Abstract
The magnetic compass of birds is embedded in the visual system and it has been hypothesized that the primary sensory mechanism is based on a radical pair reaction. Previous models of magnetoreception have assumed that the radical pair-forming molecules are rigidly fixed in space, and this assumption has been a major objection to the suggested hypothesis. In this article, we investigate theoretically how much disorder is permitted for the radical pair-forming, protein-based magnetic compass in the eye to remain functional. Our study shows that only one rotational degree of freedom of the radical pair-forming protein needs to be partially constrained, while the other two rotational degrees of freedom do not impact the magnetoreceptive properties of the protein. The result implies that any membrane-associated protein is sufficiently restricted in its motion to function as a radical pair-based magnetoreceptor. We relate our theoretical findings to the cryptochromes, currently considered the likeliest candidate to furnish radical pair-based magnetoreception.
Introduction
Millions of birds, each year, heed the call of changing seasons and migrate thousands of miles from one feeding ground to another. Scientists have shown that the Earth's magnetic field helps guide them (1–3). Even though the ability of birds to detect magnetic fields and use it for navigation during migration has been clearly established, the way in which birds and other animals sense the magnetic field has remained enigmatic. Primary magnetoreceptors have not yet been identified with certainty in any animal (1–3). The fact that magnetic fields pass freely through biological tissue has made locating magnetoreceptors particularly difficult. Magnetoreceptors need not make contact with the external environment and might plausibly be located nearly anywhere within an animal's body. Magnetoreceptors might also be tiny and dispersed throughout a large volume of tissue, or the transduction process might involve a sequence of chemical reactions, so that no obvious organ or structure devoted to magnetoreception necessarily exists. Moreover, accessory structures such as lenses, which focus sensory stimuli on receptors and are often conspicuous, are unlikely to have evolved for magnetic-field sensing because few biomaterials affect magnetic field lines (3).
Historically, migratory birds appear to be the most studied class of animals having an intrinsic magnetic compass. The typical strength of the geomagnetic field is 0.5 G (50 μT), putting severe limitations on possible physical mechanisms of magnetoreception. In the quest for explaining the origin of this sense, two models have attracted much attention, one involving iron mineral structures (4–9) in the bird's beak, the other a magnetosensitive radical pair reaction (1,10–26) in the bird's eye. The idea behind the latter mechanism, referred to as the radical pair mechanism (10,15–17,19,21), is that in the course of a photochemical reaction in the retina, a pair of reactive radicals is produced, the reaction yield of which is influenced by the orientation of the bird with respect to the geomagnetic field, and which in turn modulates visual perception (12,16,24–27). It is thought that when the bird, by moving its head, changes the angle between its head and the Earth's magnetic field; it then generates a moving visual impression that reveals the external magnetic field (16). Consistent with this suggestion, studies have found that at least some migratory birds use head-scanning behavior to detect magnetic compass information (28).
There are several pieces of evidence supporting a radical pair-based visual magnetic compass rather than one based on iron mineral particles, though likely both types of magnetic sensing mechanisms are realized side-by-side in animals. The avian compass is an inclination compass, sensitive only to the inclination of the Earth's magnetic field lines and not to their polarity (2,29). The avian compass is known to be highly sensitive to the strength of the ambient magnetic field, requiring a period of acclimation before orientation can occur at intensities differing from that of the natural geomagnetic field (30). Low-intensity radio frequency radiation affects bird orientational behavior (20,31) as expected for radical pair processes (32). The avian compass is light-dependent, as first suggested by theory (14). It normally requires light in the blue-green range in order to function properly (33–36). A protein harboring blue-light-dependent radical pair formation, cryptochrome, is found localized in the retinas of migratory birds (12,13,22,37) where its effects could use the visual neuronal pathway. During magnetic compass orientation, a visual brain region named Cluster N is the most active forebrain region (24,25,27). This activation region requires light perceived through the eyes for its neuronal activation (11,27) and differences in activation between migratory and nonmigratory birds have been documented (24,27). European robins with bilateral lesions of Cluster N are unable to show oriented magnetic compass-guided behavior, whereas their ability to perform sun compass and star compass orientation behavior is unaffected by Cluster N lesions (26); in contrast, bilateral section of the ophthalmic branch of the trigeminal nerve leading to the putative iron-mineral-based receptors in the upper beak of European robins did not influence the birds' ability to use their magnetic compass for orientation (26).
A radical pair model in which a light-driven, magnetic field-dependent chemical reaction in the eye of a bird modulates the visual sense indeed predicts all these properties (14–16). As cryptochromes are the only known class of photoreceptor molecules known from vertebrates to form radical pairs upon photoexcitation (16,22,38–41), they represent the only currently suggested candidate molecules which could function as the primary receptor molecules in the radical pair-based magnetic compass mechanism. In Mouritsen et al. (12), it was demonstrated that cryptochrome exists in noticeable quantities in retinal ganglion cells and in the photoreceptor cells of the retina.
Cryptochrome is activated via light-induced electron transfer, which probably involves a chain of three tryptophan amino acids and a molecule called flavin adenine dinucleotide (FAD) (10,17,21,22,39,41,42). Cryptochrome internally binds FAD in its oxidized state before light activation. In the active (signaling) state, FAD is transformed to the FADH form. The magnetic field could influence the photoactivation process of cryptochrome acting on the unpaired electron spins as described in Solov'yov et al. (17) and Solov'yov and Schulten (21). Cryptochrome's signaling state has a lifetime of 1–10 ms as the FADH state slowly reverts to the FAD state (22,39,41). The back-reaction, that may involve the superoxide radical O2•–, could also be modulated by the Earth's magnetic field (18,20).
The notion that superoxide might play a role in avian magnetoreception arises principally from the observation that European robins display a resonant disorientation response to weak radiofrequency fields at the electron paramagnetic resonance frequency (20,31), investigations that had been inspired by earlier theoretical work (32). In terms of the radical pair mechanism, the radiation effect can be readily understood if one of the radicals has no hyperfine interactions ≳0.2 G, a condition that excludes most biologically plausible paramagnetic molecules. O2•–, by contrast, contains no magnetic nuclei, and is ubiquitous in animal cells. However, a viable radical pair magnetoreceptor must satisfy other conditions as well (43). To account for the resonant response to a 1.3-MHz radiofrequency field, the radical in question must have a reasonably isotropic g-value close to 2 and should not undergo electron spin relaxation faster than ∼1 μs. In addition, the chemistry of the radicals must generate a spin correlated initial state and to permit appropriate spin-selective reactions. As discussed in Hogben et al. (43), these constraints are quite stringent for O2•– due to its orbital angular momentum. In the case of O2•–, it appears that these requirements can only be satisfied if the radical is complexed tightly enough to cryptochrome to quench the majority of its orbital angular momentum and to prevent rapid reorientation, but in such a way that any hyperfine interactions with the cryptochrome are ≲0.2 G.
One essential requirement for cryptochromes to act as magnetic compass sensors is that they must be orientationally restricted, which may be a challenging condition, because intracellular structures, like membranes and cytoskeleton, are dynamic and wobbly. In this article, we study theoretically how much disorder is permitted for the cryptochrome-based magnetic compass in the eye to remain functional. For our calculations, the radical pairs are assumed to be fixed inside the protein and their relative orientation change, during one reaction cycle of the cryptochrome, is considered negligible. This treatment is justified if the wiggling motion of the protein, for instance due to motion of the membrane, takes place on a much slower timescale than the spin-correlated part of radical pair reactions, which occur on a 1–10 ms timescale (22,39,41). Thus, the suggested theory allows us to account not only for individual cryptochrome misalignments, but also for membrane deformations, which disturb cryptochrome orientation in a similar fashion. We base our analysis on a quantitative theory of magnetic field effects in cryptochrome photochemistry and on recent experimental observations. We also present arguments on how the vision-based compass may function and pinpoint; important questions that remain to be answered. The question of how disorder inherent in biological cells affects the ability of radical pair systems to provide directional information has been addressed independently in two other articles, which appeared while this article was under review (44,45), albeit from a different perspective than we have taken here.
Signaling of cryptochromes may work in the eye by interfering with the normal rhodopsin-based visual process or independently from this process. For the principle results of the calculations below, the exact signaling mechanism is irrelevant. All we assume is that the currently unknown cryptochrome activation cascade involves amplification steps that result in a similar degree of amplification as known from the rhodopsin signaling cascade (46) (see Fig. 1).
Figure 1.
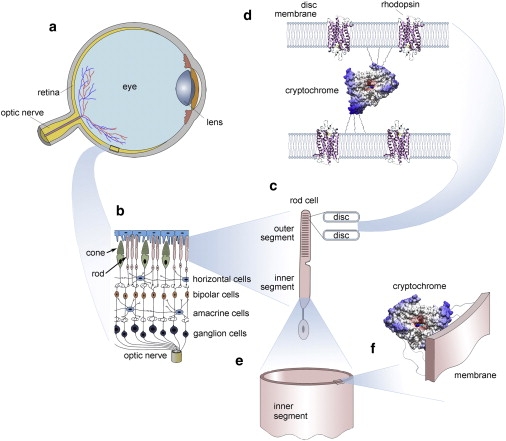
Schematic illustration of a bird's eye and its important components. The retina (a) converts images from the eye's optical system into electrical signals sent along the ganglion cells forming the optic nerve to the brain. (b) An enlarged retina segment is shown schematically. (c) The retina consists of several cell layers. The primary signals arising in the rod and cone outer segments are passed to the horizontal, the bipolar, the amacrine, and the ganglion cells. (d) The primary phototransduction signal is generated in the receptor protein rhodopsin shown schematically at a much reduced density. The rhodopsin containing membranes form disks with a thickness of ∼20 nm (46), being ∼15–20 nm apart from each other (46). The putatively magnetic-field-sensitive protein cryptochrome may be localized in a specifically oriented fashion between the disks of the outer segment of the photoreceptor cell, as schematically shown in panel d or the cryptochromes (e) may be attached to the oriented, quasicylindrical membrane of the inner segment of the photoreceptor cell (f).
In mathematical terms, the vision-based compass in birds is characterized through a filter function, which models the magnetic field-mediated visual signal modulation recorded on the bird's retina. We study different factors that can affect the acuity of the filter function, in particular, the possibility of repetitive action of cryptochrome, and how day and night flight regimes may influence the magnetic field-mediated visual pattern on the bird's retina and, thereby, its compass sense.
Theory
The key idea of vision-based magnetoreception is the spread of an orientationally constrained, magnetically responding molecule, i.e., cryptochrome, over the retina of a bird's eye that influences visual perception by forming a filter over the visual field. At each point on the retina, we define a filter function where 〈···〉 denotes that the filtering arises as an average over a local ensemble of magnetically responding molecules. Although it is interesting and relevant how many molecules are involved in the average (44) and how such an average is established, we do not consider this important issue further. The filtering depends on the direction of the Earth' magnetic field as specified further below.
The magnetic response of cryptochrome involves a magnetic field dependence of the protein's signaling yield and signaling time as described in Solov'yov et al. (17) and Solov'yov and Schulten (18). This response depends on the orientation of relative to cryptochrome. As shown in Fig. 2, the orientation of cryptochrome is captured through an x, y, z-coordinate system affixed to the FADH moiety of the protein, the z axis being oriented perpendicular to the flavin group of FADH. The overall orientation of the eye is described by an X, Y, Z-coordinate system.
Figure 2.
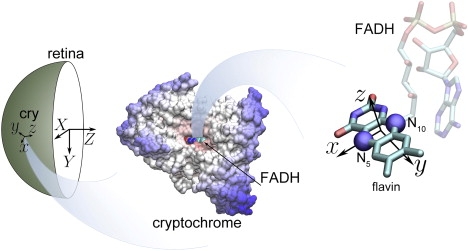
Coordinate frames used in the computations. The fixed (X, Y, Z) coordinate frame is associated with the bird's retina, such that the Z axis is pointing in the direction of the bird's sight, the Y axis is pointing down (toward the ground), and the X axis is perpendicular to the Y and Z axes. The local coordinate frame, associated with a cryptochrome is denoted as (x, y, z). At each point of the retina, the z axis is perpendicular to its surface, and the x, y, z axes form a right-handed coordinate frame. Cryptochrome's magnetic field-sensing anisotropy axis is roughly perpendicular to the plane of the flavin radical, responsible for cryptochrome's functioning (17,18,21,23). We suggest in this study that cryptochrome's magnetic field-sensing anisotropy axis is collinear with the z axis. Cryptochrome's magnetic field-sensing anisotropy is dominated by the anisotropic hyperfine interactions in the two nitrogen atoms, highlighted here (23).
Key to establishing a magnetic field-dependent visual impression that can be readily interpreted by the bird's visual neural pathways is a systematic orientation of cryptochrome at positions of the retina, i.e., the orientation of cryptochrome should be a simple function of . For the sake of illustration, we choose a particular rule for cryptochrome's orientation at any point on the retina. The rule is based on the so-called spherical coordinates specifying , namely (r, ϑ, ϕ) as shown in Fig. 3 a. To specify the rule we introduce a rotational transformation that specifies the orientation of cryptochrome at as follows: rotates the eye-fixed coordinate system X, Y, Z into the coordinate system x, y, z that specifies the local (at ) orientation of cryptochrome. We choose, following mathematical convention,
| (1) |
Figure 3.
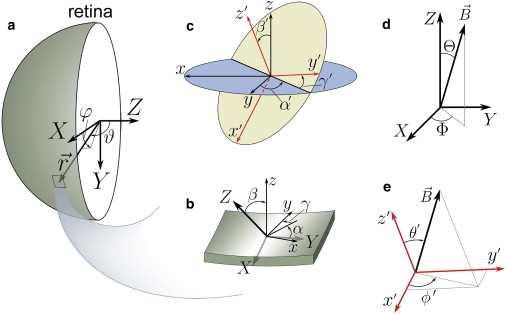
Relative orientation of coordinate frames used in the computations. The fixed (X, Y, Z) coordinate frame (a) is associated with the bird eye retina as shown in Fig. 2. The orientation of the cryptochrome molecules distributed over the retina are specified through the x, y, z-coordinate systems, which can be obtained from the initial (X, Y, Z) coordinate frame though a rotational transformation defined by the angles α, β, γ shown in panel b. Cryptochrome wiggling in the retina introduces rotational disorder of the ideally oriented proteins. (c) As a result, the ideal x, y, z-coordinate frame is to be replaced by a randomly oriented x′, y′, z′-coordinate frame, defined by the three Euler angles α′, β′, and γ′. (d) The external magnetic field vector in the (X, Y, Z) coordinate frame is characterized by the polar angle Θ and azimuthal angle Φ. (e) However, in the x′, y′, z′-coordinate frame, it can be written in terms of angles θ′ and φ′.
Here are the so-called Euler angles that specify, mathematically, rotational transformations and orientations of asymmetric objects like cryptochrome. D(α, β, γ) is specified in the Supporting Material. For the -dependence of the Euler angles, we choose
| (2) |
as explained in the Supporting Material.
The key issue of this study is not the role of the specific choice of α, β, γ, but rather in how far this choice has to be precise, or in other words, how much orientational disorder the suggested mechanism can accommodate. To investigate this systematically, we introduce now the critical assumption that all cryptochromes experience a local orientational disorder. Such disorder can be introduced mathematically in an elegant way, namely by postulating that on top of the cryptochrome orientation is actually specified by an additional random rotational transformation T′ that has the same characteristics for all retina locations. The random characteristics are introduced in the Supporting Material where T′ is specified through
| (3) |
The disorder is characterized through an angular mean-square deviation
| (4) |
where Δ = 0.17, indicating the relative change of cryptochrome's signaling yield. The transformation (Eq. 3) is illustrated in Fig. 3 c. The overall orientation of any cryptochrome relative to the eye's X, Y, Z system is then specified through the transformation D(α′, β′, γ′)D(α, β, γ) where for each location the angles α′, β′, γ′ are independent random variables. In the Supporting Material we establish how the random orientation can be accounted for through a Boltzmann distribution in a potential Epot(α′, β′, γ′) and we show that only orientational disorder in β′ matters, i.e., disorder in α′, γ′ has no effect. We therefore assume for Epot the functional form Epot = V(β′) where we choose
| (5) |
where ɛ0 is a parameter. The filtering function that is subject to the random disorder characterized here is denoted as 〈F〉 and described below.
What controls the filtering function at each location is the relative orientation of the Earth's field and the cryptochrome FADH moiety. It is straightforward to specify the orientation of relative to the eye's coordinate system X, Y, Z as shown in Fig. 3 d; is specified through its spherical coordinates (B, Θ, Φ) in the X, Y, Z system. Likewise, one can specify in the x′, y′, z′ coordinate system of the randomly oriented cryptochrome at location , using for the purpose the spherical coordinates of in the x′, y′, z′ system, namely (B, θ′, φ′) as shown in Fig. 3 e. Here (θ′, φ′) depend on the transformation D(α′, β′, γ′)D(α, β, γ) and, hence, can be expressed in terms of the angles (α, β, γ, α′, β′, γ′, Θ, Φ). In the Supporting Material, this relationship is established. One can calculate then a local filtering function F(α, β, γ, α′, β′, γ′, Θ, Φ).
As pointed out above, what is of interest is to determine, actually, the average 〈F〉. This function is defined as
| (6) |
where
| (7) |
is a function of (α, β, γ, α′, β′, γ′, Θ, Φ). We demonstrate in the Supporting Material the following relationship between cos θ′ and the stated angles
| (8) |
where
| (9) |
| (10) |
| (11) |
The 〈F〉 averages over all random orientations, i.e., over α′, β′, γ′ as stated in Eq. 6. As a result, 〈F〉 does only depend on α, β, Θ, Φ. Below we utilize 〈F(α, β, Θ, Φ)〉 to calculate the effect of cryptochrome orientational disorder on the visual impression of a navigating bird.
Lastly, we also consider the case that cryptochromes act repeatedly in establishing the filtering. Suppose that cryptochrome, like many other sensory proteins, affects a signaling cascade, which results in the activation of specific molecules, that in turn perform a further biological function such as opening or closing an ion-channel. Let N0 be the number of activated molecules generated in this step in the absence of the external magnetic field. The external magnetic field alters the number of activated molecules, described by the filter function 〈F〉, defined in Eq. 6. In general, cryptochrome activation may occur η times, thereby significantly changing the number of the activated molecules in the magnetic field-mediated step of the transduction process. The number Nη of activated molecules defines the efficiency of a cryptochrome-containing receptor cell, which shows to which extent the cell characterized through its retinal position (α, β) (see Eq. 2) contributes to the retinal image
| (12) |
Here the efficiency I(α, β) is measured in arbitrary units varying between 0 and 1, reflecting the modulation level of the virtual visual image in a bird's eye by the magnetic field.
From Eqs. 6 and 12, it follows that at a fixed orientation of the magnetic field the varying efficiency of the cells in the retina leads to a formation of a disk-shaped virtual visual pattern in the bird's field of view. The size and the intensity of this pattern are related to the acuity of the vision-based magnetic compass. Let Imax and Imin be the maximal and the minimal values of I(α,β), respectively. Then the maximal intensity of the magnetic field-mediated pattern, A, is defined as
| (13) |
The modulation level of the visual signal through the magnetic field, defined in Eq. 12, defines the total intensity of the magnetic field-mediated pattern S as
| (14) |
Here we integrate over the surface of the semi-spherical retina, and therefore the integration over β is limited by π/2. According to the definition, it holds that 0 ≤ S ≤ 2π. The integration over α and β, according to Eq. 2, corresponds to an integration over retinal positions θ, φ. Another important characteristic of the magnetic filter function is the size of the magnetic field-mediated disk-shaped pattern at half intensity, ΔΩ, which can be calculated numerically as the solution of the equation
| (15) |
where Ωmax = (α, β)max denotes α and β at which I(α, β) reaches its maximal value and A is the maximal intensity of the magnetic field-mediated pattern defined in Eq. 13. The quantities A, S, and ΔΩ in Eqs. 13–15 define the acuity of the visual-based compass. A is the measure of the maximal intensity of the magnetic field-mediated pattern (increasing A leads to an increase of the magnetic field-mediated signal in the retina), S indicates to which extent the retina is influenced by the magnetic field, and ΔΩ defines the size of the magnetic field-mediated pattern. A small value of ΔΩ corresponds to a small magnetic field-mediated spot on the retina, thus allowing the bird to resolve the magnetic field more readily.
Results
In the following, the effect of cryptochrome orientational disorder on the magnetic filter function is studied. The magnetic filter function renders a disk-shaped pattern in the bird's field of view, described by Eqs. 6 and 12. The position of this pattern in the retina of a bird depends on the heading of the animal relative to the geomagnetic field; size and intensity of the magnetic field-mediated pattern defines the sensitivity of the magnetic compass.
Cryptochrome orientational disorder
In order to understand how the orientational disorder affects the filter function, we consider first a single cryptochrome characterized by specific retinal coordinates at which α = β = 0, namely according to Eq. 2, retinal position (ϑ, ϕ) = (π, 0). We study the filter function, defined in Eq. 6, as a function of Θ with Φ = π/2 fixed. Fig. 4 shows the Θ-dependence of the signaling yield of cryptochrome averaged over possible orientations of the protein, normalized to the yield at Θ = 0.
Figure 4.
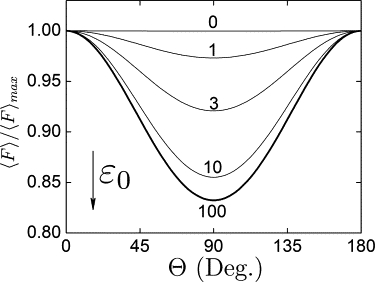
Averaged signaling yield of cryptochrome normalized on its maximal value 〈F〉max. The signaling yield is calculated using Eq. 6 as a function of protein orientation with respect to the external magnetic field, characterized by the angle Θ (see Fig. 3d), for different values of the parameter ɛ0, that label the yield curves.
The results in Fig. 4 were calculated using σ defined in Eq. 4, assuming Δ = 0.17 in accordance with prior studies (17,18). An increased orientational disorder (decrease of ɛ0) alters the filter function: 〈F〉/〈F〉max is 0.17, 0.14, 0.08, and 0.03 for ɛ0 = 100, 10, 3, and 1, respectively.
The parameter ɛ0 determines the wiggling range of cryptochrome, Δβ, which can be calculated according to statistical mechanics (45,47,48):
| (16) |
Thus, for ɛ0 = 100, 10, 3, and 1 the corresponding values of Δβ are Δβ ≈ ±5°, ±17°, ±37°, and ±50°. Fig. 4 shows that a very weak cryptochrome restriction is sufficient to produce a detectable magnetic field-mediated signal. Even for Δβ = ±50° the signal from cryptochrome is still changing by ∼3% in the geomagnetic field.
Magnetic field-mediated pattern in the visual field of a bird
The position of the magnetic field-mediated pattern in the retina (ϑ, ϕ) is determined by the angle θ′ defined in Eq. 8 (see Fig. 3), which in turn is α- and β-dependent (and therefore ϑ- and ϕ-dependent as well; see Eq. 2) as follows from Eqs. 8–11. The value θ′ also depends on the angles Φ and Θ, which change upon rotation of the animal in the horizontal plane, causing a displacement of the magnetic field-mediated pattern in the retina. The magnetic field-mediated pattern can be conveniently mapped to the plane of the visual field by the so-called Miller cylindrical projection, as described in the Supporting Material, and as illustrated in Fig. 5 for ɛ0 = 100 (equivalent to a wiggling range of ±5°). The magnetic field-mediated pattern shown in Fig. 5, for the sake of illustration, is in grayscale. How a bird's magnetic field-mediated visual impression exactly manifests itself is presently completely unknown.
Figure 5.
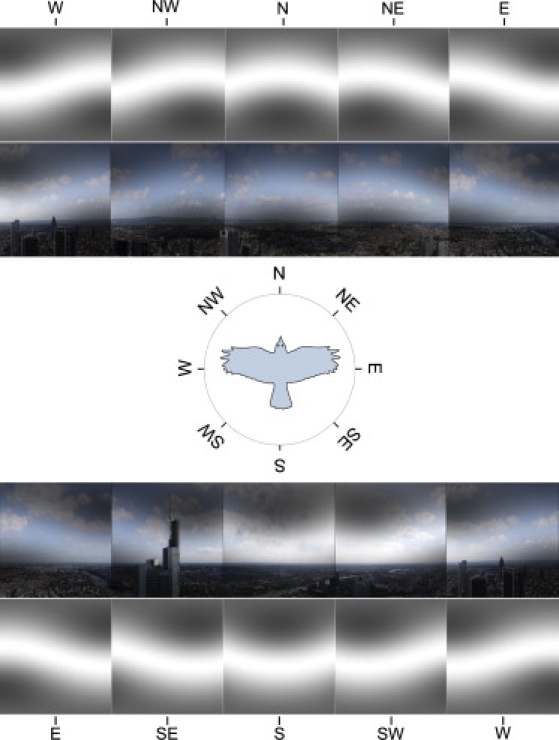
Panoramic view at Frankfurt am Main, Germany. The image shows the landscape perspective recorded from a bird flight altitude of 200 m above the ground with the cardinal directions indicated (images of Frankfurt provided by Vita Solovyeva). The visual field of a bird is modified through the magnetic filter function according to Eq. 12 with η = 1 and ɛ0 = 100. For the sake of illustration we show the magnetic field-mediated pattern in grayscale alone (which would reflect the perceived pattern if the magnetic visual pathway is completely separated from the normal visual pathway) and added onto the normal visual image the bird would see, if magnetic and normal vision uses the same neuronal pathway in the retina. The patterns are shown for a bird looking at eight cardinal directions (N, NE, E, SE, S, SW, W, and NW). The geomagnetic field inclination angle is 66°, being a characteristic value for the region.
Fig. S3 in the Supporting Material shows the pattern in the visual impression of a bird modulated through the geomagnetic field for the animal flying at daytime, allowing for different cryptochrome wiggling regimes. From the comparison in Fig. S3, it follows that the intensity of the magnetic field-mediated pattern decreases with the increase of cryptochrome orientational disorder; the magnetic field-mediated pattern in the visual field is hardly discernable for ɛ0 = 1.
As follows from Eq. 5, the parameter ɛ0 characterizes the degree of wiggling, i.e., the wiggling range of cryptochrome, Δβ, as discussed above. Using Eq. 16, we estimate the wiggling range of cryptochrome corresponding to Fig. S3 b, Fig. S3 c, and Fig. S3 d to be ±17°, ±37°, and ±50°, respectively, while in Fig. S3 a it is ±5°.
Repeated activation of cryptochrome
From Eq. 12, it follows that the repeated activation of cryptochrome leads to a sharpening of the magnetic filter function. Fig. S4 shows the modulation patterns in the visual field through the geomagnetic field, calculated for ɛ0 = 3, assuming cryptochromes in the retina to undergo one, two, three, and five activation cycles. The patterns in Fig. S4 were calculated in analogy to Fig. 5.
The intensity of the magnetic field-mediated pattern increases with the number of cryptochrome activation cycles, enhancing the acuity of the cryptochrome-based compass. The magnetic field-mediated pattern in Fig. S4 was calculated for ɛ0 = 3. For other values of ɛ0, the repetitive activation of cryptochrome is expected to enhance the magnetic field-mediated pattern in the visual field in a similar fashion to Fig. S4; for example, for ɛ0 = 1 and η = 5 the pattern is visible, while for ɛ0 = 1 and η = 1 it is not.
According to Eq. 12, the magnetic field-mediated pattern in the retina has a disklike shape. For a quantitative characterization of the angular acuity of the magnetic compass in the eye of a bird, Fig. 6 shows the total intensity of the disk-shaped pattern S, its size at half-intensity, ΔΩ, and the maximal intensity, A, plotted as a function of the parameter ɛ0 for different numbers η of repetitive cryptochrome activation cycles. A, S, and ΔΩ were calculated from Eqs. 13–15.
Figure 6.
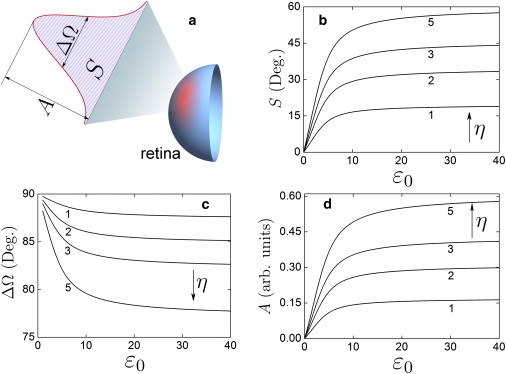
Angular acuity of the magnetic compass in the eye. The acuity of the magnetic compass is measured by the size and intensity of the disk-shaped magnetic field-mediated pattern in the visual field of a bird (a). The total intensity of the pattern S (b), its size at half-intensity ΔΩ (c), and the maximal intensity of the pattern A (d) are plotted as a function of the parameter ɛ0 defining the wiggling amplitude of cryptochrome for different numbers η of cryptochrome activation cycles. The labels in the figures indicate the corresponding η-values.
Fig. 6 shows that a single activation of cryptochrome (η = 1) allows a moderate orientational disorder of cryptochrome, at which a detectable magnetic field-mediated signal in the retina is still produced. For example, as follows from Fig. 6 d, the maximal intensity of the magnetic field-mediated pattern decreases twofold at ɛ0 = 4. Increasing the number of cryptochrome's activation cycles leads to an enhancement of the magnetic field-mediated pattern. Thus, S = 9°, 16°, 21°, 27°, ΔΩ = 89°, 88°, 87°, 85°, and A = 0.08, 0.13, 0.18, 0.24 are expected for η = 1, 2, 3, 5, respectively, at ɛ0 = 3 (wiggling range ±37°).
Night vision
Many migratory birds fly during nighttime (2,3,10). It is interesting to investigate how the filter function would alter the field of view of a bird flying at nighttime. For the sake of illustration, Fig. S5 shows the night-time panoramic view at Frankfurt am Main, Germany, modified through the filter function defined in Eq. 6 with ɛ0 = 100.
The irradiance level of the environment should exceed a certain threshold value to activate the cryptochrome-based compass. Below this threshold, there are insufficient photons to maintain the magnetic compass function. The number of photons hitting the retina per unit time can be estimated from the known values of light intensity at different day times. Fig. S5 shows that at nighttime there is enough illumination to activate the cryptochrome blue-light receptors. The typical light irradiance level on a sunny day, at sunrise/sunset, on a full moon night and on a moonless starry night (dark night) is 10,000 lux, 10 lux, 0.01 lux, and 0.001 lux, respectively (49). For the irradiance level of 1 lux at 380–720 nm the photon density (photon irradiance) can be estimated to be 1.2 × 1016 quanta/s·m2 (50). Thus, the photon density at daytime is typically 1.2 × 1020 quanta/s·m2 and at nighttime 1.2 × 1014 quanta/s·m2, while at dark night and sunset it can be estimated as 1.2 × 1013 and 1.2 × 1017 quanta/s·m2, respectively. Assuming the diameter of a retina equal to 1 cm one estimates that ∼3.7 × 107 photons hit the retina per millisecond at night. This number is highly likely to excite sufficiently many cryptochromes in the retina to act as a magnetic compass, as photoreceptor cells found in birds can be activated by just a few photons (46). Free-flying Catharus-thrushes (night migrating songbirds) used the magnetic field for orientation also on very dark natural nights, when the illuminance was as low as 0.0003 lux (51).
Nevertheless, it is still unclear why the magnetic compass in some species seems to be more functional at night (24,27): the neuronal activity in Cluster N (the brain area required for magnetic compass orientation in European robins) is high at weak moonlight conditions (0.04 lux), but its neuronal activity drops dramatically both toward room-light conditions (∼275 lux) and total darkness (24,27,52). A possible explanation is that the visual image of the night landscape has a more uniform background color and exhibits sharper contrast between light and dark areas; therefore, the magnetic field-mediated transformation of the visual impression may be easier to resolve at night than during the day (53). The signal/noise ratio of the magnetoreceptor may pull in the opposite direction, as one expects the noise to decrease with the square root of the number of activated magnetic field receptors participating in signaling events. Thus, at low light conditions, when fewer receptors are activated, one expects high noise.
The presented data show that a cryptochrome-based compass can be functional at night. However, from the performed analysis, it is not possible to conclude whether constraints on the radical pair mechanism may help to explain why some bird species prefer night navigation over day navigation. This uncertainty should be investigated soon.
Discussion
Earlier investigations (16–18,21) demonstrated how a biochemical magnetic compass in birds can be realized through light-induced electron transfer reactions in the protein cryptochrome. An essential requirement for cryptochromes to act as magnetic compass sensors is that they must be systematically oriented across the retina and exhibit a limited degree of orientational disorder. In this article, we assumed a simple ordering scheme and investigated for this scheme how much disorder is permitted for the cryptochrome-based magnetic compass in the eye to remain functional. Our study showed that rotational degrees of freedom of cryptochrome do not need to be rigidly fixed for cryptochrome to act as a magnetic compass. In particular, we demonstrated that only one of three rotational degrees of freedom of cryptochrome needs to be partially constrained, while the other two do not impact the magnetoreceptive properties of the protein. This finding is in agreement with earlier results (17,18) and with the conclusion reached by Lau et al. (45), who performed computer simulations on a collection of radical pairs undergoing restricted rigid-body rotation, coherent anisotropic spin evolution, electron spin relaxation, and spin-selective recombination reactions.
This is a biologically important finding, as proteins embedded in membranes typically are free to rotate around their own axes and membrane proteins are known to diffuse quite a lot within the plane of the membrane. Thus, if rotational disorder would not be allowed, it would be challenging to understand how any membrane-associated protein could function as a radical pair-based magnetic compass detector. While membranes are not completely rigid in the third dimension (i.e., along the axis perpendicular to the membrane plane), their wiggling movement is restricted. Our theoretical calculations demonstrate that even very moderate (within a cone of ∼90°) orientational alignment of a primary magnetic compass sensing protein is sufficient for a compass function in bird's eyes to be robust enough to potentially detect the reference direction provided by the geomagnetic field.
Having these theoretical results in mind, can we estimate what degree of disorder of the primary sensory protein is actually expected to occur in the retina of a bird? The answer to this question is strongly dependent on
-
1.
The identity of the primary sensory molecule;
-
2.
In what specific part of the primary sensory cell the primary sensory molecule is located; and
-
3.
What cell type in the retina harbors the primary sensory molecule.
If the primary magnetic compass sensor molecule in birds is cryptochrome, a number of predictions can be made. The most likely structures within a cell, which could reduce orientational disorder to a degree where cryptochrome may become a magnetic compass sensor, are membrane and/or cytoskeleton elements. However, cryptochromes almost certainly are not directly embedded into any membrane.
Antibody staining against cryptochromes in migratory garden warblers suggests that cryptochrome 1 is mainly located in the cytosol and possibly in cell membranes, whereas garden warbler cryptochrome 1 seems to be absent in the cell nucleus. If the cryptochromes are floating freely in the cytosol, they cannot function as magnetic compass sensors. Consequently, if they do work as magnetic compass detectors, they must be tied to cytoskeleton proteins or more likely to one or more membrane proteins (see Fig. 1, c–f). The putative interaction partners of cryptochromes are not currently known.
Assuming for the moment that cryptochromes are actually associated with membranes, what cell types in the retina and what specific membranes would be the most suitable candidates? The retina consists of six major cell types: photoreceptors (rods and cones), horizontal cells, bipolar cells, amacrine cells, ganglion cells, and Müller cells. Antibody staining against cryptochromes in migratory garden warblers suggests that at least some types of cryptochrome are mainly located in ganglion cells and in photoreceptor cells (12). As many ganglion cells in garden warblers are not perfectly spherical (12) and as the cryptochromes could be concentrated on specific membrane portions, the ganglion cells, in principle, could harbor the primary magnetic compass-sensing proteins in their membranes. However, the photoreceptor cells are the much more likely candidate cell type for harboring magneto-sensory cryptochromes, as the outer segments of the photoreceptor cells (see Fig. 1 c) contain stacks of highly ordered disk-shaped membranes with a thickness of ∼20 nm, being ∼15–20 nm apart from each other, and are all oriented parallel to the retina surface/eyeball (46). One highly efficient way to achieve orientational constraint would be if cryptochromes were located in the inter-disk space, as schematically shown in Fig. 1 d. Another, slightly less efficient, but still good, way to achieve orientational constraint of cryptochrome would be cryptochromes bound to membrane proteins populating the inner segments of the photoreceptor's membranes, because the inner segment photoreceptor membranes provide an array of quasicylindrical tubes oriented perpendicular to retina surface/eyeball, as schematically shown in Fig. 1, e–f.
The results of our calculations show that rotation and wiggling of up to ±50° is allowed without cryptochrome losing its potential to work as a magnetic compass detector. Therefore, both of the above-mentioned putative cryptochrome locations will almost certainly fulfill the required motion restriction, and the additional effects of the many cryptochromes that could be embedded with very similar orientations in the two suggested types of photoreceptor membranes are likely to help enhance the signal and to reduce noise. Further reduction of noise could come from repetitive activation of cryptochrome, which can lead to an enhancement of acuity of the magnetic compass even if the degree of cryptochrome motion or disorder in the retina is relatively high.
In a recent study, Hill and Ritz (44) investigated the minimum number of receptors necessary for detection of the change in chemical signal owing to changes in magnetic field direction, quantifying the required increase in the number of receptors to compensate for the signal attenuation through increased disorder. The authors concluded that radical pair-based compass systems are relatively robust against disorder, in agreement with our findings.
To test whether the ideas presented here are relevant for bird navigation, more information on cryptochromes, their interaction partners, and on the neuronal mechanisms underlying bird navigation is needed.
Supporting Material
Five figures and 47 equations are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00419-4.
Supporting Material
Acknowledgments
The authors thank Vita Solovyeva, Alexander Yakubovich, Eduard Schreiner, and Andrey Korol for useful discussions and help in the preparation of the manuscript. They acknowledge the use of resources at the Frankfurt Center for Scientific Computing.
K.S. thanks the Alexander von Humboldt Foundation for support. H.M. thanks the VolkswagenStiftung for support. I.A.S. thanks the Illinois Beckman Institute for hospitality and support during visits. This work has been supported also by the Stiftung Polytechnische Gesellschaft Frankfurt am Main, by the Deutsche Forschungsgemeinschaft (grant No. FOR 701 to H.M.), and by the National Science Foundation (grant Nos. NSF MCB-0744057 and NSF PHY0822613), and the National Institutes of Health (P41 RR005969).
References
- 1.Mouritsen H., Ritz T. Magnetoreception and its use in bird navigation. Curr. Opin. Neurobiol. 2005;15:406–414. doi: 10.1016/j.conb.2005.06.003. [DOI] [PubMed] [Google Scholar]
- 2.Wiltschko R., Wiltschko W. Magnetoreception. Bioessays. 2006;28:157–168. doi: 10.1002/bies.20363. [DOI] [PubMed] [Google Scholar]
- 3.Johnsen S., Lohmann K.J. Magnetoreception in animals. Phys. Today. 2008;61:29–35. [Google Scholar]
- 4.Fleissner G., Stahl B., Fleissner G. A novel concept of Fe-mineral-based magnetoreception: histological and physicochemical data from the upper beak of homing pigeons. Naturwissenschaften. 2007;94:631–642. doi: 10.1007/s00114-007-0236-0. [DOI] [PubMed] [Google Scholar]
- 5.Solov'yov I.A., Greiner W. Theoretical analysis of an iron mineral-based magnetoreceptor model in birds. Biophys. J. 2007;93:1493–1509. doi: 10.1529/biophysj.107.105098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Solov'yov I.A., Greiner W. Iron-mineral-based magnetoreceptor in birds: polarity or inclination compass? Eur. Phys. J. D. 2009;51:161–172. [Google Scholar]
- 7.Solov'yov I.A., Greiner W. Micromagnetic insight into a magnetoreceptor in birds: on the existence of magnetic field amplifiers in the beak. Phys. Rev. E. 2009;80 doi: 10.1103/PhysRevE.80.041919. 041919-1–10. [DOI] [PubMed] [Google Scholar]
- 8.Kirschvink J.L., Walker M.M., Diebel C.E. Magnetite-based magnetoreception. Curr. Opin. Neurobiol. 2001;11:462–467. doi: 10.1016/s0959-4388(00)00235-x. [DOI] [PubMed] [Google Scholar]
- 9.Falkenberg G., Fleissner G., Fleissner G. Avian magnetoreception: elaborate iron mineral containing dendrites in the upper beak seem to be a common feature of birds. PLoS One. 2010;5:e9231. doi: 10.1371/journal.pone.0009231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rodgers C.T., Hore P.J. Chemical magnetoreception in birds: the radical pair mechanism. Proc. Natl. Acad. Sci. USA. 2009;106:353–360. doi: 10.1073/pnas.0711968106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Heyers D., Manns M., Mouritsen H. A visual pathway links brain structures active during magnetic compass orientation in migratory birds. PLoS One. 2007;2:e937. doi: 10.1371/journal.pone.0000937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mouritsen H., Janssen-Bienhold U., Weiler R. Cryptochromes and neuronal-activity markers colocalize in the retina of migratory birds during magnetic orientation. Proc. Natl. Acad. Sci. USA. 2004;101:14294–14299. doi: 10.1073/pnas.0405968101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Möller A., Sagasser S., Schierwater B. Retinal cryptochrome in a migratory passerine bird: a possible transducer for the avian magnetic compass. Naturwissenschaften. 2004;91:585–588. doi: 10.1007/s00114-004-0578-9. [DOI] [PubMed] [Google Scholar]
- 14.Schulten K., Swenberg C.E., Weller A. A biomagnetic sensory mechanism based on magnetic field modulated coherent electron spin motion. Z. Phys. Chem. 1978;NF111:1–5. [Google Scholar]
- 15.Schulten K. Magnetic field effects in chemistry and biology. In: Treusch J., editor. Advances in Solid State Physics [Festkörperprobleme] Vol. 22. Vieweg, Braunschweig/Wiesbaden; Germany: 1982. [Google Scholar]
- 16.Ritz T., Adem S., Schulten K. A model for photoreceptor-based magnetoreception in birds. Biophys. J. 2000;78:707–718. doi: 10.1016/S0006-3495(00)76629-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Solov'yov I.A., Chandler D.E., Schulten K. Magnetic field effects in Arabidopsis thaliana cryptochrome-1. Biophys. J. 2007;92:2711–2726. doi: 10.1529/biophysj.106.097139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Solov'yov I.A., Schulten K. Magnetoreception through cryptochrome may involve superoxide. Biophys. J. 2009;96:4804–4813. doi: 10.1016/j.bpj.2009.03.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Maeda K., Henbest K.B., Hore P.J. Chemical compass model of avian magnetoreception. Nature. 2008;453:387–390. doi: 10.1038/nature06834. [DOI] [PubMed] [Google Scholar]
- 20.Ritz T., Wiltschko R., Wiltschko W. Magnetic compass of birds is based on a molecule with optimal directional sensitivity. Biophys. J. 2009;96:3451–3457. doi: 10.1016/j.bpj.2008.11.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Solov'yov I.A., Chandler D.E., Schulten K. Exploring the possibilities for radical pair effects in cryptochrome. Plant Signal. Behav. 2008;3:676–677. doi: 10.4161/psb.3.9.5809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liedvogel M., Maeda K., Mouritsen H. Chemical magnetoreception: bird cryptochrome 1a is excited by blue light and forms long-lived radical-pairs. PLoS One. 2007;2:e1106. doi: 10.1371/journal.pone.0001106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cintolesi F., Ritz T., Hore P. Anisotropic recombination of an immobilized photoinduced radical pair in a 50-μT magnetic field: a model avian photomagnetoreceptor. Chem. Phys. 2003;294:707–718. [Google Scholar]
- 24.Liedvogel M., Feenders G., Mouritsen H. Lateralized activation of cluster N in the brains of migratory songbirds. Eur. J. Neurosci. 2007;25:1166–1173. doi: 10.1111/j.1460-9568.2007.05350.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Feenders G., Liedvogel M., Jarvis E. Molecular mapping of movement-associated areas in the avian brain: a motor theory for vocal learning origin. PLoS ONE. 2008;3:e1768. doi: 10.1371/journal.pone.0001768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zapka M., Heyers D., Mouritsen H. Visual but not trigeminal mediation of magnetic compass information in a migratory bird. Nature. 2009;461:1274–1277. doi: 10.1038/nature08528. [DOI] [PubMed] [Google Scholar]
- 27.Mouritsen H., Feenders G., Jarvis E.D. Night-vision brain area in migratory songbirds. Proc. Natl. Acad. Sci. USA. 2005;102:8339–8344. doi: 10.1073/pnas.0409575102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mouritsen H., Feenders G., Kropp W. Migratory birds use head scans to detect the direction of the earth's magnetic field. Curr. Biol. 2004;14:1946–1949. doi: 10.1016/j.cub.2004.10.025. [DOI] [PubMed] [Google Scholar]
- 29.Wiltschko W., Wiltschko R. Magnetic compass of European robins. Science. 1972;176:62–64. doi: 10.1126/science.176.4030.62. [DOI] [PubMed] [Google Scholar]
- 30.Wiltschko W., Stapput K., Wiltschko R. Avian magnetic compass: fast adjustment to intensities outside the normal functional window. Naturwissenschaften. 2006;93:300–304. doi: 10.1007/s00114-006-0102-5. [DOI] [PubMed] [Google Scholar]
- 31.Ritz T., Thalau P., Wiltschko W. Resonance effects indicate a radical-pair mechanism for avian magnetic compass. Nature. 2004;429:177–180. doi: 10.1038/nature02534. [DOI] [PubMed] [Google Scholar]
- 32.Canfield J.M., Belford R.L., Schulten K. A perturbation treatment of oscillating magnetic fields in the radical pair mechanism using the Liouville equation. Chem. Phys. 1995;195:59–69. [Google Scholar]
- 33.Wiltschko W., Munro U., Wiltschko R. Red light disrupts magnetic orientation of migratory birds. Nature. 1993;364:525–527. [Google Scholar]
- 34.Wiltschko W., Wiltschko R. Light-dependent magnetoreception in birds: the behavior of European robins, Erithacus rubecula, under monochromatic light of various wavelengths and intensities. J. Exp. Biol. 2001;204:3295–3302. doi: 10.1242/jeb.204.19.3295. [DOI] [PubMed] [Google Scholar]
- 35.Stapput K., Thalau P., Wiltschko W. Orientation of birds in total darkness. Curr. Biol. 2008;18:602–606. doi: 10.1016/j.cub.2008.03.046. [DOI] [PubMed] [Google Scholar]
- 36.Muheim R., Bäckman J., Åkesson S. Magnetic compass orientation in European robins is dependent on both wavelength and intensity of light. J. Exp. Biol. 2002;205:3845–3856. doi: 10.1242/jeb.205.24.3845. [DOI] [PubMed] [Google Scholar]
- 37.Liedvogel M., Mouritsen H. Cryptochromes—a potential magnetoreceptor: what do we know and what do we want to know? J. R. Soc. Interface. 2010;7(Suppl 2):S147–S162. doi: 10.1098/rsif.2009.0411.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zeugner A., Byrdin M., Ahmad M. Light-induced electron transfer in Arabidopsis cryptochrome-1 correlates with in vivo function. J. Biol. Chem. 2005;280:19437–19440. doi: 10.1074/jbc.C500077200. [DOI] [PubMed] [Google Scholar]
- 39.Giovani B., Byrdin M., Brettel K. Light-induced electron transfer in a cryptochrome blue-light photoreceptor. Nat. Struct. Biol. 2003;10:489–490. doi: 10.1038/nsb933. [DOI] [PubMed] [Google Scholar]
- 40.Kottke T., Batschauer A., Heberle J. Blue-light-induced changes in Arabidopsis cryptochrome 1 probed by FTIR difference spectroscopy. Biochemistry. 2006;45:2472–2479. doi: 10.1021/bi051964b. [DOI] [PubMed] [Google Scholar]
- 41.Biskup T., Schleicher E., Weber S. Direct observation of a photoinduced radical pair in a cryptochrome blue-light photoreceptor. Angew. Chem. Int. Ed. Engl. 2009;48:404–407. doi: 10.1002/anie.200803102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.O'Day K.E. Shedding light on animal cryptochromes. PLoS Biol. 2008;6:1359–1360. doi: 10.1371/journal.pbio.0060168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hogben H.J., Efimova O., Hore P. Possible involvement of superoxide and dioxygen with cryptochrome in avian magnetoreception: origin of Zeeman resonances observed by in vivo EPR spectroscopy. Chem. Phys. Lett. 2009;490:118–122. [Google Scholar]
- 44.Hill E., Ritz T. Can disordered radical pair systems provide a basis for a magnetic compass in animals? J. R. Soc. Interface. 2010;7(Suppl 2):S265–S271. doi: 10.1098/rsif.2009.0378.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lau J.C.S., Wagner-Rundell N., Hore P.J. Effects of disorder and motion in a radical pair magnetoreceptor. J. R. Soc. Interface. 2010;7(Suppl 2):S257–S264. doi: 10.1098/rsif.2009.0399.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Mayhew T.M., Astle D. Photoreceptor number and outer segment disk membrane surface area in the retina of the rat: stereological data for whole organ and average photoreceptor cell. J. Neurocytol. 1997;26:53–61. doi: 10.1023/a:1018563409196. [DOI] [PubMed] [Google Scholar]
- 47.Landau L., Lifshitz E. Elsevier Butterworth-Heinemann; Oxford, UK: 1980. Statistical Physics. [Google Scholar]
- 48.McQuarrie D.A. University Science Books; Sausalito, CA: 2000. Statistical Mechanics. [Google Scholar]
- 49.Clark R.N. Sky Publishing; Cambridge, MA: 1990. Visual Astronomy of the Deep Sky. [Google Scholar]
- 50.Wetzel R.G., Likens G.E. Springer Verlag; Berlin, Heidelberg, New York: 2000. Limnological Analysis. [Google Scholar]
- 51.Cochran W.W., Mouritsen H., Wikelski M. Migrating songbirds recalibrate their magnetic compass daily from twilight cues. Science. 2004;304:405–408. doi: 10.1126/science.1095844. [DOI] [PubMed] [Google Scholar]
- 52.Hein C.M., Zapka M., Mouritsen H. Night-migratory garden warblers can orient with their magnetic compass using the left, the right or both eyes. J. R. Soc. Interface. 2010;7(Suppl 2):S227–S233. doi: 10.1098/rsif.2009.0376.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ritz T., Ahmad M., Wiltschko W. Photoreceptor-based magnetoreception: optimal design of receptor molecules, cells, and neuronal processing. J. R. Soc. Interface. 2010;7:S135–S146. doi: 10.1098/rsif.2009.0456.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


