Intramolecular Fluorescence Correlation Spectroscopy in a Feedback Tracking Microscope

Abstract

We derive the statistics of the signals generated by shape fluctuations of large molecules studied by feedback tracking microscopy. We account for the influence of intramolecular dynamics on the response of the tracking system and derive a general expression for the fluorescence autocorrelation function that applies when those dynamics are linear. We show that in comparison to traditional fluorescence correlation spectroscopy, tracking provides enhanced sensitivity to translational diffusion, molecular size, heterogeneity, and long-timescale decays. We demonstrate our approach using a three-dimensional tracking microscope to study genomic λ-phage DNA molecules with various fluorescence label configurations.

Introduction

Fluorescence correlation spectroscopy (FCS) is a method for optically measuring local concentration fluctuations of fluorescence-labeled molecules in solution (1–4). The fluorescence autocorrelation function—referred to as the FCS curve—contains signatures of the dynamic properties of those molecules, such as diffusion coefficients or reaction rates, which are inferred by comparing the curve to theoretical predictions. Modern approaches to FCS use tightly focused laser beams and confocal detection to probe diffraction-limited sample volumes, are sensitive enough to measure fluorescence from single dye-labeled molecules, and can resolve fluctuations on timescales as fast as the fluorescence lifetimes of the dyes (5,6). These methods have achieved success in a wide range of applications in biology and chemistry.

One relatively new application of FCS is the study of the intramolecular dynamics of large polymer chains. Such motions were first described theoretically over 50 years ago (7,8), but were only coarsely probed experimentally because of the insensitivity of the experimental methods available at the time. As first demonstrated in 2003, FCS is sensitive to the internal motions of polymers that are large relative to the focused waist of the probe laser (9). These initial measurements suggested that the internal dynamics of large double-stranded DNA (dsDNA) molecules are dominated by the stiffness of the polymer chain and by hydrodynamic couplings between spatially proximate polymer segments. Later measurements conflicted with these conclusions (10), however, and the resulting controversy has yet to be fully resolved, despite several iterations of experimental and theoretical improvements (11–13).

In a recent article (14), we argued that FCS is not a sufficiently sensitive technique for characterizing the internal dynamics of large-polymer molecules, because the theoretical FCS curves contain too many free parameters, resulting in underdetermined numerical fits to the data. We instead used a technique based on feedback tracking microscopy, a technology that has been developed by our and other groups over the past few years (15–22) (and reviewed recently in Cang et al. (23)) by which a feedback system tracks the translational motion of a single molecule and keeps it in the focus of the microscope. In the particular variant of feedback microscopy developed by our group, we compute the autocorrelation function of the fluorescence measured from the tracked molecule and analyze it in a manner analogous to traditional FCS (24–26). This tracking FCS (tFCS) approach generates statistics that are related to traditional FCS (which we will refer to as stationary FCS for clarity in this article), but it provides enhanced sensitivity to both translational and intramolecular motion. Our tFCS measurements revealed that the translational statistics and radius of gyration of large dsDNA molecules were together consistent with strong hydrodynamic interactions, as commonly expected, but that the intramolecular relaxation statistics are surprisingly not consistent with the Zimm polymer model (8,14,27).

This article provides the mathematical foundation for intramolecular tFCS. In The Intramolecular Tracking FCS Curve, we compute the tFCS curve for a molecule exhibiting conformation fluctuations. We account for the effect of those fluctuations on the response of the tracking system, as well as the systematic artifacts that the tracking system adds to the tFCS curve. We focus in particular on molecules described by linear dynamical models, both because these include the standard polymer dynamics theories and because it is possible to derive closed-form expressions for the tFCS curve for such models. We illustrate characteristics of the intramolecular tFCS approach with a simple sample model for molecular motion. In Application to Double-Stranded DNA, we demonstrate the application of tFCS to the study of the intramolecular motion of fluorescence-labeled genomic λ-phage DNA using a variation on the apparatus we described in a previous article (28). Our measurements are consistent with predictions for molecules with three different label configurations, and furthermore, they reveal sensitivity to heterogeneity among molecules with random labeling schemes with a noise floor consistent with the predicted photon-counting noise level.

Materials and Methods

We made all measurements using the three-dimensional tracking microscope described in our previous article (28), which we enhanced by the addition of a second excitation laser at 444 nm and a confocal detection channel with peak sensitivity at 480 nm, also described previously (14).

We purchased genomic λ-phage DNA (48,502 basepairs (bp)) from New England Biolabs (Ipswich, MA) and Invitrogen (Carlsbad, CA) and produced three different DNA-dye conjugates. One conjugate was labeled with the intercalating dyes POPO-3 (for tracking) and POPO-1 (for tFCS), both purchased from Invitrogen. Molecules with mean interdye spacings of 300 bp for the tracking dye and between 300 and 48,000 bp for the tFCS dye were prepared by adding DNA to dilute solutions of dye in TE buffer (10 mM TRIS, 1 mM Na₂EDTA, pH 8.0) and incubating at room temperature for 20 min. At these relatively low dye densities, we anticipate little alteration of the DNA dynamics (9).

One conjugate was labeled by incorporation of a single Atto-425 conjugated dATP (Jena Biosciences) into a terminal single-stranded overhang using Klenow exo-DNA polymerase (New England Biolabs). The reaction was cleaned up using the QIAEX II silica adsorption procedure (Qiagen, Venlo, The Netherlands) and repeated ultrafiltration in a Microcon YM-100 unit (Millipore, Billerica, MA) until no free dyes were detected in solution. This conjugate was then labeled with POPO-3 for tracking, as described below.

A final conjugate was prepared by ligating the biotinylated oligonucleotide sequence 5′-GGGCGGCGACCT-3′-Bio (Integrated Device Technology, San Jose, CA) onto the free single-stranded overhang of the Atto425-labeled conjugate using T4 DNA ligase (New England Biolabs). This molecule was purified as described above and then mixed with an excess of streptavidin-coated quantum dots (qd655, Invitrogen) and incubated at room temperature. The qdot-DNA conjugate was purified by repeated ethanol precipitation until few free quantum dots were detected in solution.

All molecules were imaged in TE buffer with 1% v/v 2-mercaptoethanol added to enhance the fluorescence yield.

The Intramolecular Tracking-FCS Curve

We begin with a description of the experimental scenario we are concerned with (see Fig. 1). A molecule is labeled with a collection of two types of fluorescent dyes, distinguished in the figure by their colors. The red dyes are excited by the tracking laser to determine the position of the molecule, and the cyan dyes are excited by a probe laser for intramolecular tFCS measurements. The tracking system reacts to the motion of the molecule by adjusting the position of the laser beams to follow the center of mass of the tracking dyes. Fundamental localization noise induces tracking errors, so the beams do not follow the target position precisely, as emphasized by their off-center displacement in the figure. The tFCS dyes emit fluorescence bursts whenever the intramolecular motion causes them to drift through the probe laser beam. The goal of this section is to calculate the statistics of this tFCS signal as determined by the dynamics of the tracking system and the statistics of the molecule's motion.

Figure 1.

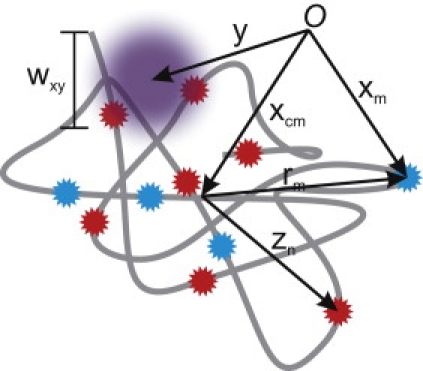
Typical experimental scenario. The gray curve represents a molecule sparsely labeled with red and cyan dyes. The circular violet region represents the tFCS probe beam (the larger tracking beam is not illustrated). Vectors x_cm, x_m, and y relative to the arbitrary origin O represent the center of mass of the molecule, position of tFCS dye m, and beam position, respectively. Dye positions relative to x_cm (r_m for tFCS dyes and z_n for tracking dyes) are used in the text for convenience.

We begin with the standard definition of the FCS curve,

$$g_2\left(\tau \right)=\frac{\langle I\left(t\right)I\left(t+\tau \right)\rangle }{\langle I\left(t\right)\rangle \langle I\left(t+\tau \right)\rangle }-1,$$ (1)

where angled brackets denote an average over time, equivalent to an ensemble average due to the ergodicity of the fluorescence signal. In this article, we deal with g₂(τ) for a collection of M dyes moving along a set of trajectories {x_m^t}, each with its own possibly distinct dynamics (superscript notation will be used throughout as shorthand to indicate the time dependence of various quantities). We define the brightness of dye m, b_m, so that b_mϕ₀ is the fluorescence rate we detect when that dye is excited by a laser with intensity ϕ₀. We can then write I(t) in terms of the dye positions and brightnesses and the spatially varying laser intensity ϕ(x):

$$I\left(t\right)=\sum _{m=1}^M{b}_m\varphi \left({\mathbf{y}}^t-{\mathbf{x}}_m^t\right),$$ (2)

where y^t is the position of the laser beam over time. In the case where y^t is constant, this I(t) is exactly that of stationary FCS.

We express Eq. 2 in terms of the Fourier transform of ϕ(x), $\tilde{\varphi }\left(\mathbf{k}\right)$, to facilitate calculations. The unnormalized autocorrelation G(τ) ≡ 〈I(t)I(t + τ)〉 is then given by

$$G\left(\tau \right)=\sum _{m,\mu =1}^M{b}_m{b}_{\mu }\int \frac{{\text{d}}^6\overline{\mathbf{k}}}{{\left(2\pi \right)}^6}\langle e^{i{\overline{\mathbf{k}}}^{\text{T}}({\overline{\mathbf{x}}}_{m\mu }-\overline{\mathbf{y}})}\rangle \Phi \left(\overline{\mathbf{k}}\right),$$ (3)

where we have simplified notation by defining the concatenated vectors $\overline{\mathbf{k}}=\left(\begin{array}{c}\mathbf{k}\\ {\mathbf{k}}^{\prime }\end{array}\right)$, $\overline{\mathbf{y}}=\left(\begin{array}{c}{\mathbf{y}}^{t+\tau }\\ {\mathbf{y}}^t\end{array}\right)$ and ${\overline{\mathbf{x}}}_{m\mu }=\left(\begin{array}{c}{\mathbf{x}}_{\mu }^{t+\tau }\\ {\mathbf{x}}_m^t\end{array}\right)$, and the product of the beam profiles $\Phi \left(\overline{\mathbf{k}}\right)=\tilde{\varphi }\left(-\mathbf{k}\right)\tilde{\varphi }\left(-{\mathbf{k}}^{\prime }\right)$. A similar expression exists for the time average 〈I(t)〉.

Equations 1 and 3 together define g₂(τ) in terms of the properties of the tracked molecule and tracking system; all that remains is to insert appropriate models for these dynamics. In the general case, Eq. 3 cannot be simplified because ${\overline{\mathbf{x}}}_{m\mu }$ and $\overline{\mathbf{y}}$ are highly correlated. The tracking system responds to both the center-of-mass and intramolecular motions of the molecule, and these motions may be correlated with each other. For example, a molecule's shape fluctuations may couple into variations in its apparent translational diffusion coefficient (13), and spatial inhomogeneities within the sample may cause the intramolecular dynamics to depend on the center-of-mass position. As a consequence, the only general approach to calculating the tFCS curve relies on solving for the joint statistics of the laser and the dyes from a set of coupled equations of motion.

Linear models in homogeneous samples

Linear models such as the Rouse and Zimm polymer models predict Gaussian statistics for the molecular motion because the Brownian force is Gaussian. Our feedback system is linear as well, so it exhibits Gaussian statistics in response to the molecular motion (26). If we assume that ${\overline{\mathbf{x}}}_{m\mu }$ and $\overline{\mathbf{y}}$ are jointly Gaussian random variables, we can make a fairly dramatic simplification to the average in Eq. 3 (see Supporting Material):

$$\langle e^{i{\overline{\mathbf{k}}}^{\text{T}}\left({\overline{\mathbf{x}}}_{m\mu }-\overline{\mathbf{y}}\right)}\rangle =\exp \left\{-\frac{1}{2}{\overline{\mathbf{k}}}^{\text{T}}\langle {\left({\overline{\mathbf{x}}}_{m\mu }-\overline{\mathbf{y}}\right)}^2\rangle \overline{\mathbf{k}}\right\},$$ (4)

where we have adopted the notation for the outer product, x² ≡ xx^T, and have assumed that ${\overline{\mathbf{x}}}_{m\mu }-\overline{\mathbf{y}}$ has a zero mean, a condition that is enforced by the tracking system. This simplification is helpful because it separates the average into second-order correlation matrices that are relatively easy to calculate.

Linear models further predict that the center-of-mass motion and intramolecular motion are uncorrelated, provided the absence of any spatially inhomogeneous fields. These models express the dynamics using an eigenfunction expansion in which the center-of-mass motion appears as the zeroth-order mode, whereas the intramolecular motion is superposed in the higher-order modes. If we write ${\mathbf{x}}_m^t$ as a sum of the center-of-mass position, ${\mathbf{x}}_{\text{cm}}^t$, and the dye position relative to the center of mass, ${\mathbf{r}}_m^t$, then the autocorrelation function is just the sum of autocorrelations. For example,

$$\langle {\mathbf{x}}_{\mu }^{t+\tau }{\left({\mathbf{x}}_m^t\right)}^{\text{T}}\rangle =\langle {\mathbf{x}}_{\text{cm}}^{t+\tau }{\left({\mathbf{x}}_{\text{cm}}^t\right)}^{\text{T}}\rangle +\langle {\mathbf{r}}_{\mu }^{t+\tau }{\left({\mathbf{r}}_m^t\right)}^{\text{T}}\rangle \text{.}$$ (5)

In a similar way, we can write y^t as a sum over components that respond to the center-of-mass motion, ${\mathbf{y}}_{\text{cm}}^t$; to the intramolecular motion, which we denote as ${\mathbf{y}}_z^t$; and to localization noise arising from photon counting, as described previously (29), which we denote as ${\mathbf{y}}_F^t$. These three components are also uncorrelated, the first two because of the assumption of independence between center-of-mass and intramolecular motions, and the third because the photon-counting process is independent of dye position.

We now insert these decomposed terms into Eq. 4 to get

$$\langle e^{i{\overline{\mathbf{k}}}^{\text{T}}\left({\overline{\mathbf{x}}}_{m\mu }-\overline{\mathbf{y}}\right)}\rangle =\exp \left\{-\frac{1}{2}{\overline{\mathbf{k}}}^{\text{T}}\left[{\Lambda }_{m\mu }^{\tau }+{\Sigma }^{\tau }\right]\overline{\mathbf{k}}\right\},$$ (6)

where

$${\Lambda }_{m\mu }^{\tau }=\langle {\left({\overline{\mathbf{r}}}_{m\mu }-{\overline{\mathbf{y}}}_z\right)}^2\rangle$$ (7)

and

$${\Sigma }^{\tau }=\langle {\left({\overline{\mathbf{x}}}_{\text{cm}}-{\overline{\mathbf{y}}}_{\text{cm}}\right)}^2\rangle +\langle {\left({\overline{\mathbf{y}}}_F\right)}^2\rangle ,$$ (8)

and in these definitions we have used the $\overline{\cdot }$ notation to indicate concatenated two-time vectors, as in Eq. 3. Defined in this way, Σ^τ constitutes a tracking error arising from the finite system response bandwidth and from localization noise and is identical to that described in our previous work (26). The intramolecular motion therefore adds a new time-dependent variance term to the systematic tracking error variance that was characterized previously.

We now approximate the excitation laser beam with a three-dimensional Gaussian, as is standard practice in the FCS literature. We denote the covariance of this Gaussian by the diagonal matrix $\frac{1}{4}W$, where the elements of W—denoted $w_x^2$, $w_y^2$, and $w_z^2$ —are the squares of the beam waists along the x, y, and z axes. Combining this with Eq. 6, we can compute the integrals in Eq. 3 to write the FCS curve in terms of the matrices Σ^τ and Λ_mμ^τ:

$$g_2\left(\tau \right)+1\propto \sum _{m,\mu =1}^M{b}_m{b}_{\mu }{\left\{\det \left[{\Lambda }_{m\mu }^{\tau }+{\Sigma }^{\tau }+\frac{1}{4}\left(\begin{array}{cc}W& 0\\ 0& W\end{array}\right)\right]\right\}}^{-1/2},$$ (9)

where the constant of proportionality can by found by direct computation of 〈I(t)〉, or more simply by requiring that g₂(∞) = 0.

Equation 9 is suitable for any intramolecular model with linear dynamics. In general, there may be coupling between the intramolecular motion along different Cartesian axes; for example, dye movement can induce fluid flows in the solvent that act upon adjacent dyes in a manner that must be described by a mobility tensor. However, the models we work with in this article do not contain this feature. In this case, we may write the matrices Λ_mμ^τ and Σ^τ in terms of smaller, diagonal matrices (denoting the 3 × 3 identity by Id₃):

$${\Lambda }_{m\mu }^{\tau }=\left(\begin{array}{cc}{\lambda }_{mm}^0{\text{Id}}_3& {\lambda }_{m\mu }^{\tau }{\text{Id}}_3\\ {\lambda }_{\mu m}^{\tau }{\text{Id}}_3& {\lambda }_{\mu \mu }^0{\text{Id}}_3\end{array}\right)$$ (10)

$${\Sigma }^{\tau }=\left(\begin{array}{cc}{\sigma }^0{\text{Id}}_3& {\sigma }^{\tau }{\text{Id}}_3\\ {\sigma }^{\tau }{\text{Id}}_3& {\sigma }^0{\text{Id}}_3\end{array}\right)\text{.}$$ (11)

For example, ${\lambda }_{m\mu }^{\tau }=\frac{1}{3}\langle {\left({\mathbf{r}}_{\mu }^{t+\tau }-{\mathbf{y}}_z^{t+\tau }\right)}^{\text{T}}\left({\mathbf{r}}_m^t-{\mathbf{y}}_z^t\right)\rangle$. The quantities λ^τ_mμ and σ^τ must then be found from the models chosen for the intramolecular and tracking system dynamics. We note that, in addition to requiring independence, when expressed in this way, Λ_mμ^τ and Σ^τ also require that the dynamics are identical along all three Cartesian axes. In practice this idealization is rarely realized because the x and y axes and the z axis usually do not perform identically in our apparatus. We will therefore distinguish between the dynamics along different axes, when necessary, using the notation (λ_mμ^τ)_x and σ_x^τ to indicate the x axis, and likewise for the y and z axes.

We can now write the tFCS curve in the most general form necessary in this article:

$$g_2\left(\tau \right)=\sum _{m,\mu =1}^M\frac{b_m{b}_{\mu }{\left\{\sum _{m=1}^M{b}_m{\prod _{\alpha \in \{x,y,z\}}\left[{\left({\lambda }_{mm}^0\right)}_{\alpha }+\frac{1}{4}{w}_{\alpha }^2+{\sigma }_{\alpha }^0\right]}^{-1/2}\right\}}^{-2}}{{\prod _{\alpha \in \left\{x,y,z\right\}}\left\{\left[{\left({\lambda }_{mm}^0\right)}_{\alpha }+\frac{1}{4}{w}_{\alpha }^2+{\sigma }_{\alpha }^0\right]\left[{\left({\lambda }_{\mu \mu }^0\right)}_{\alpha }+\frac{1}{4}{w}_{\alpha }^2+{\sigma }_{\alpha }^0\right]-{\left[{\left({\lambda }_{m\mu }^{\tau }\right)}_{\alpha }+{\sigma }_{\alpha }^{\tau }\right]}^2\right\}}^{1/2}}-1,$$ (12)

which reduces determination of g₂(τ) to the problem of finding ${\lambda }_{m\mu }^{\tau }$ and σ^τ for the particular models chosen for the intramolecular dynamics and the tracking system. In the next section, we compute the system response to the motion of the tracked molecule both to fully calculate σ^τ and to derive the necessary equations for calculation of the y_z-dependent terms in ${\lambda }_{m\mu }^{\tau }$.

Tracking system dynamics

Earlier work by our group described the tracking stage as a linear control system that responds continuously to differences in position between it and the tracked particle, and furthermore characterized the fluorescence fluctuations that arise due to imperfect tracking fidelity (26). Here, we expand upon this work by incorporating the effect of intramolecular shape fluctuations on the tracking statistics. The approach taken here differs significantly from previous work in that we use a Langevin equation, rather than a Fokker-Planck equation, to compute the statistics we require. The advantage of this approach is that it is simpler to incorporate generalized intramolecular dynamics as a stochastic input to a deterministic tracking system than to find and solve a Fokker-Planck equation that describes the joint molecular and tracking-stage statistics.

We let the molecule be labeled by a set of N dyes to which the tracking system responds; these may be the same as those used to compute the FCS curve, but need not be. Therefore, we must be somewhat careful in distinguishing between tracking dyes and FCS dyes. We let the tracking dyes move along a set of trajectories that we write as {${\mathbf{x}}_{\text{cm}}^t$ + ${\mathbf{z}}_n^t$}, where ${\mathbf{z}}_n^t$ are positions relative to the center of mass that fluctuate according to the molecule's internal dynamics. As with ${\mathbf{x}}_{\text{cm}}^t$ and ${\mathbf{r}}_m^t$, discussed previously, we assume that ${\mathbf{x}}_{\text{cm}}^t$ and ${\mathbf{z}}_n^t$ are uncorrelated.

Provided that the molecule is smaller than the rotation radius and axial modulation distance of the tracking laser beam, the fluorescence from any individual dye on it will produce a localization signal that is proportional to the dye's distance from the tracking fixed point (24,30). These signals add linearly for multiple dyes, so that the tracking system follows the average position of the N tracking dyes.

We let y^t be the position of the tracking stage along the x axis, without loss of generality, as a function of time. Similarly, $x_{\text{cm}}^t$ and $z_{\text{n}}^t$ are the x-axis components of their corresponding vectors. We write a linear dynamical system to describe the evolution of y^t in response to these dye positions and to a localization noise F^t arising from photon counting, as described previously (29):

$$\begin{array}{c}\frac{\text{d}}{\text{d}t}{\mathbf{q}}^t=\mathbf{A}{\mathbf{q}}^t+\mathbf{B}\left(x_{\text{cm}}^t+\frac{1}{N}\sum _{n=1}^N{z}_{\text{n}}^t+F^t\right)\\ y^t=\mathbf{C}{\mathbf{q}}^t,\end{array},$$ (13)

where q^t is an internal-state variable and the matrices A, B, and C are a state-space realization of the tracking system dynamics. This abstract matrix formalism is used because the dynamics of the tracking system depend on those of all of its constituent components and, particularly with mechanical stages like our piezoelectric one, some of the system components may have nontrivial responses within the operational feedback bandwidth. Although we can sometimes obtain satisfactory results with a simple first-order system (in which A, B, and C are scalars), often we require a two-dimensional system to account for the finite bandwidth of the mechanical stage (26).

We now solve Eq. 13 in terms of its inputs:

$$y^t=\mathbf{C}{e}^{\mathbf{A}t}{\mathbf{q}}^0+\mathbf{C}\underset{0}{\overset{t}{\int }}\text{d}\xi e^{\mathbf{A}\left(t-\xi \right)}\mathbf{B}\left(x_{\text{cm}}^{\xi }+\frac{1}{N}\sum _{n=1}^N{z}_n^{\xi }+F^{\xi }\right)\text{.}$$ (14)

The first term in this equation is a transient one reflecting the state of the system at the initiation of tracking; we avoid consideration of such transients because the linearity assumption for the localization signal is often violated, and the resulting nonlinear statistics are quite complicated (30). Fortunately, the stability of the tracking system requires A < 0, so that the transients decay sharply for t larger than the time constant set by |A|⁻¹.

We will use Eq. 14 in the steady-state limit $\left|\mathbf{A}\right|t\gg 1$ to compute the statistics of y^t. This limit can only be interpreted when ${\mathbf{z}}_n^t$ is stationary, but this will essentially always be the case. We assume that the center of mass moves by ordinary Brownian motion. The inputs $z_n^t$ and F^t both have mean zero, so that 〈y^t〉 = x_cm⁰. For simplicity, we define our coordinate system so that x_cm⁰ = 0.

The two-time correlation functions are more substantial. We break y^t into its uncorrelated constituent parts, as described earlier: y^t ≡ y_cm^t + y_z^t + $y_F^t$. For each part, we write out the product, insert the appropriate correlations, compute the integrals and take the steady-state limit. Beginning with the center-of-mass motion, we insert the Brownian correlation $\langle x_{\text{cm}}^{t_1}{x}_{\text{cm}}^{t_2}\rangle =2D\min \left\{t_1,t_2\right\}$ and find, after some manipulation,

$$\langle y_{\text{cm}}^{t+\tau }{y}_{\text{cm}}^t\rangle =2Dt-2D\mathbf{C}{\mathbf{A}}^{-1}\left[{\mathbf{A}}^{-1}\left(\text{Id}+e^{\mathbf{A}\tau }\right){\Gamma }^{\infty }+{\Gamma }^{\infty }{\left({\mathbf{A}}^{\text{T}}\right)}^{-1}\right]{\mathbf{C}}^{\text{T}},$$ (15)

where ${\Gamma }^{\infty }={\lim }_{t\to \infty }{\int }_0^t\text{d}\xi e^{\mathbf{A}\left(t-\xi \right)}\mathbf{B}{\mathbf{B}}^{\text{T}}{e}^{{\mathbf{A}}^{\text{T}}\left(t-\xi \right)}$, as defined in a previous article (26). Γ^∞ may alternatively be expressed as the solution of the equation AΓ^∞ + Γ^∞A^T = – BB^T, which we exploit to simplify expressions containing this term. The simplification to Eq. 15 also requires CA⁻¹B = −1, which indicates that the tracking system has no deterministic steady-state error and is guaranteed by the use of an integrating controller in the feedback loop (26). The τ-independent term in Eq. 15 represents the lag between the molecule and stage positions resulting from finite feedback bandwidth. As |A|→∞, the lag term goes to zero, because the tracking system follows the molecule with perfect fidelity.

We next assume that F^t is a white-noise process with power spectral density f. Following the same procedure as for $y_{\text{cm}}^t$ yields

$$\langle y_F^{t+\tau }{y}_F^t\rangle =f^2\mathbf{C}{e}^{\mathbf{A}\tau }{\Gamma }^{\infty }{\mathbf{C}}^{\text{T}}$$ (16)

and puts us in position to compute σ^τ as defined in Eq. 11. We combine Eqs. 15 and 16 to get

$${\sigma }^{\tau }=\mathbf{C}{e}^{\mathbf{A}\tau }\left[2D{\mathbf{A}}^{-1}{\Gamma }^{\infty }{\left({\mathbf{A}}^{\text{T}}\right)}^{-1}+f^2{\Gamma }^{\infty }\right]{\mathbf{C}}^{\text{T}},$$ (17)

which is independent of t, because all 2Dt terms stemming from the center-of-mass motion have been canceled. This is the mathematical statement of the fact that the tracking system cancels the molecule's center-of-mass motion on timescales longer than the tracking and intramolecular relaxation times.

We cannot compute the component of the stage motion due to z_n^t until we specify the model that we will use for the intramolecular dynamics. We next present a simple example model that captures the essential features of intramolecular tracking FCS.

Example: independent harmonically bound dyes

We consider the example of a collection of dyes bound by a harmonic potential to a central point that is undergoing Brownian motion. Despite being somewhat artificial, this example will contain all of the essential details of intramolecular tracking FCS and is convenient in that it is exactly solvable.

We let all dyes move independently of each other and with the same dynamics, and we require that motion along different Cartesian axes is uncorrelated. The dyes' intramolecular correlation function is a well-known result from the Ornstein-Uhlenbeck theory (31),

$$\langle {\mathbf{r}}_{\mu }^{t+\tau }{\left({\mathbf{r}}_m^t\right)}^{\text{T}}\rangle =e^{-\beta \tau }{a}^2{\delta }_{m\mu }{\text{Id}}_3,$$ (18)

where β is the stiffness of the attractive bond to the central point and a² is the variance of the dye position. The distribution of these dyes is Gaussian, so the formula for g₂(τ) in Eq. 9 applies.

For simplicity, we choose a first-order dynamical model for our tracking system, with A ≡ −γ, B = γ, and C = 1. We can now compute the intramolecular response matrix elements λ^τ_mμ. If the sets of FCS dyes and tracking dyes are distinct, we have

$${\lambda }_{m\mu }^{\tau }=a^2{e}^{-\beta \tau }{\delta }_{m\mu }+\frac{a^2\gamma }{N}\left[\frac{\gamma e^{-\beta \tau }-\beta e^{-\gamma \tau }}{{\gamma }^2-{\beta }^2}\right]\text{.}$$ (19)

The first term in this expression is the intramolecular correlation function (Eq. 18). The second term arises because tracking errors add fluctuations to the fluorescence signal; it is strictly positive, indicating that in this configuration the fluorescence fluctuations are always larger than if the tracking system had an exact estimate of the center-of-mass position (as in the limit N→∞). In the particular case where the same set of dyes are used as both tracking indicators and tFCS probes, the result is

$${\lambda }_{m\mu }^{\tau }=a^2{e}^{-\beta \tau }{\delta }_{m\mu }-\frac{a^2\gamma }{M}\left[\frac{\gamma e^{-\beta \tau }-\beta e^{-\gamma \tau }}{{\gamma }^2-{\beta }^2}\right]\text{.}$$ (20)

Here, the tracking error component is strictly negative, because the fluctuations in the dye position relative to the probe beam are suppressed by the tracking system.

Fig. 2 illustrates the tFCS curves for the harmonic model with varied values for β, including the limit β→∞, representing a solid particle (this limit does not account for rotational motion, so the particle it represents is densely labeled). For β ≫ γ, the timescales of the intramolecular motion and of the tracking system response are separated and the curves for the harmonic models approach that of the solid particle for τ > β⁻¹. In this case, the molecule's rapid internal fluctuations average away on timescales relevant to the tracking system. The tracking system is able to follow the intramolecular motion for smaller β; consequently, the fluorescence fluctuations increase significantly when the tracking and probe dyes are distinct and decrease significantly when the dyes are identical.

Figure 2.

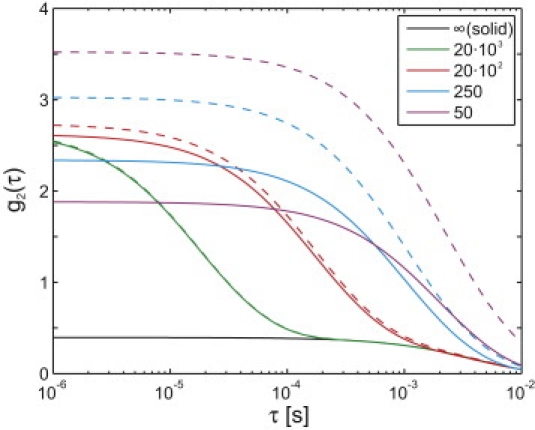
Sample tracking-FCS curves for the harmonic model. Dashed curves indicate distinct tracking and probe dyes (Eq. 19), and solid curves indicate identical tracking and probe dyes (Eq. 20). The legend indicates the value of β for each curve. All curves used N = M = 1, a = 200 nm, σ⁰ = (250 nm)² for all axes, w_xy = 280 nm, and w_z = 800 nm.

In the next section, we use the harmonic model to demonstrate features of the tFCS approach that generalize qualitatively to other models of molecular motion.

General features of intramolecular tFCS

Tracking FCS shares many general properties with stationary FCS. This section is not a survey of these familiar properties, but instead points out the tFCS differences in approach or features that distinguish it from the latter methodology. For a general survey of stationary FCS, see Krichevsky and Bonnet (4). We also include in the Supporting Material a more detailed discussion of the differences between stationary FCS, tFCS, and related image correlation techniques.

Center-of-mass statistics and tracking errors

The independent measurement of the position of the tracked molecule over time is a hallmark difference between stationary FCS and tracking techniques, allowing us to make very accurate diffusion coefficient measurements while simultaneously greatly suppressing the fluorescence decay due to translational motion. This is covered extensively in our previous works (25,26) for the case where the tracked molecule is a point particle; here, we examine the effect that intramolecular motion has on the center-of-mass statistics.

The most basic characterization of the performance of a particle-tracking system is the size of its center-of-mass tracking error, which we usually define for each axis by σ⁰, the variance of the stationary distribution of the quantity y^t − x_cm^t. Using the harmonically bound dye model with first-order tracking dynamics as an example, we find

$$\text{Var}\left[y^t-x_{\text{cm}}^t\right]=\frac{D}{\gamma }+\frac{f^2\gamma }{2}+\frac{a^2\gamma }{N\left(\gamma +\beta \right)},$$ (21)

where the first two terms are familiar from point-particle tFCS and the third results from the response of the stage to the intramolecular motion. Thus, the intramolecular term adds a steady-state error that, when N is small and $\beta <\gamma$, can actually dominate the tracking system's response. In some cases, this may be desirable, for instance, if we were tracking the diffusion of a single point on a molecule as it moves within the molecule itself. In such cases, it may be more sensible to define the tracking error differently, because x_cm is no longer the relevant target position; the derivations in this article would facilitate doing so.

Although the tracking error is important as a figure of merit, a more general and practically useful quantity is the variance of the stage increment, to which we fit curves to determine γ, f, and D from our data. Fig. 3 illustrates the effect of the intramolecular motion on the quantity $\widehat{D}\left(\tau \right)\equiv \text{Var}\left[y^{t+\tau }-y^t\right]{\left(2\tau \right)}^{-1}$, defined so that $\widehat{D}\left(\infty \right)=D$. The sigmoidlike shape of the curve for small β is what is typically observed due to pure center-of-mass tracking (26). The curve peaks as a function of both τ and β due to the tracking system's response to the intramolecular motion. The peak along τ indicates the tradeoff between intramolecular motion on short timescales and center-of-mass motion on long timescales. The peak along β occurs because slow intramolecular fluctuations (small β) are dominated by center-of-mass motion, whereas fast intramolecular fluctuations (large β) are not tracked well due to latency in the feedback loop.

Figure 3.

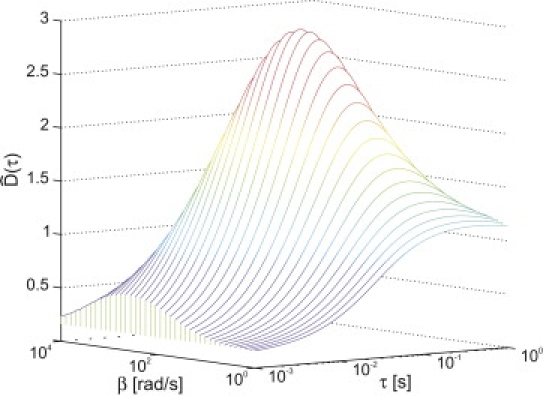
$\widehat{D}\left(\tau \right)$, as defined in the text, evaluated for the harmonic model over a range of values for β. We used D = 1 μm²/s, a = 500 nm, γ = 10 Hz, f = 8 nm/$\sqrt{\text{Hz}}$, and N = 1.

Concentration and molecular size

An obvious practical difference between stationary FCS and tFCS is that the tracking approach is not directly sensitive to the sample concentration. The concentration determines how frequently molecules drift into focus, but once a single molecule is detected and tracked, its fluctuations are independent of the number of molecules elsewhere in the sample. By contrast, the sample concentration has a large influence in stationary FCS, determining the variance of the fluorescence fluctuations and consequently the overall scaling of the FCS curve through the value g₂(0).

The fluorescence variance is somewhat more complicated in tFCS, as it is partially determined by tracking errors (exclusively so in point-particle tFCS). Unlike in stationary FCS, however, the fluorescence variance in tFCS also contains a component due to intramolecular fluctuations. We demonstrate this using the harmonic model as an example, and for simplicity, we assume that the tracking errors are small and unaffected by intramolecular motion, i.e., ${\sigma }^0\ll a^2$ and N→∞. In the limit where the molecule is much bigger than the beam waists, i.e., $a\gg w/2$, the variance of the FCS curve is

$$g_2\left(0\right)\approx \frac{1}{M}\frac{2^{3/2}{a}^3}{w_{xy}^2{w}_z}\equiv \frac{1}{\overline{C}\overline{V}},$$ (22)

where $\overline{C}=M/a^3$ gives the effective intramolecular dye concentration and $\overline{V}=2^{-3/2}{w}_{xy}^2{w}_z$ the imaging volume. Equation 22 has exactly the same form as in stationary FCS except with the sample concentration replaced by its tFCS analog, $\overline{C}$.

It is straightforward to show that the tFCS variance is dominated by tracking errors in the small-particle limit $a\ll w/2$, where it approaches its value for point particles. Hence, intramolecular tFCS has the same general property as intramolecular stationary FCS, in which the FCS curve is dominated by intramolecular motion for molecules larger than the excitation beam and by translational motion for smaller molecules (9). An important difference, however, is that g₂(0) is affected—strongly so for large particles—by molecular size in tFCS, whereas it is determined by the sample concentration alone in stationary FCS (11). This fact makes tFCS more sensitive to molecule size than stationary FCS and improves the numerical conditioning of fits to g₂(τ).

Sensitivity to heterogeneity

Stationary FCS is a true single-molecule method in the sense that it generates fluorescence signals from only one molecule at a time. However, the signal from a single molecule is never sufficient to determine a detailed FCS curve, because only a small number of photons are typically detected from each molecule, so that statistical counting errors are very large. This is quite unlike tFCS, in which long observation times with the tracked molecule located in the brightest part of the excitation beam can enhance the signal/noise ratio by a factor of 100 or more (28). Tracking FCS can therefore be used to determine complete FCS curves on individual molecules over a wide range of timescales, providing the unique ability to resolve differences in the dynamics of different molecules. We will demonstrate this in our measurements in the next section.

Sensitivity to decays on long timescales

Another characteristic feature of tFCS is sensitivity to fluorescence decays on timescales much longer than the characteristic diffusion time of a molecule through the laser focus. g₂(τ) only decays to zero when the quantities ${\lambda }_{m\mu }^{\tau }$ and σ^τ are both approximately zero; this means that decays in the intramolecular term ${\lambda }_{m\mu }^{\tau }$ are detectable even if they occur at times much longer than the center-of-mass diffusion time. Stationary FCS, by contrast, contains a decay of the form g₂(τ) ∝ τ⁻¹ for τ longer than the characteristic diffusion time (4), so that any longer decays are sharply attenuated.

Application to Double-Stranded DNA

We now apply the theory developed in the previous sections to measurements on double-stranded DNA.

Linear polymer models

The simplest dynamical model for the motion of a flexible polymer chain was developed by Rouse (7,27) and forms the basis for subsequent refinements by Zimm (8) and others of the physics incorporated into the models. The Rouse model describes the polymer as a sequence of beads connected and held together by springs and driven by independent Brownian forces. The discrete set of equations of motion for these beads is transformed into a partial differential equation for the polymer backbone by taking a continuum limit, assuming that the RMS distance between beads is much smaller than the overall length, L, of the molecule. The resulting equation defines a time-dependent space curve R(u, t) parameterized by the position u ∈ [0, L] along the backbone contour, and is solved using a Fourier series expansion. From this solution, we find the correlation function needed to compute g₂(τ) (27),

$$\langle \mathbf{R}\left(u,t+\tau \right)\mathbf{R}{\left(u^{\prime },t\right)}^{\text{T}}\rangle =2Dt{\text{Id}}_3+\frac{2r_0^2}{{\pi }^2}\sum _{q=1}^{\infty }\frac{1}{q^2}{e}^{-\tau /{\tau }_q}\cos \left[\frac{\pi qu}{L}\right]\cos \left[\frac{\pi q{u}^{\prime }}{L}\right]{\text{Id}}_3,$$ (23)

where r₀² is the mean-squared distance between the end and center of mass of the polymer and τ_q is the relaxation time of Fourier mode q, which scales as q⁻² for the Rouse model and approximately as q^−3/2 for the Zimm model. We provide λ_mμ for a polymer with probe dyes at contour positions {u_m} and tracking dyes at {v_n} in Eq. S2 in the Supporting Material.

We have already demonstrated that the Rouse model is sufficient to describe tFCS measurements on λ-phage DNA, and that in fact the Zimm model is not consistent with our data (14). We therefore use only the Rouse model in our fits in this article. The results here are intended to illustrate the theoretical consistency and capabilities of the tFCS technique and the technical aspects of measurements on labeled polymers. We focus more on the specific quantities to which tFCS is sensitive than on the scientific interpretation of those quantities, although, together with our closely related work (14), the technical developments described in this article have provided a significant advance in the field of experimental DNA dynamics.

Labeling

The simplest way to incorporate fluorescence labels into DNA is with intercalating dyes that insert themselves randomly at sites approximately uniformly distributed over the DNA backbone. It is possible to incorporate many of these dyes, which makes them valuable for tracking, since the molecule becomes brightly fluorescent with little influence of intramolecular motion on the dynamics of the tracking system. Intercalating dyes are less useful for the probe dyes which, in contrast to the tracking dyes, should be incorporated quite sparsely to maximize sensitivity to intramolecular motion. The difficulty is that the dye positions are random and are different for each molecule; both tFCS and stationary FCS are sensitive to these differences, but not sufficiently sensitive to infer the dye label configurations precisely. This configuration uncertainty must be properly addressed when analyzing tFCS and stationary FCS data, and inevitably reduces the sensitivity of these techniques to the underlying polymer dynamics.

An alternative labeling procedure uses methods from molecular biology to incorporate dyes site-specifically into the DNA backbone. This is more challenging but provides much greater experimental sensitivity, because the dye configurations are exactly known and are identical for all molecules.

We prepared three different DNA-dye conjugates for our experiments: one molecule with intercalating tracking and probe labels; one molecule with intercalating tracking labels and a single probe label on the molecule's terminus; and one molecule with individual tracking and probe labels on opposite termini. We provide theoretical formulae for the tFCS curves for each of these molecules, derived from Eq. 23, in the Supporting Material.

Measurements

Fig. 4 shows g₂(τ) measured from the three DNA-dye conjugates along with fits to theoretical curves for the Rouse polymer model in which the polymer parameters τ₁ and r₀ were fit for all three curves and the mean number, $\tilde{M}$, of intercalating dyes was also fit for the POPO-1/POPO-3 curve. All fits used a first-order tracking system model with γ_xy = 15 Hz, γ_z = 2 Hz, σ⁰_x = σ⁰_y = (100 nm)², and σ_z⁰ = (250 nm)², as determined from $\widehat{D}\left(\tau \right)$, described above. All fits were corrected for attenuation due to background counts (14). The fits for the POPO-3-labeled molecules include high-frequency triangle-wave oscillations, accounting for our excitation scheme described previously (14), by which we alternatingly expose the molecules to the two excitation lasers to prevent cross talk between tracking and probe fluorescence. Furthermore, all fits span the range 10⁻⁴ s ≤ τ ≤ 10⁻¹ s due to interference by a systematic decay in our data spanning 0.2 s ≤ τ ≤ 1 s, likely caused by an imperfection in the z-axis tracking (14). Although this systematic decay is very small compared to the primary tFCS decay, the high statistical resolution on these longer timescales would place too much emphasis on this spurious component of the tFCS curves if it were included in the fits.

Figure 4.

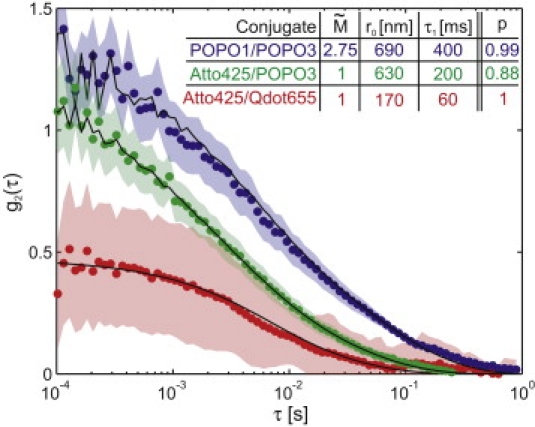
tFCS data for genomic λ-phage DNA with varied label configurations. Mean values of g₂(τ) are indicated by circles, and 2σ bounds by the shaded regions. Fit curves to the Rouse model are superimposed in black. The legend indicates the fit parameters and goodness-of-fit p-values, as described in the text. The POPO-3/POPO-1 conjugate was prepared with POPO-1 label density of 1 dye/24,000 bp (for an expected $\tilde{M}\approx 2$ dyes/molecule).

We evaluated the goodness of the fits to the data by assuming that the statistical noise on each of the measured curves is Gaussian, so that the sum of the squared residuals has a χ² distribution. The size of the statistical uncertainty in the Atto425/POPO-3 and Atto425/Qdot655 conjugates was determined by computing the variance in g₂(τ) over the set of observed molecules. The uncertainty in the POPO-1/POPO-3 conjugate was determined using the bootstrap method after processing the data to account for dye configuration uncertainty, as described later in this section.

All three curves fit the data satisfactorily from a statistical perspective, as indicated by the p-values given in Fig. 4. The large p-values for the POPO-3/POPO-1 and Atto425/Qdot655 conjugates suggest that our estimates for the noise in these curves are probably too large. The consequence of overestimated uncertainty is reduced ability to discriminate between different models or between different parameter values. Fortunately, we showed in our model discrimination experiments that the difference between the Rouse and Zimm models was great enough to resolve using tFCS on the Atto425/POPO-3 conjugate (14).

The POPO-1/POPO-3 and Atto425/POPO-3 conjugates yielded fairly consistent values for r₀ and τ₁. As discussed in our previous work (14), these fit parameters, together with the measured translational diffusion statistics (we find D = 0.8 μm²/s), are internally consistent with the predictions from basic polymer theories. By contrast, both fit parameters for the Atto425/Qdot655 conjugate are consistent with those of a molecule that is smaller by a factor of 3. We attribute this difference to nonspecific interactions between the DNA and the streptavidin on the qdot surface. It is interesting that such interactions would be very difficult to rule out using stationary FCS because of that technique's insensitivity to molecular size, so that the unfortunate problems with this conjugate highlight a strength of our technique.

Although data from the Atto425/POPO-3 and Atto425/Qdot655 conjugates were both straightforward to analyze, the sensitivity of tFCS to the precise positions of dyes in the POPO-1/POPO-3 conjugate demands a more sophisticated approach. For example, Eq. 23 predicts both a slower relaxation time and a larger relaxation amplitude for a molecule with a single dye on its end (u = 0) compared to a single dye in the middle of the chain (u = L/2). Briefly, we account for configuration uncertainty in the POPO-1/POPO-3 conjugate by treating each measured g₂(τ) as the sum of an ensemble average curve, g^∗(τ), a contribution due to dye configuration, η(τ), and a statistical noise term, ξ(τ). We estimate the value of g^∗(τ) from a set of measured g₂(τ) by using a maximum-likelihood estimator; the data in Fig. 4 are the output of this estimator. Furthermore, since it is difficult to compute g^∗(τ) exactly for the purpose of fitting, we determine the fit curve in the figure by generating 1000 random dye configurations at a fixed dye density and averaging their tFCS curves. Complete details regarding the maximum-likelihood estimator are given in the Supporting Material.

We performed experiments on POPO-1/POPO-3 conjugates over a wide range of POPO-1 densities to fully demonstrate the ability of tFCS to resolve differences between molecules based on their dye configurations. During these experiments, we varied the probe excitation intensity to keep the average count rate, and therefore the measurement noise, roughly constant. The variations between molecules can be evaluated most simply by computing the variance of the measured tFCS curves: expressing the measured curves as a sum of g^∗(τ), η(τ), and ξ(τ), as described above, we have Var[g₂(τ)] = Var[η(τ)] + Var[ξ(τ)]. Since the measurement noise is constant, any differences in Var[g₂(τ)] observed in these experiments must derive from the dependence of η(τ) on dye-label density. Fig. 5 shows the results of these measurements. As expected, at sufficiently low dye densities (large dye spacings), the observed variations between molecules exceed the values predicted for measurement noise alone and therefore suggest that we are indeed observing heterogeneity within our sample due to differences in dye configuration.

Figure 5.

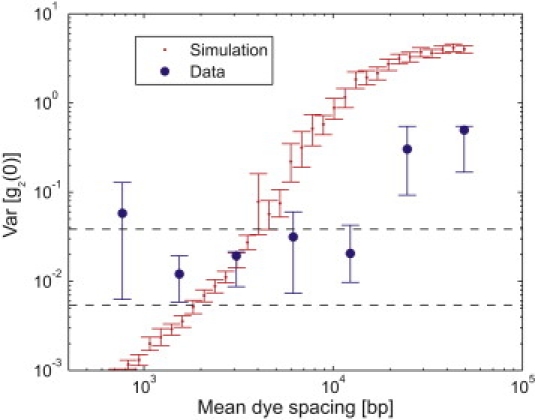
Sensitivity to labeling heterogeneity. The measured variances of g₂(0) within individual DNA samples (blue) are compared to the variances predicted by simulations (red) of ensembles of polymers with uniformly distributed dyes. Dashed lines indicate the shot-noise variances for 15-s tracking times with 2.5 kHz count rates (upper) and 40-s tracking times with 8 kHz count rates (lower). Experimental tracking times averaged 25 s, and count rates averaged 3.8 kHz; 95% error bars were determined by bootstrap sampling.

To evaluate the observed heterogeneity quantitatively, we determined the expected variance as a function of dye spacing by using Monte Carlo simulations. These simulations suggest that our observed variances are smaller than expected by a factor of ∼3. There are several possible reasons for this discrepancy. One is that our prepared dye densities may differ from the true densities, as would be the case, for example, if some of our DNA were adsorbed to the walls of our sample tubes. However, given that the fitted $\tilde{M}$ in Fig. 4 roughly matches the prepared density, and that the variances in Fig. 5 apparently saturate at similar dye densities, we suspect this is not a major source of error. Another possibility is that our data suffer from selection bias, because we choose to quantitatively examine only fluorescence trajectories for which we clearly see both a POPO-1 and a POPO-3 signal. This selection process is necessary to ensure that dim molecules, which have very poor signal/noise and signal/background ratios, do not contribute too much noise to our measurements. However, as a consequence of selecting data this way, we discard data from molecules that are either labeled with very few dyes or labeled more toward their ends than their centers (because labels near the ends tend to remain farther from the molecule's center of mass and, therefore, from the probe beam focus). Both exclusions will tend to lower the observed variances, although it is difficult to be certain of the extent to which they have done so in our measurements.

Conclusions

We derived the FCS statistics measured on large molecules tracked via feedback control. We demonstrated several distinguishing features of these statistics by using a pair of simple molecular models, and demonstrated the application of the tracking-FCS technique to the study of large double-stranded DNA molecules. These results demonstrated our ability to recover realistic and consistent parameters for the dynamics of DNA labeled in two different ways, as well as to identify alterations in the dynamics of the molecule due to attachment of a streptavidin-coated quantum dot label. Furthermore, we demonstrated the ability to resolve configuration differences between different molecules in a sample subjected to a random labeling scheme. We have demonstrated that tFCS is a method with unique capabiliites; we believe that these capabilities will establish it as a valuable tool for a range of difficult problems in molecular biophysics.

Supporting Material

One figure and 29 equations are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00410-8.