Driving Forces for Transmembrane α-Helix Oligomerization

Abstract

We present what we believe to be a novel statistical contact potential based on solved structures of transmembrane (TM) α-helical bundles, and we use this contact potential to investigate the amino acid likelihood of stabilizing helix-helix interfaces. To increase statistical significance, we have reduced the full contact energy matrix to a four-flavor alphabet of amino acids, automatically determined by our methodology, in which we find that polarity is a more dominant factor of group identity than is size, with charged or polar groups most often occupying the same face, whereas polar/apolar residue pairs tend to occupy opposite faces. We found that the most polar residues strongly influence interhelical contact formation, although they occur rarely in TM helical bundles. Two-body contact energies in the reduced letter code are capable of determining native structure from a large decoy set for a majority of test TM proteins, at the same time illustrating that certain higher-order sequence correlations are necessary for more accurate structure predictions.

Introduction

Transmembrane (TM) proteins are estimated to make up a quarter of all biological proteins (1), yet, relative to aqueous proteins, only a small number of these are known in atomic-level detail. Structure determination is difficult, because the native state depends on the bilayer environment, and so traditional aqueous crystallization is typically impractical. The class of associated α-helical membrane proteins constitutes a large fraction of TM proteins, including channels, such as voltage-gated ion channels (2), ligand-gated ion channels (3), aquaporins (4), other transporters (5,6), and α-helical bundles such as rhodopsin (7). Due to the oily bilayer environment, the driving force for TM protein assembly is different than for aqueous proteins, since the association of transmembrane helices is not as strongly driven by the hydrophobic interaction (8). In addition, secondary structure seems to be more regular within the transmembrane region, with a number of protein complexes largely being α-helices that criss-cross the bilayer (9,10).

Stabilizing features for TM protein structures have been interpreted in terms of a number of factors, including side-chain size, polarity (hydrophobic or hydrophilic identity), hydrogen bonding, side-chain packing effects, and helix tilt angles (11–18). Eilers et al. analyzed the differences between aqueous helix bundles and transmembrane bundles, and found that helices pack more tightly in the membrane than in aqueous proteins; they found that although aqueous helix bundles pack Ala, Leu, Val, Gly, and Ile most frequently, there was a prevalence for amino acids Gly, Ser, and Thr to pack in the helix-helix interface of TM helix bundles, compatible with an argument that side-chain size appears to be better correlated with helix binding propensity than simple polarity identity (8). In contrast, Gimpelev et al. were able to find most TM helix sequence packing patterns in aqueous bundles (19). Adamian and Liang (20) performed a similar study and were able to differentiate, for example, the tightly packed bacteriorhodopsin from the loosely packed mechanosensitive channel, perhaps indicating a functional role for van der Waals packing. A more recent study by Harrington and Ben-Tal (21) found that considering hydrogen bonding, aromatic interactions, salt bridges, and packing motifs effectively determined the structure of 15 diverse TM proteins, consistent with a more dominant role for polarity. Experimentally, it is known that the dimerization of apolar polyleucine helices is enhanced by polar single-residue mutations (22), and polar residues can enhance or induce dimerization (23–28). A big limitation of drawing more definitive conclusions with regard to molecular driving forces is the poor structural and ambiguous sequence statistics for characterizing TM proteins relative to their aqueous counterparts, with underrepresentation of polar groups in particular.

In this work, we devise a quasichemical theory to analyze the dependence of TM α-helical driving forces on sequence and membrane environment. The method used in this study is to first determine statistical amino acid contact frequencies based on actual observations found in TM α-helical protein structures, similar in spirit to statistical potentials developed for aqueous (29,30) and TM (31,32) proteins. Our approach differs from past efforts in that it compares against a novel null distribution to determine the expected frequencies of the 20 × 20 contact potential matrix for TM α-helical proteins, and then methodically reduces the amino-acid alphabet size, allowing us to extract trends in the broader driving forces for packing of TM α-helix bundles with greater statistical confidence. Our reduced letter code shows that generic polarity is a more dominating feature than size in determining whether a residue is found at a helix-helix interface, and in identifying correlations in sequence that place like residues on the same or opposite faces. Two-body contact energies in the reduced letter code are capable of determining the native structure from a large decoy set for a majority of test TM α-helical proteins, at the same time illustrating that certain higher-order sequence correlations are necessary for more accurate structure predictions.

Models and Methods

Quasichemical theory

The contact energies between peptide or lipid beads are determined under the assumption of a quasichemical equilibrium, that is, that the bead pairs are in equilibrium with the lipid bilayer such that

$$P-Q+L-L\iff P-L+Q-L,$$ (1)

where P and Q are a pair of amino acid interaction sites and L is an element of the lipid bilayer. The resulting interaction energy for P-Q is interpreted to be

$$E_{PQ}=-k_{\text{B}}T\log \left(\frac{K_{PQ}}{K_{PQ}^0}\right)\text{.}$$ (2)

Here, K_PQ, defined as

$$K_{PQ}=\frac{N_{PQ}{N}_{LL}}{N_{PL}{N}_{QL}},$$ (3)

is the equilibrium constant formulated from the native distribution of TM helix contact pairs observed, a corresponding equilibrium constant, $K_{PQ}^0$, is defined from an appropriate null distribution of expected contact pairs (described in more detail below), and T is assumed to be room temperature.

It has been shown previously that differentiation between the bilayer interior and surface is useful (33,34). We apply explicit surface beads to model the very different environment at the bilayer surface, and these define alternate, explicit interactions with the protein beads that exclude bilayer interactions but, like the implicit lipid contacts, are also limited by the expected number of contacts, as discussed below. A grid of surface beads is placed a distance of 13 Å above and below the bilayer midpoint.

The actual N_PQ contact distribution is sampled from the crystal structures of TM α-helical proteins taken from the Protein Data Bank (PDB) TM database (9,10); analysis was restricted to those structures interpretable as simple bundled collections of α-helices, and we ignored all PDB structures that were pore or channel structures (which may indeed have substantially different contacts (35)), had substantial ambiguity in secondary-structure assignment, or whose structure obviously depended on the presence of ligands or prosthetic groups. (See Table 4 for a list of the proteins.)

Table 4.

Percentile ranking of native-state interfaces relative to decoy states that differ from the native state by rotation of their helices

PDB code	Helices	Full rank	LOOCV rank	PDB code	Helices	Full rank	LOOCV rank
1p49	2	11.2%	11.9%	1c3w	21 (3)	99.5%	99.4%
2qts	6 (3)	30.4%	20.3%	1kf6	12 (2)	99.7%	99.7%
2wit	36 (3)	47.2%	30.7%	3hqk	24 (2)	99.5%	99.7%
3b44	6 (3)	91.4%	84.9%	2rdd	39 (3)	99.9%	99.7%
3h9v	6 (3)	86.8%	86.9%	2h8a	4	99.8%	99.7%
2zuq	4	95.3%	89.7%	2zxe	12	99.9%	99.8%
2gfp	12	92.4%	91.1%	2qjp	20 (2)	100.0%	99.8%
2uui	12 (3)	94.0%	92.9%	1ott	20 (2)	99.9%	99.9%
3ddl	7	95.0%	93.4%	3cap	14 (2)	100.0%	99.9%
3gia	12	94.6%	93.5%	3d4s	7	100.0%	99.9%
1iwo	10 (2)	93.4%	94.2%	3b9w	33 (3)	100.0%	100.0%
2jln	10	95.0%	94.5%	3f3e	24 (2)	99.9%	100.0%
2zjs	11	96.4%	96.0%	1yew	39 (3)	100.0%	100.0%
2jaf	21 (3)	96.4%	96.1%	2b2h	33 (3)	100.0%	100.0%
3eml	7	98.4%	98.7%	2bl2	40 (10)	100.0%	100.0%
3b8c	10	99.0%	98.8%	2vpz	16 (2)	100.0%	100.0%
2z73	7	98.7%	99.0%	2yvx	10 (2)	100.0%	100.0%

The table lists the percentage of 5000 decoy structures with higher energy than that of the native state, as well as the number of helices (with multiplicity in parentheses). The ranking with the full-set energy matrix and the energy matrix with the ranked structure left out are given.

The neutral ensemble of structures used to determine $N_{PQ}^0$ is generated from the same set of helical-bundle TM structures used to generate N_PQ, but with the set of structures expanded by sampling configurations in which the helices are rotated randomly about their axes. The axis of rotation was determined by minimizing the sum-squared distances of α-carbons from a trial axis. Five thousand structures (including the native structures) for each TM protein were generated by assigning random rotations to each helix and then relaxing the positions in the xy plane to minimize $f\left(r\right)$, defined as

$$f\left(r\right)=\sum _{ij}{\frac{r_{ij}^{\min }}{3.6}}^{-12}+\sum 0.01{(r_{ij}-r_{ij}^0)}^2\text{.}$$ (4)

Here, $r_{ij}$ is the minimum distance between helices i and j, and $r_{ij}^0$ is the value for the native structure, always relative to α-carbons. P-Q contacts in either ensemble were assigned on the basis of a spatial cutoff separation of α carbons (7.75 Å), and by a restriction on the orientations of the residues relative to their parent helices, meant to exclude side chains presumably not near each other. Angles ${\varphi }_1$ and ${\varphi }_2$ are assigned for a candidate interaction by using as a reference point the nearest point along each residue's helix axis:

$${\varphi }_1={\cos }^{-1}\left(r_{11}\mathrm{\times }{r}_{12}\right),$$ (5)

where r₁₁ is the unit vector from residue 1 to the nearest point on the axis of helix 1, and r₁₂ is the unit vector from residue 1 to the nearest point on the axis of helix 2. In addition, a righthand rule is used to determine sign. If the magnitude of either angle is >100°, or if the sum is >100°, the distance contact is discarded. Center-of-mass side chains were not used as the interaction centers, based on the logic that substantial side-chain reorientation would be likely for a randomized configuration. Our method of contact determination differs from that of previous work due to the necessity of judging contacts between neutral and PDB structures on the same basis. By specifying hypothetical side-chain positions for the neutral states, perhaps one could use the more sophisticated contact methodology employed by others, but this would entail significant computational expense. Surface contacts were detected with only a distance cutoff (6 Å). The corresponding observed and expected contact propensities (N_PQ and $N_{PQ}^0$), along with an illustration of how contacts are defined, are given in the Fig. S17 in the Supporting Material.

In either ensemble, we assume that the likely maximum number of contacts that any α-helical peptide residue could make is 4 (we don't limit residue-residue contacts, only surface and bilayer tail contacts), since a greater number of contacts (>4) is much less likely using our contact measure. Thus, the (implicit) peptide-lipid contacts, N_PL and N_QL, are calculated as the difference between the likely maximum number of contacts and the actual number of residue contacts, with negative values set to zero. Due to the nature of the null ensemble we generate, which is not meant to characterize helix dissociation, N_LL is nearly identical for all native and decoy structures, and hence cancels. A similar quasichemical expression can be used to define peptide beads exposed to material on the bilayer surface, N_PS and N_QS, to give a total energy per TM structure i based on the 20-letter code:

$$E_{20}^i=\sum _{P,Q>P}{N}_{PQ}^i{E}_{PQ}+\sum _P{N}_{PS}^i{E}_{PS}\text{.}$$ (6)

The final step is to reduce the full 20 × 20 interaction matrix to an n-type interaction set, where amino acid alphabet reduction (n < 20) is a common technique for analysis of protein interactions (36–38). We explore the case n = 4 in this work. Expanding the alphabet introduces problems with smaller groups having poor statistics, and as more TM structures become available, a larger alphabet could be explored. We do this by first classifying the 20 amino acids according to the 4-letter code by reexpressing the equilibrium constant in Eq. 3 as

$$K_{pq}=\frac{\sum _{P\in p,Q\in q}{N}_{PQ}{N}_{LL}}{\sum _{P\in p,Q\in q}{N}_{PL}{N}_{QL}}\text{.}$$ (7)

for both the actual and null distributions, where p and q refer to residue types in the reduced letter code (when P and Q are the same, the sum is restricted so as not to double-count). This allows us to redefine the energy for TM structure i as

$$E_4^i=\sum _{p,q>p}{N}_{pq}^i{E}_{pq}+\sum _p{N}_{pS}^i{E}_{pS},$$ (8)

where N_pq, N_pS, E_pq, and E_pS now refer to contacts and energies with peptide, lipid, and surface material in the 4-letter code. The final amino acid assignment to one of the four bead types is optimized by minimizing the summed energy over all TM α-helical structures

$$E_{Total}=\sum _i{E}^i{h}_i^{-1},$$ (9)

where h_i is the number of helical bundles in the crystal cell of structure i, for homooligomers. The search procedure used for P assignments into p is a naive, brute-force combination of swaps and switches, checking all swaps (exchange of two residues) and group switches (moving one residue to another group) that lowered the total energy in Eq. 9. A simulated annealing protocol found the same optimal set of groups as did the brute-force minimization. Table 1 lists the final classification of residues into the four bead classes, and Table 2 gives the corresponding interaction energy matrix.

Table 1.

Classification of 20 amino acids into four bead types, L, N, V, and B

20	4	20	4	20	4	20	4
Trp	B	Met	V	Tyr	V	Asn	N
Val	B	Cys	V	Ser	N	Gln	N
Leu	B	Pro	V	Gly	N	Glu	L
Ile	B	Ala	V	His	N	Asp	L
Phe	B	Thr	V	Lys	N	Arg	L

The grouping is determined by minimizing Eq. 9.

Table 2.

Statistical potential in the 4-letter code

Bead type	L	N	V	B	Surface
L	−1.479 (0.39)	−0.771 (0.18)	−0.789 (0.16)	−0.303 (0.14)	−0.507 (0.09)
N	−0.771 (0.18)	−0.493 (0.10)	−0.303 (0.07)	0.091 (0.06)	−0.165 (0.04)
V	−0.789 (0.16)	−0.303 (0.07)	−0.193 (0.07)	0.102 (0.05)	0.002 (0.03)
B	−0.303 (0.14)	0.091 (0.06)	0.102 (0.05)	0.517 (0.05)	0.102 (0.02)

All entries are the interaction strength parameter, E_pq, derived from Eq. 7 given the optimal grouping in Table 1. Units are in k_BT. Error bars are estimated by adding/subtracting one standard deviation of the contact number from the neutral distribution.

Results

Helix-helix contact propensities

A comparison of the neutral and PDB distributions yields information about the propensity of the various side chains to be in contact with other side chains or in contact with the lipid bilayer tails. The contact propensities given here depend on the TM helices being stable in the bilayer. In Fig. 1, we plot a quasichemical (free) energy difference for residue P being in contact with a helix interface versus an oily lipid, according to

$$E_P=-k_{\text{B}}T\log \left[\frac{{\sum }_Q{N}_{PQ}{N}_{PL}^0}{{\sum }_Q{N}_{PQ}^0{N}_{PL}}\right],$$ (10)

as a function of its partial volume, given in Harpaz et al. (39). In general, large hydrophobic amino acids are less likely to be found at helix-helix interfaces, instead favoring interfaces with the lipid bilayer region. We explain the contact propensity of Lys by its ability to act as a snorkel (40,41), with its positive charge near the charged bilayer surface. Note that it falls nicely on the hydrocarbon residue line (Trp, Phe, Ile, Leu, Val, Pro, and Ala, although with large uncertainty), possibly indicating that surface Lys residues act similarly to Leu or Ile residues in terms of a contact model. Those residues that are smaller and/or capable of hydrogen-bonding have a modest tendency to be at TM α-helical interfaces. In a class by themselves are the most polar residues, with net charge in the aqueous phase, Asp, Glu, His, and Arg, which display only modest size dependence but are most consistent with driving interhelical contact formation. However, these residues occur infrequently in TM helix sequences relative to amino acids such as Gly, Ala, Ile, Val, and Leu. Furthermore, the strength of a hydrophilic residue contact is likely greatly modulated by its depth in the lipid bilayer; were a hydrophilic residue at the bilayer midpoint, its propensity to make contacts with other helices, rather than with the apolar bilayer tails, could be much greater than calculated by our statistical potential.

Figure 1.

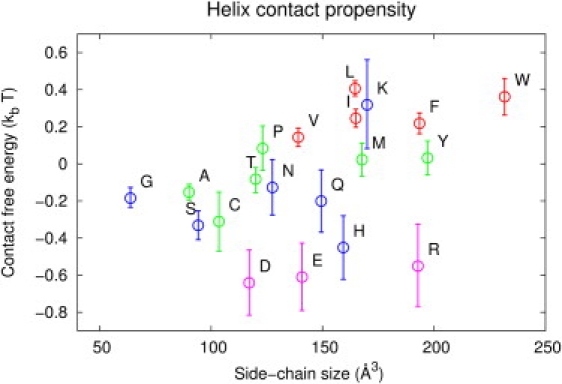
The residue-residue contact free energy for each amino acid. Side-chain volumes are taken from Harpaz et al. (39). Residues are colored/shaded according to the reduced-alphabet grouping (Table 1).

Reduced alphabet for TM α-helices

The four-site energy model formed from the statistical contact procedure (see Methods) is shown in Table 1. The group breakdown seems to reflect size and polarity as important features of the four-bead classification. The B-type bead contains large hydrophobic amino acids consisting of Leu, Ile, Phe, Trp, and Val, which are residues that typically face the oily bilayer, whereas the L-type bead group contains the acidic/basic residues Arg, Asp, and Glu. The N- and V-type beads seem to balance the importance of size versus polar/apolar character. The N-type bead includes the smaller amino acids, such as Gly, and/or amino acids that are capable of hydrogen-bonding, such as Ser, Asn, His, and Gln, whereas the V-type bead includes less polar amino acids, such as Ala, Met, Cys, and Pro. The amino acids Lys, Tyr, and Thr have dual polar/apolar character, in which the polar amino terminal group interaction of Lys with the bilayer surface favors its polar classification with group N, whereas the aliphatic or aromatic component of Tyr and Thr outweigh their ability to hydrogen-bond, so that they are classified into the V group. The strongest member (i.e., with the largest energy penalty to move to another group) of the B group is Leu, and that of the L group is Arg, presumably due to its large size. The strongest member of the N group is Ser, whereas those of the V group are Ala and Thr.

Size and polarity sequence motifs

Our contact propensities in Fig. 1 show clear trends with both side-chain size and side-chain polarity. If polar interactions such as salt-bridges and hydrogen bonding, for example, are significant, polar residues might tend to group on the same face of a given TM α-helix to help stabilize the interface with other TM helices. Fig. 2 shows the well-known result that α-helical structure gives rise to sequence patterning with sequence positions 3, 4, and 7 occurring on the same helical face and positions 2, 5, and 6 on the opposite face. We use our four-letter bead classification to analyze polarity (L and N versus V and B), as well as a reassignment of the groupings based on size (Table 3), to calculate the actual and expected frequency of pairs of amino acids at different sequence distances (registers) on a single TM helix. We use the analysis method of Senes, Gerstein, and Engelman (SGE) (42), but because we group residues by the reduced alphabet and by size, we may determine more general sequence motif correlations than discovered previously. We state here the modifications we have made to the SGE study (42), but for details of the calculation, we refer the reader to that study. We used the SwissProt database v21, accessed on August 19, 2009 (48), and we calculated homology scores according to

$$S_H=\sum _{ij}{\log }_{10}\left(\frac{M_{ij}}{f_j}\right),$$ (11)

where M_ij is the mutation probability matrix (raised to the 100th power) and f_j are the residue frequencies, given in Dehouck et al. (49). From an initial set of 323,071 TM sequences we pruned homologous sequences to yield 30,082 sequences. Sequences with scores >6 were candidates for rejection using the same sequence priority classification as in the SGE analysis (42). Instead of determining the 18-residue maximum hydrophobic region of the TM sequences, we centered our 18-residue sequences around the midpoint given in the database, which reduces end effects where the SGE analysis gave the unphysical result of placing hydrophobic residues at the membrane boundary (tending to shift the odds by <4% in a face-independent way, i.e., not significantly changing the results from the SGE analysis (42)). No sequences were rejected due to high residue frequencies or low hydrophobicity. Expected frequencies were calculated considering the distribution of a particular group of residues at each of the 18 positions; a particular random sequence was weighted by the probability of finding the relevant groups at those positions. When we break the analysis down to individual amino acids, the reported odds are not weighted by the distributions.

Figure 2.

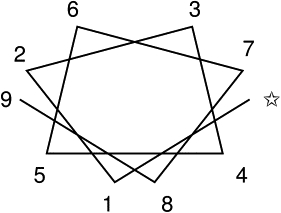
A helix wheel depicting the facial positions assuming 3.6 residues/turn.

Table 3.

Classification of amino acids by residue size

20	2	20	2	20	2	20	2
Trp	L	Met	ML	Ala	S	Asn	MS
Val	MS	Cys	MS	Ser	S	Gln	ML
Leu	ML	Pro	MS	Gly	S	Glu	ML
Ile	ML	Tyr	L	His	ML	Asp	MS
Phe	L	Thr	MS	Lys	ML	Arg	L

The grouping is determined by equating van der Waals volumes >190 ų with large beads (L), 140–190 ų with medium-large beads (ML), 140–100 ų with medium-small beads (MS), and <100 ų with small beads (S). Volumes were taken from a study by Harpaz et al. (39).

In Figs. 3 and 4, we consider the odds of particular pairings on a helix face with residues grouped by size (Table 3) or by statistical alphabet reduction into polar through apolar categories (Table 1), with enhancements at positions 4 and 7 and depletion at positions 1 and 2 indicating preference for same-helix-face positions. The original SGE analysis found that the motif GG4 (two glycine residues, with one at i and the other at i + 4) had the largest deviation from the expected probability of 1.0 (odds ratio of 1.32; Table 2 of SGE (42)), and that the β-branched residues Ile and Val also had large deviations (II4, 1.15; VV4, 1.13; II2, 0.86). We therefore separate the odds-ratio analysis, in which we include as well as exclude these residues so that they don't overwhelm other trends.

Figure 3.

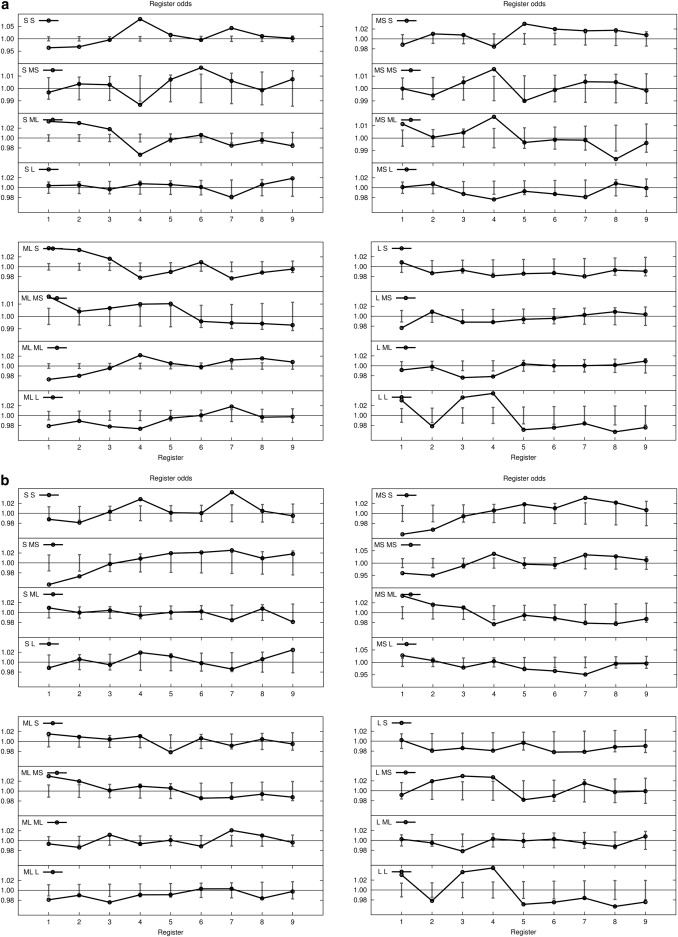
The found/expected odds ratio of finding small (S), medium-small (MS), medium-large (ML), and large (L) residues on TM sequences with Gly, Val, and Ile included (a) and excluded (b). See Table 3 for residue classification.

Figure 4.

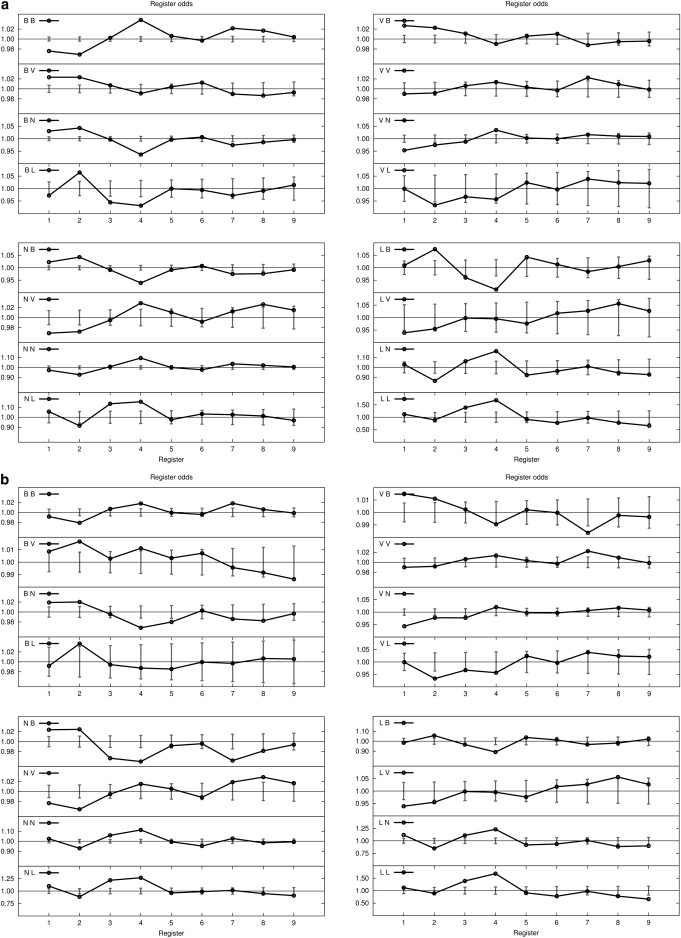
The found/expected odds ratio of finding polar and apolar residues on TM sequences with Gly, Val, and Ile included (a) and excluded (b). See Table 1 for residue classification.

Fig. 3 shows the odds of particular pairings on a helix face with residues grouped by size, but with Gly, Val, and Ile included (Fig. 3 a) and excluded (Fig. 3 b). Fig. 3 shows that even with Gly and Val eliminated, the odds of the S/S and MS/MS residue pairs being found on the same face are still greater, whereas with Ile removed, the odds pattern for the ML/ML residue pairs being on the same face is flatter, that is, with less chance of them being found on the same helical face. The L/L pattern also shows a significant increase in odds ratio for at least one large residue on the same face. By contrast, the elimination of Gly, Val, and Ile from the S/MS and S/ML trends removes the strong tendency of these size residue pairs to deplete the same face, and like the S/L category, these distributions are now within expected odds. The elimination of Val and Ile causes a modest odds-ratio tendency to occupy different faces for the MS/ML categories, but it causes an overall flat trend for MS/L, ML/ML, and ML/L correlations. Certain residues identified by their amino acid identity do not fit the trend of their broader group. Leu has a reduction of odds at position 4 when correlated with similar-sized polar residues (Lys, Gln, Glu, and Arg), but enhancement is observed at this position for the rest of the group. Although MS/MS shows enhancement at position 4, the most statistically significant pairs (NN4, odds 1.49, p = 3e-08; TC4, odds 1.18, p = 4e-5; TT4, odds 1.08, p = 2e-4; DN4, odds 1.52, p = 3e-04) are more naturally interpreted by polarity. The L/L enhancement at position 4 is dominated by FF4 (odds 1.06, p = 5e-5) but is counteracted by YF4 (odds 0.89, p = 9e-6). In summary, the size categorization emphasizes the accumulation of multiple small residues on the same face, with other size-pairing categories being less informative.

Fig. 4 shows that the sequence motifs based on our reduction to four groups based on polarity shows far more statistically significant patterning based on helix sequence than on size. The apolar-apolar BB and VB motif sequencing shows a weak enhancement on the same face, even though an apolar residue has some preference for the bilayer rather than a helix interface. The Leu, Ile, and Val pairings provide a clear explanation of the relative importance of the polarity of the B groups and the role of β-branching (42). Although Leu tends to associate on the same face (LL4, 14,193 observed, 13,632 expected, standard deviation (SD) 95), it does not rival II4 (7804 observed, 6562 expected, SD 68) or VV4 (5710 observed, 5046 expected, SD 61). The flattening of the odds-ratio pattern for BB correlations when Gly, Val, and Ile are zremoved makes this evident. By contrast, there are highly amplified preferences for placing charged residues (L) or polar residues capable of hydrogen-bonding (N) on the same face, whereas residue groups of unlike polarity tend to associate on different helical faces. The group pair BN (which has a large population and a large disparity in polarity) displays statistically significant enhancement at the opposite-face positions (1 and 2) and depletion at positions on the same face (4 and 7); for example, among the 18 BN4 pairings, only one has enhancement on the same face (FQ4) with better than 5e-2 statistical significance (p = 2e-2).

Energy ranking of native TM helix bundle against decoy structures

We use the contact energy matrix (Table 2) to perform a native ranking analysis to determine whether our four-letter code residue-residue pair contact is sufficient for picking the native helical interface of TM bundles. We note two caveats: 1), that the set of decoys is limited to an ensemble of helices positioned the same as the native structure, but with helices free to rotate; and 2), although statistical potentials of this kind are not accurate enough to predict globular protein structures ab initio (in part due to the limitations of the ensemble), they have still been conceptually influential in analyzing protein structure, stability, and folding features (43–47). We performed leave-out-one-cross-validation (LOOCV) analysis on each member of the PDB set, and the ranking with and without LOOCV analysis is given in Table 4.

In Fig. 5, we show root-mean square deviation (RMSD) versus energy plots for three structures: one for which the potential performed poorly (2wit; Fig. 5 upper), one for which the potential performed moderately well (3b44; Fig. 5 middle), and one for which the potential performed well (2yvx; Fig. 5 lower). We sampled additional near-native structures to expand the range of RMSDs sampled (gray points). The native structure is denoted with an asterisk at RMSD = 0. For 2yvx and 3b44, the energy increases, generally, with RMSD.

Figure 5.

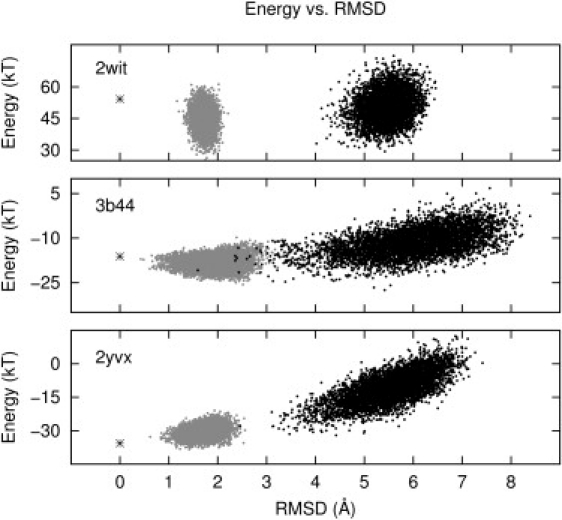
RMSD versus energy for the TM section of three proteins. The model performs poorly for the upper system (2wit), moderately well for the middle system (3b44), and well for the lower (2yvx). The black points are members of the ensemble from which the potential is derived, whereas the gray points are structures closer to the native state.

Overall, the coarse-grained contact energy model ranks 18 of 34 of the native TM helix bundles in the top 1%, with good discrimination for native structures for another five to eight native structures (ranked in the top 5%). Overall, native structures ranked at the top of their set, for example, particulate methane monooxygenase (1YEW) (50) and ammonium transporter 2b2h (51) have fewer hydrophobic contacts than the lowest ranked decoys.

The poorly ranked acid-sensing ion channel 2qts (52) is likely due to a substantial void that is occupied by a detergent molecule in the crystal structure at the active-site opening, which is not considered by our model. The worst-ranked structure, estrone sulfatase, 1p49, has two TM helices whose interacting helix faces are lined with hydrophobic residues, whereas small and/or polar residues, such as Thr, Gln, Gly, and Ser, appear to be facing the bilayer, even though potentially dimerizing TT3 (odds 1.06, p = 7e-3) and GS4 (odds 1.09, p = 3e-5) motifs are present, defying the usual trends of TM helix interactions. The best-ranked decoy of the Na⁺/betaine symporter 2wit (53) has ∼20 more small-residue contacts and ∼30 fewer large-residue hydrophobic contacts than the native structure (and the decoy set for 2wit is likely unrealistic, as this TM protein has a substantially kinked and interlaced set of helices). The poorly ranked intramembrane protease GlpG (3b44) native state (54) has more BB contacts and fewer small residue contacts than the lowest ranked decoys.

Structures with many large hydrophobic groups, such as Ile, Val, Leu, Trp, and Phe, tend to be ranked poorly by the contact energy, since these residues have lower relative odds of making contacts with each other, and so contacts between these residues are penalized with a positive contact energy. It is likely that the contact energy is overemphasizing the role of effective mutual repulsion of large bulky residues, which tend to point at the oily bilayer, washing out the preferences of branched hydrophobic side chains to pack at a helical interface. The dual role of the large hydrophobic residues, of interacting with lipid tails and flanking helix-helix interfaces, is also likely not captured in the statistical contact energy. Of particular interest for 3b44 is a helix pair in which there is a GLxxGL motif on one helix that interacts with a YAxxGY motif on the other helix. We see in the ranking of structure 3b44 that the energy functional was not able to properly assess the stability of a helix with a motif of large and small residues with a clear ridge-in-groove interaction, suggesting a breakdown of the pair interaction assumption.

For comparison, the scoring function (based primarily on packing propensities) of Fleishman and Ben-Tal (55) was used to rank the same ensemble of structures. The average ranking of their function was 94.4%, compared with this work's average LOOCV ranking of 90.3%. Omitting the one case of 1p49, each system is ranked at >92% by either the scoring function in this work or that of Fleishman and Ben-Tal (55).

Discussion

As our approach is markedly different from the other TM studies of helical contacts, we compare our method of computing single-residue contact propensities with those of other studies that use direct van der Waals contacts or backbone distances to interpret single-residue contact propensities. In the study of Adamian and Liang (25), which evaluates contact propensity by counting atomic van der Waals contacts of side chains (and also the propensity for a side chain to be in a void or pocket of the structure), the authors note that the TM contacts appear to be less identity-dependent than the contacts in soluble bundles, but with some preference for Met, Cys, and Trp to make helix-helix contacts. Lo and co-workers (56) use the contact assignment scheme of Walters and DeGrado (57), in which atomic van der Waals radii contacts are determined with a residue-residue C_α atom distance cutoff of 6 Å, compensating for the poor statistics of certain residue contacts using a Bayesian analysis. The authors determine that Cys has the highest contact propensity, whereas some of the strongly hydrophilic residues (Asp, Glu, Lys, and Arg) have poor contact propensities.

Instead of van der Waals contacts, Eilers et al. (8) used a simple cutoff based on the backbone-to-backbone distance between helices to determine which helices interact, after which interface residues are determined by evaluating minima (with respect to residue number) in the backbone interhelical distance plot. They found a compelling correlation between side-chain size and helix-helix contacts for TM bundles in contrast to aqueous bundles. They determined that the residue with the largest propensity to be at a helix-helix interface is Pro, although small residues Gly, Ala, Ser, and Cys also had very high propensities. Unlike the van der Waals definitions (20,56), we also see a correlation between size and helical interface propensity. For the most part, this is probably due to our assessment of contacts in which backbone atoms are used to determine those residues participating in the helix-helix interface. Our view is that using the distance between backbone atoms does not obscure the size and polarity dependence of the identity-dependent driving force of helix association. We note that the hydrophobic free energy (measured by partitioning between water and nonpolar solvents) has been shown to correlate linearly with total surface area in contact with water (58,59), which makes separation of size and polarity somewhat complicated. However, we find that polarity is a stronger influencing factor of identity-dependent driving forces for TM helical bundle assemblies than has been found in previous studies.

Conclusions

We have developed a novel statistical contact potential based on solved structures of TM proteins, which we use to investigate the amino acid likelihood of stabilizing TM helix-helix faces based on the full amino acid alphabet. We found that the most polar residues with net charge in the aqueous phase, Asp, Glu, His, and Arg, have a strong propensity to participate in helix-helix contact formation, although they occur rarely in TM helical bundles, playing more specialized stabilizing roles near the surface. To increase statistical significance, we further reduced the 20 × 20 contact-energy matrix to a four-flavor reduced alphabet of amino acids, automatically determined by our methodology, in which we find that polarity is a more dominant factor of group identity than is size. We found that there are indeed broad trends of aqueous charged or polar groups capable of hydrogen-bonding to occupy the same face, whereas polar/apolar residue pairs occupied opposite faces.

When our contact energy is applied to native target selection against a large decoy set of native intermolecular helical positions that have been rotated to generate nonnative helical interfaces, we can predict the native structure for 34 TM helical bundles a majority of the time. We also have reasonable RMSD trends with energy that perhaps make the statistical potential a useful first-pass filter for structure prediction, comparable to the scoring potential of Fleischman and Ben-Tal (55), but we would clearly need to rely on a more sophisticated energy model for reliable native-state discrimination against misfolds. Of more importance, the failures of our pair-based contact energies provide a good step toward identifying the higher-order sequence motifs with significant cooperation between residues. Of particular significance for future studies will be the packing of the large hydrophobic residues around the helix-helix interface, amino acid motifs that allow for ridge-in-groove interactions, and differences among these motifs for dimerization versus oligomerization. McAllister and Floudas (60) have used a sophisticated categorization of contacts (for example, a separate classification of primary and secondary contacts, with primary contacts nearer), and are able to include three-body effects in their prediction model, but statistical noise remains an issue for these higher-order effects in contact propensities. A structure prediction algorithm may need to incorporate motif-specific heuristics of many-residue motifs (61) or evaluate the relative side-chain entropy of configurations (62) to accurately predict the native structure of TM helical bundles.

Supporting Material

Seventeen figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00482-0.