The Potential Landscape of Genetic Circuits Imposes the Arrow of Time in Stem Cell Differentiation

Abstract

Differentiation from a multipotent stem or progenitor state to a mature cell is an essentially irreversible process. The associated changes in gene expression patterns exhibit time-directionality. This “arrow of time” in the collective change of gene expression across multiple stable gene expression patterns (attractors) is not explained by the regulated activation, the suppression of individual genes which are bidirectional molecular processes, or by the standard dynamical models of the underlying gene circuit which only account for local stability of attractors. To capture the global dynamics of this nonequilibrium system and gain insight in the time-asymmetry of state transitions, we computed the quasipotential landscape of the stochastic dynamics of a canonical gene circuit that governs branching cell fate commitment. The potential landscape reveals the global dynamics and permits the calculation of potential barriers between cell phenotypes imposed by the circuit architecture. The generic asymmetry of barrier heights indicates that the transition from the uncommitted multipotent state to differentiated states is inherently unidirectional. The model agrees with observations and predicts the extreme conditions for reprogramming cells back to the undifferentiated state.

Introduction

During cell differentiation, the gene regulatory network governs a unidirectional progressive change of the cell's gene expression pattern through which the cells adopt the expression pattern that implements the cell type-specific phenotype (1–4). Whereas in equilibrium systems time-irreversibility is a direct reflection of the second law of thermodynamics, the cell's gene regulatory network represents a nonequilibrium system (far from thermodynamic equilibrium) and time-irreversibility of development is not a direct manifestation of thermodynamics. As in most metazoa, differentiation is not associated with the irreversible loss of genes (5) but instead, each gene can be reversibly turned on and off. This raises the question: What is the origin of the macroscopic directionality of the temporal evolution of the gene expression pattern during development, if, at the microscopic level, the activation and repression of individual genes are reversible?

To address this question, one can formalize the problem by studying a gene regulatory network of N genes (X₁, X₂, …, X_N) that governs differentiation of a cellular state S. Then the gene expression profile of these N genes, representing the phenotypic state S, is a time-dependent state vector S(t) = [x₁, x₂, …, x_N] = x(t), where the values x_i represents the activation levels of gene i at time t. The dynamical behavior of the network is described as an N-dimensional dynamical system with rate equations for the vector x(t), namely: dx(t)/dt = F(x), where the vector F is the force that drives the movement of S(t). But what causes the directionality in the time evolution of S(t) across fate decisions?

The standard evaluation of such dynamical systems relies on linear stability analysis around fixed-points (stable steady states, or attractors) that represent cell types. Directionality of change in gene expression pattern is simply explained by the local relaxation toward a stable steady state (i.e., attractor) due to dissipative dynamics (6) or by hysteresis around bifurcations (7). While these effects arise from circuits as dynamical systems considered in isolation, such nonlinear phenomenon can stem from often-neglected interaction with host physiology. Indeed, a recent work reveals a new mechanism of generating bistability that underscores the need to account for host physiology (8).

We summarize in the following the most salient existing but disparate concepts that implicitly explain directionality of cell differentiation (see also Fig. S1, A–D, in the Supporting Material):

Linear regulatory cascades and gene expression avalanches

The simplest explanation of directionality of cellular differentiation relies on the traditional notion in molecular biology of signaling cascades that drives development (9). In this view, the gene expression changes S(t) associated with development is governed by a chainlike gene regulatory pathway, such as GeneA → GeneB → GeneC → GeneD, etc. (Fig. S1 A). Models of such circuits may exhibit branching and feed-forward loops, but typically contain few or are devoid of feedback loops. The almost circular network structure naturally affords the system a directionality, as the gene activation avalanches propagate, akin to the domino-effect, through the network down the cascade of one-way gene interactions. Regulatory interactions fanning out from master genes to large numbers of differentiation gene batteries (9) then establish the cell type-specific gene expression profiles S. This idea of activation avalanche is best elaborated for the development of sea urchin (9).

Development in higher organisms, such as vertebrates, however, exhibits features that are not compatible with this picture of avalanchelike progression.

First, the architecture of the gene regulatory network is replete with positive and negative feedback control loops. Moreover, many developmental control genes, such as BMPs, GATAs, STATs, Wnt, Notch, etc., are reused at multiple stages and in multiple lineages of development.

Second, the development of cell types proceeds through a succession of intermediate phenotypes that are discrete and stable, such as the multipotent stem and progenitor cells, that can be physically isolated as distinct entities. In contrast, the avalanche model would instead produce a continuum in time and would not account for the stability of gene expression profiles of discrete cell types, including those representing intermediate stages, such as tissue stem cells.

Molecular fixation of S(x) by covalent modification

Cell types, and hence their associated circuit states S(t), are maintained even after the action upstream regulators have subsided (often referred to by biologists as the memory effect). We denote here such stable stationary expression profiles with an asterisk: S^∗. To explain the stability and terminal character of cell type-specific, stationary gene expression profiles, S^∗, molecular biologists commonly invoke covalent modifications, including methylation of DNA and histones, at specific residues (10). These modifications are thought to affect gene expression by controlling chromatin structure and hence, the access of transcription factors to their binding regions on the genomic DNA. Because they are chemically stable and appear to permanently control the reading of the genomic DNA without altering the gene sequence, they have been interpreted as epigenetic marks that remember the activation status of individual genes once cells have differentiated (10).

However, it is clear that such molecular marks need to be erased at each generation when gametes fuse to produce pluripotent embryonic stem cells. Similarly, the successful reprogramming of nuclei of somatic, differentiated cells by transfer into oocyte cytoplasm (11) or by genetic manipulation (12–14) demonstrates the inherent reversibility of genetic programs. Moreover, from the accumulating characterization of chromatin modifying enzymes, notably those controlling histone lysine (de)methylation (10,15–17), it is increasingly recognized that the covalent epigenetic modifications are bidirectional (reversible). Thus, the epigenetic marks invoked to explain the irreversible sealing of cell fates are actually reversible. Moreover, as chromatin modifying enzyme complexes are not locus specific, ultimately, TFs have to guide these modifying machineries. In fact, the picture is emerging that DNA and chromatin modifying enzymes are recruited by TFs to specific gene loci, thus they are themselves subjected to the control by a network of transcription factors (18,19). This underscores the fundamental role of transcriptional network dynamics in cell fate control.

Nonlinear dynamics and bifurcations

At the center of differentiation control by gene circuit dynamics is the idea that each distinct cell phenotype S^∗ corresponds to an asymptotically stable state of the network, or attractor (20–23). This concept solves the difficulties of relying on linear cascades and covalent molecular marks to explain stability and the discontinuous nature of cell fates, lineages, and cell types, as well as the existence of temporally stable, discrete immature states (stem cells, progenitor cells). In brief, gene regulatory circuits that contain at least one positive feedback loop (or a composite positive feedback loop consisting of an even number of sequential negative regulation) exhibit multistability (24). This is the coexistence of multiple stable steady states S^∗_i, in which dS^∗_i/dt = 0 and S^∗_i are at least linearly stable in the sense that when the circuit state S(t) is perturbed by being kicked slightly away from S^∗_i, the circuit will spontaneously return to S^∗_i.

In this framework, each observable distinct cell phenotype i that can be identified biologically maps into an attractor state S^∗_i. The attractors naturally explain the discreteness and stability of individual cell phenotypes, such as cell types (20–23). Then, differentiation is the macroscopically quasidiscontinuous process by which a cell transitions from one attractor state S^∗₁ to another attractor at a different state space position S^∗₂. Although accumulating evidence points to the presence of attractor states (23,25,26), it remains unclear how the actual differentiation process, or the motion of S in state space between different stable states, is to be conceptualized, and what would account for the directionality.

In a first class of dynamical models, the transition occurs as a parameter of the dynamical system is altered, so that the system undergoes a bifurcation, i.e., a sudden change of the structure of the state space. For instance, the one-dimensional system dx/dt = F(x, λ) with the variable x and parameter λ can undergo a (supracritical) pitchfork bifurcation in which an attractor S^∗ in a monostable system becomes unstable as the parameter λ crosses a critical value λ_c. At this point, the stable state branches into two new stable states that correspond to different values of S, and hence, represent different stable gene expression programs (Fig. S1 B). It has been postulated that development is a succession of multiple such bifurcations that generate an increasing diversity of stable states (26–29). Importantly, in this model directionality in time hinges upon the external, explicit change of a control parameter as a function in time, e.g., λ = f(t), thus, is not reduced to a natural elementary and intrinsic process. Reversion of the control parameter would play the tape of development backward, so to speak, and allow the system to reoccupy the original stable branch.

Reversibility of differentiation due to time reversibility of control parameters is avoided in another type of dynamical model where differentiation occurs in a hysteresis loop and corresponds to the transition (i.e., the jump) from the lower branch to a higher branch as the critical parameter value λ_c is crossed (Fig. S1 C). Because of hysteresis, partial reversibility is naturally achieved, as reversal of the parameter to below the λ_c point does not cause a return to the lower stable branch until the another critical value, λ′_c. Because the hysteresis loop is not structurally stable, appropriate choice of other parameters can create a fully irreversible situation when the critical point for the return jump λ′_c is shifted out of the physically accessible state space, as shown in Fig. S1 D. Such irreversible state transitions due to extreme hysteresis have been observed in various enzymatic reactions (30) and described for hormone-induced differentiation of Xenopus oocytes (7).

Stochastic systems

Although extreme hysteresis with an open loop can impose a directionality, all the deterministic dynamical models above still require an external, explicitly modeled monotonic change of a control parameter, such as λ = f(t), to impose the arrow of time (even with time invariant λ) (6). Therefore, it is still hard to explain the spontaneity of a time-irreversible process. In reality, the dynamics of regulatory circuits is subjected to stochastic fluctuations caused, in part, by gene expression noise (31). Thus, a second class of dynamical model treats differentiation as a noise-induced transition from one stable attractor to another, which corresponds to a hopping, from one stable branch to another, in the bifurcation diagram, without the need for a parameter change. Ample experimental findings indicate stochastic state transitions during metazoa cell differentiation (32,33). The notion of noise-driven state transitions obviates the need for an externally imposed, explicitly introduced directionality, because the noise term introduces an odd variable (6) that can impose time-asymmetry—equivalent to entropy in classical thermodynamics.

If we expand this analogy to the idea of attractors as nonequilibrium stable stationary states, we will need an equivalent of free energy to address the following question: given two attractor states, S^∗₁ and S^∗₂, and noise-induced transitions, how does one determine an asymmetry of transition probability for the transitions in either direction? In dynamical systems, the identification of attractor states is based on linear stability analysis, i.e., the exploration of the immediate neighborhood around the attractor state. Such local stability analysis does not relate attractors in a multistable system to each here.

These explanations address only behaviors near attractors or require an explicit external influence, such as the deliberate change of a control parameter in one direction. In contrast, irreversibility of development pertains to spontaneous processes taking place at a larger scale, in state space, encompassing transitions between multiple attractors in a multistable nonequilibrium system (34). Thus, explaining directionality requires analysis of the global dynamics of the network as a nonequilibrium system by computing an equivalent of the potential (35,36) that would permit answering specific question: Given two stable attractor states S^∗₁ and S^∗₂ (far from equilibrium), and noise-induced state transition, what is the relative transition rate in either direction?

One can not obtain a global potential function as one would for an equilibrium system because F(x) is, for more than one-dimensional system in general, nonintegrable. Here we show that a generalized global nonequilibrium landscape (6,37–47) can be applied to a simple canonical regulatory circuit that exhibits a multistability which can describe the fate decision of a bipotent progenitor cell. Using this system, we show that directionality of differentiation is a system-immanent feature that emerges from such a gene regulatory circuit that is wired to produce the diversification of one stable cellular state S(t) into two distinct ones.

Results and Discussions

The canonical gene regulatory circuit module shown in Fig. 1 A, consisting of the mutual regulation of two opposing fate determining master transcription factors (TF) X₁ and X₂, has been shown to control cell fate decision and commitment in several instances of multipotent stem or progenitor cells (26,29,48). X₁ and X₂ are coexpressed in the multipotent undecided cell, and commitment to either one of the two alternative lineages leads to expression patterns in which they are, then, expressed in a mutually exclusive manner (49–51). Importantly, note that, in many cases, the genes X₁ and X₂ also positively autoregulate themselves (Fig. 1 A).

Figure 1.

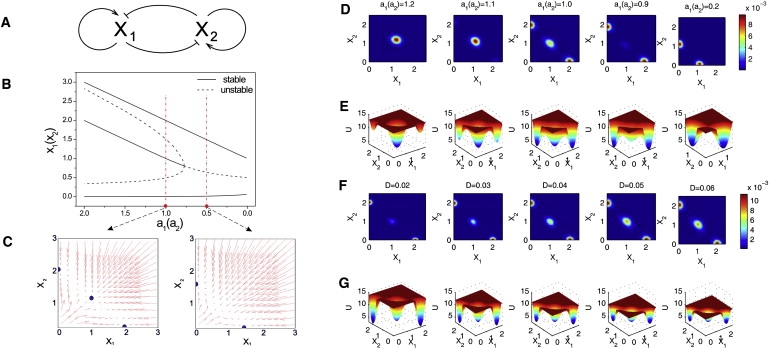
Dynamics of the canonical gene regulatory circuit of two mutually opposing transcription factors that positively self-regulate themselves. (A) Circuit architecture for the two genes X₁ and X₂. (B) Bifurcation diagrams indicating the stable position of S(x₁, x₂) where x₁ = x₂ for the symmetric case (vertical axis), during the symmetric change of a = a₁ = a₂ over the indicated range of values (horizontal axis), for the other parameter values b₁ = b₂ = 1, k₁ = k₂ = 1, and S = 0.5, n = 4. (C) Force field in the X₁ – X₂ state space for two parameter values for parameter a on both sides of the respective critical point in the bifurcation diagram. (D and F) Steady-state probability distribution P_ss(S) calculated from the Fokker-Planck equation (Eq. 1) as function of the parameter a in panel D or the noise parameter D in panel F. Colors indicate the probability P as shown in the color bar. (E and G) The corresponding quasipotential landscape where the elevation of the landscape (quasipotential) represents –ln(P(S)).

The circuit can be described by the following minimal system equations (26),

$$\frac{d{x}_1}{dt}=\frac{a_1{x}_1^n}{S^n+x_1^n}+\frac{b_1{S}^n}{S^n+x_2^n}-k_1{x}_1=F_1\left(x_1,x_2\right),$$ (1)

$$\frac{d{x}_2}{dt}=\frac{a_2{x}_2^n}{S^n+x_2^n}+\frac{b_2{S}^n}{S^n+x_1^n}-k_2{x}_2=F_2\left(x_1,x_2\right),$$ (2)

or, in vector form, dx/dt = F(x) = [F₁(x₁, x₂), F₂(x₁, x₂)] where x₁ and x₂ are the cellular expression or activation levels of the two lineage-determining transcription factors X₁ and X₂, and a₁, a₂, b₁, b₂, and k₁, k₂ are positive parameters that denote the strength of the following interactions or processes: The first expression represents, in the common formalization (26), a self-activation of strength a₁, a₂ that obeys a sigmoidal transfer function. The second term represents mutual inhibition, given a basal expression of strength b₁, b₂. The last term is the first-order inactivation (degradation) of either factor with the rate k₁, k₂. For our purpose, it will suffice to consider the symmetric situation a = a₁ = a₂; b = b₁ = b₂; and k = k₁ = k₂.

Such circuits robustly generate a tristable dynamics with three asymptomatically stable attractor states (see bifurcation diagram in Fig. 1 B): the two outer asymmetric attractor states S^∗_A and S^∗_B representing the differentiated states with almost mutually excluding expression of X₁ and X₂, and a third central symmetric attractor state, S^∗_C, characterized by approximately equal levels of X₁ and X₂ expression: x^∗₁ ∼ x^∗₂ (Fig. 1 C) (26,29). This central attractor represents the multipotent state that exhibits the characteristic balanced or promiscuous expression of the two opposing, fate-determining TFs (49)—a hallmark of the indeterminacy of the undecided multipotent stem cell.

Commitment of progenitor cells at S^∗_C to the two differentiated cells (S^∗_A and S^∗_B) is thought to involve two mechanisms:

• 1.Destabilization of the central progenitor attractor S^∗_C due to a subcritical pitchfork bifurcation as parameter values are gradually changed, for instance, as self-activation a is decreased (roughly symmetrically for both equations) (Fig. 1 B) (26); and
• 2.Noise-driven transition from the S^∗_C attractor into either one of the asymmetric attractors.

The observed direction of state transitions, representing fate commitment is indeed S^∗_C → S^∗_A or S^∗_C → S^∗_B. Once in S^∗_A or S^∗_B (= committed cell), spontaneous reversion to the S^∗_C (immature progenitor) state does not occur. Experimental evidence supports the role of both destabilization of the progenitor attractor (26,52,53) and of gene expression noise-induced state transitions (52,33,25). If directionality of attractor transitions is to be intrinsic, it must come from the noise-driven component, as the bifurcation requires an explicit externally driven parameter change.

Potentials for nonequilibrium and nonintegrable systems

We first evaluated the global dynamics of this circuit so that we can assign potentials to the attractor states and determine their distinct relative depth within the same frame of reference. The idea of a potential landscape describes how forces acting in a system relate to its global behavior. They are particularly useful for systems of interacting components, such as chemical reactions and protein dynamics, motion, and folding (54–56). However, these applications deal with equilibrium systems where the potential function is a priori knowable. For nonequilibrium systems, such as gene circuits that exhibit stable stationary states in higher (N > 1) dimensional state space, the intuition of some form of a potential is still warranted and widely used metaphorically (36), however, its functional form is not easy to obtain (6,37–47). In the gene circuit dx/dt = F(x), exemplified in Eq. 1, the vector F(x) is the force that drives the system. However, F(x) cannot, in general, be written as a gradient of a potential U: F(x) ≠ –grad(U) for systems of more than one dimension. In other words, F(x) is not a pure gradient of a potential, but there is another force, F_c, stemming from the nonintegrability that contributes to the dynamics (46) as

$$\mathbf{F}\left(\mathbf{x}\right)={\mathbf{F}}_c-{\mathbf{D}}^{\ast }\text{grad}\left(U\right),$$ (3)

where D is the diffusion coefficient tensor. Here D appears in front of the gradient accounting for the most general case when the system is inhomogeneous and anisotropic. It is not easy to separate these two components of the driving force, i.e., to calculate F_c and grad(U). However, in a stochastic system in which each state x is described probabilistically, the information about the probability in time and state space position x, P(x, t) can be found by solving the corresponding probabilistic equation or through Monte Carlo simulations. It allows one to correlate information provided by the steady-state probability distribution with the dynamics (46).

Although in nonequilibrium systems, at steady state, the divergence of the probability flux J_ss vanishes, the flux itself need not vanish. When local flux is equal to zero, the detailed balance is preserved and the system is in equilibrium state. When local flux is not equal to zero, the detailed balance is broken and the system is in nonequilibrium state. We found (see Supporting Material) that (46) F_c = J_ss/P_ss reflects the additional force linking the divergence-free steady state (long time limit) probability flux J_ss (velocity current) and the steady-state probability P_ss (density). Divergence-free flux has no place to start or end. It is in this sense that the flux has a “curl” nature. Importantly, in Eq. 2, we have decomposed the force driving the dynamics of the system into two terms, the curl force F_c and the gradient of the potential U where U is linked with the steady-state probability by U = –ln(P_ss).

Nonequilibrium landscape

The above discussion allows us to naturally introduce the nonequilibrium landscape U as U ∼ –ln(P_ss), analogous to the equilibrium situation. The difference between equilibrium systems (i.e., protein folding; local detailed balance preserved) and general nonequilibrium systems (i.e., gene regulatory circuit; local detailed balance broken) is that although the potential is linked to the steady-state probability in a similar way, the dynamics of the former follows a gradient of the potential whereas the dynamics of the latter is governed by both the gradient of the potential plus the curl flux (46). The origin of the nonzero flux is the energy pump to the open system (through, for example, ATP hydrolysis or phosphorylation). The presence of the nonzero curl flux breaking the detailed balance introduces a direction that can cause the asymmetry in time series, which is unique for nonequilibrium systems. This provides a physical foundation for arrows or directions in times for the underlying nonequilibrium process (57).

To obtain the stochastic time evolution of the probability distribution, P(x,t) and hence, U(x), we solved the Fokker-Planck diffusion equation for the system (Eq. 1; see also details in the Supporting Material) (58). With certain initial conditions and taking the long time limit, we obtained the steady-state solution using a finite difference method. The probability distribution P_ss(x) is shown as a function of the parameter a = a₁ = a₂ (Fig. 1 D) or of noise D (Fig. 1 F), with other parameters fixed. Consistent with the vector field and the bifurcation diagram (Fig. 1, B and C), at high values of the parameter a (strong positive feedback) the system has one central maximum (highest probability), corresponding to the central attractor S^∗_C.

As the parameter a is gradually decreased, this central maximum is destabilized (decreasing probability) as the two marginal states with locally higher probability S^∗_A and S^∗_B appear. The probability was converted to an elevation over each state space position x to obtain a landscape picture using

$$U\left(\mathbf{x}\right)=-ln{P}_{ss}\left(\mathbf{x},t\to \infty \right),$$

as shown in Fig. 1, E and G, where the z axis represents the dimensionless potential U(x). Here the attractor states appear as valleys—reminiscent of Waddington's “epigenetic landscape” (36). At the critical point, a_crit, the metastable central attractor S^∗_C flattens, disappears, and is converted to a hill-top—corresponding to the bifurcation point (Fig. 1 B) near which minimal stochastic fluctuations can drive the fate decision into either attractor S^∗_A and S^∗_B as soon as they become reachable.

Differentiation dynamics on the potential landscape

By applying the experimentally confirmed interpretation that the central attractor state S^∗_C represents the uncommitted bipotential progenitor state with its characteristic equal, intermediate expression levels of X₁ and X₂ (x₁ ∼ x₂) (25,26) and can differentiate into either cell fates (attractors S^∗_A or S^∗_B), we next evaluated the dynamics of circuit states S. We consider a scenario where the differentiation is achieved when a₁ and a₂ are decreased at the same timescale as the dynamics of x, hence, destabilizing the progenitor attractor S^∗_C while at the same time stochastic fluctuations drive the circuit into either one of the two attractors S^∗_A or S^∗_B as soon as they become reachable during the bifurcation, when a < a_crit (see Fig. 1).

To evaluate the dynamics of circuit states S, mimicking noise-driven and signal-induced cell lineage commitment, we numerically computed the probabilistic temporal evolution of the progenitor state S^∗_C driven by the dynamical system (Eq. 1) by solving the corresponding Fokker-Planck diffusion. In the model, as time evolves, a₁ and a₂ are also reduced according to a₁∼exp(–λ₁^∗t) and a₂∼exp(–λ₂^∗t) (25,26). Fig. 2 shows the probability flux vectors mapped onto the state space with the probability distribution P(x, t), indicated by the colors, for constant noise, D = 0.05. Note that the vector field does not reflect the probability gradients as in equilibrium systems. This is manifest in the curl flow rotating out of and into attractors because the driving force F(x) is not –D·grad(U(x)), but F(x) = F_c –D·grad(U(x)) (Eq. 2). The evidence of a circular flow out of the progenitor attractor predicted by the potential landscape was hinted in the experiments for the differentiation in common myeloid progenitor cells in the PU.1/GATA1 state space in the PU.1/GATA2 state space (26).

Figure 2.

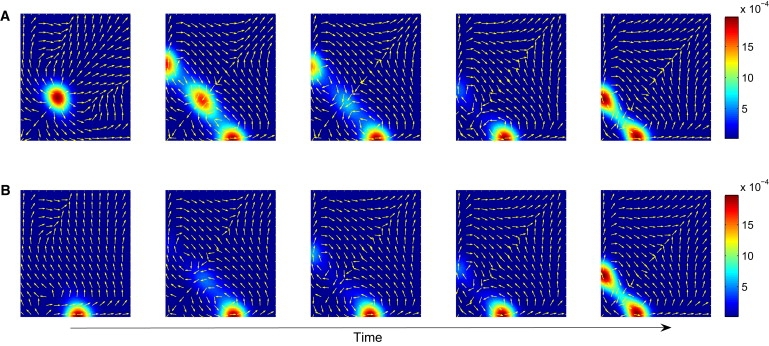
Dynamical behavior of the probability P(S, t) and flux vectors during fate decision of a stem cell in the multipotent state S^∗_C. P(S, t) is evaluated during bifurcation from tristable to the bistable regime as the parameters a₁ and a₂ are decreased according to a₁ ∼ exp(–λ₁^∗t) and a₂ ∼ exp(–λ₂^∗t) with λ₁ = 0.01 and λ₂ = 0.015. In panel A, the initial state is near the central attractor S^∗_C, P(S = (0.3, 0.3), t = 0) = 1, whereas in panel B, the initial state is near the attractor S^∗_A, i.e., P(S(1.0, 0.0), t = 0) = 1. Other parameters are the same as Fig. 1.

As time progresses and the landscape undergoes a change according to the bifurcation driven by the reduction of a₁ and a₂, the maximum probability is redistributed from the initial state S₀ = (1, 1) around the central attractor S^∗_C to the two marginal ones (Fig. 2 A). If we assume artificial asymmetry, namely, λ₁ = 0.01 and λ₂ = 0.015 for the sake of instructive fate commitment (26) (i.e., for a₂ decreasing faster than a₁, hence favoring the deepening of the attractor S^∗_B over that of S^∗_A), then the system tends to preferentially first occupy the attractor S^∗_B (x₂ >> x₁) after the bifurcation, as expected. This corresponds to a biased bifurcation and may represent the influence of specific fate-determining differentiation signals, such as Epo and G/CM-CSF in the case of myeloid progenitor cells (2,26), which introduce the symmetry breaking. However, stochasticity still plays a role in fate determination by instructive signals. In the model, after the landscape change has reached stationarity, noise-driven transitions between S^∗_A and S^∗_B equilibrate the two states. A similar scenario but with a different initial state, S₀ = (1, 0) (i.e., closer prospective site of the attractor S^∗_A; Fig. 2 B), will, under otherwise identical conditions, also end with a similar two-population steady state despite transient dominance of S^∗_B occupancy.

Transition between attractors-barrier height and transition dynamics

Although the computation in Figs. 1 and 2 exhibits spontaneous occupation of the two differentiation attractors S^∗_A and S^∗_B, this was achieved by the explicit directional change of the parameter a, in combination with noise-induced state transition. Thus, we have so far not formally demonstrated directionality. What prevents the circuit from noise-driven jumping, back from the differentiated states S^∗_A and S^∗_B, to the restored progenitor state S^∗_C? Time asymmetry at the scale of interattractor dynamics only exists if the noise-driven, nonphysiological back-transitions S^∗_A → S^∗_C (or S^∗_B → S^∗_C) are less probable than the physiological forward transitions S^∗_C → S^∗_A (or S^∗_C → S^∗_B).

To demonstrate the directionality of interattractor dynamics conferred by the noise-driven component, we calculated the relative probability for hopping between the stable branches at various parameter values a. The global potential landscape now offers a framework for comparing the relative stability of any state S(x), and hence, for computing the apparent height of the potential barriers U for individual transitions, such as the physiological transitions S^∗_C → S^∗_A (or S^∗_C → S^∗_B) versus the reverse transitions, S^∗_A → S^∗_C (or S^∗_B → S^∗_C). Fig. 3, A–C, shows the landscapes reflecting the barrier heights for various values of the parameter a around the bifurcation. From the link between barrier height and steady-state probability distribution of the states, we can then infer that lower potential basins correspond to larger cell populations while higher potential basins correspond to smaller populations.

Figure 3.

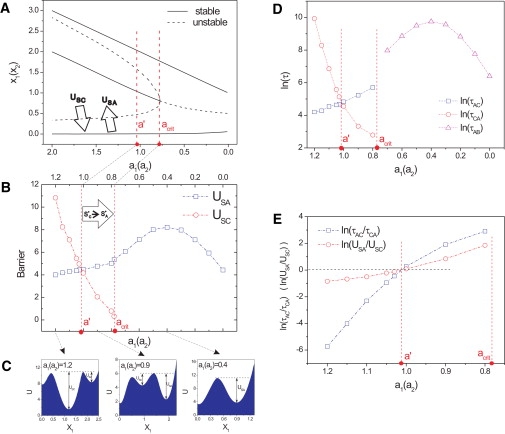
Relative barrier height as a function of parameter a accounts for directionality of state transitions around the bifurcation. (A) The bifurcation diagram for same parameters as in Fig. 1B with large arrows representing the transitions across the respective barriers U_SC and U_SA that separate the central stem cell attractors S^∗_C and the differentiated cell attractors S^∗_A and S^∗_B. (B) Computed heights of the barriers U_SC and U_SA as a function of a = a₁ = a₂ (for noise level D = 0.05). Here a_crit = bifurcation point, a′= value of a at which the relative barrier heights reverse. (C) Sections through the potential landscape illustrating the barriers at the three indicated values of a (dashed arrows). (D) The transitions mean first passage times τ for $S_C^{\ast }\to S_A^{\ast }$ (τ_CA) and S^∗_A → S^∗_C (τ_AC). (E) Direct comparison of U and τ as function of a: log-scale relative barrier heights or transition times for the transitions S^∗_A → S^∗_C and S^∗_C → S^∗_A, respectively. Other parameters are the same as Fig. 1.

The height of barriers between two attractors is defined here as follows: U_SC = U_saddle – U_C and U_SA = U_saddle – U_A. (Fig. 3 C). U_saddle is the potential at the saddle point between the two stable basins of attraction. U_C and U_A are the potentials at the minima for the attractors S^∗_C and S^∗_A, respectively. However, the relevant quantity for directionality is the observable average transition time for the transitions between the attractor states in forward (physiological) and backward (nonphysiological) directions, τ_CA and τ_AC, for the transitions S^∗_C → S^∗_A and S^∗_A → S^∗_C, respectively. Importantly, for a nonequilibrium system, there is in general no guarantee that the steady-state population ratio of cells in state S^∗_A (or S^∗_B) is related to the transition times between these states as in the equilibrium situation. Thus, we need to see if the relative barrier heights connected to the population ratio by definition is related to transition times. This relationship is expected to be true if in the relevant region, the gradient force dominates the flux force or they are perpendicular to each other. Fig. 4 shows (for a = 1) that the apparent barrier heights U decreased with increasing diffusion coefficient, reflecting the flattening of the landscape due to the fluctuations (Fig. 4 A)—as does the respective transition times reflecting the faster kinetics (Fig. 4 B)—corroborating the physical meaning of the computed barrier heights. In fact, the transition timescales monotonically with the barrier height U (Fig. 4, C and D); however, it increases sharply as barrier height exceeds some value (U > 10). Thus, U_SC < U_SA implies the directionality for the noise-driven transition S^∗_C → S^∗_A, suggesting that we can directly obtain information on directionality from the landscape topography. In other words, because the steady-state probability distribution is directly related to the underlying potential landscape, a shift of dominance of the center state S^∗_C to the outer state S^∗_A. (Fig. 3 C), supports the kinetic argument of time directionality from a steady-state perspective.

Figure 4.

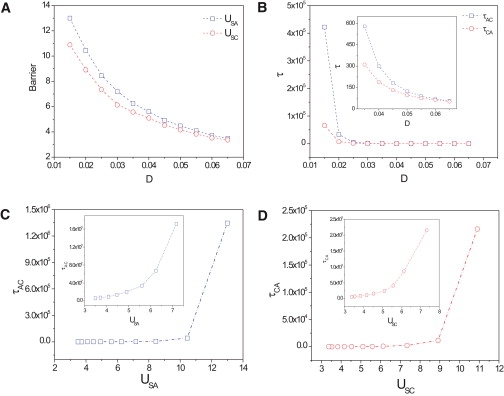
Dependence from the noise level D of barrier heights U and state transition times τ (A and B) and their equivalence (C and D), regime a = 1. The values τ_AC, τ_AB, and τ_CA denote the transition times (given a noise level D) for noise-driven transitions between the respective attractors, and U_SA and U_SC represent the barrier heights separating the respective attractors. Here a₁ = a₂ = 1 (other parameters the same as Fig. 1).

Note that for all values of D considered (D = 0.01–0.07) and parameter value a = 1, the barrier U_SC is substantially lower than the barrier U_SA and accordingly, τ_CA is shorter than τ_AC, confirming that the (S^∗_C → S^∗_A) transition is preferred over the (S^∗_A → S^∗_C) transition this regime. The difference does diminish as noise is increased to D > 0.05 (Fig. 4 B).

Transition around bifurcation: time directionality

To examine the robustness of directionality, a detailed analysis of U and τ for varying parameter a is needed. Doing so revealed a new critical point a′, not uncovered in standard bifurcation analysis, that delineates a regime just before loss of the attractor S^∗_C (namely from a′ (a′ > a_crit) down to a_crit) in which U_SC < U_SA, and therefore transition times, τ_CA < τ_AC. This provides a formal confirmation of the topographic intuition that the vanishing attractor basin of S^∗_C must flatten (Fig. 3, B–D). In this critical zone the relative barrier heights dictate the physiological directionality S^∗_C → S^∗_A. In other words, the critical zone (a′ > a > a_crit) in which U_SC < U_SA,SB and therefore transition times τ_CA < τ_AC holds, acts as a one-way filter protecting, to some extent, against temporary uncontrolled (noisy) reversal of the parameter a and guaranteeing the robustness of the arrow of time in noise and bifurcation-driven fate decision. However, at a > a′, deeper in the tristable regime, the relative barrier heights reverse, with U_SC > U_SA, favoring reverse transitions to the now much more stable multipotent state. Thus, only with very strong positive feedback (a > a′) can there be significant probabilistic spontaneous reverse differentiation. Interestingly, the transition time between differentiated cells in the postfate commitment bistable regime is, in general, higher than that for reverse differentiation to the progenitor state in tristable regime (Fig. 3 D).

We also note that the network system, in building its robustness, seems to evolve so as to minimize the dissipation cost to its stability, as characterized by the barrier heights and transition time between the basins. Therefore, minimization of the dissipation and increasing the barrier height might provide an evolutionary optimization principle for the network design.

These new dynamical features around the bifurcation point, obtained only by computing the quasipotential landscape, reveal the generic and intrinsic nature of a given gene circuit architecture. These novel properties help explain salient observations in stem cell control beyond directionality. The model presented here also defines the extreme conditions under which reversal of the arrow of time is possible, as epitomized in the reprogramming of differentiated cells back to a multi- or pluripotent state. They predict the extreme conditions needed for reverse differentiation as recently achieved in the reprogramming of differentiated cells into an embryonic stem-cell-like induced pluripotent state (59). This procedure requires first the simultaneous overexpression of the mutually regulating genes X₁ and X₂, embodied by Oct4 and Nanog, which are critical to maintain the pluripotent state. This corresponds to resetting of the S^∗_C state. But second, ectopic expression of a third TF, Klf4, is also needed. Klf4 binds to the promoter region of Oct4 and Nanog and has been suggested to enhance the transcriptional self-stimulation autoregulation of Nanog (60,61). Thus, Klf4 would specifically increase autoregulation, corresponding to increasing a, which the theory predicts is needed to reverse the directionality filter around the bifurcation. In addition, deep in the stem cell regime when the autostimulation is strong (a >> a′) the pluripotent state behaves, in fact, like a robust attractor (62,63). However, as predicted by our model, it can also visit distinct, detectable, short-lived precommitment states characterized by low Nanog (52), and may—at least with respect to the Nanog state space dimension—correspond to states S^∗_A or the S^∗_B that exist in this regime (a >> a′) but are metastable.

Conclusions

Our potential landscape analysis here adds a new dimension to the standard dynamical system analysis. This information pertains to the probability for noise-induced transitions between various attractors crucial for the differentiation and developmental process. We show that a change in a control parameter is not only important for bifurcations but also leads to directionality (of spontaneous processes given some level of noise). This explains one-way process of stem cell differentiation not achieved by standard dynamical system analysis.

The canonical gene circuit discussed here (Fig. 1) where the master transcription factors X₁ and X₂ inhibit each other and positively regulate their own repression, appears to be a general network motif that controls binary branch points of cell lineage commitment during development. Examples of X₁-X₂ pairs (where the positive autoregulation can also be indirect) are widespread and include GATA1-PU.1, PU.1-C/EBP, C/EBP-cJun, Egr2-Gfi1, Runx2-Sox9; Oct4-Cdx2, Nanog-Gata6, and Sox2-Oct4 (61,51,50). Although we discussed the dynamics of one individual circuit, eukaryotic gene regulatory circuits are, in reality, coupled to each other, forming genomewide networks whose dynamics remains to be studied. But they certainly will generate more complex potential landscapes that will be manifested in the multilevel succession of branching valleys, as Waddington depicted in his famous 1957 picture of an epigenetic landscape (36).

The self-activation loops, implemented by nonzero value of the parameter a in Eq. 1, are essential to locally stabilize the undecided state of indeterminacy which is characterized by the coexpression at intermediate low levels of the opposing lineage-determining factors X₁ and X₂ and to ensure that this poised state is an attractor state and not an unstable equilibrium state (26). Such promiscuous expression of opposing fate-determining transcription factors is a hallmark of multipotency (49). In fact, the multipotent stem cell is, given not too-intense noise, a self-maintaining metastable entity and has metaphorically been dubbed a ground state (63). Importantly, our potential landscape computation shows that near the bifurcation point where this central attractor disappears it has a higher potential level than the differentiated states. This explains the familiar general tendency of embryonic stem or progenitor cells to eventually differentiate-away in random directions when conditions are not optimized for maintaining “stemmedness” despite the ground state character (63).

Recent experiments show that disabling P53, an essential tumor-suppressor protein, improves the efficiency of stem-cell production, implying the fundamental similarity between cancer and stem cells regulated through some common regulators (64). The landscape here may not only provide a new global picture and quantitative model in understanding stem-cell development but also a possible physical origin of cancer: the stem, cancer, and normal cells can all be thought of as states of the gene network and thus cancer cells result from regulation rather than gene mutation alone (65–67). In the normal condition, the differentiated cells are more stable, with lower basins than stem or cancer cells (see Fig. 3 C; in our example, S^∗_A, _B at self-regulating wiring strength a < a′), which have higher basins of attraction (S^∗_C at a < a′). When the environment changes, and affects certain wiring strengths (at a > a′), the stem or cancer state S^∗_C can become more stable than the normal state S^∗_A, _B. Now stem or cancer states have a higher chance of occurring. The increasing elevation of cancer attractor cells is the formal basis of differentiation therapy of cancer. Although the drug industry is engaged in developing the differentiation therapy of cancer based on observations of rare spontaneous differentiation (which could be explained by the exit from the cancer state due to stochastic state transitions), it is worthwhile to point out that this may be a too-simplistic view—because effective therapy can only be achieved if all cells can be stimulated to undergo the state transition.

We want to stress the importance of our specific analysis of the gene circuitry, upon which we apply the potential landscape approach. This type of analysis has, since the submission of our manuscript, been popularized among stem cell biologists (68,69). However, those discussions do not provide a formal and quantitative explanation of the landscape. As our knowledge of gene network architectures increases, the computation of their potential landscape should become an integral part of analyzing these networks—inasmuch as such computation exposes inherent phenotypic behaviors encoded by the network that are not uncovered by traditional dynamical system analysis.

Supporting Material

Eleven equations and one figure are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00424-8.