Cell Segmentation Using Front Vector Flow Guided Active Contours

Abstract

Phase-contrast microscopy is a common approach for studying the dynamics of cell behaviors, such as cell migration. Cell segmentation is the basis of quantitative analysis of the immense cellular images. However, the complicated cell morphological appearance in phase-contrast microscopy images challenges the existing segmentation methods. This paper proposes a new cell segmentation method for cancer cell migration studies using phase-contrast images. Instead of segmenting cells directly based on commonly used low-level features, e.g. intensity and gradient, we first identify the leading protrusions, a high level feature, of cancer cells. Based on the identified cell leading protrusions, we introduce a front vector flow guided active contour, which guides the initial cell boundaries to the real boundaries. The experimental validation on a set of breast cancer cell images shows that the proposed method demonstrates fast, stable, and accurate segmentation for breast cancer cells with wide range of sizes and shapes.

1 Introduction

Cell migration plays pivotal roles in cancer cell scattering, tissue invasion, and metastasis. Metastasis is a major cause of morbidity and mortality in most of cancer patients [1]. For breast cancer, five-year relative survival in local invasive breast cancer patients is 98.1%, whereas it is only 26% in patients with distant metastases in USA [2]. These dismal prognoses can be partly explained by the fact that a large majority of the drugs used today to treat cancer are pro-apoptotic, but migrating cells involved in metastases are known to show a decreased proliferation rate and are thus less sensitive to such chemotherapy. Thus the anti-migration drugs hold great promise for both anti-metastasis therapy and increasing the efficacy of the existing pro-apoptotic anti-cancer drugs. Phase-contrast microscopy is a common tool for study of dynamic behaviors of a population of cells under different treatments [3]. However, the complicated cell morphological appearance and the low signal to noise ratio (SNR) of the phase-contrast images, as seen in Figure 1, challenge the existing segmentation methods, new segmentation methods are needed.

Fig. 1.

Two representative MDA-MB231 breast cancer cell images (column-(a)), the MIP images of the multi-scale LoG filtered original images for bright region detection (column-(b)), the MIP images of the multi-scale LoG filtered complemented images for dark region detection (column-(c)), and the cell body detection results (column-(d)). The green, blue and red curves imposed on the cell images indicate the boundaries of the detected bright regions, dark regions and cell centers respectively.

Although a number of cell segmentation methods have been proposed, cell segmentation remains an open problem [4]. For example, thresholding methods [5] cannot accurately separate cells from background because regions inside cells often have similar intensity as the background in the phase-contrast image. Voronoi based methods can only estimate the rough regions of cells [6]. Watershed methods assume that the edges (watersheds) have the maximum intensity (or maximum gradient) between two cells [7]; however, it is not always true. Graph cut based methods are robust to weak boundaries. Nevertheless, they require closed boundaries [8]. Active contours has two kinds of methods: region based [9] and edge based [10]. The region based active contours are robust to the initial boundaries and fast, but they always require that the intensity of objects is homogenous and different with background [9]. The edge based active contours are sensitive to the initial boundaries and a set of parameters. The evolution of contours may stop before reaching the real boundaries or pass through the real boundaries, without good initial boundaries or well-tuned parameters.

The limitation of above methods, which do the segmentation directly based on low-level features, e.g. intensity and gradient, is that they all assume the edges or regions inside objects have simple, distinct features, e.g. large gradient or homogenous intensity. In practice, we cannot distinct the real boundaries with other features by assuming clear cut gradient or homogenous intensity information. In this paper, we propose to segment cancer cells in phase-contrast images by introducing a high-level feature, fronts (leading protrusions), as seen in Figure 1. We identify the cell fronts first and then introduce the front vector flow to direct the active contours unambiguously to where the real boundaries are. We name this method as front vector flow guided active contour.

2 Methods

2.1 Problem Description

We provide two representative phase contrast cell images of living breast cancer cells MDA-MB231 in the column-(a) of Figure 1. We can see that 1) the cell centers have two distinct regions with lower (dark region) and higher intensity (bright region), 2) the leading protrusions of cells is far away from the cell centers and has non-closed arc shape, see the ridge-like structures, 3) the regions between the cell centers and leading protrusions have similar intensity as the background. The first property enables us to detect the cell bodies easily by detecting the two regions, which can be used as the initial boundaries of cells. However, the second and third properties make the segmentation very challenging. For example, the evolution of cell boundaries using edge-based active contours [10] will stop near the cell centers due to the rapid intensity variation, or easily go outside the cells due to the non-closed leading protrusions and the regions that have homogenous intensity as the background. To deal with these challenges, we proposed the following method of front vector flow guided active contour.

2.2 Front Vector Flow Guided Active Contour

The proposed front vector flow guided active contour method consists of the following steps: 1) cell center detection, 2) front (leading protrusions) detection, and 3) contour evolution following the front vector flow.

A. Cell center detection

To detect the cell center, we first detect the dark and bright regions inside cells respectively, and then combine the detection results together, as seen in Figure 1. In this paper, we make use of the multi-scale representation to detect the bright regions [11]. Specifically, we filter the original image using a series of Laplacian of Gaussian (LoG) filters with different scales, i.e., the σ s of Gaussians. Then the maximum intensity projection (MIP) image of the filtered image is generated, and we use a three-class fuzzy c-means clustering [12] method to detect the bright regions accurately, as seen in the column-(b) of Figure 1. Since a dark region can be viewed as a bright region in the complemented cell image, we can detect it using the same method, as seen in the column-(c) of Figure 1. Finally, we employ the convex hull operation to obtain the cell center, as seen in the column-(d) of Figure 1.

B. Front detection

The first stage of cell migration consists of initial cell polarization caused by localized actin polymerization to form filaments, and this is followed by the extension of cytoplasmic protrusions. The quantitative analysis of the cytoplasmic protrusion formation, disappearance, and variation is important for studies of cell migration. Considering the ridge shape of fronts, we detect the cell fronts using the curvilinear structure detectors [13, 14].

For a 1D ridge profile, f (x) = c if |x|≤b, and f (x) = 0 otherwise, we can detect the center point of f (x) using the criterion: k′ (x, σ) = 0, and k″ (x, σ) ≪ 0, where $k\prime (x,\sigma )=c\sqrt{\sigma }\left(g(x+b,\sigma )-g(x-b,\sigma )\right)$, k″ (x, σ) = cσ(g′(x + b, σ) − g′(x − b, σ)), and g(x, σ), g′(x, σ) represent the Gaussian density function and its derivative respectively. For ridge profiles with different width, we can use a series of scales (multiscale) to let k″ (x, σ) reaches its maximum value. In discrete case, a point x_n is labeled as center point, if $\stackrel{t=-\sqrt{{\sigma }_n^{\ast }}{\times }^{k\text{'}\left(x_n,{\sigma }_n^{\ast }\right)}}{}/\underset{k"\left(x_n,{\sigma }_n^{\ast }\right)}{}\in [-\frac{1}{2},\frac{1}{2}]$, and $|k"\left(x,{\sigma }_n^{\ast }\right)|$ is larger than a given threshold, where σ_n* = arg min_σ {k″ (x_n, σ)}.

It is straightforward to extend the method to 2D space because the cross-section of the 2D ridge profile in direction perpendicular to ridge center line is a 1D ridge profile. The eigenvector, (n_x, n_y), which corresponds to the minimum eigen-value, λ_x,y, of the Hessian matrix at a given point (x, y), indicates the cross-section direction at that point. In a 2D discrete case, a point is labeled as a center point if |λ_x,y| is larger than a given threshold, and the following equation holds:

$$(t{n}_x,t{n}_y)\in [-1/2,1/2]\times [-1/2,1/2]$$ (1)

where $t=-\frac{k_x({\sigma }_{x,y}^{\ast })n_x+k_y({\sigma }_{x,y}^{\ast })n_y}{k_{xx}({\sigma }_{x,y}^{\ast })n_x^2+2k_{xy}({\sigma }_{x,y}^{\ast })n_x{n}_y+k_{yy}({\sigma }_{x,y}^{\ast })n_y^2}$, k_x, k_y, k_xx, k_xy and k_yy are the normalized partial derivatives of 2D cellular images convolved with 2D Gaussian kernels, and ${\sigma }_{x,y}^{\ast }=arg,{min}_{\sigma }{\lambda }_{x,y}(x,y;\sigma )$. To remove the false center points, the hysteresis thresholding technique is employed, and then a link process links the broken center lines together [14]. The detected cell front is represented by a binary image, as seen in Figure 2-(e).

Fig. 2.

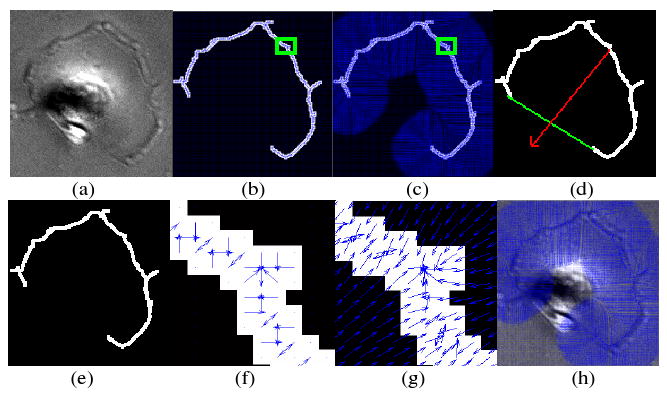
An illustration of the front vector flow. (a) Original cell image, (e) detected front image, (b) gradient vectors, (c) front vector flow, (f) zoom in image of the green square in (b), (g) zoom in image of the green square in (c), (d) the red arrow, which is obtained by linking the midpoints of the front and the chord linking two endpoints of the front, points to the corresponding cell center, and (h) the front vector flow was imposed on the original cell image. The blue arrows represent the gradient vectors.

C. Contour evolution following the front vector flow

After obtained the cell centers and fronts, we still cannot obtain the accurate cell boundaries because the regions that locate between cell centers and the fronts are missed. To obtain the accurate boundaries, we propose to evolve the initial cell boundaries (the boundaries of the cell centers) to the real boundaries following the front vector flow.

We calculate the front vector flow as in the following:

$${\widehat{\mathbf{\text{V}}}}_{\mathbf{\text{fvf}}}=\underset{\mathbf{\text{V}}}{min}\iint \mu \left(u_x^2+u_y^2+v_x^2+v_y^2\right)+{\left|\nabla {\mathit{\text{I}}}_{\mathbf{\text{f}}}\right|}^2\left|\mathbf{\text{V}}-\nabla {\mathit{\text{I}}}_{\mathbf{\text{f}}}\right|\mathit{\text{dxdy}},$$ (2)

where, I_f represents the detected cell front image; $\nabla I_{\mathbf{\text{f}}}=\langle \frac{\partial }{\partial x}{I}_{\mathbf{\text{f}}},\frac{\partial }{\partial y}{I}_{\mathbf{\text{f}}}\rangle$ denotes the gradient of the detected front image; and V = 〈u(x, y), v(x, y)〉 is the front vector flow. Figure 2 illustrates the relationship between the gradient and the front vector flow. As we can see, the front vector flow extends the gradient vector to a large region and converges to the detected front [15], as seen in Figure 2-(b), (c), (f), and (g). This motivates us to evolve the initial cell boundaries along with the front vector flow to reach the real boundaries. A problem is posed that the front vector flow may attract initial cell boundaries of different cells to one front. To avoid this, we associate each front with its corresponding cell uniquely using the convex property (arc shape) of the fronts, as seen in Figure 2(d). The red arrow, which is obtained by linking the midpoints of the front and the chord linking two endpoints of the front points, points to the corresponding cell. Thus we can find the corresponding cell along the direction of the red arrow, and evolve its initial boundary following the front vector flow of the front.

The contour evolution process along with front vector flow can be easily implemented under the active contour (level set) framework. The mathematical evolution equation is as follows.

$$\frac{d}{dt}\psi =-\left({\widehat{V}}_{\mathbf{\text{fvf}}}\cdot \nabla \psi \right)+\beta \kappa \left|\nabla \psi \right|,$$ (3)

where ψ denotes the level set function, κ is the curvature, and β is the parameter that controls the smoothness of the boundary. This equation is straightforward and robust because the only parameter β, which controls the smoothness of the contour, will not influence the evolution much.

$$\kappa =\mathit{\text{div}}\left(\frac{\nabla \psi }{\left|\nabla \psi \right|}\right)+\frac{{\psi }_{xx}{\psi }_y^2-2{\psi }_x{\psi }_{xy}{\psi }_y+{\psi }_x^2{\psi }_{yy}}{{\left({\psi }_x^2+{\psi }_y^2\right)}^{3/2}},$$ (4)

3 Experiments and Results

The MDA-MB231 breast cancer cell line was grown in Dulbecco's Modified Eagle's Medium (DMEM) containing 10% fetal bovine serum. Cell cultures were maintained in a humidified incubator at 37C, with 5% CO2. Images of cells were acquired in phase contrast mode of a FluoView™ FV1000 laser scanning confocal microscope (Olympus) using a 20× objective. We selected 50 cells and manually segmented them as the ground truth. To validate the performance of the proposed front vector flow guided (FVF) active contour method, we compared it with two kinds of widely used active contours: edge-based geodesic active contour (GAC) [10], region based Chan and Vese active contour (CV) [9], and the manually analyzed ground truth. The goal of the comparison is merely to show the robustness of the proposed method, which can handle the intensity variation and prevent the contour from leaking. GAC and CV are two widely used methods, which have been tested in certain phase contrast images. Therefore, we chose them for comparison. Both GAC and CV methods could be adapted by incorporating the front detection. However, it is not trivial, and instead we propose the new method that is straightforward and fast. In this validation, the active contour (level set) evolution equation of GAC and CV are as: $\frac{d}{dt}\psi =\alpha \left(\nabla g\cdot \nabla \psi \right)+g\left(\kappa +c\right)\left|\nabla \psi \right|,\frac{d}{dt}\psi ={\delta }_{\epsilon }(\psi )\left[\mu \cdot \kappa -\nu -{\lambda }_1{\left(I-c_1\right)}^2+{\lambda }_2{\left(I-c_2\right)}^2\right]$ Table 1 lists the detailed parameters settings of the three methods (GAC, CV, and FVF). Figure 3 shows the comparison among GAC, CV, FVF and manual segmentation results. The boundaries of cell centers, as seen in Figure 1-(d), were used as the initial boundaries, and the stopping criterion is setting a maximum iteration number. As we can see, the edge leaks outside of cells in the results of GAC due to the non-closed cell fronts. The CV method works like a threshold method that only separates the bright regions from the background and dark regions. Whereas, the proposed FVF method delineates the cell boundaries accurately compared with the ground truth. To quantitatively analyze the accuracy of the segmentation, we employed following two error measures: false positive rate, FPR = (S_A − S_M)/S_M, and false negative rate, FNR = (S_M − S_A)/S_M, where S_M means the manual segmentation result and S_A means the automated segmentation results. The average FPRs of GAC, CV and FVF are as: 27.8%, 0%, and 7.8%, while the average FNRs are as: 15.6%, 63.5%, and 6.7%. The results indicate that the propose FVF method demonstrates accurate segmentation results compared with the ground truth, while the GAC and CV results are not reliable. The computational complexity is also important for segmentation methods. In Table 2, we compared the computational complexity of the three methods in terms of number of iterations and computational time. We implemented the three methods in Matlab (version 2007), and the comparison were did on a standard desktop PC (Intel core 2, 1.86 GHz). The CV method is the fastest, and the FVF method has similar complexity as the CV method. However, the computational complexity of the GAC method increased rapidly. In conclusion, the proposed FVF method is fast, stable, and accurate compared with the GAC and CV methods.

Table 1.

Parameters settings of the GAC, CV and FVF active contours

	Parameter setting
GAC	dt = 0.05, c = 1, α = 0.2
CV	dt = 0.1, λ1 = 1, λ2 = 1, μ = 0, v = −65
FVF	dt = 0.1, β = 1

Fig. 3.

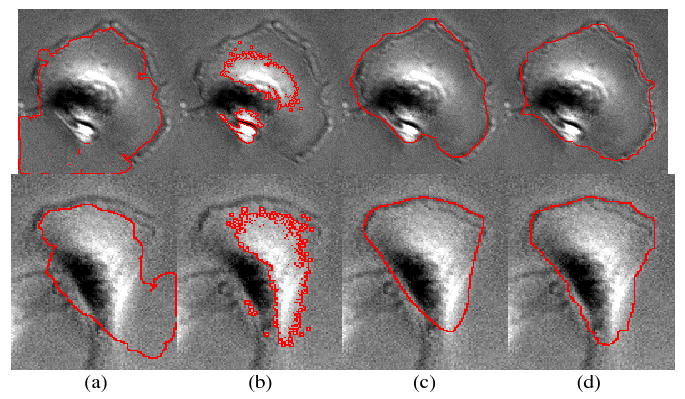
Comparison of segmentation results. (a) Segmentation results of GAC, (b) segmentation results of CV, (c) segmentation results of FVF, and (d) manual segmentation results.

Table 2.

Computational complexity comparison in terms of number of iteration and time

	GAC		CV		FVF
	Img1	Img2	Img1	Img2	Img1	Img2
# of iteration	400	400	400	400	40	40
time (seconds)	240	210	11	8	18	11

4 Discussion and Conclusions

In this paper, we propose a new method for segmenting breast cancer cell images obtained by phase-contrast microscopy. The segmentation method takes advantage of the prior knowledge that the leading protrusion in cancer cells is a distinct high-level feature of cell boundaries compared to the commonly used low-level features such as edge gradient or cell intensity. Thus we propose to identify the protrusions first, which tell the segmentation algorithms clearly where the real boundaries are, and then introduce the front vector flow and implement the cell segmentation in the framework of active contour. The initial cell boundaries, which are obtained after the cell center detection, are attracted to the real edges following the front vector flow. The proposed method deals with the aforementioned challenges existing in the phase-contrast images well. The algorithm is fast, stable, and accurate compared with the manually segmented ground truth and is used to segment large amounts of breast cancer cells in the phase-contrast images of our high content screening studies. One limitation of the proposed method is the requirement of the accurate boundary detection results. It may fail when the noise or inaccurate boundary detection results exist. To improve the proposed method, we may integrate the edge detection and vector flow into active contour methods.

Although designed for breast cancer cells in phase contrast images, it is possible to generalize the proposed algorithm, including the cell center detection, front detection, and contour evolution, to other applications. For example, the center detection and front detection can be generalized to the blob and ridge structure detection in other biomedical images, e.g. nuclei and neurite images. For the contour evolution, it can be customized to other applications where part of boundaries of objects can be identified. In the future work, we will extend the proposed segmentation method for tracking live cancer cells in phase-contrast image movies.