Loss Function Based Ranking in Two-Stage, Hierarchical Models

Abstract

Performance evaluations of health services providers burgeons. Similarly, analyzing spatially related health information, ranking teachers and schools, and identification of differentially expressed genes are increasing in prevalence and importance. Goals include valid and efficient ranking of units for profiling and league tables, identification of excellent and poor performers, the most differentially expressed genes, and determining “exceedances” (how many and which unit-specific true parameters exceed a threshold). These data and inferential goals require a hierarchical, Bayesian model that accounts for nesting relations and identifies both population values and random effects for unit-specific parameters. Furthermore, the Bayesian approach coupled with optimizing a loss function provides a framework for computing non-standard inferences such as ranks and histograms.

Estimated ranks that minimize Squared Error Loss (SEL) between the true and estimated ranks have been investigated. The posterior mean ranks minimize SEL and are “general purpose,” relevant to a broad spectrum of ranking goals. However, other loss functions and optimizing ranks that are tuned to application-specific goals require identification and evaluation. For example, when the goal is to identify the relatively good (e.g., in the upper 10%) or relatively poor performers, a loss function that penalizes classification errors produces estimates that minimize the error rate. We construct loss functions that address this and other goals, developing a unified framework that facilitates generating candidate estimates, comparing approaches and producing data analytic performance summaries. We compare performance for a fully parametric, hierarchical model with Gaussian sampling distribution under Gaussian and a mixture of Gaussians prior distributions. We illustrate approaches via analysis of standardized mortality ratio data from the United States Renal Data System.

Results show that SEL-optimal ranks perform well over a broad class of loss functions but can be improved upon when classifying units above or below a percentile cut-point. Importantly, even optimal rank estimates can perform poorly in many real-world settings; therefore, data-analytic performance summaries should always be reported.

1 Introduction

Performance evaluation burgeons in many areas including health services (Goldstein and Spiegelhalter 1996; Christiansen and Morris 1997; Normand et al. 1997; McClellan and Staiger 1999; Landrum et al. 2000, 2003; Daniels and Normand 2006; Austin and Tu 2006), drug evaluation (DuMouchel 1999), disease mapping (Devine and Louis 1994; Devine et al. 1994; Conlon and Louis 1999; Wright et al. 2003; Diggle et al. 2006), and education (Lockwood et al. 2002; Draper and Gittoes 2004; McCaffrey et al. 2004; Rubin et al. 2004; Tekwe et al. 2004; Noell and Burns 2006). Goals of such investigations include valid and efficient estimation of population parameters such as average performance (over clinics, physicians, health service regions or other “units of analysis”), estimation of between-unit variation (variance components) and unit-specific evaluations. The latter includes estimating unit specific performance, computing the probability that a unit's true, underlying performance is in a specific region, ranking units for use in profiling and league tables (Goldstein and Spiegelhalter 1996), identification of excellent and poor performers.

Bayesian models coupled with optimizing a loss function provide a framework for computing non-standard inferences such as ranks and histograms and producing data-analytic performance assessments. Inferences depend on the posterior distribution, and how the posterior is used should depend on inferential goals. Gelman and Price (1999) showed that no single set of estimates can simultaneously optimize loss functions targeting the unit-specific parameters (e.g, unit-specific means, optimized by the posterior mean) and those targeting the ranks of these parameters. For example, as Shen and Louis (1998) and Liu et al. (2004) showed, ranking the unit-specific maximum likelihood estimates (MLEs) performs poorly as does ranking Z-scores for testing whether a unit's mean equals the population mean. In some situations, ranking the posterior means of unit-specific parameters can perform well, but in general an optimal approach to estimate ranks is needed.

In the Shen and Louis (1998) approach, SEL operates on the difference between the estimated and true ranks. But, in many applications interest focuses on identifying the relatively good (e.g., in the upper 10%) or relatively poor performers, a down/up classification. For example, quality improvement initiatives should be targeted at health care providers that have the highest likelihood of being the poorest performers; geography-specific, environmental assessments should be targeted at the most likely high incidence locations (Wright et al. 2003); genes with differential expression in the top 1% (say) should be selected for further study.

We construct new loss functions that focus on down/up classification and derive the optimizers for a subset of them. We develop connections between the new optimizers and others in the literature; report performance evaluations among the new ranking methods and other candidates; identify appropriate uncertainty assessments including a new performance measure. We evaluate performance for a fully parametric hierarchical model with unit-specific Gaussian sampling distributions and assuming either a Gaussian or a mixture of Gaussians prior. We evaluate performance and robustness under the prior and loss function that was used to generate the ranks as well as under other priors and loss functions. Shen and Louis (1998) showed that when the posterior distributions are stochastically ordered, maximum likelihood estimate based ranks, posterior mean based ranks, SEL-optimal ranks and those based on most other rank-specific loss functions are identical. We report performance assessments for the stochastically ordered case and compare approaches for situations when the posterior distributions are not stochastically ordered. We illustrate approaches using Standardized Mortality Ratio (SMR) data from the United States Renal Data System (USRDS).

2 The two-stage, Bayesian hierarchical model

We consider a two-stage model with independent identically distributed (iid) sampling from a known prior G with density g and possibly different unit-specific sampling distributions f_k:

$$\begin{array}{c}\hfill {\theta }_1,\dots ,{\theta }_K\mathit{\text{iid}}G({\theta }_k),k=1,\dots ,K\hfill \\ \hfill Y_k|{\theta }_k\sim f_k(Y_k|{\theta }_k).\hfill \end{array}$$ (1)

From model (1) we can derive the independent (ind) posterior distributions for Bayesian inferences:

$$[{\theta }_k|Y_k]\mathit{\text{ind}}{g}_k({\theta }_k|Y_k)=\frac{f_k(Y_k|{\theta }_k)g({\theta }_k)}{{\displaystyle \int f_k(Y_k|u)g(u)du}}.$$

For computing efficiency, we assume that the θs are iid, though model (1) can be generalized to allow a regression structure in the prior and extended to three stages. Our theoretical results hold for these more general situations.

2.1 Loss functions and decisions

Let θ = (θ₁ ,…, θ_K) and Y = (Y₁, …, Y_K). For a loss function L(θ, a), the optimal Bayesian a(Y) minimizes the posterior Bayes risk,

$${\text{Risk}}_G(\mathbf{a}(\mathbf{Y}),\mathbf{Y})={\mathrm{E}}_{\mathbf{\theta }|\mathbf{Y}}[L(\mathbf{\theta },\mathbf{a}(\mathbf{Y}))|\mathbf{Y}],$$

and thereby the pre-posterior risk

$${\text{Risk}}_G(\mathbf{a})={\mathrm{E}}_{\mathbf{Y}}[{\text{Risk}}_G(\mathbf{a}(\mathbf{Y}),\mathbf{Y})].$$

Also, for any a(Y) we can compute the frequentist risk:

$$\text{Risk}(\mathit{\theta },\mathbf{a}(·))={\mathrm{E}}_{\mathbf{Y}|\mathit{\theta }}[L(\mathit{\theta },\mathbf{a}(\mathbf{Y}))|\mathit{\theta }].$$

3 Ranking

Laird and Louis (1989) represented the ranks by,

$$R_k(\mathit{\theta })=\text{rank}({\theta }_k)={\displaystyle \sum _{j=1}^K{I}_{\{{\theta }_k\ge {\theta }_j\}}},$$ (3)

with the smallest θ having rank 1 and the largest having rank K. The non-linear form of (3) implies that, in general, the optimal ranks are neither the ranks of the observed data nor the ranks of the posterior means of the θs. A loss function is necessary to formalize developing estimates and related uncertainties.

3.1 Squared-error loss (SEL)

Square error loss (SEL) is the most common loss function used in estimation. It is optimized by the posterior mean of the target parameter. For example, under the model (1), with the unit-specific θs as the target, the loss function is L(θ, a) = (θ – a)² and the optimal estimator is posterior mean (PM) ${\theta }_k^{pm}=E({\theta }_k|\mathbf{Y})$.

When ranks are the target, producing SEL-optimal ranks by minimizing

$$\widehat{L}=\widehat{L}({\mathbf{R}}^{\mathbf{\text{est}}},R(\mathbf{\theta }))=\frac{1}{K}{\displaystyle \sum _k{(R_k^{\mathit{\text{est}}}-R_k(\mathbf{\theta }))}^2}$$ (4)

and setting $R_k^{\mathit{\text{est}}}$ equal to,

$${\overline{R}}_k(\mathbf{Y})=E_{\theta |\mathbf{Y}}[R_k(\theta )|\mathbf{Y}]={\displaystyle \sum _{j=1}^K\text{pr}({\theta }_k\ge {\theta }_j|\mathbf{Y}).}$$ (5)

The R̄_k are shrunk towards the mid-rank (K + 1)/2, and generally are not integers (Shen and Louis 1998). Optimal integer ranks are reached by

$${\widehat{R}}_k(\mathbf{Y})=\text{rank}({\overline{R}}_k(\mathbf{Y})).$$ (6)

See Section Appendix A for additional details on producing optimal ranks under weighted SEL.

3.2 Notation

Henceforth, we drop dependency on θ and omit conditioning on Y whenever this does not cause confusion. For example, R_k stands forR_k(θ) and R̂_k stands for R̂_k(Y). Furthermore, use of the ranks facilitates notation in mathematical proofs, but percentiles

$$P_k=R_k/(K+1);{\widehat{P}}_k={\widehat{R}}_k/(K+1),\text{etc}.$$ (7)

normalize large sample performance and aid in communication. For example, Lockwood et al. (2002) showed that mean square error (MSE) for percentiles rapidly converges to a function that does not depend on K; the same normalization strategy applies in the loss functions below.

4 Upper 100(1 − γ)% loss functions

L ^(Equation 4) evaluates general performance without specific attention to identifying the relatively well or poorly performing units. To attend to this goal, for 0 < γ < 1 we investigate loss functions that focus on identifying the upper 100(1 − γ)% of the units, with loss depending on the correctness of classification and, possibly, a distance penalty; identification of the lower 100γ% group is similar. For notational convenience, we assume that γK is an integer, so γ(K + 1) is not an integer and in the following it is not necessary to distinguish between (>, ≥) or (<, ≤).

4.1 Summed, unit-specific loss functions

For 0 < γ < 1, let

$$\begin{array}{c}{\mathit{\text{AB}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})=I_{\{P_k>\gamma ,P_k^{\mathit{\text{est}}}<\gamma \}}=I_{\{R_k>\gamma (K+1),R_k^{\mathit{\text{est}}}<\gamma (K+1)\}},\hfill \\ {\mathit{\text{BA}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})=I_{\{P_k<\gamma ,P_k^{\mathit{\text{est}}}>\gamma \}}=I_{\{R_k<\gamma (K+1),R_k^{\mathit{\text{est}}}>\gamma (K+1)\}.}\hfill \end{array}$$ (8)

AB_k and BA_k indicate the two possible modes of misclassification. AB_k indicates that the true percentile is above the cutoff, but the estimated percentile is below the cutoff. Similarly, BA_k indicates that the true percentile is below the cutoff while the estimated percentile is above it.

For p, q, c ≥ 0 define,

$$\begin{array}{cc}\tilde{L}(\gamma ,p,q,c)\hfill & =\frac{1}{K}{\displaystyle \sum _k\{|\gamma -P_k^{\mathit{\text{est}}}{|}^p{\mathit{\text{AB}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})+c|P_k^{\mathit{\text{est}}}-\gamma {|}^q{\mathit{\text{BA}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})\},}\hfill \\ L^{†}(\gamma ,p,q,c)\hfill & =\frac{1}{K}{\displaystyle \sum _K\{|P_k-\gamma {|}^p{\mathit{\text{AB}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})+c|\gamma -P_k{|}^q{\mathit{\text{BA}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})\},}\hfill \\ L^{‡}(\gamma ,p,q,c)\hfill & =\frac{1}{K}{\displaystyle \sum _k\{|P_k-P_k^{\mathit{\text{est}}}{|}^p{\mathit{\text{AB}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})+c|P_k^{\mathit{\text{est}}}-P_k{|}^q{\mathit{\text{BA}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})\},}\hfill \\ \hfill L_{0/1}(\gamma )& =\frac{{\displaystyle {\sum }_k\{{\mathit{\text{AB}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})+{\mathit{\text{BA}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})\}}}{K}=2\frac{{\displaystyle {\sum }_k{\mathit{\text{AB}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})}}{K}\hfill \\ \hfill & =\frac{\#(\text{misclassifications})}{K}=\tilde{L}(\gamma ,0,0,1)=L^{†}(\gamma ,0,0,1)=L^{‡}(\gamma ,0,0,1).\hfill \end{array}$$ (9)

The loss functions confer no penalty if the pair of estimated and true unit-specific percentiles, $(P_k^{\mathit{\text{est}}},P_k)$, are either both above or both below the γ cut point. If they are on different sides of γ, L̃ penalizes by an amount that depends on the distance of the estimated percentile from γ, L^† by the distance of the true percentile from γ and L^‡ by the distance between the true and estimated percentiles. Parameters p and q adjust the intensity of the penalties; p ≠ q and c ≠ 1 allow for different penalties for the two kinds of misclassification. L_0/1(γ) counts the number of discrepancies and is equivalent to setting p = q = 0, c = 1; we use the relation ${\displaystyle {\sum }_k{\mathit{\text{AB}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})={\displaystyle {\sum }_k{\mathit{\text{BA}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}}})}$ in its definition. In practice, L^† and L^‡ would be harder to use than L̃ because their penalizing quantities depend on unknown P_k. However, inclusion of them in our investigation does help to calibrate the robustness of other estimators.

Our mathematical analyses apply to the general loss functions (9), but our simulations are conducted for p = q = 2, c = 1. Within this setting, we denote the first three loss functions in (9) as L̃(γ), L^†(γ) and L^‡(γ).

We do not investigate the “all or nothing, experiment-wise” loss function with zero loss, when all units are correctly classified as above γ or below γ and penalty 1 if any unit is misclassified. While this loss function is one of the most fundamental and provides framework in many multiple comparison methods, it does not provide a good guideline in our ranking problem. Finding the optimal classification is challenging in computation and there will be many nearly optimal solutions. Furthermore, in the spirit of computing the false detection rate, loss functions that compute average performance over units or a subset of units are more appropriate in most applications.

5 Optimizers and other candidate ranks

We find ranks/percentiles that optimize L_0/1 and L̃ and study an estimator that performs well for L^‡, but is not optimal. First, note that optimizers for the loss functions in (9) and L̂ are equal when the posterior distributions are stochastically ordered (the G_k(t | Y_k) never cross). So, in this case P̂_k, which minimizes L̂ (see equations (4), (6) and (7)), is optimal for a broad class of loss functions (see Theorem 4). Also, it is straightforward to show that all rank/percentile estimators operating through the posterior distribution of the ranks are monotone transform invariant; that is, they are unchanged by monotone transforms of the target parameter.

5.1 Optimizing L_0/1

Theorem 1

L_0/1 loss is minimized by

$$\begin{array}{cc}{\tilde{R}}_k(\gamma )\hfill & =\text{rank}\{\text{pr}(P_k\ge \gamma |\mathbf{Y})\},\hfill \\ \hfill {\tilde{P}}_k(\gamma )& ={\tilde{R}}_k(\gamma )/(K+1).\hfill \end{array}$$ (10)

These are not unique optimizers.

See Section Appendix B.

5.2 Optimizing L̃

Theorem 2

The P̃_k(γ) optimize L̃. In Section Appendix C, we show in detail that the P̃_k(γ) are also optimal for more general loss functions with the distance penalties $|\gamma -P_k^{\mathit{\text{est}}}{|}^p\text{and}c|P_k^{\mathit{\text{est}}}-\gamma {|}^q$ replaced by any nondecreasing functions of $|\gamma -P_k^{\mathit{\text{est}}}|$. The proof has three steps: first, classify the units into (above γ)/(below γ) groups; second, inside each group, rewrite the posterior risk as the inner product of the discrepancy vector and the misclassification probability vector; third, repeatedly use the rearrangement inequality (Hardy et al. 1967) to minimize the inner product.

The Normand et al. (1997) estimate

Normand et al. (1997) proposed using the posterior probability pr(θ_k > t| Y) and ranks based on it to compare the performance of medical care providers. The cut point t is an application-relevant threshold. Using this approach, we define $P_k^{*}(\gamma )$ with properly chosen cut point t and show that $P_k^{*}(\gamma )$ is essentially identical to P̃_k(γ).

Definition of ${\mathit{P}}_{\mathit{k}}^{*}(\gamma )$: Let

$${\overline{G}}_{\mathbf{Y}}(t)=\frac{1}{K}{\displaystyle \sum _{j=1}^K\text{pr}({\theta }_j\le t|\mathbf{Y}),}$$ (11)

and define $P_k^{*}(\gamma )$ as the percentiles produced by ranking the pr(θk ≥ ${\overline{G}}_{\mathbf{Y}}^{-1}$ (γ)|Y). Section 6.2 gives a relation among P̄_k, P̃_k(γ) and $P_k^{*}$. Theorems 5 and 6 show that P̃_k(γ) is asymptotically equivalent to $P_k^{*}(\gamma )$.

By making a direct link to the original θ scale, $P_k^{*}(\gamma )$ is straightforward to explain and interpret. Furthermore, for a desired accuracy, computing $P_k^{*}(\gamma )$ is substantially faster than computing P̃_k(γ), since the former requires only accurate computation of individual posterior distributions and of Ḡ_Y.

5.3 Optimizing L^†

Section Appendix D presents an optimization procedure for the case p = q = 2, −∞ < c < ∞. However, other than use of brute force (complete enumeration), we have not found an algorithm for general (p, q, c). As for L_0/1, performance depends only on optimal allocation into the (above γ)/(below γ) groups. Additional criteria are needed to specify the within-group order.

5.4 Optimizing L^‡

We have not found a simple means of optimizing this loss function, but Section Appendix E develops a helpful relation.

5.5 Other ranking estimators

Traditional rank estimators include ranks based on maximum likelihood estimates, those based on posterior means of the θs and those based on hypothesis testing statistics (Z-scores, P-values). MLE-based ranks are monotone transform invariant, but the others are not. As shown in Liu et al. (2004), MLE-based ranks will tend to give units with relatively large variances extreme ranks, while hypothesis testing statistics based ranks will tend to place units with relatively small variances at the extremes. Though not an optimal solution to this problem, modified hypothesis testing statistics moderate this shortcoming by reducing the ratio of the variances (Tusher et al. 2001; Efron et al. 2001).

A two stage ranking estimator

Ranking estimator P̃_k(γ) optimize the (above γ)/(below γ) misclassification loss L_0/1 and P̂_k optimize the L̂, which penalizes on the distance |P^est_k P_k|. A convex combination loss function, ${\widehat{L}}_{0/1}^w(\gamma )=(1-w)L_{0/1}(\gamma )+w\widehat{L},(0\le w\le 1)$, thus addresses both inferential goals, as L^‡ similarly does, and motivates $\widehat{\tilde{P}}(\gamma )$, a two stage hybrid ranking estimator.

Definition of $\widehat{\tilde{P}}(\gamma )$: Use P̃_k(γ) to classify into (above γ)/(below γ) percentile groups. Then, within each percentile group order the estimates by P̂_k.

Theorem 3

$\widehat{\tilde{P}}(\gamma )$ minimizes L_0/1 and conditional on this (above γ)/(below γ) classification, produces optimal SEL estimates within the two groups.

See Section Appendix F.

Furthermore, it is straightforward to show that for ${\widehat{L}}_{0/1}^w(\gamma )$ there exists a w_* > 0 such that for all w ≤ w_*, $\widehat{\tilde{P}}(\gamma )$ is optimal and there exists a w* < 1 such that for all w ≥ w*, P̂_k is optimal.

6 Relations among estimators

In this section we develop relations among estimators using ranks or percentiles depending on the context for convenience.

6.1 A general relation

Let ν = [γK] and define

$$R_k^{+}(\nu )=\frac{K(K+1)}{2(K-\nu +1)}\text{pr}(R_k\ge \nu ).$$

Then the ranked $R_k^{+}(\nu )$ equal the ranked pr(R_k ≥ ν) and so each generates the R̃_k(γ). Note that $\frac{K(K+1)}{2(K-\nu +1)}$ is a constant used to standardize $R_k^{+}(\nu )$ such that:

$${\displaystyle \sum _k\frac{K(K+1)}{2(K-\nu +1)}\text{pr}(R_k\ge \nu )={\displaystyle \sum _k{R}_k^{+}(\nu )=\frac{K(K+1)}{2}={\displaystyle \sum _k{R}_k.}}}$$

Theorem 4

R̅_k is a linear combination of the $R_k^{+}(\nu )$ with respect to ν and so for any convex loss function the R̅_k outperform the $R_k^{+}(\nu )$ for at least one value of ν = 1,…,K. For SEL, R̅_k dominates for all ν. As shown in Section Appendix A, the R̂_k = rank(R̅_k) also dominate rank $(R_k^{+}(\nu ))=\widetilde{R_k}(\gamma )$ for all ν.

See Section Appendix G.

6.2 Relating P̂_k, P̃_k(γ) and $P_k^{*}$

From (3), (5) and (11), we have that,

$$\begin{array}{ccc}{\overline{G}}_{\mathbf{Y}}({\theta }_k)\hfill & =\hfill & \mathrm{E}[R_k|{\theta }_k/K,\hfill \\ \hfill {\overline{R}}_k& =\hfill & \mathrm{E}[R_k]=K\mathrm{E}[{\overline{G}}_{\mathbf{Y}}({\theta }_k)]=\mathrm{E}\{\mathrm{E}[R_k|{\theta }_k]\}.\hfill \end{array}$$

The $R_k^{*}(\gamma )$ are generated by ranking the pr $({\theta }_k\ge {\overline{G}}_{\mathbf{Y}}^{-1}(\gamma ))$, which is equivalent to ranking pr(Ḡ_Y (θ_k) ≥ γ). By the foregoing, it is equivalent to ranking the pr(E[R_k|θ_k] ≥ γK), which is similar to pr(R_k ≥ γK), the generator of P̃_k(γ). The R̂_k are produced by ranking the R̄_k which is the same as ranking the expectation of the random variables used to produce the $R_k^{*}$ or R̃_k(γ).

6.3 Approximate equivalence of P̃_k(γ) and $P_k^{*}$

Theorem 5

Assume that ${\theta }_k\stackrel{\mathit{\text{iid}}}{\sim }G,Y_k|{\theta }_k\stackrel{\mathit{\text{ind}}}{\sim }f(Y_k|{\theta }_k)$ and that the posterior cumulative distribution function (cdf) of each θ_k is continuous and differentiable at G⁻¹(γ). If G_k(· |Y) has a universally bounded second moment, then for K → ∞, $P_k^{*}(\gamma )$ is equivalent to P̃_k(γ).

See Section Appendix H.

Theorem 6

Assume that ${\theta }_k\stackrel{\mathit{\text{iid}}}{\sim }G,Y_k|{\theta }_k\stackrel{\mathit{\text{ind}}}{\sim }f(Y_k|{\theta }_k,{\zeta }_{\mathit{k}})$ and that the posterior cumulative distribution function (cdf) of each θ_k is continuous and differentiable at G⁻¹(γ). Furthermore, assume that the empirical distribution function (edf) of the ζ_k converges to a probability distribution. If G_k(·|Y, ζ) has a universally bounded second moment, then for K → ∞, $P_k^{*}(\gamma )$ is equivalent to P̃_k(γ).

Proof

Regard ζ_k as part of the observed data and use $Y_k^{\prime }=(Y_k,{\zeta }_k)$ in Theorem 5.

Theorems 5 and 6 imply that $P_k^{*}(\gamma )$ is asymptotically optimal for L̃ and provides a loss function basis for the Normand et al. (1997) estimates.

6.4 A unifying score function

We provide a unified approach to loss function based ranking. To this end, we define a non-negative, nondecreasing scoring function S(P) : (0, 1) → [0, 1]. The function can be regarded as the scores (reward) a unit would get if its percentile was P. It relates percentiles, P, to “consequences” S(P). These relations can help in eliciting an application-relevant loss function and in interpreting loss-function based percentiles. We use SEL for S(P) to produce percentiles and ranks, specifically:

$$L_s=L({\mathbf{S}}^{\mathbf{\text{est}}},S(P(\mathit{\theta })))=\frac{1}{K}{\displaystyle \sum _k{(S_k^{\mathit{\text{est}}}-S(P_k(\mathit{\theta })))}^2.}$$ (12)

The optimal S^est satisfy $S_k^{\mathit{\text{est}}}=\mathrm{E}[S(P_k)|\mathbf{Y}]$ and we use the ranks and percentiles based on them.

When S(P) = aP + b, a > 0, i.e. the reward is linear in the estimated percentile, we have L̂_s = a²L̂ and so P̂_k is associated with linear rewards. When S(P) = I_{P>γK}, i.e., the reward only depends on whether the percentile of a unit is beyond the threshold γ, there is no constraint on the rankings of units inside each of the (above γ)/(below γ) groups. With this setting, there exist many optimizers and P̃_k(γ) is one of them. For the two stage ranking estimator ${\widehat{\tilde{P}}}_k(\gamma )$, let S(P) = aP + I_{P>γ} and so $S_k^{\mathit{\text{est}}}=a{\overline{P}}_k+\text{pr}(P_k>\gamma )$. When a is sufficiently close to zero, $\widehat{\tilde{P}}(\gamma )$ is optimal. More S(P) are given in Section Appendix I.

7 Performance evaluations and comparisons

7.1 Posterior and pre-posterior performance evaluations

In a Bayesian model, an estimator’s performance can be evaluated by using the posterior distribution (data analytic evaluations) and by using the marginal distribution of the data (pre-posterior evaluations). For example, preposterior SEL performance is the sum of expected posterior variance plus expected squared posterior bias.

We provide evaluations relative to the loss function used to produce the estimate and other potentially relevant loss functions. For example, performance with respect to SEL should be computed for the SEL optimizer and for other estimators. These comparisons help to determine the efficiency of an estimator that optimizes one loss function when evaluated for other loss functions. Procedures that are robust to the choice of loss functions will be attractive in applications.

7.2 The (above γ)/(below γ) operating characteristic

For (above γ)/(below γ) classification, plots of the posterior probability of exceeding γ versus estimated percentiles are informative (see Figure 4). Such plots can be summarized by the a posteriori operating characteristic (OC). For any percentiling method, define,

$$\begin{array}{ccc}\mathit{\text{OC}}(\gamma )\hfill & =\hfill & \text{pr}(P_k<\gamma |P_k^{\mathit{\text{est}}}>\gamma ,\mathbf{Y})+\text{pr}(P_k>\gamma |P_k^{\mathit{\text{est}}}<\gamma ,\mathbf{Y})\hfill \\ \hfill & =\hfill & \text{pr}(P_k>\gamma |P_k^{\mathit{\text{est}}}<\gamma ,\mathbf{Y})/\gamma =\frac{{\mathrm{E}}_{\theta |\mathbf{Y}}{L}_{0/1}(\gamma )}{2\gamma (1-\gamma )},\hfill \end{array}$$ (13)

with the last equality following from identity ${\displaystyle {\sum }_k{\mathit{\text{BA}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})={\displaystyle {\sum }_k{\mathit{\text{AB}}}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}}})}$. OC(γ) is the sum of two misclassification probabilities and so is optimized by P̃_k(γ). It is normalized so that if the data provide no information on the θ_k, then for all γ, OC(γ) ≡ 1. Evaluating performance using only one of the probabilities, e.g., pr $(P_k>\gamma |P_k^{\mathit{\text{est}}}<\gamma ,\mathbf{Y})$ is analogous to computing the false discovery rate (Benjamini and Hochberg 1995; Storey 2002, 2003).

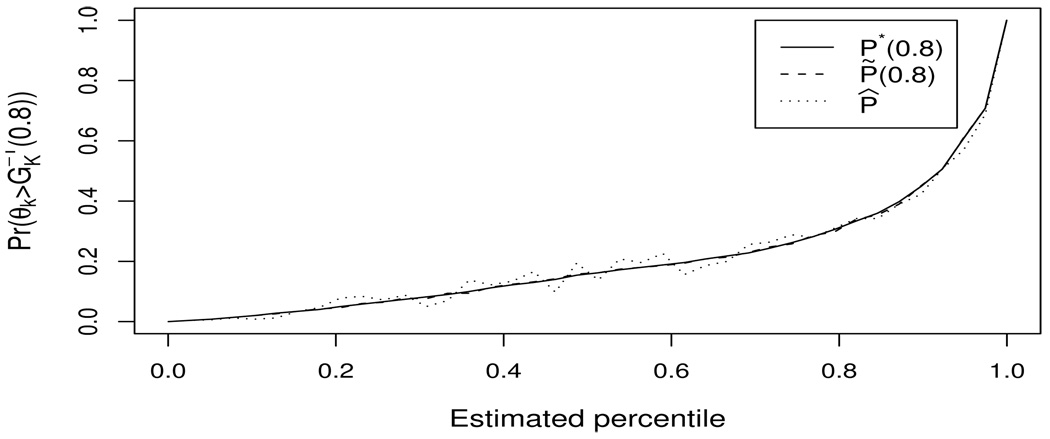
Figure 4.

Pr(θ_k > 0.18 | Y) with X-axis percentiles determined separately by the three percentiling methods.

7.3 Unit-specific performance

For loss functions that sum over unit-specific components, performance can also be evaluated for individual units and, in a frequentist evaluation, for individual θ vectors. These evaluations are in Section 9.3.

8 Simulation scenarios

We evaluate pre-posterior performance for the Gaussian sampling distribution with K = 200 using 2000 simulation replications. We compute pr(R_k = ℓ | Y) using an independent sample Monte Carlo with 2000 draws. All simulations are for loss functions with p = q = 2 and c = 1.

8.1 The Gaussian-Gaussian model

We evaluate estimators for the Gaussian/Gaussian, two-stage model with a Gaussian prior and Gaussian sampling distributions and allow for varying unit-specific variances. Without loss of generality we assume that the prior mean is µ = 0 and the prior variance is τ² = 1. Specifically,

$$\begin{array}{ccc}\hfill {\theta }_k& \mathit{\text{iid}}\hfill & N(0,1)\hfill \\ \hfill Y_k|{\theta }_k& \sim \hfill & N({\theta }_k,{\sigma }_k^2).\hfill \end{array}$$

This derives:

$${\theta }_k|Y_k\mathit{\text{ind}}N({\theta }_k^{\mathit{\text{pm}}},(1-B_k){\sigma }_k^2),$$

where ${\theta }_k^{\mathit{\text{pm}}}=(1-B_k)Y_k\text{and}{B}_k={\mathrm{\sigma }}_k^2/({\mathrm{\sigma }}_k^2+1)$. When unit-specific variances $({\sigma }_k^2\equiv {\sigma }^2)$ are all equal, the posterior distributions are stochastically ordered and all ranking methods we investigate are identical. Evaluation for this case provides a baseline performance with respect to the set of loss functions. In practice, the $\{{\sigma }_k^2\}$’s can vary substantially and we evaluate this situation using two departures from the ${\sigma }_k^2\equiv {\sigma }^2$ case. In each case, the equal variance scenario is produced by rls = 1:

1. log uniform: Ordered, geometric sequences of the $\{{\sigma }_k^2\}$ with ratio of the largest σ² to the smallest $\mathit{\text{rls}}={\sigma }_K^2/{\sigma }_1^2$ and geometric mean $\mathit{\text{gmv}}=\mathit{\text{GM}}({\sigma }_1^2,\dots ,{\sigma }_K^2)$.

2. two clusters: The first half of the ${\sigma }_k^2\equiv {(\mathit{\text{rls}})}^{-\frac{1}{2}}$; for the second half, ${\sigma }_k^2\equiv {(\mathit{\text{rls}})}^{\frac{1}{2}}$. Here, $\mathit{\text{rls}}={\sigma }_K^2/{\sigma }_1^2$ and gmv = 1.

In both cases the variance sequence is monotone in k, but simulation results would be the same if the indices were permuted. These variance sequences — constant, uniform in the log scale, clustered at the extremes of the range — triangulate possible patterns, though specific applications can, of course, have their unique features.

8.2 A Mixture prior

This prior is a mixture of two Gaussian distributions with the mixture constrained to have mean 0 and variance 1:

$${\theta }_k\stackrel{\mathit{\text{iid}}}{~}(1-\epsilon )N\left(-\frac{\epsilon \mathrm{\Delta }}{A},\frac{1}{A^2}\right)+\epsilon N\left(\frac{(1-\epsilon )\mathrm{\Delta }}{A},\frac{{\xi }^2}{A^2}\right)$$

where

$$A^2=A^2(\epsilon ,\mathrm{\Delta },\xi )=(1-\epsilon )+\epsilon {\xi }^2+\epsilon (1-\epsilon ){\mathrm{\Delta }}^2$$

We present results for ε = 0.1, Δ = 3.40, ξ² = .25, γ = 0.9 and compute the preposterior risk for estimators that are computed from the posterior produced by this mixture and for estimators that are based on a standard, Gaussian prior.

9 Simulation results

9.1 SEL for P̂_k and estimated θ-based percentiles

Table 1 documents SEL (L̂) performance for P̂_k, the optimal estimator, for percentiled Y_k (the MLE), percentiled ${\theta }_k^{\mathit{\text{pm}}}$ and percentiled $\text{exp}\left\{{\theta }_k^{\mathit{\text{pm}}}+\frac{(1-B_k){\sigma }_k^2}{2}\right\}$ (the posterior mean of e^θk).

Table 1.

Simulated preposterior SEL (10000 L̂) for gmv = 1.

	percentiles based on
rls	P̂k	${\theta }_k^{\mathit{\text{pm}}}$	exp $\left\{{\theta }_k^{\mathit{\text{pm}}}+\frac{(1-B_k){\sigma }_k^2}{2}\right\}$	Yk
1	516	516	516	516
25	517	517	534	582
100	522	525	547	644

The posterior mean of e^θ_k is presented to assess performance for a monotone, non-linear transform of the target parameters. For rls = 1, the posterior distributions are stochastically ordered and the four sets of percentiles are identical, as is their performance. As rls increases, performance of Y_k-derived percentiles degrades, those based on the ${\theta }_k^{\mathit{\text{pm}}}$ are quite competitive with P̂_k but performance for percentiles based on the posterior mean of e^θ_k rapidly degrades. Results show that though the posterior mean can perform well for some models and target parameters, in general it is not competitive with rank-based approaches.

9.2 Comparisons among loss function-based estimates

Table 2 reports results for P̂_k, P̃_k(γ) and $\widehat{\tilde{P}}(\gamma )$ under four loss functions and for the “log-uniform” variance pattern. For the “two-clusters” pattern, differences between estimators are modified relative to those for the log-uniform pattern, but preference relations are unchanged. For example, the L̂ risks are generally smaller for the “two-clusters” variance pattern than for the “log-uniform” pattern, but the reverse is true for L̃.

Table 2.

Simulated preposterior risk for gmv = 1. All values are 10000×(Loss). The first block is for the Gaussian-Gaussian model; the second for the Gaussian mixture prior assuming the mixture; the third for the Gaussian mixture prior, but with analysis based on a single Gaussian prior.

		L0/1		L̂			L̃			L‡
γ	rls	P̂k	P̃k(γ)	P̂k	P̃k(γ)	$\widehat{\tilde{P}}(\gamma )$	P̂k	P̃k(γ)	$\widehat{\tilde{P}}(\gamma )$	P̂k	P̃k(γ)	$\widehat{\tilde{P}}(\gamma )$
0.5	1	2508	2511	517	518	517	104	105	104	336	337	336
0.5	25	2506	2508	519	524	519	98	96	98	340	335	340
0.5	100	2503	2503	521	530	521	93	90	93	342	334	342
0.6	100	2432	2422	522	537	523	91	87	91	324	316	327
0.8	25	1740	1717	517	558	517	67	59	67	175	170	181
0.8	100	1742	1689	523	595	523	71	57	71	178	170	189
0.9	1	1059	1058	515	520	515	30	30	30	73	73	73
0.9	25	1060	1032	518	609	519	37	29	37	75	72	81
0.9	100	1048	1005	523	673	523	43	29	42	77	70	86
0.8	1	1469	1471	565	567	565	54	54	54	150	150	150
0.8	25	1524	1494	566	606	567	59	51	59	161	158	168
0.9	1	782	782	565	575	565	14	14	14	42	42	42
0.9	25	823	783	564	699	564	23	14	23	51	48	58
0.8	1	1473	1470	565	566	565	54	54	54	150	150	150
0.8	25	1496	1493	567	615	567	58	52	59	159	158	168
0.9	1	782	782	565	570	565	14	14	14	42	42	42
0.9	25	788	783	565	664	564	22	14	23	50	45	58

When rls = 1, ${\tilde{P}}_k(\gamma )\equiv {\widehat{P}}_k\equiv \widehat{\tilde{P}}(\gamma )$ and so differences in the SEL results in the first and seventh rows quantify residual simulation variation and Monte Carlo uncertainty in computing the probabilities used in equation (1) to produce the P̃_k(γ). Results for other values of rls show that under L̂, P̂_k outperforms P̃_k(γ) and $\widehat{\tilde{P}}(\gamma )$ as must be the case, since P̂_k is optimal under SEL. Similarly, P̂_k(γ) optimizes L_0/1 and L̃, and for rls ≠ 1 outperforms competitors. Though $\widehat{\tilde{P}}(\gamma )$ optimizes ${\widehat{L}}_{0/1}^w(\gamma )$ (see Section 5.4) for sufficiently small w, it performs relatively poorly for the seemingly related L^‡; P̃_k(γ) appears to dominate and P̂_k performs well. The poor performance of $\widehat{\tilde{P}}(\gamma )$ shows that unit-specific combining of a misclassification penalty with squared-error loss is fundamentally different from using them in an overall convex combination.

Similar relations among the estimators hold for the two component Gaussian mixture prior and for a “frequentist scenario” with a fixed set of parameters and repeated sampling only from the Gaussian sampling distribution conditional on these parameters.

Results in Table 2 are based on gmv = 1. Relations among the estimators for other values of gmv are similar, but a look at extreme gmv is instructive. Results (not shown) indicate that for rls = 1, the risk associated with L_0/1 is of the form a(gmv)γ(1 − γ), where a(gmv) is a constant depending only on the value of gmv. By identity (13), this implies that the expectation of OC(γ) is approximately constant. When gmv = 0, the data are fully informative, Y_k ≡ θ_k and all risks are 0. When ${\sigma }_k^2\to \infty$, gmv = ∞ and the Y_k provide no information on the θs nor on P_k. Table 3 displays the preposterior risk for this no information case, with values providing an upper bound for results in Table 2.

Table 3.

Preposterior risk for rls = 1 when gmv = ∞. All values are 10000×Risk.

	L0/1	L̂	L‡	L̃ and L†
γ	200γ(1−γ)	1667	3333γ(1−γ)	3333γ(1−γ)[γ3 + (1−γ)3]
0.5	5000	1667	833	208
0.6	4800	1667	800	224
0.8	3200	1667	533	277
0.9	1800	1667	300	219

Under L_0/1 P̃_k(γ) is the optimal and the difference between P̂_k and P̃_k(γ) depends on the magnitude of rls. That P̃_k(γ) is only moderately better than P̂_k under L̃ is due in part to our having considered only the case p = q = 2, c = 1, which makes L̃ very similar to L̂. For larger p and q there would be a more substantial difference.

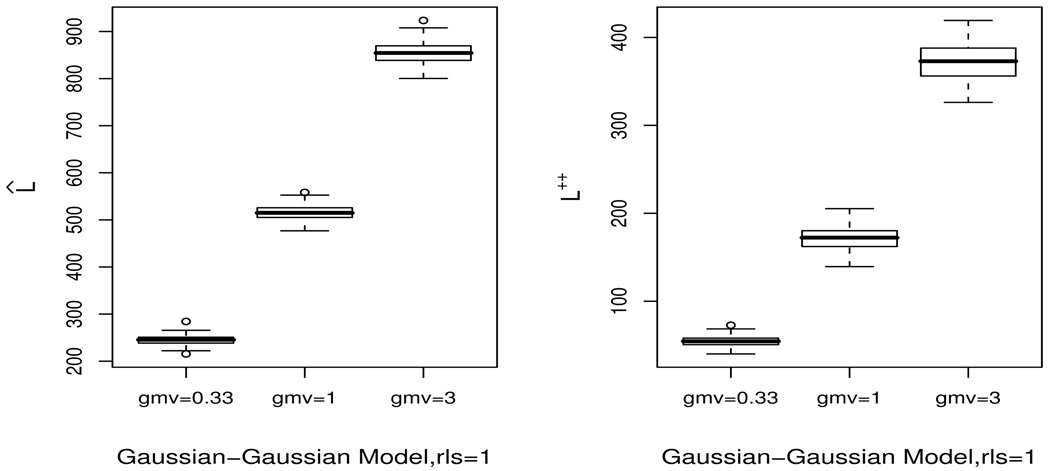
Figure 1–Figure 3 are based on the Gaussian-Gaussian model. Figure 1 displays the dependence of risk on gmv for the exchangeable model (rls = 1). As expected, risk increases with gmv. For rls = 1, expected unit-specific loss equals the overall average risk and so the box plots summarize the sampling distribution of unit-specific risk.

Figure 1.

Unit-specific, L̂ and L^‡ risk classified by gmv for K = 200, γ = 0.8.

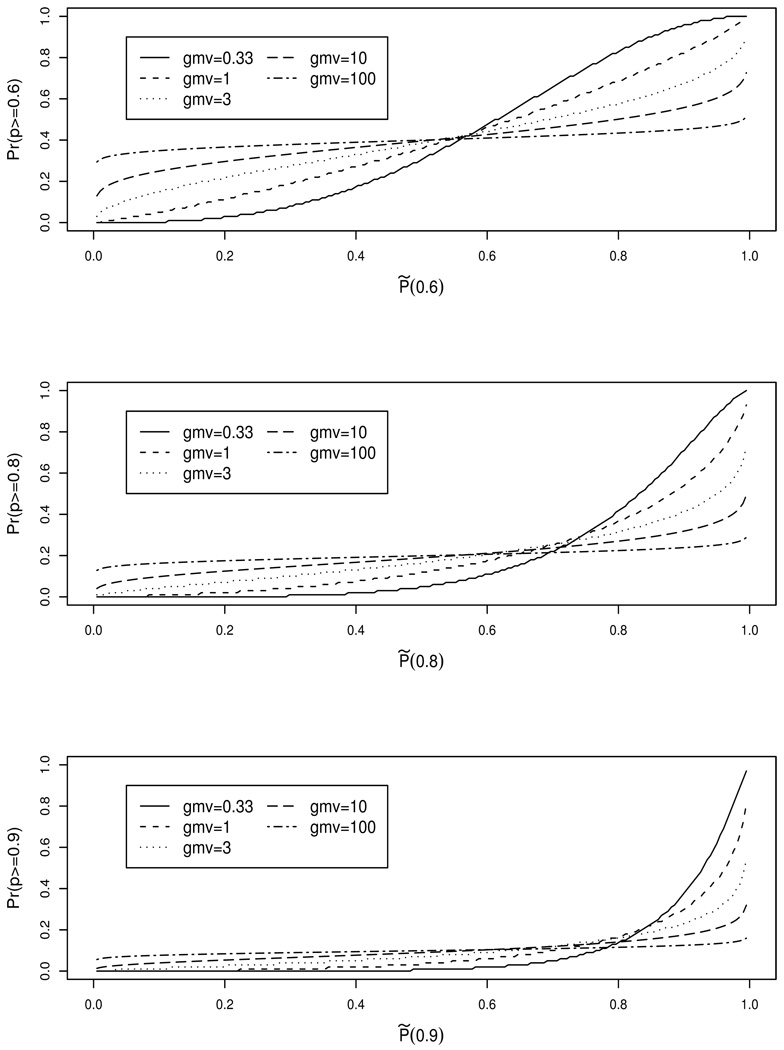
Figure 3.

Average posterior classification probabilities as a function of the optimally estimated percentiles for rls = 1, γ = (0.6, 0.8, 0.9).

9.3 Unit-specific performance

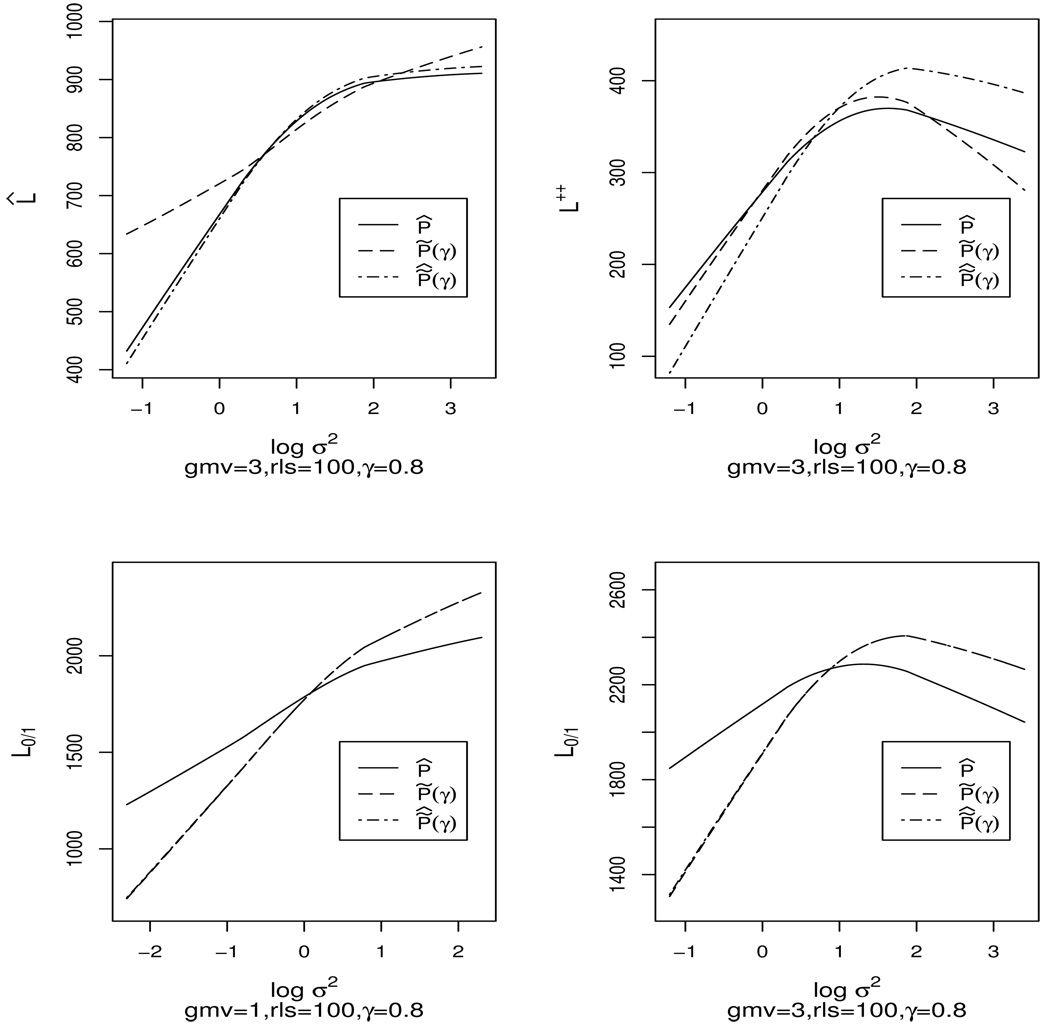
When rls = 1, pre-posterior risk is the same for all units. However, when rls > 1, the ${\sigma }_k^2$ form a geometric sequence and preposterior risk depends on the unit. We study this non-exchangeable situation by simulation. Figure 2 displays loess smoothed performance of P̂_k, P̃_k(γ) and $\widehat{\tilde{P}}(\gamma )$ for L_0/1, L̂ and L^‡ as a function of unit-specific variance for gmv = 1 and 3, rls = 100 and γ = 0.8. Results for L̂ (gmv = 3) and L_0/1 (gmv = 1) are intuitive in that risk increases with increasing unit-specific variance. However, in the displays for L_0/1 (gmv = 3) and for L^‡, for all estimators the risk increases and then decreases as a function of ${\sigma }_k^2$. For gmv and rls sufficiently large, similar patterns hold for other γ-values with the presence and location of a downturn depending on | γ − 0.5 |.

Figure 2.

Loess smoothed, unit-specific performance of P̂_k, P̃_k(γ) and $\widehat{\tilde{P}}(\gamma )$ under L̂, L^‡, and L_0/1 as a function of unit-specific variance (${\sigma }_k^2$).

These apparent anomalies are explained as follows. If γ is near 1 (or equivalently, near 0) and if the ${\sigma }_k^2$ differ sufficiently (rls ≫ 1), estimates for the high variance units perform better than for those with mid-level variance. This relation is due to the improved classification of high-variance units into (above γ)/(below γ) groups, with substantial shrinkage of the percentile estimates towards 0.5. For example, with γ = 0.8, a priori 80% of the percentiles should be below 0.8. Estimated percentiles for the high variance units are essentially guaranteed to be below 0.8 and so the classification error for the large-variance units converges to 0.20 as rls → ∞. Generally, low variance units have small misclassification probabilities, but percentiles for units with intermediate variances are not shrunken sufficiently toward 0.5 to produce a low L_0/1.

9.4 Classification performance

As shown in the foregoing tables and by Liu et al. (2004) and Lockwood et al. (2002), even the optimal ranks and percentiles can perform poorly unless the data are very informative. Figure 3 displays average posterior classification probabilities as a function of the optimally estimated percentile for gmv = 0.33, 1, 10, 100 and γ = 0.6, 0.8, 0.9, when rls = 1. The pattern shown by the three panels should hold for other γ choices and we use the γ = 0.8 panel as the typical example for further comments. Discrimination improves with decreasing gmv, but even when gmv = 0.33 (the σ_k are 1/3 of the prior variance), the model-based, posterior probability of P_k > 0.8 is only 0.42 for a unit with P̃_k(0.8) = 0.8. For this probability to exceed 0.95 (i.e., to be reasonably certain that P_k > 0.80) requires that P̃_k(0.8) > 0.97. It can be shown that as gmv → ∞ the plots converge to a horizontal line at (1 − γ) and that as gmv → 0 the plots converge to a step function that jumps from 0 to 1 at γ.

9.5 The Poisson-Gamma model

We conducted investigations analogous to the all of the foregoing for the Poisson sampling distribution with a Gamma prior, with constant or unequal variances (e.g., expected values) for the unit-specific MLEs. Results are qualitatively and quantitatively very similar to those we report for the Gaussian sampling distribution.

10 Analysis of USRDS standardized mortality ratios

The United States Renal Data System (USRDS) uses provider specific, standardized mortality ratios (SMRs) as a quality indicator for its nearly 4000 dialysis centers (Lacson et al. 2001; End-Stage Renal Disease (ESRD) Network 2000) and (United States Renal Data System (USRDS) 2005). Under the Poisson likelihood (last line of model (14)), with Y_k the observed and m_k the expected deaths computed from a case-mix adjustment (Wolfe et al. 1992), the MLE is ρ̂_k = Y_k/m_k, with variance ρ_k/m_k. For the “typical” dialysis center ρk ≈ 1 and the m_k control the variance of the MLEs. The observed m_ks range from around 0 to greater than 100. The ratio of the largest m_k to the smallest m_k, which is analogous to the rls in the foregoing simulations, is around 258,000.

In this “profiling” application, the loss function should reflect the end use of the ranks or percentiles. For example, suppose that the following monetary reward (increased reimbursement) and penalty (increased scrutiny) system is in place:

• A provider either does or does not receive the reward depending on whether its percentile is or is not beyond (for SMRs, below) a γ threshold.

• Providers that do get rewards receive varying amounts depending on their position among those receiving rewards.

• Providers not receiving rewards undergo increased scrutiny from an oversight committee.

• The distance from the threshold γ is used to monetize rewards or intensify scrutiny.

Loss function L̃ embodies this system with the values of p, q and c controlling the award/penalty differences within the (above γ)/(below γ) groups. If rewarded providers all get the same amount, then L_0/1(γ) can be used. Alternatively, rewards and scrutiny can depend on the posterior probability of exceeding or falling below γ, with both P̃_k(γ) and $P_k^{*}(\gamma )$ optimizing the evaluation.

Liu et al. (2004) analyzed 1998 data and Lin et al. (2004) extended these analyses to 1998 – 2001 for 3173 centers with complete data using an autoregressive model. We illustrate the new loss functions and performance measures using 1998 data and the model,

$$\begin{array}{ccc}\hfill \xi \stackrel{\mathit{\text{iid}}}{\sim }N(\mathrm{0,\; 10}),& \hfill & \lambda ={\tau }^{-2}\stackrel{\mathit{\text{iid}}}{\sim }\text{Gamma}(0.05,0.2)\hfill \\ [{\theta }_1,\dots ,{\theta }_K|\xi ,\tau ]\hfill & \stackrel{\mathit{\text{iid}}}{\sim }\hfill & N(\xi ,{\tau }^2,{\theta }_k=\text{log}({\rho }_k)\hfill \\ \hfill [Y_k|m_k,{\rho }_k]& \sim \hfill & \text{Poisson}(m_k{\rho }_k).\hfill \end{array}$$ (14)

For these data, ${\overline{G}}_K^{-1}(0.8)=0.18(\rho =1.20)$. Table 4 gives the posterior risks. For all loss functions investigated, the MLE based rank has the poorest performance; methods based on the posterior distributions generally perform well. As Theorem 6 indicates, P̃_k(γ) and $P_k^{*}(\gamma )$ have almost identical risk.

Table 4.

Posterior, loss function risk for different ranking methods using the USRDS 1998 data. All values are 10000×(Loss). ${\widehat{P}}_k^{\mathit{\text{PM}}}$ and ${\widehat{P}}_k^{\mathit{\text{MLE}}}$ are percentiles based on the ${\theta }_k^{pm}$ and the Y_k respectively.

	${\widehat{P}}_k^{\mathit{\text{PM}}}$	${\widehat{P}}_k^{\mathit{\text{MLE}}}$	P̂k	P̃k(γ)	$\widehat{\tilde{P}}(\gamma )$	$P_k^{*}(\gamma )$
L̂	741	872	740	769	741	769
L̃	108	164	107	100	107	100
L†	97	130	96	102	102	102
L‡	281	401	279	275	285	276
L0/1	2001	2062	2006	1992	1991	1995

Figure 4 displays pr(θ_k > 0.18 | Y) with X-axis percentiles determined separately by the three percentiling methods. As shown by Theorem 6, the $P_k^{*}(0.18)$ and P̃_k(0.8) curves are monotone and approximately equal; the P̂_k curve is not monotone, but is close to the other curves. The OC(0.8) value for $P_k^{*}(\gamma )$ and P̃_k(0.8) is 0.64 (the optimal classification produces an error rate that is 64% of that for the no information case) and for P̂_k is 0.65, showing that for γ = 0.8, using P̂_k to classify is nearly fully efficient. Figure 4 also shows that for centers classified in the top 10%, the probability that they are truly in the top 20% (γ = 0.8) can be as low as 0.45. Lin et al. (2004) showed that, by using data from 1998–2001, this probability increases to 0.57. Evaluators should take this relatively poor classification performance into account by tempering rewards and scrutiny.

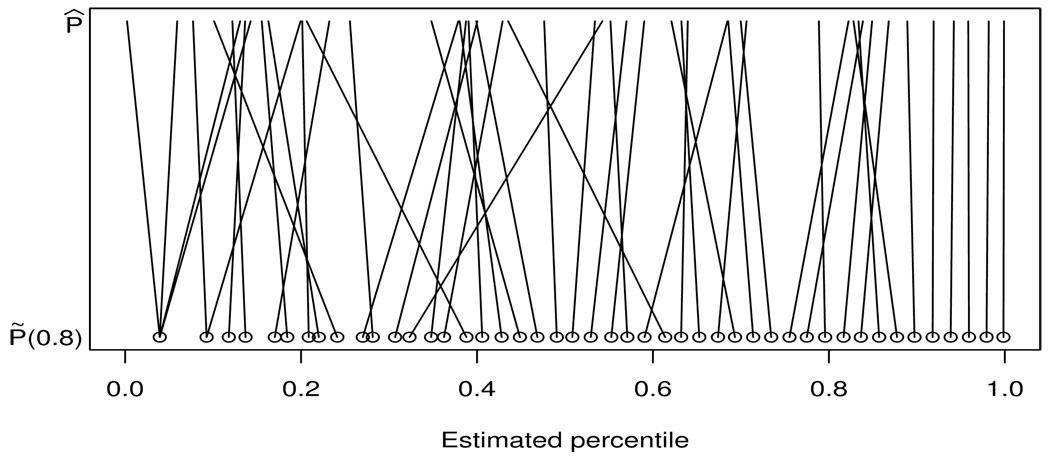
Figure 5 displays the relation between P̃_k(0.8) and P̂_k for 50 dialysis centers spaced uniformly according to P̃_k(0.8). Since P̃_k(0.8) is based on the pr(P_k > .8|Y) calculated from MCMC samples, ties appear when this probability is close to zero. Among 3173 dialysis centers, 249 centers have the exceeding probability 0 and all are estimated with percentile 125/3174=0.039. Though P̃_k is highly efficient, some percentiles are substantially different from the optimal. As further evidence of this discrepancy, of the 635 dialysis centers classified by P̃_k(0.8) in the top 20%, 39 are not so classified by P̂_k with most of these near the γ = 0.8 threshold. Estimated percentiles are very similar for centers classified in the top 10%.

Figure 5.

Circles represent 50 USRDS dialysis centers evenly spread across percentiles determined by P̃_k(0.8) using 1998 SMR data. Lines connect P̃_k(0.8) and P̂_k. Ties appear in the lower percentile area.

11 Discussion

Effective ranking or percentiling should be based on a loss function computed from the estimated and true ranks, or be asymptotically equivalent to such loss function based estimates. Doing so produces optimal or near optimal performance and ensures desirable properties such as monotone transform invariance. In general, percentiles based on MLEs or on posterior means of the target parameter can perform poorly. Similarly, hypothesis test-based percentiles perform poorly.

Our performance evaluations are primarily for the fully parametric model with a Gaussian sampling distribution, though we do investigate departures from the Gaussian prior. Simulations for the Poisson/Gamma model produce relative performance very similar to those for the Gaussian. The P̂_k that optimize L̂ (SEL) are “general purpose” with no explicit attention to optimize the (above γ)/(below γ) classification. The optimal (above γ)/(below γ) ranks are asymptotically equivalent to the “exceedance probability” procedure proposed in Normand et al. (1997). This near-equivalence provides insight into goals and a route to efficient computation.

We report loss function comparisons and plots based on unit-specific performance. These can be augmented by bivariate and multivariate summaries of properties, for example pair-wise posterior distributions or pair-wise operating characteristics.

When posterior distributions are not stochastically ordered and the choice of ranking methods does matter, our simulations show that though P̃_k(γ) and $\widehat{\tilde{P}}(\gamma )$ are optimal for their respective loss functions and outperform P̃_k, P̃_k performs well for a broad range of γ values. And, P̂_k(γ) can have poor SEL performance. However, for some scenarios the relative benefit of using an optimal procedure is considerable and so a choice of estimator should be guided by goals.

Performance evaluations for three-level models with a hyper-prior and robust analyses based on the non-parametric maximum likelihood prior or a fully Bayesian nonparametric prior (Paddock et al. 2006) showed that SEL-optimal ranks perform well over a wide range of prior specifications.

Other loss functions and estimates can be considered. Weighted combinations of several loss functions can be used to broaden the class of loss functions. If an application relevant loss function cannot be optimized, our evaluations provide a framework to compare candidate estimators. Our scoring function approach can help practitioners elicit a meaningful loss function with an intuitive interpretation.

Though there are a wide variety of candidate loss functions and, thereby, candidate estimated percentiles, our investigations show that in most applications one can choose between P̂_k and $P_k^{*}(\gamma )$ (equivalently, P̃_k(γ)). The P̂_k are for general purpose and are recommended in situations where the full spectrum of percentiles is important, for identifying units as low, medium or high performers. This is the case in educational assessments. Schools and school districts want to track their performance over time irrespective of whether they are low, high or in the middle. The $P_k^{*}(\gamma )$ focus on a specific (above γ)/(below γ) cut point and are recommended in situations where identifying one extreme is the dominant goal. Selection of the most differentially expressed genes, with γ selected to deliver a manageable number for further analysis, is a prime example.

Whatever percentiling method is used, plots such as Figure 4 can be constructed with those percentiles on the X-axis. In general, the plot will not be monotone unless the $P_k^{*}(\gamma )$ are used, but use of the P̂_k produces a nearly monotone plot and very good OC(γ) performance. Therefore, unless there is a compelling reason to optimize relative to a specific (above γ)/(below γ) cut point, the P̂_k are preferred.

Importantly, as do Liu et al. (2004) and Lockwood et al. (2002), we show that unless data are highly informative, even the optimal estimates can perform poorly. It is thus very important to select proper estimates for as good as possible inference, especially when performance differences between estimators are large. Data analytic performance summaries such as SEL, OC(γ) and plots like Figure 3 and Figure 4 should accompany any analysis.

Appendix

Appendix A Optimizing weighted squared error loss (WSEL)

Theorem 7

Under weighted squared error loss:

$${\displaystyle \sum _k{\omega }_k{(R_k^{\mathit{\text{est}}}-R_k)}^2,}$$ (15)

the optimal rank estimates are

$${\overline{R}}_k=E(R_k|\mathbf{Y})={\displaystyle \sum _j\mathit{\text{pr}}({\theta }_k\ge {\theta }_j|\mathbf{Y}).}$$

(We drop conditioning on Y)

$$\begin{array}{ccc}\mathrm{E}{\displaystyle \sum _k{\omega }_k{(R_k^{\mathit{\text{est}}}-R_k)}^2}\hfill & =\hfill & {\displaystyle \sum _k{\omega }_k\mathrm{E}{(R_k^{\mathit{\text{est}}}-{\overline{R}}_k+{\overline{R}}_k-R_k)}^2}\hfill \\ \hfill & =\hfill & {\displaystyle \sum _k{\omega }_k\mathrm{E}[{(R_k^{\mathit{\text{est}}}-{\overline{R}}_k)}^2+{({\overline{R}}_k-R_k)}^2]}\hfill \\ \hfill & \ge \hfill & {\displaystyle \sum _k{\omega }_k\mathrm{E}{({\overline{R}}_k-R_k)}^2}\hfill \end{array}$$

Thus, the R̄_k are optimal.

When all w_k ≡ w,

$${\widehat{R}}_k=\text{rank of}({\overline{R}}_k)$$

optimizes (15) subject to the $R_k^{\mathit{\text{est}}}$ exhausting the integers (1;…K). To see this, if 0 ≤ E(R_i) = m_i ≤ E(R_j) = m_j, r_i < r_j, then

$$\begin{array}{ccc}\mathrm{E}{(R_i-r_i)}^2+\mathrm{E}{(R_j-r_j)}^2\hfill & =\hfill & \text{Var}(R_i)+\text{Var}(R_j)+{(m_i-r_i)}^2+{(m_j-r_j)}^2\hfill \\ \hfill & <\hfill & \text{Var}(R_i)+\text{Var}(R_j)+{(m_i-r_j)}^2+{(m_j-r_i)}^2\hfill \\ \hfill & =\hfill & \mathrm{E}{(R_i-r_j)}^2+\mathrm{E}{(R_j-r_i)}^2\hfill \end{array}$$

and the R̂_k are optimal.

For general w_k there is no closed form solution, but a sorting-based algorithm based on,

$$\begin{array}{cc}\hfill & {\omega }_i{(m_i-r_i)}^2+{\omega }_j{(m_j-r_j)}^2<{\omega }_i{(m_i-r_j)}^2+{\omega }_j{(m_j-r_i)}^2,\text{if}{r}_j>r_i\hfill \\ \iff \hfill & (r_j-r_i)((1-\frac{{\omega }_j}{{\omega }_i})(r_i+r_j-2m_j)+2(m_j-m_i))>0,\text{if}{r}_j>r_i\hfill \\ \iff \hfill & (1-\frac{{\omega }_j}{{\omega }_i})(r_i+r_j-2m_j)+2(m_j-m_i)>0,\text{if}{r}_j>r_i.\hfill \end{array}$$ (16)

guides the optimization. By the above inequality, reversing any two estimated ranks that do not align with R̄_k results in a smaller squared error.

Theorem 8

Start from any initial ranks and implement the recursion: If inequality (16) is satisfied, switch the position of unit i and unit j, i, j = 1,…, K. The unique fixed point will minimize weighted squared error loss (15).

Since each switch will decrease the expected loss and there are at most n! possible values of the expected loss, a fixed point will be reached. At the fixed point, no (i, j) pair produces inequality (16) and so gives the SEL minimum.

In the standard sorting problem, the quantities to sort do not depend on the current positions of the units, while the quantity in (16) does. For this reason, the convergence of the algorithm can be very slow. After units i and j are compared and ordered, if unit i is compared to some other unit k and a switch happens, then unit i should be compared to unit j again and so this pairwise-switch optimization algorithm is computationally impractical.

Appendix B Optimizing L_0/1

Proof of Theorem 1

Rewrite the loss function as a function of the number of units that not classified in the top (1 − γ)K, but that should have been. Then, $L_{0/1}=\frac{1}{K}(K-|A\cap T|)$, where A is the set of indices of the observations classified in the top and T is the true set of indices for which rank(θ_k) > (1 − γ)K. We need to maximize the expected number of correctly classified coordinates:

$$\begin{array}{ccc}\mathrm{E}|A\cap T|\hfill & =\hfill & \mathrm{E}{\displaystyle \sum I(k\in A\cap T})\hfill \\ \hfill & =\hfill & \mathrm{E}{\displaystyle \sum _{k\in A}I(k\in T)={\displaystyle \sum _{k\in A}\text{pr}(P_k>\gamma |\mathbf{Y}).}}\hfill \end{array}$$

To optimize L_0/1, for each θ_k calculate pr(P_k > γ|Y), rank these probabilities and select the largest (1−γ)K of them to minimize L_0/1, creating the optimal (above γ)/(below γ) classification. This computation can be time-consuming, but is Monte Carlo implementable.

The P̂_k(γ) optimize L_0/1. There are other optimizers because L_0/1 requires only the optimal (above γ)/(below γ) categorization but not the optimal ordering. For example, permutations of the ranks of units classified in A or permutations of the ranks in A^C yield the same posterior risk for L_0/1.

Appendix C Optimizing L̃

Lemma 1

If a₁ + a₂ ≥ 0 and b₁ ≤ b₂, then

$$a_1{b}_1+a_2(1-b_2)\le a_1{b}_2+a_2(1-b_1).$$

$$\begin{array}{ccc}(a_1+a_2)b_1\le (a_1+a_2)b_2\hfill & \Rightarrow \hfill & a_1{b}_1-a_2{b}_2\le a_1{b}_2-a_2{b}_1\hfill \\ \hfill & \Rightarrow \hfill & a_1{b}_1+a_2(1-b_2)\le a_1{b}_2+a_2(1-b_1).\hfill \end{array}$$

Lemma 2

Rearrangement Inequality (Hardy et al. 1967): If a₁ ≤ a₂ ≤ … ≤ a_n and b₁ ≤ b₂ ≤ … ≤ b_n, b₍₁₎; b₍₂₎, …b_(n) is a permutation of b₁; b₂, … b_n, then

$${\displaystyle \sum _{i=1}^n{a}_i{b}_{n+1-i}\le {\displaystyle \sum _{i=1}^n{a}_i{b}_{(i)}\le {\displaystyle \sum _{i=1}^n{a}_i{b}_i.}}}$$

For n = 2 we use the ranking inequality:

$$a_1{b}_2+a_2{b}_1\le a_1{b}_1+a_2{b}_2\iff (a_2-a_1)(b_2-b_1)\ge 0.$$

For n > 2, there exists a minimum and a maximum in all n! combinations of sums of products. By the result for n = 2, the necessary condition for the sum to reach the minimum is that any pair of indices (i₁, i₂), (a_i1, a_i2) and (b_i1, b_i2) must have the inverse order; to reach the maximum, they must have same order. Therefore, except in the trivial cases where there are ties inside {a_i} or {b_i}, ${\displaystyle {\sum }_{i=1}^n{a}_i{b}_{n+1-i}}$ is the only candidate to reach the minimum and ${\displaystyle {\sum }_{i=1}^n{a}_i{b}_i}$ is the only candidate to reach the maximum. Proof of Theorem 2 Denote by R_(i) the rank random variables for units whose ranks are estimated as i. Then,

$$\begin{array}{ccc}E(L_{R_K^{\mathit{\text{est}}}}(\gamma ,p,q,c))=\hfill & \hfill & {\displaystyle \sum _{i=1}^{[\gamma (K+1)]}|\gamma (K+1)-i{|}^p\text{pr}(R_{(i)}\ge \gamma (K+1))}\hfill \\ \hfill & +\hfill & {\displaystyle \sum _{i=[\gamma (K+1)]+1}^{K}c|i-\gamma (K+1){|}^q(1-\text{pr}(R_{(i)}\ge \gamma (K+1))).}\hfill \end{array}$$

For optimum ranking, the following conditions are necessary:

1. By Lemma 1, for any (i₁; i₂) satisfying (1 ≤ i₁ ≤ [γ(K + 1)], [γ(K + 1)] + 1 ≤ i₂ ≤ K), it is required that pr(R_(i1) ≥ γ (K + 1)) ≤ pr(R_(i2) ≤ γ(K + 1)). To satisfy this condition, divide the units into two groups by picking the units with largest (1 − γ)K values of pr(R_k ≥ γ(K + 1)) into the (above γ) group.

2. By Lemma 2

   1. For the set {k : R_k = R_(i), i = 1, …, [γ(K + 1)]} , since |γ(K + 1) − i|^p is a decreasing function of i, we require that pr(R_(i1) ≥ γ(K + 1)) ≥ pr(R_(i2) ≥ γ(K + 1)) if i₁ > i₂. Therefore, for the units with ranks (1,… γK), the ranks should be determined by ranking the pr(R_k ≥ γ(K + 1)).

   2. For the set {k : R_k = R_(i), i = [γ(K + 1)] + 1, … ,K} since |i − γ(K + 1) |^q is an increasing function of i, we require that pr(R_(i1) ≥ γ(K + 1)) ≥ pr(R_(i2) ≥ γ(K + 1)) if i₁ > i₂. Therefore, for the units with ranks (γK + 1,…,K), the ranks should be determined by ranking the pr(R_k ≥ (K + 1)).

These conditions imply that the R̃_k(γ) (P̃_k(γ)) are optimal. By the proof of Lemma 2, we know that the optimization is not unique, when there are ties in pr(R_k ≥ γ (K + 1)).

Appendix D Optimization procedure for L^†

As in the proof of Theorem 2, we begin with a necessary condition for optimization. Denote by R_(i1), R_(i2) the rank random variables for units whose ranks are estimated as i₁, i₂, where i₁ < γ(K + 1), i₂ > γ(K + 1). Let,

$$\text{pr}(R_{(i_1)}\ge \gamma (K+1))=p_1,\text{pr}(R_{(i_2)}\ge \gamma (K+1)=p_2.$$

For the index selection to be optimal,

$$\begin{array}{cc}\hfill & \mathrm{E}[{(R_{(i_1)}-\gamma (K+1))}^2|R_{(i_1)}\ge \gamma (K+1)]p_1+c\mathrm{E}[(R_{(i_2)}-\gamma {(K+1))}^2|R_{(i_2)}<\gamma (K+1)](1-p_2)\hfill \\ \le \hfill & c\mathrm{E}[{(R_{(i_1)}-\gamma (K+1))}^2|R_{(i_1)}<\gamma (K+1)](1-p_1)+\mathrm{E}[{(R_{(i_2)}-\gamma (K+1))}^2|R_{(i_2)}\ge \gamma (K+1)]p_{2.}\hfill \end{array}$$

The following is equivalent to the foregoing:

$$\begin{array}{cc}\hfill & \mathrm{E}[{(R_{(i_1)}-\gamma (K+1))}^2|R_{(i_1)}\ge \gamma (K+1)]p_1-c\mathrm{E}[R_{(i_1)}-\gamma {(K+1))}^2|R_{(i_1)}<\gamma (K+1)](1-p_1)\hfill \\ \le \hfill & \mathrm{E}[{(R_{(i_2)}-\gamma (K+1))}^2|R_{(i_2)}\ge \gamma (K+1)]p_2-c\mathrm{E}[R_{(i_2)}-\gamma {(K+1))}^2|R_{(i_2)}<\gamma (K+1)](1-p_2).\hfill \end{array}$$

Therefore, with p_k = pr(R_k ≥ γ(K + 1)) the optimal ranks split the θs into a lower fraction and an upper fraction by ranking the quantity,

$$\mathrm{E}[{(R_k-\gamma (K+1))}^2|R_k\ge \gamma (K+1)]p_k-c\mathrm{E}[{(R_k-\gamma (K+1))}^2|R_k<\gamma (K+1)](1-p_k).$$

This result is useful and different from that of WSEL in Section Appendix A in the sense that we can now successfully get a quantity depend on unit index k only. However, as for L_0/1 optimization of L^† does not induce an optimal ordering in the two groups. A second stage loss, for example SEL, can be imposed within the two groups.

Appendix E Optimizing L^‡

As for optimizing WSEL in Section Appendix A, a pairwise switch algorithm is computationally challenging, since the decision on switching a pair of units depends on their relative position and on their estimated ranks. Thus, in each iteration all pair-wise relations have to be checked. We have not identified a general representation or efficient algorithm for the optimal ranks. However, we have developed the following relation between L^†, L̃ and L^‡. Note that when either $A{B}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})\ne 0\text{or}B{A}_k(\gamma ,P_k,P_k^{\mathit{\text{est}}})\ne 0$ it must be the case that either $P_k^{\mathit{\text{est}}}\ge \gamma \ge P_k\mathrm{\text{or}}{P}_k\ge \gamma \ge P_k^{\mathit{\text{est}}}$. Equivalently,

$$|P_k-\gamma |+|P_k^{\mathit{\text{est}}}-\gamma |=|P_k-P_k^{\mathit{\text{est}}}|\text{or}\frac{|P_k-\gamma |}{|P_k-P_k^{\mathit{\text{est}}}|}+\frac{|P_k^{\mathit{\text{est}}}-\gamma |}{|P_k-P_k^{\mathit{\text{est}}}|}=1.$$

Now, suppose c > 0, p ≥ 1, q ≥ 1 and let m = max(p,q). Then, using the inequality 2^1−m ≤ a^m + (1 − a)^m ≤ 1 for 0 ≤ a ≤ 1, we have that (L̃ + L^†) ≤ L^‡ ≤ 2^m−1(L̃ + L^†). Specifically, if p = q = 1, L^‡ = L̃ + L^†; if p = q = 2, then (L̃ + L^†) ≤ L^‡ ≤ 2(L̃ + L^†). Similarly, when c > 0, p ≤ 1, q ≤ 1, (L̃ + L^†) ≥ L^‡ ≥ 2^m−1 (L̃ + L^†). Therefore, L̃ and L^† can be used to control L^‡.

Appendix F Proof of Theorem 3

Since the (above γ)/(below γ) groups are formed by P̃_k(γ), $\widehat{\tilde{P}}(\gamma )$ minimizes L_0/1. For constrained SEL minimization we prove the more general result that for any (above γ)/(below γ) categorization, ordering within the groups by P̂_k produces the constrained solution. To see this, without loss of generality, assume that coordinates (1,…, γK) are in the (below γ) group and (γK + 1,…,K) are in the (above γ) group. Similar to Section Appendix A,

$$\mathrm{E}{\displaystyle \sum _k{(R_k^{\mathit{\text{est}}}-R_k)}^2={\displaystyle \sum _{k}V(R_k)+{\displaystyle \sum _k{(R_k^{\mathit{\text{est}}}-{\overline{R}}_k)}^2}.}}$$

Nothing can be done to reduce the variance terms. The summed squared bias partitions into,

$${\displaystyle \sum _k{(R_k^{\mathit{\text{est}}}-{\overline{R}}_k)}^2={\displaystyle \sum _{k=1}^{\gamma K}{(R_k^{\mathit{\text{est}}}-{\overline{R}}_k)}^2+{\displaystyle \sum _{k=\gamma K+1}^K{(R_k^{\mathit{\text{est}}}-{\overline{R}}_k)}^2}}}$$

which must be minimized subject to the constraints that $(R_1^{\mathit{\text{est}}},\dots ,R_{\gamma K}^{\mathit{\text{est}}})\in \{1,\dots ,\gamma K\}\text{and}(R_{\gamma K+1}^{\mathit{\text{est}}},\dots ,R_K^{\mathit{\text{est}}})\in \{\gamma K+1,\dots ,K\}$. We deal only with the (below γ) group; the (above γ) group is handled in the same manner. Without loss of generality assume that R̄₁ < R̄₂ < … < R̄_γK and compare SEL for $R_k^{\mathit{\text{est}}}=\text{rank}\left({\overline{R}}_K\right)=k,k=1,\dots ,\gamma K$ to any other assignment. It is straightforward to show that switching any pair that does not follow the R̄_k order reduces SEL. Iterating this and noting that the R̂_k = rank(R̄_k) produces the result.

Appendix G Proof of Theorem 4

Recall that for a positive, discrete random variable the expected value can be computed as the sum of (1 − cdf) at mass points, where cdf is the cumulative distribution function, so

$$\begin{array}{ccc}{\overline{R}}_k\hfill & =\hfill & {\displaystyle \sum _{\nu =1}^K\nu \text{pr}[R_k=\nu ]={\displaystyle \sum _{\nu =1}^K\text{pr}[R_k\ge \nu ]}}\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{\nu =1}^K\frac{2(K-\nu +1)}{K(K+1)}\frac{K(K+1)}{2(K-\nu +1)}\text{pr}[R_k\ge \nu ]}\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{\nu =1}^K\frac{2(K-\nu +1)}{K(K+1)}{R}_k^{+}(\nu ).}\hfill \end{array}$$ (17)

Relation (17) can be used to show that when the posterior distributions are stochastically ordered, R̂_k ≡ R̃_k(γ) because the order of pr[R_k ≥ ν] does not depend on γ and the R̄_k inherit their order.

Appendix H Proof of Theorem 5

In this proof we use Y_K rather than Y to stress that as K goes to infinity, the length of Y changes. For ${\overline{G}}_{{\mathbf{Y}}_{\mathbf{K}}}(t)=\frac{1}{K}{\displaystyle {\sum }_{k=1}^K\text{pr}({\theta }_k\le t|{\mathbf{Y}}_{\mathbf{K}})}$, we prove: as $K\to \infty ,|\text{pr}(P_k\ge \gamma |{\mathbf{Y}}_{\mathbf{K}})-\text{pr}({\theta }_k\ge {\overline{G}}_{{\mathbf{Y}}_{\mathbf{K}}}^{-1}(\gamma )|{\mathbf{Y}}_{\mathbf{K}})|\to 0$, where P_k is the true percentile of θ_k, Y_K is the vector (Y₁; Y₂,… , Y_K).

The posterior independence of θ_k is straightforward. Denote θ = (θ₁, …, θ_k,…, θ_K) and θ^(−k) = (θ₁,…, θ_k−1, θ_k+1,…,θ_K), where ${\theta }_k\stackrel{\mathit{\text{ind}}}{\sim }g(\cdot |Y_k)=g_k(\cdot )$. Let θ_(γ) = θ_(i,K) be the γ_th quantile of θ, if $\frac{i}{K}\le r<\frac{i+1}{K}$, where θ_(i,K) is the i_th largest number of θ. Respectively, ${\theta }_{(\gamma )}^{(-k)}$ is the γ_th quantile of θ^(−k). We also denoted θ_{(i−1,K−1)} as the (i − 1)_th largest number of θ^(−k).

For the P̃_k(γ)’s generator:

$$\begin{array}{ccc}\text{pr}(P_k\ge \gamma |{\mathbf{Y}}_{\mathbf{K}})\hfill & =\hfill & \mathrm{E}[I({\theta }_k\ge {\theta }_{(\gamma )})|{\mathbf{Y}}_{\mathbf{K}})]\hfill \\ \hfill & =\hfill & \mathrm{E}[I({\theta }_k\ge {\theta }_{(\gamma )}^{(-k)}|{\mathbf{Y}}_{\mathbf{K}})]+\mathrm{E}[I({\theta }_k\ge {\theta }_{(\gamma )})-I({\theta }_k\ge {\theta }_{(\gamma )}^{(-k)})|{\mathbf{Y}}_{\mathbf{K}}]\hfill \end{array}$$ (18)

For the second term in (18)

$$\mathrm{E}[I({\theta }_k\ge {\theta }_{(\gamma )})-I({\theta }_k\ge {\theta }_{(\gamma )}^{(-k)})|{\mathbf{Y}}_{\mathbf{K}}]=-\text{pr}({\theta }_{(\gamma )}^{(-k)}\le {\theta }_k<{\theta }_{(\gamma )}|{\mathbf{Y}}_{\mathbf{K}})+\text{pr}({\theta }_{(\gamma )}\le {\theta }_k<{\theta }_{(\gamma )}^{(-k)}|{\mathbf{Y}}_{\mathbf{k}})$$

We have the inequality $\frac{i-1}{K-1}<\frac{i}{K}\le \gamma <\frac{i+1}{K}$, θ_(γ) = θ_(i,K) by definition. Consider the relation between $\frac{i}{K-1}$ and γ:

• If $\gamma <\frac{i}{K-1},\text{then}\frac{i-1}{K-1}<\frac{i}{K}\le \gamma <\frac{i}{K-1}<\frac{i+1}{K},{\theta }_{(\gamma )}^{(-k)}={\theta }_{(i-1,K-1)}$ pr(θ_{(i−1,K−1)} ≤ θ_k < θ_(i,K)|Y_K) = 0 and pr(θ_(i,K) < θ_k ≤ θ_{(i−1,K−1)}|Y_K) = 0;

• If $\frac{i}{K-1}\le \gamma ,\text{then}\frac{i-1}{K-1}<\frac{i}{K}<\frac{i}{K-1}\le \gamma <\frac{i+1}{K},{\theta }_{(\gamma )}^{(-k)}={\theta }_{(i,K-1)}$ pr(θ_(i,K−1) < θ_k ≤ θ_(i,K)|Y_K) = 0 and pr(θ_(i,K) < θ_k ≤ θ_{(i−1,K−1)}|Y_K) = 0.

Thus the second term in (18) is zero,

$$\begin{array}{ccc}\text{pr}(P_k\ge \gamma |{\mathbf{Y}}_{\mathbf{K}})\hfill & =\hfill & \mathrm{E}[I({\theta }_k\ge {\theta }_{(\gamma )}^{(-k)})|{\mathbf{Y}}_{\mathbf{K}}]=\mathrm{E}[\mathrm{E}[I({\theta }_k\ge {\theta }_{(\gamma )}^{(-k)})|{\mathit{\theta }}^{(-k)}]|{\mathbf{Y}}_{\mathbf{K}}]\hfill \\ \hfill & =\hfill & \mathrm{E}[\text{pr}({\theta }_k\ge G^{-1}(\gamma )|{\mathbf{Y}}_{\mathbf{K}})+g_k(G^{-1}(\gamma ))({\theta }_{(\gamma )}^{(-k)}-G^{-1}(\gamma ))+o_p({\theta }_{(\gamma )}^{(-k)}-G^{-1}(\gamma ))|{\mathbf{Y}}_{\mathbf{K}}]\hfill \\ \hfill & =\hfill & \text{pr}({\theta }_k\ge G^{-1}(\gamma )|Y_k)+g_k(G^{-1}(\gamma ))\mathrm{E}[({\theta }_{(\gamma )}^{(-k)}-G^{-1}(\gamma ))+o_p({\theta }_{(\gamma )}^{(-k)}-G^{-1}(\gamma ))|{\mathbf{Y}}_{\mathbf{K}}]\hfill \end{array}$$ (19)

In (19), ${\theta }_{(\gamma )}^{(-k)}$ is the γ_th quantile of non-iid K − 1 samples from K − 1 posterior distributions. By theorem 5.2.1 of David and Nagaraja (2003) and large sample theorem of order statistics from iid sampling, we have ${\theta }_{(\gamma )}^{(-k)}\to G^{-1}(\gamma )$ in probability as K goes to ∞. Since we assume that θ_k|Y_k has a uniformly bounded finite second moment, so does ${\theta }_{(\gamma )}^{(-k)}|{\mathbf{Y}}_{\mathbf{K}}$. Thus $\mathrm{E}[{\theta }_{(\gamma )}^{(-k)}|{\mathbf{Y}}_{\mathbf{K}}]\to G^{-1}(\gamma )$.

The generator of $P_k^{*}(\gamma )$ is:

$$\begin{array}{ccc}\text{pr}({\theta }_k\ge {\overline{G}}_{{\mathbf{Y}}_{\mathbf{K}}}^{-1}(\gamma )|{\mathbf{Y}}_{\mathbf{K}})\hfill & =\hfill & \text{pr}({\theta }_k\ge G^{-1}(\gamma )|{\mathbf{Y}}_{\mathbf{K}})+g_k({\overline{G}}^{-1}(\gamma ))({\overline{G}}_{{\mathbf{Y}}_{\mathbf{K}}}^{-1}(\gamma )-G^{-1}(\gamma ))\hfill \\ \hfill & \hfill & +o({\overline{G}}_{{\mathbf{Y}}_{\mathbf{K}}}^{-1}(\gamma )-G^{-1}(\gamma ))\hfill \\ \hfill & =\hfill & \text{pr}({\theta }_k\ge G^{-1}(\gamma )|Y_k)+g_k({\overline{G}}^{-1}(\gamma ))({\overline{G}}_{{\mathbf{Y}}_{\mathbf{K}}}^{-1}(\gamma )-G^{-1}(\gamma ))\hfill \\ \hfill & \hfill & +o({\overline{G}}_{{\mathbf{Y}}_{\mathbf{K}}}^{-1}(\gamma )-G^{-1}(\gamma ))\hfill \end{array}$$ (20)

Since ${\overline{G}}_{{\mathbf{Y}}_{\mathbf{K}}}^{-1}(\gamma )\to G^{-1}(\gamma )$ by (19) and (20), |pr(P_k ≥ γ|Y_K) − pr(θ_k ≥ ${\overline{G}}_{{\mathbf{Y}}_{\mathbf{K}}}^{-1}(\gamma )|{\mathbf{Y}}_{\mathbf{K}})|\to 0$.

Appendix I Scoring function

For each function S(P), there will be an optimal SEL ranking estimator. For instance,

$$S(P)=(aP+b)\ast {\mathrm{I}}_{\{P>\gamma \},}a>0$$

indicates that the reward or penalty is the same for all units below the threshold γ; for units above γ the reward/penalty is linearly related to the rank.

We study the (above γ)/(below γ) classification, but more than two ordinal categories can be of interest. For example, educational institutions might be classified into three categories, the poor, the average and the excellent. The following two S(P) capture this goal. Let J ≥ 3 be the number of ordered categories, then

$$S(P)={\displaystyle \sum _{j=1}^J{a}_{j}I(P\le {\gamma }_j),0<{\gamma }_1<\cdots <{\gamma }_J,a_j\ge 0}$$

or

$$S(P)={\displaystyle \sum _{j=1}^J{a}_{j}I(P\le {\gamma }_j)+a_{0}P,0<{\gamma }_1<\cdots <{\gamma }_J,a_j\ge 0.}$$