CLIC: clustering analysis of large microarray datasets with individual dimension-based clustering

Taegyun Yun; Taeho Hwang; Kihoon Cha; Gwan-Su Yi

doi:10.1093/nar/gkq516

. 2010 Jun 6;38(Web Server issue):W246–W253. doi: 10.1093/nar/gkq516

CLIC: clustering analysis of large microarray datasets with individual dimension-based clustering

Taegyun Yun ¹, Taeho Hwang ¹, Kihoon Cha ², Gwan-Su Yi ^1,2,3,^*

PMCID: PMC2896182 PMID: 20529873

Abstract

Large microarray data sets have recently become common. However, most available clustering methods do not easily handle large microarray data sets due to their very large computational complexity and memory requirements. Furthermore, typical clustering methods construct oversimplified clusters that ignore subtle but meaningful changes in the expression patterns present in large microarray data sets. It is necessary to develop an efficient clustering method that identifies both absolute expression differences and expression profile patterns in different expression levels for large microarray data sets. This study presents CLIC, which meets the requirements of clustering analysis particularly but not limited to large microarray data sets. CLIC is based on a novel concept in which genes are clustered in individual dimensions first and in which the ordinal labels of clusters in each dimension are then used for further full dimension-wide clustering. CLIC enables iterative sub-clustering into more homogeneous groups and the identification of common expression patterns among the genes separated in different groups due to the large difference in the expression levels. In addition, the computation of clustering is parallelized, the number of clusters is automatically detected, and the functional enrichment for each cluster and pattern is provided. CLIC is freely available at http://gexp2.kaist.ac.kr/clic.

INTRODUCTION

Microarray analysis is used to monitor the expression patterns of tens of thousands genes simultaneously (1–5). The identification of gene clusters showing correlated expression patterns is one of the most important steps in microarray analyses as it helps to reveal the novel function of genes, gene expression regulation and concerted gene functions in pathogenesis (6–9).

Recently demand has increased for the analysis of large microarray data sets as the number of genes in commercially available probe sets increases and as the number of test samples for an experimental set increases (10). However, most available clustering methods cannot conduct clustering analysis properly with large microarray data sets. Agglomerative clustering approaches such as the hierarchical clustering method require a quadratic increase in the distance matrix size as the number of genes increases. Partitioning approach (such as k-center or k-means methods) conduct distance comparisons iteratively to determine the find optimal cluster centers. They also require additional iterative processes to determine the appropriate number of clusters (k) to evaluate the cluster validity for different k sets of clusters. Model-based clustering approaches decrease the computational cost from gene-to-gene comparison to gene-to-cluster comparisons. Moreover, the number of clusters can be determined automatically during the clustering process in some model-based approaches such as the Bayesian infinite mixture model method (11,12). In spite of its advanced features, the use of a model-based approach with high-dimensional data or large-scale microarray data is limited due to the computational complexity and the difficulty in specifying data distributions (13). In summary, clustering tasks for large microarray data sets are computationally expensive and often technically infeasible when using only an ordinary personal computer.

To avoid this complexity, a filtering step to select a manageable number of significant genes often antecedes a clustering analysis. However, this approach can lead to information loss as it can exclude genes which may have meaningful biological functions.

In addition, the expression patterns of lowly expressed genes can easily be ignored when clustering is accomplished with a conventional Euclidean distance metric because these genes can show small expression changes. The correlation-based similarity metric can be used to identify similar expression patterns having various levels of expression differences, but the information pertaining to the absolute expression differences can be lost. This dilemma is aggravated when the size of the microarray data set increases as the levels of expression changes become diversified. To tackle this problem, it is necessary to cluster large data sets successively into smaller sub-clusters using both the absolute expression differences and expression profile patterns iteratively. This may involve considerable computation complexity and memory usage if conventional clustering methods are used.

CLIC was developed to address the aforementioned problems. Instead of clustering genes based on all N dimensional array conditions, CLIC clusters genes separately in each array dimension first and N distinct clustering results are combined later. The computation of clustering in each array becomes a single-dimensional problem and N distinct jobs can be distributed to a cluster of computing nodes. The memory requirement for the distance measure decreases to the size of the genes (M) from an M × N matrix. CLIC constructs N dimensional clusters by aligning the genes with their cluster indices that are assigned ordinally with the expression levels in 1D clustering. The resulting clusters are subjected to further sub-clustering via the same procedure successively as long as the validity of the resulting clusters is maintained. The patterns of cluster indices of genes are re-examined against the entire set of clusters to find similar patterns of expression profiles that are hidden in different clusters due to the different amplitudes of expressions.

In summary, CLIC provides advanced features particularly in clustering analyses that are not limited to large microarray data sets via the following functions: (i) parallelized computation of individual dimension-based clustering including automatic determination of the number of clusters, (ii) intrinsic normalization of expression values along the array dimensions and clusters via the ordinal labeling of a cluster instead of the gene expression values during the full dimension-wide clustering, (iii) the iterative discovery of the sub-clusters of a given cluster and the evaluation of discovered clusters with cluster homogeneity, (iv) the identification and grouping of the common expression profile patterns of genes hidden in the same and different clusters, (v) visual inspection of the discovered clusters and patterns using a heatmap and (vi) functional enrichment of each cluster and pattern.

ALGORITHM OF INDIVIDUAL DIMENSION-BASED CLUSTERING

One-dimensional clustering

The first step of CLIC is the decomposing of the M × N microarray data matrix into N separate M × 1 vectors (M is the number of gene probes, and N is the number of array conditions). Genes in each array dimension are clustered using k-means clustering for a series of k, the number of clusters. The time complexity of k-means clustering with a 1D data set is substantially decreased compared to that with a d-dimensional data set (d > 1) (14). The optimal k is determined after evaluating the validity of k clusters using a modified version of the Silhouette statistic, which is optimized for the evaluation of clusters having sequentially listed 1D values. The modified Silhouette statistic is defined as follows:

Here, a′(i) is the distance between gene i and the center of its own cluster, and b′(i) is the minimum distance between the values obtained from gene i and the centers of its two adjacent clusters. The validity of the given clusters is estimated from the average s′(i) of all genes. The overall computation of cluster validation for an M × N microarray data matrix is reduced considerably from M × M to 3 × M × N (M >> N).

Identification of the clusters for combined matrix

After the 1D clustering process, the genes in each dimension are labelled with ordinal variables, cluster indices, in an ascending order of cluster centers. With this process, the ratio variables of the microarray expression values are replaced by the ordinal variables. The systematic variation of the expression levels among the arrays and clusters can be neutralized by these discretized cluster indices.

Individual array dimensions (or columns in a microarray matrix) are prioritized and rearranged in a descending order of the average approximated Silhouette statistics of the clusters in each dimension. The genes are re-aligned in an ascending order of cluster indices successively from the leftmost column that has the maximum average approximated Silhouettes statistics to the rightmost column that has the lowest cluster validity. In this step, genes having a similar cluster index pattern over N dimensional arrays are aligned together in the reconstructed matrix. Generally, lower cluster indices or lowly expressed genes reside in the upper region of the cluster index matrix. To identify the cluster boundaries, the cluster boundary distance, d(g_m,g_m+1), is measured for every adjacent gene pair, as follows:

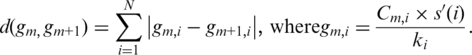Here, m ranges from 1 to M−1; C_m_,_i is a cluster index in row m and column i; s′(i) is an approximated Silhouette index of column i; and k_i is the number of clusters of column i. The cluster boundary distance, d(g_m, g_m+1), is the sum of the cluster index differences of an adjacent gene pair for all columns weighed by the cluster validity and the number of clusters in each column. From the site showing the largest cluster boundary distance to the next site, cluster boundaries are examined successively as long as the average cluster homogeneity of neighboring clusters is improved by the boundary selection. The site showing the maximum cluster homogeneity is selected as a cluster boundary. The degree of cluster homogeneity is measured by the average Pearson correlation coefficient of the expression values of the genes in each cluster.

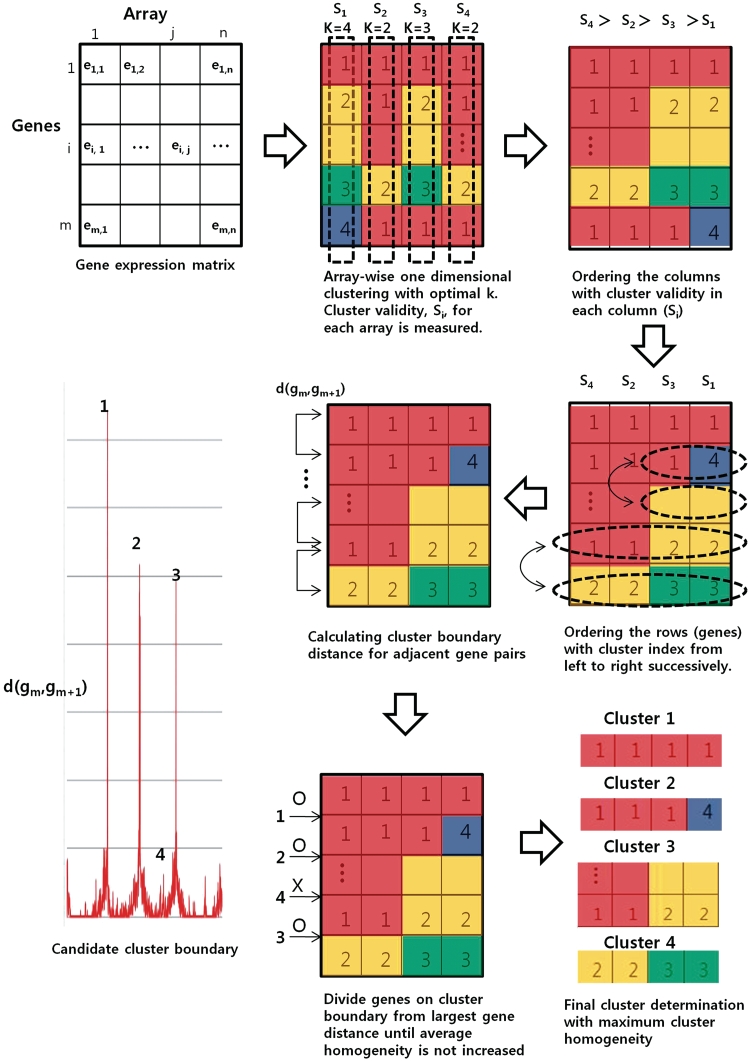
The overall process of individual dimension-based clustering is summarized at Figure 1. One set of these clustering processes generates first-round clusters in CLIC and the same processes are used for the subsequent sub-clustering step.

Sub-clustering and grouping of the rescaled expression pattern

In an analysis of a large microarray data set, the potential clusters, especially the clusters in lowly expressed genes, may not be fully separated due to the influence of several distinct clusters of large distributional differences. The repeated sub-clustering of each cluster generated in first-round clustering provides the opportunity to uncover more homogeneous groups in the clusters. Sub-clustering analysis is conducted for the previously determined first-round clusters. Sub-clustering continues until the homogeneity of a newly discovered sub-cluster is larger than that of the original cluster. In distance-based clustering, if the genes have a large difference in their expression levels, they cannot be grouped together despite the fact that they may have a similar expression pattern through the test conditions. In CLIC, the patterns of column-wide cluster indices for every gene are re-examined after the first round of the clustering and sub-clustering steps. The relative changes in the cluster indices along the different array conditions (columns in a microarray matrix) are identified as the expression profile patterns of a gene. For example, the index pattern of both 2233 and 5566 becomes 1122. Patterns with more subtle expression changes can be identified with sub-clusters because the cluster indices are rebuilt among more homogeneous sub-clusters during the sub-clustering routine.

WEB APPLICATION DESCRIPTION

Input

The input microarray data matrix format for CLIC is a tab delimited text file. CLIC allows various types of gene or probe identifiers, from Affymetrix, Agilent, Entrez Gene, UniGene, RefSeq, EMBL, ENSEMBL, SGD, RGD, MGI and HGNC. Users can choose an organism and the threshold of the corrected P-value for functional category enrichment with gene ontology (GO) (15) and KEGG pathways (16). The default parameter for the corrected P-value is set to 0.05. After uploading a microarray data file and selecting the functional enrichment parameters, clustering analysis can begin. CLIC initially checks the input file format for tab delimits and missing values. If the file passes this format check, a data filter page automatically guides headers and numerical data so that they are analyzed in an input file. The user can accept the system’s suggestion of the header and data columns or can select them manually. Users can check the progress of their submitted job during the first-round clustering, sub-clustering and pattern identification steps on the job progress page. The progress of the submitted job is renewed every 5 s, and elapsed time is displayed on this page. The progress page is moved to the result summary page and a hyperlink of this page is e-mailed when the submitted job is completed.

Interpretation of outputs

CLIC provides a result summary page which includes hyperlinks to the summary report; the first-round clustering results; sub-clustering results; and pattern identification after both the first round and sub-clustering processes. The summary report contains statistics that include the number of genes and samples in the input data, the number of discovered groups, the number of genes within each group, and a table that shows the member genes of each group. Each of clustering results and their pattern identification results include the reports of elapsed time, average homogeneity value, functional enrichment and graphical output including heatmap. Users can check the time taken to complete each analysis. Generally, a sub-clustering analysis requires much more time than other two types of analysis due to the use of repeated runs to find more homogenous groups of genes. Homogeneity information for each group helps to evaluate validity of newly generated sub-groups. Heatmaps show cluster index patterns as well as gene expression patterns. One can have a clear view of cluster integrity with the heatmaps of cluster index pattern. The functional enrichment result of different functional categories in GO and KEGG pathways for each cluster and pattern group are provided in a summarized table. The significance of the association between a given gene set and the functional annotation terms is estimated by a hypergeometric test. Multiple testing correction of the P-value in the hypergeometric test is done with a false discovery rate (FDR) method (17). The functional enrichment results for the original cluster and its sub-clusters are compared with a given threshold of the corrected P-value. After comparing significantly annotated terms, uniquely identified terms in the sub-cluster are highlighted in yellow in the functional enrichment table in a sub-cluster.

IMPLEMENTATION

The core algorithms of CLIC were implemented in R and a modified version of COFECO was used as a functional enrichment module (18). All annotation data for gene entries and functional modules for the modified version of COFECO were stored in Oracle 10g RDBMS. The web interface of CLIC was implemented in Perl. It runs on the Apache Web Server. The clustering jobs for individual dimensions were parallelized using the parallel virtual machine (PVM) via the rpvm and snow in R-packages on a Linux-based cluster system with nine nodes, each with a dual quad-core Intel Xeon 2.46 GHz CPU and 24 GB of RAM.

PERFORMANCE OF CLIC

The clustering accuracy of CLIC was compared with well known k-means method, CRC (12), MCLUST (19), CLICK (20,21), HPCluster (10) and k-boost (22) using an ARI (adjusted Rand index) (Table 1). Chinese restaurant process-based clustering (CRC) takes a model-based clustering approach that is known to be able to cluster genes and infer the number of clusters simultaneously with high accuracy. MCLUST, which is also a model-based clustering approach, finds the optimal model according to Bayesian information criteria (BIC) for expectation maximization (EM) initialized by hierarchical clustering to parameterize a Gaussian mixture model. MCLUST shows comparably good performance with the automatic detection of the optimal cluster number with the BIC criterion. CLICK is a novel clustering algorithm based on graph-theory and statistical techniques. HPCluster is a recently developed clustering method that can handle large microarray data set in significantly less time and with much less memory. The k-boost algorithm is a recently developed algorithm that clusters large microarray data sets with automatic estimation of the number of clusters based on information-theoretic principles (22). The performance of all methods except k-boost is tested on local system with Intel Xeon 2.46 GHz CPU. The k-boost algorithm is tested on AMIC@ web server (23). To test the clustering accuracy of the methods with ARI, we use used two simulated data sets (10,24) and yeast galactose microarray data set (25) that have been widely used in many previous researches for clustering performance evaluation (12). The first simulated data set was generated with four distinct clusters of 1000 gene probes in 100 array conditions. The second simulated data set was designed to have the characteristics of time series microarray data set with 100 genes in 33 array conditions. Details about the simulated data generation are provided in the Supplementary Data. Yeast galactose microarray data set is a time series data set showing the expression profiles of yeast growing with 205 genes under 20 different perturbations for the GAL pathway. The clusters of this data set have been well characterized with GO enrichment analysis in previous studies (25).

Table 1.

Adjusted rand indexes of clustering algorithms for three different data sets

	Simulated (1000, 100, 4)	Simulated (100, 33, 9)	Yeast galactose (205, 20,4)
CLIC	1 (4)	1 (9)	0.97 (4)
k-means	0.68 (4)	0.88 (9)	0.87 (4)
HPCluster	1 (4)	1 (9)	0.83 (4)
CRC	0.90 (6)	0.46 (4)	0.97 (4)
MCLUST	1 (4)	0.98 (9)	0.97 (4)
k-boost	0.72 (3)	0.20 (3)	0.95 (4)
CLICK	NA (1)	0 (2)	0.81 (2)

Open in a new tab

The details of the yeast galactose data set and simulated data sets are described in the manuscript and in the Supplementary Data. Numbers are followed by the data name (the number of genes, the number of samples and the number of true clusters).

Table 1 summarizes the performance of tested methods. ARI measures the level of agreement between the clustering result and the true cluster within the minimum value 0 to the maximum value 1.

CLIC successfully detected the true number of clusters and performed well with higher ARI accuracy for all three different data sets. Some methods showed low accuracy in simulated data sets mainly due to the wrong estimation of cluster number (CRC, k-boost and CLICK) but all methods showed comparable accuracy for yeast galactose data set which is real microarray data set. As k-means and HPCLUST require a specific number of clusters, the true number of clusters was provided. CRC required several parameters, including the number of chains, the number of cycle, the inversion flag parameter and max shift parameter. The parameter values followed the author’s recommendation in these experiments. MCLUST requires the G parameter, which represents the integer vector specifying the number of mixture components for calculating BIC. We used the default range of G which is from 1 to 9 as the true number of clusters for the three data sets is in this range. CLICK is known for its high accuracy but it underestimated the number of clusters for the three data sets. It may be due to its characteristics that produces a hard partition of genes and cannot identify very small clusters. In general, all methods are expected to have comparable clustering performance as long as the number of clusters is correctly determined.

To show the characteristics of the scalability in CLIC, experiment to measures the execution time for complete a clustering analysis with differently sized data sets was conducted. We generated different subsets of GSE4290 data set obtained from GEO database in NCBI (26). The GSE4290 has 54 765 gene probes and 104 samples. The details of data generation are described in Supplementary Data. Among the six compared clustering algorithms for the accuracy test, k-means clustering and HPCluster were not included in this comparison because these methods require a separate procedure to determine the number of clusters (see also Supplementary Data for the comparison of these methods with estimated running times for cluster number determination). Table 2 presents the results of this analysis. The execution time was measured in seconds and was averaged over five runs. The execution time for CLIC and k-boost linearly increase in reasonable time scale as the size of the data set increase. In other words, these algorithms scale well as the size of data set increases. CLICK shows good characteristics that the execution time does not increase in these gene sizes although it is relatively high and fluctuated in lower sized data sets. However, the execution time of CLICK jumped up to 2334 s when the gene size reached 40 000 genes. The model-based approaches, CRC and MCLUST, show much worse performance in execution time than the other methods and CRC was not completed in a reasonable time.

Table 2.

Execution times of clustering algorithms for data sets of different sizes

	5000	10 000	15 000	20 000	25 000	30 000
CLIC	69	132	201	273	345	466
CRC	9709	28 871	NC	NC	NC	NC
MCLUST	2023	6533	12 517	23 771	32 861	46 972
k-boost	185	432	660	1028	1183	1781
CLICK	559	930	481	373	325	587

Open in a new tab

HPCluster and k-means methods listed in Table 1 are not included in this comparison because these methods require a separate procedure to determine the number of clusters. The execution time is measured in seconds. NC: clustering analysis is not completed.

As a unique feature of CLIC, sub-clustering and pattern identification were conducted on these three data sets. A performance comparison was not provided because other competing approaches did not have these functionalities. Two of the simulated data sets could not be sub-clustered because all of the determined clusters are already very homogenous. In yeast galactose data set, CLIC identified 17 sub-clusters having more homogenous expression patterns. CLIC found 20 distinct expression profile patterns with the relative changes of cluster indices from first round clustering results and nine of those from sub-clustering results in yeast galactose data set.

Example analysis

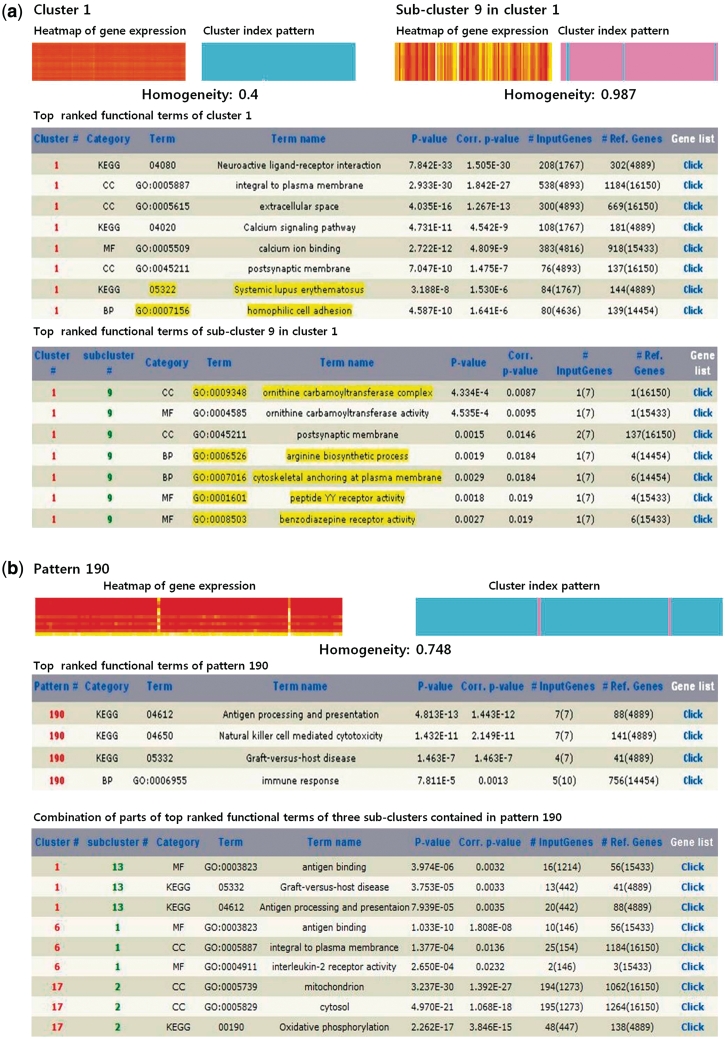
An example study to show the benefits of CLIC is presented that uses NCI 60 cell line data (27) obtained from BioGPS (28). This data set consists of 22 283 gene probes and 108 samples collected from various human cancer cell lines. This large data set was successfully clustered into 17 clusters. These clusters were sub-clustered into several more homogenous groups of genes. The execution time for the first round of clustering was ∼300 s, and that of sub-clustering steps with nine iterations including the identification of the expression patterns for both clustering results was ∼900 s in the previously described computing environments. The functional enrichment step required nearly 20 min for all identified clusters and patterns. Figure 2a shows cluster 1 and its sub-cluster 9. The homogeneity of the gene expression levels increased from 0.4 to 0.987 after cluster 1 was sub-clustered. The most significantly enriched term for cluster 1 was the ‘neuroactive ligand-receptor interaction’ (P = 1.505E−33). After sub-clustering, the GO CC term ‘ornithine carbamoyltransferase complex’ was newly found for sub-cluster 9 of cluster 1. Interestingly, three genes from the cluster 1, seven genes from cluster 6, and one gene from cluster 17 could be grouped together by sub-clustering as they showed a similar pattern (pattern 190) that was scarcely hardly recognized in the first-round cluster result due to their different expression levels (Figure 2b). The genes grouped in pattern 190 are highly expressed in the B cell leukemia and T cell leukemia cell lines and are enriched to the ‘antigen processing and presentation’ KEGG pathway (P = 1.443E−12). This pathway was enriched by the three genes from the cluster 1, which implies that the other eight genes in pattern 190 also might have a functional association with respect to this pathway, as they have common rescaled expression patterns.

Figure 2. — Example study of NCI 60 data with CLIC. (a) Heatmap (left: gene expression levels, right: pattern of cluster indices), and a part of top-ranked functionally enriched terms for cluster 1 and its sub-cluster 9. Functional terms uniquely enriched by a selected cluster 1 with a given threshold level are highlighted. Uniquely identified functional terms in sub-cluster compared to those in its original cluster 1 are highlighted. The homogeneity of sub-cluster (0.987) is increased dramatically from that of its mother cluster (0.4); (b) Heatmap, and a part of top-ranked functionally enriched terms for pattern 190 (above table) and the terms for three sub-clusters that include the genes in pattern 190 (below table).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Grant from the second stage of the Brain Korea 21 Project in 2010. Funding for open access charge: the second stage of the Brain Korea 21 Project in 2010.

Conflict of interest statement. None declared.

Supplementary Material

[Supplementary Data]

gkq516_index.html^{(737B, html)}

REFERENCES

1.Alizadeh AA, Eisen MB, Davis RE, Ma C, Lossos IS, Rosenwald A, Boldrick JC, Sabet H, Tran T, Yu X, et al. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature. 2000;403:503–511. doi: 10.1038/35000501. [DOI] [PubMed] [Google Scholar]
2.Alon U, Barkai N, Notterman DA, Gish K, Ybarra S, Mack D, Levine AJ. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc. Natl Acad. Sci. USA. 1999;96:6745–6750. doi: 10.1073/pnas.96.12.6745. [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999;286:531–537. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
4.Perou CM, Jeffrey SS, van de Rijn M, Rees CA, Eisen MB, Ross DT, Pergamenschikov A, Williams CF, Zhu SX, Lee JC, et al. Distinctive gene expression patterns in human mammary epithelial cells and breast cancers. Proc. Natl Acad. Sci. USA. 1999;96:9212–9217. doi: 10.1073/pnas.96.16.9212. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Pollack JR, Perou CM, Alizadeh AA, Eisen MB, Pergamenschikov A, Williams CF, Jeffrey SS, Botstein D, Brown PO. Genome-wide analysis of DNA copy-number changes using cDNA microarrays. Nature Genetics. 1999;23:41–46. doi: 10.1038/12640. [DOI] [PubMed] [Google Scholar]
6.Eisen MB, Spellman PT, Brown PO, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc. Natl Acad. Sci. USA. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Hughes JD, Estep PW, Tavazoie S, Church GM. Computational identification of cis-regulatory elements associated with groups of functionally related genes in Saccharomyces cerevisiae. J. Mol. Biol. 2000;296:1205–1214. doi: 10.1006/jmbi.2000.3519. [DOI] [PubMed] [Google Scholar]
8.Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, Eisen MB, Brown PO, Botstein D, Futcher B. Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell. 1998;9:3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Cho RJ, Campbell MJ, Winzeler EA, Steinmetz L, Conway A, Wodicka L, Wolfsberg TG, Gabrielian AE, Landsman D, Lockhart DJ, et al. A genome-wide transcriptional analysis of the mitotic cell cycle. Mol. Cell. 1998;2:65–73. doi: 10.1016/s1097-2765(00)80114-8. [DOI] [PubMed] [Google Scholar]
10.Sharma A, Podolsky R, Zhao J, McIndoe RA. A modified hyperplane clustering algorithm allows for efficient and accurate clustering of extremely large datasets. Bioinformatics. 2009;25:1152–1157. doi: 10.1093/bioinformatics/btp123. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Medvedovic M, Sivaganesan S. Bayesian infinite mixture model based clustering of gene expression profiles. Bioinformatics. 2002;18:1194–1206. doi: 10.1093/bioinformatics/18.9.1194. [DOI] [PubMed] [Google Scholar]
12.Qin ZS. Clustering microarray gene expression data using weighted Chinese restaurant process. Bioinformatics. 2006;22:1988–1997. doi: 10.1093/bioinformatics/btl284. [DOI] [PubMed] [Google Scholar]
13.Tseng GC, Wong WH. Tight clustering: a resampling-based approach for identifying stable and tight patterns in data. Biometrics. 2005;61:10–16. doi: 10.1111/j.0006-341X.2005.031032.x. [DOI] [PubMed] [Google Scholar]
14.Har-Peled S, Sadri B. How fast is the k-means method? Algorithmica. 2005;3:185–202. [Google Scholar]
15.Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, et al. Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nature Genetics. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Kanehisa M, Araki M, Goto S, Hattori M, Hirakawa M, Itoh M, Katayama T, Kawashima S, Okuda S, Tokimatsu T, et al. KEGG for linking genomes to life and the environment. Nucleic Acids Res. 2008;36:D480–D484. doi: 10.1093/nar/gkm882. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Benjamini Y, Drai D, Elmer G, Kafkafi N, Golani I. Controlling the false discovery rate in behavior genetics research. Behavioural Brain Res. 2001;125:279–284. doi: 10.1016/s0166-4328(01)00297-2. [DOI] [PubMed] [Google Scholar]
18.Sun CH, Kim MS, Han Y, Yi GS. COFECO: composite function annotation enriched by protein complex data. Nucleic Acids Res. 2009;37:W350–W355. doi: 10.1093/nar/gkp331. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Yeung KY, Fraley C, Murua A, Raftery AE, Ruzzo WL. Model-based clustering and data transformations for gene expression data. Bioinformatics. 2001;17:977–987. doi: 10.1093/bioinformatics/17.10.977. [DOI] [PubMed] [Google Scholar]
20.Sharan R, Shamir R. CLICK: a clustering algorithm with applications to gene expression analysis. Proceedings of the 11th. International Conference on Intelligent Systems for Molecular Biology; ISMB. International Conference on Intelligent Systems for Molecular Biology. 2000;8:307–316. [PubMed] [Google Scholar]
21.Sharan R, Maron-Katz A, Shamir R. CLICK and EXPANDER: a system for clustering and visualizing gene expression data. Bioinformatics. 2003;19:1787–1799. doi: 10.1093/bioinformatics/btg232. [DOI] [PubMed] [Google Scholar]
22.Geraci F, Leoncini M, Montangero M, Pellegrini M, Renda ME. K-Boost: a scalable algorithm for high-quality clustering of microarray gene expression data. J. Comput. Biol. 2009;16:859–873. doi: 10.1089/cmb.2008.0201. [DOI] [PubMed] [Google Scholar]
23.Geraci F, Pellegrini M, Renda ME. AMIC@: all microarray clusterings @ once. Nucleic Acids Res. 2008;36:W315–W319. doi: 10.1093/nar/gkn265. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Michaud DJ, Marsh AG, Dhurjati PS. eXPatGen: generating dynamic expression patterns for the systematic evaluation of analytical methods. Bioinformatics. 2003;19:1140–1146. doi: 10.1093/bioinformatics/btg132. [DOI] [PubMed] [Google Scholar]
25.Ideker T, Thorsson V, Ranish JA, Christmas R, Buhler J, Eng JK, Bumgarner R, Goodlett DR, Aebersold R, Hood L. Integrated genomic and proteomic analyses of a systematically perturbed metabolic network. Science. 2001;292:929–934. doi: 10.1126/science.292.5518.929. [DOI] [PubMed] [Google Scholar]
26.Sun L, Hui AM, Su Q, Vortmeyer A, Kotliarov Y, Pastorino S, Passaniti A, Menon J, Walling J, Bailey R, et al. Neuronal and glioma-derived stem cell factor induces angiogenesis within the brain. Cancer Cell. 2006;9:287–300. doi: 10.1016/j.ccr.2006.03.003. [DOI] [PubMed] [Google Scholar]
27.Ross DT, Scherf U, Eisen MB, Perou CM, Rees C, Spellman P, Iyer V, Jeffrey SS, Van de Rijn M, Waltham M, et al. Systematic variation in gene expression patterns in human cancer cell lines. Nature Genetics. 2000;24:227–235. doi: 10.1038/73432. [DOI] [PubMed] [Google Scholar]
28.Wu C, Orozco C, Boyer J, Leglise M, Goodale J, Batalov S, Hodge CL, Haase J, Janes J, Huss JW, 3rd, et al. BioGPS: an extensible and customizable portal for querying and organizing gene annotation resources. Genome Biol. 2009;10:R130. doi: 10.1186/gb-2009-10-11-r130. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]

gkq516_index.html^{(737B, html)}

gkq516_nar-00476-web-b-2010-File004.doc^{(59KB, doc)}

[B1] 1.Alizadeh AA, Eisen MB, Davis RE, Ma C, Lossos IS, Rosenwald A, Boldrick JC, Sabet H, Tran T, Yu X, et al. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature. 2000;403:503–511. doi: 10.1038/35000501. [DOI] [PubMed] [Google Scholar]

[B2] 2.Alon U, Barkai N, Notterman DA, Gish K, Ybarra S, Mack D, Levine AJ. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc. Natl Acad. Sci. USA. 1999;96:6745–6750. doi: 10.1073/pnas.96.12.6745. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B3] 3.Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999;286:531–537. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]

[B4] 4.Perou CM, Jeffrey SS, van de Rijn M, Rees CA, Eisen MB, Ross DT, Pergamenschikov A, Williams CF, Zhu SX, Lee JC, et al. Distinctive gene expression patterns in human mammary epithelial cells and breast cancers. Proc. Natl Acad. Sci. USA. 1999;96:9212–9217. doi: 10.1073/pnas.96.16.9212. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B5] 5.Pollack JR, Perou CM, Alizadeh AA, Eisen MB, Pergamenschikov A, Williams CF, Jeffrey SS, Botstein D, Brown PO. Genome-wide analysis of DNA copy-number changes using cDNA microarrays. Nature Genetics. 1999;23:41–46. doi: 10.1038/12640. [DOI] [PubMed] [Google Scholar]

[B6] 6.Eisen MB, Spellman PT, Brown PO, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc. Natl Acad. Sci. USA. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B7] 7.Hughes JD, Estep PW, Tavazoie S, Church GM. Computational identification of cis-regulatory elements associated with groups of functionally related genes in Saccharomyces cerevisiae. J. Mol. Biol. 2000;296:1205–1214. doi: 10.1006/jmbi.2000.3519. [DOI] [PubMed] [Google Scholar]

[B8] 8.Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, Eisen MB, Brown PO, Botstein D, Futcher B. Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell. 1998;9:3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B9] 9.Cho RJ, Campbell MJ, Winzeler EA, Steinmetz L, Conway A, Wodicka L, Wolfsberg TG, Gabrielian AE, Landsman D, Lockhart DJ, et al. A genome-wide transcriptional analysis of the mitotic cell cycle. Mol. Cell. 1998;2:65–73. doi: 10.1016/s1097-2765(00)80114-8. [DOI] [PubMed] [Google Scholar]

[B10] 10.Sharma A, Podolsky R, Zhao J, McIndoe RA. A modified hyperplane clustering algorithm allows for efficient and accurate clustering of extremely large datasets. Bioinformatics. 2009;25:1152–1157. doi: 10.1093/bioinformatics/btp123. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B11] 11.Medvedovic M, Sivaganesan S. Bayesian infinite mixture model based clustering of gene expression profiles. Bioinformatics. 2002;18:1194–1206. doi: 10.1093/bioinformatics/18.9.1194. [DOI] [PubMed] [Google Scholar]

[B12] 12.Qin ZS. Clustering microarray gene expression data using weighted Chinese restaurant process. Bioinformatics. 2006;22:1988–1997. doi: 10.1093/bioinformatics/btl284. [DOI] [PubMed] [Google Scholar]

[B13] 13.Tseng GC, Wong WH. Tight clustering: a resampling-based approach for identifying stable and tight patterns in data. Biometrics. 2005;61:10–16. doi: 10.1111/j.0006-341X.2005.031032.x. [DOI] [PubMed] [Google Scholar]

[B14] 14.Har-Peled S, Sadri B. How fast is the k-means method? Algorithmica. 2005;3:185–202. [Google Scholar]

[B15] 15.Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, et al. Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nature Genetics. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B16] 16.Kanehisa M, Araki M, Goto S, Hattori M, Hirakawa M, Itoh M, Katayama T, Kawashima S, Okuda S, Tokimatsu T, et al. KEGG for linking genomes to life and the environment. Nucleic Acids Res. 2008;36:D480–D484. doi: 10.1093/nar/gkm882. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B17] 17.Benjamini Y, Drai D, Elmer G, Kafkafi N, Golani I. Controlling the false discovery rate in behavior genetics research. Behavioural Brain Res. 2001;125:279–284. doi: 10.1016/s0166-4328(01)00297-2. [DOI] [PubMed] [Google Scholar]

[B18] 18.Sun CH, Kim MS, Han Y, Yi GS. COFECO: composite function annotation enriched by protein complex data. Nucleic Acids Res. 2009;37:W350–W355. doi: 10.1093/nar/gkp331. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B19] 19.Yeung KY, Fraley C, Murua A, Raftery AE, Ruzzo WL. Model-based clustering and data transformations for gene expression data. Bioinformatics. 2001;17:977–987. doi: 10.1093/bioinformatics/17.10.977. [DOI] [PubMed] [Google Scholar]

[B20] 20.Sharan R, Shamir R. CLICK: a clustering algorithm with applications to gene expression analysis. Proceedings of the 11th. International Conference on Intelligent Systems for Molecular Biology; ISMB. International Conference on Intelligent Systems for Molecular Biology. 2000;8:307–316. [PubMed] [Google Scholar]

[B21] 21.Sharan R, Maron-Katz A, Shamir R. CLICK and EXPANDER: a system for clustering and visualizing gene expression data. Bioinformatics. 2003;19:1787–1799. doi: 10.1093/bioinformatics/btg232. [DOI] [PubMed] [Google Scholar]

[B22] 22.Geraci F, Leoncini M, Montangero M, Pellegrini M, Renda ME. K-Boost: a scalable algorithm for high-quality clustering of microarray gene expression data. J. Comput. Biol. 2009;16:859–873. doi: 10.1089/cmb.2008.0201. [DOI] [PubMed] [Google Scholar]

[B23] 23.Geraci F, Pellegrini M, Renda ME. AMIC@: all microarray clusterings @ once. Nucleic Acids Res. 2008;36:W315–W319. doi: 10.1093/nar/gkn265. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B24] 24.Michaud DJ, Marsh AG, Dhurjati PS. eXPatGen: generating dynamic expression patterns for the systematic evaluation of analytical methods. Bioinformatics. 2003;19:1140–1146. doi: 10.1093/bioinformatics/btg132. [DOI] [PubMed] [Google Scholar]

[B25] 25.Ideker T, Thorsson V, Ranish JA, Christmas R, Buhler J, Eng JK, Bumgarner R, Goodlett DR, Aebersold R, Hood L. Integrated genomic and proteomic analyses of a systematically perturbed metabolic network. Science. 2001;292:929–934. doi: 10.1126/science.292.5518.929. [DOI] [PubMed] [Google Scholar]

[B26] 26.Sun L, Hui AM, Su Q, Vortmeyer A, Kotliarov Y, Pastorino S, Passaniti A, Menon J, Walling J, Bailey R, et al. Neuronal and glioma-derived stem cell factor induces angiogenesis within the brain. Cancer Cell. 2006;9:287–300. doi: 10.1016/j.ccr.2006.03.003. [DOI] [PubMed] [Google Scholar]

[B27] 27.Ross DT, Scherf U, Eisen MB, Perou CM, Rees C, Spellman P, Iyer V, Jeffrey SS, Van de Rijn M, Waltham M, et al. Systematic variation in gene expression patterns in human cancer cell lines. Nature Genetics. 2000;24:227–235. doi: 10.1038/73432. [DOI] [PubMed] [Google Scholar]

[B28] 28.Wu C, Orozco C, Boyer J, Leglise M, Goodale J, Batalov S, Hodge CL, Haase J, Janes J, Huss JW, 3rd, et al. BioGPS: an extensible and customizable portal for querying and organizing gene annotation resources. Genome Biol. 2009;10:R130. doi: 10.1186/gb-2009-10-11-r130. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

CLIC: clustering analysis of large microarray datasets with individual dimension-based clustering

Taegyun Yun

Taeho Hwang

Kihoon Cha

Gwan-Su Yi

Abstract

INTRODUCTION