Biases in Illumina transcriptome sequencing caused by random hexamer priming

Abstract

Generation of cDNA using random hexamer priming induces biases in the nucleotide composition at the beginning of transcriptome sequencing reads from the Illumina Genome Analyzer. The bias is independent of organism and laboratory and impacts the uniformity of the reads along the transcriptome. We provide a read count reweighting scheme, based on the nucleotide frequencies of the reads, that mitigates the impact of the bias.

INTRODUCTION

Transcriptome analysis using next-generation sequencing technologies, or RNA-Seq, is a promising new form of analysis already yielding breakthrough discoveries. It is well-known that spatial biases along the genome exist, resulting in a non-uniform coverage of expressed transcripts (1). These spatial biases hinder comparisons between genomic regions and will therefore adversely affect any analysis where such a comparison is integral. Two important such types of analyses, on which RNA-Seq is expected to have great impact, are the study of alternative splicing, where an alternatively spliced exon is compared with a constitutively spliced exon, and de novo inference of gene structure.

General biases in DNA sequencing using the Illumina platform have been studied in (2). Dohm et al. found that there was no fragmentation bias in DNA sequencing reads, but uneven coverage as a result of locally varying GC content.

The standard library preparation protocol (1) for transcriptome sequencing using the Illumina Genome Analyzer platform starts with extraction of total RNA, followed by poly(A) enrichment using oligo(dT) beads, RNA fragmentation and reverse transcription into double-stranded complementary DNA (dscDNA) primed by random hexamers. The resulting dscDNA is then sequenced using the DNA sequencing protocol, starting with end repair, addition of an A nucleotide and adapter ligation. Random hexamer priming is utilized to generate reads across the entire length of all expressed transcripts, although the resulting sequence coverage is far from uniform (1). Fragmenting the RNA prior to reverse transcription has been shown to make coverage more uniform within a transcript (1).

Here, we demonstrate that the use of random hexamer priming results in a bias in the nucleotide composition at the start of sequencing reads and that this bias influences the uniformity of the location of the reads along expressed transcripts. We also propose a reweighting scheme that adjusts for the bias and makes the distribution of sequencing reads more uniform.

MATERIALS AND METHODS

Data

Data were obtained according to information in the references. Additional data have been deposited to the Short Read Archive under accession number SRA009901.

The Supplementary Data section contains precise details on the number of (mapped, unmapped) reads (Supplementary Tables S1 and S2), data files and their origin (Supplementary Table S3) and an overview of experimental protocols (Supplementary Table S4). One lane worth of data was used for each sample depicted in Figures 1–3. One lane was selected at random from each experiment, except for Nagalakshmi where we chose a lane each from a randomly primed sample (RH) and an oligo(dT) primed sample (DT) and Wang where we chose a lane each from heart and brain tissue.

Figure 1.

Nucleotide frequencies versus position for stringently mapped reads. For each experiment, mapped reads were extended upstream of the 5′-start position, such that the first position of the actual read is 1 and positions 0 to −20 are obtained from the genome. The first hexamer of the read is shaded. Brief experimental protocols are indicated in the key. (a) RNA-Seq experiments conducted using priming with random hexamers, with and without RNA fragmentation. (b) DNA resequencing and ChIP-Seq experiments. (c) RNA-Seq experiments with alternative library preparation protocols, including priming with random hexamers followed by fragmentation using DNase I and priming with oligo(dT) followed by fragmentation using either DNase I, nebulization or sonication.

Figure 2.

Hexamer frequencies. (a) The logarithm (base 2) of all (4096) observed hexamer frequencies computed using positions 1–6 of the aligned reads for an experiment in H. sapiens (8) versus an experiment in S. cerevisiae (9). The two distributions have a correlation of 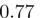. (b) As in (a), but the hexamers correspond to positions 25–30 of the aligned reads, with a correlation of .

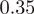Figure 3.

Nucleotide frequencies versus position for stringently mapped stranded reads for the A nucleotide. (a and b) As in Figure 1a, but split according to whether reads map to the sense or antisense strand. (c) Difference between the frequencies in (a and b).

Mapping

Reads were mapped using Bowtie (3), requiring perfect and unique matching to the genome. See Supplementary Data for additional information.

Free energies

Binding energies were computed using the program ‘DNA’, from the Mobyle webserver hosted at the Pasteur Institute, which provides access to the EMBOSS (4) suite of programs. Free energies from RNA–DNA duplexes were used.

Reweighting scheme

Each read is assigned a weight 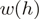based on its first heptamer 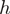(seven bases) and computed as follows. Given a set of mapped reads, let 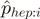be the observed distribution of heptamers starting at position (hence spanning positions to i + 6) of the reads. Specifically, 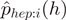is the proportion of reads which have heptamer 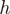at position and 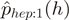is the proportion of reads starting with heptamer 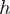. Define the weights 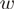by

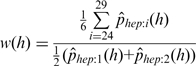(1)

(Here, we assume a read length of at least 35 nt.)

At each (stranded) genomic location , we compute the number of reads 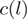with 5′-end mapping to . Each (stranded) genomic position is identified with a single heptamer 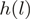and the reweighted counts are computed as 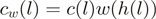. A specific example is provided in Table 1.

Table 1.

Data from a small genomic region in the sense strand of the YOL086C gene in S. cerevisiae

Strand	Location	Heptamer	Count	Weight	Reweighted count
…
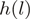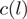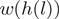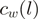−1	159792	TTGGTCG	17	1.39	23.6
−1	159793	TTTGGTC	17	0.25	4.3
−1	159794	TTTTGGT	65	0.31	20.4
−1	159795	GTTTTGG	72	0.32	23.3
−1	159796	CGTTTTG	10	1.66	16.6
…

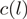denotes the number of mapped reads starting at a particular (stranded) location and 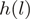is the unique heptamer associated with this location. 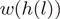are weights such as in Equation (1) and 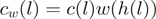are the location-specific reweighted counts. For this particular small genomic region, reweighting makes the counts more comparable between different locations. Data from the WT experiment.

The method is implemented in the R package Genominator (version 1.1.5), released through the Bioconductor Project (5).

Evaluation of the reweighting scheme

Regions of constant expression (ROCE) were defined based on existing annotation as maximal genomic regions for which each position is annotated as belonging to the same set of transcripts (for example, two overlapping transcripts are split into three ROCEs). Highly expressed ROCEs (heROCEs) were defined as ROCEs longer than 100 (Saccharomyces cerevisiae) or 50 (Homo sapiens) mappable bases, with more than one mapped read per mappable base. For the experiments considered here, roughly 10% of all ROCEs were highly expressed (Supplementary Table S2).

For each heROCE, we computed 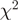goodness-of-fit statistics to the Poisson distribution with a constant intensity and coefficients of variation for the unadjusted 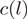and the reweighted 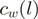counts (Figure 4 and Supplementary Figures S6–S8). Either of these two measures being lower for the reweighted counts than for the unadjusted counts was taken as evidence that reweighting improved the uniformity of the location of the reads within heROCEs. For five different data sets (four from S. cerevisiae and one from H. sapiens), we observed a consistent decrease in both measures for almost all heROCEs.

Figure 4.

Evaluation of the reweighting scheme. (a and b) Unadjusted and re-weighted base-level counts for reads from the WT experiment mapped to the sense strand of a 1-kb coding region in S. cerevisiae (YOL086C). The graey bars near the x-axis indicate unmappable genomic locations. (c) The 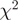goodness-of-fit statistics based on unadjusted and reweighted counts for 552 highly expressed regions of constant expression. (d) Smoothed histograms of the reduction in 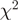goodness-of-fit statistics when using the re-weighting scheme, evaluated in five different experiments. Values greater than zero indicate that the re-weighting scheme improves the uniformity of the read distribution.

RESULTS

Positional nucleotide bias

To explore potential biases in the sequencing system, we analyzed data from a number of recently published and unpublished RNA-Seq experiments conducted using the Illumina Genome Analyzer (1,6–9). For each experiment, we determined a set of stringently mapped reads and computed the nucleotide frequencies for each position of the reads (see ‘Materials and Methods’ section).

There is a strong distinctive pattern in the nucleotide frequencies of the first 13 positions at the 5′-end of mapped RNA-Seq reads (Figure 1a). The nucleotide frequencies vary from position to position, but are almost the same across different experiments. It is striking that while the exact nucleotide frequencies differ slightly between experiments, their relative changes are nearly identical. After the first 13 positions, the nucleotide frequencies become independent of position, but are different between experiments, presumably reflecting the base content of the different transcriptomes. The pattern is thus reproducible across experiments in different organisms and laboratories. A similar pattern is also present when all unmapped (versus. only mapped) reads are considered (Supplementary Figure S1).

It is not only the frequencies of single nucleotides at the 5′-end of reads that are very similar across experiments, but also the frequencies of longer runs of nucleotides, such as hexamers. As an example, in Figure 2, we compare the distributions of hexamers corresponding to read positions 1–6 as well as positions 25 to 30 for S. cerevisiae and H. sapiens. Presumably, the sizable correlation (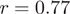) at the beginning of reads primarily reflects a bias in nucleotide content, whereas the limited correlation (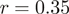) at the end reflects some similarity of hexamer composition between the transcriptomes of the two organisms.

This dependence of nucleotide frequency on position can occur either because of a reproducible bias originating from the sequencing platform or because of a spatial bias of the reads across the transcriptome.

In contrast to RNA-Seq, no strong distinctive pattern in nucleotide frequencies is observed for DNA resequencing and ChIP-Seq experiments (10–14) (Figure 1b and Supplementary Figure S2). This shows that the 5′ nucleotide bias from RNA-Seq is not caused by the Illumina Genome Analyzer DNA sequencing protocol, but rather by additional steps in the RNA-Seq library preparation, namely RNA extraction and reverse transcription into dscDNA. The standard protocol described above was used in all experiments in Figure 1a, except for two experiments that omitted RNA fragmentation.

Based on Figure 1c, we conclude that the pattern is caused by the use of random hexamers to prime the reverse transcription of RNA into dscDNA. The figure shows a number of RNA-Seq experiments employing alternative library preparation protocols (15–17). Two of these experiments used oligo(dT) priming followed by fragmentation of dscDNA using nebulization and sonication; both these experiments show no dependence of the nucleotide frequencies on position. The other two experiments employed oligo(dT) priming and random hexamer priming, both followed by fragmentation of dscDNA using DNase I. The nucleotide frequencies for these latter two experiments have similar patterns, but compared with the pattern of the RNA-Seq experiments of Figure 1a, this pattern is smaller in magnitude and extends upstream of the start position of the reads. Because the two different priming methods used in these experiments result in the same pattern, we conclude that the pattern is caused by DNase I digestion.

We find that computationally predicted binding energies associated with the random hexamers do not explain the observed hexamer frequencies at the beginning of the reads (see Supplementary Data, Supplementary Figure S3). Rather, we find that any relationship between binding energies and hexamer frequencies is a feature of the particular transcriptome and is not related to the use of random hexamers for priming.

In the standard model of second-strand synthesis of dscDNA, the second DNA strand is synthesized by DNA polymerase primed from nicks in the original RNA strand, where the nicks are created by lightly treating the RNA–DNA duplexes with RNase. This model implies that the 5′ bias caused by random hexamer priming will only affect reads from the 5′-end of the first strand. We have used the annotated coding regions of the genome to infer whether reads are likely to have originated from the sense strand (second-strand synthesis by DNA polymerase) or the antisense strand (first-strand synthesis by reverse transcriptase) (Figure 3a–b and Supplementary Figure S4). A 5′ pattern similar to the one depicted in Figure 1a is visible on both strands, suggesting that the second-strand DNA synthesis is not solely primed by nicked RNA, but also by random hexamers remaining in the solution. There is a small, but consistent difference between the patterns on the sense and antisense strands (Figure 3c and Supplementary Figure S4), perhaps reflecting different sequence specificity of reverse transcriptase and DNA polymerase or the effect of nick priming.

A model for the bias

If the reads were uniformly sampled from the transcriptome, there would be no dependence of nucleotide frequencies on position. Based on this observation, we now posit the following model: priming using random hexamers generates a biased sample of dscDNA fragments, not uniformly distributed across the transcriptome. Specifically, dscDNA fragments beginning with certain 13-mers are over- and underrepresented compared with the frequency of the 13-mers in the transcriptome. Starting with such a biased sample of fragments, the resulting reads produced by the Genome Analyzer reflect the bias in the nucleotide frequencies of these fragments. This interpretation implies that the pattern is not caused by sequencing errors and hence cannot be removed by trimming the 5′-end of the reads. Indeed, we have consistently found that more reads map by trimming their 3′-end than their 5′-end, in agreement with a higher error rate at the 3′-end of the reads. Trimming the 5′-end of the reads would thus remove the pattern only from the part of the reads that is mapped to the genome, but the pattern would be visible in the nucleotides upstream of the mapped trimmed portion of the reads. This model also explains why dscDNA fragmentation substantially alters the 5′ pattern (Figure 1c), as the fragmentation occurs after random priming and generates a new set of fragments with ends affected by DNase I.

It is surprising that the pattern extends well beyond the hexamer primer, out to 13 bases. The length of the pattern could potentially be explained by a strong bias in the first 6 bases of the reads, coupled with dependencies between adjacent nucleotides in the transcriptome. Two observations contradict this explanation. First, the pattern in the nucleotide frequencies ends immediately upstream of the first base of the reads, indicating that the dependence between adjacent nucleotides in the transcriptome is weak (Figure 1a). Note that it is possible for a pattern to extend upstream of the reads, as seen with DNase I fragmentation (Figure 1c). Second, dinucleotide transition probabilities appear biased throughout all 13 initial bases (Supplementary Figure S5). The fact that the 5′ bias extends over 13 bases could be explained by the sequence specificity of the polymerase. Alternately, due to the end repair performed as part of the standard DNA sequencing protocol, the first sequenced base of a read may not be where the primer binds.

Adjusting for the bias

In order to investigate the effect of the priming bias on the distribution of reads along expressed transcripts and adjust for this bias, we developed the following read count re-weighting scheme. Each read is assigned a weight based on its first heptamer, reflecting the fact that certain heptamers are overrepresented in the biased distribution at the start of the reads, relative to the unbiased distribution at the end. Reads beginning with a heptamer overrepresented in the heptamer distribution at the beginning relative to the end are downweighted and vice versa. Accordingly, weights are of the following general form

(2)

where 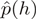is the proportion of reads starting/ending with heptamer 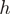[in practice, we use a slight variation of this basic idea to compute the weights, see Equation (1) in ‘Materials and Methods’ section for a precise definition]. The weights are used in the following way: instead of counting the reads mapping to a genomic region (for example, an exon), the weights of the reads mapping to the region are added, see Table 1 for an example. Simply counting the reads mapping to a genomic region is equivalent to a reweighting scheme where all weights are equal to one. The weights are constructed in such a way that the distribution of the first heptamer of the re-weighted reads is equal to the distribution of the last heptamer of the unweighted reads.

Defining the weights based on 7 nt requires computing 4⁷–1 = 16 383 frequencies. While the bias extends over the first 13 positions of the reads, we have found that weights based on only the first 7 nt perform the best (with weights based on either 6 or 8 nt performing almost as well). The reason that weights based on longer oligomers do not perform better is likely to be that the number of required oligomer frequencies increases exponentially while the amount of data stays constant. In addition, as longer sequences are used, certain sequences are only observed at the beginning or at the end of the reads, leading to weights being either zero or infinity. If sequencing depth is substantially increased, it might be possible to base the weights on >7 nt. Note that one of the data sets used for evaluation has >80 million mapped reads.

As detailed in ‘Materials and Methods’ section, we define the weights in a slightly different manner than the intuitive approach outlined above. Essentially, we average frequencies over several locations in the reads. Interestingly, we find that the performance of the reweighting scheme is substantially improved by averaging over the heptamer distributions starting at positions 1 and 2 (Supplementary Figure S8). Figure 1 shows that these two heptamer distributions are very different, since the marginal distributions of single nucleotides are very different. We propose two explanations for this improvement. First, is the well-known observation that the Illumina sequencer tends to have a higher error rate at the first base of the read (2). Second, the end repair performed as part of the standard protocol may shift the start position of the read relative to the binding of the random hexamer.

Using data from experiments in S. cerevisiae (8) and H. sapiens (9), we found that reweighting the reads improves their uniformity along expressed transcripts, although substantial heterogeneity remains (Figure 4 and Supplementary Figures S6–S8). We concentrated on non-short, highly expressed regions of constant expression, defined based on existing gene annotation (roughly equal to coding sequences in yeast and exons in human) and taking mappability into account. We used highly expressed regions (>1 read per base), because evaluating the effect of the methodology on base-level spatial heterogeneity requires a reasonable number of reads per base. For measuring the uniformity of the reads, we used the 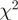goodness-of-fit statistic and the coefficient of variation. Both measures were substantially reduced (up to 50%) when re-weighting was used, although the statistics as well as qualitative evaluation suggest that the reweighted counts are still not uniformly distributed within an expressed transcript.

One possible concern with this methodology is the use of the same data set for computing the weights and evaluating the performance improvement, especially since we focus on highly expressed genes where most of the reads come from. We have also computed the weights using only reads that mapped outside of highly expressed genes and the performance improvement did not change. For convenience, we suggest using all mapped reads to compute the weights.

DISCUSSION

We have shown that priming using random hexamers biases the nucleotide content of RNA sequencing reads and that this bias also affects the uniformity of the locations of the reads along expressed transcripts. Despite this bias, we believe that priming using random hexamers is preferable to using oligo(dT) priming, as the latter is highly biased toward the 3′-end of the expressed transcripts.

Mamanova et al. recently described an alternative protocol for sequencing RNA using the Illumina Genome Analyzer (18), in which reverse transcription takes place directly on the flow cell and which yields stranded reads and avoids polymerase chain reaction amplification. RNA is not converted to dscDNA using random priming, instead sequencing adapters are ligated directly onto RNA fragments. The ligated RNA library is then reverse transcribed on the flow cell. Data from their study does not show the nucleotide biases reported here (Supplementary Figure S9).

As an alternative to poly(A) enrichment, Armour et al. describe a protocol for ribosomal depletion, where only a subset of the 4096 possible hexamers are used to prime the reverse transcription (19). There are currently no publicly available data sets generated using this protocol.

A natural question is whether the read biases observed with the Illumina Genome Analyzer also occur with other sequencing platforms. We have begun investigating SOLiD data and our preliminary results based on data from (20) indicate that similar, but smaller random priming biases may be present in addition to more important SOLiD-specific biases.

We have provided a method for adjusting the nucleotide bias and have shown that this method makes the start positions of the reads closer to being uniformly distributed across the transcriptome. The method is implemented in the R package Genominator available from Bioconductor (5).

During the review of the present manuscript, we became aware of recent related work by Li et al. (‘Modeling non-uniformity in short-read rates in RNA-Seq data’, submitted for publication). These authors consider a different approach for handling the non-uniformity of the read distribution, which involves modeling the base-level read counts of a given gene using a Poisson model with parameter that is a function of the neighboring nucleotides. Compared to our reweighting procedure, the Li et al. method relies on gene annotation and does not relate to the library preparation protocol (i.e. random hexamer priming). In a similar spirit, Bullard (21) considers generalized linear models for base-level read counts in a simulation study assessing the performance of the differential allele-specific expression method proposed in Bullard et al. (22). However, preliminary attempts in the explicit modeling of base-level read counts have had limited success and more research and benchmarking is needed before one can confidently derive expression measures based on such models.

Alleviating the positional bias induced by random hexamer priming is one step toward enabling comparisons within samples, between distinct genomic regions. Such comparisons are crucial to several aims of transcriptome sequencing, including the study of alternative splicing, transcript assembly and allele specific expression.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

U.S. National Institutes of Health, (grant U01 HG004271 to S. E. Celniker and grant R01 GM071655 to S.E.B.). Funding for open access charge: U.S. National Institutes of Health (grant U01 HG004271 to S. E. Celniker).

Conflict of interest statement. None declared.