Diffusion-Influenced Transport of Ions across a Transmembrane Channel with an Internal Binding Site

Abstract

We develop a microscopic theory for ion transport across a transmembrane channel with an internal binding site. The ion flux is determined by the rate constants for binding to the internal site from the two sides of the membrane and the corresponding unbinding rate constants. The binding rate constants are formulated in terms of diffusion-influenced reactions. The theory allows a reconciliation of experimental data on the conductance of the influenza A M2 proton channel with the structure and dynamics of the protein.

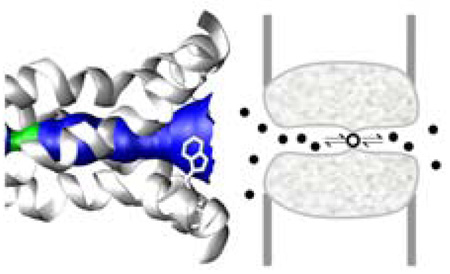
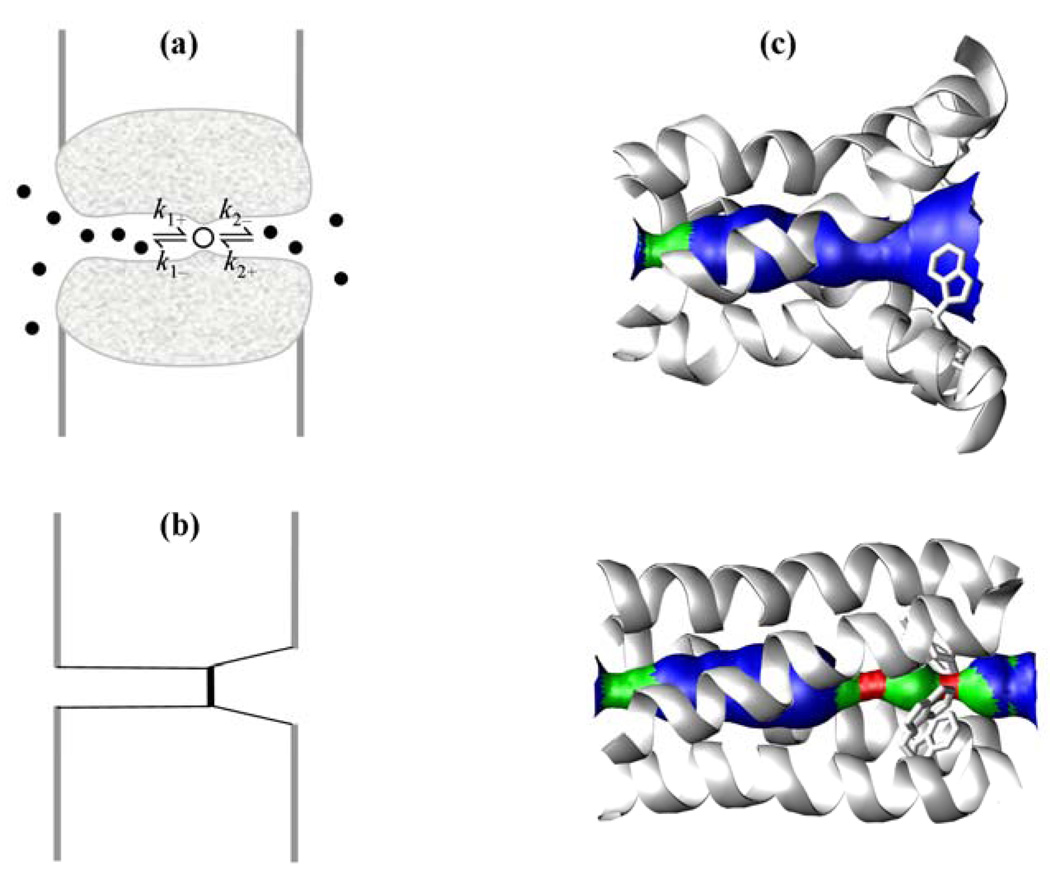
In some transmembrane ion channels, the ion selected for transport obligatorily binds to an internal site, such as a protonation site like a histidine residue in a proton channel^1–4 or a site separated by energy barriers from the two opposite entrances of the channel.^5,6 One may model by chemical kinetics the binding and unbinding on either side of the internal site (Figure 1). Specifically, an ion on the left, signified with index 1, can take up the binding site, with rate constant k₁₊, and an ion on the right side, signified with index 2, can take up the binding site, with rate constant k₂₊. Once bound (from either side), the ion can unbind either to side 1, with rate constant k₁₋, or to side 2, with rate constant k₂₋. If the ion concentrations in the bulk solutions on the two sides of the membrane are C_i, the steady-state ion flux per channel is⁵

$$I=\frac{(k_{1+}{k}_{2-}{C}_1-k_{2+}{k}_{1-}{C}_2)/(k_{1-}+k_{2-})}{1+\frac{k_{1+}{C}_1+k_{2+}{C}_2}{k_{1-}+k_{2-}}}.$$ (1)

The aim of this Letter is to present a theory for calculating the rate constants from a microscopic formulation of the binding process and use the resulting theory to characterize the structure-dynamics-function correlation of the influenza A M2 proton channel. The proton conductance function of the M2 protein is essential for viral replication.

Figure 1.

A transmembrane ion channel with an internal binding site. (a) Diffusion of ions into the pore and binding at the internal site. (b) Idealized geometry of the pore. (c) Open and closed conformations of the M2 proton channel, which consists of four identical helical subunits. Top: open conformation in which proton binding from the C-terminal side (on the right) is allowed. Bottom: closed conformation in which proton binding from the C-terminal side is prohibited by the primary gate residue Trp41, which is shown as sticks. The constriction on the left comes from Val27; the constriction near the middle of the pore seen in the bottom panel comes from His37, which is the proton binding site. Part (c) is adapted from Yi et al.⁴ with permission; copyright (2009) the National Academy of Sciences, U.S.A.

In the M2 proton channel, the obligatory binding site is provided by the His 37 tetrad (Figure 1c).^7,8 In bulk solution, the rate constant of proton binding to a histidine sidechain, i.e., an imidazole, is 10¹⁰ M⁻¹s⁻¹.⁹ Such a high binding rate constant suggests diffusion control. Diffusion-controlled proton binding to imidazole can be modeled as absorption of diffusing protons by a patch on an otherwise reflecting spherical surface. When the patch spans 60° in polar angle, the rate constant is ~2πDa₀,¹⁰ where D is the proton diffusion constant and a₀ is the proton-imidazole contact radius. The observed rate constant is reproduced with the measured proton diffusion constant¹¹ of 10³ Ų/ns and a₀ = 2.6 Å, a size that seems quite reasonable. A binding site in the channel pore is much less accessible than its counterpart in bulk solution, and hence the diffusion-limited binding rate constant would be reduced.^12,13 Consequently there is all the more reason to model proton binding to the His37 tetrad in the pore of the M2 protein as diffusion-controlled.

The binding rate constants k_i+ and the corresponding unbinding rate constants k_i− are related by the dissociation constants:

$$\frac{k_{i-}}{k_{i+}}=K_{\mathrm{d}i},i=1\text{ and }2.$$ (2)

The two dissociation constants K_d1 and K_d2 are related, since they describe the binding equilibra of the same species, i.e., the permeating ion to the same site. When the excess chemical potentials of the ion in the bulk solutions on the two sides of the membrane are the same, then we must have K_d1 = K_d2; hereafter we refer to this value as the intrinsic dissociation constant and denote it as $K_{\mathrm{d}}^0$. Note that, in this case, as expected, the ion flux given by eq (1) is zero when C₁ = C₂. More generally, when there is a difference, say ΔU, in excess chemical potential on going from the bulk solution on side 1 to the bulk solution on side 2, e.g., due to a voltage across the membrane, then corresponding differences, ΔU₁ and ΔU₂, respectively, exist between the binding site and the bulk solutions on the two sides; Δ U₁ – Δ U₂,=Δ U. Consequently

$$K_{\mathrm{d}i}=K_{\mathrm{d}}^0{e}^{\mathrm{\Delta }{U}_i/k_{\mathrm{B}}T},$$ (3a)

$$\frac{K_{\mathrm{d}2}}{K_{\mathrm{d}1}}=e^{-\mathrm{\Delta }U/k_{\mathrm{B}}T},$$ (3b)

where k_B is the Boltzmann constant and T the absolute temperature. Hereafter (k_BT)⁻¹ will be denoted as β. We take $K_{\mathrm{d}}^0$ as given; that allows us to focus on the binding rate constants k_i+.

In our model, k_i+ are diffusion-influenced rate constants for binding to a “buried” site. For notational simplicity, we specialize our description to the binding from one side, say side 1, and drop the index i for now. By applying the so-called constant-flux approximation¹⁰ on the channel entrance, k₊ can be calculated by solving two simpler problems.¹² The first is the “exterior” problem, for the diffusion-controlled binding of ions from the bulk solution to the channel entrance. For a circular entrance with radius a, the binding rate constant for the exterior problem is k_ex = 4Da.¹⁴

The second is the “interior” problem, for the diffusion-influenced binding of ions in the pore to the internal site, with a special boundary condition at the channel entrance. We model the motion of ions in the pore (between the channel entrance and the binding site) as one-dimensional diffusion along the channel axis, with the coordinate denoted as x. The diffusion may be influenced by a potential energy function, U(x), arising from interactions with the pore or an external voltage. The cross section, σ(x), along the pore may be non-uniform; then σ(x) effectively contributes an entropic term to the energy function.¹⁵ The channel entrance and the binding site are assumed to be located at x = 0 and x = d, respectively. The rate constant, k_in, for the interior problem is given by the flux of the steady-state diffusion equation, when the binding site is modeled as an absorbing boundary condition (or a radiation boundary condition when binding is only partially controlled by diffusion). For a cylindrical pore with radius a and a linear potential U(x) = αx, we find

$$k_{\text{in}}=\pi {\mathit{\text{Da}}}^2\alpha \beta /(e^{\alpha \beta d}-1).$$ (4)

When the pore is cone-shaped (see Figure 1b and 1c), with radius a at the binding site, radius a₂ at the pore entrance, and length d₂ along the pore axis, and the potential is zero, we have

$$k_{\text{in}}=\pi {\mathit{\text{Daa}}}_2/d_2.$$ (5)

The overall binding rate constant is¹²

$$\frac{1}{k_{+}}=\frac{1}{k_{\text{ex}}}+\frac{1}{k_{\text{in}}}.$$ (6)

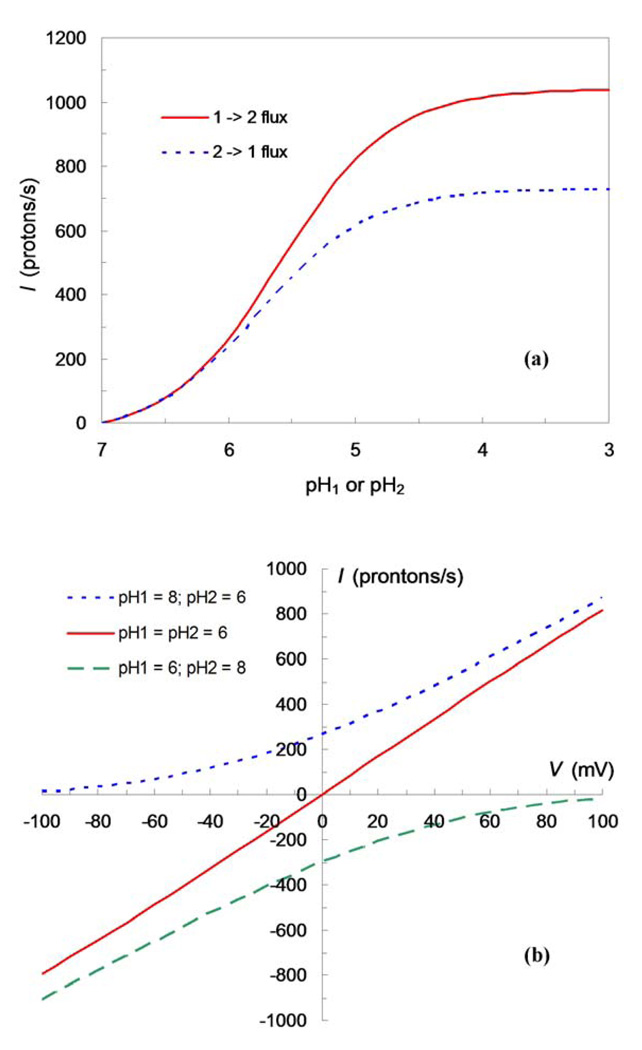
In Figure 2a, we show the flux for a cylindrical proton channel with a binding site located at d = 21 Å, or 60% through the full pore length of 35 Å, when the pH on one side is fixed at 7 while the pH on the other side is varied from 7 to 3. With D = 10³ Ų/ns and a pore radius of a = 3 Å, the rate constants for proton binding from the two sides are 0.7 × 10⁹ and 10⁹ M⁻¹s⁻¹, respectively. That k₂₊ > k₁₊ here is because the binding site is closer to the channel entrance on side 2 than to its counterpart on side 1. The intrinsic dissociation constant of the internal binding is set to 10⁻⁶ M, corresponding to the third pK_a of ~6 for the His37 tetrad of the M2 protein.^7,8 The proton flux in either direction shows saturation as the varying pH is below 4, but the saturation values in the two directions are different. According to eq (1), the saturation value of the flux is k₂₋ for the 1→2 flux (when protons are driven from side 1 to side 2) and k₁₋ for the 2→1 flux. These unbinding rate constants are given by $K_{\mathrm{d}}^0{k}_{i+}$ . The asymmetry between the fluxes in the two directions is thus due to the asymmetry in k_i+. The asymmetric and saturable fluxes shown here are qualitatively consistent with conductance measurements on the M2 protein.¹⁶ For the parameters listed above, the saturation value of the 1→2 flux is 1000 ions per channel per second. In Figure 2b, we show the flux-voltage relation for three pH gradients: pH₁ = 6, pH₂ = 8; pH₁ = 8, pH₂ = 6; and pH₁ = pH₂ = 6. Again, these results are qualitatively consistent with voltage dependences of proton currents conducted by the M2 protein.^2,16

Figure 2.

Ion fluxes driven by (a) pH gradient and (b) voltage. A cylindrical pore, with radius a = 3 Å and full length L = 35 Å, is assumed; binding to the internal site, located at d = 15 Å, is diffusion-controlled. The proton diffusion constant D is 10³ Ų/ns. When a voltage V is applied across the membrane, the potential function in the pore is taken to be a linear function: U(x) = eVx/L, where e is the proton charge.

However, the results of Figure 2 overestimate the magnitudes of the observed proton fluxes, which are of the order of 100 protons per channel per second.^2,17,18 Our model for the channel assumes a static structure for the protein, in which the binding site is always accessible to protons from the bulk solutions on both sides. In contrast, molecular dynamics (MD) simulations show that the channel is closed on both sides most of the time, and conformational gating allows protons to occasionally access the binding site.¹⁹ The ion binding rate constants are thus lower than calculated by assuming an always open channel,^12,13 leading to a reduced proton flux. We now examine the effects of conformational gating on proton flux.

It has long been known that Trp41 plays an important gating role in the M2 channel.²⁰ MD simulations further show that the gating motion of Trp41 is coupled to the global deformation of the transmembrane helix, in the form of kinking around Gly34.⁴ As previously proposed,⁴ there are two conformational states (see Figure 1c): the open state involves significant helix kinking, leading to a wider opening of the pore toward the C-terminal end (which hereafter is identified with side 2), whereas in the closed state the helix is relatively straight. Equation (1) for the ion flux can be generalized to the case where the channel protein interconverts between two conformational states.⁵ Under the condition that the conformational interconversion is much faster than proton binding/unbinding, eq (1) still holds but the rate constants are weighted averages of the two conformations. We argue that this condition is fulfilled by the M2 protein.²¹ Since only the open conformation is competent in proton binding from the C-terminal side, conformational averaging leads to

$$k_{2+}^{\text{avg}}=p_{\text{open}}{k}_{2+},$$ (7)

where p_open is the probability of the M2 protein being in the open conformation and k₂₊ is the diffusion-controlled rate constant for proton binding from the C-terminal side in that conformation.

For a cone-shaped pore with a = 3 Å, a₂ = 5 Å, and d₂ = 14 Å, k₂₊ is calculated to be 2 × 10⁹ M⁻¹s⁻¹. A $k_{2+}^{\text{avg}}$ value that is 10-fold lower than the k₂₊ value in Figure 2 is achieved if it is assumed that the M2 protein has only a 5% probability of being in the open conformation. That the open conformation is a minor population is consistent with MD simulations⁴ and the observation that NMR peaks remain in essentially the same positions upon lowering pH.²²

On the N-terminal side, Yi et al.,¹⁹ based on MD simulations, proposed that Val27 near the channel entrance serves as a “secondary” gate (see Figure 1c). The effect of a gate that stochastically switches between open and closed on the binding rate constant has been studied previously.¹² The stochastically gated rate constant, $k_{1+}^{\text{sg}}$, like the counterpart k₁₊ for an always open channel, is calculated by separately solving the exterior and interior problems. The result for diffusion-controlled binding in a cylindrical channel without a potential is

$$\frac{1}{k_{1+}^{\text{sg}}}=\frac{1}{k_{1+}}+\frac{{\omega }_{\mathrm{c}}}{{\omega }_{\mathrm{o}}}\left[\frac{1}{\omega {\widehat{k}}_{\text{ex}}(\omega )}+\frac{\text{tanh}{(\omega d^2/D)}^{1/2}}{\pi a^2{(D\omega )}^{1/2}}\right],$$ (8)

where ω_c and ω_o are the open-closed transition rates of the gate, located at the channel entrance; ω = ω_c + ω_o; and k̂_ex (s) is the Laplace transform of the time-dependent rate coefficient for the exterior problem. For a circular channel entrance, a very accurate result is²³

$$s{\widehat{k}}_{\text{ex}}(s)/4\mathit{\text{Da}}=1+(\pi /4){({\mathit{\text{sa}}}^2/D)}^{1/2}-\frac{(1-\pi /4){({\mathit{\text{sa}}}^2/D)}^{1/2}}{(1-\pi /4)\pi /2({\pi }^2/8-1)+{({\mathit{\text{sa}}}^2/D)}^{1/2}}.$$ (9)

When ω ≪ D/d² and D/a², eq (8) reduces to

$$k_{1+}^{\mathrm{\text{sg}}}=({\omega }_{\mathrm{o}}/\omega )k_{1+}.$$ (10)

At ω_o = 0.1 ns⁻¹ and ω_c = 1 ns⁻¹ (along with the other parameters used in Figure 2), $k_{1+}^{\text{sg}}$ is close to the limit of eq (10), and is reduced from k₁₊ by 10-fold. These illustrative transition rates have timescales and relative magnitudes that are consistent with the dynamics of the Val27 secondary gate seen in simulations.¹⁹ Note that the conformational interconversion important for proton binding from the C-terminal side has little effect on the binding rate constant from the N-terminal side, since the two conformations do not differ significantly in the N-terminal half (Figure 1c).

The 10-fold reductions in k_i+ by conformational gating bring the magnitude of the calculated proton flux into agreement with experimental values. Several mutations that presumably affect gating dynamics provide further test of our analysis of its effects on proton flux. For example, a mutation of Gly34 into alanine is expected to rigidify the helix backbone and hence reduce the probability of the open conformation, which we propose to be required for proton binding from the C-terminal side. Consistent with this expectation, the G34A mutation reduces the conductance of the M2 protein by 60%.²⁴ On the other hand, mutating the secondary gate residue Val27 into a smaller alanine is expected to increase the open gate probability on the N-terminal side and hence increase proton flux. Indeed, the V27A mutation leads to a 50% increase in conductance.²⁴

In summary, we have presented a microscopic theory for ion transport across a channel with an internal binding site. With this theory, we have rationalized the observed low, asymmetric, and saturable conductance of the influenza M2 proton channel in terms of the structural and dynamical properties of the protein.