Calcium(II) Site Specificity: Effect of Size and Charge on Metal Ion Binding to an EF-Hand-like Site

Abstract

The molecular mechanisms by which protein Ca(II) sites selectively bind Ca(II) even in the presence of high concentrations of other metals, particularly Na(I), K(I), and Mg(II), have not been fully described. The single Ca(II) site of the Escherichia coli receptor for D-galactose and D-glucose (GGR) is structurally related to the eukaryotic EF-hand Ca(II) sites and is ideally suited as a model for understanding the structural and electrostatic basis of Ca(II) specificity. Metal binding to the bacterial site was monitored by a Tb(III) phosphorescence assay: Ca(II) in the site was replaced with Tb(III), which was then selectively excited by energy transfer from protein tryptophans. Photons emitted from the bound Tb(III) enabled specific detection of this substrate; for other metals binding was detected by competitive displacement of Tb(III). Representative spherical metal ions from groups IA, IIA, and IIIA and the lanthanides were chosen to study the effects of metal ion size and charge on the affinity of metal binding. A dissociation constant was measured for each metal, yielding a range of K_D’s spanning over 6 orders of magnitude. Monovalent metal ions of group 1A exhibited very low affinities. Divalent group IIA metal ions exhibited affinities related to their size, with optimal binding at an effective ionic radius between those of Mg(II) (0.81 Å) and Ca(II) (1.06 Å). Trivalent metal ions of group IIIA and the lanthanides also exhibited size-dependent affinities, with an optimal effective ionic radius between those of Sc(III) (0.81 Å) and Yb(III) (0.925 Å). The results indicate that the GGR site selects metal ions on the basis of both charge and size. The site is designed to bind highly charged cations, thereby effectively excluding the abundant monovalent metals, including Na(I) and K(I). Moreover, the divalent cavity size is optimized for a metal close to Ca(II) in radius, thereby disfavoring the smaller Mg(II). These and other general factors likely to contribute to the metal specificity of protein Ca(II) sites are discussed.

Calcium (II) binding proteins play important roles in many biological systems, including intracellular signaling pathways, Ca(II) transport and storage, and stabilization of protein structure. Proper activation and function of a given Ca(II) binding protein require efficient binding of substrate Ca(II), generally present at submicromolar to micromolar concentrations inside cells (Tsien, 1989). At the same time, other metal ions are likely to be present in concentrations up to 10⁶-fold larger. Thus Ca(II) binding sites are faced with a considerable specificity problem: they must selectively bind a relatively rare substrate metal ion and exclude competing metal ions present in much higher concentrations. The structural and electrostatic mechanisms used by Ca(II) sites to provide Ca(II) specificity are not yet fully understood, in part because insufficient information is available regarding the specificities of Ca(II) sites. The present study addresses the effects of metal ion size and charge on metal binding to a model Ca(II) site.

The Escherichia coli D-galactose and D-glucose receptor (GGR, also termed the galactose binding protein) is a 36-kDa soluble protein from the aqueous periplasmic compartment between the inner and outer membranes of E. coli and similar bacteria (Hazelbauer & Adler, 1971; Scholle et al., 1987). GGR functions as the initial sugar receptor in both chemotaxis and transport systems [reviewed by Bourret et al. (1989), Meister et al. (1989), Parkinson (1988), Koshland (1988), Eisenbach and Matsumura (1988), Taylor et al. (1988), Stewart and Dahlquist (1987), MacNab (1987), and Ames (1986)] and possesses a single Ca(II) site discovered when the structure of the protein was determined by X-ray crystallography to 1.9-Å resolution (Vyas et al., 1987; Quiocho et al., 1987; Vyas et al., 1988). The function of this Ca(II) site has not yet been ascertained but may be structural rather than regulatory [Vyas et al., 1987; also, Falke et al. (unpublished results)].

Vyas, Vyas, and Quiocho have shown that the GGR Ca(II) binding loop is structurally similar to the corresponding loop of the EF-hand class of Ca(II) sites (Vyas et al., 1987; Quiocho et al., 1988), the latter found in a variety of eukaryotic regulatory proteins including calmodulin, troponin C, and others [Kretsinger, 1980; reviewed by Strynadka and James (1989)]. Figure 1A illustrates the similar backbone structures of the GGR site and calmodulin site IV (Babu et al., 1988). The backbone of the GGR site contains one unique structural feature: it consists of two stretches of polypeptide, nine and two amino acids in length, which are distant in the primary structure but adjacent in the folded structure. In contrast, EF-hand loops are composed of a single stretch of polypeptide, 12 amino acids in length. However, this difference is not likely to alter metal ion specificity, which is determined largely by the ligation structure of the bound metal. Like most EF-hand loops, the GGR site chelates Ca(II) with seven oxygen ligands in a pentagonal-bipyramidal geometry. All seven GGR ligands are protein oxygens provided by side-chain and backbone groups, such that the coordinates of these groups are similar or identical with those in EF-hand sites (Vyas et al., 1987). The ligation of the EF-hand class exhibits the greatest variability at the fifth ligand position: often the fifth ligand is provided by a water oxygen bridging the metal ion and a short side chain. Also observed, however, is direct ligation by a side-chain oxygen at the fifth ligand position, as in the GGR site (Strynadka & James, 1989). Thus, the GGR site is structurally the closest known relative of the EF-hand class. An important prediction of this picture is that the Ca(II) affinity and metal binding specificity of the GGR site should lie within the ranges observed for EF-hand sites. This prediction has recently been verified by Vyas et al. (1989). Together the available evidence indicates that a rigorous analysis of metal binding to the GGR site will be relevant to EF-hand sites.

FIGURE 1.

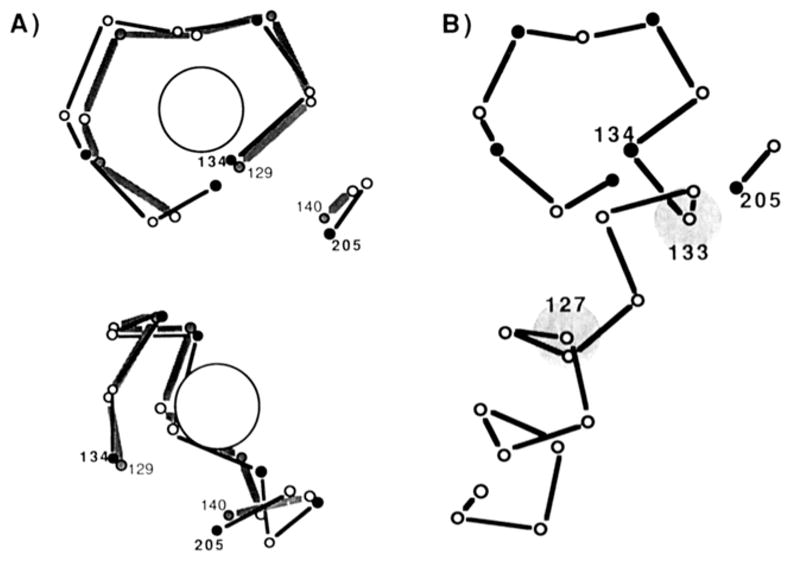
α-Carbon backbone structures of two Ca(II) sites: cal-modulin site IV and the GGR site. (A) Two views of the corresponding backbone regions of calmodulin site IV [gray line, residues 129–136 and 139–140 (Babu et al., 1988)] and of the GGR site [bold line, residues 134–142 and 204–205 (Vyas et al., 1987)]. The position of bound Ca(II) in calmodulin site IV is indicated by the large circle. Ligand positions are indicated by filled vertices in the backbone. For clarity the corresponding regions of calmodulin site IV and GGR sites are slightly offset; also, the regions of divergence are omitted (calmodulin site IV residues 137–138 are omitted, and GGR site residues 142–203 are omitted). (B) A view of the GGR site and a portion of the preceding helix (Vyas et al., 1987). The circles at helix positions 127 and 133 indicate the backbone positions of nearby tryptophan residues.

A significant experimental advantage of the GGR system is that only one Ca(II) site is present per molecule, while EF-hand proteins generally contain tightly coupled pairs of sites. Elegant studies have resolved the binding events at individual sites in such pairs (Williams et al., 1987; Forsen et al., 1988), yet cooperativity between sites, which may vary for different substrate metals, prevents rigorous analysis of metal binding specificity at individual sites. The GGR site provides no information regarding cooperativity but is ideal for a systematic study of Ca(II) site specificity. A convenient spectroscopic assay enables direct detection of metal binding: the GGR site lies within 12 Å of two tryptophan side chains and binds the phosphorescent lanthanide Tb(III) (Figure 1B). When the tryptophans are excited by absorption of photons, excitation energy is efficiently transferred to the nearby bound Tb(III), resulting in Tb(III) photon emission. Detection of emitted photons enables quantitation of Tb(III) binding, as well as binding of other metals that compete with Tb(III) for the site. This type of approach has been applied to a wide variety of Ca(II) binding proteins [for example, see Brittain et al. (1976) and Horrocks et al. (1984)], including GGR (Vyas et al., 1989).

In order to ascertain the relationship between binding to the Ca(II) site and the size and charge of metal ions, we have compared the affinities of group IA, IIA, and IIIA metal ions. These are monovalent, divalent, and trivalent cations, respectively, and all possess filled-shell spherical symmetry. We have also investigated the lanthanides, which are trivalent and essentially spherical due to their outlying filled 5s and 5p orbitals. By focusing on spherical ions with filled valence orbitals, effects due to ligation geometry, ligand field splittings, and covalent interactions are minimized. In this case the substrate ions can be treated simply as spheres of different radii and charges. The results indicate that size and charge both contribute to the binding affinity of metal ions and that the optimal radius for binding decreases as the charge of the metal ion increases. A simple model is proposed for the mechanisms underlying metal selectivity. This model will provide a framework for future site-directed-mutagenesis studies of the molecular basis of Ca(II) binding.

EXPERIMENTAL PROCEDURES

Reagents

All metal ion stock solutions were made from the highest commercially available grade of the chloride salt, in 100 mM KCl and 10 mM PIPES; all stocks were adjusted to pH 6.0. The KCl used in all phases of GGR preparation and metal binding was a grade specially purified to minimize contamination by Ca(II) [4 M KCl ionic strength adjuster solution for Ca(II) electrode work, Orion Instruments, Inc.]. The water used in all buffers was glass distilled to minimize metal contamination. Dialysis membranes were treated with two or more changes of 1 M EDTA, 100 °C, to remove metals.

Purified E. coli GGR

Plasmid pSF3 containing the E. coli GGR gene and its natural promoter was constructed according to standard techniques (Maniatis et al., 1982). The source of the promoter and gene was plasmid pMG10, graciously provided by Dr. Robert Hogg, Case Western Reserve University (Scripture & Hogg, 1983). In pMG10 the 3′ end of the GGR gene is truncated at an EcoRI site (Scholle et al., 1987); we repaired this truncation by insertion of a synthetic linker containing the missing three codons and two stop codons. Subsequently, a fragment containing the promoter and repaired gene was cloned into the polylinker of vector pEMBL19 (Dente et al., 1983) to generate pSF3, which overexpresses GGR >50-fold in E. coli.

GGR was produced by pSF3 overexpression in E. coli NM303 (F⁺ mgl-503 lacZ lacY⁺ rec A1), a mutant strain that makes no endogenous GGR (Muller et al., 1985). Cells were grown 18–24 h at 37 °C in tryptone broth (Miller, 1972) containing 25 μg/mL ampicillin to maintain the plasmid and 1 mM α-D-(+)-fucose to maximally induce the GGR promoter (Scholle et al., 1987). Standard procedures were used to isolate cells and osmotically lyse the outer membrane to release GGR (Heppel, 1971; Kellerman & Ferenci, 1982). The resulting supernatant was concentrated by ultrafiltration (Amicon YM-10 membranes) until the GGR concentration was 20 μM. Then, bound sugar and Ca(II) were removed from the protein by dialysis against 50 volumes of the following buffers, each for ≥6 h at 4 °C: (A) two times against 3 M guanidine hydrochloride (Sigma grade I), 100 mM KCl, 20 mM EDTA, 10 mM Tris, pH 7.1, with HCl, and 0.5 mM phenyl-methanesulfonyl fluoride—this buffer unfolds the protein to facilitate release of substrates (Miller et al., 1972); (B) three times against 100 mM KCl, 20 mM EDTA, and 10 mM Tris, pH 7.1, to remove substrate and denaturant; (C) two times against 100 mM KCl and 10 mM PIPES, pH 6.0. All dialysis steps were carried out with KCl, H₂O, and dialysis membranes specially purified to remove Ca(II) and other metals (see Reagents). The resulting GGR is ≥80% pure, as determined by SDS-polyacrylamide gel electrophoresis (Laemmli, 1970).

Equilibrium Dialysis to Determine K_D for Tb(III)

The dissociation constant for Tb(III) binding was measured by equilibrium dialysis in a microscale apparatus containing six pairs of 100-μL chambers separated by a MW 12000–14000 cutoff dialysis membrane. Each chamber pair contained 100 mM KCl and 10 mM PIPES, pH 6.0. One chamber contained GGR; the other initially contained added Tb(III). Following an 18-h equilibration with shaking at 23 °C, aliquots of 20 μL were removed from each chamber, and total Tb(III) was determined. Briefly, each aliquot was brought to 1% do-decyltrimethylammonium bromide (DTAB) and incubated at 95°C for 5 min to denature GGR and release bound Tb(III). Subsequently, aliquots were diluted to 1.0 mL with 1.0 mM dipicolinic acid (DPA) in 100 mM KCl and 10 mM PIPES, pH 6.0. Tb(DPA), was quantitated by excitation of the DPA at 280 nm, which in turn excites Tb(III) by energy transfer within the complex (Barela & Sherry, 1976), so that Tb(III) emission at 490 nm was detected and measured with 5-nm bandwidths on a Perkin-Elmer MPF 43A steady-state spectrofluorometer. Measured emission was converted to total Tb(III) concentration by interpolation on a Tb(DPA)₃ standard curve made with the same concentration of GGR as the experimental samples. Free and bound Tb(III) concentrations were determined as follows. The free Tb(III) concentration [Tb]_f was the concentration in the chamber lacking GGR: [Tb]_f was assumed to be the same in both chambers at equilibrium. In the protein chamber, the total Tb(III) concentration was the sum of [Tb]_f and the bound Tb(III) concentration [Tb]_b; thus, the latter quantity was obtained by subtraction of [Tb]_f.

Detection of Bound Tb(III) by Trp-Tb(III) Energy Transfer

Samples containing 2.5 μM GGR, 25 μM TbCl₃, 100 mM KCl, and 10 mM PIPES, pH 6.0, were equilibrated ≥6 h at 23 °C to ensure maximal loading of the Ca(II) site with Tb(III). GGR tryptophan residues were excited at 292 nm, and bound Tb(III) emission was measured at 543 nm. Bandwidths on both excitation and emission channels were 5 nm. The resulting emission is temperature sensitive; thus, the cuvette holder was thermostated at 25 °C.

Determination of K_D for Metal Ions That Compete with Tb(III)

Following stabilization of the bound Tb(III) emission at 543 nm, a small volume of metal ion (Cl⁻ salt) in 100 mM KCl and 10 mM PIPES, pH 6.0, was added to one of two identical emission samples in the same buffer. To the other control sample was added an equal volume of buffer only. The samples were allowed to stabilize for ~ 30 min; then, an emission reading was taken. This cycle of metal ion addition, equilibration, and emission measurement was repeated for each metal ion concentration in the titration. The ratio of emission from the experimental and control samples was F/F_max, which quantitated the fraction of bound Tb(III) remaining in the GGR site.

An advantage of the described metal affinity measurements is that the relative affinities of different metal ions will be independent of many experimental conditions. For example, E. coli encounters a broad physiological pH range due to its ubiquitous nature. In the present study the chosen pH of 6.0 was acidic so as to minimize metal hydroxide formation. It is likely that Ca(II) site ligands in the unoccupied site become increasingly protonated at lower pH and that absolute metal affinities measured at pH 6.0 are lower than those at higher pH. However, the unoccupied site is the same for all metal ions, and in known structures of occupied Ca(II) sites the protein ligands are always fully deprotonated (Strynadka & James, 1989), so that the binding equilibria of different metal ions will generally depend on pH in an identical way. Similarly, the present study utilized 100 mM KCl to minimize nonspecific ion binding. These sample parameters and many others can be described as an additive perturbation of the observed free energy of metal binding or as a multiplicative perturbation of the observed dissociation constant for metal binding:

$$\mathrm{\Delta }{G}_{\text{obs}}=\mathrm{\Delta }G+\mathrm{\Delta }{G}_{\text{p}}{K}_{\text{obs}}={KK}_{\text{p}}$$ (1)

where subscript p signifies the perturbation. Equation 1 indicates such perturbations will impact the binding of different metals equally, resulting in multiplication of measured dissociation constants by a constant factor. Thus, the relative dissociation constants, which are of primary interest, are expected to often remain the same in different experimental systems.

RESULTS

Detection of Metal Ion Binding: Energy Transfer from Tryptophan to Tb(III)

Previous studies of protein Ca(II) sites have indicated that Tb(III) is often able to effectively replace bound Ca(II) because the size of Tb(III) is similar to that of Ca(II) [effective ionic radii = 0.98 and 1.06 Å respectively (Shannon, 1976)] and because many Ca(II) sites bind both divalent and trivalent metal ions with high affinity (Britain et al., 1976; Horrocks & Albin, 1984). Tb(III) is an optically interesting metal, exhibiting multiple UV-vis absorption and emission bands due to transitions within its 4f⁸ configuration. When a suitable donor chromophore such as the indole ring of tryptophan is nearby the bound Tb(III), fluorescence energy transfer can be used to sensitively and selectively excite the bound metal. The tryptophan–Tb(III) energy-transfer pair has a characteristic distance R₀ = 3–4 Å for half-maximal energy transfer, and such energy transfer has been detected up to a distance of 12 Å in a known protein structure (Horrocks & Collier, 1981). Following excitation, Tb(III) decays to the ground state by one of several emissive transitions. The most intense emission is produced by a ⁵D₄–⁷F₅ transition in the 535–555-nm region, with a phosphorescence decay time of 0.1–10 ms. The decay time is long because the transition is Laporte forbidden, due to its intraconfigurational nature. A considerable advantage of the approach is that it detects only Tb(III) bound in the protein site near chromophores: Tb(III) free in solution does not interfere.

In the primary structure of GGR, Trp 127 and Trp 133 lie nearby the Ca(II) loop, which begins at Asp 134. In the folded protein both residues are within 12 Å of the bound metal; thus, both residues may be able to transfer energy to bound Tb(III). Figure 2 indicates that such energy transfer does indeed occur: when the five GGR tryptophans were excited at 292 nm, their emission at 340 nm was reduced by ~ 25% upon binding of Tb(III) to the Ca(II) site (Figure 2B), suggesting that one to two Trp residues were quenched by bound Tb(III). Concomitantly, two new emission bands appeared at 495 and 543 nm upon binding of Tb(III) (Figure 2B). These Tb(III) emission bands were observed only when Tb(III) occupied the Ca(II) site: they were absent when GGR was not added (Figure 2A, compare spectra 1 and 2). As expected, the ⁵D₄–⁷F₅ transition at 543 nm gave the strongest emission and was used in further experiments to selectively observe and quantitate bound Tb(III).

FIGURE 2.

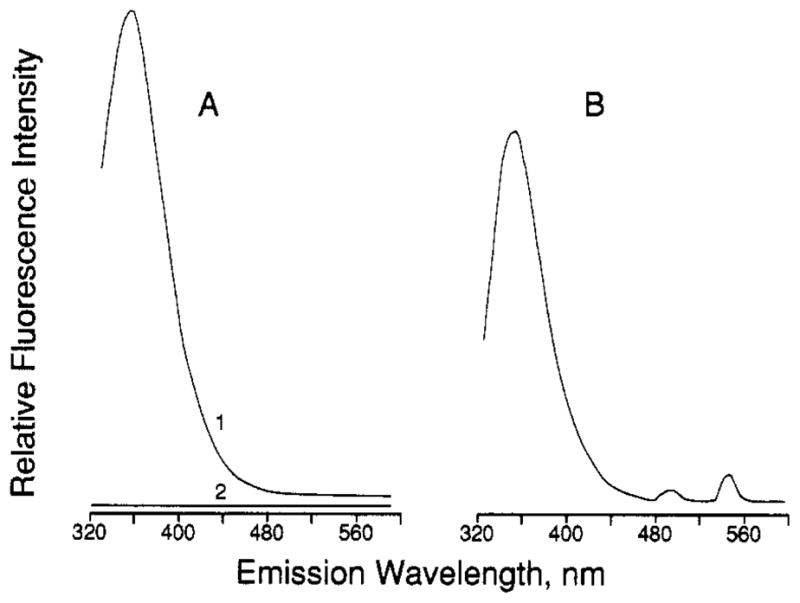
Emission spectra of the GGR-Tb(III)complex and controls. (A) Emission spectra of GGR alone (spectrum 1 ) and Tb(III) alone (spectrum 2, coinciding with the x axis but offset for clarity). (B) Emission spectrum of the GGR-Tb(III) complex. All spectra were at 25 ºC, the excitation wavelength was 292 nm, the emission wavelength was scanned, and the bandwidths on both channels were 10 nm. [GGR] = 2.5 μM; [TbCl₃,] = 25 μM. Buffer = 100 mM KCl and 10 mM PIPES, pH 6.0.

K_D Values for Metal Ion Binding

The affinities of other metal ions that bind to the Ca(II) site were measured by direct competition with Tb(III). Before a true dissociation constant could be obtained from these competition experiments, however, the dissociation constant for Tb(III) binding had to be measured. Equilibrium dialysis was carried out to obtain this quantity. The resulting data, plotted as GGR-bound Tb(III) against free Tb(III), are presented in Figure 3. The data are well approximated by a best-fit curve for a class of identical, independent Tb( III) binding sites, described by the classic hyperbolic relationship:

FIGURE 3.

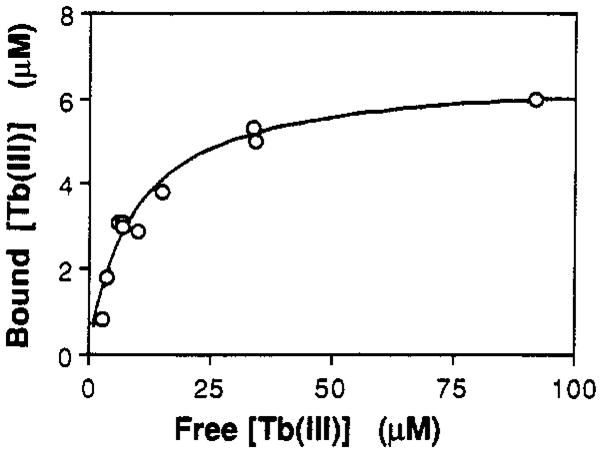
Equilibrium dialysis to determine the Tb(III) dissociation constant. Shown is the nonlinear least-squares best-fit curve for Tb(III) binding to a population of identical, noninteracting sites described by the function y = [L]x(x + K_Tb)⁻¹, where [L] is the site concentration and K_Tb is the Tb(III) dissociation constant. Best-fit parameters: [L] = 7 ± 2 μM; K_Tb = 9 ± 4 μM. Equilibrium dialysis parameters: 100 mM KCl and 10 mM PIPES, pH 6.0; [GGR] = 8 μM; 22 ºC.

$${[\text{Tb}]}_{\text{b}}=[\text{L}]\frac{{[\text{Tb}]}_{\text{f}}}{{[\text{Tb}]}_{\text{f}}+K_{\text{Tb}}}$$ (2)

where [Tb]_x is the concentration of bound or free Tb(III), [L] is the concentration of binding sites, and K_Tb is the dissociation constant for Tb(III) binding. The resulting stoichiometry of sites was 1.0 ± 0.2 per molecule of GGR, and the dissociation constant was K_Tb = 9 ± 4 μM. In a separate experiment, the site was titrated by incremental addition of Tb(III) while the bound Tb(III) emission was being monitored (data not shown). This experiment yielded K_Tb = 20 ± 10 μM, in reasonable agreement with the equilibrium dialysis result. Because the equilibrium dialysis value of K_Tb = 9 μM was determined through direct measurement of bound and free Tb(III), it was used in all subsequent calculations and is presented below in Table I and Figure 5.

Table I.

Summary of Metal Dissociation Constants

metal ion	effective ionic radius (Å)	KD (M)a	±SE (M)	calcd ΔGB (kcal/mol)b
group IA
Li(I)	0.84c	≥0.9		≥−0.1
Na(I)	1.12	≥2.4		≥0.5
K(I)	1.46	≥0.8		≥−0.1
Rb(I)	1.56	≥1.9		≥0.3
group IIA
Mg(II)	0.81c	0.20	0.06	−1.0
Ca(II)	1.06	2.5 × 10−5	1.1 × 10−5	−6.3
Sr(II)	1.21	5.4 × 10−3	0.2 × 10−3	−3.1
Ba(II)	1.38	≥0.6		≥−0.3
group IIIA
Sc(III)	0.81c	1.91 × 10−4	0.01 × 10−4	−5.1
Y(III)	0.96	3.8 × 10−5	0.1 × 10−5	−6.0
La(III)	1.10	7.29 × 10−4	0.04 × 10−4	−4.3
lanthanides
Ce(III)	1.07	4.6 × 10−4	0.6 × 10−4	−4.6
Pr(III)	1.06	3 × 10−4	1 × 10−4	−4.8
Nd(III)	1.05c	2.3 × 10−4	0.4 × 10−4	−5.0
Sm(III)	1.02	1.3 × 10−4	0.2 × 10−4	−5.3
Eu(III)	1.01	9.5 × 10−5	0.5 × 10−5	−5.5
Gd(III)	1.00	8.2 × 10−5	0.1 × 10−5	−5.6
Tb(III)	0.98	9 × 10−6d	4 × 10−6	−6.9
Dy(III)	0.97	2.5 × 10−5	0.8 × 10−5	−6.3
Ho(III)	0.96c	3.3 × −610−5	0.1 × 10−5	−6.1
Er(III)	0.945	2.6 × 10−5	0.1 × 10−5	−6.3
Tm(III)	0.94c	1.3 × 10−5	0.2 × 10−5	−6.6
Yb(III)	0.925	0.8 × 10−6	0.2 × 10−6	−8.3
Lu(III)	0.92c	1.1 × 10−6	0.2 × 10−6	−8.1

^aAll measurements were at 25 °C and 2.5 μM protein, 100 mM KCl, and 10 mM PIPES, pH 6.0.

^bBinding free energies for 1 M standard state concentration (ΔG_B = RT In K_D)

^cEffective ionic radius for coordination number = 7 was obtained by averaging EIR for CN = 6 and CN = 8. In other cases EIR are those measured for CN = 7. EIR are from Shannon (1976).

^dDetermined by equilibrium dialysis.

FIGURE 5.

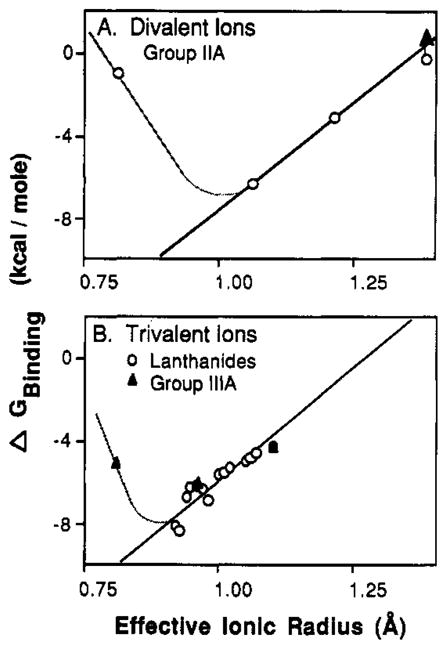
Dependence of binding free energy on metal ion size and charge. Plotted against effective ionic radius are the binding free energies, or the lower limit binding free energy (up arrow), for the spherical metal ions listed in Table I. Also shown are least-squares best-fit straight lines for radii larger than the optimal radii (bold lines) and hypothetical curves extending to radii smaller than the optimum (light lines). (A) Divalent metal ions from group IIA exhibit a best-fit slope of 21 kcal/mol per angstrom above the optimum. (B) Trivalent metal ions from group IIIA and the lanthanides exhibit a best-fit slope of 19 kcal/mol per angstrom above the optimum.

Metal ions that competitively displaced bound Tb(III) from the GGR site yielded measurable decreases in the bound Tb(III) emission. In such experiments the bound Tb(III) emission was quantitated as F/F_max, or the ratio of the emission in the presence and absence of competing metal. For each competing metal the dissociation constant was determined by titration of a sample containing fixed GGR and Tb(III) concentrations with increasing concentrations of competitor. The resulting data are again well described by expressions for a class of identical, independent sites:

$$F/F_{max}=1-\frac{{[\text{M}]}_{\text{f}}}{{[\text{M}]}_{\text{f}}+{K_{\text{D}}}^{\text{app}}}$$ (3)

$${K_{\text{D}}}^{\text{app}}=K_{\text{D}}(1+{[\text{Tb}]}_{\text{f}}/K_{\text{Tb}})$$ (4)

where K_D^app is the apparent dissociation constant for competing metal M in the presence of fixed free Tb(III) concentration [Tb]_f and K_D is the true dissociation constant for M. The concentration of free competing metal [M]_f was determined by subtracting the bound metal concentration [M]_b [=[L]( 1−F/F_max) (eq 3)] from the known total metal concentration [M]_t. In most cases [M]_f ≈ [M]_t, because the binding site concentration (=2.5 μM) was negligible relative to the total metal concentration. Figure 4 illustrates the application of eq 3 and 4 to the measurement of dissociation constants for competing group IIA metals. For example, when the concentration of Ca(II) was increased, the bound Tb(III) emission decreased and asymptotically approached zero at high Ca(II), where bound Tb(III) was completely displaced from the GGR site. The Ca(II) dissociation constant was determined from these data as follows. First, the apparent Ca(II) dissociation constant K_Ca^app was measured by best-fit of eq 3 to the titration data. K_Ca^app was then substituted into eq 4, together with the appropriate parameters for Tb(III), to generate the true dissociation constant for Ca(II) binding in the absence of Tb(III). The resulting true dissociation constant was K_ca = 25 ± 11 μM at pH 6.0,25 °C. The same procedure was used for other group IIA, group IIIA, and lanthanide metal ions possessing dissociation constants less than 0.5 M, specifically, Mg(II), Ca(II), Sr(II), Sc(III), Y(III), La(III), Ce(III), Pr( III), Nd( III), Sm( III), Eu( III), Gd( III), Dy(III), Ho( III), Er(III), Tm(III), Yb(III), and Lu(III), as summarized in Table I. Metal ions exhibiting lower affinities were analyzed by slightly different procedures, as follows.

FIGURE 4.

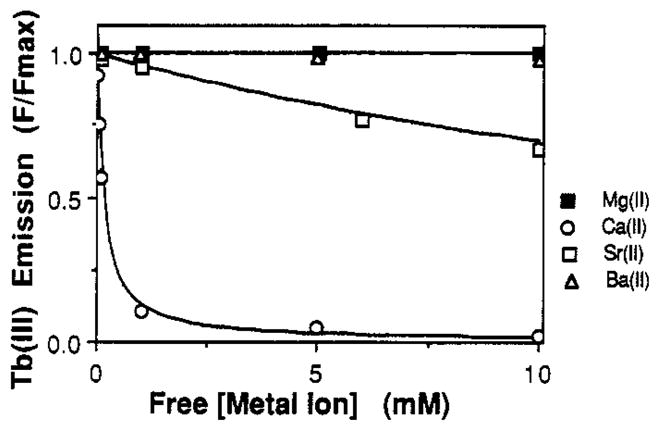
Displacement of Tb(III) from the GGR site by competing group IIA metals. Shown are nonlinear least-squares best-fit curves for the binding of group IIA metals to a population of identical, noninteracting sites equilibrated with a fixed concentration of Tb(III) described by the function y = 1 − x(x + K_D^app)⁻¹ Bound Tb(III) was monitored via its emission at 543 nm following energy transfer from protein Trp residues excited at 292 nm. The concentration of competing metal was increased, and the effect on the bound Tb(III) emission was observed. Best-fit apparent dissociation constants (K_D^app) were corrected for the presence of competing Tb(III), thereby yielding the true dissociation constants summarized in Table I. Spectral parameters: excitation 292 nm; emission 543 nm; 5-nm bandwidths on both channels. Sample parameters: 100 mM KCl and 10 mM PIPES, pH 6.0; [GGR] = 2.5 μM; [Tb(III)] = 25 μM; 25 °C.

Very low affinity metal ions yielded no detectable displacement of bound Tb(III) over the range of concentrations presented in Figure 4. For such metal ions, it was necessary to use considerably higher concentrations, typically on the order of 1 M, to measurably decrease the bound Tb(III) emission. The resulting emission decrease was then used in eqs 3 and 4 to place a lower limit on the true dissociation constant, as summarized in Table I for metals from groups IA and IIA possessing dissociation constants > 0.5 M, specifically, Li(I), Na(I), K(I), Rb(I), and Ba(II).

A recent independent study of the GGR site measured dissociation constants for Mg(II), Ca(II), Sr(II), Ba(II), Pb(II), Cd(II), and Tb(III), all at a pH of 7.0 and an ionic strength of ≤20 mM (Vyas et al., 1989). The present study was conducted at a lower pH of 6.0 to minimize metal hydroxide formation and a higher ionic strength of 110 mM to minimize nonspecific ion binding. Not surprisingly, the lower pH and higher ionic strength of the present study yielded higher dissociation constants for all the overlapping metals, Mg(II), Ca(II), Sr(II), Ba(II), and Tb(III). This observation is fully explainable in terms of the effects of pH and ionic strength on the protonation and charge screening of Ca(II) site ligands, respectively.

Comparison of Dissociation Constants for Spherical Metal lons

The true dissociation constants obtained in the present study for spherical metal ions from groups IA, IIA, IIIA and the lanthanides, including lower-limit dissociation constants, are compared in Table I. Table I also includes the effective ionic radius for each metal ion as tabulated by Shannon (1976). The radii shown are for a coordination number of seven, as appropriate for the GGR Ca(II) site.

The monovalent group IA metal ions Li(I), Na(I), K(I), and Rb(I) were observed to be very low affinity substrates, exhibiting K_D ≥0.8 M (Table I). The size of Na(I) lies within the range of divalent ion sizes observed to bind with moderate to high affinity [compare Na(I), Ca(II), and Sr(II) in Table I], indicating that monovalent ions are excluded primarily by their charge, rather than by size.

Divalent group IIA metal ions, as well as trivalent group IIIA and lanthanide ions, exhibited dissociation constants that varied as a function of ion charge and size. Table I summarizes these dissociation constants, and in Figure 5 the corresponding binding free energies are plotted against their effective ionic radii. For both divalent and trivalent metals, the binding free energies exhibit a minimum at an intermediate radius, indicating the existence of an optimal size for binding of these ions. The optimal divalent radius lies between the radii of Mg(II) (0.81 Å) and Ca(II) (1.06 Å), while the optimal trivalent radius lies between the radii of Sc(III) (0.81 Å) and Yb(III) (0.925 Å). Above the optimal radius the binding free energy approximates a linear function of radius, and similar slopes are observed for divalent and trivalent ions. Together the results indicate that the site is deformable and can accommodate a limited range of substrate sizes. The data suggest, but do not prove, that the optimal radius of the trivalents is smaller than that of the divalents. Presently it is not possible to more precisely determine the optimal radii, because (a) additional spherical metal ions with radii near the optimal radii are unavailable and (b) the mathematical relationship between the binding free energy and ionic radius, which must depend upon the details of site mechanics, is unknown.

DISCUSSION

Comparison of the dissociation constants for the binding of spherical metal ions from groups IA, IIA, and IIIA and the lanthanides indicates that both charge and size are important parameters in determining the specificity of the GGR Ca(II) site. A simple model for the binding event at a protein Ca(II) site, illustrated in Figure 6A, is consistent with the available evidence and explains the observation of optimal ionic radii for divalent and trivalent metal ions. In this model the site is locally unfolded in the absence of bound metal, such that the oxygen ligands are partly or fully hydrated. The free metal ion is also hydrated. During the binding event the metal is dehydrated, and the protein ligands are dehydrated and fully deprotonated, to yield the folded structure of the occupied site. The free energy of binding can be decomposed into three components:

$$\mathrm{\Delta }{G}_{\text{B}}=\mathrm{\Delta }{G}_{\text{dm}}+\mathrm{\Delta }{G}_{\text{dp}}+\mathrm{\Delta }{G}_{\text{m}·\text{p}}$$ (5)

where ΔG_dm, ΔG_dp, and ΔG_m·p; are the free energies of metal ion dehydration, ligand dehydration/deprotonation, and association of the dehydrated ion–site complex, respectively. The predicted dependence of these contributions on metal ion size is shown in Figure 6B. The existence of an optimal radius must stem largely from the structural constraints of the ion–site complex, although metal ion dehydration may also contribute to the observed minimum in the limit of decreasing ionic radius, where the free energy of dehydration increases as 1/r (Rashin & Honig, 1985). Evidence for local unfolding of Ca(II) sites upon removal of metal is provided by the relatively open conformation of empty EF-hand sites I and II in the structure of troponin C (Satyshur et al., 1988; Strynadka & James, 1989).

FIGURE 6.

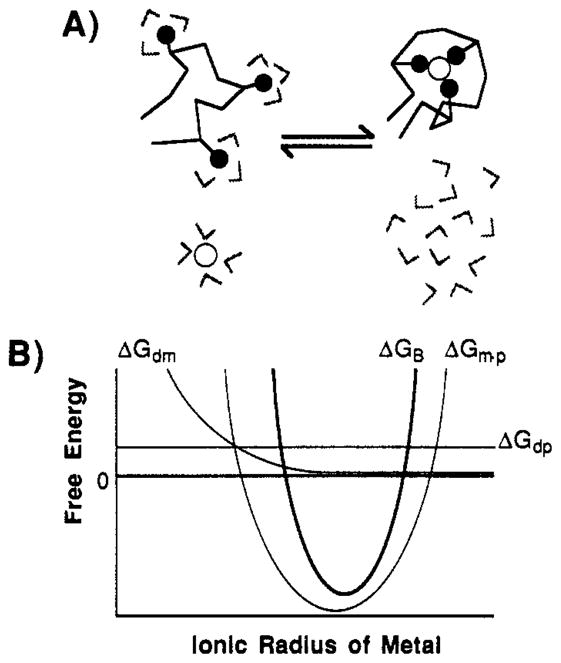
Model for metal ion binding to protein Ca(II) sites. (A) A simplified schematic view of metal ion binding to a partially unfolded, empty Ca(II) site. The binding event occurs when the binding site folds around the metal ion, releasing water of hydration from the metal ion and from ligand residues. (B) A schematic diagram of the relationship between the binding free energy and ionic radius. The total binding free energy (ΔG_B) is the bold curve, shown with its three additive components: the free energy of ligand dehydration and deprotonation (ΔG_dp) is predicted to be independent of metal ion radius; the free energy of metal ion dehydration (ΔG_dm) is predicted to increase inversely as the ionic radius decreases (Rashin & Honig, 1985); the free energy of association of the dehydrated ion and the site (Δ _m·p) is predicted to exhibit a minimum at the optimal ionic radius, while increasing both for larger radii which cause crowding in the site and for smaller radii which have reduced metal-ligand electrostatic stabilization.

The model indicates that multiple factors must be considered when the metal ion selectivity of the GGR Ca(II) site is being analyzed, as well as protein Ca(II) sites in general. These factors, many of which have been previously discussed, include the following:

(1) Number, Type, and Geometry of Ligands

The coordination of bound metal in protein Ca(II) sites appears in many cases to be optimized for selective binding of Ca(II), or Ca(II) and Mg(II) (Tsai et al., 1987; Strynadka & James, 1989). Coordination by seven oxygens, as is generally observed in protein Ca(II) sites (Strynadka & James, 1989), is one of the preferred coordination structures observed for small-molecule Ca(II) complexes. The exclusion of Mg(II) from many protein Ca(II) sites can be explained in part by the fact that Mg(II) prefers a coordination number of six and uses nitrogen as a ligand more frequently (Shannon, 1976; Martin, 1983; Einspahr & Bugg, 1983). The pentagonal-bipyramidal geometries of protein Ca(II) sites also contribute to their specificity; thus, transition metals that prefer octahedral geometries due to ligand field splitting are disfavored by this factor. Yet ligand number and geometry are not the only important factors in metal exclusion: for example, calmodulin sites I and II possess the usual pentagonal-bypyramidal coordination but are observed to bind both Mg(II) and Ca(II) (Tsai et al. 1987).

(2) Electrostatic Interactions

Electrostatic interactions between ligands and bound metal are likely to be particularly important (Sekharudu & Sundaralingam, 1988; Marsden et al., 1988). For the GGR site the following relative affinities are observed for spherical metal ions: monovalent cations ≪ divalent cations < trivalent cations. There are three negatively charged ligands in the site, and the other four oxygen ligands possess the usual oxygen partial negative charge; thus, it is likely that substantial electrostatic repulsion exists between ligands. This repulsion would be counteracted by cation binding, to a degree dependent on the cation charge. Thus, trivalent cations would counteract ligand repulsion better than divalents, enabling contraction of the site about the trivalents and yielding a smaller optimal radius, as suggested by the present data (Figure 5). Monovalents may be unable to stabilize the ligand repulsion in the folded site. Electrostatic interactions between the site and its protein environment are also likely to contribute to selectivity; for example, the net charge of the occupied site may be destabilized by interaction with nearby low dielectric regions, thereby favoring an electroneutral ion–site complex (Sekharudu & Sundaralingam, 1988). And nearby nonligand dipoles or charges may tune the specificity and affinity of the site (Linse et al., 1988).

(3) Cavity Size and Deformability of the Site

The GGR site appears to have a flexible cavity size, which can deform to accommodate ions of different radius and charge. Cavity size is an important parameter in determining the optimum substrate metal, while the deformability could play a key role in determining the range of acceptable substrates. Studies of lanthanide binding to other Ca(II) sites indicate that many sites exhibit optimal substrate radii (Curmi et al., 1982; Corson et al., 1983; Chao et al., 1984; MacManus et al., 1989) and that the deformability of different sites varies dramatically (Williams et al., 1984).

(4) Dehydration and Deprotonation of Metal and Ligands

It is likely that the dehydration of metal and ligands provides much of the driving force for metal binding, due to the increased entropy of liberated water molecules. In this regard the hydration numbers of free metal ions may contribute to binding selectivity. In addition, for a fixed hydration number the dehydration free energy increases as ionic radius decreases (Rashin & Honig, 1985); thus, dehydration will contribute to the exclusion of small ions from the site. Deprotonation of protein ligands will generally not contribute to binding selectivity, since the extent of protonation of the unoccupied site and the fully deprotonated occupied site is substrate independent.

(5) Limited Availability of Substrate Metal Ions

Protein Ca(II) sites, including the GGR site, selectively bind Ca(II) only because metal ions that are better substrates are not present in biological systems. For example, Yb(III) and Lu(III) exhibit at least 20-fold higher affinities than Ca(II) for the GGR site. Due to the limited bioavailability of trivalent metal ions, evolution has been able to design protein Ca(II) sites that are optimized to bind highly charged cations, thereby better excluding the abundant monovalent metals, particularly Na(I) and K(I). In addition the GGR site exhibits an optimal divalent radius similar to that of Ca(II), so that it is better able to exclude Mg(II).

While the above list includes most or all of the factors that contribute to Ca(II) site selectivity, further work is needed to characterize the roles of individual factors as well as their relative importance. Site-directed mutagenesis of the residues in and around Ca(II) sites has been shown to be a valuable tool in the analysis of metal binding affinity and specificity (Linse et al., 1988; MacManus et al., 1989). In addition, NMR and thermodynamic measurements should provide useful information regarding changes in Ca(II) sites triggered by substrate binding, including changes in structure, hydration, and protonation. Future studies of the GGR Ca(II) site will utilize both mutagenesis and physical approaches to further investigate the structural and electrostatic basis of Ca(II) site selectivity. These studies will be facilitated by the simplicity of a single site and the ease of mutagenesis in the GGR system.