Arrested phase separation in reproducing bacteria creates a generic route to pattern formation

Abstract

We present a generic mechanism by which reproducing microorganisms, with a diffusivity that depends on the local population density, can form stable patterns. For instance, it is known that a decrease of bacterial motility with density can promote separation into bulk phases of two coexisting densities; this is opposed by the logistic law for birth and death that allows only a single uniform density to be stable. The result of this contest is an arrested nonequilibrium phase separation in which dense droplets or rings become separated by less dense regions, with a characteristic steady-state length scale. Cell division predominates in the dilute regions and cell death in the dense ones, with a continuous flux between these sustained by the diffusivity gradient. We formulate a mathematical model of this in a case involving run-and-tumble bacteria and make connections with a wider class of mechanisms for density-dependent motility. No chemotaxis is assumed in the model, yet it predicts the formation of patterns strikingly similar to some of those believed to result from chemotactic behavior.

Microbial and cellular colonies are among the simplest examples of self-assembly in living organisms. In nature, bacteria are often found in concentrated biofilms, mat, or other colony types, which can grow into spectacular patterns visible under the microscope (1, 2). Also in the laboratory, bacteria such as Escherichia coli and Salmonella typhimurium form regular geometric patterns when they reproduce and grow on a Petri dish containing a gel such as agar. These patterns range from simple concentric rings to elaborate ordered or amorphous arrangements of dots (3–11). Their formation results from collective behavior driven by interactions between the bacteria, such as chemotactic aggregation (6), competition for food (8) or changes in phenotypes according to density (11). The question as to whether general mechanisms lie behind this diversity of microscopic pathways to patterning remains open.

Unlike the self-assembly of colloidal particles, pattern formation in motile microorganisms and other living matter is typically driven by nonequilibrium rather than thermodynamic forces. Indeed, the dynamics of both dilute and concentrated bacterial fluids is already known to be vastly different from that of a suspensions of Brownian particles. For instance, suspensions of active, self-propelled particles have been predicted to exhibit giant density fluctuations (12, 13), which have been observed experimentally (14), along with various other instabilities (15, 16). Similarly, an initially uniform suspension of self-propelled particles performing a “run-and-tumble” motion like E. coli has recently been shown theoretically to separate into a bacteria-rich and a bacteria-poor phase, provided that the swim speed decreases sufficiently rapidly with density (17). This is akin to what happens in the spinodal decomposition of binary immiscible fluids, but has no counterpart in a system of Brownian particles interacting solely by density-dependent diffusivity. (The latter obey the fluctuation-dissipation theorem, ensuring that the equilibrium state is diffusivity-independent.) Other nonequilibrium effects, such as ratchet physics, have also been observed and used either to rectify the density of bacteria (18–20) or to extract work from bacterial assemblies (21).

Some aspects of bacterial patterning show features common to other nonequilibrium systems, and a crucial task is to identify the key mechanisms that control their development. In many equilibrium and nonequilibrium phase transitions an initial instability creates density inhomogeneities; these coarsen, leading eventually to macroscopic phase-separation (22). The situation observed in bacterial assemblies often differs from this; long-lived patterns emerge with fixed characteristic length scales, suggesting that any underlying phase-separation is somehow arrested. The strong diversity of biological functions met in experiments has led to an equally diverse range of proposed phenomenological models (5–7, 9–11) to account for such effects. Most of them rely on the coupling of bacteria with external fields (food, chemoattractant, stimulant, etc.), and many involve a large number of parameters due to the complexity of the specific situation of interest. The most common mechanism used to explain the bacterial patterns is chemotaxis (6): the propensity of bacteria to swim up/down gradients of chemoattractants/repellants. This explanation is so well established in the literature for at least two organisms [E. coli and S. typhimurium (6)] that observation of similar patterns in other species might defensibly be taken as evidence for a chemotactic phenotype.

Although in principle one would like a similarly detailed mechanism for each system in which such patterns can form, it is important also to ask whether more generic explanations can be found by studying the process at a coarse-grained level. This does not abandon the search for a mechanism, but aims to subsume the complex, system-specific microscopic details into a small number of effective parameters that control the macroscopic behavior. Here we follow such an approach, offering a description on scales intermediate between the microscopic dynamics of bacteria and the macroscopic scale of the patterns. In effect we are “averaging out” all specific microscopic aspects, such as the motion of chemoattractants or steric interactions, and retaining only a coarse-grained dependence of the bacterial motility on density. This procedure allows us to identify a very general mechanism, characterized in the simplest cases by only two dimensionless numbers, that may help to explain the origin of pattern formation across a large class of experiments on bacterial colonies. This involves a density-dependent motility, giving rise to a phase separation that is then arrested, on a well-defined characteristic length scale, by the birth and death dynamics of bacteria.

To develop our approach, we first analyze a specific example of run-and-tumble bacteria whose swim speed depends directly (via unspecified interactions) on local bacterial density. This gives patterns similar to those observed in experiments (5, 6). However, the basic mechanism—density-dependent motility coupled to logistic population growth—is not limited to this example as we discuss toward the end of this paper. In particular, our work demonstrates that chemotaxis per se is not a prerequisite for observing what are sometimes colloquially referred to as “chemotactic patterns.”

It is indeed remarkable that density-dependent motility and logistic growth alone are sufficient to create some of the pattern types previously identified with specific chemotaxis mechanisms. In mechanistic terms, we find that the logistic growth dynamics effectively arrest a spinodal phase separation; the latter can follow from a density-dependent swim speed (17), but could also arise far more generally, as we discuss later. Put differently, an initially uniform bacterial population with small fluctuations will aggregate into droplets, but these will not coarsen further once a characteristic length scale is achieved, at which aggregation and birth/death effects come into balance. Starting instead from a small inoculum, we predict formation of concentric rings which, under some conditions, at least partially break up into spots at late times (5).

To exemplify our generic mechanism, we start from a minimal microscopic model of run-and-tumble bacteria, which can run in straight lines with a swim speed v and randomly change direction at a constant tumbling rate τ^-1 (23–25). To this we add our two key ingredients: a local density-dependent motility and the birth/death of bacteria, the latter accounted for through a logistic growth model. Of course, bacteria can interact locally in various ways, ranging from steric collisions (17) to chemical quorum sensing (6). [Indeed a nonspecific dependence of motility on bacterial density was previously argued to be central to bacterial patterning by Kawasaki and co-workers (8).] Here we focus on the net effect of all such interactions on the swim speed v(ρ), which we assume to decrease with density ρ. This dependence might include the local effect of a secreted chemoattractant [such as aspartate (3–5), which causes aggregation, effectively decreasing v] but does not assume one.

In addition to their run-and-tumble motion, real bacteria continuously reproduce, at a medium-dependent growth rate that ranges from about one reciprocal hour in favorable environments such as Luria broth to several orders of magnitude lower for “minimal” media such as M9. In bacterial colonies patterns may evolve on time scales of days (6), over which such population growth dynamics can be important.

We now derive coarse-grained continuum equations for the local density ρ(r,t) in a population of run-and-tumble bacteria, with swim speed v(ρ), growing at a rate of α(1 - ρ/ρ₀). The latter represents a sum of birth and death terms, in balance only at ρ = ρ₀. At large scales in a uniform system, the motion of individual bacteria is characterized by a diffusivity D(ρ) = v(ρ)²τ/d, where τ^-1 is the tumbling rate and d is the dimensionality (23, 24). Crucially, however, a nonuniform swim speed v(r) also results in a mean drift velocity V = -vτ∇v (23), which here gives V = -D^′(ρ)∇ρ/2 (17). This contribution is crucial to phase separation (17) and will again play a major role here. However, this term is absent for ordinary Brownian particles interacting solely via a variable diffusivity D(ρ) and was accordingly overlooked in previous studies that relied on phenomenological equations involving a density-dependent diffusivity and no drift (8). Such a drift term, V = -D(ρ)∇μ_ex, does, on the other hand, arise for Brownian particles whose excess chemical potential μ_ex is density-dependent. Our interacting bacterial system thus impersonates a purely Brownian one with the same D(ρ) but in addition μ_ex = log v(ρ). For v(ρ) a decreasing function, this corresponds to an attractive thermodynamic interaction that can lead to phase separation (see below), which D(ρ) alone, for Brownian particles, cannot.

Coupling the diffusion-drift equation for run-and-tumble bacteria, as derived in ref. 17, with the logistic growth term, the full dynamics is then given by

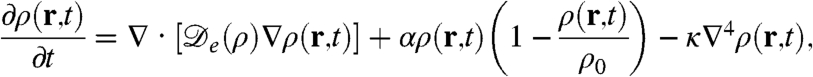[1]

where the “effective diffusivity” is

[2]

[For Brownian particles with diffusivity D(ρ) and μ_ex = ln v, 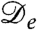would be called the “collective” diffusivity.] This results from the summed effects of the true diffusive flux -D(ρ)∇ρ and the nonlinear drift flux ρV. In Eq. 1 we have also introduced a phenomenological surface tension parameter κ > 0, which controls gradients in the bacterial density. Such a contribution has been shown to arise when the speed of a bacterium depends on the average density in a small local region around it, rather than a strictly infinitesimal one (17). Eq. 1 neglects noise, both in the run-and-tumble dynamics and in the birth/death process. The former noise source conserves density and should become irrelevant at the experimental time scale of days. On the other hand, the nonconservative noise in the birth and death dynamics may be more important, and we have verified that our results are robust to its introduction at small to moderate levels. Numerical simulations of Eq. 1 have been performed with standard finite difference methods (although noise does require careful treatment, as in refs. 26 and 27), with periodic boundary conditions used throughout. For definiteness, all our simulations have been carried out with v(ρ) = v₀e^-λρ/2, where v₀ > 0 is the swim speed of an isolated bacterium and λ > 0 controls the decay of velocity with density. The precise form of v(ρ) is, however, not crucial for the phenomenology presented here, and the instability analysis offered below does not assume it.

The logistic population dynamics alone would cause the bacterial density to evolve toward a uniform density, ρ(r) = ρ₀, which constitutes a fixed point for the proposed model. Although this homogeneous configuration is stable in the absence of bacterial interactions, it has been shown (17) that, without logistic growth, a density-dependent swim speed v(ρ) leads to phase separation via a spinodal instability whenever dv/dρ < -v/ρ. By Eq. 2 this equates to the condition 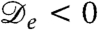, and it is indeed obvious that the diffusive part of Eq. 1 is unstable for negative 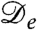. It is important, clearly, that 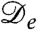can be negative although D is not. This holds for a much wider class of nonequilibrium models than the one studied here; we return to this point at the end of the paper.

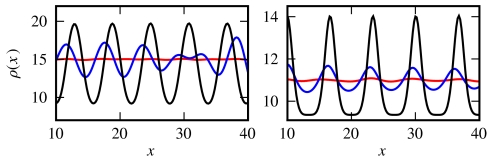
For the choice of v(ρ) made in our simulations, we have 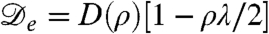, and the flat profile will thus become unstable for ρ₀ above 2/λ. We have confirmed this numerically and find that upon increasing ρ₀, the uniform state becomes (linearly) unstable, evolving in a 1D geometry into a series of “bands” of high bacterial density separated by low-density regions. Depending on the parameters, this transition can be continuous (supercritical), with the onset of a harmonic profile whose amplitude grows smoothly with ρ₀, or discontinuous (subcritical) with strongly anharmonic profiles (see Fig. 1).

Fig. 1.

Growth of the instability in the supercritical (Left) and subcritical cases (Right). The three lines correspond to three successive times. A small perturbation around ρ₀ (red line) growth toward harmonic or anharmonic patterns in the supercritical or subcritical case, respectively. (Left) Supercritical case (α = κ = 0.01, λ = 0.02, ρ₀ = 15, 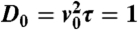; times: 10², 10³, 10⁴). (Right) Subcritical case (α = κ = 0.005, λ = 0.02, ρ₀ = 11, 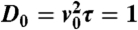; times: 3.10², 3.10³, 10⁵).

The transition to pattern formation arising from Eq. 1 is a fully nonequilibrium one: It is not possible to write down an effective thermodynamic free energy that would lead to this equation of motion. Nonetheless, it is possible to understand why the birth/death process effectively arrests the spinodal decomposition induced by the density-dependent swim speed. The latter tends to separate the system into high- and low-density domains with densities on either side of ρ₀. (Without the logistic term, these would coarsen with time.) Bacteria thus tend to be born in the low-density regions and to die in the high-density regions. To maintain a steady state, they have to travel from one to the other: Balancing the birth/death terms by the diffusion-drift transport flux between the domains then sets a typical scale beyond which domain coarsening can no longer progress. Were any domain to become much larger, the density at its center would soon regress toward ρ₀, retriggering the spinodal instability locally. [This is closely reminiscent of what happens in a thermodynamic phase separation when the supersaturation is continuously ramped (28).]

To better understand the onset of the instability, let us linearize Eq. 1 around ρ(r) = ρ₀ and work in Fourier space. Defining 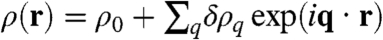yields

[3]

The flat profile ρ = ρ₀ is thus stable if Λ_q ≤ 0 for all q and is unstable otherwise. From the expression for 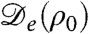, Eq. 2, one sees that instability occurs if

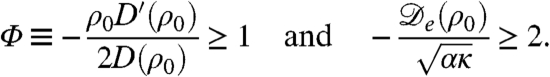[4]

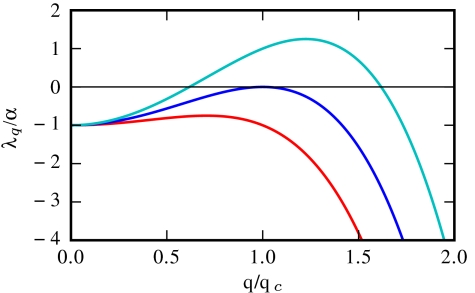
At the onset of the instability only one mode is unstable, with wave vector 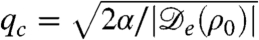, as can be seen in Fig. 2. The first condition in Eq. 4, Φ≥1, is equivalent to the requirement that 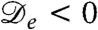given previously. From the dispersion relation, Eq. 3, we see that the resulting destabilization is balanced by the stabilizing actions of bacterial reproduction and the surface tension at large and small wavelength, respectively. The unstable modes thus lie within a band q₁ < q < q₂, where 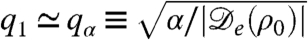and set the wavelengths below and above which the stabilizing effects of bacteria reproduction and the surface tension can compete with the destabilizing effect of the negative diffusivity, respectively. For unstable modes to exist, one needs q₁ ≤ q₂; restoring prefactors, this yields 2q_α ≤ q_κ, which is the second criterion in Eq. 4. This analysis is consistent with the view that phase separation is arrested by the birth/death dynamics, which stabilizes the long wavelength modes (Λ₀ = -α), whereas the phenomenological tension parameter κ primarily fixes the interfacial structure of the domains, not their separation.

Fig. 2.

Three plots of Λ_q(q) for 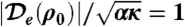, 2, 3 (from bottom to top). At the transition, only one critical mode q = q_c is unstable.

We now consider more closely the parameters controlling the transition to pattern formation. For definiteness, we address the specific case used for our simulations, D(ρ) = D₀ exp(-λρ). To put Eq. 1 in dimensionless form, we define rescaled time, space, and density as

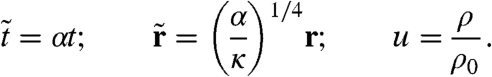[5]

The equation of motion now reads

[6]

where 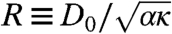and Φ = λρ₀/2 are the two remaining dimensionless control parameters. Meanwhile the conditions 4 for pattern formation become

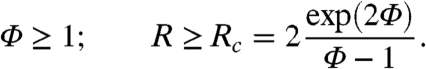[7]

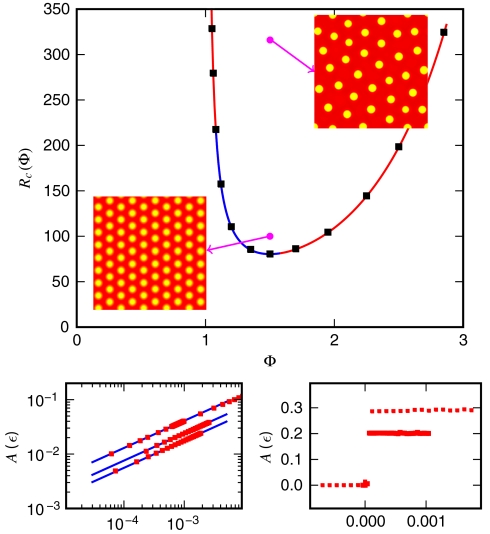
These relations, combined with the preceding linear stability analysis, define a phase diagram in the (R,Φ) plane (Fig. 3) that agrees remarkably well with numerical results for systems prepared in a (slightly noisy) uniform initial state.

Fig. 3.

(Top) Phase diagram in the (R,Φ) plane. The outer region corresponds to stable behavior, whereas within the curve, patterning occurs. The solid line is the theoretical phase boundary—Eq. 7—which accurately fits the numerics (black squares). The blue and red sections correspond to continuous and discontinuous transitions, respectively. The two magenta dots correspond to two 2D simulations that show ordered harmonic patterns close to supercriticality and amorphous patterns otherwise. (Bottom Left) Transition in the supercritical regime. The blues lines correspond to the theory—Eq. 8—whereas the squares come from simulations (Φ = 1.5, 1.35, 1.2 from top to bottom). (Bottom Right) Transition in the subcritical regime for Φ = 1.06 and Φ = 1.7 (bottom to top).

Close to the transition, the emergent steady-state pattern can be studied using an amplitude equation (see SI Appendix). Introducing ϵ = (R - R_c)/R_c, one gets in 1D that for 1.08 ≤ Φ ≤ 1.58, the transition is supercritical (continuous) and the steady state is given by

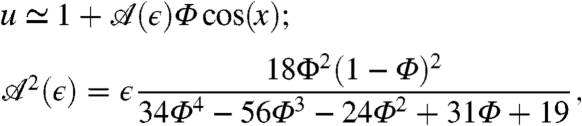[8]

which agrees with simulations (Fig. 3 Bottom Left). Outside this range, the transition becomes subcritical (discontinuous, Fig. 3, Bottom Right) and the analytical tools available become less reliable (29). We emphasize again that the basic mechanism for patterning presented above does not depend on the precise form chosen for v(ρ). Quantitatively, however, Eq. 8 and the frontier between subcriticality and supercriticality do depend on the details of the interplay between the nonlinearity in v(ρ) and the logistic growth term. We leave further analysis of such model-specific features to future work.

While the amplitude equation is more easily developed in 1D, the stability analysis offered above is valid in higher dimensions, and it is natural to ask what happens in 2D, which is the relevant geometry for Petri dish studies with growing bacterial colonies. Fig. 4 shows the simulated time evolution of ρ(r,t) for a system started with small random fluctuations around the equilibrium density ρ₀, with other parameters as in Fig. 1. Perhaps not surprisingly, bands are replaced by droplets of the high-density phase dispersed in a low-density background at large times. This is the typical steady state obtained with a near-uniform starting condition. However, the structure and organization of the bacterial drops in the steady state depends on the point (R,Φ) chosen in the phase diagram. Generally, the closer the system is to the supercritical instability curve, the more ordered the patterns. For instance, we have observed an essentially crystalline distribution of bacterial drops, which develops defects and eventually becomes amorphous on moving farther away from the phase boundary (Fig. 3 Insets to main panel). For particular choices of parameters, our model can also admit other steady-state patterns. Close to the supercritical line, where the phase transition is continuous, we can obtain long-lived stripes, whereas for fixed large values of R and Φ close to the (right) subcritical phase boundary, we have also observed “inverted droplets” with a high-density lawn punctuated by low-density “holes.”

Fig. 4.

Numerical results for a 2D simulation with size equal to (in dimensionless units, see Eq. 5) 28 × 28, R ≃ 316, and Φ = 1.5. Times corresponding to the snapshots are (from left to right) 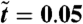, 0.12, 0.20, and 0.51. The color bar shows values of the dimensionless density u; see Eq. 5.

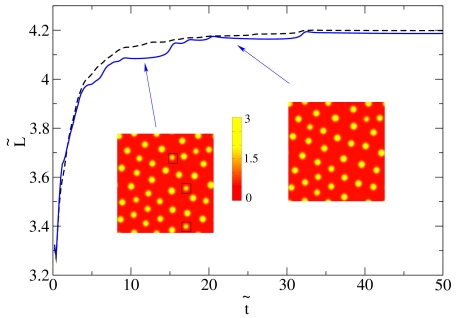
In these 2D geometries initialized from a near-uniform state, droplets can coalesce in the early stages, whereas at late times the dynamics is governed by evaporation-condensation events (see Figs. 4 and 5). However, it is already apparent from Fig. 4 that coarsening eventually stops and the droplets reach rather well-defined steady-state sizes and center-to-center distances. This can be quantified by looking at the time evolution of the characteristic domain size, L(t), which we have computed as the inverse of first moment (times 2π) of the structure factor (22). Fig. 5 suggests that L(t) at late times eventually stops increasing and reaches a steady-state value. [The visible steps in domain size mark discrete evaporation events involving smaller bacterial droplets; presumably L(t) would become smooth for a large enough system.]

Fig. 5.

Plot of the characteristic domain size, 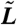, as a function of time, 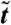(both in dimensionless units), for a system in the inhomogeneous phase, with initially random density fluctuations around ρ₀. Parameters were R ∼ 316 and Φ = 1.35, whereas the system size was 35.5 × 35.5 (in dimensionless units). The solid line corresponds to a single run, whereas the dashed line is an average over six runs. The steps in the single run curve correspond to evaporation-condensation events, highlighted by black squares in the snapshots shown in the figure (before and after one of the steps, respectively, arrows indicate positions on the plot corresponding to the two snapshots). The color bar shows values of the dimensionless density u.

These droplet patterns in steady state are very similar to those observed for E. coli in a liquid medium or S. typhimurium in semisolid agar (0.24% water-agar in ref. 5) when starting from a uniform distribution (6). For the E. coli case, interactions are believed to come from chemoattractant, emitted by the bacteria themselves, that is not degraded over time (3, 4). The chemoattractant distribution should approach uniformity so that these interactions decay to zero as time proceeds. In our framework this is analogous to decreasing Φ, which will turn any initially unstable state into a homogeneous one, and can thus explain that the patterns observed experimentally fade with time (whereas in our simulations Φ remains constant and the patterns are stable indefinitely). E. coli in a semisolid medium also shows droplet patterns of high symmetry. In our framework, such patterns result from a continuous transition, close to the supercritical line.

The growth of bacterial colonies of S. typhimurium starting from a small inoculum of bacterial cells in semisolid agar leads to quite specific (transient but long-lived) patterns, with the bacteria accumulating in concentric rings that can subsequently fragment into a pattern of dots (5, 6). Once again, although these patterns are believed to stem from a chemotactic mechanism (6), we find they can arise in principle without one, so long as our two basic ingredients of density-suppressed motility and logistic growth are both present. Indeed, initializing our simulations with a single small droplet of high-density ρ, we find that a similarly patterned bacterial colony structure develops. First, the bacteria spread radially, forming an unstructured lawn with the highest density at the center. This background density increases logistically until the onset of instability via our generic phase-separation mechanism; with circular symmetry, the instability causes concentric rings of high bacterial density to successively develop that are very stable in time (Fig. 6 third and fourth snapshots in the top row). The patterns observed at later times again depend on the position of the parameters in the (R,Φ) plane. If we fix a value of R, e.g., 100, larger values of Φ in the unstable region lead to rings being very stable. For smaller values of Φ, on the other hand, effectively corresponding to weaker interactions between the bacteria, we observe that rings initially form but rapidly destabilize through a secondary modulation of the bacterial density along them. This eventually breaks the rings into a series of drops (Fig. 6 third and fourth snapshots in the bottom row). The inner rings destabilize first, and the system evolves eventually to the same steady state as found starting from a uniform density, composed of drops with well-defined characteristic size and separation. All this phenomenology is strikingly reminiscent of the dynamics observed by Woodward et al. (5) for S. typhimurium, where rings are stable at large concentrations of potassium succinate (a “stimulant” that promotes pattern formation), but break up into drops at smaller ones. Our model shows a similar morphological change when decreasing Φ, i.e., the strength of the interactions.

Fig. 6.

Dynamics of formation of patterns in 2D, starting from a single small bacterial droplet in the middle of the simulation sample. (Top) Formation of rings in a system with R = 100 and Φ = 1.65. The simulation box has size 125 × 125 (in dimensionless units). The snapshots correspond to times equal to (from left to right) 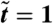, 5, 10, and 27. (Bottom) Breakage of rings into dots. The four snapshots correspond to the time evolution of a system with R = 100 and Φ = 1.3. We show a 125 × 125 fraction of the simulation box, with the boundaries far away and not affecting the pattern. The snapshots correspond to times equal to (from left to right) 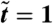, 7, 29, and 122. For both rows, the color bar shows values of the dimensionless density u.

Different views are possible concerning the ability of our generic model to reproduce some of the observed chemotactic patterns of E. coli and S. typhimurium (6). One possibility is that Eq. 1, with the interpretation we have given for it, actually does embody the important physics of pattern formation in these organisms. Indeed it is well accepted that bacteria in the high-density concentric rings are essentially nonmotile (30). The precise mechanism leading to this observation is not well understood (6), but it is possible that the chemotactic mechanism mainly acts to switch off motility at high density. If so, by focusing solely on this aspect [with a correspondingly vast reduction in the parameter space from that of explicit chemotactic models (5, 6)] our model might capture the physics of these chemotactic patterns in a highly economical way. Interestingly, our model is essentially local, whereas chemotaxis in principle mediates interactions between bacteria that are nonlocal in both space and time. It is not clear whether such nonlocality is essential for the chemotactic models in refs. 5 and 6 or if fast-variables approximations and gradient expansions would reduce these models (which involve between six and nine dimensionless numbers) into Eq. 1. In this case, we would still have in Eq. 1 a highly economical model for chemotactic pattern-formation organisms, possibly with a different interpretation of 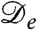and κ.

Alternatively, the success of our local model for these chemotactic organisms might be largely coincidental. But in that case, such a sparse model should be easily falsified, for instance, by using the linear stability analysis to relate the typical length scale of the patterns to microbial parameters. This length scale is of order 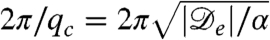, with 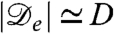, a typical bacterial diffusion coefficient [ 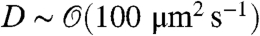for E. coli (24)]. Using the previously quoted growth rate α ≃ 1 hr^-1, we get a ring separation of ∼1 mm, in order-of-magnitude agreement with the experimental value (5).

Our phase diagram could be explored quantitatively for S. typhimurium (5) by changing both nutrient and stimulant concentration. The former affects both growth rate and motility, whereas the latter controls the dependence of motility on density. The swim speed, tumble rate, and growth rate can all be measured microscopically, fixing α and also, so long as it stems from pure run-and-tumble motion, 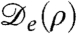. To allow for other microscopic possibilities, it would be better directly to measure this effective diffusivity in the stable regime using Fourier microscopy (31) and extrapolate these data into the unstable region. A further quantitative test of our mechanism might involve altering the growth medium with the aim of changing solely the birth/death term α, which is responsible for the arrest of phase separation at a finite length scale. Finally, the main role of κ in Eq. 1 is to determine the interfacial width between low- and high-density phases; it might be determined by careful measurement of that width.

More generally, our analysis of Eq. 1 shows that the main prerequisite for pattern formation, assuming the presence of the logistic growth term, is negativity of the effective diffusion constant 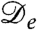. For run-and-tumble dynamics, 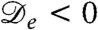was shown to arise for a sufficiently strong decay of swim speed with density; it does so because spatial variations in the true diffusivity D(ρ) create a drift flux ρV = -ρD^′(ρ)∇ρ/2, which can overcompensate the true diffusive flux -D∇ρ (17). Negative 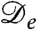could, however, equally arise for another density-dependent nonequilibrium diffusion process. Indeed, the principle of detailed balance, which holds only for systems whose steady states are governed by equilibrium thermodynamics, leads to the Einstein relation, that D = k_BTM, with D a many-body diffusivity and M the corresponding mobility. In conditions of local equilibrium, such as those governing phase separation in thermodynamic systems, the drift velocity remains V = -M∇μ_ex. Therefore, since μ_ex derives from a free energy, no drift velocity can arise purely from gradients of D. In contrast, for strongly nonequilibrium systems such as bacteria, the no detailed balance principle applies. We should then expect instead generically to find mobility-induced drift velocities, and the run-and-tumble model is merely one instance of this. Accordingly one can expect, in principle, to find cases of negative 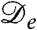in other microorganisms showing distinctly different forms of density-dependent self-propulsion.

To summarize, we have studied the dynamics of a system of reproducing and interacting run-and-tumble bacteria, in the case where interactions lead to a decreasing local swim speed with increasing local density. We have thereby identified a potentially generic mechanism for pattern formation in which an instability toward phase separation, caused by the tendency for bacteria to move slowly where they are numerous, is arrested by the birth and death dynamics of bacterial populations. We have shown that these two ingredients alone are enough to capture many of the patterns observed experimentally in bacterial colonies—including some that have only previously been explained using far more complex models involving specific chemotactic mechanisms. Indeed, if motility decreases steeply enough with density, then a spatially homogeneous bacterial population becomes unstable to density fluctuations leading to the formation of bands (1D) or droplets (2D). The length scale of the resulting pattern is set by a balance between diffusion-drift fluxes and the logistic relaxation of the population density toward its fixed-point value. Starting instead from a small initial droplet of bacteria, we predict the formation of concentric rings, each of which may eventually further separate into droplets.

In several well-studied systems, such characteristic patterns are (with good reason) believed to be the direct result of chemotactic behavior (5, 6). It is therefore remarkable that they can also arise purely from the interplay of density-dependent diffusivity and logistic growth, without explicit reference to the dynamics (or even the presence) of a chemoattractant. This suggests that similar patterns might arise in organisms having no true chemotactic behavior at all. Such patterns could then be the result of local chemical signaling without gradient detection (quorum ,sensing, not chemotaxis) or even purely physical interactions (steric hindrance, say), either of which could in principle produce the required dependence of motility on density. Last, a motility decreasing with density is not the only mechanism that could lead to 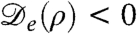in Eq. 1, and much of our analysis applies equally to other such cases.

Finally, the simplest version of our model allows identification of just two dimensionless parameters that control the entire pattern-forming process. In both homogeneous and centrosymmetric geometries, this gives predictions for how the pattern type depends on interaction strength, which are broadly confirmed by experimental data. This suggests that some of the diverse patterns formed by colonies of motile bacteria could have a relatively universal origin.