Buckley-James Boosting for Survival Analysis with High-Dimensional Biomarker Data

Abstract

There has been increasing interest in predicting patients’ survival after therapy by investigating gene expression microarray data. In the regression and classification models with high-dimensional genomic data, boosting has been successfully applied to build accurate predictive models and conduct variable selection simultaneously. We propose the Buckley-James boosting for the semiparametric accelerated failure time models with right censored survival data, which can be used to predict survival of future patients using the high-dimensional genomic data. In the spirit of adaptive LASSO, twin boosting is also incorporated to fit more sparse models. The proposed methods have a unified approach to fit linear models, non-linear effects models with possible interactions. The methods can perform variable selection and parameter estimation simultaneously. The proposed methods are evaluated by simulations and applied to a recent microarray gene expression data set for patients with diffuse large B-cell lymphoma under the current gold standard therapy.

1. Introduction

Gene expression profiling is a way of measuring the activity levels of thousands of genes at the same time. Studies have shown great promise in predicting cancer survival using the gene expression data (Rosenwald et al., 2002, Lenz et al., 2008). A typical task is to select a parsimonious subset of genes with good prediction accuracy. The analysis of the high-dimensional low-sample size gene expression datasets presented a statistical challenge. Additionally, there is growing evidence that gene-gene interactions play roles in the risk for common diseases. The investigation of such gene-gene interactions provides even more methodological challenges as the number of potential interactions among genes can grow rapidly. Time-to-event data is often censored, thus presenting another difficulty for modeling. This article is aimed to develop a unified framework on regression models for a time-to-event outcome with the gene expression data. All the above issues can be addressed within this framework.

Cox regression has been a common choice in the analysis of time-to-event data with censoring information. However, due to its limitations such as the proportional hazards assumption and lack of an intuitive interpretation compared with linear regression, the accelerated failure time (AFT) model is an important alternative. There are some advantages and motivations in developing the estimation methods for the AFT model. First, the AFT model has a familiar linear regression form, typically based on a logarithmic transformed response variable. Such a “direct physical interpretation” from the AFT model has been favored by many statisticians including Sir David Cox himself (Reid, 1994). Second, although the Cox model has been dominant for the analysis of time-to-event data, the proportional assumption may not be realistic in some settings. In theory, except for the extreme value error distributions, the Cox model and AFT model cannot simultaneously hold. Hence, the AFT model will be more appropriate in some settings. Finally, it will be demonstrated that the Buckley-James (BJ) estimation (Buckley and James, 1979) for the AFT model can be conveniently extended to describe more complex data structures with existing software, such as MART Friedman (2001) and MARS Friedman (1991).

For the theoretical work with the AFT model, see Lai and Ying (1991) and the references therein. In applications, the BJ method has been utilized in many disciplines including medicine (Hammer et al., 2002), genetics (Bautista et al., 2008), astronomy (Steffen et al., 2006) and economics (Deaton and Irish, 1984, Calli and Weverbergh, 2009). For the estimation of high-dimensional AFT models, originating from regression and classification, there have been some proposals on regularized estimation methods, combining with a variety of approaches adjusting for censoring. Huang et al. (2006) applied the least absolute shrinkage and selection operator (LASSO) (Tibshirani, 1996) and the threshold gradient directed regularization (TGDR) (Friedman and Popescu, 2004), with the inverse probability censoring (IPC) weighted least squares estimator (Stute, 1993). Datta et al. (2007) applied the partial least squares (PLS) and LASSO by mean imputation. Engler and Li (2009) and Wang et al. (2008a) applied an elastic net algorithm (Zou and Hastie, 2005) together with a mean imputation and the BJ method, respectively. PLS with BJ can be found in (Huang and Harrington, 2005), although PLS can’t conduct variable selection. The TGDR approach in Huang et al. (2006) relies on the threshold parameter whose small changes can dramatically vary the number of variables selected. Thus, it can be critical to obtain the optimal tuning parameter for a stable model selection. The LASSO approach in Huang et al. (2006) is based on IPC weighting which is different from BJ iterative imputation, and can produce inferior prediction accuracy, at least in some empirical studies (Huang et al., 2006).

All the aforementioned methods, however, were developed for describing simple linear effects. On the other hand, it is anticipated that the genetic architecture of the common diseases is very complex (Moore, 2003, Sing et al., 2003, Thornton-Wells et al., 2004), and many diseases are produced by the nonlinear interaction of genetic and environmental covariates (Motsinger AA, 2006). Briollais et al. (2007) claimed that “gene-gene interactions are ubiquitous in determining the susceptibility to common human diseases”. One of the major tasks using gene expression microarrays in cancer study is “identifying cancer-associated (signalling) molecular markers and their complex interactions” (Wang et al., 2008b). By capturing nonlinear effects plus high order (nonlinear) interactions can potentially improve predictive power. The success of such complex models over simple linear effects model perhaps can be explained by the somewhat famous XOR or chess-board problem, in which two uncorrelated covariates and their linear combinations have no classification power, while a simple nonlinear model is perfectly classifying (Duda et al., 2001, Guyon and Elisseeff, 2003). In addition, such an XOR problem can be generalized to higher than two-dimensional. The literature has repeated indicated that applications of complex models in cancer classification can lead to better prediction than simple models, which support the hypothesis that genetic variants in cancer genes contribute to cancer risk through complex relationship. For instance, Briollais et al. (2007) showed evidence for several two-way and higher order interactions associated with breast cancer. Huang et al. (2007) demonstrated that a four-factor model involving gene-gene and gene-environmental interactions had the best power to predict bladder cancer risk. A complicated technique, multifactor dimensionality reduction has been introduced to detect gene-gene interactions in diseases such as sporadic breast cancer (Ritchie et al., 2001). Statistical methods in genetics with complex model structure for time-to-event outcome is underdeveloped. Not surprisingly, due to the curse of dimensionality and censoring, fitting nonlinear model and interactions becomes a more challenging task. To our knowledge, one such example is gene harvesting (Hastie et al., 2001a) with pairwise interaction, despite some limitations on its prediction performance and robustness (Segal et al., 2003). In conclusion, although there is a rich literature on statistical methods for high-dimensional survival data, flexible methods are needed to fit complex structures.

This paper is motivated to develop a unified framework to model survival times with gene expression microarrays. The proposed approach can fit linear effects model, nonlinear effects model, and nonlinear effects model with high order nonlinear interactions. A key component of this framework relies on boosting techniques. Boosting is a different approach for estimation when covariates are high-dimensional, which is popular in machine learning and computer science. Developed by Freund and Schapire (1995, 1996), boosting as a classification algorithm has been proved to be successful in many applications. A typical boosting algorithm begins with a weak base learner, which is a model fitting method, and iteratively fits the weighted data to update the accuracy of predication and update the weights for each observation by giving more weights to those with more difficulty to fit. The resulting final model is a linear combination of such iterative estimates. Boosting has been generalized in various statistical estimation problems, after the discovery that boosting is a gradient descent method. When the number of noneffective covariates are large, a twin boosting (Bühlmann and Hothorn, 2010) can select more sparse models, similarly to the adaptive LASSO (Zou, 2006). For a recent review on boosting in statistical applications, see Bühlmann and Hothorn (2007). Boosting also has a clear connection with the LASSO (Hastie et al., 2001b, Efron et al., 2004). With survival data, boosting has been employed by Ridgeway (1999) and Li and Luan (2005) to optimize the partial likelihood in Cox’s model with regression trees and smoothing splines, respectively. Hothorn et al. (2006) employed boosting for the AFT models with the weighted least squares loss function. Also, see Lu and Li (2008) for non-linear transformation models and Schmid and Hothorn (2008) for parametric models.

In this article, we propose to apply the BJ iterative estimation method for the AFT models. Within each iteration, boosting is utilized for model estimation and selection. Since the proposed method is a combination of BJ and boosting, we illustrate its advantages from two aspects. First, as an iterative least squares approach, the BJ estimator is closely related to the ordinary least squares estimator without censoring. Such an interpretation can be more accessible to practitioners. In a comparison study, Heller and Simonoff (1990) concluded the BJ estimator is preferred among the commonly applied estimation methods in the literature. In addition, the validity of the BJ approach requires weaker assumptions. For instance, the IPC approach assumes the censoring time is independent of the covariates, and the support of the failure time is included in the support of the censoring time, which may not be true in practice. Under weak requirements on the censoring mechanism, in particular, the residuals are independent of the covariates, the BJ estimator is comparably efficient with the classical least squares estimator. Second, we emphasize that boosting is a method for minimizing convex loss functions via gradient descent techniques. Thus, boosting is different from some of the aforementioned methods which optimize penalized loss functions, such as the LASSO. Bühlmann (2006, section 4.3) specifically demonstrated that boosting is different from the LASSO. Efron et al. (2004) considered a version of boosting, called forward stage wise linear regression (FSLR), and they show that FSLR with infinitesimally small step-sizes generates a set of solutions which is approximately equivalent to the set of the LASSO solutions, under certain conditions. They are, however, different for many problems. The FSLR paths are much smoother and more monotone than the LASSO paths in high-dimensional problem with correlated covariates (Hastie et al., 2007, Hastie, 2007). This particularly implies that in analyzing the microarray gene expression data for which gene-gene interactions often exist, the LASSO and boosting can generate different results. Additionally, boosting and LASSO can generate different results due to the parameters selected in tuning methods. This is because boosting typically has a larger number of tuning parameter to choose from compared with LASSO. Boosting is a general and generic method which can be used to estimate models with complex data structures. Therefore, compared with the LASSO-type methods (Huang et al., 2006, Wang et al., 2008a), the BJ boosting can produce different, and sometimes better results. In the subsequent sections, we develop a unified framework with BJ boosting for linear, and non-linear effects models with possible interactions. Finally, the proposed BJ boosting is not difficult to implement. In fact, the BJ procedure can be readily implemented because it iteratively utilizes the Kaplan-Meier estimates, which is a common component in major statistical software. In addition, the boosting algorithm is straightforward to program. Both BJ estimation and boosting have been implemented in statistical software R (R Development Core Team, 2009), for instance, in Design (Harrell, 2003) and mboost (Bühlmann and Hothorn, 2007) package, respectively. The algorithm developed here including the tuning parameter selection procedure can be readily carried out.

The rest of the article is organized as follows. In section 2, we outline the BJ estimation method for the AFT models. In section 3, we give a summary of a generic boosting and twin boosting algorithms. In section 4, we propose the L₂ boosting algorithm adjusting for censoring by the BJ method. In section 5, a simulation study was conducted to evaluate and compare the proposed algorithm and other related methods. In section 6, the proposed methods are applied to the microarray data for patients with diffuse large B-cell lymphoma (DLBCL). Finally, section 7 concludes with discussions.

2. Regression Models for Survival Data

Let T_i be the logarithmic (or some other monotone function) transformed random failure time and X_i be length-p covariate vector for subject i. For right censoring T_i, the observed data are (Y_i, δ_i, X_i), where Y_i = min(T_i, C_i). C_i is the logarithmic transformed censoring time and δ_i = I(T_i ≤ C_i) is the censoring indicator function. We first assume a parametric model

$$T_i=f(X_i,\beta )+{\varepsilon }_i,\hspace{1em}i=1,\dots ,n,$$

for a parameter vector β = (β₁, β₁, …,β_p)′. The form of f, depending on the parameter vector β, may be chosen to be linear, such as the AFT model $f(X_i)=X_i^{\prime }\beta$. Later, we extend to a nonparametric model and β can be dropped out. With some abuse of notation, f(X) and f(X, β) are used interchangeably, which should be clear according to the context. We assume the random noise ɛ_i has mean zero and finite variance. If no censoring occurs, then T_i = Y_i and the function f may be estimated by minimizing a loss function, for example,

$$L(Y,f(X))=\frac{1}{2}\sum _{i=1}^n{(Y_i-f(X_i))}^2.$$ (1)

Due to censoring, f cannot be estimated directly from (1). Buckley and James (1979) suggested to impute those censored T_i with their conditional expectation given associated censoring times and covariates. Specifically, let $Y_i^{*}$ be imputed as

$$Y_i^{*}=Y_i{\delta }_i+E(T_i|T_i>Y_i,X_i)(1-{\delta }_i).$$

This implies $Y_i^{*}=T_i \text{if} {\delta }_i=1$ and $Y_i^{*}=E(T_i|T_i>Y_i,X_i) \text{if} {\delta }_i=0$. We can calculate the conditional expectation by

$$E(T_i|T_i>Y_i,X_i)=f(X_i)+{\int }_{Y_i-f(X_i)}^{\infty }\frac{tdF(t)}{1-F(Y_i-f(X_i))},$$

where F is the distribution function of T − f (X), which can be simply estimated by the Kaplan-Meier estimator F̂. Assume f (X) = X′ β and we have an estimated f̂ (X) (for instance, an initialized value f̂ (X) = 0). Note the underlying residuals T_i − f̂ (X_i) is generally not available due to censoring. Denote the observed residuals e_i = Y_i − f̂ (X_i) with ranked order such that e₁ < e₂ < ⋯ < e_n and the responses, indicators and covariates are re-arranged according to this ranking. Thus, $Y_i^{*}$ can be imputed by

$$Y_i^{*}=\widehat{f}(X_i)+\left\{e_i{\delta }_i+(1-{\delta }_i)\left[\widehat{S}{(e_i)}^{-1}\sum _{e_j>e_i}{e}_j{\delta }_j\Delta \widehat{S}(e_j)\right]\right\},$$ (2)

where Ŝ(e_i) is the Kaplan-Meier estimator of survival function for residual failure time e_i, and ΔŜ(e_j) is the jump size of Ŝ at residual time e_j. Denote $Y*={(Y_1^{*},Y_2^{*},\dots ,Y_n^{*})}^{\prime }$ and the covariates matrix X = (X₁, X₂, …, X_n)′, we can rewrite Equation (2) as follows:

$$Y*=\widehat{f}(X)+\mathbf{\text{A}}(\beta )(Y-\widehat{f}(X)),$$

where

$$\mathbf{\text{A}}(\beta )=\left(\begin{array}{cccc}{\delta }_1& (1-{\delta }_1){\delta }_2\frac{\Delta \widehat{S}(e_2)}{\widehat{S}(e_2)}& \cdots & (1-{\delta }_1){\delta }_n\frac{\Delta \widehat{S}(e_n)}{\widehat{S}(e_n)}\\ 0& {\delta }_2& \cdots & (1-{\delta }_2){\delta }_n\frac{\Delta \widehat{S}(e_n)}{\widehat{S}(e_n)}\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\delta }_n\end{array}\right).$$ (3)

To update the estimate f̂ (X) based on the current ( $X_i,Y_i^{*}$), a least squares estimator can be obtained. Specifically, substituting Y_i with $Y_i^{*}$, β may be obtained by minimizing the loss function (1). The BJ estimator has a simple least squares solution

$${\widehat{\beta }}_{BJ}={(X^{\prime }X)}^{-1}{X}^{\prime }Y*$$

An iterative procedure is expected to solve for β as the imputed value $Y_i^{*}$ involves unknown parameter β. For linear regression with an intercept β₀, we first center both responses and covariates. After the iterations are completed and the estimated coefficients β̂ are claimed, the intercept can be estimated as β̂₀ = Ȳ* − X̄β̂, where Ȳ* is the sample mean of $Y_i^{*}$ and X̄ is the vector of sample means of the covariates.

3. Generic Boosting

In this section, we present a generic boosting algorithm and discuss the selection of loss function, base learner and tuning parameter.

3.1. Generic boosting algorithm

We first summarize a generic boosting algorithm, or functional gradient descent algorithm (Friedman, 2001, Bühlmann and Yu, 2003, Bühlmann and Hothorn, 2007). Given (X_i, Y_i) for i = 1,2, …, n, the goal is to approximate Y with a function f such that Y = f (x) + ɛ, with ɛ being random noise with mean 0 and finite variance. To optimize a loss function L(Y, f), boosting proceeds as follows:

1. Initialize f̂₀ = Ȳ, where $\overline{Y}=\frac{1}{n}{\sum }_{i=1}^n{Y}_i$, set m = 0.

2. At the mth iteration, compute the residuals, defined as negative gradient of loss function, $U_{i,m}=\frac{\partial L(Y_i,f)}{\partial f}{|}_{f={\widehat{f}}_m(X_i)}$.

3. Fit a base learner (see section 3.3) g(U_m, X) to the residuals U_i,m with covariates X_i, for i = 1,2, …, n.

4. Update the estimated function f̂_m+1 (X) = f̂_m(X) + νg(U_m, X) for a learning rate 0 < ν ≤ 1.

5. Increase m by one and repeat steps 1–4 until m = M for some tuning parameter M determined by the procedures to be described in section 3.4.

As an example, if we consider L₂ boosting, i.e., a squared loss function L = (Y_i − f (X_i))²/2, then in step 2, U_i,m = Y_i − f̂_m(X_i). Similarly, with nonnegative w_i and a weighted squares loss function L = w_i(Y_i − f (X_i))²/2, we can simply make a change in step 2, U_i,m = w_i(Y_i − f̂_m(X_i)). In our simulations and applications, we chose ν = 0.1. This choice of ν does not determine the predictive performance (Friedman, 2001). A smaller value of ν typically requires a larger boosting step M.

3.2. Twin boosting

It has been demonstrated that the L₂ boosting can falsely select a larger number of covariates when the ratio of the effective number of covariates to the total number of covariates is low (Bühlmann and Yu, 2006, Bühlmann and Hothorn, 2010). A possible remedy is sparse boosting (Bühlmann and Yu, 2006) which is related to nonnegative garrote estimator (Breiman, 1995). Another more general strategy is twin boosting (Bühlmann and Hothorn, 2010) which has connections with the adaptive LASSO. Roughly speaking, the twin boosting (or adaptive LASSO) is to apply a second round of boosting (or LASSO) and only those covariates selected in the first round will be considered as the remaining candidates in the second round. These remaining candidates are weighted by their magnitudes of the estimated coefficients from the first round. This principle can be generalized to a generic base learner as described below. The twin boosting is especially useful in the settings with small n and large p, since it can select more sparse solutions and typically maintains or improves the predictions. The twin L₂ boosting algorithm with a generic base learner g follows (Bühlmann and Hothorn, 2010).

1. First round of boosting to obtain the initial function estimates f̂_init and the covariates selected by the model. Without loss of generality, assume the selected covariates are X₁, X₂, …, X_s where s ≤ p.

2. Among the remaining covariates selected by the first round of boosting, second round of boosting resembles the first round by selecting the best base learner which mostly reduces the penalized residual sum of squares

   $$\widehat{l}=\underset{1\le j\le s}{\text{arg}\text{min}{\widehat{\mathit{\text{cor}}}}^2}(g,{\widehat{f}}_{\mathit{\text{init}}})\sum _{i=1}^n{(u_i-g(X_i^{(j)}))}^2,$$ (4)

   where $\widehat{\mathit{\text{cor}}}$ is the sample correlation which measures the strength of the similarity. The estimate is used to replace step 3 in section 3.1 and the rest of twin boosting is the same as boosting.

3.3. Base learner

Boosting requires a weak base learner g to iteratively fit the residuals U obtained from the last iteration. Three common base learners in the literature (Friedman, 2001, Bühlmann and Yu, 2003) are incorporated for the survival data in this article. In the following description, we sometimes suppress the subscript m, which should be clear from the context.

3.3.1. Componentwise linear least squares

At each iteration, one single covariate is chosen which minimizes the residual sum of squares most:

$$\begin{array}{l}\widehat{l}=\underset{1\le j\le p}{\text{arg}\text{min}}\sum _i^n{(U_i-{\beta }_j{X}^{(j)})}^2,{\widehat{\beta }}_j=\sum _{i=1}^n{X}_i^{(j)}{U}_i/\sum _{i=1}^n{(X_i^{(j)})}^2.\\ \text{The} \text{base} \text{learner} \text{is} \widehat{g}(x)={\widehat{\beta }}_{\widehat{l}}{X}^{(\widehat{l})}.\end{array}$$

We choose the initial offset value f̂⁽⁰⁾ = Ȳ and center the covariates to avoid shrinking the intercept.

3.3.2. Smoothing splines

At mth iteration, fit a univariate cubic smoothing spline g_m(X^(j)) based on U_i,m against X^(j), for j = 1, 2, …, p, with a large amount of smoothing. Then select the covariate which explains the variability most. Specifically,

$$\widehat{l}=\underset{1\le j\le p}{\text{arg}\text{min}}\sum _{i=1}^n{(U_{i,m}-g(X_i^{(j)}))}^2+\lambda \int {(g^{″}(x))}^{2}dx,$$

where λ is the smoothing tuning parameter, and the base learner is ĝ(X^(l̂)). We fix a corresponding small degrees of freedom, say 4 for each of covariate. As a result, such a choice implies a weaker learner having an estimate with large bias and small variance. Applications of boosting with smoothing splines may be found in Li and Luan (2005), Meier et al. (2009).

3.3.3. Regression trees

Regression trees have the advantages that the response variables are invariant to monotone transformations, and are insensitive to outliers. Friedman (2001) studied gradient boosting trees to improve prediction over a single regression tree. If we employ a base learner by constructing a regression tree having two terminal nodes (degree=1), the boosting estimate will be an additive model in the original predictor covariates. With at most 3 terminal nodes (degree=2), boosting estimate is a nonparametric model having interaction terms between pairs of covariates.

3.4. Tuning parameter

The number of boosting step M is a tuning parameter. Because of the connection between the boosting and L₁ regularization, this tuning parameter plays a regularization role. It should be chosen in a trade-off of the model fitting and parsimony. A general strategy is to estimate M by the K-fold cross-validation. With the componentwise linear least squares as the base learner, Bühlmann (2006) developed a computational efficient Akaike information criterion (AIC) for the selection of M. The results can be summarized as below. Let

$$H_j=X^{(j)}{X}^{(j)T}/{\Vert X^{(j)}\Vert }^2,\hspace{1em}j=1,2,\dots ,p,$$

be the n × n hat matrix for the linear least squares fitting operator with the jth covariate variable vector X^(j), where || || is the Euclidean norm. At mth iteration, it was shown that L₂ boosting hat matrix is

$${\mathbf{\text{b}}}_{\mathbf{\text{m}}}=I-(I-v{H}_{c^m})(I-v{H}_{c^{m-1}})\cdots (I-v{H}_{c^1}),$$

where I is the identity matrix and c^k is the component identified in the boosting procedure in the kth iteration, for k = 1, …,m. In an operator notation, the L₂ boosting estimate in iteration m is

$${\widehat{f}}_m={\mathbf{\text{b}}}_{\mathbf{\text{m}}}Y.$$ (5)

An AIC is defined to penalize the model complexity in the boosting algorithm:

$$\text{AIC}(m)=\text{log}({\widehat{\sigma }}^2)+\frac{1+df/n}{1-(df+2)/n},$$

where

$${\widehat{\sigma }}^2=\frac{1}{n}\sum _{i=1}^n{(Y_i-{\widehat{f}}_m(X_i))}^2,$$

and the degrees of freedom d f can be approximated by the number of covariates selected at the mth boosting step (Hastie, 2007). The tuning parameter M can be chosen to minimize the AIC(m), for m = 1,2, …M_stop, where M_stop is a prespecified large number. This procedure, however, may not exist for some boosting base learner, for instance, regression trees. Therefore, for tuning parameter selection, one may simply use the K-fold cross-validation technique, as suggested in Hastie (2007). Specifically, define the CV score as

$$CV(m)=\sum _{v=1}^K\sum _{(X_i,Y_i)\in D^v}{(Y_i^{(k)}-{\widehat{f}}_m^{-D^v}(X_i))}^2,$$ (6)

where D^v and D^(−v) are the test and training data, respectively, and $f_m^{-D^v}$ is estimated from the training data.

In survival data analysis, the above tuning parameter selection strategies can be implemented, although some modifications are required to take into account of censoring (Hothorn et al., 2006, Luan and Li, 2008). Details on tuning parameter selection in the current setting will be given in the next section.

4. Boosting Survival Data

To estimate the AFT model with right-censoring survival times and high-dimensional covariates, we propose a method combining BJ estimator and boosting.

4.1. Buckley-James boosting algorithm

1. Initialization of β̂⁽⁰⁾ or f̂⁽⁰⁾. Set R = 0.

2. At the Rth iteration,

   1. Update $Y_i^{*}$ from Equation (2):

      $$Y_i^{*}=\widehat{f}{(X_i)}^{(R-1)}+\left\{e_i{\delta }_i+(1-{\delta }_i)\left[\widehat{S}{(e_i)}^{-1}\sum _{e_j>e_i}{e}_j{\delta }_j\Delta \widehat{S}(e_j)\right]\right\},$$

      where e_i = Y_i − f̂ (X_i)^(R−1).
   2. With ( $X_i,Y_i^{*}$), fit the model $Y_i^{*}=\widehat{f}{(X_i)}^{(R)}+{\epsilon }_i$ by the L₂ boosting or twin boosting outlined in section 3 for a chosen m iterations. Also see remarks below for tuning parameter selection.
3. Increase R by one and repeat step (2) until some stopping criterion or R = M_BJ for some prespecified number M_BJ. With the componentwise linear least squares, the stopping criterion is chosen to be |β^(R) − β^(R−1)| < η, where η is a prespecified small number. Otherwise, the stopping rule is

   $$\frac{\Vert \widehat{f}{(X)}^{(R)}-\widehat{f}{(X)}^{(R-1)}\Vert }{\Vert \widehat{f}{(X)}^{(R-1)}\Vert }<\eta ,$$ (7)

   where for a length-n vector f = (f₁, f₂, …, f_n), we define $\Vert f\Vert ={\sum }_{i=1}^n{f}_i^2$. The Buckley-James algorithm can generate oscillated estimates among iterations, due to the nature of the discontinuity of the estimating function for β or f in relation to the Kaplan-Meier estimator. We stopped the iterative algorithm whenever such an oscillation occurred or convergence was reached. See, e.g., Huang and Harrington (2005), Wang et al. (2008a), Cai et al. (2009).

Remarks: When computing tuning parameters, both AIC and cross-validation involve the squared difference between the observed outcome and the predicted outcome. Since the observed outcome Y is subject to censoring, we replace Y with the imputed Y*, for instance, in (6), which is the same strategy as in Johnson (2009). There are a variety of tuning parameter selection methods in regularized survival data analysis (Huang et al., 2006, Wang et al., 2008a). While some approaches such as the one in Wang et al. (2008a) can be adopted for linear model in the current setting, the approach is not directly applicable for some nonparametric base learners including smoothing splines and regression trees.

5. Simulation Studies

This section is to evaluate the performance of the BJ boosting, and compare with various relevant methods for the high-dimensional AFT models, which will be briefly presented here. Initially we consider linear models only. Hothorn et al. (2006) proposed a boosting method minimizing an IPC loss function (IPC-B):

$$L_w(Y,f(X))=\frac{1}{2}\sum _{i=1}^n{w}_i{(Y_i-f(X_i))}^2,$$

where $w_i=\frac{{\delta }_i}{S_c(Y_i-)}$, and S_c(Y_i−) (− denotes a left limit) is the conditional censoring survivor function, which is calculated by the Kaplan-Meier estimate. To apply the twin boosting, we first obtain the initial estimates f_init from the above IPC boosting. Then, the twin boosting is employed using estimator (4).

Huang et al. (2006) considered the LASSO estimator (IPC-LASSO):

$$\widehat{\beta }(\lambda )=\underset{\beta }{\text{arg}\text{min}}\frac{1}{n}\sum _{i=1}^n{w}_i{(Y_i-X_i\beta )}^2+\lambda \sum _{j=1}^p\left|{\beta }_j\right|,$$

where λ is the regularization tuning parameter. The adaptive LASSO with the IPC model can be estimated as well. In the sequel, we use an * to denote the twin boosting or adaptive LASSO. Zou and Hastie (2005) considered an elastic net estimator which can select groups of correlated covariates and the number of selected covariates can exceed the total sample size n, which is one of the limitations of the LASSO. For survival data, Wang et al. (2008a) applied the elastic net method to the BJ regression (BJ-EN) by replacing the step 2(b) in section 4 with the elastic net estimator.

The simulations contain three scenarios for linear effects model with p = 30 and two scenarios for non-linear effects model. Since methods for non-linear effects model are quite different, we present the results separately from those for linear effects model. For each scenario, 50 random replications were conducted to evaluate the methods unless otherwise specified. In the first three scenarios, the transformed survival time log(T) = 0.5 + X′β + ɛ with ɛ ∼ N(0,1). For each scenario, the censoring time is generated from the uniform distribution such that the censoring rates are about 30% and 70%, respectively. It is worth mentioning no distribution assumptions were made for the BJ boosting although it is convenient to simulate data from some distributions, as we did here. The tuning parameters were chosen by the AIC for the (first round) BJ boosting with linear least squares (BJ-LS) and IPC boosting, and 5-fold cross validations for the IPC-LASSO. For the twin BJ-LS, IPC-B and adaptive IPC-LASSO, tuning parameters were chosen by the 5-fold cross validations. For BJ-EN, the tuning parameters were chosen by the generalized cross validation as proposed in the original article. To evaluate the predictive performance of the proposed methods, we consider the mean squared error in the simulation study. For linear models, the estimated parameters obtained from the training data are used to predict

$$\text{MSE}=E[{(\widehat{f}(X)-f(X))}^2],f(X)=E[Y|X=x],$$ (8)

where X is a new test observation with the same distribution as in the training sample. More details of data generation are described below.

Scenario 1

In this scenario, the components of β is 0.4 for the first half and 0 for the second half. The covariate X is generated from a multivariate normal distribution N₃₀(0,Σ), where

$$\Sigma =\left(\begin{array}{cccc}J& & & \\ & J& & \\ & & J& \\ & & & I\end{array}\right),$$

with J being a 5 × 5 matrix with diagonal elements to be 1.01 and off-diagonal elements to be 1, and I being a 15 × 15 identity matrix. The model has five members in each of three equally important groups (cf. Zou and Hastie (2005)). In gene expressing data with large p and small n, the ‘grouped variables’ scenario has attracted some attention (Hastie et al., 2000, Segal et al., 2003).

Scenario 2

The first 10 components of β are set to be 1, and 0 otherwise. The design matrix X is generated as X ∼ N₃₀(0,Σ) where [Σ]_ij = 0.5^|i−j|.

Scenario 3

The first half of components of β are set to be 0.4, and 0.2 for the other half. The design matrix X is the same as in Scenario 2.

We summarize the simulation results. The intercepts were not counted in computing the number of non-zero coefficients. Table 1 and 2 support the following findings:

1. For sparse models, it is almost always beneficial to run the twin boosting or adaptive LASSO. The applications of such procedures will typically result in more parsimonious models while maintaining similar prediction performances. When the ratio of noneffective number of covariates to the total number of covariates is large, the advantage is more substantial. When the true underlying models are not sparse, the twin boosting or adaptive LASSO are not favored compared with their counterparts, respectively. For instance, in Scenario 3, the twin BJ-LS, IPC-B and adaptive IPC-LASSO can generate larger MSE and underestimate the effective covariates more severely compared with their counterparts, respectively.

2. BJ-LS, IPC-B and BJ-EN have similar prediction performances while IPC-LASSO can generate larger MSE when censoring rate is high with small sample sizes.

3. When a grouping effect exists, such as the data generated in Scenario 1, BJEN can capture more grouped effects since this is the method specially designed for. However, BJ-EN may overestimate the grouped effects with high censoring data. Other methods that typically underestimate the grouped effects, however, can still maintain good prediction accuracy. In this case, the grouped effects are absorbed in a subset of the effective covariates. It is worth noting that boosting with ridge regression as developed in Tutz and Binder (2007) may be utilized in the BJ framework to account for grouping effect.

4. When the censoring rate increases, the estimation problem becomes more difficult. We suggest to apply some dimension-reduction techniques first to reduce the dimension of the problem. Then, more important covariates are kept for the analysis using the techniques described here.

5. With larger sample sizes, all methods improve the prediction performances.

Table 1:

Mean squared error (MSE) E[(f̂(X) − f (X))²], (f (X) = E[Y|X = x]) for different censoring rate (CR). The twin boosting BJ-LS, IPC-B, or adaptive IPCLASSO is denoted by an asterisk *. Tuning parameter is selected by AIC or cross-validation as specified in the text. Estimated standard deviations are given in parentheses.

Method	Scenario 1		Scenario 2		Scenario 3
	CR 30%	CR 70%	CR 30%	CR 70%	CR 30%	CR 70%
n=100
BJ-LS	0.22 (0.09)	0.62 (0.30)	0.39 (0.18)	1.67 (0.92)	0.64 (0.21)	1.84 (0.67)
BJ-LS*	0.25 (0.11)	0.54 (0.27)	0.40 (0.17)	1.96 (1.27)	0.94 (0.30)	2.62 (1.18)
IPC-B	0.25 (0.11)	1.24 (0.59)	0.46 (0.21)	2.89 (1.53)	0.69 (0.18)	2.64 (1.17)
IPC-B*	0.26 (0.11)	0.85 (0.50)	0.45 (0.22)	3.01 (1.97)	1.02 (0.27)	3.34 (1.53)
IPC-LASSO	0.43 (0.36)	2.81 (2.44)	0.51 (0.28)	7.78 (12.6)	0.80 (0.28)	10.02 (22.3)
IPC-LASSO*	0.24 (0.20)	2.13 (3.67)	0.39 (0.21)	10.79 (19.9)	1.15 (0.35)	15.56 (34.8)
BJ-EN	0.32 (0.19)	1.60 (0.71)	0.41 (0.23)	1.77 (1.02)	0.62 (0.23)	2.07 (0.94)
n=200
BJ-LS	0.12 (0.06)	0.28 (0.12)	0.19 (0.06)	0.53 (0.21)	0.31 (0.09)	0.78 (0.19)
BJ-LS*	0.14 (0.05)	0.26 (0.12)	0.21 (0.08)	0.60 (0.24)	0.42 (0.14)	1.11 (0.30)
IPC-B	0.14 (0.07)	0.60 (0.29)	0.23 (0.07)	0.99 (0.41)	0.33 (0.10)	0.99 (0.35)
IPC-B*	0.14 (0.05)	0.48 (0.22)	0.21 (0.08)	0.75 (0.38)	0.47 (0.13)	1.35 (0.38)
IPC-LASSO	0.22 (0.14)	1.33 (0.72)	0.22 (0.08)	1.29 (1.30)	0.35 (0.11)	1.45 (0.79)
IPC-LASSO*	0.18 (0.14)	0.49 (0.30)	0.19 (0.08)	0.63 (0.31)	0.50 (0.17)	1.56 (0.54)
BJ-EN	0.13 (0.08)	0.45 (0.21)	0.20 (0.08)	0.51 (0.20)	0.32 (0.09)	0.74 (0.17)

Table 2:

Estimated number of covariates with non-zero coefficients for different censoring rate (CR). The twin boosting BJ-LS, IPC-B or adaptive IPC-LASSO is denoted by an asterisk *. The selected number (No.) of covariates: A is the total number selected; T is the correctly selected number; F is the falsely selected number. Tuning parameter is selected by AIC or cross-validation. Estimated standard deviations are given in parentheses.

Method	No.	Scenario 1		Scenario 2		Scenario 3
		CR 30%	CR 70%	CR 30%	CR 70%	CR 30%	CR 70%
n=100
BJ-LS	A	12.1 (2.9)	12.3 (3.4)	15.1 (3.0)	17.3 (4.0)	27.2 (2.0)	23.1 (4.0)
	T	7.9 (1.5)	6.8 (1.4)	10.0 (0.0)	9.9 (0.4)	27.2 (2.0)	23.1 (4.0)
	F	4.2 (2.6)	5.5 (3.0)	5.1 (3.0)	7.4 (3.9)	-	-
BJ-LS*	A	7.1 (2.4)	7.2 (2.0)	14.4 (2.3)	15.6 (3.0)	22.6 (2.8)	17.8 (3.0)
	T	4.4 (1.0)	3.9 (0.7)	10.0 (0.0)	9.6 (0.6)	22.6 (2.8)	17.8 (3.0)
	F	2.7 (2.1)	3.2 (1.8)	4.4 (2.3)	6.0 (2.9)	-	-
IPC-B	A	13.7 (3.2)	20.9 (3.5)	18.8 (4.7)	27.4 (1.3)	27.5 (1.9)	27.8 (1.3)
	T	8.1 (1.4)	8.0 (1.9)	10.0 (0.0)	10.0 (0.2)	27.5 (1.9)	27.8 (1.3)
	F	5.6 (3.1)	12.9 (2.4)	8.8 (4.7)	17.5 (1.2)	-	-
IPC-B*	A	9.9 (2.3)	13.6 (2.7)	16.6 (3.2)	20.0 (2.2)	24.6 (1.9)	20.4 (2.0)
	T	5.4 (0.9)	5.1 (1.1)	10.0 (0.0)	9.6 (0.7)	24.6 (1.9)	20.4 (2.0)
	F	4.4 (2.3)	8.5 (2.5)	6.6 (3.2)	10.4 (2.1)	-	-
IPC-LASSO	A	10.8 (4.5)	17.9 (8.2)	14.9 (4.4)	21.5 (6.2)	25.7 (2.3)	22.2 (6.2)
	T	7.0 (1.8)	7.4 (3.1)	10.0 (0.0)	9.6 (0.7)	25.7 (2.3)	22.2 (6.2)
	F	3.8 (4.0)	10.4 (5.9)	4.9 (4.4)	11.9 (6.1)	-	-
IPC-LASSO*	A	5.8 (2.7)	8.4 (6.3)	12.9 (3.0)	17.0 (7.6)	20.2 (2.8)	17.0 (8.4)
	T	4.4 (1.6)	4.2 (2.1)	10.0 (0.0)	8.7 (1.4)	20.2 (2.8)	17.0 (8.4)
	F	1.3 (1.9)	4.2 (4.6)	2.9 (3.0)	8.3 (7.1)	-	-
BJ-EN	A	17.7 (5.0)	26.1 (4.6)	19.8 (4.9)	23.6 (3.6)	28.0 (1.3)	25.6 (1.8)
	T	8.7 (2.0)	11.8 (2.9)	10.0 (0.0)	10.0 (0.0)	28.0 (1.3)	25.6 (1.8)
	F	9.0 (4.0)	14.3 (2.3)	9.8 (4.9)	13.6 (3.6)	-	-
n=200
BJ-LS	A	13.4 (3.3)	13.7 (3.7)	17.3 (3.9)	19.9 (4.2)	29.0 (1.2)	27.1 (1.8)
	T	9.5 (1.5)	8.2 (1.4)	10.0 (0.0)	10.0 (0.0)	29.0 (1.2)	27.1 (1.8)
	F	3.9 (3.0)	5.5 (3.2)	7.3 (3.9)	9.9 (4.2)	-	-
BJ-LS*	A	6.8 (1.6)	6.2 (2.0)	15.5 (3.3)	16.5 (2.7)	26.6 (1.8)	20.9 (2.7)
	T	5.3 (1.0)	4.2 (0.7)	10.0 (0.0)	10.0 (0.0)	26.6 (1.8)	20.9 (2.7)
	F	1.5 (1.5)	2.0 (3.1)	5.5 (3.3)	6.5 (2.7)	-	-
IPC-B	A	14.9 (3.8)	21.2 (3.8)	19.8 (4.1)	27.8 (2.2)	29.1 (1.2)	28.8 (1.3)
	T	9.3 (1.3)	9.2 (1.6)	10.0 (0.0)	10.0 (0.0)	29.1 (1.2)	28.8 (1.3)
	F	5.6 (3.6)	12.0 (2.8)	9.8 (4.1)	17.8 (2.2)	-	-
IPC-B*	A	7.1 (2.5)	7.3 (2.9)	14.9 (3.6)	17.5 (3.8)	26.7 (1.4)	21.7 (2.5)
	T	5.2 (1.2)	4.2 (1.1)	10.0 (0.0)	10.0 (0.0)	26.7 (1.4)	21.7 (2.5)
	F	1.8 (1.9)	3.1 (2.4)	4.9 (3.6)	7.5 (3.8)	-	-
IPC-LASSO	A	12.7 (5.2)	9.0 (4.1)	15.7 (3.8)	14.9 (4.0)	29.1 (1.1)	22.6 (3.8)
	T	8.7 (1.6)	6.1 (2.9)	10.0 (0.0)	10.0 (0.3)	29.1 (1.1)	22.6 (3.8)
	F	4.0 (4.7)	2.9 (3.5)	5.7 (3.8)	5.0 (4.0)	-	-
IPC-LASSO*	A	6.8 (4.2)	5.7 (2.5)	12.8 (2.6)	13.4 (3.4)	25.6 (1.8)	18.0 (3.5)
	T	5.0 (2.0)	4.3 (1.4)	10.0 (0.0)	10.0 (0.0)	25.6 (1.8)	18.0 (3.5)
	F	1.7 (2.9)	1.3 (1.9)	2.8 (2.6)	3.4 (3.4)	-	-
BJ-EN	A	16.4 (3.9)	23.7 (5.6)	20.0 (5.1)	22.7 (2.8)	29.0 (1.0)	26.4 (1.3)
	T	9.7 (2.1)	10.9 (2.6)	10.0 (0.0)	10.0 (0.0)	29.0 (1.0)	26.4 (1.3)
	F	6.7 (4.1)	12.8 (3.5)	10.0 (5.1)	12.7 (2.8)	-	-

We have conducted additional simulations with extreme censoring 5% and 95%, respectively. The results with sample size n = 200 can be found in Supplementary Table 1 and 2, which also support the above findings. Furthermore, we plotted the MSE of test data against BJ iterations in Supplementary Figure 1. The plots suggest that in BJ iterations, the MSE curves can quickly become flat so that the stable predictions are reached.

Scenario 4

We present a simulation study with p = 50, to evaluate the performance of the proposed BJ boosting methods for non-linear effects. The model considered here has the same functional forms as those in Li and Luan (2005):

$$f(X)=f_1(X^{(1)})+f_2(X^{(2)})+f_3(X^{(3)})+f_4(X^{(4)}),$$

where f₁(X⁽¹⁾) = 4[X⁽¹⁾]² + X⁽¹⁾, f₂(X⁽²⁾) = sin[6X⁽²⁾], f₃(X⁽³⁾) = cos[6X⁽³⁾] − 1, f₄(X⁽⁴⁾) = 4[X⁽⁴⁾]³ + [X⁽⁴⁾]². Along with other 46 noneffective covariates, X^(j), j = 1, …,50 are generated from uniform [−0.5,0.5] distribution. The logarithmic transformed survival time T is generated from a normal distribution T = f (X) + ɛ where ɛ has a normal distribution N(0,0.75). Thus the survival time follows a log-normal distribution. The logarithmic transformed censoring time C is generated from a normal distribution N(0,0.75) to obtain 36.5% censoring.

We conducted analysis of simulated data by BJ boosting with smoothing splines (BJ-SS) and regression trees with degree 1 (BJ-Tree). For non-linear effects models, we also combine BJ estimator with other nonparametric methods including ACOSSO and MARS to compare with the boosting approach. Storlie et al. (2009) developed ACOSSO which is a version of the adaptive LASSO in the nonparametric framework. Another popular algorithm MARS was developed in Friedman (1991) which is a stepwise forward-backward procedure, and can overcome some limitations of regression trees such as discontinuity. At each BJ iteration, we fit a model for the imputed survival times with ACOSSO or MARS, and the tuning parameters for these methods were appropriately set. These methods are denoted by BJ-ACOSSO and BJ-MARS, respectively.

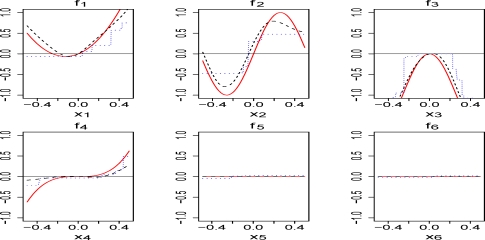
We begin with investigating how well the proposed BJ boosting method can recover the underlying functional forms. For illustration, estimated function forms for a sample are shown in Figure 1. It can be seen that the estimated functional forms with smoothing splines are similar to the true ones. The regression trees apparently misspecify the model. It is worth noting that the estimated functional forms for covariates X⁽¹⁾−X⁽⁴⁾ are typically shrunk toward zero, which is the anticipated feature of the shrinkage estimates. The functional form for X⁽⁴⁾ is more difficult to estimate due to the lower signal-to-noise ratio (SNR = var(f (x))/var(ɛ)) compared with the first 3 covariates. For noneffective covariates X⁽⁵⁾ and X⁽⁶⁾, the estimated functions are close to their true values zero. The results for other noneffective covariates are similar. To further evaluate the importance of the remaining covariates selected in the model, Friedman (2001) suggested the relative influence measure (RIF):

$$I_j={\left(E_X{\left[\frac{\partial \widehat{f}(X)}{\partial X^{(j)}}\right]}^2{\text{var}}_X(X^{(j)})\right)}^{1/2},$$ (9)

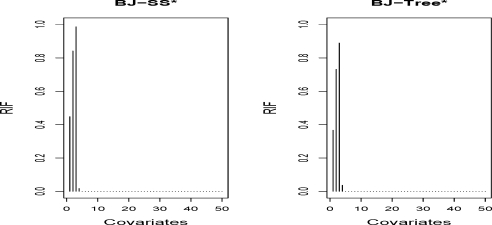
for j = 1, …, p, where E_X can be computed by the sample average. A larger value of I_j suggests a more important contribution from the covariate X^(j) to the model. If I_j = 0, then the corresponding covariate is not selected in the model. It can be shown that I_j is equivalent to the coefficients for some special linear regression models (Friedman, 2001). RIF can be computed for the boosting with smoothing splines, but not for the regression trees since Equation (9) does not exist. One solution is the measure proposed in Friedman (2001). Here we consider a simplified measure by approximating (9) with numerical differentiation so that the measure can be evaluated for both smoothing splines and regression trees. It is simple to implement even for twin boosting. The usage of the measure is illustrated in a simulation study. Figure 2 shows the medians with 100 replications for the proposed measure by applying BJ twin boosting with smoothing splines and regression trees. Despite of misspecification of the model, regression trees indeed provide informative importance measures, similarly to smoothing splines.

Figure 1:

The true functional forms (solid line), the estimated functional forms with smoothing splines (dashed line) and regression trees (dotted line).

Figure 2:

Median of relative influence measure (RIF) for each covariate in 100 simulations (n=200) by BJ twin boosting with smoothing splines and regression trees (degree=1). Data generated in the same setting as Scenario 4.

For non-linear effects models, the integrated squared error (ISE) is estimated by Monte Carlo integration using 2000 test points from the same distribution as the training points. In Table 3, BJ-SS has similar ISE compared with BJ-ACOSSO. BJ-Tree and BJ-MARS generate larger ISEs which is not unanticipated. Compared with boosting, twin boosting appears to improve the prediction accuracy, and generate more parsimonious models. Additionally, we compared the methods with a relatively small sample size n = 100 in Supplementary Table 3. BJ-SS and its twin boosting counterpart clearly outperform other methods.

Table 3:

Average ISE and total number of selected covariates (standard deviations in parentheses) in Scenario 4.

Method	ISE		No.
	n=200	n=400	n=200	n=400
BJ-SS	0.16 (0.047)	0.10 (0.021)	13.5 (3.3)	12.1 (1.8)
BJ-SS*	0.10 (0.038)	0.05 (0.020)	6.9 (1.8)	4.9 (1.2)
BJ-Tree	0.34 (0.072)	0.21 (0.029)	44.7 (2.1)	41.5 (2.7)
BJ-Tree*	0.32 (0.094)	0.20 (0.042)	12.0 (5.4)	11.7 (4.4)
BJ-MARS	0.43 (0.112)	0.27 (0.072)	16.0 (3.7)	17.8 (4.0)
BJ-ACOSSO	0.15 (0.107)	0.06 (0.023)	4.7 (1.0)	4.6 (1.2)

Scenario 5

We present a simulation study with p = 20, to demonstrate that BJ boosting can be utilized to detect nonlinear high order interactions. With four effective covariates, the model follows:

$$f(X)=0.25[X^{(1)}+X^{(2)}+X^{(3)}+X^{(4)}]+8X^{(1)}{X}^{(2)}{X}^{(3)}{X}^{(4)}.$$

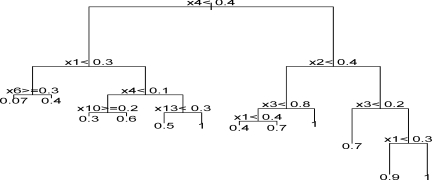
The covariates X^(j), j = 1, …,20 are generated from uniform [−0.5,0.5] distribution. The logarithmic transformed survival time T is equivalent to f (X) + ɛ where ɛ ∼ N(0,0.25). The logarithmic transformed censoring time C is generated from uniform [0,3] distribution to obtain 35% censoring. With sample size n = 200, we applied the BJ boosting trees with degree 4 to fit a model with up to four-way interactions. At the first iteration in the outer BJ loop, the algorithm was run only one inner boosting iteration. A corresponding model is shown in Figure 3. The leaves right side of the first node X₄ < 0.4 clearly demonstrate four-way interactions among X₁,X₂,X₃,X₄. BJ boosting can generate different trees and some of them can detect four-way interactions such as those illustrated in Figure 3. Thus, the final assembled model can contain complex structures including interactions. To show the benefits of modeling interactions, we apply the comprehensive BJ boosting algorithm to the simulated data and evaluate the prediction accuracy with 2000 test data, with 100 replications. As a comparison, we also run BJ boosting trees with main effects only (i.e., tree with degree 1). The mean squared error of model with four-way interactions is 72% of that for the main effects model (standard deviation 6%), which clearly illustrates the advantages of modeling the interactions.

Figure 3:

Four-way interactions with BJ boosting trees in Scenario 5.

6. An Application to DLBCL Data

We apply the proposed methods to a DLBCL study. Lymphoma is a type of cancer involving cells of the immune system. DLBCL is an aggressive lymphoma of B-cells, which can grow quickly, and can spread fast to diverse parts of the body. DLBCL often occur in men with age above 50 years. At the time of diagnosis of DLBCL, patients may have extensive disease requiring chemotherapy, which may lead to 35 to 40% of cure (Rosenwald et al., 2002). To predict therapy success of DLBCL, high-profile microarray gene expression studies have been conducted, in the hope that the gene level analysis can provide better prediciton of disease prognosis than that obtained from clinical predictors only. In the literature, DLBCL data sets for the combination chemotherapy with cyclophosphamide, doxorubicin, vincristine and prednisone (CHOP) have been analyzied, for instance, see Rosenwald et al. (2002), Segal (2006) and the references therein. The current gold standard therapy, however, has evolved into to include rituxima immunotherapy in addition to the chematherapy (R-CHOP), which has improved overall survival among patients with DLBCL by 10 to 15% (Lenz et al., 2008). It is interesting to identify genes that predict survival among patients who received CHOP also retain their prognositc power among patients who received R-CHOP. Studying those robust genes can lead to better understanding of biologic variation among DLBCL tumors. Using R-CHOP data, some recent medical articles have re-evaluated the prediction accuracy of the models previously developed for CHOP data (Alizadeh et al., 2009, Malumbres et al., 2008).

We analyzed the microarray data of DLBCL reported in Lenz et al. (2008). There are 181 CHOP patients as training data, and 233 R-CHOP patients as testing data, each with 54675 probe sets or covariates. Loosely, we will use the terms genes and probe sets interchangeably. The censoring rate in the training data is about 40%. The goal of the analysis was to build a model with good prediction based on a small subset of probe sets, which was believed to be the truth. The training data were used to build models and the testing data is used to validate the models. Due to the nature of p ≫ n, we first conducted a preselection procedure on the training data by filtering out the genes with lower variations if a sample variance for a gene was smaller than the 10th percentile for that gene. Genes with weak variations were less likely to correlate with biological functions, and removing such genes can increase the signal to noise ratio. Testing data with the same remaing genes as in the training data will be used for validation.

With the remaining 3833 probe sets in the sequel, we applied the methods described in the previous sections. For the AFT models, before the logarithmic transformation was applied to the survival times, a value 1 was added to the observed survival times due to a few zero values. The interpretation, however, is based on the predicted values after transforming back to the original time scale. For comparison, other high-dimensional data analysis tools based on the Cox proportional hazards model were included: the Cox model with L₁ penalty (Park and Hastie, 2007) denoted as Cox-LASSO; and supervised principal components (Bair et al., 2006) denoted as Superpc. To assess prediction, the survival times estimated from the testing data were dichotomized into two groups at year 3 for the AFT models, or the median for the Cox model. We then constructed the Kaplan-Meier curves for the two groups with their corresponding observed survival times in the testing data, and conducted the log-rank tests. Selected results are presented in Table 4. If the twin boosting improved the prediction on the testing data, then the results were shown. Otherwise, the boosting results were shown. For instance, with smaller log-rank test p-value, BJ-LS* was preferred to BJ-LS. With the same principle, the results from the IPC-LASSO rather than the adaptive LASSO were shown. The results for BJ-EN and Cox-LASSO are based on a different strategy on tuning parameter selection. Our first attempt was to follow the original strategies proposed in the authors’ papers. For BJ-EN, it is the generalized cross-validation (GCV). It appears that further pre-selection is required for BJ-EN due to the high demanding computation for the GCV. Thus, a univariate BJ procedure was employed to select the top 1000 most significant probe sets, as in Wang et al. (2008a). This procedure is called supervised gene screening in Ma (2006). With the tuning parameters selected by the GCV, the model resulted in a large p-value for the log-rank test. In addition, pre-selection of top 100 most significant probe sets resulted in a p-value 0.05 and 78 probe sets were selected. Since the tuning parameter selection for BJEN is out of the scope of this manuscript, we chose the tuning parameters so that the corresponding log-rank test is the most significant based on 3833 probe sets without supervised gene screening. The results were shown in Table 4. This procedure was also employed for the supervised principal components with the similar reasoning. For nonparametric model estimation, we adopted a supervised gene screening to select the top 100 probe sets based on univariate BJ estimation. With other selection such as top 1000, BJ-Tree still had good prediction, although it became a computational burden to BJ-SS or BJ-ACOSSO. Apparently, gene screening itself is an important topic and Ma (2006) provided some discussion.

Table 4:

Prediction results for testing data with R-CHOP therapy for different methods. The models were estimated using the training data with CHOP therapy. The third column is the number of probe sets selected by a method. The fourth column displays the number of overlapping probe sets in BJ-LS* and other methods. P-value is calculated by a log-rank test for high risk and low risk groups.

Model	Method	No.	Overlap	P-value
AFT linear	BJ-LS*	12	-	0.004
	IPC-B*	57	1	0.012
	IPC-LASSO	64	1	0.011
	BJ-EN	17	12	<0.001
AFT non-linear	BJ-Tree (degree=1)	61	8	<0.001
	BJ-Tree (degree=4)	66	8	<0.001
	BJ-SS*	23	8	<0.001
Cox linear	Cox-LASSO	118	12	0.016
	Superpc	97	8	<0.001

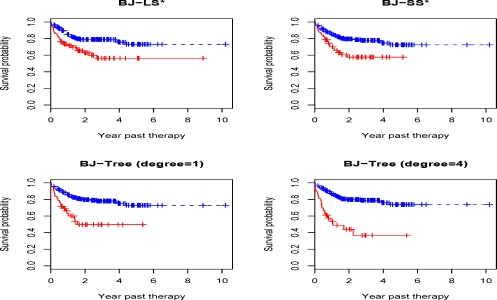
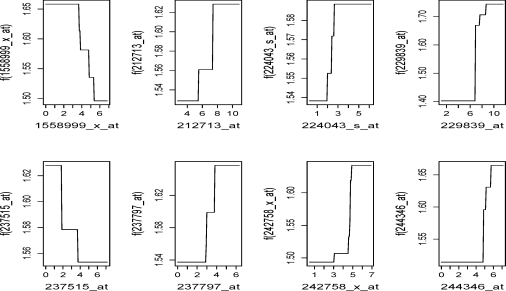
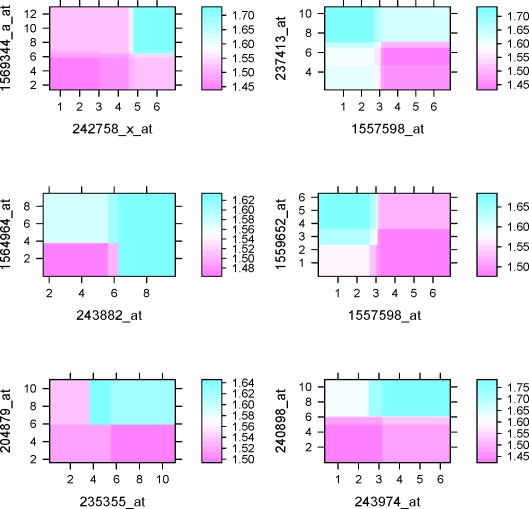
The results can be summarized as follows. In Table 4, all methods show good prediction accuracy despite that p-values vary. The results for BJ-LS* was used as benchmark since only 12 probe sets were chosen in the model, with coefficients presented in Table 5. With good separation, the Kaplan-Meier survival curves for the BJ boosting methods were illustrated in Figure 4. Kaplan-Meier survival curves for BJ-EN, IPC-LASSO and IPC-B* can be found as Supplementary Figure 2 online. Figure 4 contained the results with BJ-Tree (degree=4), which allows for interactions among 4 probe sets, at least. This model further enhanced the prediction accuracy compared with the additive model BJ-Tree (degree=1). In fact, the resulting p-value was less than 5 × 10⁻⁸ which was the smallest among all methods under investigation, while BJ-Tree (degree=1) resulted in a p-value 9 × 10⁻⁵). With regression trees, in particular with interactions, partial dependence plots (Friedman, 2001) can be utilized to show the impact of one or more covariates on the response after taking account the average effects of all other covariates in the model. For the BJ-Tree (degree=4) model, the partial plots were depicted in Figure 5 for the 8 overlapping probe sets to BJ-LS*. These plots clearly indicated the same monotonic patterns for the corresponding probe sets. For instance, a negative coefficient for probe set 1558999_x_at in Table 5 perhaps was better illustrated in a monotonic decreasing curve in Figure 5. The two-way interaction partial plots in Figure 6 suggested gene-gene interactions for the survival. To determine the top dominant interactions shown in the figure, we adopted the method described in Elith et al. (2008). Since the IPC based methods selected a different subset of probe sets, in the following, we summarize the variable selection results from other methods excluding IPC based methods. BJ-LS* selected 8 or more common probe sets with other methods. Furthermore, there was a high degree of consensus on the probe sets. Except for 224043_s_at, the 7 probe sets presented in Figure 5 were selected by all methods. Probe set 224043_s_at was not selected by Superpc, but selected by all the remaining methods. Additionally, BJ with MARS or ACOSSO, after supervised gene screening, also typically selected the 8 probe sets. However, due to the less accurate prediction, the results were not shown here. In summary, BJ-LS* selected a small subset of probe sets with good prediction accuracy, and BJ-Tree had greater fidelity to the data to potentially improve the prediction accuracy. BJ-Tree with higher degree can capture the gene-gene interactions in a flexible nonparametric fashion, which also further added the prediction power.

Table 5:

Probe set ID, gene symbol, and the estimated coefficient for the model selected by the BJ twin boosting with componentwise linear least squares (BJ-LS*) based on training data with CHOP therapy. The intercept is estimated as −0.596.

Probe set	Gene symbol	Coefficient
1558999_x_at	LOC283922 / PDPR	−0.104
1561016_at		−0.098
1562727_at		−0.045
1568732_at		0.116
212713_at	MFAP4	0.058
224043_s_at	UPB1	0.121
229839_at	SCARA5	0.112
237515_at	TMEM56	−0.019
237797_at	DNM1L	0.212
240811_at		−0.010
242758_x_at	JMJD1A	0.112
244346_at		0.111

Figure 4:

Kaplan-Meier survival curves of the testing data with R-CHOP therapy patients. Models are fitted by boosting methods with different base learner using training data with CHOP therapy patients: high risk group (solid line); low risk group (dashed line). Log-rank test p-values are in Table 4.

Figure 5:

Partial plots of overlapping probe sets for DLBCL CHOP patients based on BJ-Tree with degree=4.

Figure 6:

Interactions between probe sets selected by BJ-Tree with degree=4 for training data with CHOP therapy patients.

We briefly report the biological relevance of the selected probe sets. Probe set 1558999_x_at is described as pyruvate dehydrogenase phosphatase regulatory subunit pseudogene. Probe 212713_at_is microfibrillar-associated protein 4, which involves in cell adhesion and signal transduction. Probe 224043_s_at (gene UPB1) encodes a protein that belongs to the CN hydrolase family. UPB1 deficiencies may lead to abnormalities in neurological activity (van Kuilenburg et al., 2004). It is our hypothesis that such abnormalities may be associated with primary lymphomas of the central nervous system (PCNSL), which are highly malignant Bcell lymphomas confined to the central nervous system. Since PCNSL cannot be distinguished histologically and immunophenotypically from DLBCL (Richter et al., 2009), UPB1 deficiencies perhaps are also associated with DLBCL. Probe 229839_at (gene SCARA5) was identified as a new candidate tumor suppressor gene in human hepatocellular carcinoma (Huang et al., 2010). Probe 237515_at is transmembrane protein 56, which is integral to membrane. Probe 237797_at can contribute to cell communication, mitochondrial fragmentation during apoptosis, mitochondrial membrane organization and biogenesis, and multicellular organismal development. The protein encoded by this gene is a member of the dynamin superfamily of GTPases. Recent studies (see Krieg et al. (2010) and the references therein) show that probe 242758_x_at (gene JMJD1A) regulates the expression of adrenomedullin and growth and differentiation factor 15 (GDF15) under hypoxia. In addition, hypoxic regulation of JMJD1A can ultimately enhance tumor growth.

7. Discussion

We have presented the boosting procedures for estimating the AFT models, adjusting for censoring with BJ estimator. The proposed BJ twin boosting can generate more sparse models. It is worth noting that the choice of componentwise linear least squares as the base learner facilitates the interpretation as the estimated coefficients of covariates are the linear combination of the covariates through the iteration of boosting. We further extended the boosting methods to reflect more complex model structures including non-linear effects and interactions for survival data. This is an important advantage of boosting over some other regularization methods, where extensions to nonparametric form become more difficult. Whether to use linear or non-linear methods is often guided by the relevant scientific theories for the questions under investigation. In our case study with the DLBCL gene expression microarray data, we have built non-linear effects models in addition to simple linear models since there is strong evidence that non-linear effects including complex interactions exist among cancer genes. A linear model can approximate complex data, although it might not capture the data structure at a satisfying level, compared with non-linear effect models. Nevertheless, in our case study, the estimated gene effects on survival times have the similar impact with linear and non-linear models. Thus, the BJ methods are robust in our applications. In summary, both the BJ estimator and boosting can fit models with a high degree of prediction accuracy. A combination of these two methods can be utilized to model time-to-event data with high-dimensional covariates and complex model structures. The results in the paper also assure further theoretical investigation.

A corresponding R package bujar for Buckley-James regression with high-dimensional covariates can be downloaded from the supplementary website.