The Origin of Nonmonotonic Complex Behavior and the Effects of Nonnative Interactions on the Diffusive Properties of Protein Folding

Abstract

We present a method for calculating the configurational-dependent diffusion coefficient of a globular protein as a function of the global folding process. Using a coarse-grained structure-based model, we determined the diffusion coefficient, in reaction coordinate space, as a function of the fraction of native contacts formed Q for the cold shock protein (TmCSP). We find nonmonotonic behavior for the diffusion coefficient, with high values for the folded and unfolded ensembles and a lower range of values in the transition state ensemble. We also characterized the folding landscape associated with an energetically frustrated variant of the model. We find that a low-level of frustration can actually stabilize the native ensemble and increase the associated diffusion coefficient. These findings can be understood from a mechanistic standpoint, in that the transition state ensemble has a more homogeneous structural content when frustration is present. Additionally, these findings are consistent with earlier calculations based on lattice models of protein folding and more recent single-molecule fluorescence measurements.

Introduction

The energy landscape theory of protein folding (1–5) has been an invaluable theoretical framework for understanding protein folding (6–10), oligomerization (11–13), and functional transitions (14–18). According to the theory, the energy landscape associated with protein folding lacks large energetic traps and has an overall funnel shape where the native ensemble is the lowest energy state. These minimally frustrated landscapes can be idealized as being devoid of energetic roughness, which enables the use of structure-based (Gō-like) models (8,10,19–23) to study the thermodynamic and kinetic properties of the folding process. Because these structure-based models lack energetic trapping, they also provide a means to characterize the topological contributions to folding.

Although there is a strong correlation between simulated barrier heights and experimental folding times (24), rates are a consequence of both the free-energy profile and the diffusion coefficient (25,26). Accordingly, direct comparison between experiments and theory requires both quantities. In principle, one may circumvent the need for the diffusion coefficient by simulating many thousands of folding trajectories and calculating the mean first passage time of folding (27–29). Such approaches are often computationally intractable and they do not always advance our physical understanding of the process. Therefore, it is desirable to calculate both the free energy F and the diffusion coefficient D as functions of a global folding coordinate Q (30–34). If D is constant, then it only serves as a prefactor to the folding rate. However, when D is not constant, as we describe below, it can give rise to kinetic barriers in addition to the thermodynamic barriers (32).

The diffusion coefficient D is a result of the underlying energy landscape. As every conformation has a unique set of locally accessible interactions, D is a function Q. Although Q can be defined by a variety of measures, here we use the fraction of native contacts, as it has been shown to capture, accurately, the transition state ensemble of two-state proteins (35). Low values of Q correspond to the unfolded state and high values correspond to the folded ensemble. When Q is low, energetic contributions are largely from water-protein interactions. In the folded state (high Q), the burial of hydrophobic surface area can be the dominant energetic contribution. In these two regimes, the local energetic roughness can be quite different, which can lead to different diffusion coefficients.

Many recent efforts have attempted to characterize D(Q) via experimental methods (36–42) and theoretical calculations (26,32–34,43–49). These studies have found that diffusion is not constant as a protein folds to the native state. This naturally leads to the question: Does diffusion vary with the degree of compactness because of energetic trapping, or topological constraints? To address this, we calculate D for a structure-based model that lacks energetic roughness and compare the findings to variants of the model that include energetic frustration.

In this article, we present the diffusive properties of a C_α structure-based model in molecular dynamics simulations. We compare the results obtained from the unfrustrated model (i.e., only native interactions are stabilizing) with an energetically frustrated variant of the model, which allows for a quantitative, and qualitative, comparison of topological and energetic contributions to the diffusion coefficient. As there is a large body of experimental data available, including denaturant-dependent diffusion coefficient measurements, we chose to study the cold shock protein from the hyperthermophilic bacterium Thermotoga maritima known as TmCSP (36) (Fig. 1 a). TmCSP is a 66-amino-acid β-barrel protein that is known to have well-defined two-state folding behavior (50–53). Through comparison with previous computational, theoretical, and experimental results, we provide evidence of the degree of roughness present in TmCSP.

Figure 1.

Cold-shock protein from Thermotoga maritima (TmCSP Protein DataBank entry 1G6P (36)), shown in (a) cartoon representation and (b) C_α representation. The size of the atoms in panel b correspond to the excluded volume radii used in this model. The structures are colored from red (C-terminus) to blue (N-terminus) and were visualized with VMD (82). The TmCSP is a small globular protein with 66 amino acids, molecular mass of 7.5 kDa, and a three-dimensional structure known as a Greek-key β-barrel (five β-strands divided in two antiparallel β -sheets).

Models and Methods

Structure-based C_α model

Here, we employ a well-studied coarse-grained structure-based model (8). In this model, each residue is represented as a single bead, located at the position of the C_α atom (Fig. 1 b). For unfrustrated simulations, only native interactions are stabilizing and all residue pairs not in contact in the native structure are given a repulsive interaction to prevent chain crossing. In this model, the native structure is the global energetic minimum and the landscape lacks energetic traps. Native contacts were determined by the Contact of Structural Units software package (54). The functional form of the potential is

$$\begin{array}{l}V=\sum _{\text{bonds}}{\epsilon }_r{\left(r-r_o\right)}^2+\sum _{\text{angles}}{\epsilon }_{\theta }{\left(\theta -{\theta }_o\right)}^2\\ +\sum _{\text{dihedrals}}{\epsilon }_{\varphi }\left\{\left[1-\text{cos}\left(\varphi -{\varphi }_o\right)\right]+\frac{1}{2}\left[1-\text{cos}\left(3\left(\varphi -{\varphi }_o\right)\right)\right]\right\}\\ +\sum _{\text{contacts}}{\epsilon }_C\left[5{\left(\frac{{\sigma }_{ij}}{r}\right)}^{12}-6{\left(\frac{{\sigma }_{ij}}{r}\right)}^{10}\right]+\sum _{\text{noncontacts}}{\epsilon }_{NN}{\left(\frac{{\sigma }_{NN}}{r}\right)}^{12},\end{array}$$ (1)

where ε_r = 100, ε_θ = 20, ε_φ = 1, ε_C = 1, ε_NN = 1, and σ_NN = 4.0 Å. r_o, θ_o, φ_o, and σ_ij are given the values found in the native structure.

To model nonspecific energetic frustration, we introduced an additional attractive interaction between all residue pairs that are not in contact in the native state and are separated by at least four residues in sequence. The functional form of the nonnative interactions is

$$V_f\left(r\right)=-{\epsilon }_{NC}\exp \left\{-\frac{{\left(r-r_g\right)}^2}{{\sigma }_g^2}\right\},$$ (2)

with r_g = 6.5 Å and σ_g = 1.0 Å. The degree of energetic frustration is determined by ε_NC. In this study, we performed simulations with ε_NC = 0.1–0.7.

Biasing potential

To calculate the diffusion coefficient about a specific value of Q, we introduced umbrella potentials (55,56) that restrained each simulation to a specified range of Q values. See Supporting Material for technical details.

φ-values analysis

Experimentally, the structural content of the transition state ensemble in proteins is often studied by measuring changes in native stability and folding/unfolding rates upon point mutations. An approximate kinetic measure of the protein structure around a mutated residue is given by (57,58)

$$\varphi \equiv \frac{-RT\ln k_{\text{mut}}/k_{\text{wt}}}{\Delta \Delta G^0},$$ (3)

where k_mut and k_wt are the mutant and the wild-type folding rates, and ΔΔG⁰ is the change in stability of the folded state upon mutation.

From a simulation, one may also calculate φ-values by determining the change in the thermodynamic free energy barrier upon site mutation and comparing it to the change in native stability ΔΔG^F–U. Computationally, this is less demanding than trying to determine differences in folding rates upon mutation. The φ-values from structure-based simulations for each native contact pair (residues i and j) can be further approximated as (8,59)

$${\varphi }_{ij}=\frac{\Delta \Delta G^{TS-U}}{\Delta \Delta G^{F-U}}\approx \frac{P_{ij}^{TS}-P_{ij}^U}{P_{ij}^F-P_{ij}^U},$$ (4)

where P_ij^X is the probability of a contact between i and j being formed in state X (with X being F, TS, or U). For ease of discussion, here, we report φ_i-values averaged over all native contacts with residue i.

Results

Diffusion coefficient is robust to changes in restraining potential

The primary objective of this study was to determine how the diffusion coefficient D, in reaction coordinate space, changes during the folding process of TmCSP (Fig. 1 a). To calculate D, we employed a C_α structure-based model (Fig. 1 b) with a restraining potential to ensure that each simulation sampled the phase space local to a particular value of Q (see Models and Methods for full description). The restraining potential was harmonic, centered at Q^∗, and was given a strength of K_Q. When adding such a restraint, one must first ensure that the quantities of interest are not dependent on the strength of the restraint. To ensure that the diffusion coefficients are a result of the underlying energy landscape, and not the biasing potential, several sets of simulations were performed, each with a different strength of the restraint.

To calculate the diffusion coefficient from a simulation, we employed a quasiharmonic diffusive approximation (25)

$$D=\frac{\Delta Q{\left(T\right)}^2}{2\tau \left(T\right)},$$ (5)

where ΔQ(T)² is the mean-squared fluctuations in Q, and τ(T) is the relaxation time associated with the decay of the autocorrelation function of Q, i.e., C_Q(t). Here, Q(t) is defined as the fraction of native C_α-C_α contacts formed as a function of time (see Models and Methods). To use Eq. 5, the value of K_Q must be in a range for which a quasiharmonic approximation is warranted and D is not dependent on K_Q.

To determine values of K_Q for which the quasiharmonic approximation is valid, we compared the probability distributions in Q for a variety of K_Q values. Fig. 2 a shows the probability distributions for several values of K_Q (where the harmonic restraint is centered at Q^∗ = 0.5), each at the folding temperature in the unrestrained case. For K_Q = 10, the probability distribution is clearly bimodal, with one peak corresponding to nativelike structures (Q ≈ 0.8) and one peak corresponding to the unfolded ensemble (Q ≈ 0.2). For K_Q = 50, the probability distribution possesses a single peak near the minimum of the restraining potential Q = 0.5. For K_Q = 100, the width of the distribution is further reduced. This additional reduction of the width is undesirable. Because the diffusion coefficient describes the multidimensional process of the protein escaping from local energetic/topological minima, an overly-strong restraint may lead to artifacts by disallowing some possible routes of escape. In that scenario, our calculations of D could probe the restraining potential and not the underlying energy landscape.

Figure 2.

(a) Probability distributions in Q for biased (K_Q > 0, Q^∗ = 0.5) simulations with different strengths of the restraining potential K_Q. As K_Q increases, the distribution changes from a bimodal distribution, with peaks corresponding to the native and unfolded ensembles, to a single peak centered about the minimum of the restraining potential Q^∗. The distribution is quasiharmonic for K_Q > 10. (b) The diffusion coefficient D is shown, on a semilog plot, as a function of K_Q for five values of Q^∗. For 10 < K_Q < 50 (region delimited by the vertical dashed lines) D(Q) is relatively constant, demonstrating that estimates of D will be independent of K_Q over this interval. Simulations were performed at the folding temperature of the pure structure-based model T_f⁰.

In addition to identifying a range of value of K_Q for which a quasiharmonic approximation is valid, we also determined a range of K_Q-values for which the calculated diffusion coefficients are not K_Q-dependent. Fig. 2 b shows D as a function of K_Q for a wide range of Q values. For low values of K_Q (< 10), all calculated values of D increase with K_Q. As discussed above, this is due to the probability distribution being altered from a bimodal distribution to a distribution centered about the Q value of interest. For 10 < K_Q < 50 the calculated D is nearly constant for all Q values. Above K_Q = 50, the values of D again increase for Q > 0.7. Based on these data, we concluded that K_Q = 50 will provide reliable values for the position-dependent diffusion.

Diffusion coefficient dependence on Q

To understand the origins of the Q-dependence of the diffusion coefficient, one must consider the fluctuations in Q and the decay time of these fluctuations τ_Q. As our calculated values of D are not sensitive to K_Q at K_Q ∼ 50, all further values are reported for simulations performed at the folding temperature of the unrestrained simulations T_f⁰ with K_Q = 50. Fig. 3 a shows the time autocorrelation functions of Q for a variety of Q^∗ values. As Q^∗ is increased from 0.2 to 0.5 the characteristic decay time, τ_Q, increases. At higher Q values (>0.5), the decay time decreases to a value smaller than in the unfolded ensemble (larger 1/τ_Q values in Fig. 3 b). The dispersion in Q (ΔQ²) also displays a nonlinear dependence on Q (Fig. 3 b). Similar to τ_Q, ΔQ² initially increases with increasing Q (0.2–0.5) and then decreases as the native ensemble is reached (Q = 0.8). Fluctuations in Q, shown in Fig. 3 b, rise considerably near the transition state due to the intrinsic instability of the transition state ensemble (TSE). In other words, Q exhibits large amplitude fluctuations as it overcomes the free energy barrier. For high and low Q values (the folded and unfolded ensembles), Q is highly localized, which results in a small dispersion in Q. While ΔQ² is roughly symmetric about the TSE, the autocorrelation time, as well as its inverse, is asymmetric. This symmetry-breaking in τ_Q leads to an asymmetric relationship between D and Q.

Figure 3.

(a) Normalized correlation functions of Q, C_Q(t), shown on a log-log plot (time in reduced units) for different values of Q^∗. Because a single exponential did not always fit well, each curve was fit to the sum of three exponentials to obtain an average decay time τ_Q. K_Q = 50 was used and the temperature was the folding temperature of the unbiased simulations T_f⁰. The characteristic decay time τ_Q is used to calculate the diffusion coefficient D. (b)The dispersion of the reaction coordinate ΔQ² as a function of the reaction coordinate Q (left axis), with and without energetic frustration. The inverse correlation time of Q (1/τ_Q) shown as a function of Q (right axis), with and without the frustration term. Calculations are shown at T_f of each ε_NC.

The diffusion coefficient as a function of Q, D(Q), is proportional to the product of ΔQ² and 1/τ_Q, and is shown in Fig. 4. We find D has large variations as a function of the folding reaction, which is in agreement with earlier studies on lattice models (32) and analytic studies (30,31,33,43). As discussed above, D(Q) (Fig. 4) largely follows 1/τ_Q (Fig. 3 b). Fluctuations of the reaction coordinate ΔQ² appear to have less influence on D(Q), as ΔQ² changes only modestly with Q. The fact that D(Q) reaches a minimum around the TSE suggests the presence of a kinetic barrier, in addition to a thermodynamic one. After the protein moves from the TSE to the folded state, D(Q) once again increases and eventually reaches values that are 10-times larger than those corresponding to the unfolded ensemble.

Figure 4.

Comparison of the diffusion coefficients calculated without energetic frustration (black circles) and with energetic frustration (ε_NC = 0.2, red squares) as functions of Q. All results were calculated with a restraining potential of strength K_Q = 50 and at the T_f of each ε_NC.

The one-dimensional position-dependent diffusion coefficient variations indicate that the ruggedness of the energy landscape is not the same over the one-dimensional configuration space. D(Q) describes the local moves over microscopic barriers that connect states with similar values of Q. If the microstate is deep, it acts like a speed bump slowing both the drift and the superimposed Brownian movement (60) (i.e., the diffusion coefficient becomes small and escape-time from traps increases (7)). Because our energetically unfrustrated model gives rise to values of D that vary with Q, our results clearly indicate that the topology of the ensemble about a particular value of Q is inextricably linked to the diffusive dynamics. In other words, each configuration of the protein has a particular set of accessible escape routes, independent of the energetic roughness, which lead to the nonconstant form of D(Q).

Energetic frustration alters the diffusive dynamics

Due to the funnel-like nature of protein-folding energy landscapes, completely unfrustrated models, such as the one employed in this study, are sufficient to capture many aspects of protein folding (7,9,59,62–73). However, there is mounting evidence that a low degree of frustration can lead to accelerated folding rates (63) and provide a more accurate description of the unfolded ensemble (74). Such findings suggest a potential influence of energetic frustration on the diffusive properties associated with protein folding. To investigate this further, we employed a modified structure-based model in which the degree of frustration may be controlled. Specifically, we used the structure-based C_α-model and added nonspecific attractive interactions between all nonnative atom pairs, where the functional form is a Gaussian with an energetic weight ε_NC (see Models and Methods). Accordingly, ε_NC = 0 corresponds to the purely structure-based model.

Thermodynamic quantities were calculated for each frustrated system (ε_NC > 0.0) with K_Q = 0. For each parameter set, the fraction of native proteins f_N(T) was defined as

$$f_N\left(T\right)=\frac{{\int }_{\text{native}}\exp \left[-F\left(Q\right)/k_{\text{B}}T\right]dQ}{{\int }_0^1\exp \left[-F\left(Q\right)/k_{\text{B}}T\right]dQ},$$ (6)

where F(Q) is the free energy as a function of Q, the integral in the numerator is over all native conformations, and the denominator is over all possible Q values. We define the folding temperature T_f as the temperature where f_N = 0.5 (dotted horizontal line in Fig. 5 a). As the degree of frustration is increased from 0, T_f initially increases and reaches its maximum at ε_NC = 0.2. Because T_f measures thermodynamic stability, an increase in native-state stability with increased nonnative interaction strength may be surprising. This feature has two origins. First, in the native state ensemble, proteins are constantly fluctuating (75), which allows nonnative residue pairs to fluctuate toward and away from each other and form transient nonnative interactions (10). When nonspecific interactions are stabilizing, these transient nonnative interactions increase the stability of near-native conformations. The second contribution to the increased native-state stability may be due to using a C_α representation. All nonnative interactions were given energetic minima at 6.5 Å. When coarse-graining, C_α pairs may be within that distance, but the side-chain configurations may lead to these pairs being considered not-in-contact. Thus, the noncontacting residues may stabilize these native configurations via the nonspecific interactions. Above ε_NC = 0.2, the energetic frustration stabilizes the unfolded ensemble more than the folded ensemble and the folding temperature decreases, as expected. These findings are consistent with experimental results indicating that weakly attractive nonspecific interactions can increase the stability of Src homology 3 domain (70). In addition to affecting native stability, these experiments also revealed variations in the thermodynamic properties of the transition state ensemble, which were manifested as increased unfolding and refolding rates.

Figure 5.

(a) Fraction of native protein f_N versus temperature T for different degrees of frustration ε_NC. The value f_N was calculated using Eq. 6. (b) Folding temperature T_f as a function of ε_NC for K_Q = 0. The folding temperature T_f has a maximum at ε_NC = 0.2.

Increased levels of frustration also have direct effects on the calculated D(Q) profiles (Fig. 4). Similar to the unfrustrated simulations, the majority of the changes in D(Q) may be attributed to fluctuations in τ_Q (Fig. 3). When energetic frustration is introduced, ΔQ² is only marginally perturbed while 1/τ_Q exhibits substantial deviations (Fig. 3). Comparison of the frustrated and unfrustrated simulations (Fig. 3) indicates that frustration has little effect on the ΔQ² and 1/τ_Q values associated with the unfolded ensemble (Q < 0.5). After the protein has reached the folding transition state (Q ≈ 0.5) and moves to higher Q values, 1/τ_Q increases for both the unfrustrated and ε_NC = 0.2 simulations, although there is a larger increase in 1/τ_Q for the frustrated simulations than the unfrustrated ones. This finding may be counterintuitive, but it shows that a low degree of frustration can actually reduce the height of the microscopic barriers that are described by the diffusion coefficient.

Residual entropy of the native state ensemble

The fact that D(Q) reaches a maximum in the folded ensemble can be understood by analyzing the density of states as a function of Q. Fig. 6 shows the density of states as a function Q for a lattice model (32) and the presented C_α model. Although there is an increase in D(Q) as Q goes to 1, D(Q) remains on the same scale for large Q as for small Q. This is due to the ensemble nature of the native state. That is, in the C_α model, the protein may interconvert between local structures without changing the value of Q, even when all native contacts are formed (Q = 1). This leads to a degenerate native state, residual entropy, and nonzero correlation times. In contrast, in the lattice model, every possible move from the Q = 1 state results in a decrease in Q. This nondegenerate native state leads to very low correlation times, and hence very large diffusion coefficients for the native state. Additionally, in the lattice model, single rearrangements can result in multiple contacts being formed or broken simultaneously. This lack of residual entropy in the lattice model has prevented previous evaluation of D(Q = 1). Here, by using an off-lattice C_α model, we are able to calculate D(Q) for the full range of Q.

Figure 6.

Density of states n as a function of Q for (a) the C_α model and (b) a lattice model (32). High Q represents the folded ensemble and low Q is the unfolded ensemble. Panel a shows the density of states for the unfrustrated (ε_NC = 0.0) and frustrated (ε_NC = 0.2) systems. The C_α model has a highly degenerate folded state, indicating the presence of residual entropy which allows for an increase in D after the protein passes through the TSE. For the lattice model there is a rapid decrease in the density of states with a nondegenerate folded state (n(E_folded) = n(Q_folded) = 1) and monotonically decreasing values of D (32).

Folding mechanism and φ-values analysis

The introduction of attractive nonnative interactions, or energetic frustration, changes the folding energy landscape (62,63,76) and can alter the structural content of the transition state ensemble. The ε-values are commonly used experimentally to measure the degree of native structural content in the TSE about each residue. Computationally, φ-values can also be determined, where a value of 0 indicates no native structural content and 1 indicates full structural content in the TSE. Fig. 7 shows φ_i (φ-value for each residue i) obtained from simulations with no frustration (ε_NC = 0.0) and a low degree of frustration (ε_NC = 0.2). When ε_NC = 0.2, there is a shift in structural content from the C-terminus to the N-terminus. Specifically, when ε_NC is increased from 0.0 to 0.2 the φ-values for residues 0–20 increase and residues 55–65 decrease. Additionally, other regions with low φ-values, such as residues 42–45, increase when frustration is introduced.

Figure 7.

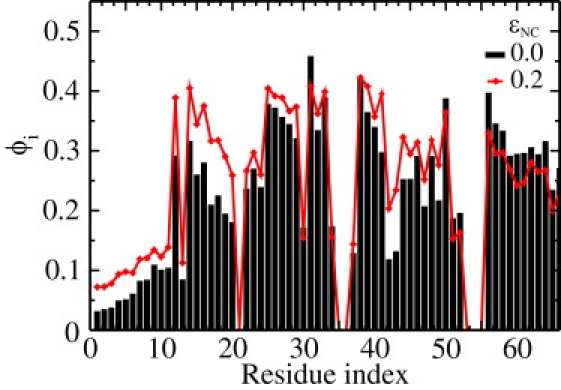
The φ-values calculated for the unfrustrated simulations (ε_NC = 0.0, black bars) and a weakly-frustrated system (ε_NC = 0.2, red diamonds). Many residues with lower φ_i-values increase, and high values decrease, upon the addition of frustration. This indicates a more homogeneous TSE when a low level of frustration is introduced. Simulations were performed without a restraining potential (K_Q = 0) and at T_f(ε_NC).

Overall, introducing a low-degree of frustration appears to (partially) homogenize the φ-values. Because residues that are less native (low φ-values) are not surrounded by formed native interactions, they are more exposed to nonnative interactions. Accordingly, nonspecific stabilizing interactions are more accessible to less-native residues than highly-native ones. These nonspecific attractive interactions can then localize the residues involved in native-contacts, which results in additional native structure formation and a shift in the φ-values.

To characterize the effects of frustration on the unfolded and folded basins, in addition to the TSE, we calculated the probability of contacts being formed with each residue, as functions of Q (Fig. 8). The probabilities for the unfrustrated case are shown in Fig. 8 a. For low Q, the probabilities are not homogeneously distributed, but are high around residues 22, 53, and 56, and nearly zero for all other residues. At approximately the transition state (Q = 0.5), the probabilities follow the φ-values, and have peaks around residues 22, 35, and 55. After passing the transition state, these regions may be considered nucleation sites, about which the rest of the protein's native structure is formed. Fig. 8 b shows the changes in the probabilities when frustration is introduced. Blue corresponds to decreased structure and red indicates increased structure formation. Similar to the φ-values, in the TSE there is a shift in probabilities from the C-terminal residues to the N-terminal residues. Surprisingly, the effects of the energetic frustration appear to be isolated to the TSE. One explanation for this feature is that frustration in the unfolded ensemble may not be well described by Gaussian potentials, as we have employed here. Instead, longer-range, screened-electrostatic interactions may be a larger contributor to frustration in the unfolded ensemble (74). In contrast, using a coarse-grained structure-based model, Das et al. (77) showed that introducing nonnative interactions and energetic heterogeneity has a large effect on the TSE, and improves agreement between experimental and theoretical φ-values for Src homology 3 domain. Although our finding suggest short-range frustration is most important in the TSE, real proteins likely exhibit a combination of short-range and long-range nonnative interactions. Further investigation will be necessary to untangle the relationship among different types of frustration, the folding mechanism, and the diffusive dynamics of the folding process.

Figure 8.

Probability of contacts being formed for each residue P(i, Q, ε_NC) as a function of the reaction coordinate Q, for the unfrustrated and weakly frustrated system. (a) P(i, Q, 0) increases (blue to red) as the protein folds. (b) Difference between the probabilities for the frustrated and unfrustrated simulations, P(i, Q, ε_NC) – P(i, Q, 0.0), where ε_NC = 0.2. The simulations were performed at T = T_f . (Open bars) Residues lacking any native contacts.

Perl et al. (78) explored the role of the chain termini residues on the folding stability by comparing the cold shock proteins BcCSP from the thermophile Bacillus caldolyticus with its homolog BsCSPB Bacillus subtilis. These two cold shock proteins have nativelike activated states of folding, similar to that of the hyperthermophilic Thermotoga maritima TmCSP (50) studied in this work. Their studies illustrate that major contributors to the difference in stability are residue 3 (which takes on nativelike structure in the TSE) and the C-terminal residue 66 (which forms late in the folding process) (78). Despite the fact that the C-terminal residues have high φ-values in experiments and low φ-values for the unfrustrated model, as discussed above, the φ-values of the termini increase with increased energetic roughness. As suggested by our analysis of stability as a function of roughness, this comparison also demonstrates that cold shock protein likely has a modest degree of energetic roughness, though the exact degree, and type, of frustration cannot be unambiguously determined from the presented simulations.

Conclusions

In this work, we have studied the folding of TmCSP using a coarse-grained structure-based model and we calculated the diffusion coefficient as a function of a reaction coordinate Q. Our main results can be outlined as follows: The diffusion coefficient displays nonmonotonic behavior as a function of Q, which can be attributed to a residual entropy of the native state ensemble. A role of residual entropy has been suggested previously (33), though here we explicitly calculate it and show its relationship to the diffusive dynamics. By introducing varied degrees of energetic roughness, we have shown that for low levels of frustration, TmCSP displays increased thermal stability and diffusion coefficients, relative to the unfrustrated regime, which agrees with previous findings (62,63). As frustration is increased, the stability reaches a maximum, after which increased frustration leads to a less stable protein. At this optimum degree of frustration, the transition state is characterized by a more homogeneous distribution of φ-values, relative to the unfrustrated case. In addition to changes in the structural content of the TSE, the diffusion coefficient is also affected by a low-degree of energetic frustration.

This work has shown that the diffusive dynamics are intimately linked to the topological and energetic aspects of a protein, and lays a foundation for understanding the diffusive properties of protein folding. Many examples can be found where the diffusion coefficient provides a nontrivial contribution to the folding dynamics. For example, as the presence of additional small free-energy barriers can actually accelerate folding rates (79,80), there must be a balance between folding barriers and diffusion along the reaction coordinate. The folding of proteins with smaller free-energy barriers, such as BBL (81), will also depend more on the precise structure of the diffusion coefficient (44,41,42), such that the nonmonotonic behavior of the diffusion may be the limiting factor that determines folding rates. With the presented framework, further investigation will explore the details of how the diffusive dynamics contributes to the folding of these and other systems.

Uncited reference

61.

Supporting Material

Additional text and one reference is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00539-4.