JAMIE: joint analysis of multiple ChIP-chip experiments

Abstract

Motivation: Chromatin immunoprecipitation followed by genome tiling array hybridization (ChIP-chip) is a powerful approach to identify transcription factor binding sites (TFBSs) in target genomes. When multiple related ChIP-chip datasets are available, analyzing them jointly allows one to borrow information across datasets to improve peak detection. This is particularly useful for analyzing noisy datasets.

Results: We propose a hierarchical mixture model and develop an R package JAMIE to perform the joint analysis. The genome is assumed to consist of background and potential binding regions (PBRs). PBRs have context-dependent probabilities to become bona fide binding sites in individual datasets. This model captures the correlation among datasets, which provides basis for sharing information across experiments. Real data tests illustrate the advantage of JAMIE over a strategy that analyzes individual datasets separately.

Availability: JAMIE is freely available from http://www.biostat.jhsph.edu/∼hji/jamie

Contact: hji@jhsph.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

ChIP-chip is a powerful approach to study protein–DNA interactions (Ren et al., 2000). By coupling chromatin immunoprecipitation with genome tiling arrays, this technology allows one to create genome-wide maps of transcription factor binding sites (TFBSs; Boyer et al., 2005; Carroll et al., 2005; Cawley et al., 2004). With rapid growth of ChIP-chip data in public repositories such as Gene Expression Omnibus (Barrett et al., 2009), it becomes more and more common that multiple datasets related to the same TF, pathway or biological system are collected. When multiple such datasets are available, it is often desirable to analyze them jointly. Looking at all data together not only enables one to study commonality and context-dependency of protein–DNA association, but also creates opportunities to borrow information across datasets to improve statistical inference. This is particularly useful if the data of primary interest are noisy and information from other datasets is required to distinguish signals from noise.

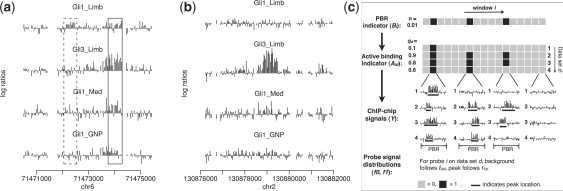
Figure 1a provides an example that illustrates the potential advantage of joint data analysis. The figure shows four related ChIP-chip experiments (GEO GSE11062, Vokes et al., 2008; GSE17682, Lee et al., 2010) performed by two different labs using Affymetrix Mouse Promoter 1.0R arrays. The purpose of these experiments is to locate binding sites of two TFs, Gli1 and Gli3, in different cellular contexts. Both Gli1 and Gli3 are members of Gli family of TFs, which recognize the same DNA motif. The figure shows log₂ fold enrichment between the normalized ChIP and control probe intensities. The first experiment (‘Gli1_Limb’) measures Gli1 binding in developing limbs of mouse embryos. This experiment has low signal-to-noise ratio due to an unoptimized ChIP protocol and use of a mixed cell population (Gli1 is active only in the posterior fraction of the limb, but ChIP-chip was performed using the whole limb. As a result, cells from the anterior limb may dilute signals in the posterior limb). In spite of the weak signals, one still wants to find true Gli1 binding sites in this dataset, since Gli1 is a key transcriptional regulator for controlling proper development of limb. A careful examination of the data shows that ‘peaks’ in these four datasets are correlated. In other words, they tend to occur at the same locations in the genome. This correlation can be potentially used to improve statistical inference. For example, the weak peak highlighted by the solid box in ‘Gli1_Limb’ cannot be easily distinguished from background noise if one looks at this dataset alone. However, if all datasets are analyzed together, the observation that all other datasets have strong peaks at the same location suggests that the weak peak in ‘Gli1_Limb’ is a real binding site. In contrast, the peak highlighted by the dashed box has approximately the same magnitude in the ‘Gli1_Limb’ data, but no binding signal has been observed in the other datasets, suggesting that it is less likely to be a real binding signal.

Fig. 1.

Motivation and model structure of JAMIE. (a) Four Gli ChIP-chip datasets show co-occurrence of binding sites at the same genomic locus. This correlation may help to distinguish real and false TFBSs. Each bar in the plot corresponds to a probe. Height of the bar is the log₂ ratio between ChIP and control intensities. Med, medulloblastoma; GNP, granule neuron precursor cells. (b) An example that shows context dependency of TF-DNA binding. (c) An illustration of the JAMIE model.

When multiple datasets are analyzed jointly, it is important to keep in mind that some TFBSs are context-specific. For example, the location shown in Figure 1b is bound by Gli in ‘Gli3_Limb’ but not in ‘Gli1_Limb’ and ‘Gli1_GNP’ (GNP stands for granule neuron precursor cells). In this case, even without referring to the other datasets, the enrichment in ‘Gli3_Limb’ is sufficiently strong and should be called as a peak. On the other hand, one should avoid claiming that ‘Gli1_Limb’ and ‘Gli1_GNP’ have peaks in this region only because there is a strong peak in ‘Gli3_Limb’. Ideally, there should be a mechanism that automatically integrates and weighs different pieces of information, and rank peaks according to the combined evidence. This cannot be achieved by simply analyzing each dataset separately and then taking intersections of the results.

In the past few years, a number of algorithms and software tools have been developed for analyzing ChIP-chip data. Examples include Tiling Analysis Software (TAS) from Affymetrix (Kapranov et al., 2002), MAT (Johnson et al., 2006), TileMap (Ji and Wong, 2005), HGMM (Keles, 2007), Mpeak (Zheng et al., 2007), Tilescope (Zhang et al., 2007), Ringo (Toedling et al., 2007), BAC (Gottardo et al., 2008) and DSAT (Johnson et al., 2009). However, they are all designed for analyzing one dataset at a time, and the full advantage of data is not exploited when multiple related datasets are available. A recent hierarchical hidden Markov model (HHMM) approach developed by Choi et al. (2009) allows joint analysis of one ChIP-chip data and one ChIP-seq data. This represents a new progress towards using information more efficiently via correlating two types of high-throughput ChIP experiments. Nevertheless, this method does not target analyzing two related ChIP-chip experiments. More importantly, its current form does not support the analysis of more than two datasets, and it is not easy to generalize the method to handle multiple datasets since its number of parameters grows exponentially when the number of datasets increases. In summary, although jointly analyzing multiple ChIP-chip datasets is conceptually appealing, currently there is no convenient tool to perform such analysis. Here we develop JAMIE, an R package for Joint Analysis of Multiple ChIP-chip Experiments, to support convenient and efficient mapping of TFBSs by jointly analyzing two or more related ChIP-chip experiments.

JAMIE uses a hierarchical mixture model to capture correlations among datasets. The model provides the basis for sharing information across datasets. Its number of parameters grow linearly with the number of datasets. A computationally efficient algorithm is developed to estimate the model parameters. Given the estimated parameters, the model is applied to scan the genome and find TFBSs. Our tests on real data show that by pooling information, JAMIE improves peak detection over the traditional approach that analyzes individual datasets separately.

2 METHODS

2.1 Data model

Suppose there are D datasets (Fig. 1c). Consider an L base pair (bp) window starting at an arbitrary probe. It is assumed that a priori, the window can either become a potential binding region (PBR) with probability π, or become background with probability 1 − π. Let B_i = 1 indicate that the window starting at probe i is a PBR, and B_i = 0 otherwise. If a window is a PBR, it can either become an active binding region in dataset d (d = 1,…, D) with probability q_d, or it can remain silent in dataset d with probability 1 − q_d. Let A_id (=1 or 0) indicate whether the PBR is active in dataset d or not. Conditional on B_i = 1, A_ids are assumed to be independent. If B_i = 0, then A_id = 0 for all d. Under these assumptions, the prior probability that a randomly chosen genomic window represents an active binding region in dataset d is πq_d. The joint prior probability that a window is active in all datasets is π(∏_dq_d). In general, this probability is not equal to ∏_d(πq_d), the joint probability one would expect if locations of binding sites occur independently in different datasets. This explains why the hierarchical model, while assuming conditional independence of A_ids given B_i = 1, can be used to describe correlations among datasets.

Now consider a PBR. Suppose it starts at probe i and is active in dataset d (i.e. B_i = 1 and A_id = 1). It is assumed that a PBR active in dataset d should contain an active binding site (i.e. ‘peak’) in that dataset. The peak starts at a randomly chosen probe within the PBR and has length W_id (≤L) (Fig. 1c). W_id is randomly chosen from a set of allowable lengths W. The peak start and peak length are chosen subject to the constraint that the peak should be fully contained within the PBR. For a particular PBR and a particular dataset in which the PBR is active, all possible peak configurations that meet this constraint are sampled with equal prior probability. Within the same PBR, peaks in different datasets can have different starts and different lengths, i.e. peaks within a PBR are not required to overlap exactly. This provides some flexibility to model binding sites of different TFs that co-occupy the same promoters or enhancers but do not bind to the same DNA motif. Both the length of PBRs (L) and the allowable peak lengths (W) are configurable. By default, we use L = 1000 bp and W = {500, 600,…, 1000} bp, which match peak lengths observed in typical ChIP-chip data.

For probe i, let H_id = 1 denote that it is located within a peak in dataset d, and H_id = 0 otherwise. H_id = 0 can correspond to one of the following scenarios: (i) probe i is in a background window; (ii) probe i is covered by a PBR, but the PBR is silent in dataset d; (iii) probe i is covered by a PBR, which is active in dataset d, but the probe is not covered by the active binding site (i.e. the peak) in that dataset.

Given H_id, probe intensities are modeled as follows. Suppose dataset d has K_d1 replicated ChIP (IP) samples and K_d0 replicated control samples. Let X_idjk denote the normalized and log₂ transformed probe intensity of probe i in the k-th replicate under condition j (j = 1: IP; j = 0: control) of dataset d. Define the observed mean IP–control difference Y_id = , where 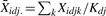. It is assumed that

(1)

and the probability density functions of μ_id are given by

(2)

Here, ϕ(x; m, τ²) represents probability density at a point x of a normal distribution with mean m and variance τ², mixing proportion ϵ is a small positive number, and m_d > 0. This model implies that for most background probes, the true IP–control difference μ_id follows a normal distribution N(0, τ_d²), and for most probes in peaks, μ_id follows N(m_d, τ_d²). However, there is a small probability ϵ to have outliers, i.e. μ_id of a background probe can show a real IP–control difference that follows N(m_d, τ_d²), and a probe in a peak may not respond to TF-binding and has μ_id ∼ N(0, τ_d²). Assuming equal variance (τ_d²) of the two normal distributions guarantees that the likelihood ratio f(μ_id|H_id = 1)/f(μ_id|H_id = 0) is monotone in μ_id.

Integrating out μ_id gives the probability density of Y_id conditional on H_id. Defining f_hid ≡ f(Y_id|H_id = h), we have

(3)

where m_d, σ_id² and τ_d² are parameters that can be estimated from data (see below). Once they are estimated, they will be treated as fixed and known parameters. The role of ϵ is to bound the likelihood ratio f_1id/f_0id that a single probe can contribute to making a peak call (the bound is [ϵ/(1 − ϵ), (1 − ϵ)/ϵ]). For considerations of computational efficiency, we fix ϵ to be 0.001. Empirically, this produces reasonable results.

Together, these assumptions provide a probabilistic model that describes how the observed data Y in a genomic window are generated (Fig. 1c). Let U = (L, W) be the configurable window size parameters. Define T_i to be the set of probe indices in the L bp genomic window starting at probe i. Y_id = {Y_ld : l ∈ T_i} is the collection of all enrichment measurements in window i and dataset d. Y_i = (Y_i1,…, Y_iD). Define m = (m₁,…, m_D), Σ be the collection of all σ_id²s, Ψ the collection of all τ_d²s and q = (q₁,…, q_D). Let Λ = (Σ, m, Ψ, π, q) be the collection of all parameters that need to be estimated from the data, and let A_i = (A_i1,…, A_iD). The basic idea of JAMIE is to first estimate Λ, and then scan the genome using a sliding window and the estimated parameters to find active binding regions in each dataset based on the posterior probability P(A_id = 1|Y_i, Λ, U).

2.2 Likelihood and posterior probabilities

If the L bp window starting from probe i is inactive in dataset d, the probability to produce Y_id is

(4)

If the window is active in dataset d, let u_id denote the probe that starts the active peak within the window, T_i^W_id,u_id be probe indices covered by a W_id bp peak starting at u_id and T_i\T_i^W_id,u_id be the remaining probe indices. Let |Z| counts the number of elements in a set Z and T_i(W_id) be the set of probe indices that can be used to start a peak of length W_id that is fully covered by the window. The probability of Y_id, after integrating out peak start u_id and peak length W_id is

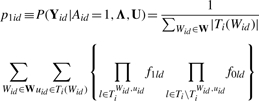(5)

The joint probability of (Y_i, A_i, B_i) is given by

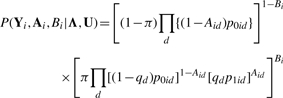(6)

The posterior probability of B_i given Y_i and (Λ, U) is

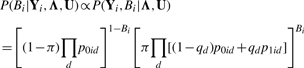(7)

Let 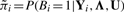. The posterior probability of A_id = 1 is

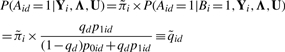(8)

The computation of P(A_id = 1|B_i = 1, Y_i, Λ, U) only involves information from the dataset d, while 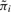is determined using information from all datasets. The formula above makes it clear that information from dataset d is weighed by information from other datasets in order to determine whether the window in question is an active binding region in dataset d.

2.3 Parameter estimation

We originally sought to divide the genome into non-overlapping windows and develop iterative algorithms such as Expectation Maximization (EM) or Markov Chain Monte Carlo to estimate the parameters using all windows. This approach turned out to be computationally too intensive to be practically useful. As a result, we decided to use an alternative approach, which is computationally much more efficient but only provides approximate estimates of parameters that may not be optimal. Our tests show that this ad hoc approach performed well in real data.

First consider Σ = (σ_id²). Let S_id be the standard error of Y_id, computed using the replicate samples in dataset d. We estimate σ_id² by an empirical Bayes approach described in Ji and Wong (2005). Briefly, 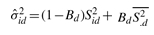. Here, B_d is a shrinkage factor that takes a value between zero and one. The value is automatically determined by the data. The term 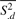is the mean of all S_id²s in dataset d. If there is no degree of freedom to estimate σ_id² within a dataset (e.g. only one IP and one control sample are available), we use probe intensities from all datasets to estimate σ_id² via a robust procedure (see Supplementary Material A.1).

Next consider m and Ψ. For the purpose of estimating m and Ψ, we analyze each dataset separately and assume that Y_ids within a dataset are independently drawn from either N(0, σ_id²+τ_d²) or N(m_d, σ_id²+τ_d²). Under this mixture model assumption, and conditional on the estimated Σ, parameters m and Ψ can be estimated using an EM algorithm (Dempster et al., 1977) (see Supplementary Material A.2).

Lastly, we estimate π and q. Instead of using all genomic windows, we first select windows that are likely to contain peaks. This is done by performing an initial peak detection for each dataset separately, using a fast moving average method described previously (Ji and Wong, 2005). The initial peak detection uses a loose false discovery rate (FDR) cutoff (default = 30%) so that loci with weak peak signals and many background windows are also included. The union of the initial peaks detected from different datasets are obtained. Each peak is extended or truncated to form an L bp window. Resulting windows that are not overlapping are retained. The retained windows often comprise a small fraction of the raw data (<5%). By assuming that PBRs occur only in these retained windows, we developed a fast EM algorithm to estimate π and q (see Supplementary Material A.3). Since the assumption that only the retained windows contain PBRs are generally not true (it only represents a crude approximation of the reality), this assumption is used only for the purpose of estimating π and q. The estimated π and q will then be used in conjunction with a sliding window to scan the whole genome to find active binding regions.

2.4 Peak detection

Given the estimated parameters, an L bp sliding window is used to scan the genome. For each dataset, we first find locations with 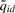[Equation (8)] bigger than a user specified threshold. Then for each of these locations, we look for probes within its neighborhood to find the one with the local maxima (i.e. the maximal 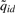). That probe is used as the start of a PBR, and subsequent probes within L bp from the start are included within the PBR. We report the most likely peak from all possible peaks in the PBR, after comparing all (W_id, u_id) pairs. 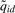was used as the score to rank the reported peaks. Since the posterior probabilities 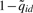can also be viewed as the estimated local FDRs, the global FDR of a list of peaks can be obtained by averaging their .

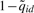3 IMPLEMENTATION

JAMIE has been implemented in an R package. The engine functions were written in C for computational efficiency. The input required by JAMIE is CEL and BPMAP files (for Affymetrix arrays) or text files with raw intensities (all other platforms), and a text file for parameter configurations. With two lines of R codes, JAMIE will report ranked peaks for all datasets and the estimated parameters. In a test involving four datasets, each with 3 IP, 3 control and 3.8 million probes, the whole process took around 15 min on a PC running Linux with 2.2 GHz CPU and 4 G RAM.

4 RESULTS

4.1 Simulations

We first tested JAMIE using simulations. Data were created by adding computationally simulated peaks to real data of input control samples. Four publicly available datasets generated using Affymetrix Mouse Promoter 1.0R arrays were collected (Supplementary Table S1). Each dataset had three input control samples. For each dataset, we selected one input control sample, planted in a number of simulated peaks, and generated a new CEL file. The newly created CEL file was used as the simulated ChIP sample. The other two input control samples chosen from the same dataset served as the corresponding controls. This produced four simulated datasets, each with one IP and two control samples. To simulate the peaks, we first generated 3000 PBRs, each 1000-bp long, at randomly chosen genomic loci covered by the array design. For each dataset, a random half of the PBRs were then chosen to be active. Peaks were generated within the active PBRs. Lengths of the peaks were uniformly distributed between 300 and 800 bp. Relative locations of the peaks within PBRs were uniformly distributed. For probes within peaks, we simulated true IP–control differences μ_id from N(m_d, τ_d²) where m_d = 1 and τ_d² = 0.09. These values were chosen to match observed values in real data. μ_ids were then added to the log₂ probe intensities of the input samples used to plant peaks.

After quantile normalization (Bolstad et al., 2003), JAMIE was applied to analyze the simulated data in two different modes. In the first mode, referred to as ‘JAMIE pooling’, all datasets were analyzed together as described in Section 2. In the second mode, referred to as ‘JAMIE single’, four datasets were analyzed separately. This was done by forcing q_d = 1 and fitting a different π for each dataset. These two modes of data analysis were compared in order to investigate whether the joint analysis was able to improve performance of peak detection. In addition to JAMIE, we also performed peak detection using two other peak callers MAT and TileMap, which showed favorable performance compared to other tools in the recent analyses of ENCODE spike-in data (Ji et al., 2008; Johnson et al., 2008). Comparison results for the first dataset are shown in Figure 2, and results for the other datasets are presented in Supplementary Figures S1–S3.

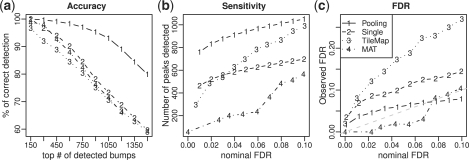
Fig. 2.

Comparisons of peak detection results of different methods (JAMIE pooling, JAMIE single, TileMap and MAT) in simulated data. (a) Peak detection accuracy. X-axis is number of top-ranked peaks. Y-axis is the percentage of peaks being true positives. (b) Sensitivity at various nominal FDR cutoffs. X-axis is the nominal FDR. Y-axis is the number of peaks reported under the corresponding nominal FDR. (c) Observed true FDR versus nominal FDR.

Each method reported a ranked list of peaks for each dataset. Figure 2a and Supplementary Figure S1 compare the peak detection accuracies by showing percentages of top-ranked peaks that are true positives. These figures show that JAMIE pooling had the best ranking performance. The observed differences among JAMIE, MAT and TileMap could be attributed to a number of factors, such as use of different data normalization procedures and different peak detection algorithms. For this reason, the comparisons among them did not provide direct evidence to show the advantage of joint data analysis. In contrast, the comparison between JAMIE pooling and JAMIE single was carefully controlled. The only difference between these two methods was data pooling. The observation that JAMIE pooling consistently performed better than JAMIE single illustrates that jointly analyzing multiple related datasets can indeed improve peak ranking compared to analyzing each dataset separately.

From Figure 2a one can also see that the gain of joint analysis was more substantial when the signal was weak. The improvement in accuracy was bigger for peaks that were ranked lower. For example, for the top 300 peaks, 99.6% called by JAMIE pooling and 96.7% called by JAMIE single were true positives. The improvement in accuracy was only 3%. However, for the top 1500 peaks, the true positive rates were 79.4% and 59.7%, respectively, and the improvement was 33%. This is consistent with the intuition that peaks ranked on top usually have strong signals. For these peaks, data from a single experiment contain adequate information, and borrowing information from other datasets has little effects on changing their ranks.

Figure 2b and Supplementary Figure S2 show the number of peaks reported by each algorithm under the same nominal (i.e. estimated) FDR cutoff. In Figure 2c and Supplementary Figure S3, the nominal FDRs are compared with the observed true FDRs. These results show that JAMIE pooling consistently reported more peaks than JAMIE single at the same nominal FDR cutoff (Fig. 2b). This happened even when the FDR estimated by JAMIE pooling was more conservative than the FDR estimated by JAMIE single (Fig. 2c), indicating higher sensitivity of JAMIE pooling. Similar results were observed when JAMIE pooling was compared to TileMap and MAT.

Figure 2c and Supplementary Figure S3 also show that all methods tested here can provide accurate FDR estimates in some datasets but not the others, and no method was able to consistently provide the best FDR estimates. In general, the accuracy of FDR estimation depends on how well the data fit the model assumptions and how accurate the model parameters can be estimated. If these do not match the data well, one may obtain biased FDR estimates. For this reason, in practice we recommend users to use JAMIE mainly as a tool to rank peaks, and use qPCR to obtain a more reliable FDR estimates whenever possible.

JAMIE is based on a number of model assumptions, such as the normality of observed and true log ratios Y_id and μ_id, equal variance τ_d² of the signal and noise components of μ_id, independence of probe signals conditional on the peak status H_id, etc. We examined these assumptions using real data, and performed additional simulations to test JAMIE's performance when these assumptions did not hold true. The results are presented in detail in Supplementary Material B, Supplementary Figures S4–S7 and Supplementary Tables S2–S5. These analyses indicate that JAMIE is fairly robust to deviations from the model assumptions.

4.2 Real data tests

We next tested JAMIE on real data (Supplementary Table S6). The first test involved three ChIP-chip datasets for detecting TFBSs of OCT4, SOX2 and NANOG in human embryonic stem (ES) cells (Boyer et al., 2005). The second test contained four datasets for locating binding sites of transcription factors Gli1 and Gli3 in different developmental and pathological contexts. The third test involved four datasets used to identify DNA binding of p130, E2F4, LIN9 and LIN54 in G0 phase of the cell cycle (Litovchick et al., 2007). These four proteins are components of a p130 complex termed DREAM. Data in the three tests were generated using Agilent promoter arrays, Affymetrix mouse promoter 1.0R and Affymetrix human promoter 1.0R arrays, respectively. They are referred to as ‘Agilent’, ‘Gli’ and ‘DREAM’ data hereafter. In all three tests, one expects both common and TF- or context-specific binding sites. Each dataset in the Agilent data contained two replicates, and each dataset in the Gli and DREAM data contained three replicates. The Agilent data had a low probe density, and the average probe spacing was 250 bp. In the Gli and DREAM data, the average probe spacing was 35 bp. A detailed description of the data collection and preprocessing can be found in Supplementary Material C.

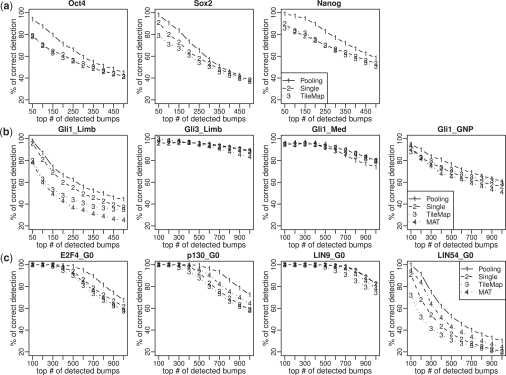
Since comprehensive lists of true binding sites for these real datasets were unknown, we were unable to evaluate the FDR estimates of different algorithms. For this reason, we focused on comparing the peak rankings. For each test, we first applied JAMIE single, TileMap and MAT (if applicable) to each individual dataset. For each dataset, a gold standard peak list was constructed by collecting common peaks reported by all three algorithms at the 30% FDR cutoff. We then excluded one replicate from each dataset, applied these algorithms to the reduced data and applied JAMIE-pooling to jointly analyze all reduced datasets together. Figure 3 compares the accuracies of the peak detection results. Accuracy was defined as the percentage of top peaks overlapping with the gold standard. For a dataset with N replicates, the test was performed N times by excluding a different replicate from the analysis each time. The figure compares the median performance. MAT cannot be applied to Agilent arrays and was not included in the Agilent test.

Fig. 3.

Comparisons of peak detection accuracies of JAMIE pooling, JAMIE single, TileMap and MAT in real ChIP-chip data. X-axis is the number of top-ranked peaks. Y-axis is the average percentage of correct detections. The first row shows the results for Agilent data, the second row is for Gli data and the third row is for DREAM data.

Figure 3 shows that JAMIE pooling performed better than or comparable to JAMIE single in almost all datasets, even though the gold standard was constructed in a way that was in favor of analyzing datasets separately. ‘LIN54_G0’ had the lowest signal-to-noise ratio in the DREAM data (Litovchick et al., 2007), and substantial improvement was observed for this dataset. Similarly, ‘Gli1_Limb’ had the lowest signal-to-noise ratio in the Gli data (Vokes et al., 2008), and improvement in this dataset was bigger than improvement observed in the other Gli datasets. Agilent arrays had low probe density. Clear improvement was observed for all three datasets in the Agilent data. Together, these reinforce the idea that joint analysis can greatly improve peak detection when the noise level is high or when the amount of information for peak detection is limited. Figure 3 also shows that JAMIE pooling performed better than TileMap and MAT.

Since the gold standard constructed by a particular algorithm may bias the results in favor of that algorithm, in a second test, each of the four algorithms was applied to the reduced data and compared to the gold standard constructed by itself using the full data. JAMIE pooling again provided the best performance in terms of self-consistency (Supplementary Fig. S8).

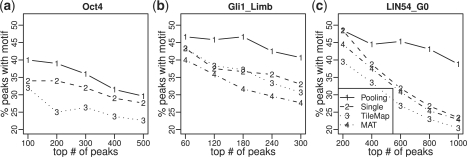
The TFs involved in the tests have known DNA binding motifs. We further compared different methods by enrichment of motifs in their reported peaks. To avoid bias caused by peak lengths, all peaks were truncated or extended to have the same length. This was done by taking the highest point of each peak and extending it to both ends by 500 bp. For each ranked peak list, the percentage of peaks that contained at least one motif site was computed. Motif sites were mapped using CisGenome (Ji et al., 2008). The TRANSFAC (Matys et al., 2006) Oct4 and Gli motifs were used for analyzing the Agilent data and Gli data, respectively. For the DREAM data, four motifs E2F4, NRF2, CREB and n-MYC were previously shown to be relevant (Litovchick et al., 2007). All of them were used in the analysis. Figure 4 shows the results for the Oct4 dataset from the Agilent data, Gli1_Limb dataset from the Gli data and E2F4 motif in LIN54_G0 dataset from the DREAM data. The comprehensive results can be found in Supplementary Material D and Figures S9–S14. The results show that peaks reported by JAMIE-pooling generally had higher or comparable motif enrichment than peaks reported by the other methods. For example, in the LIN54_G0 dataset, 39% out of the top 1000 peaks reported by JAMIE pooling contained the E2F4 motif. The percentage was 23% for JAMIE single, 23% for MAT and 20% for TileMap.

Fig. 4.

Comparisons of motif enrichment in top peaks detected by different algorithms. (a) Oct4 motif in Oct4 data, (b) Gli motif in Gil1_Limb data and (c) E2F4 motif in LIN54_G0 data. X-axis is the number of top-ranked peaks. Y-axis is the percentage of peaks with at least one motif site.

5 DISCUSSION

In summary, we have introduced a novel hierarchical mixture model for jointly analyzing multiple ChIP-chip datasets. The model was implemented using an efficient algorithm JAMIE. Our simulation and real data analyses showed that by sharing information across data, JAMIE can improve the analysis of multiple correlated ChIP-chip datasets. The well-controlled comparison between JAMIE pooling and JAMIE single showed that the improvement can be consistently observed in different test data, and it can be substantial in datasets with low signal-to-noise ratio. In our tests, JAMIE was also compared with two other popular ChIP-chip peak detection methods. Unlike the comparison between JAMIE pooling and JAMIE single, these additional comparisons were less well-controlled in the sense that the observed differences among these algorithms could be attributed to a number of factors. Knowing how much each factor contributes to the difference generally is difficult. As a result, these comparisons do not allow one to conclude that joint data analysis is better than separate analysis. From this perspective, the comparison between JAMIE pooling and JAMIE single is more informative, as it is able to illustrate a generalizable design principle that can be used to improve future algorithm design.

In the past few years, a number of important design principles have been developed for building good ChIP-chip data analysis algorithms. For example, by using a probe-sequence-dependent background correction model, MAT can remove systematic biases in the background (Johnson et al., 2006); using hundreds of publicly available samples in GEO database, TileProbe (Judy and Ji, 2009) allows one to further remove residual probe effects that cannot be explained by MAT; TileMap uses the variance shrinkage technique to improve peak detection when only a limited number of replicates are available (Ji and Wong, 2005); Mpeak shows that incorporating peak shape can improve peak detection (Zheng et al., 2007); various hierarchical, mixture and/or latent stochastic models have been shown to be useful to model varying peak lengths, non-constant probe spacing, probe outliers and correlation structures among probes (Gottardo et al., 2008; Johnson et al., 2009; Keles, 2007). The contribution of the current work is the addition of another design principle as well as a model framework for implementing it to our toolbox. Principles in our current toolbox provide basic building blocks for assembling new algorithms for future applications. By carefully assembling them together, one could expect more powerful algorithms to become available in future.

The hierarchical mixture model used by JAMIE is easily scalable to a large number of datasets. Although our current description of the model assumes that all datasets in the analysis are based on the same tiling array platform, the model can be tailored to accommodate data from different array platforms. Currently, JAMIE is implemented for analyzing multiple ChIP-chip experiments. With the rapid development of the next-generation sequencing technologies, ChIP-seq (Johnson et al., 2007) emerged as another powerful approach for mapping TFBSs. Conceptually, by tailoring the data generating distributions f_1id and f_0id to the tag count data, the hierarchical mixture model used by JAMIE can be applied to process ChIP-seq data as well. With the ability to analyze multiple ChIP datasets jointly, the huge amount of genome-wide ChIP data deposited in public databases could be reused to improve analysis of new ChIP-chip and ChIP-seq experiments.

JAMIE is developed based on a number of model assumptions. Successful application of this algorithm depends on how much benefit from using the model is compromised by violations of the model assumptions. Our simulations and real data analyses show that JAMIE is reasonably robust. Indeed, it provided better peak ranking compared to the other algorithms even when the assumptions were not perfectly satisfied. To avoid misleading results caused by dramatic violations of the assumptions, in practice one can analyze data using JAMIE and a few other peak detection algorithms and compare their performance using methods similar to Figures 3 and 4.

The current implementation of JAMIE assumes that within a PBR, whether a dataset contains an active binding site is a priori independent of the other datasets, and the corresponding probability q_d is constant across all PBRs. In real data, some datasets are more similar than others (e.g. Gli1 and Gli3 binding in limb tend to co-occur more often than Gli1 binding in brain tissues GNP and Med). This induces correlation between active binding events within a PBR. How to model this more complex correlation structure is an interesting topic for future research. In JAMIE, it is implicitly assumed that the shape of peaks is rectangular. In reality, however, peaks tend to have a triangle or bell shape, which has not been incorporated into our model. Using this additional information can potentially increase the detection power further. How to incorporate this information will be another topic for future investigation.