Abstract
The two-state model of receptor activation, in which a receptor population exists in equilibrium between a single on-state and a single off-state, has long been considered a viable model for the signaling behavior of bacterial chemoreceptors. Here, we show that this simple, homogeneous two-state model is adequate for a pure receptor population with just one adaptation state, but fails to account quantitatively for the observed linear relationship between the apparent attractant affinity (K1/2) and kinase activity ( ) as the adaptation state is varied. Further analysis reveals that the available data are instead consistent with a heterogeneous two-state model in which covalent modification of receptor adaptation sites changes the microscopic properties of the on-state or off-state. In such a system, each receptor molecule retains a single on-state and off-state, but covalent adaptation generates a heterogeneous population of receptors exhibiting a range of different on-states or off-states with different microscopic parameters and conformations. It follows that covalent adaptation transforms the receptor from a simple, two-state toggle switch into a variable switch. In order to identify the microscopic parameters most sensitive to covalent adaptation, six modified, two-state models were examined in which covalent adaptation alters a different microscopic parameter. The analysis suggests that covalent adaptation primarily alters the ligand-binding affinity of the receptor off-state (KD1). By contrast, models in which covalent adaptation alters the ligand-binding affinity of the receptor on-state, the maximal kinase stimulation of the on-state or off-state, cooperative interactions between receptors, or the assembly of the receptor-kinase signaling complex are inconsistent with the available evidence. Overall, the findings support a heterogeneous two-state model in which modification of the receptor adaptation sites generates a population of receptors with heterogeneous off-states differing in their attractant affinities.
In the process of testing the effects of covalent adaptation on the assembly of the receptor-kinase signaling complex, a new method for estimating the stoichiometric ratio of receptor and CheA in the ternary signaling complex was devised. This method suggests that the ratio of receptor dimers to CheA dimers in the assembled complex is 6:1 or less.
Keywords: bacterial chemotaxis, receptor adaptation, covalent modification, CheA, two-state model
Introduction
Mechanistic aspects of signal transduction continue to be the focus of intense interest. Many signaling proteins, including many ligand-regulated receptors, have been proposed to function as simple, two-state toggle switches in which two distinct conformations corresponding to the “on” and “off” signaling states exist at equilibrium.1–4 Typically, a signal is transmitted by agonist binding or covalent modification, which is proposed to shift an equilibrium between the on-state and the off-state. 3,5 At the other extreme, for a few specific channel and receptor proteins, ligand binding or covalent modification have been proposed to generate multiple signaling states that extend beyond a simple two-state model of protein conformations.6–11 Such multi-state systems are analogous to variable switches with multiple settings. Bacterial chemotaxis receptors have long been believed to exhibit purely two-state behavior, in which both attractant binding and covalent modification of the cytoplasmic adaptation sites are assumed to drive a simple equilibrium between two homogeneous conformations representing the kinase-activating and inactivating states.12,13 The present study develops a generalizable approach that can ascertain whether a covalently modified switch protein is a two-state switch or a more complex switch, and applies this approach to a bacterial chemoreceptor.
Bacterial chemotaxis receptors are key elements of conserved two-component signaling pathways found in all motile prokaryotes that detect and respond to external chemical stimuli.14–21 These transmembrane receptors possess a periplasmic domain that binds attractant and sends a well-characterized conformational signal through transmembrane helices to the cytoplasmic domain.16 The cytoplasmic domain serves as a scaffold to which the other elements of the signaling pathway dock, including the histidine kinase CheA, which is regulated by the receptor. There is mounting experimental evidence that interactions exist between neighboring chemotaxis receptors. Chemotaxis receptors form trimers-of-dimers22–25 that are localized to the cell pole in vivo where they may form larger lattices that serve to modify or amplify chemotactic signals.26–38
The aspartate receptor of Eschericia coli and that of Salmonella typhimurium, together with the cytoplasmic histidine kinase CheA and coupling protein CheW, forms a kinetically stable signaling complex with a dissociation half life of greater than five minutes.39 Although attractant binding to the receptor changes CheA kinase activity dramatically, the stability of the assembled signaling complex is unaffected by the presence of receptor ligand and the kinase substrates.39,40 The molar ratios of proteins in the fully assembled complex remain ambiguous, with estimates of the receptor to CheA to CheW ratios ranging from 2:2:2 to 28:4:6.39,41,42 The primary function of the signaling complex is to regulate the phosphorylation of the response regulators CheB and CheY.43,44 Phospho-CheB controls receptor adaptation by determining the covalent modification state of receptor adaptation sites, while phospho-CheY controls swimming behavior by regulating the rotational direction of the flagellar motor.45
The kinase activity of the chemoreceptor signaling complex is regulated both by the binding of chemical attractants and by the covalent modification state of the receptor adaptation sites.43,44,46 Together, these two types of signals enable a quantitative test of the predictions of the two-state model. Attractant binding to the receptor periplasmic domain inhibits CheA kinase activity, providing the first signal termed the attractant signal. In the cytoplasmic domain, specific glutamate side-chains serve as adaptation sites that are modified covalently by cytoplasmic adaptation enzymes CheR and CheB.47 The aspartate receptor possesses four adaptation sites located at positions 295, 302, 309, and 491, which in the wild-type receptor are expressed as the amino acid residues QEQE. Covalent methylation or amidation of these adaptation sites neutralizes the glutamate negative charge and stimulates receptor-mediated CheA kinase activity, thereby giving rise to the second signal, termed the adaptation signal.47–49 By contrast, CheB-catalyzed demethylation or deamidation restores the anionic glutamate side-chain and inhibits CheA kinase activity, thereby reversing the adaptation signal. The adaptation sites modulate the receptor-mediated kinase activity of the signaling complex, and serve as a chemical memory that allows the chemotaxis pathway to chemically store the attractant concentration in the recent past for comparison to the current attractant level.50
The conformational signal that travels from the periplasmic attractant-binding site through the transmembrane helices is well understood, but the structural regulation of the receptor cytoplasmic domain, including the mechanism by which the attractant and adaptation signals control kinase activity, is poorly understood.16,51 There is some evidence that, in contrast to attractant binding, modification of the cytoplasmic adaptation sites may affect the stability of the signaling complex.31,41 Thus, while the attractant signal appears to utilize a purely conformational mechanism, the cytoplasmic events triggered by the adaptation signal could involve either a conformational change or modulation of signaling complex stability.
Recent data obtained in our laboratory quantified the effects of receptor adaptation site modifications on both the apparent attractant affinity and kinase activity of the receptor population.13 In order to generate different covalent adaptation states, this prior study utilized combinations of Glu and Gln side-chains at the adaptation sites. The amidated Gln side-chain is known to mimic accurately the effect of the methyl esterification carried out by CheR in vivo.46,48,49 This approach generated engineered chemoreceptors spanning the entire range of covalent adaptation states, then reconstituted each chemoreceptor with the other components of the signaling pathway to generate a functional receptor-kinase signaling complex, and finally examined the effect of increasing attractant concentration on the kinase activity of the signaling complex. The results provided an attactant dose–response curve for each covalent adaptation state defining the apparent attractant affinity and maximal kinase activity of that state. Strikingly, the data revealed a strong linear correlation between the apparent dissociation constant for attractant (K1/2) and the apparent relative kinase activity in the absence of attractant ( ) as the covalent modification state of the receptor adaptation sites was varied. The correlation clearly demonstrated that the adaptation sites are coupled tightly to both the periplasmic attractant binding site and the cytoplasmic CheA kinase protein.
The present study carries out the first quantitative test of the ability of the simple, homogeneous two-state model to fit the available data, including the observed linear relationship between K1/2 and . This quantitative analysis reveals that the homogeneous two-state model can, for an individual receptor adaptation state, explain the observed dependence of kinase activity on attractant concentration. The analysis shows that the homogeneous two-state model predicts an approximately linear relationship between K1/2 and in the range examined experimentally, but the slope predicted by the homogeneous two-state model deviates significantly from the experimentally observed slope. Thus, although the homogeneous two-state model can explain the effect of attractant concentration on the kinase activity of a given adaptation state, it cannot account quantitatively for the effects of adaptation site changes on both the apparent attractant affinity and kinase activity of the signaling complex.
The simplest way to modify the two-state model, in order to improve its fit of the available data, is to propose that covalent modification of the receptor adaptation sites alters at least one microscopic parameter of the on-state or off-state. The present analysis indicates that only one parameter, the attractant affinity of the receptor off state (KD1), can be changed by covalent adaptation in a way that fits the linear relationship between K1/2 and quantitatively and accounts for the other available data. Notably, for a mixed receptor population, the effect of covalent adaptation on KD1 generates a heterogeneous population of off-states with different attractant affinities, reinforcing the idea that a heterogeneous, rather than homogeneous, two-state model is required to explain the signaling behavior of chemoreceptors. Five other types of modified two-state models are tested but are found to be inadequate. These unsuccessful models assume that covalent adaptation changes (i) the attractant affinity of the on-state, (ii) and (iii) the microscopic kinase activity of the on-state or off-state, (iv) the affinity of the receptor-kinase assembly, or (v) cooperative interactions between receptor dimers.
The present analysis includes a new experimental study of the effects of the adaptation signal on the stability of the signaling complex. The results indicate that modification of adaptation site glutamate residues increases signaling complex stability slightly, but the effect is too small to account for the observed deviations from two-state behavior. Fortuitously, the findings allow a novel determination of the receptor to CheA mole ratio in the fully assembled signaling complex, providing additional constraints on the oligomeric structure of the signaling complex. Overall, the results presented herein demonstrate the inadequacy of the simple, homogeneous two-state model but support a heterogeneous two-state model in which receptor covalent adaption changes one or more microscopic parameters of the on-state or off-state. The findings will be useful in quantitative simulations of receptor signal output during attractant and adaptation signaling events in the intact chemotaxis pathway.
Results
General features of the homogeneous two-state model
To analyze a switch protein for two-state behavior, it is helpful to be familiar with the general features of a two-state system. The general form of the homogeneous two-state model is illustrated in Figure 1, which presents an equilibrium between two pure signaling states, 1 and 2, representing the high-activity and low-activity states, respectively. These states have different affinities for ligand L. In the absence of ligand, the equilibrium between the two states is defined by the equilibrium constant K12 = [R2]/[R1], which describes the ratio of the two state populations. Switching between the two states is regulated by the binding of ligand, which drives the equilibrium toward the state that has the higher ligand affinity. In the presence of saturating ligand, the equilibrium constant becomes . Because the general two-state model is a thermo-dynamic cycle (Figure 1), K12 is related to the other equilibrium constants of the cycle:
| (1) |
where the microscopic ligand dissociation constants of states 1 and 2 are KD1 = [R1][L]/[LR1] and KD2 = [R2][L]/[LR2].
Figure 1.
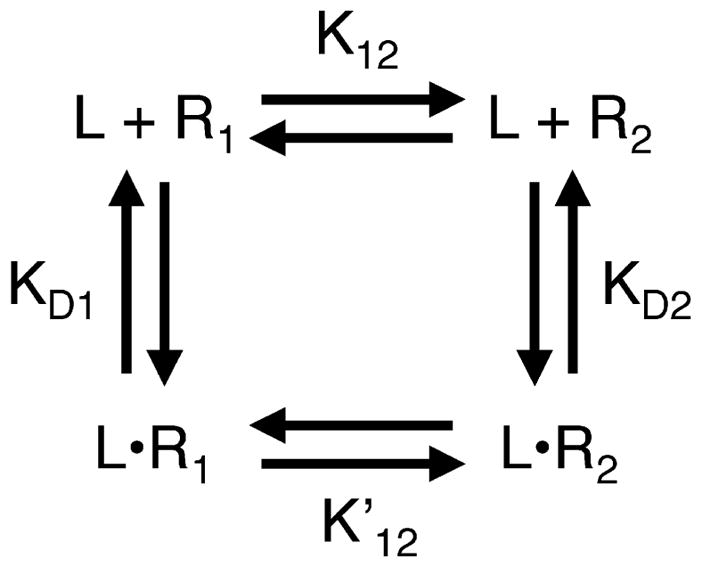
The homogeneous two-state model of receptor activation. In the homogeneous two-state model, the receptor exists in an equilibrium between two signaling states, 1 and 2, that have different ligand-binding affinities and signal output levels. State 1 is defined as the low-activity state, while state 2 is the high-activity state. In the absence of ligand (L), the equilibrium constant K12 describes the distribution between the two states. For the ligand-occupied receptor, the equilibrium constant describes the distribution between the two states. The ligand affinities are given by the microscopic dissociation constants KD1 and KD2, respectively. For bacterial chemoreceptors, state 1 (R1 and LR1) corresponds to the off-state, which possesses no measurable kinase activity, while state 2 (R2 and LR2) corresponds to the on-state. Attractants are inhibitory ligands that possess a higher affinity for state 1, and thus decrease kinase activity by driving the receptor population toward the off-state. By contrast, covalent modification of the receptor adaptation sites (either methylation or amidation) increases kinase activity by driving the equilibrium toward the on-state.
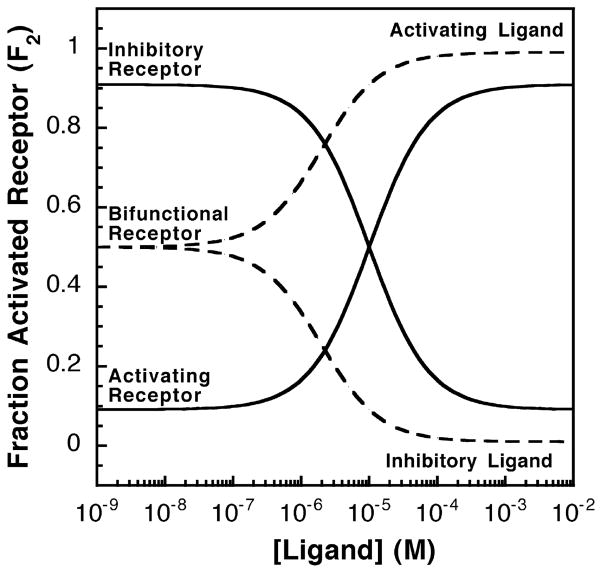
A receptor can be classified as activating or inhibitory depending on whether its ligand-saturated state exhibits maximal or minimal output signal, as illustrated in Figure 2. Ligand binding to an activating receptor shifts some or all of the receptor population toward the high-activity state, thereby increasing activity. Conversely, ligand binding to an inhibitory receptor shifts the population toward the low-activity state, thereby decreasing activity. In principle, a receptor could be bifunctional and bind both activating and inhibitory ligands. The signal output of such a receptor would be intermediate in the absence of ligand, and either increase or decrease when an activating or inhibitory ligand is added, respectively. Activating and inactivating ligands fundamentally differ in their affinities for the two signaling states. An activating ligand has a higher affinity for the high-activity state 2, while an inhibitory ligand has a higher affinity for the low-activity state 1. Thus, the binding of an activating or inhibitory ligand drives the equilibrium toward state 2 or state 1, respectively.
Figure 2.
Activating or inhibitory receptor systems and the effects of increasing activating or inhibitory ligand concentrations. Shown in continuous lines are the relative receptor-regulated activities of activating and inhibitory receptors over varying ligand concentrations. The homogeneous two-state model was used and the fraction of receptors in the activated state was calculated as described in the text (see equation (4)). The activating receptor shown has a low K12 value (K12 = 0.1) such that less than 10% of the receptor population is in the on-state in the absence of ligand. For this activating receptor, the activating ligand has a higher affinity for the on-state (KD2 = 1 μM) than for the off-state (KD1 = 100 μM), thus the binding of activating ligand to the activating receptor biases the receptor toward the on-state (state 2). In contrast, the inhibitory receptor shown has a high K12 value (K12 = 10) such that over 90% of the receptor population is in the on-state in the absence of ligand. The inhibitory ligand has a higher affinity for the off-state (KD1 = 1 μM) than for the on-state (KD2 = 100 μM), thus binding of the inactivating ligand to the the inhibitory receptor shifts the equilibrium toward the off-state (state 1). Finally, the broken lines indicate a bifunctional receptor with an intermediate K12 value (K12 = 1.0), indicating that the receptor populations of the on-state and the off-state are equal in the absence of ligand. This bifunctional receptor has two sets of dissociation constants for activating (KD1 = 100 μM, KD2 = 1 μM) and inhibitory ligands (KD1 = 1 μM, KD2 = 100 μM).
The behavior of a homogeneous two-state receptor in varying concentrations of ligand depends on the equilibrium between the two states in the absence of attractant, and on the ligand affinities of the two states. The net observed signal output Vobs of a given receptor population is determined by the fractional populations of states 1 and 2 (F1 and F2, respectively) and the microscopic activities of these states (V1 and V2, respectively):
| (2) |
For example, this output Vobs could be the velocity of a receptor-regulated kinase reaction, in which case V1 and V2 would be the microscopic kinase velocities of states 1 and 2, respectively. Equation (2) shows that if the microscopic activities V1 and V2 are known, the net signal output can be calculated from the fractional occupancy of the high activity state (F2).
In a two-state system, the fractional occupancy of the high-activity state is determined by the concentrations of individual species, where the net population of a given state includes both the apo and ligand-occupied receptors in that state:
| (3) |
Substitution of the individual concentration terms with standard expressions for the relevant equilibrium constants (KD1, KD2, K12, ) and use of mass balance transforms equation (3) into an equation relating the fractional occupancy of the high-activity state to the free ligand concentration [L] and the fixed parameters of two homogeneous signaling states:2,3
| (4) |
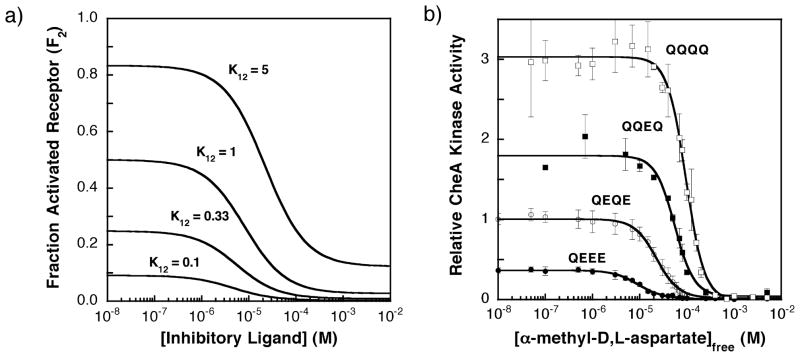
This equation indicates that the fractional occupancy of the high-activity state increases or decreases with ligand concentration [L] for an activating or inhibitory ligand, respectively (see Figure 2). For example, when a receptor population is titrated with an inhibitory ligand, the fraction of activated receptor (F2) decreases and the shape of the titration depends on K12 as illustrated in Figure 3(A). Note that the apparent ligand affinity decreases with K12, since an inhibitory ligand binds more tightly to the low-activity state 1 and the fractional population of this state decreases as K12 increases.
Figure 3.
(A) Fraction of receptor in the activated state as the concentration of an inhibitory ligand increases. The ligand-binding parameters used in this homogenous two-state model are those estimated for the binding of an inhibitory attractant (α-methyl aspartate) to the aspartate receptor (KD1 = 4 μM, KD2 = 150 μM; see the text), while the K12 value was varied as indicated. The fraction of receptor in the activated state (F2) was calculated using the homogeneous two-state model as described by equation (4). (B) The experimentally determined effects of increasing concentration of ligand on the kinase activities of signaling complexes containing the QEEE, QEQE (wild-type), QQEQ, and QQQQ receptor modification states, determined using the in vitro receptor-coupled kinase assay under standard conditions (see the text).13 The measured kinase activities are directly proportional to the fractional occupancy of receptor in the activated state (F2). For each modified receptor, the CheA kinase activity was measured at different concentrations of α-methyl aspartate. The resulting CheA kinase activities versus [attractant] data were then fit to a multisite Hill model (equation (11)). Each point is the average of at least three independent measurements. All indicated kinase activities are relative to that of the wild-type receptor (QEQE) in the absence of attractant, which is assigned a kinase activity of unity.
The apparent dissociation constant (K1/2) for ligand binding is defined operationally as the ligand concentration that yields the half-maximal change in the fractional occupancy of the high-activity state (see Figure 3(A)). More precisely, K1/2 is the ligand concentration that shifts the fraction of activated receptor to a value halfway between its extreme values observed in the absence of ligand and the presence of saturating ligand ( and , respectively):2,3
| (5) |
This equation confirms that the apparent ligand dissociation constant depends on the microscopic ligand dissociation constants of the two homogeneous states (KD1 and KD2) and on the equilibrium constant between the two states in the absence of attractant (K12). Examination of the limiting conditions indicates that as the equilibrium constant K12 goes to zero or infinity, the apparent dissociation constant K1/2 becomes KD1 or KD2, respectively, as expected.
Fitting the homogeneous two-state model to the aspartate receptor
The homogeneous two-state model makes quantitative predictions regarding the responses of bacterial chemoreceptors to attractant and adaptation signals. To analyze these predictions, it is first necessary to identify the subclass of two-state receptors that the chemoreceptors are most likely to resemble. The chemoreceptors are typically bifunctional receptors that respond to both activating and inhibitory ligands.16–18 Attractants are inhibitory ligands, since they decrease kinase activity. In Figure 1, state 1 is assumed to be the low-activity state (R1 and LR1) while state 2 is the high-activity state (R2 and LR2). Attractant binds with higher affinity to state 1, thereby decreasing kinase activity by driving the equilibrium toward the off-state. To a first approximation, which is fully valid for the aspartate receptor utilized in the present study, the low-activity state is completely inactive, such that states 1 and 2 can be simply termed the off-state and the on-state, respectively.
Figure 3(B) depicts titrations of the S. typhimurium aspartate receptor with the attractant α-methyl aspartate, in which attractant binding to the receptor inhibits the kinase activity of the receptor-regulated signaling complex. Attractant titrations of kinase activity have been carried out for all 16 covalent adaptation states of the homodimeric receptor, including the four representative adaptation states illustrated in Figure 3(B) (QEEE, QEQE, QQEQ, and QQQQ).13 In all 16 cases, the kinase activity observed at saturating attractant concentration is immeasurably low, such that state 1 is a true off-state with no detectable activity, or V1 ~0 in equation (1). In this limit, the net kinase activity of the receptor population becomes Vobs ~F2V2, enabling direct calculation of the fractional occupancy of the high-activity state (F2) from Vobs when the microscopic kinase rate of the high-activity state (V2) is known. Such a system simplifies measurement of F2 and is therefore ideal as a test case in which to probe the adequacy of the homogeneous two-state model.
Comparison of Figure 3(A) and (B) for a homogeneous two-state receptor and the aspartate receptor, respectively, indicates that the aspartate receptor exhibits certain two-state features. In particular, titration of any one adaptation state with attractant inhibits CheA kinase activity in a sigmoidal fashion, as would be expected for a homogeneous two-state receptor possessing limited positive cooperativity between receptors. Moreover, when the receptor adaptation state is varied by converting adaptation site glutamate residues to glutamine, the apparent dissociation constant for aspartate (K1/2) and the maximal kinase activity of the receptor population ( ) both increase in the qualitative fashion expected for a homogeneous two-state receptor (Figure 3(A) and (B)). As shown previously, when dose–response curves are measured for all 16 receptor adaptation states, a strong linear correlation between K1/2 and emerges, as illustrated by Figure 4(A) and Table 1.13
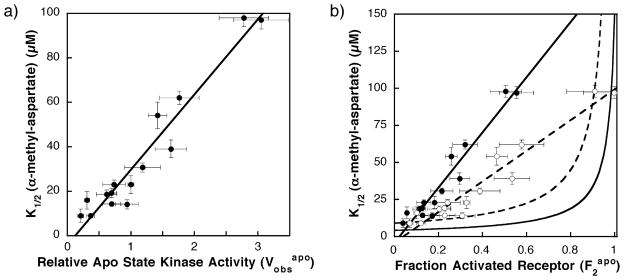
Figure 4.
(A) Previously observed correlation between the α-methyl aspartate apparent dissociation constant (K1/2) and the kinase activity in the absence of attractant ( ) for different covalent adaptation states.13 Shown is the best fit straight line. (B) Plot of apparent dissociation constant for α-methyl aspartate (K1/2) versus the fractional population of the on-state ( ) for different covalent adaptation states. The estimated fraction of receptor in the on-state ( ) was determined using equation (6) and the values summarized in Table 1. Shown are points calculated assuming that the full kinase activity of the on-state is V2 = 5.5 (filled circles) or 3.1 (open circles) relative to the activity of the wild-type receptor (QEQE) in the absence of attractant. Also shown are best fit straight lines for these data (broken and continuous lines, respectively). The calculated curves indicate the predicted behavior of homogeneous two-state model (equation (4) for two different sets of microscopic parameters: one set estimated to be the most accurate (continuous curve; KD1 = 4 μM, KD2 = 150 μM; see Appendix A), the other set providing the best fit to the data (broken curve; KD1 = 9 μM, KD2 = 1 × 109 μM). The initial regions of these two-state curves are approximately linear for values of 0.6 or less. Comparison of the line for the V2 = 5.5 experimental data (continuous line) to the initial lines for the most accurate (continuous curve) and best fit (broken curve) two-state models reveals that the slope of the experimental line is 25-fold and 11-fold higher than predicted by the two-state models, respectively. Comparison of the line for V2 = 3.1 experimental data (broken line) to the best fit two state model (broken curve) indicates that the experimental slope is still sixfold higher than the predicted two-state slope. Thus, in all cases, the homogeneous two-state model deviates significantly from the experimentally determined K1/2 and values.
Table 1.
Key parameters of the homogeneous two-state model, and heterogeneous two-state models with variable KD1 or variable V2
| Receptor modification | Homogeneous two-state model |
Variable KD1 model |
Variable V2 model |
|||
|---|---|---|---|---|---|---|
| Measured K1/2 (μM)a | Measured (relative)a | Calculated b | Modified KD1 (μM)c | Modified V2 (relative)d | Modified d | |
| (No receptor)e | NDf | 0.03 ± 0.02 | ND | ND | ND | ND |
| EEEEe | ND | 0.04 ± 0.02 | 0.007 | ND | ND | ND |
| QEEE | 9 ± 1 | 0.36 ± 0.06 | 0.066 | 8.4 | 0.64 | 0.57 |
| EQEE | 16 ± 4 | 0.31 ± 0.04 | 0.056 | 15 | 0.40 | 0.77 |
| EEQE | 23 ± 2 | 0.7 ± 0.2 | 0.13 | 20 | 0.87 | 0.85 |
| EEEQ | 9 ± 3 | 0.21 ± 0.05 | 0.038 | 8.7 | 0.37 | 0.57 |
| QEQE | 23 ± 4 | 1.0 ± 0.1 | 0.18 | 19 | 1.2 | 0.85 |
| QQEE | 31 ± 2 | 1.2 ± 0.3 | 0.22 | 25 | 1.3 | 0.89 |
| EQQE | 14 ± 2 | 0.9 ± 0.2 | 0.17 | 12 | 1.3 | 0.73 |
| QEEQ | 19 ± 2 | 0.70 ± 0.08 | 0.13 | 17 | 0.85 | 0.81 |
| EQEQ | 14 ± 1 | 0.7 ± 0.1 | 0.13 | 12 | 0.95 | 0.73 |
| EEQQ | 19 ± 2 | 0.6 ± 0.2 | 0.11 | 17 | 0.76 | 0.81 |
| QQQE | 98 ± 4 | 2.8 ± 0.4 | 0.51 | 72 | 2.8 | 0.99 |
| QQEQ | 54 ± 6 | 1.4 ± 0.1 | 0.26 | 44 | 1.5 | 0.95 |
| QEQQ | 62 ± 3 | 1.8 ± 0.3 | 0.32 | 49 | 1.8 | 0.96 |
| EQQQ | 39 ± 4 | 1.6 ± 0.2 | 0.30 | 30 | 1.8 | 0.92 |
| QQQQ | 97 ± 4 | 3.1 ± 0.4 | 0.55 | 67 | 3.1 | 0.99 |
K1/2 is the apparent dissociation constant for attractant α-methyl-aspartate regulation of kinase activity in the reconstituted signaling complex. is the relative kinase activity of the reconstituted signaling complex observed in the absence of attractant. Both and K1/2 were measured under standard assay conditions (see Figure 3(B) and Materials and Methods) utilizing monomeric protein concentrations of 2 μM aspartate receptor, 2 μM CheW, and 0.5 μM CheA.13 was determined using three or more independent measurements of two or more membrane preparations (with the exception of QEEQ, where the data shown are from one membrane preparation).
is the fractional population of the receptor on-state calculated from the ratio (equation (6)), where V2 is the kinase activity measured when the entire population is in the on-state. The V2 value utilized here is 5.5 (see Results).
KD1 is the microscopic dissociation constant of the off-state for attractant α-methyl-aspartate. In the KD1 heterogeneous two-state model (see Results and equation (7)) this parameter is altered by modification of the receptor adaptation sites, while other parameters are fixed including the values of V2 (5.5) and KD2 (150 μM).
In the V2 heterogeneous two-state model (see Results and equation (10)) the V2 parameter is altered as indicated by modification of the receptor adaptation sites. In turn, this changes the ratio (equation (6)) as indicated. Other parameters are fixed including the values of KD1 (4 μM) and KD2 (150 μM).
A negative control (no receptor) utilized membranes lacking the aspartate receptor when reconstituting the signaling complex. For this negative control, and for membranes containing the EEEE receptor, the kinase activity was too low to measure K1/2.
ND, not determined.
To test whether the homogeneous two-state model can account for the observed linear relationship between K1/2 and , the best-fit values of the two-state parameters KD1, KD2, and K12 must first be determined for this receptor–ligand pair. These parameters, when introduced into equation (4) with the experimentally determined F2 (see above), fully define the predicted shape of the attractant dose-response curve for each receptor adaptation state. The values of KD1 and KD2 are constrained by the minimum and maximum values of K1/2 observed when the adaptation state is varied, which place limits on the microscopic attractant affinities of the two states. Since glutamate residues at the adaptation sites drive the equilibrium toward the low-activity state 1, the lowest measured K1/2 obtained for the QEEE and EEEQ receptors (9 μM) serves as an upper limit on KD1. The true KD1 must be even lower than this limiting value, since the QEEE and EEEQ modification states do not drive the receptor completely into low-activity state 1, as indicated by the fact that the EEEE receptor exhibits even lower kinase activity (which is unmeasurable under standard assay conditions, thus preventing determination of K1/2 for this receptor). Similarly, since glutamine residues at the adaptation sites drive the equilibrium toward the high-activity state 2, the value of KD2 should be at least as high as the largest K1/2 measured for the QQQE and QQQQ receptors. Given these constraints, KD1 < 9 μM and KD2 > 97 μM. Currently, the best estimates of these constants are KD1 = 4 μM and KD2 = 150 μM (see Appendix).
The value of the equilibrium constant K12 can be calculated from the fractional receptor population in the high-activity state when no ligand is present ( ):
| (6) |
(note that while the relationship between and K12 is general, the relationship between , and V2 is specific for an inhibitory receptor with an inactive state 1 such that V1 = 0). Experimentally, the quantity can be determined from the ratio of the observed relative kinase activity in the absence of attractant ( ) to the maximal kinase activity observed when the receptor population is driven completely into high-activity state (V2, see equation (1)). The parameter has been measured for each receptor adaptation state and ranges from ~0.0 to 3.1 under standard conditions (Table 1), thus knowledge of V2 would enable direct calculation of the values for these states. Previous studies have identified a series of six receptor superactivating mutations that, when expressed in the QQQQ adaptation state background, appear to provide an upper limit on the value of V2. Of the over 200 receptor mutations screened to date, these are the most active, yielding kinase activities five-to sixfold higher than observed for the wild-type receptor (QEQE), and 1.6 to 1.9-fold higher than observed for the most highly modified receptor (QQQQ).52–56 One of them, G278V in the QQQQ background, appears to trap the receptor in the high-activity state 2, since it prevents both attractant-triggered inhibition of kinase activity and the loss of kinase activity normally caused by glutamate residues at the adaptation sites.13 Together, these observations suggest that G278V/QQQQ and the other superactivating mutations drive the receptor population fully into the high-activity state.13 Assuming this is the case, it follows that V2 ~5.5 under standard conditions, thereby enabling calculation of in equation (6) for each receptor adaptation state as summarized in Table 1.
Figure 4(B) compares the predictions of the homogeneous two-state model, calculated from equation (4), with the observed linear correlation between the apparent attractant affinities and kinase activities. The experimental data were obtained from Figure 4(A) simply by converting the horizontal axis parameter from to (where for V2 = 5.5). Again, the experimental plot of apparent affinity versus activity is well approximated by a straight line (Figure 4(B), continuous line). Predicted curves for the homogeneous two-state model were generated using the most accurate current estimates of the microscopic attractant affinities (KD1 = 4 μM and KD2 = 150 μM, continuous curve) or the attractant affinities that provide the best fit to the data while still satisfying the constraints discussed above (KD1 = 9 μM and KD2 ~∞, broken curve). For values between 0.0 and 0.6, which includes the experimental points (filled circles), the homogeneous two-state model predicts that K1/2 will increase approximately linearly. However, the slope of the experimental data is observed to be 25-fold and 11-fold higher than the initial slopes of the most accurate and best fit homogeneous two-state models, respectively. The fit is improved slightly by assuming that the fully modified receptor adaptation state (QQQQ) drives the population completely into the high-activity state 2, such that rather than 5.5. This assumption reduces the slope of the experimental data (broken line). However, the experimental slope remains sixfold higher than that predicted by the best fit two-state model. As increases further from 0.6 toward 1.0, where the receptor population is primarily in state 2, the curves predicted for the homogeneous two-state model increase rapidly and deviate even more from the experimental data. In short, the homogeneous two-state model is able to explain the qualitative effect of attractant binding on kinase activity for any one receptor adaptation state (Figure 3(A) and (B)), but is unable to account for the changing attractant affinities and kinase activities observed when the adaptation state is varied (Figure 4(A) and (B)).
Modifying the two-state model to fit the aspartate receptor data
The traditional, homogeneous two-state model assumes that receptor covalent modification has no effect on the microscopic parameters of the on-state and off-state. The simplest way to modify this model is to allow each microscopic parameter to vary as the adaptation sites are modified. The result is a heterogeneous two-state model, since the on-state or the off-state becomes heterogeneous when different adaptation states are introduced. There are at least six microscopic parameters that could be altered by covalent adaptation, yielding six different modified two-state models. In particular, covalent adaptation could alter (i) the microscopic attractant affinity of the off-state KD1, (ii) the microscopic attractant affinity of the on-state KD2, (iii) the kinase activity of the low-activity state V1, (iv) the kinase activity of the high-activity state V2, (v) cooperative interactions between receptor dimers, or (vi) the stability of the receptor-kinase signaling complex. All six of these modified two-state models assume that each covalently adapted receptor retains just two signaling states, corresponding to states 1 and 2 of the homogeneous two-state model. The following analysis tests each of the six models, assuming for the sake of simplicity that the deviation from homogeneous behavior arises from alteration of a single parameter. While this is likely an oversimplification, the approach identifies the single parameter most likely to dominate.
The first possibility is that covalent modification of the receptor adaptation sites alters the microscopic attractant dissociation constant KD1 of the off-state, while retaining fixed KD2 and V2 parameters. The fixed values of KD2 and V2 utilized are the most accurate current estimates as determined above (KD2 = 150 μM, V2 = 5.5). For a given covalent adaptation state exhibiting a known K1/2 and K12 (from Table 1), the KD1 value required to fit the experimental data can be calculated by rearranging equation (5):
| (7) |
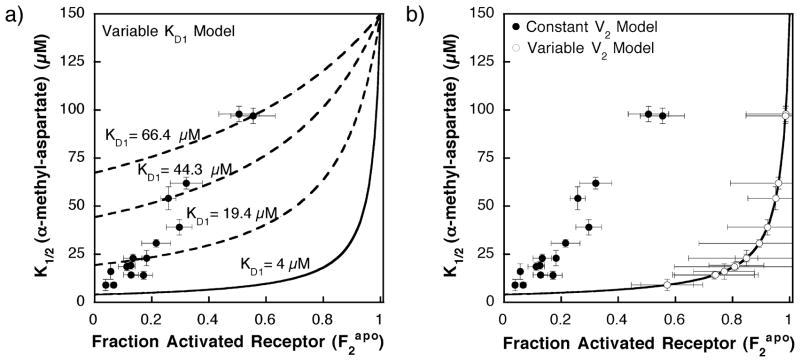
By allowing KD1 to vary as specified in equation (7), this approach yields a heterogeneous modified two-state model that quantitatively fits the experimental results as illustrated in Figure 5. The resulting modified KD1 values for the attractant α-methyl aspartate are summarized in Table 1 and range from 8 μM to 72 μM, in most cases differing significantly from the fixed KD1 value of 9 μM or 4 μM used in the homogeneous two-state model in Figure 4(B). In this scenario, KD1 increases gradually with the introduction of glutamine residues at the adaptation sites, thereby shifting the K1/2 values predicted by the homogenous two-state model (equation (4)) up toward the higher K1/2 values observed by experiment as illustrated in Figure 5(A). Note that the thermodynamic cycle (Figure 1) requires that , thus can be calculated from the values of KD1, KD2, and K12 for each adaptation state as glutamine residues are introduced (equation (1)). The resulting values increase 600-fold from the QEEE state to the QQQQ state, indicating that the fractional population in the on-state should shift substantially in the presence of saturating ligand. Unfortunately, this prediction cannot be tested currently, since the kinase activity of the ligand-occupied receptor is not measurable. Thus, the KD1 model provides an adequate fit to the available data, and further consideration is warranted of the proposal that receptor covalent adaptation alters the microscopic dissociation constant for the low-activity state. Figure 5(A) illustrates how the varying KD1 shifts the curve predicted for the homogeneous two-state model in a way that fits the experimental data.
Figure 5.
(A) Plot of the α-methyl aspartate apparent dissociation constant (K1/2) versus the fractional activated receptor in the absence of attractant ( ), illustrating how the KD1 heterogeneous two-state model fits the data. Filled circles represent the experimentally determined K1/2 and calculated values for different receptor covalent adaptation states. The fractional activated receptor in the absence of attractant ( ) was determined from equation (6) using the data in Table 1 and V2 = 5.5 (see the text). The continuous curve represents the predicted behavior for a homogeneous two-state model with fixed parameters set at the most accurate current estimates (KD1 = 4 μM and KD2 = 150 μM). The broken lines represent a subset of the 16 curves obtained by allowing the KD1 parameter of the heterogeneous two-state model to change with the receptor adaptation state (equation (7)) as summarized in Table 1, thereby intersecting specific data points. The broken curves shown are those that fit the QEQE modification state (KD1 = 19.4 μM), the QQEQ modification state (KD1 = 44.3 μM), and the QQQQ modification state (KD1 = 66.4 μM), with fixed parameters of KD2 = 150 μM and a relative V2 of 5.5. (B) Plot of the α-methyl aspartate apparent dissociation constant (K1/2) versus the fractional activated receptor in the absence of attractant ( ), illustrating how the V2 heterogeneous two-state model fits the data. Filled circles represent the experimentally determined K1/2 and calculated values for different receptor covalent adaptation states assuming a fixed relative V2 of 5.5. The open circles represent a heterogeneous two-state model (equation (10)) in which the kinase activity of the activated state (V2) is allowed to vary with the receptor adaptation state as summarized in Table 1, thereby shifting each value to the right, since (equation (6)). The continuous curve is the homogeneous two-state model (equation (5)) in which the microscopic parameters are fixed at the most accurate current estimates (KD1 = 4 μM and KD2 = 150 μM).
The second possibility is that receptor covalent adaptation modulates the microscopic dissociation constant for the high-activity state (KD2). To determine the KD2 values needed to provide agreement with the experimental data, equation (5) can be rearranged:
| (8) |
However, substitution of the experimentally determined K1/2 values together with the optimal fixed values of KD1 and V2 determined above (KD1 = 4 μM, V2 = 5.5) yields a negative KD2 for most values of K12. Since KD2 cannot be negative, the variable KD2 model is physically implausible. This is not surprising, since the estimated K12 values for the various adaptation states are all less than or approximately equal to unity (F2 less than or approximately equal to 0.5), while the ratio KD2/KD1 is significantly greater than unity. For these conditions, equation (5) indicates that K1/2 is relatively independent of KD2, thus modification of KD2 by covalent adaptation could not account for the observed deviation from homogeneous two-state behavior.
The next two possibilities focus on the effect of receptor covalent adaptation on the microscopic kinase activities of the low and high-activity states (V1 and V2, respectively). The data indicate that V1 never becomes measurable, since the net kinase activities of all receptor covalent adaptation states are immeasurably low in the presence of saturating attractant.13 It follows that state 1 is a stable off-state that cannot modulate the observable parameters in a significant way, and thus does not account for the deviation from homogeneous two-state behavior. By contrast, if covalent adaptation changes V2, the observable parameters will be altered significantly. To calculate the modified V2 values needed to fit the experimental results, it is useful to first rearrange equation (5) to determine K12:
| (9) |
Combining equations (6) and (9) yields equation (10), which enables calculation of a modified V2 value for each receptor adaptation state from the other parameters , KD1, KD2, and K1/2:
| (10) |
The resulting modified V2 values vary over an eightfold range and decrease as the adaptation sites are restored to glutamate side-chains. Subsequently, the modified V2 for a given adaptation state, together with its measured , can be used to calculate K12 for that state as indicated in equation (6). The resulting modified V2 and values are summarized in Table 1. The modified values are all larger than those obtained above using a fixed value of V2, while the modified V2 values are all smaller than the fixed value utilized above (V2 = 5.5). The smaller modified V2 values are closer to , thus the fractional occupancy of the high-activity state in the absence of attractant ( , see equation (6)) increases significantly. This shift of to larger values can provide arbitrarily close fits to the experimental results, as illustrated in Figure 5(B). Thus, a model proposing that covalent adaptation changes V2 can account for the deviation from homogeneous two-state behavior and is worthy of further consideration. However, this model is disfavored by a lock-on mutant believed to trap the receptor in state 2, for which V2 is observed to be independent of adaptation state (see Discussion).
In the fifth potential model, the receptor adaptation state modulates cooperative interactions between receptors, which in turn perturbs the apparent dissociation constant for attractant regulation (K1/2). Previous studies quantifying the attractant dependence of kinase regulation have detected positive cooperativity between receptor dimers in the binding of attractant, and have shown that this positive cooperativity generally increases with modification state.23,31 For the aspartate receptor, the incorporation of glutamine residues into the adaptation sites causes the measured Hill coefficient for attractant regulation to increase from approximately 1.5 to 3.0 due to increased cooperativity between the aspartate-binding sites of different dimers.13,23 In principle, positive cooperativity between receptors could either increase or decrease the apparent ligand binding affinity relative to the ligand-binding affinity observed in the absence of cooperativity.57 Recent evidence suggests that, for a given aspartate receptor adaptation state, increasing the cooperativity between receptors causes the apparent attractant affinity to increase.24,58 It follows that the increased positive cooperativity known to arise from glutamine incorporation into the adaptation sites13,23 should increase the apparent attractant affinity as well. By contrast, the observed deviations from homogenous two-state behavior are associated with a rapid loss of attractant affinity as glutamine residues are incorporated. Thus, the available evidence indicates that the increased positive cooperativity between receptors caused by glutamine incorporation at adaptation sites does not account for the failure of the homogeneous two-state model.
Effects of receptor covalent modification on signaling complex assembly
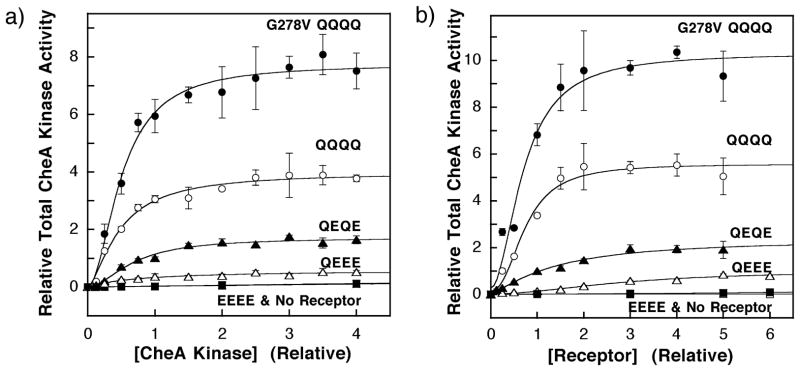
In the sixth and final model tested, covalent receptor adaptation perturbs the observed kinase activity of the two-state system, but not simply by altering the microscopic V2 of the high-activity state as considered above. Instead, the perturbation alters the total number of active signaling complexes. In this model, covalent adaptation of the receptor changes the affinity of signaling complex formation. Thus, the model predicts that two-state behavior will be restored under conditions where signaling complex formation is driven to completion for all adaptation states. To test this possibility experimentally it was first necessary to determine the relative concentrations of the receptor and kinase components needed to maximize signaling complex formation. For the G278V/QQQQ, QQQQ, QEQE, QEEE and EEEE receptors, two titrations were carried out in which (i) the concentrations of soluble components CheA, CheW and CheY were covaried or (ii) the concentration of receptor-containing membranes was varied. Even if different adaptation states modulate receptor–receptor interactions to yield different numbers of receptor oligomers capable of forming signaling complexes, the increasing total receptor concentration of the first titration should ensure that all adaptation states form the same number of signaling complexes due to saturation of the fixed kinase population. Plots of relative CheA kinase activity against receptor or kinase concentration indicate that, for a given receptor adaptation state, kinase activity asymptotically approaches maximal level as illustrated in Figure 6(A) and (B). The results of control studies (not shown) indicate that these experiments utilized sufficient CheY to ensure that the kinase activity was independent of the CheY concentration, and that the formation of phospho-CheY was linear with time during the entire initial rate measurement. Thus, even at the maximal kinase activities, the autophosphorylation of CheA remains rate-determining, and the substrates of the reaction are not depleted significantly. Similarly, the CheW concentrations utilized were sufficient to yield maximal kinase activity (not shown). For each titration, best-fit analysis utilizing the Hill equation provided an apparent dissociation constant for signaling complex assembly ( ) and an asymptotic maximal kinase activity ( ) as summarized in Tables 2 and 3, as well as a Hill coefficient. The best-fit Hill coefficients (Figure 6 legend) are difficult to interpret, due to the complicated dependence of signaling complex assembly on the CheW concentration and CheA dimerization.17,59–61 However, these Hill coefficients range from 1.0 to 2.5, consistent with current models in which the signaling complex contains multiple copies of each component.22–25,32,41
Figure 6.
(A) The effect of increasing concentration of CheA on the kinase activities of reactions containing fixed concentrations of receptor. The in vitro assay of receptor-coupled kinase activity was used to monitor the increase in signaling complex formation upon the titration of CheA into reactions containing 2 μM receptor monomer. The soluble components of the chemotactic signaling complex were covaried at a fixed molar ratio of 1:4:20 for CheA to CheW to CheY, such that CheW and CheY are always present in excess of CheA. Measured kinase activities were normalized relative to that of the wild-type (QEQE) receptor under standard assay conditions (0.5 μM CheA kinase monomer), such that both the relative kinase activity and relative CheA concentration of this reaction were set equal to unity. The resulting data were best-fit by a Hill model that yielded an apparent dissociation constant ( ) and an asymptotic kinase activity in the absence of attractant ( ) as summarized in Table 2. The fit provided Hill coefficients that are difficult to interpret due to the complexities of signaling complex assembly (see the text): H = 1.0 ± 0.3 for QEEE, 1.8 ± 0.4 for QEQE, 1.5 ± 0.2 for QQQQ, and 1.8 ± 0.3 for G278V/QQQQ. The EEEE modification state (filled boxes) showed no significant activity above that of membranes containing no overexpressed receptors (underlying open boxes), preventing measurement of parameters for this state. (B) The effect of increasing concentration of receptor on the kinase activities of reactions containing fixed concentrations of CheA kinase (0.5 μM), CheW (2 μM), and CheY (10 μM). Measured kinase activities were normalized relative to that of the wild-type (QEQE) receptor under standard assay conditions (2.0 μM receptor monomer), such that both the relative kinase activity and relative receptor concentration of this reaction were set equal to unity. The resulting data were best fit by a Hill model that yielded an apparent dissociation constant ( ) and an asymptotic kinase activity in the absence of attractant ( ) as summarized in Table 3. The fit provided Hill coefficients that approach 2.0 but are difficult to interpret due to the complexities of signaling complex assembly (see the text): H = 1.9 ± 0.6 for QEEE, 1.3 ± 0.3 for QEQE, 2.3 ± 0.5 for QQQQ, and 1.9 ± 0.5 for G278V/QQQQ. Other details are as for A.
Table 2.
Effects of receptor modifications on the apparent CheA kinase affinity of the signaling complex
| Receptor modification | for CheA binding (μM monomer)a | (relative)b |
|
|
|---|---|---|---|---|
| QEEE | 0.40 ± 0.09 | 0.6 ± 0.1 | 0.075 | |
| QEQE | 0.34 ± 0.04 | 1.7 ± 0.2 | 0.21 | |
| QQQQ | 0.23 ± 0.03 | 4.1 ± 0.3 | 0.51 | |
| G278V/QQQQ | 0.25 ± 0.02 | 8.0 ± 0.5 | 1.0 |
is the apparent dissociation constant for CheA binding to the signaling complex determined by best-fit Hill analysis of Figure 6(A). For a fixed receptor concentration (2 μM), the concentrations of CheA kinase, CheW, and CheY were covaried at constant molar ratios (CheA:CheW:CheY was 1:4:20). All protein concentrations are given in monomeric units.
is the maximal kinase activity attained under saturating conditions in the absence of attractant, relative to the kinase activity of the QEQE receptor under standard conditions, which is set equal to unity (see for QEQE in Table 1). The parameter is determined by best-fit Hill analysis of Figure 6(A) as indicated for . No significant kinase activity was observed for EEEE.
is the fractional population of the on-state in the absence of attractant at saturating levels of CheA (as well as CheW and CheY). This parameter is calculated as the ratio , where the kinase activity observed when the entire population is in the on-state (V2sat) is operationally defined as the kinase activity of G278V/QQQQ under saturating conditions.
Table 3.
Effects of receptor modifications on the apparent receptor affinity of the signaling complex
| Receptor modification | for receptor binding (μM monomer)a | (relative)b,c |
|
|
|---|---|---|---|---|
| QEEE | 6 ± 2 | 1.0 ± 0.2 | 0.097 | |
| QEQE | 2.8 ± 0.7 | 2.3 ± 0.4 | 0.22 | |
| QQQQ | 1.5 ± 0.2 | 5.4 ± 0.4 | 0.52 | |
| G278V/QQQQ | 1.4 ± 0.2 | 10.3 ± 0.9 | 1.0 |
is the apparent dissociation constant for receptor binding to the signaling complex determined by best-fit Hill analysis of Figure 6(B). While the concentrations of CheA, CheW and CheY were fixed (CheA 0.5 μM; CheW 2 μM; CheY 10 μM), receptor-containing membranes were titrated into the sample. All protein concentrations are given in monomeric units.
is the maximal kinase activity attained under saturating conditions in the absence of attractant, relative to the kinase activity of the QEQE receptor under standard conditions, which is set equal to unity (see for QEQE in Table 1). The parameter is determined by best-fit Hill analysis of Figure 6(B) as indicated for .
At high concentrations of receptor (10, 12 μM) a small but measurable amount of kinase activity was observed for EEEE. The level of activity was approximately 25-fold lower than that of QEQE under identical conditions, and the activity was eliminated by saturating attractant. The EEEE state therefore appears to have a low but measurable affinity for the signaling complex ( ). This observation is consistent with previous reports of small levels of CheA kinase activity stimulated by the EEEEE serine receptor.31
is the fractional population of the on-state in the absence of attractant at saturating levels of receptor, determined as indicated in the legend to Table 2.
Examination of the values obtained when the concentration of total receptor or kinase components is varied (Tables 2 and 3) indicates that the apparent signaling complex affinity does not vary widely for different receptor adaptation states, increasing two-or fourfold, respectively, as the covalent modification of the receptor increases from QEEE to QQQQ. Similarly, previous studies have shown that the signaling complex affinity is relatively independent of the receptor ligand occupancy.39,40 Together, these observations demonstrate that the signaling state of the receptor does not greatly alter the affinity of signaling complex formation. However, the results indicate that the standard concentrations of protein utilized in the in vitro signaling complex activity assay (see Materials and Methods) are slightly below the saturating concentrations needed to drive signaling complex formation to completion. Thus, when conditions are changed from standard to saturating, the kinase activity observed in the absence of attractant increases from 1.4-fold to threefold (compare in Table 1 with in Tables 2 and 3) depending on the adaptation state. This increased kinase activity represents a population shift from the unassembled state to the high-activity state, and the shift is largest for QEEE and smallest for G278V/QQQQ. If this increased occupancy of the high-activity state is responsible for deviations from homogeneous two-state behavior, then the signaling complexes assembled under saturating conditions would need to exhibit fractional occupancies of their high-activity states ( , Tables 2 and 3) ranging up to 14-fold higher than observed under standard conditions ( , Table 1; by analogy with the modified V2 model discussed above, which provides the model-independent increases needed to fit the data). Almost identical values are observed when increasing the receptor or kinase concentration to saturation (compare Tables 2 and 3), as expected, since the fully assembled signaling complex should exhibit the same fractional occupancy of the on-state regardless of how full assembly is achieved. However, the largest measured increase is less than twofold for the QEEE receptor. Such small increases cannot explain the large deviations from homogeneous two-state behavior. Moreover, when conditions are changed from standard to saturating, the K1/2 values values measured for attractant regulation of kinase activity are unchanged within error (as observed for QEQE,23 and for QQQQ, unpublished data). Thus, neither the nor the K1/2 parameters measured under standard conditions change substantially under saturating conditions. Overall, the data of Tables 2 and 3 provide strong evidence that the effects of receptor adaptation state on signaling complex assembly are too small to account for the observed deviations from homogeneous two-state behavior.
Estimation of the receptor:CheA mole ratio in chemotactic signaling complexes
By comparing the maximal kinase activity measured under saturating receptor and CheA conditions, it is possible to estimate the maximum receptor:CheA mole ratio in the assembled signaling complex. The approach is based on the fact that the observed kinase activity of a given number of assembled signaling complexes will be the same, regardless of whether saturation is achieved by varying the receptor concentration or the CheA concentration. Table 4 shows how the receptor to CheA mole ratio, ranging from 5.2 to 6.7, was determined for the QEEE, QEQE, QQQQ and 278V/QQQQ receptors. For example, for QQQQ, a fixed receptor monomer concentration of 2.6 μM would, under saturating CheA conditions, give the same maximal kinase activity as a fixed CheA monomer concentration of 0.5 μM under saturating receptor conditions. It follows that the number of signaling complexes is the same for these two saturated systems, and that the receptor to CheA mole ratio is 2.6/0.5 = 5.3. These calculations assume that receptor molecules are fully accessible to the soluble components during complex assembly, and that all receptor and CheA molecules are active. The E. coli membranes containing the receptors are membrane fragments produced by sonication, and at least 95% of the receptor population is accessible to cleavage within five minutes of addition of the 29 kDa tobacco etch virus (TEV) protease, indicating that most membrane compartments are accessible. However, the 132 kDa CheA dimer is considerably larger than TEV and could, in principle, be excluded from some internal compartments that admit a catalytic quantity of protease. In addition, it is not known whether all copies of the receptor, which is overexpressed approximately 30-fold higher than its native abundance, are properly folded and competent for incorporation into signaling complexes. Thus, the calculated receptor to CheA mole ratio is best regarded as an upper limit.
Table 4.
Estimation of the receptor:CheA mole ratio in chemotactic signaling complexes
| Receptor modification | for saturating CheA at 2.0 μM receptora | for saturating receptor at 0.5 μM CheAb | Calculated receptor:CheA mole ratioc |
|---|---|---|---|
| QEEE | 0.6 ± 0.1 | 1.0 ± 0.2 | 6.7 ± 1.7 |
| QEQE | 1.7 ± 0.2 | 2.3 ± 0.4 | 5.4 ± 1.1 |
| QQQQ | 4.1 ± 0.3 | 5.4 ± 0.4 | 5.3 ± 0.5 |
| G278V/QQQQ | 8.0 ± 0.5 | 10.3 ± 0.9 | 5.2 ± 0.6 |
The for saturating CheA was obtained as shown in Figure 6(A). The soluble chemotaxis components were covaried at a relative CheA to CheW to CheY ratio of 4:1:20, while the receptor concentration was fixed at 2.0 μM. Under these conditions, the CheW and CheY concentrations were always saturating, and the receptor concentration limited the maximum number of signaling complexes that could be formed. All concentrations are monomeric, and all receptors are assumed to be accessible to complex assembly.
The for saturating receptor was obtained as shown in Figure 6(B). The soluble chemotaxis components were fixed at a relative CheA to CheW to CheY ratio of 4:1:20, with a total CheA monomer concentration of 0.5 μM. Under these conditions, the CheW and CheY concentrations were always saturating, and the CheA concentration limited the maximum number of signaling complexes that could be formed. All concentrations are monomeric, and all receptors are assumed to be accessible to complex assembly.
Estimated receptor to CheA mole ratio. To obtain this value, the concentration of receptor needed to increase the value of column 2 to match the value of column 3 is calculated. Subsequently, this receptor concentration is divided by the CheA concentration from column 3 (0.5 μM) to give the calculated receptor to CheA mole ratio of the fully assembled signaling complex.
Discussion
The homogeneous two-state model of receptor activation has been proposed to describe the signaling behavior of bacterial chemoreceptors (see Introduction). A quantitative analysis reveals that the homogeneous two-state model fails to account for the linear relationship between the apparent attractant affinities (K1/2) and maximal kinase activities ( or ) of different receptor covalent adaptation states (Figure 4). In particular, the homogeneous two-state model predicts an initial slope for this linear relationship that is sixfold to 25-fold lower than the experimentally determined slope (Figure 4(B)). By contrast, the data are consistent with a heterogeneous two-state model in which covalent modification of the receptor adaptation sites changes the microscopic parameters of the on-state or the off-state.
Altogether, six different modified two-state models were tested for their ability to reproduce the linear relationship between apparent affinities and kinase activities as the adaptation state is varied (see Results). Each of these models proposes that covalent adaptation alters only one microscopic parameter of the on-state or the off-state. Two of the six models were found to provide an adequate fit. The first successful model proposes that covalent adaptation alters the microscopic dissociation constant (KD1) for attractant binding to the signaling complex off-state. The other successful model proposes that covalent adaptation alters the kinase activity of the on-state (V2). However, evidence disfavoring the latter V2 model is provided by the 278V mutant, which is believed to trap the receptor in the on-state. Previous results have shown that covalent modifications of the adaptation sites on the 278V receptor have little or no effect on kinase activity, suggesting that the kinase activity of the on-state is not altered significantly by covalent adaptation.13 Quantitative analysis also rules out the four remaining models by demonstrating that covalent adaptation does not alter significantly the dissociation constant for attractant binding to the on-state (KD2), or the kinase activity of the off-state (V1), or the cooperativity between receptors, or the stability of the signaling complex. Thus, the present findings suggest that covalent adaptation most likely alters the dissociation constant for attractant binding to the off-state (KD1). However, the present findings do not rule out the possibility that covalent adaptation could alter combinations of the six microscopic parameters, which is quite plausible.
In the successful KD1 heterogeneous two-state model, neutralization of adaptation site glutamate residues by methyl esterification or amidation causes the microscopic attractant affinity of the off-state to decrease up to eightfold, representing a transmembrane perturbation of the periplasmic ligand-binding site. As a result, covalent modification of the adaptation sites generates a mixed population of off-states with different attractant affinities. In this picture, a typical population of receptors will have homogeneous on-states, but heterogeneous off-states, thereby accounting for the deviation from homogeneous two-state behavior. Since the heterogeneous off-states have different microscopic parameters and conformations, they can be considered new signaling states that are not present in a homogeneous two-state system. Further examination of the KD1 model reveals that a significant fraction of the receptor population exists in state 1, the off-state, even in the absence of attractant, ranging from approximately 45% for the QQQQ receptor to 95% for the QEEE receptor. As a result, the apparent attractant affinity is highly sensitive to changes in KD1 (see equation (5)).
The KD1 heterogeneous two-state model further proposes that the effect of covalent modification on KD1 has likely evolved, at least in part, because it enables a chemotaxing bacterial cell to sense a broader range of concentrations of attractant. During chemotaxis, as a bacterial cell swims up an attractant gradient, the level of methylation increases and causes K1/2 to increase as well, thereby decreasing the apparent attractant affinity. The decreased affinity helps the receptor population avoid saturation by the increasing concentration of attractant, thereby extending the dynamic range of the chemotaxis pathway. In the KD1 model, methylation of the receptor population generates considerably larger K1/2 increases than predicted by the homogeneous two-state model; thus the effect of covalent adaptation on KD1 extends the dynamic range of the chemotaxis pathway even further than allowed by a homogeneous two state system. The increasing may also help the receptor population adapt to the changing concentration of attractant, since at high levels of attractant the majority of receptors will eventually be driven to the off-state by attractant binding. The increased kinase activity of the apo receptors could maintain the net kinase output of the signaling complex population at a useful level even when the majority of the population is inhibited. Finally, the striking linear relationship between K1/2 and may have evolved to ensure that the net attractant affinity and kinase activity of the receptor population gradually change in a similar fashion as the receptor population is driven into the fully modified state. Alternatively, the linear relationship between K1/2 and may arise from an underlying physical mechanism directly coupling these parameters that is not understood.
The molecular mechanism by which covalent modification of the cytoplasmic adaptation sites alters the attractant affinity of the periplasmic attractant binding site is not known. The simplest model proposes that this transmembrane communication arises from a reversal of the piston displacement of the signaling helix, which transmits the signals across the membrane.16 Evidence for such a covalent modification-driven reversal of the piston displacement has been detected by disulfide formation rate changes in a related receptor.62 This model proposes that neutralization of the adaptation sites causes subtle piston displacements of the signaling helix toward the cytoplasm, and that these displacements are slightly larger than would be expected for a homogeneous two-state system. In such a picture, the effects of covalent modification could perturb the piston position for both the on-state and the off-state, thereby altering the microscopic attractant affinities of both states (KD1 and KD2). The present analysis does not rule out such a possibility, since only one microscopic parameter was varied at a time.
The failure of the homogenous two-state model to explain the quantitative data for different covalent adaptation states adequately may have implications for quantitative simulations of chemotaxis pathway function. For example, the homogeneous two-state system has been utilized recently in several computational models of the chemotaxis pathway.35,63–66 On a qualitative level, these computational models have successfully reproduced key features of pathway function. The present study suggests that even more accurate pathway simulations could be carried out by including the effects of receptor covalent modification on the microscopic parameters of the on-state and the off-state, particularly the attractant affinity of the off-state.
Finally, the estimated mole ratio of approximately six receptor monomers to one CheA monomer, measured by a novel approach, is consistent with a simple oligomeric model for the chemotactic signaling complex. In this model, two receptor trimers-of-dimers are bridged by a single CheA dimer. Evidence that the receptor forms stable trimers-of-dimers is provided by the crystal structure of a receptor cytoplasmic fragment,22 while CheA is known to form a stable dimer.61,67 A similar oligomeric model was appeared after submission of the current work.42 The bridging of two trimers-of-dimers via dimeric CheA is consistent with Hill coefficients measured in vitro and in vivo for the attractant regulation of the kinase response, which range from 1 to 3.13,58 These Hill coefficients suggest that there are strong cooperative interactions between receptors within a single trimer-of-dimers,24 while little or no cooperativity is transmitted through the CheA dimer to the other trimer-of-dimers in the complex. It should be noted that if a significant fraction of the receptor population is improperly folded or inaccessible to the soluble proteins during complex assembly, then the receptor to CheA mole ratio could be considerably less than 6:1. Thus the present findings do not rule out previous models suggesting receptor to CheA mole ratios of 1:139 and 2:1.32
Materials and Methods
Materials
Membranes containing overexpressed S. typhimurium aspartate receptor (tar) were isolated from the E. coli strain RP3808 (Δ(cheA-cheZ)DE2209 tsr-1 leuB6 his-4 eda-50 rpsL136 [thi-1 Δ(gal-attl)DE99 ara-14 lacY1 mtl-1 xyl-5 tonA31 tsx-78]/mks/) provided by Dr John S. Parkinson, University of Utah.59 The materials used to express the S. typhimurium histidine kinase CheA (HB101/pMO4) and the S. typhimurium coupling protein CheW (HB101/pME5) were kindly provided by Dr Jeff Stock (Princeton University, Princeton, NJ).68,69 The E. coli CheY expression strain and plasmid (RBB455/pRBB40) were provided by the Drs Bob Bourret (University of North Carolina, Chapel Hill, NC), and Mel Simon (California Institute of Technology, Pasadena, CA).70 Radiolabeled enzyme substrate [γ-32P]ATP (6000 Ci/mmol) was purchased from NEN Lifesciences. tobacco etch virus (TEV) protease was obtained from Invitrogen.
The generation and expression of the modified receptors used in this study was performed as described.13 Briefly, engineered receptors were expressed from variants of the plasmid pSCF656 transformed into the E. coli strain RP3808, which lacks functional major chemotaxis receptors and the cytoplasmic chemotaxis components CheA, CheW, CheY, CheR, CheB, and CheZ. Preparation of native E. coli membrane fractions containing the overexpressed engineered receptors were carried out as described.53 The soluble chemotaxis components CheA, CheW, and CheY, were overexpressed and purified in E. coli as described.52 The concentration and purity of the engineered receptors in isolated membranes as well as soluble chemotaxis proteins was determined by means of BCA assay and quantification of protein band intensities following SDS-PAGE as described.23
Proteolysis assay
Kunkel mutagensis was utilized to replace residues 267–275 with the seven residue recognition sequence ENLYFQG in the QQQQ aspartate receptor modification state background as described.13 Sonicated native membrane preparations of the modified receptor were produced as described. TEV protease (ten units) was added to 150 μl of receptor vesicles containing 2.8 μM receptor and incubated in 50 mM Tris–HCl (pH 8.0), 0.5 mM EDTA at 23 °C. The reaction was quenched by the addition of SDS-PAGE buffer (10% (v/v) glycerol, 62.5 mM Tris–HCl (pH 6.8), 2% (w/v) SDS) and incubation for two minutes at 95 °C. Proteolysis of the receptor was assayed by SDS-PAGE. WT receptor was not digested upon incubation with TEV protease for one hour under these conditions.
In vitro activity assays
The reconstituted in vitro receptor-coupled kinase assay was performed as described but with the following modifications.13,23,43,44 To reconstitute the receptor kinase signaling complex a reaction mixture consisting of attractant (if included), the aspartate receptor in native membrane vesicles, as well as the purified cytoplasmic components (CheW, CheA, CheY), was incubated at ambient temperature (23(±1) °C) for one hour to allow for the complete formation of the ternary signaling complex. Unless indicated otherwise, the concentration of components used to determine the relative kinase activity and attractant affinity of the modified receptors as shown in Table 1 were 2 μM receptor, 2 μM CheW, 0.5 μM CheA and 10 μM CheY, where all protein concentrations are given in terms of a single subunit or monomer. All reactions were carried out at 22 °C in buffer containing 50 mM Tris–HCl (pH 7.5), 50 mM KCl, and 5 mM MgCl2. Each reaction was initiated by the addition of [γ-32P]ATP (diluted with cold ATP to a total concentration of 100 μM total ATP) to the reaction mixture and quenched after ten seconds incubation. The radiolabeled [32P]phospho-CheY was resolved by SDS-PAGE and quantified by phosphorimaging. The excess CheY present in these rate experiments was present in sufficiently high concentration to ensure that the rate-limiting step in phospho-CheY formation was the autophosphorylation of CheA. In each experiment, the ten second timepoint was found to be in the linear range of the [32P]phospho-CheY formation reaction even for the most superactivating receptors, indicating that this ten second timepoint could be used to determine the initial rate of the rate-determining CheA autophosphorylation step.23,56 Furthermore, titration of CheW concentration relative to the other chemotaxis components at concentrations of 2 μM receptor, 0.5 μM CheA and 10 μM CheY, revealed that kinase activity reached a maximum at approximately 2 μM CheW.
The apparent ligand-binding affinity, K1/2, of the receptor was determined using the ligand α-methyl-D,L-aspartate as described.13,23 This assay detects only those receptors in productive signaling complexes, thereby ensuring that the measured K1/2 arises from active receptors complexed with active CheA, CheW, and CheY molecules.
In experiments measuring the concentration-dependence of a reaction rate, a cooperative, multi-site Hill equation was used to best fit the rate versus concentration curve:
| (11) |
where R is the normalized receptor-regulated CheA kinase rate, is the maximal rate of kinase activation, m is the minimal CheA kinase activity (typically zero under standard conditions), [X] is the concentration of the component being varied, K1/2 is the concentration at which the receptor-coupled CheA kinase activity is half-maximal, and H is the Hill coefficient.
Data analysis and error determination
Modeling studies utilized Excel 2001 (Microsoft, Redmond, WA). Non-linear and linear best fits of data were carried out using Kaleidagraph 3.0 for Macintosh (Synergy Software, Reading, PA). Errors represent standard deviation for n ≥ 3.
Acknowledgments
We thank Rick Dahlquist for insightful discussions regarding the predictions of the two-state model. We also thank Howard Berg, Dennis Bray, Sandy Parkinson, Tom Shimizu, and Victor Sourjik for helpful conversations, the Parkinson laboratory for essential bacterial strains, and Victor Sourjik and Howard Berg for discussions of unpublished data. Finally, we are grateful to Matt Trammell, Noah White, and Katrina Eike for technical assistance. This work was supported by NIH Grant GM R01-40731 to J.J.F.
Abbreviations used
- L
the receptor ligand
- R1 and R2
the receptor low-activity and high-activity states, respectively
- KD1
the ligand dissociation constant for the receptor low-activity state 1
- KD2
the ligand dissociation constant for the receptor high-activity state 2
- K12
the equilibrium constant that defines the ratio of the two receptor state populations in the absence of ligand
the equilibrium constant that defines the ratio of the two receptor state populations in the presence of saturating ligand
- F1
the fractional receptor population in low-activity state 1
- F2
the fractional receptor population in high-activity state 2
- V1
the output signal (such as kinase velocity) produced by the receptor low-activity state 1
- V2
the output signal (such as kinase velocity) produced by the receptor high-activity state 2
- K1/2
the concentration of ligand that gives half-maximal signal output (such as kinase activity) in an attractant dose-response curve
the asymptotic kinase velocity exhibited by the aspartate receptor signaling complex in the absence of attractant, relative to the asymptotic velocity observed for the wild-type receptor (QEQE) utilizing standard assay conditions
the asymptotic kinase velocity exhibited by the aspartate receptor signaling complex in the absence of attractant at saturating levels of receptor or kinase
the fractional population of the aspartate receptor signaling complex in state 2, the high-activity state, in the absence of attractant
the fractional receptor population of the aspartate receptor signaling complex in state 2, the high-activity state, in the absence of attractant at saturating levels of receptor or kinase
the apparent dissociation constant for assembly of the aspartate receptor signaling complex
- BCA
bicinchoninic acid
- TEV
tobacco etch virus
Appendix
Determination of best-fit values for KD1 and KD2. Although the KD1 and KD2 of the receptor are not known, estimates can be made for their values. Like the plot of K1/2 versus (Figure 4(A) of the main text) for the experimentally determined values of the receptor modification states the plot of K1/2 versus K12 is linear when calculated using a V2 value of 5.5 (data not shown). The error-weighted linear best-fit plot of K1/2 versus K12 has a Y-intercept of 4 μM. This value can be used as an estimate of ligand binding affinity of the inactive state (KD1), since when K12 = 0 the receptor is completely in the inactive state. The estimated KD1 value (4 μM) is lower than the lowest K1/2 value (9 μM) measured for the receptor modification states, as is expected for the completely inactive state. To date, the highest K1/2 value measured for a superactivating receptor modification that can be almost completely downregulated by attractant is 150 μM for A387C in the QQQQ background.A1 As this superactive modified receptor is believed to be almost completely in the activated state, the value of 150 μM serves as a lower limit estimation of the value of KD2.
- A1.Bornhorst JA, Falke JJ. Evidence that both ligand binding and covalent adaptation drive a two-state equilibrium in the aspartate receptor signaling complex. J Gen Physiol. 2001;118:693–710. doi: 10.1085/jgp.118.6.693. [DOI] [PMC free article] [PubMed] [Google Scholar]
References
- 1.Monod J, Wyman J, Changeux J. On the nature of allosteric transitions: a plausible model. J Mol Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 2.Colquhoun D. The relation between classical and cooperative models for drug action. In: Rang HP, editor. Drug Receptors A Symposium. University Park Press; London: 1972. pp. 149–181. [Google Scholar]
- 3.Leff P. The two-state model of receptor activation. Trends Pharmacol Sci. 1995;16:89–97. doi: 10.1016/s0165-6147(00)88989-0. [DOI] [PubMed] [Google Scholar]
- 4.Hall DA. Modeling the functional effects of allosteric modulators at pharmacological receptors: an extension of the two-state model of receptor activation. Mol Pharmacol. 2000;58:1412–1423. doi: 10.1124/mol.58.6.1412. [DOI] [PubMed] [Google Scholar]
- 5.Volkman BF, Lipson D, Wemmer DE, Kern D. Two-state allosteric behavior in a single-domain signaling protein. Science. 2001;291:2429–2433. doi: 10.1126/science.291.5512.2429. [DOI] [PubMed] [Google Scholar]
- 6.Strange PG. G-protein coupled receptors: conformations and states. Biochem Pharmacol. 1999;58:1081–1088. doi: 10.1016/s0006-2952(99)00144-6. [DOI] [PubMed] [Google Scholar]
- 7.Eghbali M, Curmi JP, Birnir B, Gage PW. Hippocampal GABA(A) channel conductance increased by diazepam. Nature. 1997;388:71–75. doi: 10.1038/40404. [DOI] [PubMed] [Google Scholar]
- 8.Ruiz ML, Karpen JW. Single cyclic nucleotide-gated channels locked in different ligand-bound states. Nature. 1997;389:389–392. doi: 10.1038/38744. [DOI] [PubMed] [Google Scholar]
- 9.Rosenmund C, Stern-Bach Y, Stevens CF. The tetrameric structure of a glutamate receptor channel. Science. 1998;280:1596–1599. doi: 10.1126/science.280.5369.1596. [DOI] [PubMed] [Google Scholar]
- 10.Keynes RD, Elinder F. The screw-helical voltage gating of ion channels. Proc Roy Soc Lond. 1999;266:843–852. doi: 10.1098/rspb.1999.0714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gether U. Uncovering molecular mechanisms involved in activation of G protein-coupled receptors. Endocr Rev. 2000;21:90–113. doi: 10.1210/edrv.21.1.0390. [DOI] [PubMed] [Google Scholar]
- 12.Asakura S, Honda H. Two-state model for bacterial chemoreceptor proteins. The role of multiple methylation. J Mol Biol. 1984;176:349–367. doi: 10.1016/0022-2836(84)90494-7. [DOI] [PubMed] [Google Scholar]
- 13.Bornhorst JA, Falke JJ. Evidence that both ligand binding and covalent adaptation drive a two-state equilibrium in the aspartate receptor signaling complex. J Gen Physiol. 2001;118:693–710. doi: 10.1085/jgp.118.6.693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Stock AM, Robinson VL, Goudreau PN. Two-component signal transduction. Annu Rev Biochem. 2000;69:183–215. doi: 10.1146/annurev.biochem.69.1.183. [DOI] [PubMed] [Google Scholar]
- 15.Bourret RB, Stock AM. Molecular information processing: lessons from bacterial chemotaxis. J Biol Chem. 2002;277:9625–9628. doi: 10.1074/jbc.R100066200. [DOI] [PubMed] [Google Scholar]
- 16.Falke JJ, Hazelbauer GL. Transmembrane signaling in bacterial chemoreceptors. Trends Biochem Sci. 2001;26:257–265. doi: 10.1016/s0968-0004(00)01770-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Falke JJ, Bass RB, Butler SL, Chervitz SA, Danielson MA. The two-component signaling pathway of bacterial chemotaxis: a molecular view of signal transduction by receptors, kinases, and adaptation enzymes. Annu Rev Cell Dev Biol. 1997;13:457–512. doi: 10.1146/annurev.cellbio.13.1.457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Armitage JP. Bacterial tactic responses. Advan Microb Physiol. 1999;41:229–289. doi: 10.1016/s0065-2911(08)60168-x. [DOI] [PubMed] [Google Scholar]
- 19.Wurgler-Murphy SM, Saito H. Two-component signal transducers and MAPK cascades. Trends Biochem Sci. 1997;22:172–176. doi: 10.1016/s0968-0004(97)01036-0. [DOI] [PubMed] [Google Scholar]
- 20.Swanson RV, Simon MI. Signal transduction. Bringing the eukaryotes up to speed. Curr Biol. 1994;4:234–237. doi: 10.1016/s0960-9822(00)00052-x. [DOI] [PubMed] [Google Scholar]
- 21.Le Moual H, Koshland DE., Jr Molecular evolution of the C-terminal cytoplasmic domain of a superfamily of bacterial receptors involved in taxis. J Mol Biol. 1996;261:568–585. doi: 10.1006/jmbi.1996.0483. [DOI] [PubMed] [Google Scholar]
- 22.Kim KK, Yokota H, Kim SH. Four-helical-bundle structure of the cytoplasmic domain of a serine chemotaxis receptor. Nature. 1999;400:787–792. doi: 10.1038/23512. [DOI] [PubMed] [Google Scholar]
- 23.Bornhorst JA, Falke JJ. Attractant regulation of the aspartate receptor-kinase complex: limited cooperative interactions between receptors and effects of the receptor modification state. Biochemistry. 2000;39:9486–9493. doi: 10.1021/bi0002737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Falke JJ. Cooperativity between bacterial chemotaxis receptors. Proc Natl Acad Sci USA. 2002;99:6530–6532. doi: 10.1073/pnas.112214199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ames P, Studdert CA, Reiser RH, Parkinson JS. Collaborative signaling by mixed chemoreceptor teams in Escherichia coli. Proc Natl Acad Sci USA. 2002;99:7060–7065. doi: 10.1073/pnas.092071899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Le Moual H, Quang T, Koshland DE., Jr Methylation of the Escherichia coli chemotaxis receptors: intra- and interdimer mechanisms. Biochemistry. 1997;36:13441–13448. doi: 10.1021/bi9713207. [DOI] [PubMed] [Google Scholar]
- 27.Maddock JR, Shapiro L. Polar location of the chemoreceptor complex in the Escherichia coli cell. Science. 1993;259:1717–1723. doi: 10.1126/science.8456299. [DOI] [PubMed] [Google Scholar]
- 28.Lybarger SR, Maddock JR. Polarity in action: asymmetric protein localization in bacteria. J Bacteriol. 2001;183:3261–3267. doi: 10.1128/JB.183.11.3261-3267.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Li J, Li G, Weis RM. The serine chemoreceptor from Escherichia coli is methylated through an inter-dimer process. Biochemistry. 1997;36:11851–11857. doi: 10.1021/bi971510h. [DOI] [PubMed] [Google Scholar]
- 30.Sourjik V, Berg HC. Localization of components of the chemotaxis machinery of Escherichia coli using fluorescent protein fusions. Mol Microbiol. 2000;37:740–751. doi: 10.1046/j.1365-2958.2000.02044.x. [DOI] [PubMed] [Google Scholar]
- 31.Li G, Weis RM. Covalent modification regulates ligand binding to receptor complexes in the chemosensory system of Escherichia coli. Cell. 2000;100:357–365. doi: 10.1016/s0092-8674(00)80671-6. [DOI] [PubMed] [Google Scholar]
- 32.Shimizu TS, Le Novere N, Levin MD, Beavil AJ, Sutton BJ, Bray D. Molecular model of a lattice of signalling proteins involved in bacterial chemotaxis. Nature Cell Biol. 2000;2:792–796. doi: 10.1038/35041030. [DOI] [PubMed] [Google Scholar]
- 33.Bray D. Bacterial chemotaxis and the question of gain. Proc Natl Acad Sci USA. 2002;99:7–9. doi: 10.1073/pnas.022641699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Stock J. Sensitivity, cooperativity and gain in chemotaxis signal transduction. Trends Microbiol. 1999;7:1–4. doi: 10.1016/s0966-842x(98)01429-2. [DOI] [PubMed] [Google Scholar]
- 35.Duke TA, Bray D. Heightened sensitivity of a lattice of membrane receptors. Proc Natl Acad Sci USA. 1999;96:10104–10108. doi: 10.1073/pnas.96.18.10104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bray D, Levin MD, Morton-Firth CJ. Receptor clustering as a cellular mechanism to control sensitivity. Nature. 1998;393:85–88. doi: 10.1038/30018. [DOI] [PubMed] [Google Scholar]
- 37.Shi Y. Effects of thermal fluctuation and the receptor-receptor interaction in bacterial chemotactic signaling and adaptation. Phys Rev ser E. 2001;64:021910. doi: 10.1103/PhysRevE.64.021910. [DOI] [PubMed] [Google Scholar]
- 38.Gestwicki JE, Kiessling LL. Inter-receptor communication through arrays of bacterial chemoreceptors. Nature. 2002;415:81–84. doi: 10.1038/415081a. [DOI] [PubMed] [Google Scholar]
- 39.Gegner JA, Graham DR, Roth AF, Dahlquist FW. Assembly of an MCP receptor, CheW, and kinase CheA complex in the bacterial chemotaxis signal transduction pathway. Cell. 1992;70:975–982. doi: 10.1016/0092-8674(92)90247-a. [DOI] [PubMed] [Google Scholar]
- 40.Schuster SC, Swanson RV, Alex LA, Bourret RB, Simon MI. Assembly and function of a quaternary signal transduction complex monitored by surface plasmon resonance. Nature. 1993;365:343–347. doi: 10.1038/365343a0. [DOI] [PubMed] [Google Scholar]
- 41.Liu Y, Levit M, Lurz R, Surette MG, Stock JB. Receptor-mediated protein kinase activation and the mechanism of transmembrane signaling in bacterial chemotaxis. EMBO J. 1997;16:7231–7240. doi: 10.1093/emboj/16.24.7231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Levit MN, Grebe TW, Stock JB. Organization of the receptor-kinase signaling array that regulates Escherichia coli chemotaxis. J Biol Chem. 2002;277:36748–36754. doi: 10.1074/jbc.M204317200. [DOI] [PubMed] [Google Scholar]
- 43.Borkovich KA, Kaplan N, Hess JF, Simon MI. Transmembrane signal transduction in bacterial chemotaxis involves ligand-dependent activation of phosphate group transfer. Proc Natl Acad Sci USA. 1989;86:1208–1212. doi: 10.1073/pnas.86.4.1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ninfa EG, Stock A, Mowbray S, Stock J. Reconstitution of the bacterial chemotaxis signal transduction system from purified components. J Biol Chem. 1991;266:9764–9770. [PubMed] [Google Scholar]
- 45.Barak R, Eisenbach M. Correlation between phosphorylation of the chemotaxis protein CheY and its activity at the flagellar motor [published erratum appears in Biochemistry 1992 May 19;31(19):4736] Biochemistry. 1992;31:1821–1826. doi: 10.1021/bi00121a034. [DOI] [PubMed] [Google Scholar]
- 46.Borkovich KA, Alex LA, Simon MI. Attenuation of sensory receptor signaling by covalent modification. Proc Natl Acad Sci USA. 1992;89:6756–6760. doi: 10.1073/pnas.89.15.6756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Terwilliger TC, Koshland DE., Jr Sites of methyl esterification and deamination on the aspartate receptor involved in chemotaxis. J Biol Chem. 1984;259:7719–7725. [PubMed] [Google Scholar]
- 48.Park C, Dutton DP, Hazelbauer GL. Effects of glutamines and glutamates at sites of covalent modification of a methyl-accepting transducer. J Bacteriol. 1990;172:7179–7187. doi: 10.1128/jb.172.12.7179-7187.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Dunten P, Koshland DE., Jr Tuning the responsiveness of a sensory receptor via covalent modification. J Biol Chem. 1991;266:1491–1496. [PubMed] [Google Scholar]
- 50.Blair DF. How bacteria sense and swim. Annu Rev Microbiol. 1995;49:489–522. doi: 10.1146/annurev.mi.49.100195.002421. [DOI] [PubMed] [Google Scholar]
- 51.Murphy OJ, III, Yi X, Weis RM, Thompson LK. Hydrogen exchange reveals a stable and expandable core within the aspartate receptor cytoplasmic domain. J Biol Chem. 2001;276:43262–43269. doi: 10.1074/jbc.M105585200. [DOI] [PubMed] [Google Scholar]
- 52.Danielson MA, Bass RB, Falke JJ. Cysteine and disulfide scanning reveals a regulatory alpha-helix in the cytoplasmic domain of the aspartate receptor. J Biol Chem. 1997;272:32878–32888. doi: 10.1074/jbc.272.52.32878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Bass RB, Falke JJ. Detection of a conserved alpha-helix in the kinase-docking region of the aspartate receptor by cysteine and disulfide scanning. J Biol Chem. 1998;273:25006–25014. doi: 10.1074/jbc.273.39.25006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Bass RB, Coleman MD, Falke JJ. Signaling domain of the aspartate receptor is a helical hairpin with a localized kinase docking surface: cysteine and disulfide scanning studies. Biochemistry. 1999;38:9317–9327. doi: 10.1021/bi9908179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Chervitz SA, Falke JJ. Lock on/off disulfides identify the transmembrane signaling helix of the aspartate receptor. J Biol Chem. 1995;270:24043–24053. doi: 10.1074/jbc.270.41.24043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Chervitz SA, Lin CM, Falke JJ. Transmembrane signaling by the aspartate receptor: engineered disulfides reveal static regions of the subunit interface. Biochemistry. 1995;34:9722–9733. doi: 10.1021/bi00030a010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Sackett DL, Saroff HA. The multiple origins of cooperativity in binding to multi-site lattices. FEBS Letters. 1996;397:1–6. doi: 10.1016/s0014-5793(96)01020-4. [DOI] [PubMed] [Google Scholar]
- 58.Sourjik V, Berg HC. Receptor sensitivity in bacterial chemotaxis. Proc Natl Acad Sci USA. 2002;99:123–127. doi: 10.1073/pnas.011589998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Liu JD, Parkinson JS. Role of CheW protein in coupling membrane receptors to the intracellular signaling system of bacterial chemotaxis. Proc Natl Acad Sci USA. 1989;86:8703–8707. doi: 10.1073/pnas.86.22.8703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Liu JD, Parkinson JS. Genetic evidence for interaction between the CheW and Tsr proteins during chemoreceptor signaling by Escherichia coli. J Bacteriol. 1991;173:4941–4951. doi: 10.1128/jb.173.16.4941-4951.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Surette MG, Levit M, Liu Y, Lukat G, Ninfa EG, Ninfa A, Stock JB. Dimerization is required for the activity of the protein histidine kinase CheA that mediates signal transduction in bacterial chemotaxis. J Biol Chem. 1996;271:939–945. doi: 10.1074/jbc.271.2.939. [DOI] [PubMed] [Google Scholar]
- 62.Beel BD, Hazelbauer GL. Signalling substitutions in the periplasmic domain of chemoreceptor Trg induce or reduce helical sliding in the transmembrane domain. Mol Microbiol. 2001;40:824–834. doi: 10.1046/j.1365-2958.2001.02446.x. [DOI] [PubMed] [Google Scholar]
- 63.Morton-Firth CJ, Shimizu TS, Bray D. A free-energy-based stochastic simulation of the Tar receptor complex. J Mol Biol. 1999;286:1059–1074. doi: 10.1006/jmbi.1999.2535. [DOI] [PubMed] [Google Scholar]
- 64.Barkai N, Leibler S. Robustness in simple biochemical networks. Nature. 1997;387:913–917. doi: 10.1038/43199. [DOI] [PubMed] [Google Scholar]
- 65.Alon U, Surette MG, Barkai N, Leibler S. Robustness in bacterial chemotaxis. Nature. 1999;397:168–171. doi: 10.1038/16483. [DOI] [PubMed] [Google Scholar]
- 66.Yi TM, Huang Y, Simon MI, Doyle J. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc Natl Acad Sci USA. 2000;97:4649–4653. doi: 10.1073/pnas.97.9.4649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Bilwes AM, Alex LA, Crane BR, Simon MI. Structure of CheA, a signal-transducing histidine kinase. Cell. 1999;96:131–141. doi: 10.1016/s0092-8674(00)80966-6. [DOI] [PubMed] [Google Scholar]
- 68.Stock A, Mottonen J, Chen T, Stock J. Identification of a possible nucleotide binding site in CheW, a protein required for sensory transduction in bacterial chemotaxis. J Biol Chem. 1987;262:535–537. [PubMed] [Google Scholar]
- 69.Stock A, Chen T, Welsh D, Stock J. CheA protein, a central regulator of bacterial chemotaxis, belongs to a family of proteins that control gene expression in response to changing environmental conditions. Proc Natl Acad Sci USA. 1988;85:1403–1407. doi: 10.1073/pnas.85.5.1403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Bourret RB, Drake SK, Chervitz SA, Simon MI, Falke JJ. Activation of the phospho-signaling protein CheY. II. Analysis of activated mutants by 19F NMR and protein engineering. J Biol Chem. 1993;268:13089–13096. [PMC free article] [PubMed] [Google Scholar]