Bacterial ratchet motors

Abstract

Self-propelling bacteria are a nanotechnology dream. These unicellular organisms are not just capable of living and reproducing, but they can swim very efficiently, sense the environment, and look for food, all packaged in a body measuring a few microns. Before such perfect machines can be artificially assembled, researchers are beginning to explore new ways to harness bacteria as propelling units for microdevices. Proposed strategies require the careful task of aligning and binding bacterial cells on synthetic surfaces in order to have them work cooperatively. Here we show that asymmetric environments can produce a spontaneous and unidirectional rotation of nanofabricated objects immersed in an active bacterial bath. The propulsion mechanism is provided by the self-assembly of motile Escherichia coli cells along the rotor boundaries. Our results highlight the technological implications of active matter’s ability to overcome the restrictions imposed by the second law of thermodynamics on equilibrium passive fluids.

The modern nanofabrication tools allow us to shape matter with nanometer resolution. However, we usually have to resort to external driving fields when it comes to actuating microdevices. The possibility of producing all-in-one, self-propelled microdevices requires the availability of micromotors that include all that is needed for propulsion in a few picoliters of volume. Motile bacteria are a beautiful example of self-propelling “machines” all packaged in less than a femtoliter. The possibility of harnessing bacterial power opens up interesting ways to generate motion at the micron scale. Pioneering work in this field has been carried out in the past demonstrating the possibility of propelling microstructures by permanently attaching a layer of motile bacteria (“bacterial carpet”) on the surfaces of various synthetic objects like latex beads (1) or polydimethylsiloxane structures (2). Phototactic control of such bacterial-actuated structures has been recently demonstrated (3, 4) by exposing localized regions of the swarm to ultraviolet light. It has also been shown that motile bacteria can be permanently attached on patterned microbeads resulting in random walks having diffusion coefficients larger than thermal ones (5). A common drawback of the previous approaches is that the resulting motions are random and unpredictable, reflecting the chaotic dynamics of propelling bacteria. External fields, such as optical or magnetic (6), are usually required whenever a unidirectional and controllable motion is needed. But can we conceive a totally autonomous microdevice that is propelled by bacteria in a predictable motion with no need for external controlling fields? Or, in other words, can bacteria spontaneously rectify their random motions and cooperatively work on the same task? Such questions are inevitably connected with the more fundamental problem of what the necessary conditions are for the emergence of an ordered behavior by a self-organization mechanism. Symmetries play a fundamental role in this sense. As already recognized by Curie (7), reproducible asymmetric effects always need corresponding asymmetric causes to occur. If such an asymmetry does not exist, the phenomenon is impossible. The phenomenon we aim to produce is a long run, unidirectional rotation around a fixed symmetry axis z, of a microfabricated system immersed in a bacterial bath. Such a phenomenon breaks three main symmetries: (i) time reversal, (ii) mirror reflection σ_v through a plane containing the axis of rotation z, and (iii) a rotation of 180° around an axis perpendicular to z that is also equivalent to the two subsequent mirror reflections σ_vσ_h respectively through a plane containing the symmetry axis z and a plane perpendicular to it. In other words, a rotary motor that looked at from above spins in a given direction (i.e., clockwise) would spin in the opposite direction (i.e., counterclockwise) when looked: (i) at backward in time, (ii) at reflected in a mirror containing the rotation axis, or (iii) from the bottom side. If our device looks symmetric under at least one of the above transformations, there is no hope for it to spontaneously break that symmetry in a predictable and reproducible way. Breaking time reversal symmetry necessarily requires that our system is out of equilibrium. Suspensions of self-propelling bacteria can be viewed as a class of strongly nonequilibrium fluids, often referred to as active matter (8–12). Though at a first look bacterial motions resemble the chaotic kinetic dynamics of molecules in a gas, the underlying dynamics is intrinsically irreversible. The constant action of the flagellar rotary motor results in a propelling force pushing the cell body against the fluid drag force. Such propelling forces act as a nonconservative external force field resulting in a dynamics that is not symmetrical under time reversal. In particular, Escherichia coli cells are propelled by thin helical filaments driven by bidirectional rotary motors embedded in the cell wall (13–15). When all motors rotate counterclockwise (when looked at from behind), the cell body is propelled in an almost linear run. Forward runs are intercalated by randomly distributed tumble events, during which one or more motors start rotating clockwise, unbundling flagella and causing a random reorientation of the cell body. The chiral nature of flagellar propulsion clearly breaks symmetry under mirror reflections σ_v and σ_h but not their combination σ_vσ_h. This last symmetry has to be explicitly broken by appropriately designing a device with a proper asymmetric geometry.

Here we propose a few designs for nanofabricated devices that, by breaking the σ_vσ_h symmetry, can be driven in a directional and reproducible rotation by the self-organization of bacteria.

Results and Discussion

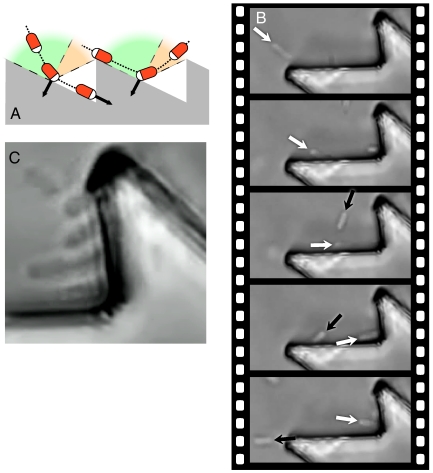
A first simple design is that of a rotating micro saw-toothed disk having an external diameter of 48 μm and 10-μm thickness (type I in Fig. 1). It is evident that such a structure breaks both σ_v and σ_vσ_h symmetries so that no other symmetry would prevent unidirectional rotation when immersed in an out of equilibrium bacterial bath, even if using achiral motile cells such as spermatozoa. Low aspect ratio, quasi-planar shapes are easily fabricated from SU-8 resist by using optical lithography. The gears are then dispersed in a bacterial suspension of E. coli cells in a motility buffer. A drop of the resulting suspension hangs from the concave part of a glass slide, leaving an air gap between the liquid suspension and the bottom coverslip (Fig. S1). Gears then sediment on that liquid–air interface where they are free from strong adhesion to solid surfaces. Interactions between cells and object boundaries are well described by a repulsive contact force directed along the surface normal. As a consequence, when a swimming cell hits a wall, it aligns and slides parallel to it in a direction determined by its incoming angle (Fig. 2 A and B and Movie S1). Cells sliding towards a concave corner get stuck and start pushing until a tumbling event occurs, reorienting the cell and eventually setting it free to swim back into the solution. Bacteria that got stuck at a corner are observed to remain in a “locked” pushing configuration for a time interval varying from a few seconds up to a couple of minutes. In a concentrated suspension of bacteria, wall interactions and intercellular repulsion lead to local packing and ordering of bacteria at concave corners (Fig. 2C). When the concentration reaches a value of about 10¹⁰ bacteria/mL, the cooperative action of rectified bacteria results in a total torque that is large enough to rotate the microgear at an average rotation frequency of about 1 rpm. Lying on a liquid–air interface, half of the bulk drag force acting from the bottom surface is negligible so that the torque exerted on the gear can be estimated assuming a rotational drag coefficient that is twice that of a disk suspended in bulk buffer solution:

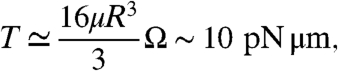[1]

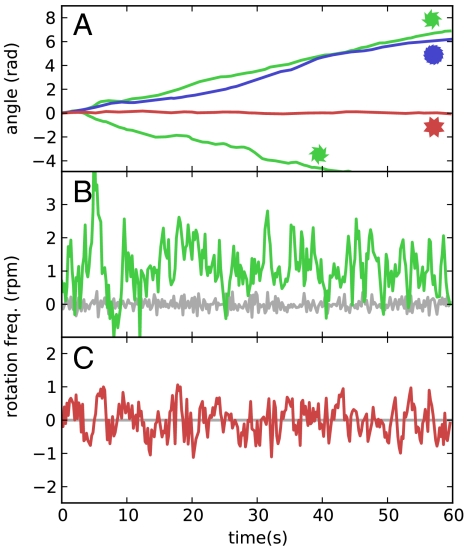
where μ is the buffer viscosity and R = 20 μm is an average gear radius. We have filmed our rotary motor for 1 min (Fig. 3 and Movie S2) and extracted angular velocity and rotation angle as a function of time (Fig. 4) by using a custom-made video tracking routine. Fig. 4A shows a comparison between the angular motions of asymmetric (type I) and symmetric type II gears in a bacterial bath. It is important to note that the presence of a liquid–gas boundary already breaks σ_h and hence σ_hσ_v symmetry. Although symmetric gears could then spin, without involving any symmetry breaking, they are observed only to fluctuate with a negligible average rotation angle. Fluctuations are better appreciated in angular velocity plots Fig. 4 B and C. Asymmetric and symmetric gears display quite large and comparable fluctuations in angular velocities because of fluctuations in the number and local arrangement of bacteria on the boundaries. An asymmetric gear in a bacteria-free buffer fluctuates much less as shown by the gray line in Fig. 4B. Both mean velocities and fluctuations resemble very closely the predictions of molecular dynamics simulations (16). The swimming velocity of a single bacterium provides the maximum achievable linear rotation of the microgear edge. At higher rotation rates bacteria would not be able to catch up to the moving walls. In our case the linear speed of the edge is only 2.5 μm/s whereas bacteria swim at approximately 20 μm/s. This observation leaves a large margin of improvement on the achievable rotation rates. Asymmetric gears can sediment in two different orientations that are observed to spin in opposite directions. All these observations exclude the possibility that rotation could be because of circular swimming of bacteria close to interfaces. Bacterial adhesion to microgears seems to be negligible as can be observed in Movie S1. The original movie lasts for much longer, and pushing bacteria are observed to swim away from the boundary even after several minutes of contact. In the course of time, nutrients decrease whereas the concentration of metabolic by-products increases. Bacteria will slowly lose their motility and eventually die. Other phenomena like bacteria clustering or biofilm formation set a limit to the durability of bacteria-propelled devices. Although one could think of strategies to delay such processes, a finite lifetime is the price we always have to pay when aiming at a self-contained micromotor that does not rely on external power sources.

Fig. 1.

Gear shapes. Optical microscopy images of microfabricated gears suspended in water. A SEM image of type I gear is also shown in B.

Fig. 2.

Rectifying bacterial motions with asymmetric boundaries. (A) A pictorial representation of the mechanism through which the asymmetric shape of the inclined teeth induces spontaneous alignment and locking of self-propelled bacteria in the concave corners. Bacteria are drawn with a white head pointing in the direction of self-propulsion. Black arrows represent the forces exerted by bacteria on the walls. Equal and opposite reaction forces reorient the cell body along the wall. (B) Two E. coli cells interacting with gear boundaries. The cell pointed out by the white arrow aligns parallel to the wall and slides towards the corner where it gets stuck, contributing a torque. The other one, pointed out by the black arrow, aligns along the wall and slides back into the bulk solution. See also Movie S1. (C) Four bacterial cells spontaneously align and cooperatively push in the same direction against the wall.

Fig. 3.

Bacterial driven micromotor. A nanofabricated asymmetric gear (48-μm external diameter, 10-μm thickness) rotates clockwise at 1 rpm when immersed in an active bath of motile E. coli cells, visible in the background. The gear is sedimented at a liquid–air interface to reduce friction. The yellow circle points to a black spot on the gear that can be used for visual angle tracking.

Fig. 4.

Analysis of rotational motion at a liquid–air interface. (A) Cumulative rotational angle of microgears in a bacterial bath. Green lines refer to type I asymmetric gears. The two gears have opposite orientations, resulting in opposite spinning directions. The blue line refers to a type III asymmetric gear with smaller teeth. No net rotation is observed for type II symmetric gears as shown by the red line. (B) Time fluctuations of rotational frequency for type I gear. Fluctuations around the nonzero mean value are because of randomness in bacterial number and local arrangement along the boundaries. The same gear in a bacteria-free buffer fluctuates much less as shown by the gray curve. (C) A symmetric type II gear in a bacterial bath fluctuates with an angular velocity of zero mean and a standard deviation comparable to the asymmetric case.

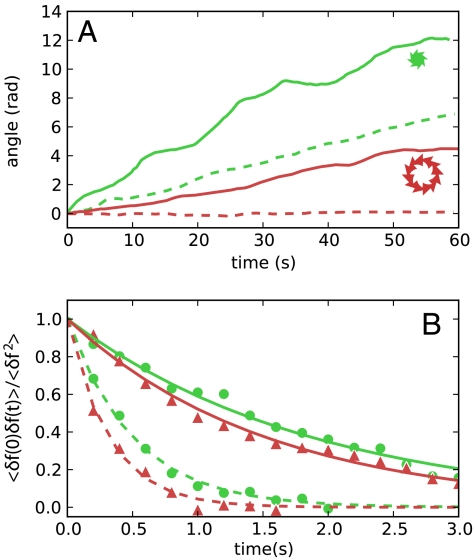
Gears of different geometry were also produced in order to investigate the role of shape. In particular, we tested another asymmetric gear having the same size of 48 μm but a larger number of teeth (type III in Fig. 1). We report in Fig. 4 the cumulative angle of one of the fastest spinning gears of this second geometry. Although large variations in angular speed may occur even within the same geometry and in the same bath, the better spinning type III gears rotate at about the same angular speed of type I. Large variations in rotational speed also make it hard to extract a quantitative concentration dependence. However, when going to densely packed suspensions (about 10¹¹ bacteria/mL), bacteria start to display large scale collective motions that enhance the rotational frequency of suspended gears. In particular, type I gears, in a 7 × 10¹⁰ bacteria/mL suspension, are observed to spin at 2 rpm, which is twice the speed observed in the lower concentration bath (Fig. 5A). Such a high concentration regime is also characterized by strong fluctuations in angular speed (or, equivalently, applied torque) that decay exponentially with a time constant of 1.9 s, which is 3.8 times longer than for the lower concentration (Fig. 5B).

Fig. 5.

Effect of bacterial concentration on rotational motion. (A) The green solid line is the cumulative rotational angle of a type I gear in a highly concentrated bacterial suspension (7 × 10¹⁰ bacteria/mL). As a comparison, we report as a dashed green line data for the same gear at a lower concentration (∼10¹⁰ bacteria/mL). By increasing the concentration, the average angular speed increases by about a factor of 2 but fluctuates much more. Solid and dashed red lines refer to the large type IV gears respectively in the higher and lower concentrations. (B) Time correlations of rotational speed fluctuations. Green disks refer to type I gears whereas red triangles to gears of type IV. Solid and dashed lines are exponential fits for, respectively, the higher and lower concentrations.

When moving to larger sizes, the torque is expected to increase as the size squared as both perimeter and moment arm increase with the size. On the other hand, the rotational mobility of the gear is expected to decrease as the inverse third power of the size. As a result, we expect a rotational speed decreasing as the inverse size. Therefore, when designing a larger gear (external diameter 80 μm) we tried to reduce the drag with a hole in the middle and to increase the torque by using a saw-toothed inner profile (type IV in Fig. 1). Such large gears were observed to spin only in a high bacterial concentration (7 × 10¹⁰ bacteria/mL), with an average rotational frequency of 0.7 rpm. On the basis of the above scaling argument, one would expect that type IV gears would spin at least at 1 rpm, which is half the speed of type I gear in the same bath. The lower value of the observed speed suggests that the size scaling of rotational frequencies could be more complicated than the simple argument provided above. On the other hand, fluctuations in angular speed decay on a time scale that depends on bacterial concentration rather than on gear size and therefore could be thought of as a characteristic property of the bacterial bath alone (Fig. 5B).

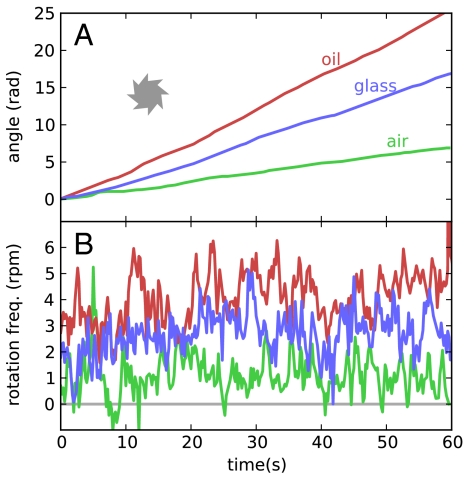
Watching microgears spontaneously rotating on a liquid–gas interface is an intriguing phenomenon, but it also looks hard to implement in a microfluidic device. We have started to investigate the behavior of rotary micromotors when sitting on a liquid–solid interface. The presence of a strongly perturbing interface, such as a solid boundary, already breaks σ_h and hence σ_vσ_h symmetry, so that we do not need to break that symmetry through the gears’ shape. This geometry results in a much stronger rectification mechanism, driving type I gears at a rotational frequency of 2.6 rpm, which is more than twice faster than that observed on a liquid–gas interface. The cumulative angle for an asymmetric gear spinning over a solid surface is reported in Fig. 6. In the same figure we also reported the rotation angle for a gear spinning over a liquid–oil interface. Although we used immersion oil, with a viscosity about 100 times larger than water, and therefore practically analogous to a solid surface in any hydrodynamic respect, we reached even higher rotational speeds (4 rpm) probably because of reduced friction (see Movie S3). Such a speed corresponds to a boundary moving at 10 μm/s, which is about half the maximum achievable speed with bacteria moving at 20 μm/s. As opposed to the case of a liquid–air interface, a strong clockwise (from above) rotation is observed even for symmetric gears or asymmetric gears of opposite orientation. We expect that such a mechanism is connected to the tendency of E. coli cells to swim along circular clockwise trajectories above a solid wall (17). It is worth noting that, on the basis of symmetry arguments, such a mechanism would be impossible if using achiral motile cells (i.e., spermatozoa) with symmetric gears because mirror symmetry σ_v would prevent the phenomenon.

Fig. 6.

Effect of boundary condition on rotational motion. (A) The blue (red) line is the cumulative rotational angle of a type I asymmetric gear spinning over a liquid–glass (liquid–oil) interface. As a comparison, we report as a green line data for the same gear on a liquid–air interface. (B) Time fluctuations of rotational frequency. Color coding is the same as in A.

When judged on the basis of the achievable torque, microelectromechanical systems technology will probably be superior to bacterial-driven motors. However, microelectromechanical systems devices need to be connected to external electrical power sources, and if we need a self-propelling motor of the size of a few tens of microns, we might have no other option than to use bacteria to convert biochemical energy into mechanical motion. A bacterial driven micromotor was previously achieved by forcing the unidirectional gliding of bacteria along circular tracks by a careful chemical patterning of microstructures (18, 19). A microrotor was then docked on the microtrack and observed to rotate unidirectionally at about 2 rpm. Our approach is fundamentally different, relying on a self-organization mechanism. We demonstrate that the underlying off-equilibrium nature of a bacterial bath allows one to rectify the chaotic motions of bacteria by geometry alone. Once the microstructures are fabricated with a proper asymmetric shape, no further chemical patterning or externally induced taxis is needed to produce a directional and predictable motion.

The idea that, in nonequilibrium states, a directional motion can arise from the chaotic dynamics of small molecules was first put forward by Feynman in his famous “ratchet and pawl” thought experiment (20). The combination of asymmetry and nonequilibrium was soon recognized to be at the origin of the “ratchet effect,” opening the way to the stimulating concept of Brownian motors in physical and biological contexts (21). Many ways have been considered to drive a system out of thermal equilibrium, such as cycling temperature or applying time-dependent external fields (22). Our experiment demonstrates an intriguing realization of a ratchet mechanism, where bacteria can be thought of as intrinsically off-equilibrium “molecules.” Asymmetric environments can be used to break the remaining spatial symmetries and allow the emergence of an ordered, reproducible motion that could serve as the driving mechanism for completely autonomous, self-propelling microdevices. Applications at the micrometer scale, such as self-propelling micromachines or pumps and mixers for microfluidics, are the most promising, but it will also be important to answer the question whether bacterial motors are confined to the microworld, or we can think of a macroscopic exploitation of bacteria as mechanical power sources.

Materials and Methods

Gear Microfabrication.

A pattern of 100 × 100 microgears was written by e-beam lithography onto a glass-chromium substrate, coated by electron-resist [polymethyl methacrylate (PMMA)]. The exposure dose is 320 mJ/cm². After resist development and selective chromium wet etching, a negative pattern of 10,000 gears was obtained on the glass mask. A silicon substrate is coated by a bilayer of 50 nm PMMA (as sacrificial layer) and 15 μm SU-8 negative resist. A pattern of target objects is written on the sample by UV lithography by using an exposure density power of 22 mW/cm². After optical lithography the structures are still attached onto the PMMA sacrificial layer, which can be removed by rinsing and sonicating the whole sample in acetone. Microgears are finally sedimented by centrifugation and resuspended in water.

Cell Growth.

E. coli (MG1655) strain was grown at 33 °C in tryptone broth (TB; Difco) containing 1% tryptone and 0.5% NaCl. The saturated culture was then diluted 1∶100 into fresh medium and grown for 3.5 h at 33 °C until OD₆₀₀ = 0.4 was reached, corresponding to a middle-log phase. Bacterial cells were harvested from culture media by centrifugation at 2,200 rpm for 10 min at room temperature, and the pellet was resuspended by gently mixing in prewarmed motility buffer [10 mM potassium phosphate, 0.1 mM Na-EDTA (pH 7.0), 76 mM NaCl, and 0.002% Tween 20 (23)]. This process was repeated three times to achieve growth medium depletion and a suitable final bacteria concentration.