Independent filtering increases detection power for high-throughput experiments

Abstract

With high-dimensional data, variable-by-variable statistical testing is often used to select variables whose behavior differs across conditions. Such an approach requires adjustment for multiple testing, which can result in low statistical power. A two-stage approach that first filters variables by a criterion independent of the test statistic, and then only tests variables which pass the filter, can provide higher power. We show that use of some filter/test statistics pairs presented in the literature may, however, lead to loss of type I error control. We describe other pairs which avoid this problem. In an application to microarray data, we found that gene-by-gene filtering by overall variance followed by a t-test increased the number of discoveries by 50%. We also show that this particular statistic pair induces a lower bound on fold-change among the set of discoveries. Independent filtering—using filter/test pairs that are independent under the null hypothesis but correlated under the alternative—is a general approach that can substantially increase the efficiency of experiments.

In many experimental contexts which generate high-dimensional data, variable-by-variable statistical testing is used to select variables whose behavior differs across the set of studied conditions. Each variable is associated with a null hypothesis which asserts that behavior for that variable does not differ across conditions. A null hypothesis is rejected when observed data, summarized into a per-variable p-value, are deemed to be inconsistent with the hypothesis. In biology, for example, microarrays or high-throughput sequencing may be used to identify genes (variables) whose expression level shows systematic covariation with a treatment or phenotype of interest. The evidence for such covariation is assessed by applying a statistical test to each gene separately. In the case of microarrays, gene-by-gene t-tests are frequently used for two-class comparisons. This approach can be generalized to more complex experimental designs through the use of ANOVA (1); it has also been refined for experiments with small sample sizes by the introduction of moderated variance estimators (2), as in the SAM (3) and limma (4) software. When transcript abundance is measured by high-throughput sequencing rather than microarrays, gene-level p-values may instead be computed on the basis of gene-level read count statistics (5).

Because a large number of hypothesis tests are performed in such variable-by-variable analyses, many true-null hypotheses will produce small p-values by chance. As a consequence, numerous false positives, or type I errors, will result if p-values are compared to standard single-test thresholds. There are well-established procedures which address the multiple testing problem by adjusting the p-values to control various experiment-wide false positive measures, e.g., the family-wise error rate (FWER) or the false discovery rate (FDR). (See ref. 6 for a review).

Multiple testing adjustment provides control over the extent to which false positives occur, but such control comes at the cost of reduced power to detect true positives. Further, this power reduction worsens as more hypotheses are tested. Typically, the number of genes represented on a microarray is in the tens of thousands, while the number of differentially expressed genes may be only a few dozen or hundred. As a consequence, the power of an experiment to detect a given differentially expressed gene could potentially be quite low.

In the microarray literature, several authors have suggested filtering to reduce the impact that multiple testing adjustment has on detection power (7–12). Conceptually similar screening approaches have also been proposed for variable selection in high-dimensional regression models (13, 14). In filtering for microarray applications, the data are first used to identify and remove a set of genes which seem to generate uninformative signal. Second, formal statistical testing is applied only to genes which pass the filter. An effective filter will enrich for true differential expression while simultaneously reducing the number of hypotheses tested at stage two—making multiple testing adjustment less severe. Such filtering is further motivated by the observation that the set of genes which are not differentially expressed can be partitioned into two groups: (i) genes that are not expressed in any of the conditions of the experiment or whose reporters on the array lack sensitivity to detect their expression; and (ii) genes that are expressed and detectable, but not differentially expressed across conditions.

This two-stage approach, the use of which need not be restricted to gene expression applications, assesses each variable on the basis of both a filter statistic (U^I) and a test statistic (U^II). Both statistics are required to exceed their respective cutoffs. Note, however, that the two-stage approach is not equivalent to standard hypothesis testing based on the joint distribution of the filter and test statistics: the latter uses a joint null distribution to compute type I error rate, while the former only considers the null distribution of the stage-two test statistic.

Some authors specifically recommend using nonspecific or unsupervised filters which do not make use of sample class labels, and they suggest that nonspecific filtering will not interfere with formal statistical testing (7, 9). Nonspecific filter statistics include, for example, the overall variance and overall mean—computed across all arrays, ignoring class label. Some Affymetrix arrays permit Present/Absent calls for each gene; requiring a minimum fraction of Present calls across all arrays also yields a nonspecific filter (15).

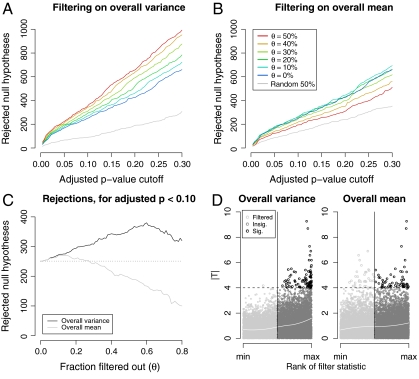
While filtering has the potential to substantially increase the number of discoveries (Fig. 1), its validity has been debated. One criticism is that data-based filtering constitutes a statistical test. Ignoring this fact, and computing and adjusting the remaining p-values as if filtering had not taken place, may result in overly optimistic adjusted p-values and a true false positive rate which is larger than reported. Clearly, increasing the number of discoveries only implies an increase in statistical power if the additional discoveries are enriched for real differential expression. If, on the other hand, filtering simply increases the false positive rate without our knowledge, matters have been made worse rather than better.

Fig. 1.

Power assessment of filtering applied to the ALL data (12,625 genes). R, the number of genes called differentially expressed between the two cytogenetic groups, was computed for different stage-one filters, filtering stringencies, and FDR-adjusted p-value cutoffs. In all cases, a standard t-statistic (T) was used in stage two, and adjustment for multiple testing was by the method of ref. 24. Similar results were obtained with other adjustment procedures. Filter cutoffs were selected so that a fraction θ of genes were removed. A random filter, which arbitrarily selected and removed one half of the genes, was also considered. (A) Filtering on overall variance (S²). At all FDR cutoffs, increasingly stringent filtering increased total discoveries, even though fewer genes were tested. This effect was not, however, due to the reduction in the number of hypotheses alone: filtering half of the genes at random reduced total discoveries by approximately one half, as expected. (B) Filtering on overall mean (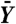), on the other hand, produced a small increase in rejections at low stringency, but then substantially reduced rejections, and thus power, at higher stringencies. (C) Effect of increasing filtering stringency for fixed adjusted p-value cutoff α = 0.1. At higher stringencies, both filters eventually reduced rejections. For the ALL data, this effect occurred much more quickly for the overall mean filter. With the overall variance filter, the number of rejections increased by up to 50%. (D) Filtering on overall mean (θ = 0.5 is shown) removed many significant |T_i| (e.g., |T_i| > 4), while filtering on overall variance retained them.

In the remainder of this article, we clarify these issues. We first point out pitfalls that can arise when an inappropriate filter statistic is used. We then show that with an appropriate choice of filter and test statistics, discoveries are increased while type I error control is maintained, thereby producing a genuine increase in detection power.

Results

Filtering Increases Discoveries.

We considered a dataset obtained from samples of 79 individuals with B-cell acute lymphoblastic leukemia (ALL), for which mRNA profiles were measured using Affymetrix HG-U95Av2 microarrays (16, 17). The samples fell into two groups: 37 with the BCR/ABL mutation and 42 with no observed cytogenetic abnormalities. The Robust Multichip Average algorithm (RMA) was used to preprocess the microarray data and produce an expression summary for each gene in each sample (18). Instructions for accessing these data, and for reproducing the analyses reported here, are given in SI Text.

We considered both overall variance and overall mean as filtering criteria. In both cases, the fraction θ∈[0,1] of genes with the lowest overall variance (or mean) were removed by the filter. The special case θ = 0 corresponds to no filtering. We then applied a standard t-test to those genes which passed the filter.

Fig. 1 A and B shows R, the total number of rejections, as a function of the cutoff on FDR-adjusted p-values. A good choice of filter substantially increased the number of null hypotheses rejected. For the overall variance filter and θ in (0,0.5), procedures with higher values of θ dominated those with lower values over a wide range of adjusted p-value cutoffs. The overall mean filter, on the other hand, was less effective, particularly for θ > 0.10. In fact, for θ > 0.25 the overall mean filter led to substantially fewer rejections than a standard unfiltered approach (Fig. 1 B and C).

This difference between the performance of the two filters is not surprising, and provides an example of how prior knowledge can be incorporated into the analysis via choice of filter. Probes on Affymetrix arrays are known to produce a wide range of fluorescence intensities, even in the absence of target, making overall mean a poor predictor for nonexpression (19).

Pitfalls: Type I Error Control Is Lost.

In the preceding section, we showed that a well-chosen filter can substantially increase the number of null hypotheses rejected. Of course, increased rejections correspond to increased power only if the false positive rate is still under control. In this section, we present several examples which demonstrate that filtering can, for an inappropriate choice of statistics, lead to loss of such control. In subsequent sections, however, we show how to avoid this problem.

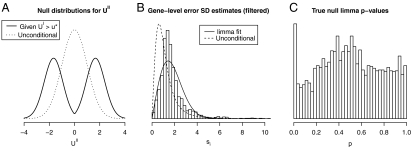
In ref. 8 the authors discuss a filter which requires the fraction of present calls to exceed a threshold in at least one condition. Similar results are obtained by requiring the average expression value to be sufficiently large in at least one condition. Although such filters do not meet the nonspecificity criterion, they have a sensible motivation: genes whose products are absent in some conditions but present in others are typically of biological interest. Fig. 2A shows, however, that such a strategy has the potential to adversely affect the false positive rate. The conditional null distribution for test statistics passing the filter is not the same as the unconditional distribution, and under some conditions, it can have much heavier tails. If one nonetheless uses the unconditional null distribution to compute p-values, these will be overly optimistic, and excess false positives will result.

Fig. 2.

(A) The null distribution of the test statistic is affected by filtering on the maximum of within-class averages. In this example, all genes have a known common variance, the filter statistic is the maximum of within-class means, and the test statistic is a z-score. The unconditional distribution of the test statistic for nondifferentially expressed genes is a standard normal. Its conditional null distribution, given that the filter statistic (U^I) exceeds a certain threshold (u^∗), however, has much heavier tails. Using the unconditional null distribution to compute p-values after filtering would therefore be inappropriate. See SI Text for full details. (B and C) Overall variance filtering and the limma moderated t-statistic. Data for 5,000 nondifferentially expressed genes were generated according to the limma Bayesian model (n₁ = n₂ = 2, d₀ = 3, 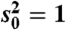). (B) Filtering on overall variance (θ = 0.5) preferentially eliminated genes with small s_i, causing gene-level standard deviation estimates for genes passing the filter (histogram) to be shifted relative to the unconditional distribution used to generate the data (dashed curve). The limma inverse χ² model was unable to provide a good fit (solid curve) to the s_i passing the filter. (C) The fitting problems lead to a posterior degrees-of-freedom estimate of ∞. As a consequence, p-values were computed using an inappropriate null distribution, producing too many true-null p-values close to zero, i.e., loss of type I error rate control. An analogous analysis comparing biological replicates from the ALL study—so that real array data were used but no gene was expected to exhibit significant differential expression—yielded qualitatively similar results.

Certain nonspecific filters, for which the filter statistic does not depend on sample class labels, can also invalidate type I error control. Consider applying the following procedure to a two-class dataset: ignore class labels but cluster the samples using, for example, k-means clustering with k = 2; filter based on the absolute value of a gene-level t-statistic computed for the two inferred clusters. Test genes which pass the filter with a t-statistic computed for the two real classes. If there are genes with strong differential expression, clustering will recover the true class labels with high probability, making the filter and test statistics identical. In effect, this procedure computes gene-level t-statistics as usual but only formally tests the most extreme results. If the standard t-distribution is used to obtain p-values, type I error rate control will clearly be lost.

More realistic nonspecific filters can also detrimentally affect the conditional distribution of the test statistic. The limma t-statistic (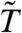) is based on an empirical Bayes approach which models the gene-level error variances 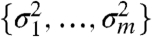with a scaled inverse χ² distribution. For many microarray datasets, this distribution provides a good fit (4). In ref. 7, an overall variance filter is combined with the limma 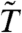. Because the within-class variance estimator (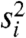) and the overall variance are correlated, filtering on overall variance will deplete the set of genes with low 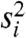(Fig. 2B). A scaled inverse χ² will then no longer provide a good fit to the data passing the filter, causing the limma algorithm to produce a posterior degrees-of-freedom estimate of ∞. This has two consequences: (i) gene-level variance estimates will be ignored, leading to an unintended analysis based on fold change only; and (ii) the p-values will be overly optimistic (Fig. 2C). See SI Text for details.

Conditional Control Is Sufficient.

Having shown that a two-stage approach need not maintain control of type I error rates, even when a nonspecific filter is used, we now examine conditions under which control is maintained.

First, observe that with filtering, false positives and rejections in general are only made at stage two. Therefore, type I errors cannot arise from those hypotheses that have been filtered out, since none of these are rejected. Second, observe that the distributions of the test statistics at stage two are conditional distributions, since we only consider test statistics corresponding to hypotheses which have passed the filter. (The pitfalls we describe above demonstrate that for some filters, this conditioning can in fact change the null distribution.) Combining these two observations, we see that the overall FWER is given by the conditional probability of a false positive at stage two; and the overall FDR, by the conditional expectation of the ratio of false to total discoveries at stage two. To control these type I error rates, we therefore require a filter that leads to a conditional distribution of the 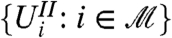which is consistent with the requirements of the p-value computation and multiple testing adjustment procedures. One may, of course, adapt these procedures to accommodate conditioning-induced changes in the null distributions. In the next section, however, we will consider a simpler alternative: the use of filters that leave the distributions of true-null test statistics unchanged. In this case, the same procedures which are appropriate for unfiltered data are still appropriate after conditioning on filter passage.

Marginal Independence of Filter and Test Statistics.

For gene i, the two-stage approach employs two statistics, 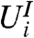and 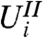, but only compares 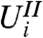—for those hypotheses passing the filter—to a null distribution. The unconditional null distribution of 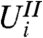is often used for this purpose, but will only produce correct p-values if the conditional and unconditional null distributions of 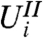are the same. When the null distribution of 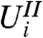does not depend on the value of 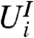, we call this marginal independence for gene i.

Several commonly used pairs of statistics satisfy this marginal independence criterion for true-null hypotheses. Let 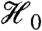denote the set of indices for true nulls, and Y_i = (Y_i1,…,Y_in)^t, the data for gene i. If Y_i1,…,Y_in are independent and identically distributed normal for each 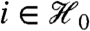, then both the overall mean and overall variance filter statistics are marginally independent of the standard two-sample t-statistic. If, on the other hand, Y_i1,…,Y_in are only exchangeable for each 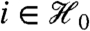, then every permutation-invariant filter statistic—including overall mean and variance, and robust versions of the same—is independent of the Wilcoxon rank sum statistic. ANOVA or the Kruskall-Wallis test permit extension to more than two classes. Proofs are given in SI Text.

In summary, the pairs of filter and test statics described above are such that for true-null hypotheses, the conditional marginal distributions of the test statistics after filtering are the same as the unconditional distributions before filtering. As a consequence, the unadjusted stage-two p-values will have the correct size for single tests. This is an important and necessary starting point for multiple testing adjustments which attempt to control the experiment-wide type I error rate.

FWER: Bonferroni and Holm Adjustments.

Independence of 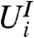and 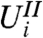for each 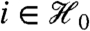means that stage-two p-values computed using the unconditional null distribution of 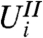will be correct. Furthermore, the marginal independence property can be used to directly understand the impact of using the Bonferroni adjustment (or, by extension, the Holm step-down adjustment) in combination with filtering. The Bonferroni correction would ideally adjust p-values with multiplication by the expected number of hypotheses passing the filter (see SI Text). In fact, we multiply by the observed value of 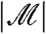. Often, the researcher fixes 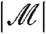, meaning that the two quantities are equal; even when 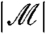is random, the ratio of 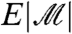to 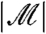will be close to 1 with high probability when the number of hypotheses is large.

FWER: Westfall and Young Adjustment.

The Westfall and Young minP or maxT adjustments (20) typically provide the greatest power among generally applicable methods for FWER control. They take full advantage of correlation among p-values (or test statistics), and when all null hypotheses are true, the nominal FWER is exact, not an upper bound. The single-step minP adjusted p-values, for example, are given by

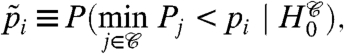[1]

where 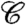denotes {1,…,m}, 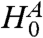denotes the intersection of all null hypotheses whose index is in A, p_i are the observed p-values, and P_i, the random variables. The step-down minP procedure is even less conservative, adjusting the ordered p-values p_I(1) ≤ p_I(2) ≤ … ≤ p_I(m) in a similar but progressively less aggressive fashion. See ref. 6 or 20 for details.

When filtering, the Westfall and Young minP adjustment for those p-values passing the filter now becomes

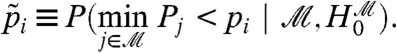[2]

The same reasoning used to prove that [1] controls the FWER may also be used to show that [2] provides conditional control of the FWER, given 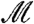. Further, we have shown above that conditional control for each 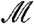implies overall control.

Importantly, the distributions of the minima in [1] and [2] are rarely known. In practice, they are typically estimated by bootstrapping or by permuting sample labels from the original data. Estimation by sample label permutation is appropriate only when, under H_i, the Y_i1,…,Y_in are exchangeable. In the SI Text we show that if filtering is based on a permutation-invariant statistic (like the overall variance or overall mean) and if the distributions of the components of true-null Y_i are exchangeable before filtering, then they are also conditionally exchangeable after filtering. Further, filters which change the correlation structure among the p-values but which preserve exchangeability will not adversely affect permutation-based Westfall and Young p-value adjustment: permutation is performed after filtering, and thus on data which reflect the conditional correlation structure, as required for estimation of the conditional distribution of the minimum in [2].

FDR Control and the Joint Distribution.

FDR-controlling procedures which adjust p-values require, at a minimum, accurate computation of single-test type I error rates. When the unconditional null distribution is used to compute p-values after filtering, equivalence of the unconditional and conditional null distributions of U^II is therefore necessary for FDR control—to ensure that the unadjusted, postfilter p-values are in fact true p-values. The marginal independence criterion guarantees this equivalence.

Adjustment procedures which make no further requirements on dependence among the p-values, such as that of ref. 21, can then be applied directly to the postfilter p-values to control the FDR. Less conservative and more widely used adjustments such as refs. 22 and 23, on the other hand, make additional assumptions about the joint distribution of the test statistics. A sufficient condition for the method of ref. 22, for example, is positive regression dependence (PRD) on each element from 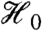(21). Filtering can, however, change the correlation structure among the p-values for null hypotheses passing the filter, even when the marginal independence criterion is satisfied. It is therefore possible that the conditional dependence structure after filtering is inappropriate for some adjustment procedures, even though the unconditional dependence structure before filtering did not present any problems.

In our experience with microarrays, reasonable filters do not create substantial differences between the unconditional and conditional correlation structure of the p-values. Further, the dependence conditions under which the more powerful FDR adjustments have been shown to work are more general than even PRD (23). However, if exploration of the data suggests filter-induced problems with the joint distribution, one can revert to the method of ref. 21; whether the loss of power associated with this more conservative approach is offset by gains due to filtering will then depend on the particulars of the data. Alternatively, if strong correlations are present between the variables, a multivariate analysis strategy that takes these into account more explicitly might be preferable to variable-by-variable testing.

Filtering and the Weighted FDR.

In ref. 24 the authors describe a weighted p-value adjustment procedure which increases detection power for those hypotheses of greatest interest to the researcher. Their original procedure uses a priori weights, but ref. 25 suggests the use of data-derived weights based on the overall variance. Filtering, using overall variance and the p-value adjustment of ref. 22, is closely related to this data-based weighted adjustment. The two-stage approach compares the ordered p-values which pass the filter to progressively less stringent thresholds. Under the weighted procedure, if weight zero is assigned to hypotheses with low overall variance, and weight 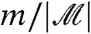is assigned to hypotheses with high overall variance, this set of p-values is compared to the exact same set of thresholds. The two-stage and weighted approaches are not, however, identical. The two-stage approach never rejects null hypotheses which have been filtered out. In the weighted approach, on the other hand, a weight of zero leads to a less favorable adjustment to the p-value, but the corresponding null hypothesis may still be rejected if the evidence against it is strong. As a consequence, under the weighted approach, zero-weight hypotheses can contribute to the number of false positives and the total number of rejections, and thus to the FDR.

The weighted false discovery rate (WFDR) provides a better analog to two-stage filtering. Let R_i be an indicator for rejection of H_i, and for a fixed weight vector w, define

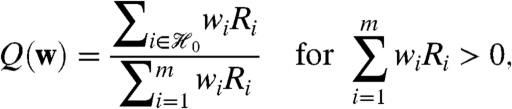and Q(w) = 0 otherwise. Then WFDR(w) is defined to be the expected value of Q(w) (24). Unlike the weighted approach to the FDR, hypotheses assigned weight zero make no contribution to the WFDR. As a consequence, two-stage FDR control using the procedure of ref. 22 is exactly equivalent to weighted WFDR control using the procedure of ref. 24. Further, for fixed w, this procedure controls the WFDR under the PRD assumption (26). Data-derived weights W, however, are random. If PRD also holds conditionally given W (or, equivalently, 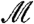), then this procedure controls WFDR(W), and by implication the two-stage filtering procedure controls the standard FDR.

Variance Filtering, Fold Change, and the t-Statistic.

Practitioners frequently compute per-variable p-values, adjust these for multiple testing, but then only pursue findings for which the adjusted p-value is significant and the observed fold change exceeds some value relevant for their application. While this approach improves interpretability of results, the effective type I error rate is not obvious.

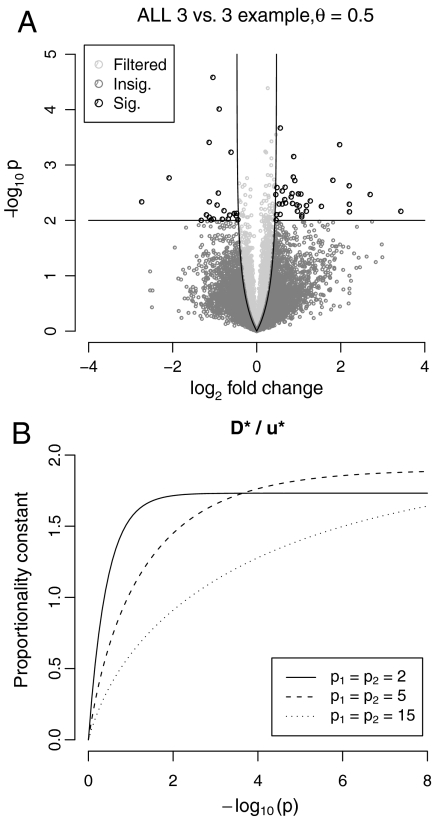
It turns out that such a strategy is related to two-stage filtering. There is a straightforward relationship linking the overall variance, the difference in within-class means (the logarithm of the fold change), and the standard within-class variance estimator used in the t-statistic (see [S3] in SI Text). As a consequence, filtering on overall variance, or equivalently, on overall standard deviation, induces a lower bound on fold change. This bound’s value increases somewhat as the p-value decreases, and Fig. 3 illustrates the effect. For small samples, this increase is negligible; for larger sample sizes, however, it is appreciable. Importantly, the induced log-fold-change bound is a multiple of the threshold used in an overall standard deviation filter.

Fig. 3.

Overall variance (or equivalently, overall standard deviation) filtering example, using the ALL data, comparing 3 BCR/ABL and 3 control subjects. (A) Volcano plot contrasting log-fold change (D_i) with p-value, as obtained from a standard t-test. The impact of filtering is shown: overall variance filtering is equivalent to requiring a minimum fold change—where the bound increases as the p-value decreases. For n₁ = n₂ = 3, the induced fold change bound was essentially constant for p_i < 10^-2 (dashed line). As a consequence, the two-stage approach—removing the 50% of genes with lowest overall variance and then applying a standard t-test to what remains—was approximately equivalent to applying a t-test to the full dataset but only rejecting null hypotheses when p_i < 0.01 and the fold change exceeded 1.35× (0.43 on the log ₂ scale). (B) The rate at which the induced fold-change bound converges to its limit depends on sample size. For small samples, this bound, D^∗(p), is essentially a constant multiple of the cutoff on overall standard deviation (u^∗) for all p-values of practical interest; for larger sample sizes, however, genes producing more significant p-values are also subject to a more stringent bound.

Discussion

In the context of variable-by-variable statistical testing, numerous authors have suggested filtering as a means of increasing sensitivity. This suggestion is typically motivated by a general purpose experimental technology which interrogates a large number of targets, a substantial (but unknown) fraction of which are in fact uninformative. In the context of gene expression, one often uses stock arrays that interrogate all known or hypothesized gene products. In a given experiment, however, many genes may not be expressed in any of the samples, or not expressed sufficiently to generate informative signal. Similar situations exist in other application domains. We and other authors have shown that filtering has the potential to increase the number of discoveries. Increasing discoveries, however, is only beneficial if the overall false positive rate can still be correctly controlled or estimated.

In this article we have shown that inappropriate filtering has the potential to adversely affect type I error rate control. This effect can occur in two different ways:

The first, more immediate problem arises from dependence between the filter and test statistics. If the two are not independent under the null hypothesis, but the unconditional distribution of the test statistic is nonetheless used to compute nominal p-values, single-test error rates may be underestimated. Multiple testing adjustment procedures rely on correct unadjusted p-values; without these, control of the experiment-wide error rate can be lost. We provide one solution—the use of filter and test static pairs which are marginally independent under the null hypothesis—and we give some concrete examples. When the sample size is large enough, the use of an empirical null distribution offers another potential solution, provided that the effects of conditioning can be correctly incorporated. Importantly, the filter and test statistics need not be independent when the null hypothesis is false. Indeed, positive correlation between the two statistics under the alternative hypothesis (Fig. 1D) is required if one hopes to increase detection power by filtering.

A second, more subtle, problem may also arise; namely, some commonly used p-value adjustments only accommodate a certain degree of dependence among the unadjusted p-values. Filtering can affect dependence between p-values, even when the marginal independence criterion is satisfied. The relevance of this concern is application dependent, but in our experience, it is not a serious problem for microarray gene expression data. Further, we show above that permutation-based implementations of the FWER-controlling procedure of ref. 20 can be safely combined with permutation-invariant filters. The FDR-controlling procedure of ref. 21 can also be applied without additional restrictions, and less conservative FDR-controlling procedures can be applied as well if their requirements are met conditionally.

In addition to analyzing power and type I error rate, we have also pointed out a relationship between filtering by overall variance and filtering by fold change. This relationship has important implications. If variation among samples is low, effects whose size is not of practical importance can nonetheless achieve statistical significance—when, for example, the numerator of the t-statistic is small but the denominator is smaller still. Fig. 3 shows that if the t-test is preceded by overall variance filtering, discoveries with small effect size are avoided. The magnitude of the induced lower bound on fold change is not obvious from the variance threshold, so we provide software for making the necessary computations in the genefilter package for Bioconductor (27).

Moderated t-statistics like the limma 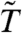are also often used to avoid discoveries with small effect sizes. Further, the null distribution for 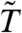is typically more concentrated than that of the standard t-statistic. In many cases, this concentration also produces power gains—gains which may exceed those obtained by the combination of variance filtering and the standard t-statistic. Can even greater power gains be obtained by combining filtering and moderation? Perhaps, but Fig. 2C shows that such an approach has the potential to inflate the false positive rate when the sample size is small. Thus, we do not recommend combining limma with a filtering procedure which interferes with its distributional assumptions. We are therefore left with two options: variance filtering combined with the standard T, or an unfiltered 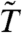. Each option addresses the issue of small effect sizes, and each can improve power. Which one provides the best improvement is data dependent, and we provide further examples and discussion in SI Text.

We have pointed out a close relationship between filtering, a weighted approach to FDR, and WFDR control. Filtering is analogous to the use of a common weight (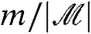) for all hypotheses passing the filter, and weight zero for the remainder. The use of continuously varying weights, on the other hand, has been shown to be optimal for certain experiment-wide definitions of type I error rate and power, and schemes for data-based estimation of these weights have been proposed (28, 29). Our aim in this article, however, has not been to identify an optimal procedure, but rather to better understand filtering and to explore its effect on power and error rate control. Further, the simplicity of filtering—in terms of both implementation and interpretation—is very appealing and may offset a degree of suboptimality.

Finally, Fig. 1 shows that a poor choice of filter statistic or cutoff can actually reduce detection power. Power can be substantially improved, on the other hand, when the filter and cutoff are chosen to leverage prior knowledge about the assay’s behavior and the underlying biology. Because such choices are application specific, data visualization is crucial. Tools which generate diagnostic plots like those of Fig. 1 are provided in the genefilter package. In summary, filtering is not just an algorithmic improvement to p-value adjustment; instead, when applied appropriately, it is an intuitive way of incorporating additional information, resulting in a better model for the data.