Elusive transition state of alcohol dehydrogenase unveiled

Abstract

For several decades the hydride transfer catalyzed by alcohol dehydrogenase has been difficult to understand. Here we add to the large corpus of anomalous and paradoxical data collected for this reaction by measuring a normal (> 1) 2° kinetic isotope effect (KIE) for the reduction of benzaldehyde. Because the relevant equilibrium effect is inverse (< 1), this KIE eludes the traditional interpretation of 2° KIEs. It does, however, enable the development of a comprehensive model for the “tunneling ready state” (TRS) of the reaction that fits into the general scheme of Marcus-like models of hydrogen tunneling. The TRS is the ensemble of states along the intricate reorganization coordinate, where H tunneling between the donor and acceptor occurs (the crossing point in Marcus theory). It is comparable to the effective transition state implied by ensemble-averaged variational transition state theory. Properties of the TRS are approximated as an average of the individual properties of the donor and acceptor states. The model is consistent with experimental findings that previously appeared contradictory; specifically, it resolves the long-standing ambiguity regarding the location of the TRS (aldehyde-like vs. alcohol-like). The new picture of the TRS for this reaction identifies the principal components of the collective reaction coordinate and the average structure of the saddle point along that coordinate.

Enzymes enhance the rates of chemical reactions by many orders of magnitude, and extensive studies have uncovered many aspects of how they do so. The prevailing theory that enzymes stabilize the transition state (TS) relative to the reactants explains many phenomena, and a great deal of contemporary research focuses on how enzymes stabilize the TS. An unfortunate hindrance to developing an understanding of how enzymes stabilize the TS lies in the enigmatic nature of the TS. Many enzymatic hydrogen (proton, hydrogen, or hydride) transfers, for example, occur by quantum mechanical tunneling, where a particle passes through an energy barrier because of its wave properties (1–6).

Yeast alcohol dehydrogenase (yADH) serves as an excellent model system for enzyme-catalyzed H transfer because unlike many other enzymes, the chemical step, oxidation of a primary alcohol to an aldehyde by NAD⁺, is rate-limiting with aromatic substrates (7). Furthermore, the thermodynamics of the reaction allow for examination of both the forward (alcohol to aldehyde) and reverse (aldehyde to alcohol) reactions under similar conditions (8). This type of nicotinamide-dependent redox reaction appears ubiquitously in biology, and a detailed picture of the TS of such reactions may facilitate many medical and industrial applications.

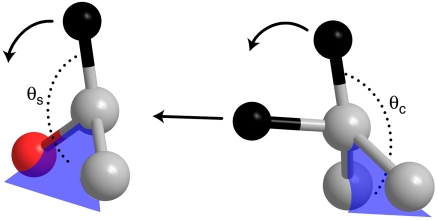
Intriguingly, decades of experiments on the reaction catalyzed by yADH have returned what appear to be contradictory results, some suggesting an early TS, whereas others point to a late TS (7–10). In pioneering studies, Klinman measured linear free energy relationships (LFERs) by using benzyl substrates in both forward and reverse directions and found evidence to support an alcohol-like TS (7, 8), despite the fact that Hammond’s postulate predicts a late TS for this slightly endothermic reaction (internal K_eq = 0.15, i.e., ∼1 kcal/mol) (9). Klinman also examined 2° kinetic isotope effects (KIEs) only to implicate an aldehyde-like TS (8). 2° KIEs measure the ratio of reaction rates of substrates that differ only in isotopic substitution of a bond that is not cleaved during the reaction. They serve as tools for determining TS structure because they reflect changes in hybridization along the reaction coordinate. The traditional formulation of 2° KIEs predicts that a very early TS will give a KIE of unity and a very late TS will give a KIE equal to the equilibrium isotope effect (EIE) (11). A few years later, though, experiments on the homologous horse liver ADH (hlADH) found that 2° KIEs on the nicotinamide exceeded the 2° EIEs. To explain these results, Cleland and co-workers suggested that the reaction involves quantum mechanical H tunneling and coupled motion between the 1° and 2° hydrogens (Fig. 1) (12). Subsequently, H tunneling appeared to be a common feature for H transfer in both enzymatic and nonenzymatic reactions (1, 13).

Fig. 1.

Schematic TRS of the reverse reaction (aldehyde to alcohol) showing 1°–2° coupling. The hydrogens are black, the carbons are gray, the oxygen is red, and the three heavy atoms define the blue plane. Traditional models of tunneling and coupled motion proposed that the reaction coordinate involved motion of all three hydrogens (shown with arrows). The model presented here parameterized the out-of-plane bending angles of the benzyl substrate and nicotinamide cofactor, θ_s and θ_c, respectively, in order to obtain a symmetric double-well potential along the H-transfer coordinate.

Concurrent with these experimental findings, several theoreticians developed a simplified empirical underpinning to the concept of tunneling and coupled motion and predicted that deviations from the semiclassical Swain–Schaad exponents (SSEs) (14) could serve as strong evidence for such behavior (15–17). Semiclassically, the SSE is

[1]

where k_i is the reaction rate with isotope i. Confirmation of this prediction came quickly thereafter in a seminal paper by Klinman’s group that found a glaringly elevated mixed-labeling SSE (mSSE) for 2° KIEs in yADH (18), where

[2]

where 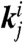is the rate when i is the hydrogen isotope at the 1° position and j is the hydrogen isotope at the 2° position. An elevated mSSE later appeared in other ADHs (19, 20) as well as other types of enzymatic hydrogen transfers (21).

Some empirical models (22, 23) as well as quantum mechanical/molecular mechanical simulation (QM/MM) studies (24–27) have achieved moderate success in replicating the observed 2° mSSEs. While not rigorously defined in those studies, the concept of “tunneling and coupled motion” complicated the traditional interpretation of 2° KIEs, so that the location of the TS need not be proportional to the 2° KIEs. A more comprehensive empirical model is proposed below.

Here we report measurements of H/T and D/T 2° KIEs (cf. k_H/k_T and k_D/k_T) on benzaldehyde in the reverse reaction that fall outside the range of the EIE to unity, a finding that mirrors 2° KIEs on the nicotinamide cofactor (12). The KIEs reported here completed the set of 2° KIEs for this reaction (both substrates in both directions). This set guided our development of a more complete empirical model that explains all the apparently contradictory findings regarding the ADH reaction. This model implies a “tunneling ready state” (TRS), which is a special case of the more general TS (28). The TRS is the ensemble of states from which H tunneling occurs and like the general case of TS is a saddle point along a coordinate that represents the motions that bring the system from the ground state to the TRS. The present approach uses the framework of Marcus-like models of hydrogen tunneling (1, 4, 28–32) and identifies some of the principle components of the collective reaction coordinate. This empirically parameterized model quantitatively replicates all of the 2° KIEs in the forward and reverse directions, as well as their mSSEs, and the LFER findings. The model also indicates an asynchronized hybridization for the donor and acceptor carbons, which was first identified for dihydrofolate reductase (DHFR) by QM/MM calculations (33). Finally, in accordance with the ensemble-averaged variational transition state theory (VTST) results from Truhlar, Gao, and co-workers (24, 25), the model supports the recently articulated hypothesis that the inflated mSSEs reported for many ADHs since 1989 result from deflated 2° D/T KIEs because of the shorter donor–acceptor distance (DAD) required for D transfer (1, 34). The present model mirrors some of the previous empirical calculations on ADH and other systems (16, 17, 22, 23, 35) but provides a more comprehensive molecular and electronic interpretation. The interpretation of experiment by this method agrees well with the results from QM/MM simulations (24, 25) that also led to deviations from semiclassical 2° mSSEs in the forward direction.

Results and Discussion

Measuring 2° H/T and D/T KIEs on Benzaldehyde Reduction.

Traditionally, models expected the magnitude of 2° KIEs to vary between unity for a reactant-like TS and the EIE for a product-like TS (see ref. 33 for a thorough discussion), but quantum mechanical tunneling and 1°–2° coupled motion have given experimental results that elude such simplistic interpretations. The 2° H/T KIE measured here for the reduction of benzaldehyde by NADH clearly escapes interpretation by semiclassical models. The value we measured (as described in Materials and Methods) was 1.05 ± .01, which is obviously outside the range of unity to the inverse EIE (0.75, ref. 36). An early attempt to measure this KIE produced results within error of unity, which did not surprise the authors because the KIE in the forward direction (alcohol to aldehyde) was equal to the EIE, suggesting a TRS close to the aldehyde (36). Our measurements differ from unity and appear to be quite precise as a result of using only the aromatic-active isozyme of yADH (10) and a broad range of time points.

The term tunneling and coupled motion has been applied to ADHs and other systems that exhibit 2° KIEs outside the semiclassical range (12, 28, 37, 38), as well as reactions that violate the Rule of the Geometric Mean, as evidenced by inflated mSSEs (1, 18, 21). The term tunneling and coupled motion appears to be used for both abnormalities in 2° KIEs. Below, we describe the development of a model that interprets these abnormalities without any explicit inclusion of “coupled motion” and show that the two types of observations differ in their physical origins.

Modeling the TRS.

The model developed here fits into the framework of Marcus-like models of H tunneling in enzymes (1, 4, 30–32). A generalized functional form of these phenomenological models gives a rate constant (k) as

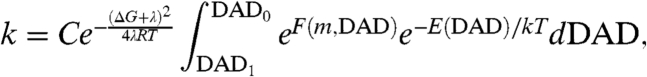[3]

where the first exponential is the traditional “Marcus term” for a reaction with driving force ΔG and reorganization energy λ at temperature T. The integral includes terms that adapt Marcus theory to the situation of H tunneling. The first exponential inside the integral, the “Franck–Condon term,” is a nuclear overlap integral, which describes the efficiency of tunneling through a given barrier and is a function of the tunneling particle’s mass (m) and the DAD. The second integrated exponential, the “Gating term,” measures the relative contributions of the ensemble of DADs, which are in dynamic equilibrium. This phenomenological model was developed to describe the temperature dependency of 1° KIEs, where most of the isotopic sensitivity is in the nuclear overlap term. The mass of the 2° hydrogens, however, does not significantly affect the integrated terms, and 2° KIEs are mostly embedded in the Marcus term of this equation.

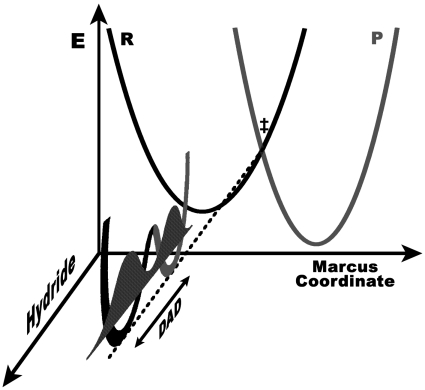
The physical interpretation of Eq. 3 mirrors the VTST treatment (39) that has been quite successful in modeling enzymatic reactions that involve H tunneling (24, 25, 33). In these models, the enzyme facilitates tunneling of the transferred particle by creating energetic degeneracy between a donor and acceptor state. When the two states are degenerate, the probability density of the transferred particle (depending on its mass and the DAD) passes from the donor well to the acceptor well (Fig. 2). Thus, the TRS is the Marcus crossing point, at which H transfer from donor to acceptor can occur. We approximated the TRS as a linear combination of two states that are degenerate distortions of the heavy atom framework and differ only as to whether the transferred hydride is in the donor or acceptor well.

Fig. 2.

Marcus-like model of a reaction with H tunneling. At the TRS (‡), the reactant (Black) and product (Gray) surfaces are degenerate, which allows the probability density of the hydrogen (Shaded) to spread from the donor well to the acceptor well (i.e., quantum mechanical tunneling) at a rate dependent on the DAD and the particle’s mass. Once degeneracy is broken, the hydride wave function can collapse into the acceptor well, giving a net transfer (i.e., dissipative tunneling). The Marcus coordinate is a complex amalgamation of many modes, some of the most important of which are discussed in the text.

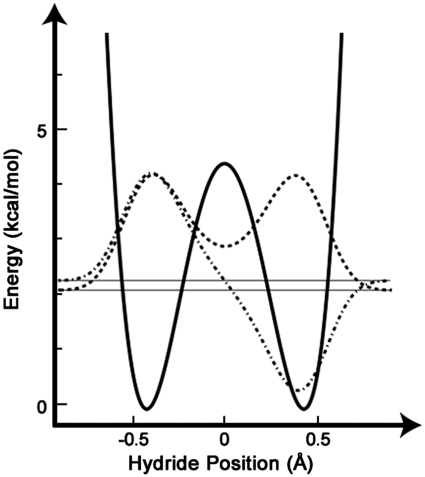
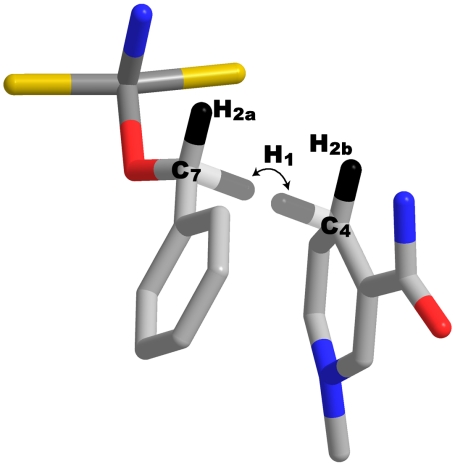
To find the structure of the heavy atom skeleton at the TRS, we adapted Redington’s method to model the TRS of the proton transfer in tropolone (40). The substrates were optimized to a geometry with the transferred H at the midpoint on a straight line between the donor and acceptor carbons by using a range of DADs. Because these structures did not yield the degenerate double-well potential necessary for tunneling, the hybridizations of the donor and acceptor carbons were parameterized (see SI Text) to give a symmetric potential energy surface for the motion of the H between the donor and acceptor (Fig. 3). The TRS was then approximated as a linear combination of the two states where the transferred H is in the donor well or the acceptor well. The geometric mean of the KIEs calculated for the donor and acceptor states of the TRS at each DAD was compared with experiment to determine the best fit. Parameterization of the Zn-O bond length at the TRS also enhanced the fit to experimental KIEs and is discussed in SI Text. Fig. 4 shows the structure that best matched experimental KIEs, Table 1 shows the values of the KIEs, and Table 2 lists important geometrical values in the TRS and their corresponding values in the ground state structures. Whereas there might be other structural solutions that fit the data, these are outside the conformational space we scanned and might not be physically relevant. The solution we report may not be the only one that reproduces some of the KIEs, but it is physically meaningful and it meets a large number of experimental restrictions that are quite sensitive to the geometric parameters surveyed.

Fig. 3.

Least-squares quartic fit to 25 single point calculations at the B3LYP/6-31 + G^∗ level along the H-transfer coordinate at the TRS. The vibrational wave functions of the ground state (Dashed Line) and first excited state (Dashed-Dotted Line) of the tunneling hydride were calculated as described in SI Text. This surface is equivalent to the 1D slice of the “hydride coordinate” at the TRS in Fig. 2.

Fig. 4.

TRS structure for H transfer found by the present methods, showing all heavy atoms used in the model along with hydrogen atoms of particular interest. The dividing surface of conformations that yield a TRS with two degenerate wells (ΔE_D-A = 0) is quite broad, so this structure represents the weighted average (via Boltzmann distribution) of the full conformational ensemble for which ΔE_D-A = 0. The 1° hydrogen is shown in both the donor and acceptor positions, but faded, because it has just half of its probability density in each position. Important geometric values are listed in Table 2.

Table 1.

Computed and experimental 2° KIEs and EIEs

	Forward*		Reverse*		Equilibrium†
	Comp	Exp	Comp	Exp	Comp	Exp
H2a (H/T)**	1.33§	1.33¶	1.05§	1.05§	1.26§	1.33¶
H2b (H/D)**	1.06§	1.08∥	1.22§	1.24∥	0.87§	0.89∥
H2a (D/T)***	1.03§	1.03††	0.97§	1.01§

Experimental errors are omitted here for clarity but are available in SI Text. The 2° hydrogens H_2a and H_2b are indicated in Fig. 4.

^*The forward direction is the oxidation of benzyl alcohol and the reverse is the reduction of benzaldehyde.

^†Equilibria refer to the forward direction.

^**H transfer.

^§This work.

^¶Ref. 36.

^∥Ref. 12.

^***D transfer.

^††Ref. 18.

Table 2.

Properties of the TRS and ground states

	Reactants*	Products*	TRS
C7-C4**	3.8 Å	3.8 Å	3.2 Å
C7-C4***	3.8 Å	3.8 Å	3.0 Å
Zn-O	1.8 Å	2.3 Å	2.25 Å
C7 hybridization	sp3	sp2	sp2.76
C4 hybridization	sp2	sp3	sp2.34

^*Reactants and products refer to those of the forward reaction.

^**H transfer.

^***D transfer.

As one would expect, the TRS in this model has a somewhat longer DAD (3.2 Å) than the distance of 2.6 Å cited in some previous ADH models (24, 27). That shorter distance referred to the saddle point for the over-the-barrier process, and the authors of those studies stressed that corrections for tunneling played a vital role in replicating experimental KIEs. The DAD in our calculations, though, refers to that of the TRS, from which tunneling occurs. In our model no barrier is present for DADs shorter than 2.8 Å, and the zero point energy of the hydride is above the barrier even beyond that. This phenomenon echoes a model by Hammes-Schiffer and co-workers that found no barrier to this reaction at such short DADs but demonstrated how tunneling can contribute to rates with a DAD in excess of 3.1 Å (26). Furthermore, a model of the H transfer in soybean lipoxygenase found that the “distance of most probable transfer” (the DAD at the TRS) could be as long as 3.25 Å (41). To clarify, the DAD refers to the distance between the two carbon atoms, but the actual distance between the two minima of the double-well potential at the TRS described here is just 0.8 Å, which is within the de Broglie wavelength of H at room temperature (1.0 Å at an energy of k_BT). Nonetheless, to ensure the feasibility of tunneling at 3.2 Å, we calculated the tunneling splitting for the double-well potential in Fig. 3 and found a value of 0.19 kcal/mol, which is similar to previous estimates of this value using other levels of theory (26). The tunneling splitting is inversely proportional to the rate of H tunneling at the TRS, and the value we found indicates that once the system reaches the TRS, all of the probability density of the hydride will pass from donor to acceptor in 250 fs (42).

Hybridization at the TRS.

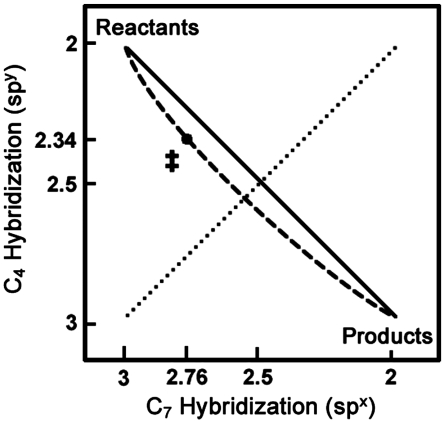
Parameterization of the donor and acceptor hybridization gave a particularly transparent view of the role of rehybridization in the reaction. By using the parameterized out-of-plane bending angle of the 2° hydrogens (Fig. 1), we calculated hybridization (sp^H) at the TRS ranging from sp² to sp³ where

[4]

Here θ is the out-of-plane bend at the TRS, and θ₀ is that angle in the relevant reduced form of each substrate. The calculated hybridizations at the TRS are sp^2.76 for the donor (C7 of the substrate) and sp^2.34 for the acceptor (C4 of the cofactor—Fig. 5). The hybridizations of the donor and acceptor carbons, therefore, are unsynchronized, as found for DHFR (33). Other models have described anomalous rehybridization like this as 1°–2° coupled motion (16, 17, 22, 23) but gave little insight into the physical source of the coupling. The present picture provides a more concrete description of the motion of the 2° hydrogens and how it is necessary to give a symmetric double-well potential at the TRS. The unsynchronized rehybridization reported here and for DHFR (33) may be a general phenomenon in nicotinamide-dependent redox reactions and even in other types of reactions involving H tunneling. We are currently examining this question in other enzymes that involve both hydride and proton transfers.

Fig. 5.

Rehybridization during the course of the reaction. The location of the TRS is marked (‡) and the dashed line indicates a reasonable reaction pathway from reactants to products that passes through the TRS. The solid line indicates a reaction pathway with perfectly synchronized rehybridization. The dotted line indicates the surface with perfectly symmetric rehybridization.

According to the current model, the physical origin of the inflated 2° H/T KIEs (relative to semiclassical predictions) is the effect of tunneling of the 1° hydrogen (delocalized at the TRS) on the 2° vibrational modes, as has been suspected since the earliest observations of 2° KIEs outside the semiclassical range (12, 18), and was first demonstrated for another ADH by QM/MM calculations (24).

The Situation with D Transfer.

Up to this point, we have addressed only the (physiological) H-transfer scenario. Some of the most inexplicable behavior of this reaction, however, particularly inflated mSSEs, occurs when D is the transferred nucleus (1). Importantly, the TRS structure we present for H transfer does not replicate the observed 2° KIEs for D transfer nor does it give inflated mSSEs or the 1° KIEs. However, prompted by the recent proposition of Klinman (1, 34), we tested whether a structure with a shorter DAD would reproduce the observed behavior for D transfer. Shortening the DAD by 0.2 Å did, in fact, give the diminished value of 1.03 for the D/T 2° KIE with D transfer in the forward direction, leading to an inflated mSSE in excellent agreement with the experimental data (18). At the shorter DAD, the effects of hybridization on energy (both total energy and degeneracy between donor and acceptor) are nearly identical to those at the longer DAD, so the hybridization at the TRS is the same with the transfer of the heavier nucleus. Nonetheless, noncovalent interactions between the substrates diminish the 2° D/T KIEs and are the main source of the inflated mSSEs that were long used to indicate tunneling and coupled motion in the ADH reaction.

Notably, the current model suggests that when a different nucleus is transferred, the system goes through a different TRS. Eq. 3 above predicts this type of behavior, because the contribution of the integral to the rate constant is greater for a heavier nucleus at shorter DADs, and similar findings resulted from ensemble-averaged variational transition state theory calculations of ADH (24). A recent VTST study of another system also showed that an H transfer from NADH proceeds via large-curvature tunneling, but the corresponding D transfer is dominated by small-curvature tunneling (43). To further explore this property, we calculated the H/D 1° KIE on the basis of the vibrational zero point energy of H and D for the double-well potential at a TRS of 3.2 and 3.0 Å, respectively, along with the difference in energy between the two TRSs (see SI Text). This simple approximation gave the value of 3.0 for the H/D 1° KIE in both directions, which agrees well with experimental measurements of this value (7, 8). This supporting evidence for Klinman’s recent suggestion of the source of the inflated 2° mSSE (1, 34) is likely to assist the development of more general and less empirical models that account for the effect of a shorter DAD on reactions with D or T transfer in both enzymatic and nonenzymatic reactions.

A Unified Picture of the Reaction Coordinate.

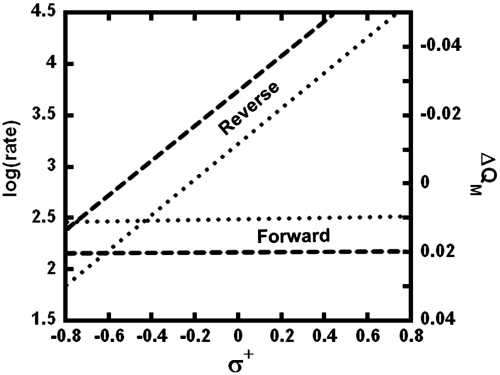
In addition to replicating all of the KIEs measured for yADH, the model presented here rationalizes the apparent paradox regarding the traditional interpretations of 2° KIEs, LFERs, and the Hammond postulate. The LFER experiments showed that substituents at the para position of the substrate have little effect on the oxidation of alcohols but substantially alter the rate of aldehyde reduction, which typically indicates a TS that more closely resembles the alcohol (7, 8, 10). For many years, this finding was seen as contradictory to the data on 2° KIEs, which, when interpreted semiclassically, suggest an aldehyde-like TS. To examine the present model’s consistency with the studies on substituent effects, we explored how two representative electron-donating and electron-withdrawing para substituents (-OCH₃ and -Br) affected the charge density on the benzylic carbon in both directions. A recent analysis of substituent effects on a similar system showed that Mulliken charge (Q_M) on the benzylic carbon, as calculated by the theory used in this model, scales linearly with Hammett substituent constants (44), suggesting that Q_M at the TRS vs. reactants (ΔQ_M) could serve as a probe for reactivity. In accordance with experimental rates, para substituents do not change ΔQ_M significantly in the forward direction, but they give drastic changes in the reverse reaction (Fig. 6). That is not to say that Q_M on the benzylic carbon does not change between the alkoxide and the TRS—only that substituents do not affect that change. In the case of aldehyde reduction, though, substituents strongly modulate how charge accumulates on the benzylic carbon during the reaction.

Fig. 6.

The effect of para substituents on the forward and reverse reactions catalyzed by yADH. In accordance with previous studies (7, 8) the experimental rates (Dotted Line) (10) showed that the forward reaction is unaffected by electronic changes (substituents with different values of σ⁺) but that electron-withdrawing substituents greatly accelerate the reverse reaction. Calculations (Dashed Line) of the reaction with a representative range of para substituents (-OCH₃,-H,-Br) showed similar trends in the change of Mulliken charge (ΔQ_M) on the benzylic carbon between reactants and the TRS. Substituents on benzyl alcohol (forward) do not affect the electronic changes along the reaction coordinate, but substituents on benzaldehyde (reverse) severely alter the electronic changes that accompany the TRS.

In terms of the Marcus-like model used as a framework for these calculations, ΔQ_M appears to be a good probe for the reorganization along the Marcus coordinate (the first exponential term of Eq. 3). Reorganization energy indicates the extent to which the electrostatic environment of the tunneling particle must change in order to reach the TRS (45). The fact that electronic changes have little effect in the forward direction suggests that the system is well preorganized for the forward reaction. That is, by binding the substrates and forming the Zn-alkoxide intermediate, the enzyme accomplishes much of the necessary changes to reach the TRS. In the reverse direction, however, reorganization after binding plays a crucial role and electronic changes affect the extent to which the system must reorganize to reach the TRS.

How can one reconcile an early TRS (for the forward reaction) with the overall endothermicity of the reaction? The Hammond postulate predicts a late TRS for an endothermic reaction. The equilibrium in solution favors the alcohol-NAD⁺ side of the reaction (at catalytically relevant pH) (7), but the solution equilibrium is not directly relevant to the rate-limiting hydride transfer step under study. Measurements of internal (on the enzyme) equilibrium gave a value of K_eq = 0.15 in favor of the alcohol-NAD⁺ side, predicting a late TRS (9), but the internal equilibrium is close to unity and very likely a combination of at least two steps: the deprotonation of the alcohol and the hydride transfer that follows (46). Indeed, QM/MM calculations for this reaction found that the hydride transfer step is exothermic, despite the fact that the overall reaction was endothermic (24, 27). Our results indicating an alkoxide-like TRS for the hydride transfer bolster the argument that this step truly is exothermic.

The overall course of the reaction appears to be the following: After the Zn alkoxide forms, the Zn-O bond lengthens, accompanied by changes in the hybridization of the donor and acceptor carbons to reach a symmetric double-well potential along the H-transfer coordinate (Fig. 3). Once the system achieves this TRS, rate-promoting vibrations of the enzyme (47) allow the substrates to sample a range of DADs. When the DAD reaches 3.2 Å (weighted average), the probability density of the hydride can spread from the donor well to the acceptor well on a time scale similar to the lifetime of the TRS. Once the degeneracy of the TRS dissolves, the wave function of the tunneling hydride collapses and it is trapped in the product state.

Conclusions

For nearly four decades, data addressing the yADH catalyzed reaction appeared contradictory and could not be rationalized within a single model. New measurements of H/T and D/T 2° KIEs for the yADH catalyzed reduction of benzaldehyde by NADH deviated from the range predicted by semiclassical theories. These data completed the set of 2° KIEs available for this enzyme and allowed us to develop an empirical model that is consistent with all the data. This model shed light on the nature of the phenomenon described in the past as H tunneling and 1°–2° coupled motion (12, 15–18).

The picture of the reaction emphasizes the dual importance of a short DAD as well as degenerate donor and acceptor wells at the TRS. Such a picture opens the doorway to a better understanding of how enzymes stabilize the TRS. The current findings are likely to spur both experimental and theoretical work to better understand the TRS of yADH and other enzymatic and nonenzymatic reactions. To test and consolidate this picture, its predictions will be assessed experimentally. The present model predicts, for example, that H/T 2° KIEs in the forward direction will be greater with H transfer than with D transfer and that the 2° SSE will conform to the semiclassical value so long as both the H/T and D/T KIEs are measured with the same nucleus at the 1° position. Additionally, the findings presented here are likely to inspire high-level theoretical studies of yADH, for which a crystal structure is now available (Protein Data Bank ID code 2HCY), to illuminate the question of how the substrates reach the TRS and what role the enzyme plays in that process.

Materials and Methods

Detailed experimental and computational methods are available in SI Text. A brief description is provided below.

Kinetic Experiments.

The H/T and D/T 2° KIEs for the reduction of benzaldehyde were measured competitively in reaction conditions designed to mimic those used in previous studies of this enzyme (18). [7-³H]-benzaldehyde was synthesized by reduction of benzoyl chloride by [³H]-NaBH₄ (48). [ring-¹⁴C]-benzaldehyde (as a trace for ¹H or ²H) was commercially available (American Radiolabeled Chemicals). [7-²H; ring-¹⁴C]-benzaldehyde was produced by CN-catalyzed exchange of the aldehydic proton with D₂O (49). R-[4-²H]-NADH (NADD) was produced by ADH-catalyzed reduction of NAD⁺ by EtOH-d₆ (50). To measure the H/T KIE, [ring-¹⁴C]-benzaldehyde was copurified with [7-³H]-benzaldehyde and the substrate was consumed by an excess of NADH in the presence of yADH. The D/T KIE used [7-²H; ring-¹⁴C]-benzaldehyde and NADD. The reactions were quenched at a range of time points, and samples were analyzed as described in SI Text to measure the depletion of tritium in the product as a function of fractional conversion, to yield the KIE.

Computational Modeling.

KIEs and EIEs were calculated on the basis of isotopic differences in vibrational frequencies between reactants and the TRS according to the Bigeleisen equation (51) by using the program ISOEFF 07 (52). Vibrational frequencies were calculated by Gaussian 03 (53) at the B3LYP level of theory. To model the effects of hydrogen tunneling on KIEs, the TRS was treated as a simple linear combination of degenerate donor and acceptor states:

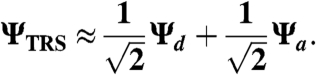[5]

Vibrational frequencies at the TRS were approximated as the average between the frequencies calculated for the individual donor and acceptor states (see SI Text for details). To obtain fits to experimentally determined KIEs, geometrical properties of the TRS were parameterized as described in the text.