Electroelastic coupling between membrane surface fluctuations and membrane-embedded charges: Continuum multidielectric treatment

Abstract

The coupling of electric fields and charges with membrane-water interfacial fluctuations affects membrane electroporation, ionic conductance, and voltage gating. A modified continuum model is introduced to study charge interaction with membrane-water interfacial fluctuations in multidielectric environments. By surrounding a point charge with a low dielectric sphere, the linear Poisson–Boltzmann equation is directly solved by calculating the reaction field potential via a method that eliminates singularity contributions. This allows treatment of charges located at dielectric boundaries. Two complementary mechanisms governing charge-fluctuation interactions are considered: (1) electroelastic deformation (EED), treating the membrane as an elastic slab (smectic bilayer model), and (2) electrohydrophobic solvation (EHS), accounting for water penetration into the membrane’s hydrophobic core. EED often leads to large membrane thickness perturbations, far larger than those consistent with elastic model descriptions [M. B. Partenskii, G. V. Miloshevsky, and P. C. Jordan, Isr. J. Chem. 47, 385 (2007)]. We argue that a switch from EED to EHS can be energetically advantageous at intermediate perturbation amplitudes. Both perturbation mechanisms are simulated by introducing adjustable shapes optimized by the kinetic Monte Carlo reaction path following approach [G. V. Miloshevsky and P. C. Jordan, J. Chem. Phys. 122, 214901 (2005)]. The resulting energy profiles agree with those of recent atomistic molecular dynamics studies on translating a charged residue across a lipid bilayer [S. Dorairaj and T. W. Allen, Proc. Natl. Acad. Sci. U.S.A. 104, 4943 (2007)].

INTRODUCTION

Electroelastic coupling of electric fields or charges to membrane surface fluctuations significantly influences membrane stability, electroporation, ionic transport, and voltage gating.^{1, 2, 3, 4, 5, 6, 7} This issue is especially significant since, in some voltage gated channels,^{8, 9, 10} its voltage sensor (gating charges) is partially embedded in the lipid bilayers. In the transduction process of opening (or closing) the channel, the gating charges move partially across the lipid bilayer membrane,⁷ raising two obvious questions. How do low dielectric environments, typically associated with the membrane hydrophobic core, stabilize charges? How can the high energy barriers for charge insertion into low dielectric environments be surmounted? Previous continuum electrostatic models,^{11, 12, 13, 14, 15, 16} not accounting for membrane deformations around buried charges, predict large energy barriers ranging from 40 to 120 kT (1 kT= 2.48 kJ∕mole at room temperature). Recent fully atomistic molecular dynamics (MD) simulations^{17, 18, 19, 20} demonstrate both significant lipid deformation and water association with the charged residues during their permeation through the membrane’s hydrophobic core. Thus, membrane shape could be significantly altered by electrostatic interactions with membrane-embedded charges. Recent continuum studies^{6, 21} combining harmonic elastic theory with electrostatics demonstrate that membrane deformations of a ponderomotive nature²² can significantly lower the energetic cost of inserting charges into the membrane. However, sometimes exceedingly large membrane deformations are predicted (e.g., ∼20 Å in Ref. 21), violating elasticity theory’s harmonic approximation;²² furthermore interfacial shapes are imposed rather than determined by equilibration.²¹ Such large unphysical deformations indicate that some new physics must be introduced in the continuum treatment. A possibility is formation of a water-filled hydrophobic plume or pore (cavity or shunt) induced by a charge buried deep within the membrane. MD simulations demonstrate the possibility of spontaneously forming such aqueous structures due to electric fields generated by transmembrane charge imbalance²³ or bilayer embedded charges.^{17, 18, 19, 20}

Near microsecond atomistic MD simulations²⁴ of systems comprising hundreds of thousands of atoms are now possible. However, conformational changes in biomolecules, ligand binding, or charge translocations across the membrane minimally require thousandfold longer times. Directly simulating such events is extremely time consuming since transition state sampling only occurs during a small fraction of the simulation time; the computation mainly samples the energy surface close to local energy minima. A solution is to focus exclusively on the rare transition events of interest, rather than on the waiting time between events, which are typically many orders of magnitude longer. This approach can be applied to problems of arbitrary atomic complexity.^{25, 26} Alternately, the molecular system can be simplified by removing those degrees of freedom less relevant to the physics of interest and simulating the residual system, in this way gaining important insights into the underlying physics. Such coarse-grained modeling²⁷ treats only a few selected degrees of freedom evolving under the mean influence of the system remainder. We apply this approach to modeling multidielectric membrane-water-charge systems. The basic idea is to decompose system dynamics into two parts: fast (noise) and slow (reaction coordinates) dynamics. To simulate transition events a realistic reaction coordinate is essential, i.e., identifying the degrees of freedom that capture the essential physics. This is usually done by predetermining a reaction coordinate and forcing system evolution along it. Such an artificially forced transition modifies system dynamics in an unspecified way, typically carried out by dragging the system from initial to final state over the energy barrier. We developed a practical procedure, kinetic Monte Carlo reaction path following (kMCRPF),²⁸ which generates a realistic pathway given the predetermined reaction coordinate and the remaining slow degrees of freedom. Here we apply this method to the membrane-water-charge assembly, to enforce transmembrane charge displacement, and to study coupling between the charge and membrane surface fluctuations and the formation of water-filled pores. The slow, dynamically significant degrees of freedom are variables characterizing the membrane-water-charge system, parameters describing the charge position, the shape of the water-membrane interface, and the water-filled pore. A natural reaction coordinate for charge translocation is the normal to the membrane (z-coordinate). The charge equilibrates its surroundings; after each thermally enforced step along the reaction coordinate, all other degrees of freedom are fully relaxed. Energy is then computed as a function of the reaction coordinate.²⁸

We study membrane fluctuations triggered by a single charge of variable strength (0.5e≤q≤1.5e) sited at selected distances from the unperturbed membrane’s midplane.^{29, 30} Were the membrane a rigid planar slab there would be a large “image force” barrier.¹¹ Our goal is to establish how membrane flexibility and charge-induced water penetration alter this picture. A novel numerical approach is developed to simulate the delicate interplay between the deformable membranes and embedded charges. The linear Poisson–Boltzmann (PB) equation³¹ is solved via a multidielectric continuum model for a range of membrane-water interfacial profiles with a point charge surrounded by a low dielectric “Born sphere.” This computational model intimately couples membrane shape, membrane elasticity, electrostatics, and interfacial tension arising from water penetration into the membrane’s hydrophobic interior. We consider two descriptions of the physical problem: electroelastic deformation (EED), where the membrane is an elastic slab (smectic bilayer model), and electrohydrophobic solvation (EHS), where water penetrates the membrane’s hydrophobic core. In both cases effects of interfacial fluctuations are analyzed. The associated energy penalties reflect elastic membrane deformation (EED) and∕or “interfacial tension” (EHS). Energetic stabilization of the charge, relative to an unperturbed membrane interface, arises from aqueous shielding of the charges’ electric field, generating fluctuations promoted by the ponderomotive force. Using kMCRPF (Ref. ²⁸) we show that the EED typically predicts instabilities leading to a charge-solvated state with deformations far exceeding the elastic limit. This suggests that at some point there is switching from EED fluctuations to EHS ones. Fluctuations are investigated using an extended family of parametrized shapes sampling a wide range of solvated states. Our results indicate that fluctuations typically originate due to EED, which then trigger the massive water penetration governed by EHS.

The article is organized as follows. Section 2 describes both physical and computational details: eliminating the singularity term, modeling elastic and hydrophobic surface fluctuation, and applying the kMCRPF method. Section 3 presents and discusses the results. Section 4 briefly outlines the conclusions.

COMPUTATIONAL MODEL AND SIMULATION METHOD

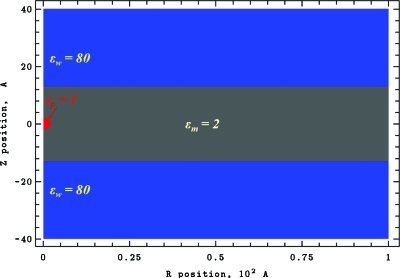
The model system is shown in Fig. 1. Azimuthal cylindrical symmetry is assumed. A point charge is embedded in a Born sphere of a dielectric constant ε_p. It is located on the cylinder axis and is freely mobile in both directions. Lipid headgroups are ignored; model membrane only describes the hydrophobic core. Membrane deformation is allowed and, to solvate the charge, a water plume can penetrate the membrane’s hydrophobic core.

Figure 1.

Two-dimensional cylindrical computational domain with R=100 Å and Z between −40 and 40 Å. This system is multidielectric: membrane with dielectric constant ε_m=2; the water domains with ε_w=80 and the charged sphere of radius 2 Å with ε_p=1. A mesh with spacings of 0.1 and 0.2 Å (1001×801 and 501×401 grid points) was used in computation. The figure is generated using our CE-MEA code.

Source-free Poisson–Boltzmann equation

To mathematically describe electrostatic interaction of the point charge in Fig. 1 with multidielectric surroundings, the linearized PB equation^{31, 32} is used. The electrostatic potential is infinite at the location of a point charge. To use a grid-based finite difference this singularity must be removed. In fact, this point charge contribution is invariant; a charge only influences energy variation through its interactions with dielectric media. In standard finite-difference approaches,^{33, 34} a point charge is projected onto the nearest grid points, and numerical solution accuracy depends on grid spacing. With smaller spacing, interactions among the charges distributed over grid points markedly accentuate the singularity contribution, affecting computational accuracy. Therefore, we use an efficient algorithm originally developed in Ref. 35 to completely project out the singularity and to directly calculate the reaction field potential. The linearized PB equation³⁵ can be written as

$$\mathbf{\nabla }\cdot \epsilon \mathbf{\nabla }\varphi ={\kappa }^2\left(q\varphi ∕k_{B}T\right)-4\pi q,$$ (1)

with ε as the position-dependent dielectric constant, κ as the inverse of Debye length, q as the unit charge, k_B as Boltzmann’s constant, T as the temperature, and ϕ as the unknown electrostatic potential. We limit consideration to low ionic strengths, where the linearized PB is known to be quite reliable.³⁶ With a point charge located at a grid point, there is a local singularity in ϕ. Within the Born sphere, where κ=0 and ε=ε_p, Eq. 1 reduces to the Poisson equation³⁵

$${\epsilon }_p{\mathbf{\nabla }}^2{\varphi }_c=-4\pi q.$$ (2)

The Coulomb potential ϕ_c can be determined analytically from Eq. 2.³⁷ This can be used to eliminate the singularity in ϕ in Eq. 1. The source-free PB equation³⁵ can be derived by subtracting Eq. 2 from Eq. 1,

$$\nabla \cdot \epsilon \nabla {\varphi }_{\delta }={\kappa }^2\left(q\varphi ∕k_{B}T\right)-\nabla \cdot \left(\epsilon -{\epsilon }_p\right)\nabla {\varphi }_c,$$ (3)

with ϕ_δ=ϕ−ϕ_c, the reaction field potential. Within the Born sphere κ=0 and ε=ε_p=1, and Eq. 3 reduces to the Laplace equation. Outside the charged sphere ϕ_c is well defined from Eq. 2; thus, the point charge singularity is eliminated and the reaction field potential ϕ_δ is determined directly from Eq. 3. The source charge q in Eq. 1 has been replaced by the analytical Coulomb potential in Eq. 3.

At the boundary points of the computational domain we define the reaction field potential as ϕ_δ=ϕ_∞−q∕(ε_pρ(r_b,z_b)) with ϕ_∞≈0. $\rho \left(r_b,z_b\right)=\sqrt{{\left(r_b-r_0\right)}^2+{\left(z_b-z_0\right)}^2}$ is the distance between a point charge located at (r₀,z₀) and the boundary points (r_b,z_b). We assume that the cylindrical boundary is located far from the point charge and that, at boundary points, the electrostatic potential ϕ=ϕ_∞≈0 is negligible. A charge can be arbitrarily sited relative to grid points, significant for one near or exactly on the dielectric bulk water-membrane boundary. Consequently there is no electrostatic potential discontinuity in crossing a dielectric boundary. Mapping of a charge onto the grid points is not needed. The reaction field potential ϕ_δ is directly distributed over all grid points. Following standard charging arguments,³⁷ the electrostatic energy is

$$E_{\text{elect}}=\frac{1}{2}q{\varphi }_{\delta }\left(r_0,z_0\right),$$ (4)

with ϕ_δ(r₀,z₀) the reaction field potential at location of the point charge.

To reliably use finite-difference methods to solve Eq. 3, the computational domain is divided into discrete cylindrical cells with dielectric discontinuities always on cell boundaries, never within a cell. The basic finite-difference algorithm described in detail in Ref. 6 and applied to Eq. 3 yields a set of algebraic equations. Despite simplifying the solvent, it remains computationally expensive to solve the PB equation. Moreover, this system of algebraic equations must be solved for each MC (Monte Carlo) step along the transition pathway. Therefore, multifrontal massively parallel solver (MUMPS),³⁸ an accurate direct method based on Lower and Upper matrix factorization, is used to solve the system of linear equations, Aϕ_δ=b, where A is an asymmetric sparse matrix, ϕ_δ is the solution vector, and b is the right-hand side vector. The MUMPS solver utilizes MPI (Message Passing Interface) for message passing and makes use of the BLAS, BLACS, and ScaLAPACK libraries.

Elastic energy

Our first model treats membranes as elastic slabs sandwiched between two aqueous phases. Due to flexibility,³² the membrane can deform in response to external forces such as a charge’s electric field. This couples electrostatics with membrane elasticity, requiring a joint and consistent treatment. In the continuum model for the elastic energy of fluidlike membranes, proposed by Helfrich in analogy to smectic phases of liquid crystals,^{39, 40} the elastic energy is expressed as the integral^{41, 42}

$$E_{\text{elast}}=2\pi {\int }_0^{R}w\left(r\right)rdr,$$ (5)

with w(r)=a⋅[z₁(r)+z₂(r)^]2+b⋅[(Δz₁(r)⁾²+(Δz₂(r)⁾²], $a=E∕\left(2h_0^2\right)$, b=K∕4, where E and K are membrane compression (dilation) and bending (tilt) elastic constants, respectively, h₀ is the thickness of the unperturbed membrane, Δ is the Laplace operator, and z_i describes the profiles of lower (i=1) and upper (i=2) membrane-water interfaces. This model has been extensively used in studying membrane fluctuations, protein insertion energetics, membrane inclusion interactions, membrane rafts, and membrane influences on ion channel gating.^{32, 43, 44, 45, 46} Both lipid tail compression (modeled by E) and tilt (or lipid leaflet bending, modeled by K) (Ref. ⁴²) contribute to the energy of nonuniform dimplelike perturbations. For the optimized dimple shapes the typical bending contribution does not exceed ∼10%–15% of that due to dilation∕compression.^{6, 47, 48} The surface tension contribution to the elastic deformation is ignored as it is assumed negligible for solvent-free membranes.^{49, 50} Reported membrane elastic constants span quite a range (see Refs. ^{6, 21, 41, 51, 52, 53, 54} for discussion and references). In our analyses of membrane elasticity^{6, 41, 45, 48} we adopted values suggested by theoretical treatments of peptide insertion (see Refs. ^{50, 51} and references therein). At 300 K these are E=0.35 kT∕Å, K=13.5 kT, and h₀=25.2 Å for dipalmitoylphosphatidylcholine⁵⁰ (DMPC) and E=0.45 kT∕Å, K=4.83 kT, and h₀=26 Å for dioleoylphosphatidylcholine⁵¹ (DOPC) bilayers. For comparative purposes we use the same constants, which are roughly comparable to values (E=0.34 kT∕Å and K=6.9 kT) used in a study of electroelastic stabilization of membrane buried charges.²¹ However, appropriate criteria for selecting elastic constants for such studies are hard to quantify. For instance, applying macroscopic moduli derived from experiments with giant bilayer vesicles^{52, 53, 54} to the nanoscales of interest here is questionable (sее Refs. ^{2, 3, 6, 48, 51} for discussion). Because of this and similar uncertainties in treating hydrophobic phenomena (see below) our approach must be viewed as semiquantitative. As will be seen later (Sec. 3B, Fig. 10 curve 5) qualitative behavior is insensitive to moderate elastic parameter variation. Surface deformations are described by either Gaussian$z_i\left(r\right)=u_i\text{\hspace{0.17em}exp}\left(-r^2∕{\mathbf{\lambda }}_i^2\right)$ or Hertzian z_i(r)=u_i Kei(r∕λ_i)∕Kei(0) profiles⁶ where u_i, either positive or negative, is the membrane displacement amplitude normal to the unperturbed surface, λ_i is the radial deformation decay length, and Kei is the zero order Kelvin function. For the Gaussian shape $\mathbf{\Delta }{z}_i\left(r\right)=-4u_i\left({\lambda }_i^2-r^2\right)\text{exp}\left(-r^2∕{\lambda }_i^2\right)∕{\lambda }_i^4$, and for the Hertzian shape $\mathbf{\Delta }{z}_i\left(r\right)=u_{i}Ker\left(r∕{\lambda }_i\right)∕\left({\lambda }_i^2\text{\hspace{0.17em}Kei}\left(0\right)\right)$. For large deformations the harmonic approximation implicit in Eq. 5 is inadequate,²² indicating that model modifications are needed at high electric field strengths.

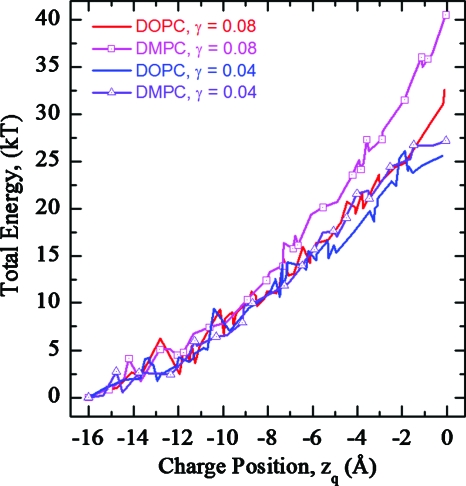
Figure 10.

Total energy profiles as functions of charge position in DOPC and DMPC membranes for hybrid fluctuations. Profiles for a γ of 0.04 and 0.08 kT∕Ų are illustrated.

Hydrophobic energy

In addition to dimplelike, purely elastic membrane perturbations maintaining bilayer integrity, water can penetrate the membrane interior. We denote this stabilization mode EHS because (due to charge solvation) water resides in or even spans the membrane hydrophobic interior.⁵⁵ EHS can be dominant when elastic treatments lead to unphysically large deformations.^{6, 21} Several studies addressed competition between the elastic and hydrophobic responses of membranes to local perturbations using phenomenological continuum models. One of these focused on hydrophobic mismatch between the inserted peptide [e.g., gramicidin A (gA) channels] and the lipid bilayer^{44, 45, 46, 47, 48, 49, 50, 56, 57, 58, 59, 60, 61} is discussed here in greater detail. The elastic energy is usually computed assuming that the mismatch 2δu=l_h−l_m between the hydrophobic length of the channel l_h and the hydrophobic thickness of the membrane l_m is completely compensated by the local adjustment of the membrane thickness, thus eliminating the hydrophobic contribution. In such studies the local thickness variation 2δu in contact with the peptide is a boundary condition establishing the elastic part of the insertion energy.^{44, 45, 46, 47, 48, 49, 58, 59, 60, 61} Such boundary conditions implicitly assume that permitting water entry to a hydrophobic region is very unfavorable energetically compared to an elastic perturbation deterring water access, a hypothesis which has been analyzed both experimentally and theoretically.^{50, 56, 59} Following Refs. ^{56, 59} consider a cylindrical “inclusion” modeling a peptide helix of radius R whose hydrophobic length l_h is less than that of the surrounding membrane. If the membrane fails to adjust elastically, the bilayer acyl chains are partially exposed to water, leading to an edge energy, γA_h=4πγRδu, where γ is the interfacial tension and A_h is the area of the hydrophobic contact opened due to the mismatch.^{56, 59} If local adjustment of membrane thickness compensates part of the mismatch, δu^′≤δu, then the total mismatch energy is δw_mis=4πγR(δu−δu^′)+4K_effδu^′2, where K_eff is an effective (elastic) spring constant depending on R, the elastic moduli, and the boundary condition describing membrane slope at the inclusion surface.^{56, 59} Optimizing δu^′ yields $\delta u_{\text{opt}}^{\prime }=\pi \gamma R∕\left(2K_{\text{eff}}\right)$. If the mismatch $\delta u>\delta u_{\text{opt}}^{\prime }$, then some “slippage” occurs resulting in hydrophobic contact in a narrow region δz∼δu−δu_opt along the border. Analogous energetic tradeoffs have been modeled similarly in analyzing membrane rafts, e.g., cholesterol enriched membrane regions.^{57, 60} Competition between the hydrophobic penalty and the electroelastic stress is also crucial in membrane electroporation, with the hydrophobic energy penalty proportional to the surface area of the water-filled cavity created in forming an aqueous plume or a membrane-spanning pore (see Ref. 62 for a review).

We now consider possible competition between the two mechanisms of charge stabilization: continuum electroelastic coupling^{6, 21} and water penetration of the membrane’s hydrophobic core. Presumably, the latter can prevent huge, unphysical elastic perturbations predicted by the elastic treatment (Sec. 2B). Once formed in the membrane’s hydrophobic interior, a water-filled cavity’s energy is most simply described by^{15, 63}

$$E_{\text{hydro}}=\gamma A,$$ (6)

with A the hydrophobic pore’s total area. A wide γ range, typically 0.04–0.12 kT∕Ų, has been proposed in studies of peptide insertion and electroporation (see Refs. ^{47, 50, 57, 64, 65, 66} and references therein). We treat γ as a model parameter and analyze its effect on competition between the two charge stabilization mechanisms. This is reasonable not only because of uncertainties in the “correct” γ, but also because our treatment of the aqueous cavity approximates it by smooth geometric shapes, ignoring atomic structure. Given this approximation, more precise specification of γ would be out of place (see also Ref. 66).

kMC reaction path following

Reaction barrier crossing is commonly analyzed by defining a physically based reaction coordinate and forcing system evolution along this path. kMCRPF (Ref. ²⁸) affects this rapidly and correctly. It has been used to study ion and water permeation through the ClC chloride and aquaporin pores^{68, 69} and gating in gramicidin A.⁷⁰ Here we apply it to force the charge or the water dimple across the membrane and find minimum-energy pathways and energy profiles along the reaction paths. For illustration, assume a charge crosses the membrane. kMCRPF navigates on the energy surface as follows: (i) choose z_q (the charge’s z-coordinate) as the reaction coordinate; (ii) allow only unidirectional (constrained) motion of the charge along the reaction coordinate, with all other degrees of freedom unconstrained and free to relax. The kMCRPF algorithm²⁸ involves the following steps. (1) Calculate the initial system energy E^old. (2) Perform a unidirectional move along the reaction coordinate. (3) Calculate the energy E^new of a new state with ΔE=E^new−E^old. (4) If ΔE≤0, accept this trial move; if ΔE>0, accept the trial move if ξ≤exp(−ΔE∕k_BT), where ξ is a random number between 0 and 1; otherwise reject it, reduce the move step length along the reaction coordinate and repeat step (2). (5) Use the unconstrained Metropolis MC method⁷¹ to perform many MC trials relaxing the other degrees of freedom while fixing the reaction coordinate and then return to step (2).

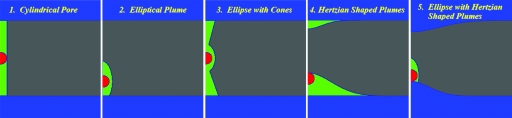
Processes such as pore formation, water plume penetration, etc. are not readily observed directly. To apply kMCRPF and simulate charge translocation we parametrize perturbation profiles. Five basic, fairly general fluctuation shapes (panels 1–5: cylinder, ellipse, ellipse-cone, dimple, and ellipse-dimple, respectively) are illustrated in Fig. 2. Shapes 1–3 depict perturbations describing the membrane’s hydrophobic core and are treated as EHS, with hydrophobic energy given by Eq. 6. Shapes 4 and 5 are treated differently. If considered as embedded in the hydrophobic core, they are described by EHS (as were shapes 1–3). However, if viewed as elastic membrane perturbations dimples are treated by EED except for the ellipse of panel 5. Shape 5 is treated in mixed mode as a hydrophobic plume (EHS) on top of an elastic dimple. In shapes 4 and 5 water dimples are parametrized as either Gaussian or Hertzian forms. Thus, shape 5 is composite, where the charge induces both membrane distortion (the lower, blue dimple, modeled as EED) and an elliptic plume (the upper, green pore, viewed as EHS). Here plume and dimple are free to separate, merge, or overlap. Dielectric constants of 40, 60, and 80 were assigned the water-filled elliptic pore.

Figure 2.

Parametrized profiles of water pores (panels 1 and 3) and water plumes (panels 2, 4, and 5) used for simulating charge translocation across the membrane. The water phase within the membrane core treated with the EHS and the EED is colored in green and blue, respectively. The water dimples with the Hertzian shapes are illustrated in panels 4 and 5. The pictures are generated using the CE-MEA code.

The various shapes permit increasing descriptive flexibility. The relaxing degrees of freedom are (1) pore radius, (2) ellipse axes’ lengths, (3) length of the cones’ base and ellipse axes’ lengths, (4) the dimple amplitudes and decay lengths u₁, u₂ and λ₁, λ₂, and (5) elliptical plume axes’ lengths (treated as EHS) and dimple amplitudes and decay lengths u₁, u₂ and λ₁, λ₂ (treated as EED). With dimple amplitude as the reaction coordinate, the charge’s z-coordinate z_q is a relaxing degree of freedom (with the charge’s location fluctuating axially). Otherwise the charge is fixed for each z_q. In this way the kMCRPF approach permits either a charge or a water dimple to navigate on an energy surface, find the minimum-energy pathways, and determine the associated energy profiles. In addition to establishing the effect of charge location, calculations were carried out at three ionic strengths, 0, 100, and 200 mM; results were ionic strength independent.

Continuum electroelastics of membrane electrolyte assembly (CE-MEA) parallel computer code was developed in mixed FORTRAN 90∕95 and C∕C++. It was implemented using the MPI-2 standard for parallel communications. This code runs on Linux or Windows Intel clusters with 64 bit addressing.

RESULTS AND DISCUSSION

Water dimple movement across a membrane: EED

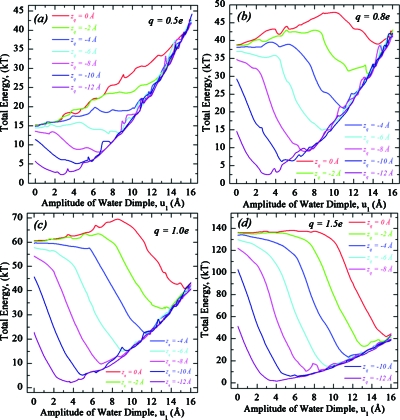
Here membrane fluctuations associated with water dimples are treated by elastic theory. By fixing the charge at some z_q, we determine energy profiles for transmembrane movement of an “elastic water dimple.” The amplitude u₁ (the reaction coordinate) of the lower dimple is unidirectionally constrained to increase while the other degrees of freedom λ₁, u₂, and λ₂ are freely variable. We explored the parameter domain (0.5e≤q≤1.5e,−12<z_q<0) to study energetics of charge-membrane-water interactions. Total energy profiles, the sum of electrostatic and elastic contributions, as functions of water dimple amplitude are illustrated in Fig. 3 for a DOPC membrane and plotted separately for four different charge values q. Each of the seven curves graphs the total energy of a membrane-embedded point charge at a specific axial position z_q. The charge is surrounded by a 2 Å radius sphere of dielectric constant ε=1 with membrane and water ε of 2 and 80, respectively. Dimples of Hertzian shape are only considered in the context of electroelastic coupling (e.g., in the EED treatment).

Figure 3.

Total energy profiles as functions of elastic water dimple amplitude for a charge crossing a DOPC membrane (h₀=26 Å). Four charge values are considered: (a) q=0.5e, (b) q=0.8e, (c) q=1.0e, and (d) q=1.5e. Each panel plots the energy of a point charge bound to the membrane at r_q=0 Å for different axial positions z_q. In all cases the energy is defined with respect to the following reference state: an unperturbed membrane with the charge immobilized in bulk water (z_q=−16 Å).

Figures 3a, 3b, 3c, 3d present total energy profiles in q−z_q space. At midmembrane (z_q=0) a 0.5e charge cannot be solvated by the elastic dimples; the total energy grows monotonically with u₁. Increasing the charge reduces the energy penalty for fluctuation (the ponderomotive effect), and for q=0.8e a local minimum is present for large u₁. Further increasing q deepens the well and reduces the activation barrier for solvation. The barrier of ∼10 kT for q=0.8e disappears for q≅1.5e, where the membrane’s only stable state corresponds to a huge perturbation (with dimple amplitude of ∼16 Å) solvating the ion. Simultaneously the solvation well deepens with q from ∼0 kT (q=0.8e) to ∼−95 kT (q=1.5e). The critical value of q leading to spontaneous (barrierless) solvation depends on z_q. It decreases as the charge approaches the surface and for z_q<∼−4 Å the ion is spontaneously solvated for all q considered. For u₁=0 Å (the corresponding u₂≈0; the other membrane surface is practically unperturbed), the total energy drops as the charge approaches the surface. The minimum-energy conformation is for an undeformed membrane with the charge in bulk water. All other conformations have higher energy. When the dimple reaches the charge and “swallows” it, the elastic energy component becomes solely responsible for the cost of further membrane deformation, while the electrostatic component stays practically unchanged. The dynamics of water dimple development, its growth and charge solvation, is illustrated in Fig. 4 (see online enhanced video). The amplitude u₁ is for elastic dimple growth in the lower part of a DOPC membrane, as seen in Fig. 4.

Figure 4.

Download video file ^{(1.2MB, mov)}

kMC reaction path following of the lower water dimple across a DOPC membrane. A charge of q=1.0e is fixed at z_q=0 Å. Dimple amplitude u₁ grows from bottom to top. Its decay length λ₁ is freely variable. The lower water dimple reaches the charge, solvates it, and then grows further. Dimple growth was followed to z_q=8 Å. The amplitude and decay length of the upper dimple are free to fluctuate. The upper membrane interface is also allowed to fluctuate upward thus protruding into the bulk water. The movie is produced using the CE-MEA code (enhanced online).

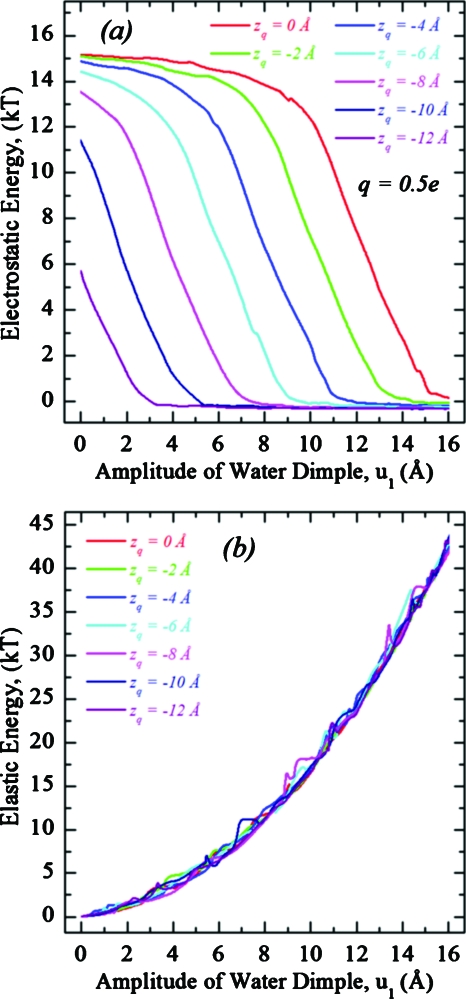
Amplitude dependent electrostatic and elastic energy profiles are illustrated in Figs. 5a, 5b, respectively, with electrostatic profiles shown for q=0.5e, roughly scaling as q². Thus, the total energy drop of ∼15 kT (q=0.5e) becomes ∼60 kT (q=1.0e). For z_q≥−4 Å, the electrostatic energy first nearly plateaus and then drops abruptly [upper three curves in Fig. 5a] with increasing dimple amplitude. For z_q<−4 Å, the electrostatic energy always drops sharply [lower four curves in Fig. 5a]. The electrostatic energy is practically constant after the charge is incorporated by the water dimple [bottom plateau in Fig. 5a]. The elastic energy steadily increases as the water dimple penetrates further into the membrane, independent of charge position or magnitude [Fig. 5b], demonstrating that the optimized shape of the dimple is most affected by the interplay between the stretching and bending elastic contributions while the charge’s electric field only plays a minor role. This also accounts for the ∼q²-dependence of the electrostatic component of the optimized energy, only possible for linear media (ε q-independent) with fixed geometry (dimple shape q-independent).

Figure 5.

Electrostatic (a) and elastic (b) energy profiles as functions of water dimple amplitude for a charge bound to a DOPC membrane at r_q=0 Å and various z_q. Electrostatic profiles are for q=0.5e. The Fig. 3 reference convention is used.

Thus, the charge’s solvation energy is bistable. For some q>0.8e there is a low-energy state where the water dimple solvates the charge. However, the associated membrane deformations are often large, apparently in excess of values consistent with the harmonic elastic treatment.²² This unphysical behavior prompts consideration of an additional route to instability, one where elastic fluctuations trigger local water penetration into the membrane’s hydrophobic core. A joint treatment is discussed next demonstrating that switching from EED to EHS reduces the upper limit of elastic dimple amplitudes dramatically to ∼7–8 Å. Put differently, allowing for this local “breakdown” suppresses the huge deformations predicted by purely elastic treatments.^{6, 21} It must be noted that our estimates of the “switching amplitude” are semiquantitative, given the approximations inherent in the EHS model.

Charge movement across a membrane: EED-EHS coupling

To describe water penetration of the membrane’s hydrophobic core, we couple the pore forming (EHS) and elastic (EED) mechanisms. As the charge position z_q and the water dimple amplitudes u₁ and u₂ can all vary, any may be the independently constrained reaction coordinate along the z-direction. We choose z_q, apply kMCRPF, and describe membrane relaxation as a process forming water dimples and∕or water-filled hydrophobic pores. The charge was tracked from the lower interface (z_q<−13 Å) to midmembrane (z_q=0 Å). After each accepted move along z_q, the other degrees of freedom were relaxed using 200 MC trials. In all calculations described a charge of 1.0e was used.

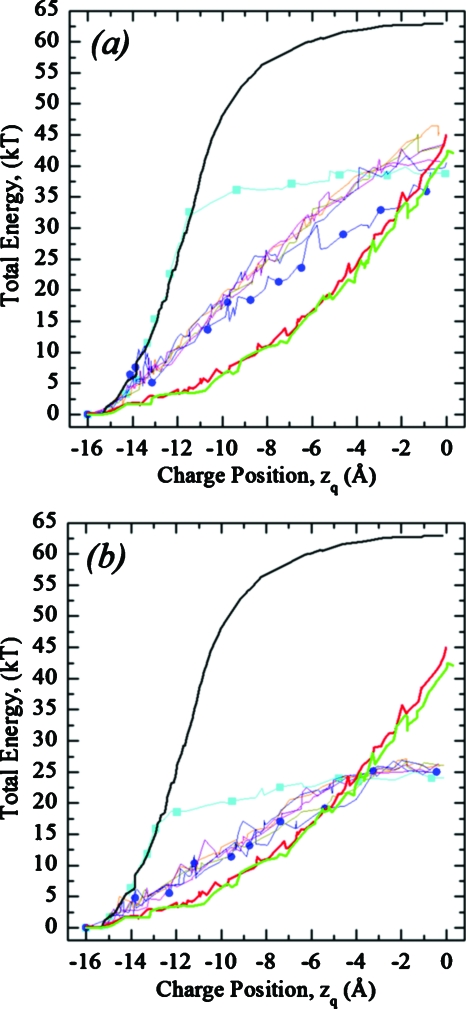
Figures 6a, 6b plot total energy profiles for the pore and plume shapes of Fig. 2 for a DOPC membrane with interfacial tension constants γ=0.08 and 0.04 kT∕Ų, respectively. Energy is measured relative to that for the charge fixed in bulk water (z_q=−16 Å) abutting an unperturbed (flat) membrane. Figure 6 shows that surface fluctuations due to water dimple formation (EED) significantly (by ∼20 kT) lower the energy barrier relative to that of the unperturbed (planar) membrane and qualitatively change the profiles from “bell-shaped” (black curve) to “parabolic” (thick red and green curves). Cyan (square) and blue (circle) curves describe cylindrical and merged ellipse-cone shapes (Fig. 2, panels 1 and 3, respectively). The cylindrical pore (Fig. 2, panel 1) initially remains closed; consequently the black and cyan (square) curves in the left part of Fig. 6 are effectively superposable. As the charge penetrates the membrane, a cylindrical pore of fluctuating radius (Fig. 2, panel 1) is created, which remains open as the charge moves toward midmembrane. The z_q at which opening a cylindrical pore occurs is a γ-dependent value [Figs. 6a, 6b]. The blue (circle) curve, corresponding to a merged ellipse-cone shape, is closer to the thick red and green curves. The five closely spaced curves intermediate between cyan (square) and blue (circle) traces describe elliptical (Fig. 2, panel 2) and Gaussian and Hertzian shaped dimples without (Fig. 2, panel 4) and with the elliptical plume (Fig. 2, panel 5). These various pore and plume shapes have essentially no effect on the energy profiles. This (generally closely bunched) set of five thin curves also illustrates energetic consequences of interfacial tension on hydrophobic pore formation (EHS). Elastic dimples are energetically favored over plumes or pores at all z_q for larger γ, ∼0.08 kT∕Ų [Fig. 6a]. Equation 6 indicates that the energy barrier should increase for γ>0.08 kT∕Ų. If γ<0.06 kT∕Ų, elastic dimples are favored near the membrane surface $\left(z_q<-4\acute{\text{Å}}\right)$ with water plumes more stable near midmembrane $\left(z_q\ge -4\acute{\text{Å}}\right)$ by ∼18 kT [Fig. 6b]. For yet smaller γ, <0.04 kT∕Ų, switching could occur even nearer the membrane-water interface.

Figure 6.

Total energy profiles as a function of charge position in a DOPC membrane. The thick black curve illustrates the energy for a flat membrane (no water dimples or plumes). Thick red and green curves are energies for elastic Gaussian and Hertzian shaped dimples, respectively, calculated using the EED model. Thin curves plot energy profiles for the water plume shapes of Fig. 2, described by the EHS model with interfacial tension γ=0.08 kT∕Ų (a) and γ=0.04 kT∕Ų (b). Cyan (squares) and blue (circles) on two thin curves are the upper and lower limiting cases that correspond to cylindrical and merged ellipse-cone shapes (Fig. 2, panels 1 and 3, respectively). The other five curves are closely spaced and intermediate between these two.

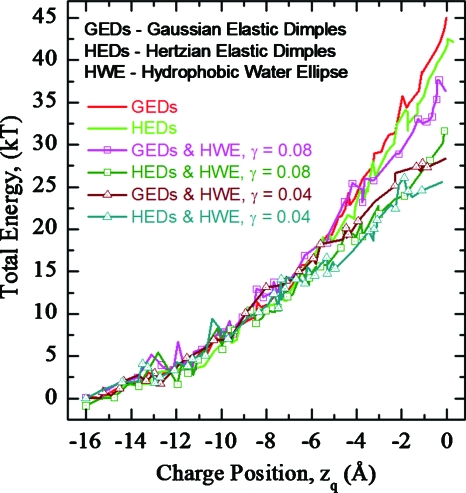
Figure 7 illustrates total energy profiles as a function of z_q in DOPC for “hybrid” fluctuations (Fig. 2, panel 5), describing plume water with an ε of 80. Charge translocation induces both elliptic water plume and elastic dimple fluctuations everywhere on the pathway (Fig. 8, see online enhanced video in .mov format where the charge moves up across a DOPC membrane). Near midmembrane (z_q>−6 Å) the water plume dominates energetics (Fig. 8) and the total energy (Fig. 7, four curves with symbols) is less than that of the pure elastic model (Fig. 7, two upper curves without symbols). Hertzian dimples are always slightly favored over Gaussian ones. The energy barrier drops as γ decreases. Elastic fluctuations at the membrane-water interface promote water penetration into the membrane interior. Both EED and EHS contribute to charge solvation.

Figure 7.

Total energy profiles as functions of z_q in a DOPC membrane for “hybrid” fluctuations with an elliptic water plume described by EHS and elastic water dimples described by EED (Fig. 2, panel 5). The water plume was assigned surface tension constants γ=0.04 kT∕Ų and γ=0.08 kT∕Ų. Effects due to both Gaussian and Hertzian dimple shapes are depicted. GED and HED refer to Gaussian and Hertzian shaped dimples, and HWE refers to plume shape: the hydrophobic water ellipse (Fig. 2, panel 5).

Figure 8.

Download video file ^{(2.5MB, mov)}

Hybrid fluctuations with an elliptic water plume (EHS) and elastic Hertzian water dimples (EED) for a charge crossing a DOPC membrane. The video depicts the case with γ=0.04 kT∕Ų. The charge moves from bottom to top. Near the membrane-water interface charge solvation mainly reflects elastic water dimple influences. As the charge approaches midmembrane, the water plume takes control. The size and shape of the plume fluctuate occasionally forming a continuous shunt. The movie is produced using the CE-MEA code (enhanced online).

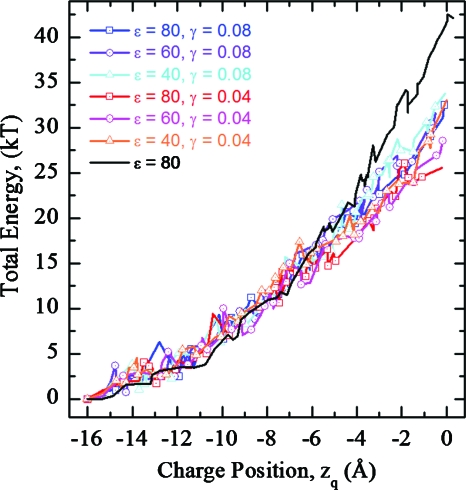
The dielectric properties of water plumes in the hydrophobic core of the membrane may differ from those of bulk water. Figure 9 illustrates the energetic effects of varying water plume ε and γ for hybrid EED∕EHS fluctuations (with Hertzian dimples). For z_q<−6 Å, the hybrid profiles of Figs. 79 closely mimic those of the pure elastic model (solid lines). However, for z_q>−6 Å energy barriers clearly drop due to water plume influences. Energy barriers are higher for water plumes with smaller ε and larger γ. For a midmembrane charge (z_q=0 Å) the energy varies within an ∼10 kT range, regardless of ε or γ.

Figure 9.

Total energy profiles as functions z_q in a DOPC membrane for hybrid fluctuations, illustrating the effects of varying water plume ε and interfacial tension γ. The black curve is the water plume-free case. Hertzian dimple shapes are used throughout.

Energy profiles are also sensitive to membrane elastic moduli. Total energies as functions of z_q in DOPC and DMPC membranes for hybrid fluctuations (panel 5) are plotted in Fig. 10 for a plume of ε 80. DOPC exhibits lower barriers, presumably due to its smaller bending modulus. Again, lowering γ also reduces the barrier.

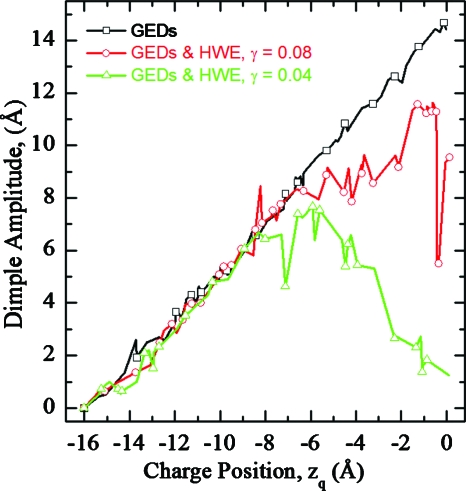
Charge solvation switches from EED to EHS at intermediate perturbation amplitudes. Figure 11 presents the mean amplitudes of Gaussian elastic dimples in DOPC membranes as functions of z_q. Amplitudes grow as the charge moves toward midmembrane. If plume formation is suppressed the amplitude grows steadily up to ∼15 Å (black curve with squares). Otherwise, dimple amplitude increases to ∼8 Å and then declines (green curve). This behavior is affected by the tension coefficient (compare green and red curves). Thus, nearer the membrane-water interface (z_q<−8 Å) charge solvation mainly reflects water dimple influences. For z_q>−8 Å and γ=0.04 kT∕Ų dimple amplitudes drop due to plume effects on charge solvation energetics and the dimple essentially disappears. Water penetrates the membrane’s interior and solvates the charge, an effect very sensitive to the tension constant for a midmembrane charge: for low γ an elliptic water-filled pore forms with a dramatic decease in dimple amplitude [green (triangles) curve in Fig. 11].

Figure 11.

Averaged (over 200 MC trials for each z_q) amplitudes of Gaussian-shaped elastic dimples in DOPC membranes as functions of z_q. Conventions of Fig. 7 apply.

CONCLUSIONS

We developed a novel continuum model for studying interactions between membrane-embedded charges and the membrane-water surface fluctuations in multidielectric environments. This model treats the reaction field of membrane-embedded charges, membrane elastic deformations, and formation of hydrophobic water-filled pores and plumes in the membrane interior. A unique feature couples electro∕elastic∕hydrophobic energy calculations with the kMCRPF method to evolve the membrane-water-charge system along the reaction coordinate. This introduces dynamics into the continuum model.

Membrane fluctuations play important roles in stabilizing membrane-bound charges. Charges far from the midplane, z_q<−4 Å, always promote significant thickness fluctuations and are solvated by elastic water dimples. Nearer midmembrane, a larger charge is required for membrane breakdown, triggering pore or plume formation. For a charge at midmembrane, this critical value is q∼0.8e. This charge-solvated state and the associated elastic deformations far exceed elastic theory’s range of validity,²² strongly suggesting that at some point there must be a switch from elastic membrane surface fluctuations to water-filled hydrophobic pore formation.

The transmembrane transition energy barrier is strongly affected by fluctuations and differs significantly from the classical picture, a planar (unperturbed) membrane. The optimized barrier shape alters from a wide bell to a parabola. Similar behavior was seen in atomistic MD simulations translating a charged arginine side chain across a lipid bilayer.¹⁷

Nearer the membrane-water interface, z_q<−6 Å, charge stabilization mainly reflects elastic dimple formation with a small additional effect from water penetration. For z_q>−6 Å a penetrating water plume dominates solvation; its formation is promoted by elastic fluctuations due to increased electric field strength near the top of the dimple.⁶ Overall charge translocation is strongly affected by the combined effect of the elastic and hydrophobic fluctuations. In the examples considered they reduce the barrier from ∼60–65 kT (planar membrane) to ∼25–30 kT. For comparison, the energy barrier found in MD simulations¹⁷ was ∼28.5 kT.

System behavior depends strongly on the parameters describing the water plume (dielectric and tension constants). The energy barrier drops with decreasing interfacial tension. Estimates of γ vary widely,^{47, 50, 57, 64, 65, 66} depending on interaction between hydrophobic bilayer organizational forces and curvature energy due to lipid head group tilt, attenuating hydrophobic influences. Our analysis indicates that the hydrophobic mechanism is competitive with elastic dimple formation for smaller γ. It should be noted that there are other important mechanisms that can assist in water penetration; among them perturbation of the packing of lipid headgroups, making the membrane interior more accessable.⁷²

The major feature of our analysis is its self-consistent treatment of electric fields and membrane perturbations, achieved by equilibrating local fluctuation profiles, crucial for the consistent analysis of charge stabilization. This differs from an earlier treatment²¹ where membrane profiles are imposed rather than determined by equilibration. That study predicted huge (∼20 Å) deformation amplitudes, suggesting the possibility of a hydrophobic mechanism.

Our analysis is likely applicable to voltage gating ion channels, which can involve large transmembrane motion of gating charges.^{8, 9, 10} Despite the voluminous simulation data available,^{17, 18, 19, 20, 23, 73, 74} the physical basis for the relatively small translocation barrier (only a few kT, consistent with transmembrane voltages of ∼<100 mV) is not yet understood. Another area where interfacial fluctuation may play a crucial role is in the transmembrane movement of ions.⁷⁵ It should be noted that charged-induced fluctuations, effectively smoothing the water∕membrane boundary, can provide a rationale for introducing a transitional region of increased dielectric constant as done in some continuous treatments.⁷⁶