Toward high-resolution homology modeling of antibody F_v regions and application to antibody-antigen docking

Abstract

High-resolution homology models are useful in structure-based protein engineering applications, especially when a crystallographic structure is unavailable. Here, we report the development and implementation of RosettaAntibody, a protocol for homology modeling of antibody variable regions. The protocol combines comparative modeling of canonical complementarity determining region (CDR) loop conformations and de novo loop modeling of CDR H3 conformation with simultaneous optimization of V_L-V_H rigid-body orientation and CDR backbone and side-chain conformations. The protocol was tested on a benchmark of 54 antibody crystal structures. The median root-mean-square-deviation (rmsd) of the antigen binding pocket comprised of all the CDR residues was 1.5 Å with 80% of the targets having an rmsd lower than 2.0 Å. The median backbone heavy atom global rmsd of the CDR H3 loop prediction was 1.6 Å, 1.9 Å, 2.4 Å, 3.1 Å and 6.0 Å for very short (4–6 residues), short (7–9), medium (10–11), long (12–14) and very long (17–22) loops respectively. When the set of ten top-scoring antibody homology models are used in local ensemble docking to antigen, a moderate to high accuracy docking prediction was achieved in seven of fifteen targets. This success in computational docking with high-resolution homology models is encouraging, but challenges still remain in modeling antibody structures for sequences with long H3 loops. This first large-scale antibody-antigen docking study using homology models reveals the level of “functional accuracy” of these structural models towards protein engineering applications.

INTRODUCTION

Therapeutic antibodies are powerful tools for the prevention and treatment of human and infectious disease because of their high affinity and specificity for target antigens. Since the first U.S. Food and Drug Administration approval of a therapeutic antibody over two decades ago, antibody drugs have become available to treat cancer, infectious and cardiovascular diseases, arthritis, inflammation and immune disorders,¹ and new therapeutic antibodies are driving further growth of the biotechnology industry. The discovery of high-affinity binders for target antigens is efficiently accomplished by the use of combinatorial libraries in various display platforms such as phage, ribosome, E. coli or yeast,^2–4 and structure-based computational techniques complement experimental methods for antibody engineering. Structures of antibodies with their antigens can yield insight into biological phenomena or drug and disease mechanisms, and the increasing sophistication of computational techniques makes it possible to increase antibody-antigen binding affinity^5,6 or deduce the structural origin of such affinity maturation.⁷ However, a crystal structure may not be readily available for most newly developed antibody sequences, in which case a high-resolution antibody homology model is needed to perform structure-based in-silico antibody engineering. Here, we describe the development and implementation of RosettaAntibody, a new protocol for high-resolution homology modeling of antibody variable domains (F_v).

Homology models can be particularly valuable if they are useful for docking or structure-based protein engineering such as increasing stability. Presumably, such downstream applications will be difficult since they require highly accurate structural models so that the atomic interactions across an interface can accurately capture the energetics of binding. Few tests have been published of the ability to use homology modeled structures in downstream predictive applications. The blind docking challenge known as CAPRI⁸ (Critical Assessment of Prediction of Interactions) has presented several homology modeling plus docking combination targets, with some predictive successes and some failures.⁹ Because antibodies are well studied structurally, they offer an ideal model system to test homology-model based docking. Template identification is considerably simpler than in generic homology tasks, and antibodies isolate the critical challenge of loop modeling which is likely to be of general interest for docking other proteins.

Whitelegg and Rees¹⁰ have authored an exhaustive review that summarizes the main issues in structure prediction of antibody variable domains. Briefly, the framework residues of the light and heavy chain variable domains (V_L and V_H) serve as the scaffolding on which the six complementarity determining region (CDR) loops are erected. The framework sequence and its β-sheet structure are generally well conserved, and the conformations of the non-H3 CDR loops are usually restricted to canonical structures that may be determined using sequence-based rules.^11–13 The difficulties in modeling the CDR H3 loop are well known:^12–16 no determinative rules can accurately predict structure from sequence for the entire loop region. Therefore, the H3 conformation is predicted de novo, which is challenging due to the hyper-variability in the sequence and length of the loop.¹⁷ At the same time, the continuous increase in the knowledge-base of solved antibody crystal structures aids in the comparative modeling aspects of F_v structure prediction.

Other groups have previously described protocols for F_v homology modeling.^18–20 The WAM¹⁰ (Web Antibody Modeling) server incorporates the antibody structure knowledge-base into a practical application that has been used by several groups, including our own, to build homology models for use in antigen docking^21–25 or to visualize the topographical location of binding site mutations.²⁶ Most of these studies required the use of experimental information such as the effect of site mutagenesis on binding in order to compensate for uncertainties in the model structures.

For use in the prediction of antigen interactions, the requirement that the paratope be modeled accurately makes antibody homology modeling a harder problem than it first appears. The geometry of the antigen binding surface is directly influenced by the particular canonical loop templates used for modeling of non-H3 CDR loops, the V_L-V_H orientation, and the accuracy of the CDR H3. There are also second-order effects on the binding site through the interactions of the CDR loops L2, L3 and H1 with H3,¹³ and the influence of the relative orientation of the V_L and V_H rigid bodies on the placement and interaction of the CDR loops.²⁷

Our main objectives are (1) to combine the existing antibody knowledge base with the high-resolution backbone and side-chain modeling capabilities of the Rosetta structure prediction suite²⁸ to generate high quality antibody F_v homology models and (2) to test those models for computational docking. To address all the relevant degrees of freedom in F_v modeling, we combine template selections with ab initio CDR H3 loop modeling and simultaneous optimization of the CDR loop conformations and the V_L-V_H orientation. The homology models are tested in antibody-antigen docking predictions, including a newly developed ensemble docking technique²⁹ that mitigates the uncertainty in the homology models by using a multiple-copy representation. To our knowledge, this is the first study to systematically benchmark docking using antibody homology models to delineate modeling aspects that are crucial for accurate prediction of the antigen interaction. Our ultimate goal is to build high-resolution antibody models that may be reliably used in various downstream docking and design applications.

RESULTS

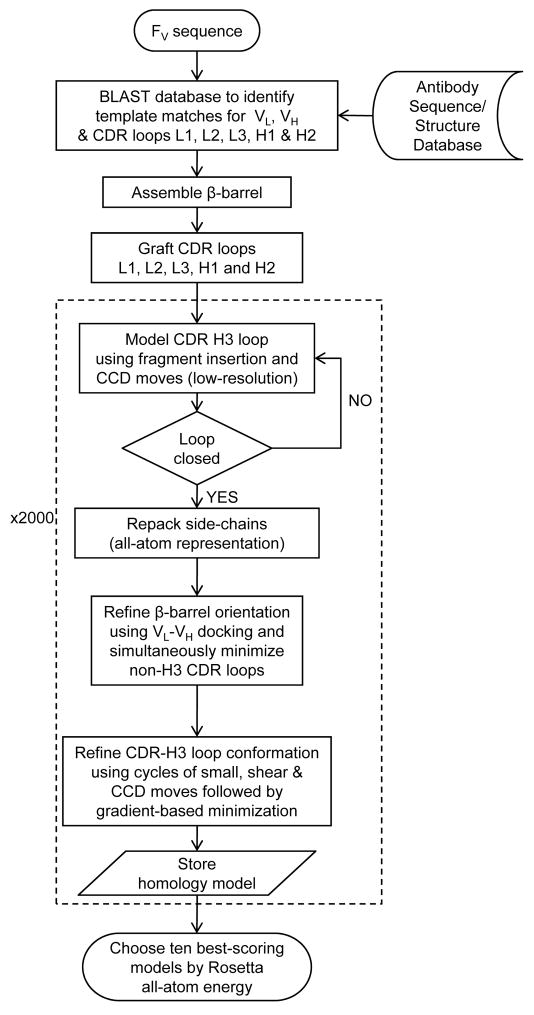
Figure 1 summarizes the antibody homology modeling algorithm which we have named RosettaAntibody. We start with the selection of the V_L and V_H framework region templates and assembly of the β-barrel, followed by the grafting of the non-H3 CDR loop conformations. The CDR H3 conformation is predicted via loop modeling, and the entire structure is refined using Monte Carlo minimization and the Rosetta all-atom energy function. To isolate the introduction of error in each step of the model building process, we first test the RosettaAntibody protocol for its ability to recover the crystallographic conformation (referred to henceforth as native) of the CDR loops given the native framework backbone (native loop recovery test). Subsequently, we test the ability to assemble a homology model starting from sequence in the absence of any information about the native structure (homology modeling test).

Figure 1.

RosettaAntibody flowchart. The dotted box envelopes the high-resolution CDR loop modeling and V_L-V_H rigid-body minimization steps.

Assembly of β-barrel

We analyzed the variation in relative V_L-V_H orientations by performing an hierarchical clustering analysis³⁰ on a set of 230 antibody crystal structures (non-redundant H3 sequences, resolution 2.8 Å or better). To focus on the domain interface, we clustered models based on the C_α rmsd of interfacial V_H residues (36–39, 46–49, 84–94 and 103–110; Chothia numbering¹²) after superposition of the V_L domains. At a radius of 2 Å, the structures collapsed into seven clusters. The largest cluster comprised 87% of the structures and consisted of κ-type light chains. λ-type light chains form the second largest cluster with 7% of the structures, due to the markedly different domain orientation in antibodies with this chain type.²⁷

Given the relatively tight clustering of the domain interface orientation, an average β-barrel approximation to represent the relative V_L-V_H orientation is reasonable.³¹ However, we follow Dyekjaer and Woods¹⁹ and use structural superposition to an antibody crystal structure from a database. That is, for each chain a template structure for the framework region is selected from the database by maximum BLAST³² bit score against the F_v chain sequence. Subsequently, the templates are oriented relative to each other using structural superposition onto a crystal structure with the highest sequence similarity for the entire F_v region. This approach captures the κ-type/λ-type differences and variations within those classes, and it reduces steric clashes across the domain interface that may result from an average β-barrel conformation.

The first section of Table I (V_H RMSD) lists the backbone heavy atom (N, C, C_α, O) rmsd-to-native of the V_H framework in the homology models created by homologous superposition alone (we will examine V_L-V_H rigid-body minimization later). The median rmsd value over 54 targets is 1.4 Å, with an rmsd under 2.0 Å for 45 of 54 targets. Most of the deviation arises from the relative V_L-V_H orientation since the individual V_L and V_H framework templates themselves have a median rmsd of 0.5 Å relative to the native backbone (data not shown). Sequence similarity between the query and template used for structural superposition varies between 75 and 85%, and the similarity does not have a strong influence on the resulting V_H rmsd. Rather, individual residues at the domain interface appear to exert a controlling influence on the relative orientation, creating the relatively small (~2 Å) differences in the orientation between different antibodies.

Table I.

Values of the backbone heavy atom (N, C_α, C, O) rmsd relative to the crystal conformation for the V_H domain after V_L superposition, CDR H3 after V_H framework superposition, and all six CDR loops after structural superposition of the loops. Targets are sorted by H3 loop length. The V_H rmsd’s are given for the initial framework template superposition (see text) and the low-rmsd RosettaAntibody homology model. The CDR H3 rmsd’s are given for the low-score and low-rmsd models from the native recovery (NatRec) and homology modeling (Homology) runs. The rmsd of the antigen binding pocket is given for the low-score and low-rmsd homology models.

Target PDB ID	H3 Length	Homology VH RMSD (Å)		H3 RMSD (Å)				Homology Antigen Binding Pocket RMSD (Å)
				Low Score		Low RMSD
		Initial	Low RMSD	NatRec	Homology	NatRec	Homology	Low Score	Low RMSD
2ddq	4	1.5	1.8	1.7	1.4	1.0	1.4	1.2	1.2
1dqq	5	0.1	0.1	0.3	0.3	0.2	0.2	0.3	0.2
1z3gb	6	1.8	2.5	1.8	2.4	1.5	1.8	1.4	1.3
2ai0	6	0.7	1.0	0.1	1.7	0.1	1.7	1.0	1.0
Median		1.1	1.4	1.0	1.6	0.6	1.6	1.1	1.1
1tet	7	2.0	1.4	0.8	1.1	0.6	1.1	0.9	0.9
1bqlb,d	7	2.6	3.6	1.5	1.6	1.4	1.6	1.1	1.1
1cgs	7	1.0	1.4	1.6	1.8	0.6	1.5	1.2	1.0
1mlbd	7	1.7	2.1	2.9	1.4	1.8	1.3	1.1	1.2
2cip	7	1.7	1.6	3.6	4.5	2.8	3.2	1.9	1.5
2bdnb,d	8	2.1	2.1	0.8	3.0	0.8	1.5	1.3	0.9
1fgnd	8	1.5	1.1	0.9	1.6	0.4	0.9	1.2	1.0
1jptd	8	1.9	1.6	0.9	2.2	0.6	1.4	1.1	1.0
1a6t	8	0.8	0.8	1.0	2.0	0.6	1.0	1.4	1.0
1kem	8	2.5	2.4	1.6	2.1	1.6	2.1	2.5	2.5
1qbld	8	1.8	1.9	1.8	3.3	1.1	2.6	1.5	1.4
1vfad	8	1.0	0.9	2.0	1.0	0.7	0.9	0.8	0.7
1iqd	8	0.1	0.6	3.7	3.4	2.7	2.7	1.4	2.7
1k4cb,d	9	0.9	1.2	0.6	2.7	0.6	1.4	2.0	1.6
1jhlb,d	9	1.2	1.2	0.9	1.1	0.8	0.7	0.8	0.7
2aepb,d	9	1.7	3.0	1.0	1.2	0.7	1.2	1.3	1.3
2fbj	9	2.4	2.4	1.1	2.7	0.8	2.6	1.9	2.2
1igt	9	2.3	2.3	1.3	1.7	0.7	1.3	1.2	1.1
2fd6b	9	2.6	2.3	1.4	1.9	0.6	1.5	2.7	1.7
2adfb	9	1.4	0.9	2.0	3.0	1.7	2.0	1.7	1.2
2jelb,d	9	1.2	2.6	2.0	1.4	2.0	1.4	1.1	1.1
1yntb,d	9	0.5	1.0	3.2	3.6	0.9	2.6	1.7	1.2
Median		1.7	1.6	1.4	1.9	0.8	1.4	1.3	1.1
1dba	10	1.4	0.7	0.7	4.0	0.7	1.4	2.2	1.4
2b2xb,d	10	2.3	3.2	0.9	7.8	0.6	3.6	3.4	1.9
1clz	10	0.9	0.8	1.0	2.0	0.6	1.9	1.3	1.3
2cju	10	1.8	1.8	1.2	1.2	1.1	1.2	1.0	1.0
1for	10	0.9	1.1	1.3	2.1	1.3	2.0	1.2	1.0
1kb5b	10	2.0	2.7	1.7	3.0	1.3	1.3	1.7	1.2
2aju	10	1.9	1.7	2.5	2.6	2.5	2.6	1.5	1.5
1ztxb,d	10	1.6	2.8	2.8	1.9	1.0	1.5	1.6	1.0
1mcp	11	1.2	1.1	1.1	2.9	1.1	2.3	1.3	1.3
1ncab,d	11	1.1	0.7	1.6	3.4	1.6	2.2	1.8	1.2
2fjgb	11	1.1	1.3	2.6	2.0	1.8	2.0	3.4	3.4
2h1pb	11	1.5	1.1	3.1	1.7	1.1	1.6	1.4	1.3
1fptb	11	0.9	1.3	3.6	2.2	1.6	1.6	1.1	1.0
2adg	11	0.9	0.9	3.7	4.2	0.6	1.1	2.1	0.8
Median		1.3	1.2	1.7	2.4	1.1	1.8	1.6	1.3
1igm	12	0.1	0.2	3.1	4.5	2.5	3.2	2.0	1.5
2fjhb	12	1.2	1.6	1.7	3.0	1.5	2.6	1.6	1.4
2g5bb	12	0.7	1.5	1.9	3.0	1.6	2.0	1.6	1.4
2h2pb	12	0.7	2.0	2.5	1.6	2.2	1.6	1.3	1.3
1fbib	13	1.9	1.8	5.7	5.8	4.7	5.8	2.6	2.6
1bj1b	14	0.1	1.0	2.0	2.8	1.5	1.6	1.2	0.9
1wc7	14	3.4	3.2	4.1	2.7	2.8	2.7	1.8	1.8
1zan	14	1.6	1.3	4.4	4.3	2.4	3.7	2.1	2.0
2aj3	14	2.4	2.0	3.3	3.8	2.6	3.7	2.3	2.1
2dqu	14	1.3	3.3	2.7	3.1	2.5	2.2	1.7	1.8
Median		1.3	1.7	2.9	3.1	2.5	2.7	1.8	1.7
1f58b	17	1.6	1.8	5.3	13.6	3.5	3.8	7.8	2.6
1hzh	18	1.1	1.8	2.7	6.4	2.7	3.0	3.1	1.5
1g9mb	19	0.1	0.7	2.3	4.6	2.3	3.5	2.2	1.9
2b4cb	22	1.2	0.9	5.9	5.6	3.3	5.1	3.3	3.0
Median		1.2	1.4	4.0	6.0	3.0	3.7	3.2	2.3

^bindicates the antibody crystal structure was determined in the antigen-complexed (bound) form.

^dindicates that the target is included in the subsequent docking studies.

The V_L-V_H orientation obtained using template superposition does not remain static during homology modeling, but is modified using rigid-body minimization of the domains subsequent to the low-resolution H3 modeling (see Methods). This step is carried out to eliminate steric clashes across the domain interface that result from threading the query F_v sequence on the framework region templates and typically results in distinct V_L-V_H orientations being obtained in individual homology models. The recovery of the native V_L-V_H orientation during homology modeling is extremely challenging not only due to the high-resolution nature of the problem (~ 2 Å), but also because the orientation is conditional on the specific CDR H3 conformation generated during de novo modeling. Therefore, the rigid-body minimization has been designed to eliminate unphysical interactions across the domain interface via minor rigid-body perturbations from the starting β-barrel, without explicitly attempting to recover the native V_L-V_H orientation.

The first section of Table I also shows the V_H framework rmsd (after V_L framework superposition) in the homology model with the lowest CDR H3 rmsd-to-native (the low-rmsd model). For 75% of the targets, V_L-V_H rigid-body minimization changes the V_H rigid-body position by 0.5 Å or less compared to the starting orientation in the β-barrel. For these targets, such minor rigid-body movement together with the side-chain repacking is sufficient to resolve high-energy interactions across the domain interface in the starting orientation. For the remaining 25% of the targets, V_L-V_H rigid-body minimization moves the V_H domain by 0.6–2.0 Å. The larger rigid-body change may be necessary either because the starting β-barrel template is sub-optimal for the query antibody sequence or because the inter-domain interactions need to be optimized given the H3 conformations generated during the low-resolution search.

Grafting of non-H3 CDR loops

Based on the analysis of antibody crystal structures available at the time, Martin and Thorton¹⁴ and Chothia and co-workers¹² spelt out the canonical paradigm for predicting non-H3 CDR loop conformations. Typically, the canonical class assignments mirror the loop lengths, and additional classes and sub-classes arise upon considering the identity of specific residue positions within the loop and the framework regions. There have been reports of antibody crystal structures with new canonical conformations that were previously unseen,³³ or modifications to the existing rules for assigning canonical classes for individual CDRs.³⁴ Recently, Whitelegg and Rees¹⁰ have revisited the issue of canonical assignments using ~100 antibody crystal structures. Their detailed analysis has confirmed the essential robustness of the original canonical rules for a majority of the loop conformations, but has also produced some new insights: in multiple cases, CDR loops were found to be conformational members of a given canonical class without complying in every detail with the sequence constraints (for instance, 11-residue L1 loops). There were also instances of loops complying with the sequence requirements for a particular canonical class, but belonging to an alternate class on conformational grounds, as is the case with the H2 loops of an anti-gamma-interferon antibody (Protein Data Bank³⁵ [PDB] ID 1b2w) and Fab fragment of a human IGG1 kappa autoantibody (1vge). It may also be deduced from their analysis that with limited exceptions, there is essentially a one-to-one correspondence between loop length and the canonical class assignment.

Due to the evidence that the loop length is an appropriate surrogate for the canonical class, we have chosen to identify the correct loop template based on the length alone without resorting to the rules for canonical class assignments. For each non-H3 CDR, the loop conformation to be used as the template for modeling is selected by maximum BLAST³² bit score to the query loop sequence. This loop template is grafted to the V_L or V_H framework by optimal superposition of the backbone atoms of two overlapping residues at each end of the loop. The BLAST search is performed against the set of known CDR loop conformations of the same length, without restricting the search to loops that belong to the same canonical class as the query. Any global sequence similarity criterion to identify loop templates may mask minor conformational effects, such as the rotation of a single peptide bond, that arise due to the identity of individual CDR or framework residues. To account for this possibility, the later stages of the protocol have been designed to incorporate minimal backbone flexibility in the non-H3 CDR loops so as to relax the loops into a conformation that is dictated by both intra-loop and CDR-framework interactions.

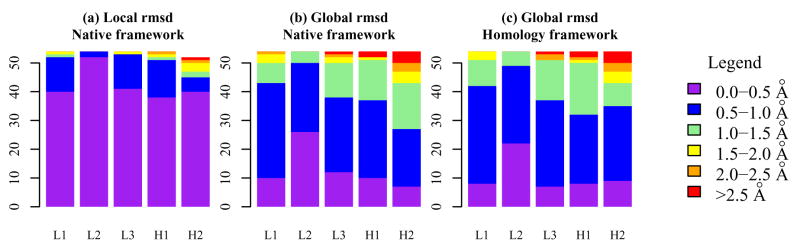
Table 1 and Figure 2 summarize the local and the global backbone heavy atom rmsd values for non-H3 CDR loops in 54 targets. Accurate predictions of the non-H3 CDR conformations to within 1 Å of the crystal conformation are achieved without first considering the canonical class assignments. A low value of the local rmsd – where the loop residue backbone atoms are optimally superposed on the reference loop without regard for the framework location – indicates that an accurate template has been chosen for the loop conformation itself. For CDR L2, the local rmsd is under 0.5 Å for 90% of the targets and under 1 Å for all targets (Figure 2A). For the other non-H3 CDRs, the local rmsd is under 0.5 Å for 60–75% of the targets depending on the CDR and under 1 Å in all but ten individual instances (Table II). These ten instances also fail by canonical classification^11–13 suggesting that the high rmsd values are due to a non-canonical conformation in the crystal structure. Extensive backbone minimization of the non-canonical non-H3 loop conformations would be a productive addition in a future version of our F_v modeling protocol.

Figure 2.

Histogram of local and global loop rmsd of non-H3 CDR loops after comparative modeling for 54 targets. (a) Local rmsd. (b, and c) Global rmsd after grafting of CDR template on (b) the native framework or (c) the BLAST-selected framework.

Table II.

Values of the local and global backbone heavy atom (N, C_α, C, O) rmsd relative to the crystal conformation for the non-H3 CDR loops.

Target	Local RMSD (Å)					Global RMSD (Å)
	L1	L2	L3	H1	H2	L1	L2	L3	H1	H2
2ddq	0.45	0.17	0.16	0.32	0.16	0.99	0.22	0.65	0.40	0.48
1dqq	0.20	0.28	0.17	0.54	0.36	0.33	0.37	0.28	1.19	1.17
1z3g	0.26	0.35	0.32	0.33	0.34	0.41	0.67	0.48	0.58	0.52
2ai0	0.41	0.18	0.21	1.00	0.66	0.82	0.30	0.69	1.29	0.81
1tet	0.48	0.16	0.28	0.38	0.41	0.68	0.27	0.59	0.82	0.55
1bqlb,d	0.65	0.28	0.22	0.53	0.77	0.95	0.54	0.29	0.91	0.96
1cgs	0.60	0.94	0.57	0.70	0.49	1.32	0.96	1.28	1.21	0.75
1mlbd	0.35	0.54	0.39	0.27	0.81	0.63	1.00	0.49	0.39	0.93
2c1p	0.33	0.17	0.32	0.37	0.35	0.51	0.38	0.93	0.96	0.61
2bdnb,d	0.30	0.29	0.34	0.52	0.15	0.48	0.78	0.61	0.77	0.30
1fgnd	0.59	0.41	0.39	0.30	0.56	0.68	0.69	0.85	0.97	1.67
1jptd	0.25	0.20	0.30	0.24	0.20	0.88	0.69	0.83	0.49	2.24
1a6t	0.33	0.67	0.82	0.28	0.34	0.87	0.88	1.65	0.66	0.58
1kem	0.41	0.24	0.94	0.57	0.27	0.76	0.42	2.66	0.77	0.71
1qbld	0.32	0.13	0.97	0.37	0.29	0.47	0.16	1.34	1.00	0.78
1vfad	0.21	0.37	0.25	0.32	0.23	0.46	0.55	0.68	0.86	1.33
1iqd	1.52	0.17	1.78	0.81	0.56	1.71	0.28	3.09	1.91	1.14
1k4cb,d	0.14	0.15	0.30	1.92	0.30	0.43	0.26	0.77	2.96	1.43
1jhlb,d	0.77	0.42	0.39	0.34	0.28	0.79	0.71	1.00	0.41	0.80
2aepb,d	0.31	0.74	0.21	0.19	0.23	0.67	1.13	0.45	0.45	1.00
2fbj	0.62	0.68	1.73	0.19	0.23	1.17	1.00	2.03	0.24	1.25
1igt	0.33	0.42	0.39	0.28	0.33	0.58	0.53	0.53	0.52	1.21
2fd6b	0.27	0.30	0.75	0.27	2.32	0.48	1.00	0.98	0.67	3.11
2adfb	0.18	0.38	0.13	0.38	0.48	0.35	0.90	0.25	0.66	0.90
2jelb,d	0.34	0.34	0.24	0.34	0.70	0.70	0.39	0.33	0.65	1.45
1yntb,d	0.52	0.43	0.62	0.39	0.44	0.73	0.52	0.77	0.86	0.97
1dba	0.39	0.32	0.74	0.42	0.48	0.69	0.44	0.86	0.73	0.86
2b2xb,d	0.25	0.19	0.48	0.24	0.14	0.61	0.35	1.00	0.73	1.00
1clz	1.34	0.33	0.28	0.34	0.41	1.59	0.49	1.00	0.55	0.70
2cju	0.41	0.57	0.14	0.42	0.91	0.99	0.80	0.52	0.59	1.64
1for	0.32	0.65	0.42	0.43	0.33	0.52	0.94	1.00	1.00	0.47
1kb5b	0.59	0.40	0.71	0.48	0.38	0.92	0.48	0.84	1.00	1.00
2aju	0.54	0.21	0.70	1.00	1.46	2.10	0.66	0.87	1.23	2.39
1ztxb,d	0.31	0.33	0.47	0.35	0.32	0.96	0.94	0.84	0.88	0.81
1mcp	0.57	0.68	0.56	0.46	0.88	0.94	0.92	0.88	0.61	1.72
1ncab,d	0.72	0.34	0.48	0.57	0.33	0.94	0.76	0.87	0.90	0.53
2fjgb	0.58	0.30	0.77	0.77	1.12	0.60	0.54	1.70	1.32	10.35
2h1pb	0.56	0.19	0.36	0.51	1.48	1.00	0.33	0.55	1.00	2.41
1fptb	0.46	0.65	0.37	0.54	0.24	0.64	0.70	0.67	0.85	0.70
2adg	0.76	0.31	0.42	0.31	0.21	1.00	0.41	0.70	0.46	0.67
1igm	0.76	0.25	0.68	0.31	0.78	0.93	0.51	1.15	0.40	1.20
2fjhb	0.55	0.17	0.43	0.76	0.34	0.92	0.64	0.79	1.12	0.93
2g5bb	0.36	0.20	0.20	0.23	0.27	1.21	0.28	0.44	0.73	0.91
2h2pb	0.89	0.34	0.97	0.31	0.42	0.93	0.70	1.13	0.54	0.81
1fbib	0.27	0.27	0.69	0.33	0.37	0.62	0.46	0.82	1.00	0.60
1bj1b	0.65	0.18	0.23	0.57	0.26	0.82	0.43	0.47	0.89	0.51
1wc7	0.41	0.65	0.59	0.29	0.30	1.85	0.99	1.40	0.46	0.90
1zan	0.24	0.20	0.70	0.37	0.41	0.37	0.61	0.74	0.93	0.65
2aj3	0.69	0.17	0.48	0.66	1.65	0.80	0.23	1.00	1.32	2.61
2dqu	0.33	0.14	0.21	0.30	0.19	0.69	0.21	0.36	0.56	1.15
1f58b	0.67	0.12	0.28	0.94	0.26	1.19	0.54	0.99	1.12	1.19
1hzh	0.26	0.44	0.43	0.33	0.36	0.63	0.46	0.51	0.86	0.98
1g9m	0.12	0.15	0.12	0.18	0.17	0.68	0.46	0.25	0.32	0.85
2b4cb	0.61	0.28	0.29	0.72	0.31	0.92	0.52	0.64	0.98	0.95
Median	0.41	0.30	0.39	0.37	0.35	0.78	0.54	0.81	0.84	0.93

^bindicates the antibody crystal structure was determined in the antigen-complexed (bound) form.

^dindicates that the target is included in the subsequent docking studies.

To test whether our predictions had identified the correct canonical loop class and whether the sequence based rules would have fared better, we examined the targets with high local rmsd (< 1 Å). In several cases, the loops did not match any canonical classification, and predictions might have to be made using sequence similarity to known loop conformations as we have done here. In cases that did match canonical rules, the rmsd of the canonical template was similar to that chosen using the BLAST search (data not shown). The large number of antibody structures in the PDB enables the use of simple database search methods to identify CDR loop conformations in most cases. However, the finite size of the database also imposes limits on the accuracies that are possible for loop lengths for which few database examples are available such as 10 and 12-residue V_κ L1 loops, or CDRs from V_λ light chains. In other cases, the accuracy is limited by the natural variation in the crystal conformation even for loops with identical sequences (for instance 16 and 17-residue L1 loops) such that the loop rmsd depends on the specific template chosen.

In addition to measuring the deviation of the loop itself, it is useful to measure the error in the global placement of the loop after grafting the CDR loop onto the scaffold. The global rmsd is the deviation of the loop residue backbone heavy atoms calculated after superposition of the framework residues, and it indicates the accuracy of the framework and the structural superposition of the loop. Figure 2b shows that when the loop template is grafted onto the native framework from the target crystal structure, the global loop conformation is modeled to an accuracy of 1 Å or better for the majority of cases. Figure 2c shows that grafting the loop template onto a scaffold identified using homology yields similar quality structures, indicating that the additional rmsd deviation from the crystal conformation arise mostly due inaccuracies in grafting the loop to the framework and not due to the choice of the loop itself or errors in the homology framework.

CDR H3 recovery on the native framework

To test our loop building procedure in isolation, we remove the CDR H3 from the crystal structure of the target and attempt to predict its conformation using loop modeling. Loop modeling consists of a low-resolution Monte Carlo-based backbone fragment assembly followed by smaller perturbations to the ϕ, ψ, and χ dihedral angles in high resolution, using cyclic coordinate descent (CCD)³⁶ to close the loops (see Methods). We perform these so-called “native recovery tests” on 54 targets with CDR H3 loops comprising between 4 and 22 loop residues.

We classify the loops as very short (4–6 residues), short (7–9), medium (10–11), long (12–14) and very long (17 and above). In the loop modeling field 11–13 residue loops are considered long,^37,38 and accuracies approaching 1–1.5 Å loop rmsd for these lengths have been demonstrated only under ideal loop modeling conditions in which the structure of the backbone and side-chains and crystal contacts outside the loop region are retained from the crystal structure. In recognition of the challenges in modeling long loops, 75% of the targets in this study contain 11 or fewer residues in the CDR H3. However, the CDR H3 length diversity of the murine and human H3 repertoire is larger, with approximately 15% and 40% respectively of the human and murine antibody sequences comprised of Kabat CDR H3 lengths longer than 11 residues.¹⁷ To capture this diversity, we have included 14 targets with 12 or more residues in the CDR H3.

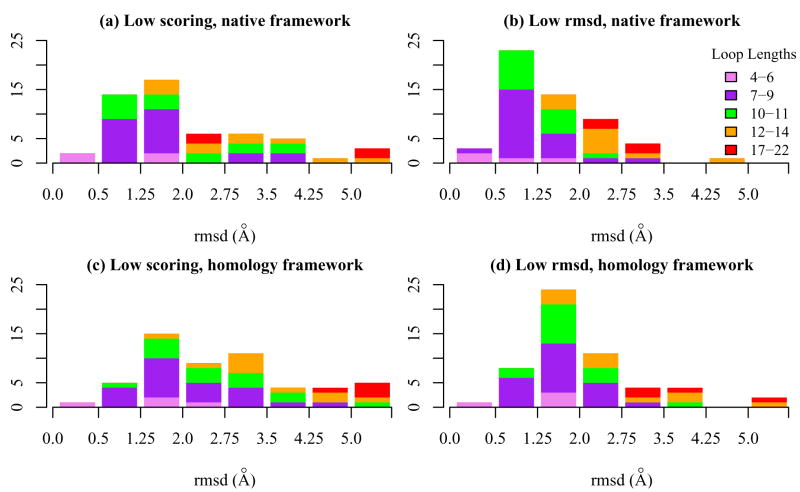
For the native recovery tests, the second section of Table I (H3 RMSD) lists the global backbone heavy-atom rmsd of the CDR H3 loop in the lowest all-atom energy model among all conformations (the “low-score model”) and the lowest global CDR H3 rmsd model among the ten lowest scoring models (the “low-rmsd model”). The low-rmsd model is not known in a blind structure prediction exercise, but serves as a useful metric to rate the ability of the protocol to discriminate near-native CDR H3 loop conformations. Histograms showing the accuracy of CDR H3 loop modeling for all loop lengths are shown in Figure 3.

Figure 3.

Global loop rmsd of CDR H3 in native recovery and homology modeling simulations for 54 targets. (a) Lowest scoring and (b) lowest rmsd models from the native recovery simulations. (c) Lowest scoring and (d) lowest rmsd models from homology modeling simulations.

11-residue and shorter CDR H3

We first present the analysis for loop lengths under 11 residues. For this set, the low-score models have a CDR H3 global rmsd-to-native of 1.25 Å or better for 16 of 40 targets, and the rmsd is under 2 Å for 30 targets (Figure 3a). If the pool is expanded to the ten lowest scoring conformations, 26 targets (~65%) have a rmsd under 1.25 Å and 37 targets (~90%) have a model with rmsd under 2 Å (Figure 3b). The median rmsd values of the predictions increase with loop length. For the low-score models, the median rmsd values are 1.0 Å for the very short loops, 1.4 Å for the short loops and 1.7 Å for the medium length loops. The corresponding values for the low-rmsd models are 0.6, 0.8 and 1.1 Å respectively.

For several targets, the loop modeling algorithm samples adequately, but the final discrimination of near-native CDR H3 loop conformations is limited by errors in the scoring function. For instance, of the ten targets that have rmsd < 1.25 Å for the low-rmsd models but not the low-score model, six produce over 15% of structures with rmsd under 1.25 Å in the 200 top-scoring homology models. In fact, for some of these targets the incorrect models score better than the native crystal structures. In other targets, sampling is a limiting issue, including two targets with an extended H3 base conformation (1bql and 1qbl) and five loops (1kem, 2jel, 2adf, 1kb5 and 2aju) that have so-called “atypical conformations” as defined by Whitelegg & Rees.¹⁰ None of the CDR H3 backbone dihedral angles in these targets are in disallowed regions of the Ramachandran plot. Low sampling is probably due to poor representation of fragments required to create a CDR H3 loop with atypical conformation in the pool of allowable fragments. Subsequent V_L-V_H rigid-body minimization improves the sampling of decoys with CDR H3 global rmsd-to-native under 1.25 Å for targets 2jel and 1kb5 (but not the final discrimination of the near-native loop conformations), suggesting that the lack of sampling diversity in the native recovery tests might be due in part to unfavorable interactions across the domain interface in the target crystal structures.

12-residue and longer CDR H3

None of the 14 targets with 12 residue or longer CDR H3 loops has a low-score or low-rmsd model with CDR H3 global rmsd under 1.25 Å. Two 12-residue loops (2g5b and 2fjh) and one 14-residue loop (1bj1) have low-score models with rmsd < 2.0 Å. If the low-rmsd models are considered, all long-loop targets except 1fbi have a model under 3 Å, with a median of 2.5 Å.

For very-long loop targets 1hzh (length 18) and 1g9m (length 19), the low-score and low-rmsd models coincide and have an rmsd value of 2.7 Å and 2.3 Å respectively. This is an impressive result, considering the conformational space that is potentially sampled by a loop of this length.

Complete antibody homology modeling

Having benchmarked the accuracy of H3 loop modeling under ideal conditions, we now combine the three modules of β-barrel assembly, CDR grafting and H3 modeling to emulate a blind prediction of the complete F_v structure. The β-barrel and the non-H3 CDR loops are modeled using homologous template structures to create the acceptor scaffold, and the CDR H3 is built on this scaffold. Furthermore, the homology model subsequently undergoes backbone minimization of the non-H3 CDR loops and rigid-body movement of the V_L and V_H domains relative to each other. Therefore, the conformations of these regions in the final homology model are different from that in the starting acceptor scaffold.

CDR H3 accuracy

The second section of Table I (H3 RMSD) lists values of the CDR H3 global backbone heavy atom rmsd values for complete homology models. Of the 40 targets with 11-residue or shorter CDR H3 loops, six targets (compared to sixteen in the native recovery test) have a low-score model with a CDR H3 rmsd-to-native of 1.25 Å better, and 20 targets (50%) have an rmsd better than 2 Å. If the low-rmsd models are considered, 31 targets (compared to 37 in native recovery) return a prediction better than 2.0 Å. Although the accuracy clearly suffers from the scaffold errors, these results are encouraging given that no aspect of the backbone or side chain conformations of the target crystal structure is used during the modeling.

For the 10 targets with loop lengths 12–14, the rmsd values of the low-score and low-rmsd models ranges from 1.6 to 5.8 Å. For the very-long loop targets, the rmsd of the low-score models range from 4.6 Å for target 1g9m to 13.6 Å for target 1f58. Three of the four very long-loop targets have a low-rmsd model with an accuracy of 3.8 Å or better.

Eighteen targets with CDR H3 lengths between 7 and 11 inclusive are also featured in the original WAM study.³¹ In the WAM publication, the final H3 loop conformation was chosen using one of so-called VFF, accessibility or rmsd screens. The rmsd screen computes the local rmsd between the loop model and known crystal structure H3 loop conformations of the same length and combines this with the sequence similarity of the two loops to rank the loop model. In ten of the eighteen targets that overlap between the respective studies, the CDR H3 rmsd in the rmsd-screened WAM³¹ model is lower than or equal to that of the low-score RosettaAntibody model. However, in two-thirds of the targets, there is at least one prediction among the ten best RosettaAntibody models that has an rmsd lower than or equal to that of the WAM prediction. These results suggest that an improved strategy to discriminate near-native conformations among the ten best models either by improvements to the scoring function or by the use of a WAM-type rmsd-screen can significantly enhance the accuracy of RosettaAntibody’s final prediction.

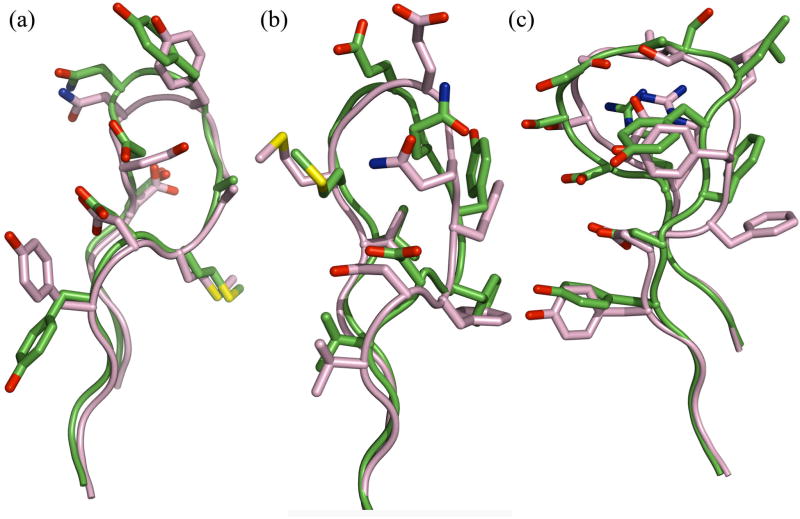
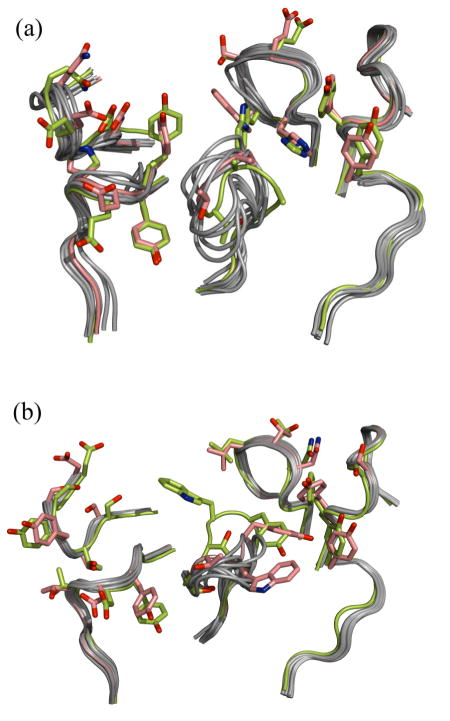
Figure 4 provides representative illustrations of high, medium and lower quality successful loop predictions obtained from homology modeling. The model for the 9-residue loop in D3H44 Fab (1jpt, Figure 4A) has a backbone rmsd value of 0.9 Å, and the high prediction quality is evident from the accurate superposition of the backbone and side chains in the homology model and the crystal structure. For jel42 Fab (2jel, Figure 4B), the prediction has an rmsd of 1.4 Å. In this medium-quality prediction, all backbone atoms are accurately positioned relative to the crystal except those of the glutamate and glutamine residues at the apex. For antibody 2H1 (2h1p, Figure 4C), an 11-residue loop target, the rmsd of the predicted loop is 1.7 Å. The loop model is faithful to the contours of the crystal loop conformation, but the backbone inaccuracies are amplified in the positioning of the side chains.

Figure 4.

Examples of high, medium and lower quality loop CDR H3 modeling predictions from homology modeling simulations with V_L-V_H rigid-body minimization. Structures are superposed using the C_α atoms of the V_H framework. (a) HyHEL-5 Fab (1jhl), CDR H3 loop length 9, global rmsd 1.1 Å (after superposition of V_H); (b) jel42 Fab (2jel), CDR H3 loop length 9, global rmsd 1.4 Å; (c) antibody 2H1 (2h1p), CDR H3 loop length 11, global rmsd 1.7 Å.

Binding surface rmsd

While local and global loop rmsd measures speak to the accuracy of structure prediction itself, the binding surface backbone heavy atom rmsd gauges the suitability of the model for applications involving antigen interactions. This rmsd is computed over the CDR residues after optimal superposition of all CDR loops, thus incorporating information in the CDR conformations within each domain as well as the relative domain orientation. The third section of Table I lists values of the binding surface rmsd for homology models for all the targets. The lowest scoring homology models have a median rmsd value of 1.5 Å and the binding surface is modeled to an accuracy of 2 Å or better in 80% of the 54 targets.

The accuracy with which RosettaAntibody predicts the geometry of the antigen binding surface is shown in Figure 5 for two targets. The figure shows all six CDR loops structurally superposed with the CDR loops in the crystal structure for the ten lowest scoring RosettaAntibody models. The CDR H3 is located at the center of the binding surface, and the loop conformation clearly varies among the different models. The figure also highlights the spread in the positioning of the non-H3 CDR loops resulting both from the V_L-V_H rigid-body minimization and the conformational variability due to direct minimization of these loops. Such variability may compensate for uncertainties in the modeling process.

Figure 5.

The antigen binding surface of the ten top-scoring homology models superposed on the antibody crystal structure for (a) D3H44 Fab (1jpt) and (b) 4F11E12 Fab (1ynt). The native conformation is colored yellow-green and the low-rmsd model is colored salmon. Side chains are shown for the native and low-rmsd structures for CDR residues that contact the antigen in the co-crystal structure.

Antibody-antigen docking

An important motivation driving high-resolution homology modeling of antibodies is that the resulting models are useful for downstream applications such as antibody-antigen docking. Here, we have benchmarked the performance of RosettaAntibody models in local antibody-antigen docking of fifteen targets with known complex structures. Local docking, where starting positions are generated from random perturbations from an input structure, attempts to identify a near-native complex conformation when sampling conformation space up to 30 Å rmsd (ligand backbone heavy atom) from the starting configuration. Local docking is often used to make blind structural predictions^9,39,40 of an antibody-antigen complex when some biological information is known about interacting residues (e.g. mutational information) to provide a reasonable estimate of the binding orientation,⁴⁰ and its success is a necessary condition for successful global docking.⁴¹

The docking studies were carried out using RosettaDock,⁴¹ a Monte Carlo-based docking algorithm that simultaneously optimizes rigid-body position and side-chain conformation. RosettaDock has been used successfully by several groups in the CAPRI (Critical Assessment of PRediction of Interactions) blind docking challenge.^9,40,42,43 As an input to the program, we use the unbound structure of the antigen except in cases where such a structure was unavailable in the PDB, in which case we use the bound backbone coordinates. The docking models are assigned CAPRI-style accuracy ratings of “high”, “medium”, “acceptable” or “incorrect” that depend on the rmsd-to-native of the ligand position, the interface rmsd to native and the fraction of native residue-residue contacts that are recovered in the model (see Methods).⁴⁴ It is typically challenging to achieve high-quality docking predictions, especially with homology models and in the absence of biological information regarding the interaction site of the protein partners. For instance, in the latest CAPRI rounds (6 through 12) predictor groups worldwide produced a high-quality prediction for only one of seven targets, and medium-quality predictions for three others.⁴⁵

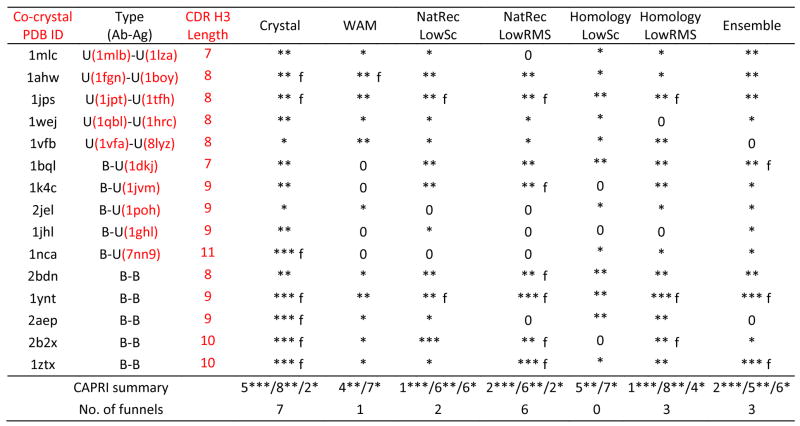
Consistent with the CAPRI assessment criteria, we report the quality of a prediction as that of the most accurate structure among the ten lowest scoring docking decoys. Additionally, we stipulate that the docking run produces an ‘energy funnel’ if at least five decoys of medium or high quality are present in the ten lowest scoring decoys. A funnel indicates convergence of the docking simulation towards the native complexed structure.⁴⁶ Creation of one model with prediction quality of at least ‘medium’ among the ten top-scoring docking models is a fairly generous criterion for docking success; the presence of an energy funnel is a conservative criterion. Table III presents a summary of the docking results, and the docking results of a monocolonal antibody complexed with surface antigen 1 of Toxoplasma gondii (1ynt) are used throughout as an example.

Table III.

Results of antibody-antigen docking simulations. PDB IDs under the “Type” column indicates the unbound component structures when available. Docking runs are annotated as unbound-unbound (U-U), bound-unbound (B-U) or bound-bound (B-B) depending on the use of bound/unbound antibody/antigen crystal coordinates in docking. Crystal indicates docking runs using crystal structure coordinates for both antibody and antigen; WAM indicates docking runs using with the Web Antibody Modeling models built using the web server. NatRec indicates docking runs using the CDR H3 native recovery models, and Homology refers to runs using RosettaAntibody homology models, respectively. For RosettaAntibody runs, results are shown for both the low-score model (LowSc) and the low-rmsd among the ten top-scoring models (LowRMS). Ensemble indicates runs using the ten top-scoring homology models. Three stars (***), two stars (**), one star (*) and “0” indicate that at least one of the ten lowest energy docking decoys is of high, medium, acceptable and incorrect quality respectively, according to the CAPRI definitions.⁴⁴ Predictions marked “f” additionally exhibit a docking funnel, i.e. five of the ten lowest scoring structures are of medium or high quality. The penultimate row shows the number of targets for which at least one of the ten lowest-energy docking decoy is of high/medium/acceptable quality, and the last row shows the number of targets with a funnel.

Docking with single antibody models

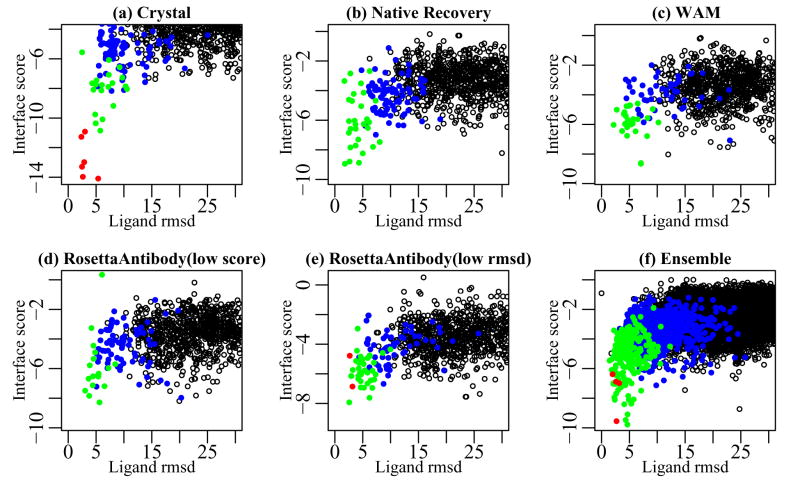
The results of docking using antibody and antigen crystal structures (bound structure if unbound is unavailable) represent the theoretical maximum of RosettaDock’s prediction accuracy for a given complex. Figure 6a illustrates a typical result for crystal structure docking using a plot of interface score vs. ligand rmsd for target 1ynt. The presence of an energy funnel is evident in the figure as nine of the ten lowest energy structures are of medium or high quality. Thirteen of the fifteen targets in our docking benchmark returned a medium or high quality prediction and seven of these cases exhibited an energy funnel. These results corroborate previous results^47,48 that while significant challenges still exist, accurate antibody-antigen docking using crystal structures is feasible and is a currently an active area of research.

Figure 6.

Docking energy landscape plots for 4F11E12 Fab complexed with surface antigen SAG1 (1ynt). High-quality decoys (CAPRI criteria⁴⁴) are indicated by red points (●), medium-quality decoys are indicated by green points (●), acceptable quality decoys are indicated by blue points (●) and incorrect predictions are indicated by open points (○).

Subsequent docking simulations, carried out using the native recovery model with the CDR H3 loop modeled de novo or with the RosettaAntibody models that retain no aspect of the native antibody conformation, reveal the extent to which deviations from the antibody crystal structure decrease docking accuracy. With the lowest scoring native-recovery model, we obtained six medium-quality and one high-quality prediction with two energy funnels, compared to seven funnels for crystal structure docking. While docking of target 1ynt with the native recovery model produces an energy funnel (Figure 6b), the best model among the ten lowest energy structures is of medium quality, compared to the high quality prediction obtained in crystal structure docking. Docking with the lowest scoring RosettaAntibody model results in lower quality predictions than those obtained using the lowest scoring native recovery models; a medium quality docking prediction was obtained for five targets, but none of the targets returned a funnel. Docking using the WAM models yields similar results with four predictions of medium quality and one funnel. For target 1ynt, docking using the RosettaAntibody model (Figure 6d) shows comparable results to that using the WAM model (Figure 6c): both produce a medium quality prediction but lack an energy funnel. These results underscore the challenges of using even high resolution, moderately accurate structural models towards functional ends such as antibody docking.

It is of interest to investigate whether docking would have been more successful if the antigen were docked to the low-rmsd model (instead of the low-score model) from the native recovery and homology modeling simulations. Such a case would be relevant if improvements in the energy function allowed the correct identification of the closest model. Docking with the low-rmsd native recovery model produces one extra high-quality prediction, but the results are otherwise similar to docking with the low-score model. Docking with the low-rmsd RosettaAntibody model not only results in one extra high and medium-quality prediction each, but also produces three funnels where there were none in the docking with the low-score models. The results for 1ynt using the low-score and low-rmsd RosettaAntibody models (Figure 6d and 6e) reflect this trend. The low-score model achieves a medium quality prediction without a funnel, while the low-rmsd model achieves a high-quality prediction with an energy funnel. The success of the low-rmsd models suggests that for several targets, structural models exist among the ten low-scoring RosettaAntibody models that are accurate enough for downstream functional applications.

Ensemble docking with ten low-scoring RosettaAntibody models

A typical real-world antibody engineering application may involve starting with the sequence of a new antibody for which a crystal structure is unavailable, building a homology model from sequence, and using this to predict the paratope-epitope interactions with the antigen via computational docking. In this scenario, the low-rmsd antibody model is not known a priori. One may perform docking with a single antibody model (for instance, the low-score model), in which case the docking accuracy may be limited by the quality of the CDR H3 loop prediction in the particular instance. Alternatively, one may use multiple antibody models (for instance, the ten top-scoring models) in independent docking runs, with a proportional increase in the computational cost and the difficulty of discriminating the near-native docking models by comparing the independent runs.

Our lab recently developed an ensemble docking method that can dock multiple input structures simultaneously in a single docking run.²⁹ The method was shown to outperform docking protocols that were based on a single-copy representation of the interacting proteins, but without a proportional increase in the computational cost. In the specific application to antibody-antigen docking, the ensemble method allows us to dock the ten (or more) top-scoring antibody models, and is especially useful in situations where an antibody model with a near-native H3 loop conformation is among the ten top-scoring models, but is not the low-score model.

Ensemble docking using the set of the ten top-scoring antibody models produces two high-quality and five medium-quality predictions, together with funnels for three targets. Ensemble docking thus achieves an overall accuracy similar to that obtained using the low-rmsd RosettaAntibody model, but does so even in cases where the identity of the low-score and low-rmsd models do not coincide. These results are also an obvious improvement over those obtained using the single low-scoring RosettaAntibody or WAM models (five and four medium-quality predictions respectively).

Figure 7 depicts the medium-accuracy ensemble docking prediction (ranked 8^th by interaction energy) of HyHEL-5 Fab-bobwhite quail lysozyme complex (1bql). This model emerged from the docking of the ensemble of RosettaAntibody models to the unbound antigen (1dkj); the latter deviates by 0.63 Å from its bound form. The antibody homology model selected from the ensemble during docking is the one with the third-lowest H3 rmsd to the native structure. In the docking model, the ligand rmsd-to-native in the docking model is 1.81 Å, the interface rmsd is 1.36 Å, and 76% of the native residue-residue contacts are recovered. Interestingly, docking with the bound antibody crystal and the unbound antigen achieves similar interface rmsd and native contacts, but a poorer ligand rmsd (4.4 Å). A backbone conformational change of the CDR loops is required to relieve the steric clashes that occur when the unbound lysozyme is superposed on the bound lysozyme in the complex. Indeed, in the antibody homology model in the predicted complex structure, the CDR L3 and the apex of CDR H3 move away from their respective bound conformation to avoid the clash, and the CDR H3 loop conformation is 1.9 Å rmsd from the native structure.

Figure 7.

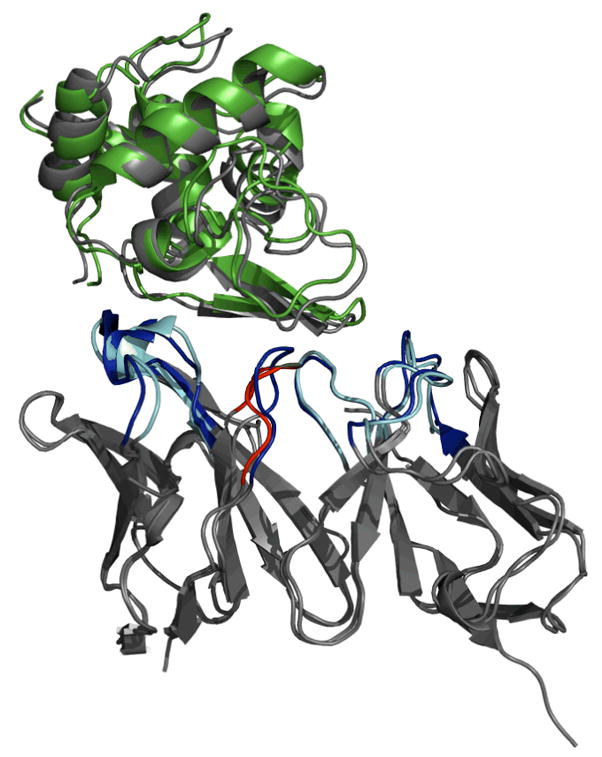
Medium accuracy antibody-antigen complex structure predicted for HyHEL-5 antibody complexed with lysozyme (1bql). Docking was performed using the ensemble of the ten low-scoring RosettaAntibody homology models. The antigen is unbound lysozyme (1dkj). The antibody framework regions and the bound antigen are gray, and the docked antigen in the model is green. The CDR loops of the native structure are blue, the non-H3 CDR loops of the homology model antibody are cyan, and the CDR H3 of the homology model antibody is red.

DISCUSSION

We have developed an antibody modeling protocol which is accurate enough to enable successful antibody-antigen docking starting with the antigen structure and the antibody sequence alone. This approach will be useful for new therapeutic antibodies for which experimentally determined coordinates are not available, as docking models can help identify epitopes, and structure-based designs can further engineer affinity or selectivity. Further, while antibodies are important to the biotechnology and pharmaceutical industry, the docking of homology models is of broad interest to biology in general. This study on antibodies serves as a model of the potential for more routine use of homology models in docking and design applications. Of course, more general applications will not be able to leverage the extensive database of structures and knowledge of antibody structures as we have done here.

We have exploited the larger antibody structural database available and combined several structural modeling techniques to create high-resolution antibody models. The antigen binding surface is collectively determined by the conformation of the CDRs as well as the relative orientation of the variable domains, and the combination of CDR loop modeling and rigid-body minimization of the entire variable region allows fine control over the geometry of the binding surface. An important contribution of this work is a detailed accounting of the accuracy and error associated with each modular task in the homology modeling process, providing benchmarks for measuring future efforts to improve antibody structural accuracy. The global conformation of the non-H3 CDRs is predicted to an accuracy of 1 Å or better in about 70% of the targets. The deviations of the CDR global conformation in the homology models usually arise as a result of the incompatibility of combining loop and framework templates from different crystal structures. In a few cases, the target CDR adopts a non-canonical crystal structure conformation in which case comparative modeling based on a database search may not produce an accurate outcome.

One of the major limitations of antibody modeling remains loop modeling, both for accuracy and computational cost. Recent advances in conformational sampling^37,38 make it possible to consistently predict the conformations of 11–13 residue loops with accuracy better than 1.5 Å. These results were obtained in simulations in which the protein side-chains except those located on the loop retained the native conformation, and the effect of crystal contacts on the loop conformation was included, although there is evidence that dropping the latter advantage does not decrease the prediction accuracy.⁴⁹ A fairer comparison to the results from our native-recovery simulations results is obtained by considering a recent loop-modeling study using the LoopBuilder protocol on a set of targets different from the ones in our benchmark. The median rmsd of the low-score native recovery models in this study is equal to or lower than the LoopBuilder values for 8-residue and 10-residue loops and larger than the LoopBuilder value for 9 and 11-residue loops. However, the median values of the low-rmsd native recovery model (0.7, 0.8, 1.05 and 1.35 Å for loop lengths eight through eleven) are lower than the corresponding LoopBuilder value for all loop lengths.

A second limitation arises from the accuracy of the energy function, as evidenced by the fact that the low-rmsd models are not always the top-scoring models. Long loops that extend into solution may require a better solvation model. Antibody interfaces are more charged than others,⁵⁰ and electrostatic energies are difficult to calculate accurately.⁵¹ Specifically, the base of the CDR H3 loop frequently has charged residues,¹⁷ resulting in dominant inter- & intra-chain electrostatic interactions.⁵² Because antibody binding regions can be more charged and contain an excess of tyrosine and tryptophan residues, the homology modeling and docking decoys (available upon request) would be useful for testing improved electrostatic models and better aromatic representations.

The antibody-antigen docking performance compares well to that in the latest rounds (Rounds 6–12) of the CAPRI challenge, where predictor groups worldwide produced high-accuracy prediction for only one of seven targets and only three targets received medium or acceptable quality predictions.⁴⁵ In the recent rounds, the two structures which required homology modeling of at least one docking partner had only acceptable quality docking predictions.⁴⁵ In this study, the antibody predictions are able to exploit more homology information than the CAPRI targets, and the docking has been limited to explorations of the local docking funnel, but the results are encouraging for the first large-scale docking study using antibody homology models. Docking using the low-rmsd RosettaAntibody models is successful for seven of the fifteen docking targets. Since the low-rmsd model is not known a priori and given the difficulties of achieving high-resolution accuracy in a homology model, an alternative approach is to generate multiple models to capture the extent of the uncertainty. In cases presented here, using the ten top-scoring models was sufficient to significantly improve docking accuracy through ensemble docking. Many flexible backbone docking methods are under active development⁵³ and may eventually enable explorations of more dimensions of the uncertainty of a homology model, such as the H2 loops which often interact with the antibody and the long L1 loops that were difficult to model accurately with grafting.

It would be useful for scientists who use the RosettaAntibody protocol in blind, predictive applications to estimate the confidence expected in docking predictions. We have observed a weak correlation in the docking accuracy (by ligand rmsd) with the mean sequence identity of the non-H3 CDRs and V_H-V_L templates and the CDR H3 length (Pearson test, significance level, α=0.05⁵⁴). Targets with template sequence identities below 90% and/or CDR H3 loop lengths of 10 or above have a less than 35% chance of producing one of the ten top-ranked docking models with a ligand rmsd below 8 Å. These conclusions have been made on the small dataset of fifteen targets, so these trends should be interpreted with caution.

The antigen docking results show that loop rmsd is not the sole indicator of the “functional accuracy” of a homology model. The functional accuracy of a homology model in docking simulations varies by target and is determined by some of the canonical loop conformations as well as the H3 modeling accuracy. Each modeling step is interdependent and the overall model quality is a complex function of the multiple structural elements. These findings are likely to apply beyond antibody modeling to homology modeling in general. That is, the value in homology models is the utility of the model for drawing scientific conclusions. Such utility could be measured by the ability to predict the effect of mutations or the ability to predict binding partners and complexed conformations, in addition to general inference of function.⁵⁵ The comparative modeling division of the Critical Assessment of Structure Prediction has recently achieved some encouraging cases of rmsd improvement on the template rmsds,⁵⁶ but as structure prediction techniques become more physically realistic, a more revealing measure might be an assessment of the functional accuracy of structural models.

CONCLUSIONS

We have introduced an antibody homology method that is more physically realistic than previous treatments³¹ through the use of an updated antibody database and a combination of interdependent protein structure prediction techniques including loop modeling, docking, and high-resolution refinement. The models were demonstrated to be useful for antigen docking, particularly when an ensemble of antibody models was used to provide robustness. RosettaAntibody models promise to widen the applicable targets for practical structure-based antibody engineering tasks such as predicting structural changes due to antigen binding,⁵⁷ predicting the structural consequences of antibody humanization^58,59 including those related to the change in the V_L-V_H orientation,⁶⁰ dissecting structural aspects relevant to antibody cross-reactivity and specificity,^61,62 and improving antibody affinity.^63,64

MATERIALS AND METHODS

Antibody structure database for comparative modeling

From the approximately 700 antibody structures in the Summary of Antibody Crystal Structures (SACS) compilation⁶⁷ (http://www.bioinf.org.uk/abs/sacs), we curated a subset of 569 structures (502 V_L-V_H dimers, 50 V_L dimers and 17 V_H dimers) by eliminating NMR structures and crystal structures with resolution above 3.5 Å. When multiple copies of structures were available, we arbitrarily chose one copy. The resulting set serves as the primary knowledge-base for the comparative modeling aspects of the protocol such as the framework and CDR template identification and CDR H3 kink modeling.

For this study, antibody residues are numbered according to the Chothia numbering scheme.¹² V_L CDR loops L1-L3 are constituted by residues 24–34, 50–56 and 89–97, respectively, and V_H CDR loops H1-H3 are constituted by residues 26–35, 50–56 and 95–102, respectively. Residues outside the CDR definitions constitute the framework regions.

Antibody benchmark set

A new set of 54 antibody crystal structures serves as the target benchmark for testing the protocol including 18 targets featured in the original WAM study.³¹ Isolated antibody structures were chosen if possible, but some antibody structures were extracted from the co-crystal structure of the antigen-bound complex. The set of 54 antibodies covers a wide range of CDR H3 loop lengths (4–22 residues) to illustrate the scope and limitations of loop modeling. To emulate blind prediction, when database information is used in modeling, only non-related (less than 90% sequence identity) antibody structures in the PDB were used.

Homology modeling protocol

Figure 1 depicts the flowchart for the steps in the RosettaAntibody protocol. The high-level steps are:

1. Identify the CDR and the framework regions in the input query sequence using known sequence motifs (http://www.bioinf.org.uk/abs).

2. Select templates for V_L and V_H framework regions and the non-H3 CDR loops by comparing the query sequence to a local antibody database via BLAST.³² The BLAST bit score is used to identify the best template match of identical sequence length for each individual region. The BLOSUM62⁶⁸ and PAM30^69,70 scoring matrices were used for the framework and CDR loops, respectively.

3. Thread the V_L and V_H framework sequences through the corresponding template matches. To create the β-barrel, the framework templates are oriented by superposing each chain onto the barrel of the template with the highest overall sequence similarity to the query. Any steric clashes at the domain interface will be remedied in the later refinement stage.

4. Graft the template non-H3 CDR loops onto the β-barrel scaffold using structural superposition of the backbone atoms (N, C_α, C and O) of the two stem residues flanking either side of the loop.

5. Model the CDR H3 conformation using a new protocol that draws from elements of Rosetta loop modeling such as fragment-insertion and CCD loop closure.

6. Refine the all-atom coordinates of the non-H3 CDR loops, with V_L-V_H rigid-body minimization of the V_L-V_H orientation, while keeping the CDR H3 fixed. Finally, minimize the H3 conformation in this new environment.

Steps 5 and 6 are more fully detailed below.

CDR H3 modeling

Creation of fragment libraries

We use fragment insertion for loop modeling of the CDR H3 loop, where three residue fragments are sets of backbone dihedral angles (ϕ,ψ,ω) obtained from known protein structures of similar sequence and secondary structure with idealized bond lengths and angles.^28,71 Fragments from H3 loops may capture the dihedral angle preferences of the H3 loop and the steric restraints due to its immediate environment. However, the Rosetta fragment database was originally constructed using a non-redundant set of protein sequences.⁷¹ The high degree of overall sequence similarity of antibodies masked the variation in the H3 sequence resulting in few database fragments from H3 loops. Therefore for CDR H3 modeling, we augmented the fragment database using the H3 loops in the set of 230 antibody structures with non-redundant H3 sequences.

The H3 C-terminus residues n-2 through n+1, or base, often exhibits a “kinked” conformation (pseudo-dihedral angle of the four C_α atoms approximately between −10° and 70°).¹⁶ We use sequence-based rules¹⁶ to detect likely kinked loops, and then we build identified loops using a special fragment library of kinked conformations from the antibody structure database, preferentially choosing fragments from loops of similar lengths or base sequence. For extended loops (pseudo-dihedral angle between 125° and 185°), we model the base using standard 3-residue Rosetta fragments.

Loop modeling strategies for CDR H3

The loop modeling strategy is a modified version of that of Rohl et al.,⁷² similar in spirit to that of Wang et al.⁷³ Since several of the details differ, we provide specifics of the algorithm in the following sections. Most notably, CDR H3 loop modeling is coupled to simultaneous optimization of non-H3 CDR conformations and refinement of the relative V_L-V_H orientation, which differs from previous loop modeling efforts. Also, the new loop modeling algorithm is approximately five times faster than the implementation by Wang et al.⁷³

Low resolution

Initially, a low-resolution Monte Carlo algorithm of fragment insertion moves generates an H3 loop library of 2000 conformations while holding constant the conformations of the non-H3 CDR loops and the V_L-V_H orientation. All residues are represented by the four backbone atoms (N, C_α, C and O) and one centroid pseudo-atom for the side chain.⁷¹ First, the backbone dihedral angles of the H3 base residues are set equal to those of a random kinked or extended fragment. Next, cycles of Monte Carlo moves attempt 25 fragment insertions in each 3-residue window for residues 1 through n-3. CCD moves close the loops after fragment insertion. The loop conformation with the best energy is recovered at the end of the Monte Carlo simulation. A final round of CCD, with a maximum tolerance of 0.01 Å for the gap at the loop discontinuity, closes the loop. If a gap persists, the protocol is repeated starting with the fragment insertion.

High resolution

Upon successful completion of the low-resolution search, the side-chain conformations of the residues are recovered from the template structures and the side chains of the H3 loop and its neighbors (8.0 Å cutoff) are repacked with a simulated annealing rotamer packing approach.⁷⁴ A 50-cycle Monte Carlo minimization docking procedure⁴¹ optimizes the V_L-V_H relative orientation by moving the V_H rigid-body via random translations of mean 0.1 Å in each Cartesian direction and by random rotations of mean 2.0° around each Cartesian axis. Subsequently, gradient-based minimization^28,73 simultaneously alters the conformations of the non-H3 CDR loops and the V_L-V_H rigid-body orientation using a fold-tree graph to control propagation of structural changes.^73,75 Finally, the backbone and side-chain positions of the CDR H3 loop are refined with an all-atom protein representation in an environment where the non-H3 CDR loops and the V_L-V_H interface are held fixed. The backbone (ϕ, ψ, ω) and side-chain dihedral angles (χ) of the loop and its neighbors are perturbed in a refinement cycle comprising of small, shear and CCD moves (five each), followed by a single instance of explicit gradient-based minimization.²⁸ The small, shear and CCD moves alter only the loop backbone. The minimization allows additional backbone flexibility in the two residues that flank the loop on each side. The loop apex is perturbed to a greater extent by this combination of moves, while the effect is minor on the stem region. The structure with the best Rosetta energy obtained during the course of the simulation is subjected to a final round of minimization.

Antibody-antigen docking

Antibody-antigen docking methodology followed that as described by Gray et al. and Wang et al.^39,41,76 Ensemble docking followed the conformation selection docking method as described by Chaudhury & Gray.²⁹ For local docking, partners are structurally superposed on the co-crystal structure of the antibody-antigen complex, and the coordinates of the antigen are perturbed to create 1000 docking models that populate a cloud of points 30–50 Å ligand rmsd about the starting position. While docking with the ensemble of the ten low-scoring RosettaAntibody models, to allow an average of 1000 docking models corresponding to each conformer in the ensemble, 10,000 docking models are generated for each target. Interface energy⁷³ is used to rank and discriminate the structures produced by the docking simulations.

Ligand rmsd is the deviation of the N, C_α, C and O backbone atoms of the antigen after superposition of the antibody backbone atoms. Interface rmsd is the deviation of the backbone atoms at the interface after optimal superposition of those same atoms, where the interface is defined as all residues within 10 Å of a non-hydrogen atom from the other docking partner. Interface score is the component of the total docking score that arises from residue-residue contacts at the antibody-antigen interface. Residue-residue contacts exist when a residue is within 5 Å of a non-hydrogen atom from the other docking partner. The docking models are assigned CAPRI⁷⁷-style “high”, “medium”, “acceptable” or “incorrect” rankings that depend on the rmsd-to-native of the ligand position, the interface rmsd to native and the fraction of native residue-residue contacts that are recovered in the docking model.⁴⁴

ALGORITHM AVAILABILITY

The antibody homology modeling methods presented here are freely available for academic and non-profit use as part of the Rosetta structure prediction suite (http://www.rosettacommons.org). The distribution includes the antibody databases, supporting scripts, documentation and full source code.

We have also implemented a web server (http://antibody.graylab.jhu.edu) which implements the algorithm to predict antibody structures from sequence. The server returns BLAST hits for each framework chain and CDR loop as well as the final ten top-scoring antibody homology models after complete refinement including V_L-V_H docking.