A Semiparametric Missing-Data-Induced Intensity Method for Missing Covariate Data in Individually Matched Case–Control Studies

Summary

In individually matched case–control studies, when some covariates are incomplete, an analysis based on the complete data may result in a large loss of information both in the missing and completely observed variables. This usually results in a bias and loss of efficiency. In this article, we propose a new method for handling the problem of missing covariate data based on a missing-data-induced intensity approach when the missingness mechanism does not depend on case–control status and show that this leads to a generalization of the missing indicator method. We derive the asymptotic properties of the estimates from the proposed method and, using an extensive simulation study, assess the finite sample performance in terms of bias, efficiency, and 95% confidence coverage under several missing data scenarios. We also make comparisons with complete-case analysis (CCA) and some missing data methods that have been proposed previously. Our results indicate that, under the assumption of predictable missingness, the suggested method provides valid estimation of parameters, is more efficient than CCA, and is competitive with other, more complex methods of analysis. A case–control study of multiple myeloma risk and a polymorphism in the receptor Inter-Leukin-6 (IL-6-α) is used to illustrate our findings.

1. Introduction

The problem of missing covariate data in individually matched case–control studies is quite common. Some of the main reasons are refusals to answer interview questions, loss to follow-up, incomplete medical records, and inability to collect information from all subjects on some variables that need expensive procedures of measurement. For example, in genetic case–control studies, researchers frequently store blood or other specimens that carry DNA information to test and determine if any specific set of genes are associated with outcome. Unfortunately, data are sometimes missing because subject’s specimens are misplaced, degraded, or have insufficient volume for a successful assay. In a study of the association between risk of multiple myeloma and some polymorphisms of the IL-6 genes (−174 GC SNP, −174 RA SNP, −572 GC SNP, −598 RA SNP), the IL-6rα receptor SNP (−174 RA) was missing in 40 pairs from a total of 112 case–control pairs due to problems related to assaying (Cozen, Gebregziabher, and Conti, 2006). Since the laboratory that processed the DNA assaying did not have information on the case–control status of the specimens, the missing data mechanism can be assumed to be independent of case–control status. Similarly, in a Danish 1:5 matched case–control study designed to identify risk factors for hospitalization due to respiratory syncytial virus infection, 233 infants were matched to controls by their age, gender, and municipality of residence (Nielsen et al., 2003). In this study, an important risk factor found was smoking status of the mother during pregnancy that was missing for 38% of the study subjects. Because smoking information was ascertained prior to the disease, missingness was not related to the case–control status. However, missingness could depend on the smoking status of the mother, since it is not unreasonable to assume that smokers might be more likely to refuse to answer a smoking question than nonsmokers due to the sensitive and personal nature of the information. A common theme in these data examples is that missingness does not depend on case–control status, which, following event time terminology, we will call predictable missingness, as defined precisely at the end of this section as well as in Section 2.

We use the nested case–control model for individually matched case–control studies in which controls are sampled from risk sets defined by the cases, failures in a cohort followed for time to disease event (Oakes, 1981; Breslow et al., 1983; Langholz, 2007). We assume that failures occur at unique times (in practice, ties can be randomly broken), so that there is only one case in each case–control set. This “continuous time” model is quite reasonable for most individually matched case–control studies. As we discuss in Section 5, our methods also apply for matched data from binary disease outcome when disease is rare. The focus of the article is the analysis of missing covariate data in individually matched case–control studies when the missingness does not depend on a disease status. To address the problem, we propose a semi-parametric partial likelihood approach. First, we derive the missing-data-induced intensity for the proportional hazards model and then propose a “semi-parametric induced model” that is consistent with the missing-data-induced intensity and depends only on observable quantities and nuisance parameters. We then give the corresponding partial likelihood that is used for estimation and to derive expressions for efficiency. The key requirements for valid estimation, over and above those nested case–control data without missing data, are (1) predictability, that conditional on covariates, missingness does not depend on case–control status, and (2) conditional independence, that the associations between covariates and disease are the same in subjects with and without missing data. Finally, our theoretical development provides a rigorous derivation of the missing indicator method and a justification for its use. Implementation of the semi-parametric induced intensity method turns out to be very easy, simply an extension of the missing indicator approach to analysis with missing data. The standard case–control data structure is retained, and a missing indicator plus, possibly, interactions between the missing indicator and known covariates, are included as variables in the analysis. We note that both cases and controls will have missing data and that, under predictable missingness, it is the relative difference in case–control missingness across known covariate values that provides the information needed for valid modeling of the missingness.

A common practice for dealing with missing data is to simply delete subjects who have missing values on variables included in the model. This method referred to as complete case analysis (CCA) is characterized by a severe loss of data. Another commonly used method is “break the matching” (BM), that is, the individual matching is ignored and the observed data from all cases and controls are analyzed as an unmatched case–control study. This method could lead to a biased inference if there is uncontrolled residual confounding by matching factors that cannot be quantified. Another method that is occasionally used is the missing indicator method (Huberman and Langholz, 1999; Greenland and Finkle, 1995; Li, Song, and Gray, 2004). For pair-matched studies, it is indicated in Huberman and Langholz (1999) that this method is always at least as efficient as CCA and always less subject to bias than BM. In simulation studies, where there is no inherent confounding in the data, it is shown to result in an improved efficiency and less bias (Li et al., 2004). Other missing data methods that can be used in individually matched case–control studies include likelihood methods (Satten and Kupper, 1993; Satten and Carroll, 2000; Rathouz, Satten, and Carroll, 2002; Rathouz, 2003), mid-point imputation (MPI; Paik and Sacco, 2000), weighted conditional likelihood (WCL; Lipsitz, Parzen, and Ewell, 1998), multiple imputation (MI; Rubin, 1987), and some recently suggested GEE-based methods (Lin, Lai, and Chuang, 2007) and Bayesian methods (Sinha, Mukherjee, and Ghosh, 2004; Sinha et al., 2005; Sinha and Maiti, 2008).

In this article, we assess the performance of the proposed method empirically in an extensive computer simulation study in which one covariate Z is known for all subjects, while a second covariate X has missing values from a predictable missing data mechanism with probability of missing possibly depending on Z or/and X but not on time to event or the binary event indicator D (dN in the counting processes notation). Suppressing time and thinking of the population in a risk set at a single failure time, the predictable missing mechanism implies that given (X,Z), missingness is independent of D. That is, pr(M = 1| X,Z,D) = Pr(M = 1| X,Z), where M is an indicator of whether X is missing or not. Relative to the commonly used missing data classification such as missing completely at random (MCAR), missing at random (MAR), or nonignorable (NI), a predictable missing mechanism covers MCAR, some MAR, and some NI situations. It excludes situations like pr(M = 1| X,Z,D) = Pr(M = 1| D) or pr(M = 1| X,Z,D) = Pr(M = 1| X,D), which in our terminology are called nonpredictable missing mechanisms. We consider the implications of X missing data when either X or Z are of primary interest in the study. We also compare the performance of the proposed methods with CCA, MPI, WCL, and MI.

2. Missing Data Methods Based on an Induced Intensity

Following Borgan, Goldstein, and Langholz (1995), let N_i (t) be the binary indicator whether subject i has experienced the event by time t, t ∈ [0, τ < ∞] with N_i (0) = 0, Y_i (t) a binary indicator whether subject i is still at risk at time t, X_i (t) (subject to missing) and Z_i (t) (not subject to missing) be the corresponding covariates at time t and M_i (t) be a binary random variable indicating whether X_i (t) is missing (i = 1, … , n). We assume that M_i (t) can depend on X_i (t) and Z_i (t) but not on dN_i (t), the disease status at time t. We call this a predictable missing mechanism. Define filtration, which is the history of the observed values of the variables in brackets, ℱ_t = {N_i (u), Y_i (u), (X_i (u),M_i (u), Z_i (u)), u ≤ t, i = 1, … , n} where, as usual, the X_i, Z_i ℱ-predictable and the N_i ℱ-adapted. We also include the missing indicator variables M_i and assume that they are ℱ-predictable, that is, it only depends on data available or known just prior to time t. Let ℛ(t) = {i : Y_i (t) = 1}. Note that X_i, Z_i, N_i, M_i are as defined above with their dependence on time t suppressed. The goal is to make the “best guess” possible of disease risk at t from the information in ℱ_t−.

To represent a nested case–control study in which controls are sampled from each failure time risk set, let N_i,r (t) be a counting process jointly indicating if subject i has experienced the event by time t and r is sampled as a case–control set. Define a filtration ℋ_t = {N_i,r (u), Y_i (u), (X_i (u),M_i (u), Z_i (u)), u ≤ t, i ∈ r ⊂ ℛ(t)}. We consider the following Cox model for the rate of disease as a function of covariates X and Z:

$$\lambda (t,x,z;\alpha (.),{\beta }_1,{\beta }_2)=\alpha (t)\text{exp}({\beta }_{1}x+{\beta }_{2}z),$$ (1)

where λ is hazard rate, t denotes the elapsed time, β₁ and β₂ are unknown parameters to be estimated, and α(t) is an unspecified baseline hazard function. Suppose there are ${\beta }_1^0,{\beta }_2^0,$, and λ₀ such that the model (1) coincides with the intensity λ_i,r(t,ℋ) corresponding to the counting process N_i,r (t) and the information available right before time t,ℋ _t⁻, given by,

$${\lambda }_{i,r}(t,\mathscr{H})=Y_i(t){\lambda }_0(t)\exp \left({\beta }_1^0{X}_i(t)+{\beta }_2^0{Z}_i(t)\right){\pi }_t(r|i),$$ (2)

where ℛ̃(t) is the sampled case–control set and π_t (r | i) = pr(ℛ̃(t) = r |dN_i (t) = 1,ℋ _t⁻) (Borgan et al., 1995). Note that given X and Z, the ℋ-intensity defined in equation (2) does not depend on the missing indicator M_i (t). This is a conditional independence assumption that the effect of X and Z on disease rates in missing is the same as in nonmissing subjects.

When X is partially missing, let 𝒢_t = {Y_i (u),N_i,r (u), (X_i (u)(1 − M_i (u)),M_i (u), Z_i (u)); u ≤ t, i ∈ r ⊂ ℛ(t)} be the missing data filtration.

Our objective is to derive a missing data “induced” intensity from the complete data intensity (2) and then extend the complete data model (1) to encompass the possible forms of the induced intensity. Since the filtrations are nested with 𝒢_t ⊂ ℋ_t , by applying the innovation theorem (Aalen, 1978; Andersen et al., 1992), suppressing possible dependence on t of X, Z, and M, the missing-data-induced intensity is,

$$\begin{array}{cc}{\lambda }_{i,r}(t;𝒢)\mathit{\text{dt}}\hfill & =\mathrm{E}[d{N}_{i,r}(t)|{𝒢}_{t^{-}}]=E[{\lambda }_{ir}(t;\mathscr{H})|{𝒢}_{t^{-}}]\mathit{\text{dt}}{\pi }_t(r|i)\hfill \\ & =Y_i(t){\lambda }_0(t)\text{exp}[{\beta }_1^0{X}_i(1-M_i)\hfill \\ & \hfill +{\beta }_2^0{Z}_i+\varphi (t,Z)M_i]\mathit{\text{dt}}{\pi }_t(r|i).\end{array}$$ (3)

where

$$\varphi (t,Z)=\text{log}\mathrm{E}[\text{exp}({\beta }_1^0{X}_i)|M_i=1,Z_i,Y_i(t)=1].$$ (4)

Equation (4) is the rate of disease when some subjects have missing X values and is the expectation of exp(βX) conditional on not being observed, and the fully observed data. This expectation can vary over time due to the selective elimination of subjects with higher risk from the risk sets over time known as differential censoring pattern that depends on X or time dependence of X, and, if X and Z are correlated, can vary over Z as well. In order to accommodate the missing data, we must extend the full data model (1) so that (3) is in the model space. We propose to replace ϕ(t, Z) in (3) by a model, ϕ(t, Z; η), a function of the “observables” t and Z, and a parameter vector η = (η₁, …, η_p ). The novelty here is that we can handle missing data by appropriately modeling ϕ(t, Z; η) as long as the missingness process is predictable. Moreover, the parameters in the distribution of X |Z in subjects for whom X is missing are accommodated in the induced intensity model instead of being estimated separately as done in other studies (Rathouz et al., 2002). A semi-parametric missing-data-induced hazards model extension of (1) is then given by

$$\begin{array}{c}\lambda (t,x,z,m;\alpha (.),{\beta }_1,{\beta }_2;\mathbf{\eta })\hfill \\ \hfill =\alpha (t)\text{exp}({\beta }_{1}x(1-m)+{\beta }_{2}z+\varphi (t,z;\mathbf{\eta })m).\end{array}$$ (5)

The complexity of ϕ(t, z; η) depends on the number of parameters in η and the form of ϕ function. The simplest case is when ϕ(t, z; η) = η₁, a single parameter that is independent of t or any components of the vector Z and defined as the log rate ratio for missingness. This leads to the single missing indicator (SMI) method. To accommodate variation over Z assuming no effect from t, we could define ϕ(t, z; η) = η₁ + η₂Z, which we call a modeled missing indicator (MMI) method. This leads to the inclusion of a linear interaction parameter between M and Z on to SMI. On the other extreme, the completely unstructured model ϕ(t, z; η) leads to CCA. To see this, note that ϕ(t, Z) will vary and be common to all subjects with the same Z values at each failure time and will drop-off from the partial likelihood in the same way as λ₀(t). This will lead to a likelihood that is proportional to the CCA likelihood (see Web Appendix A). In practice, we could use standard modeling techniques to find a model for ϕ that adequately fits the data.

2.1 Partial Likelihood

Model (5) is of proportional hazards form, so that a partial likelihood can be derived in the usual way (Borgan et al., 1995) as,

$$L({\beta }_1,{\beta }_2,\eta )={\pi }_0^{\tau }{\displaystyle \prod _{r\subset \widetilde{ℛ}}{\displaystyle \prod _{i\in r}{\left\{\frac{\text{exp}({\beta }_1{X}_i(1-M_i)+{\beta }_2{Z}_i+\varphi (u,Z;\mathbf{\eta })M_i){\pi }_u(r|i)}{{\displaystyle \sum _{j\in r}\text{exp}({\beta }_1{X}_j(1-M_j)+{\beta }_2{Z}_j+\varphi (u,Z;\mathbf{\eta })M_j){\pi }_u(r|j)}}\right\}}^{d{N}_{i,r}\left(u\right)},}}$$ (6)

where ${\pi }_0^{\tau }$ is a product integral. Under the conditional independence assumption, and assuming that, in addition to model (2), there exists an η₀ such that ϕ(t, Z) = ϕ(t, Z; η₀), standard likelihood properties can be established. In particular, the score is a martingale and the predictable variation differs from the expected information by a martingale. Further, consistency and asymptotic normality of all parameter estimates holds if conditions 1–4 of Borgan et al. (1995) hold for the particular sampling scheme π(r | i) when applied to the induced model and intensity (3).

2.2 Asymptotic Efficiency Comparison for Simple Random Sampling of Controls

In this section, we give analytic expressions for the asymptotic information from the partial likelihood for full (nonmissing) data, for CCA and SMI for missing data, and compare their efficiency to each other, for 1:m − 1 simple random sampling of controls. A general expression for the asymptotic information under independence for a single covariate X with missing values is given in Theorem 1 of Web Appendix B.

The general expression can be used to make asymptotic efficiency comparisons in some informative special cases. Consider dichotomous X with pr(X(t) = 1| Y (t) = 1) = π, pr(X(t) = 1,M(t) = 0| Y (t) = 1) = π₁, pr(X(t) = 0, M(t) = 1| Y (t) = 1) = π₀, and pr(M(t) = 1| Y (t) = 1) = q, respectively; assumed constant over time, see 6.3(B) in Goldstein and Langholz (1992). Let m₀,m₁,m₂ be the number of observations in a case–control set with X = 0, X = 1, and X = missing, respectively, and define

$$\begin{array}{cc}{\mathrm{\Gamma }}^{*}(a,b)=\hfill & \frac{1}{m}{\displaystyle \sum _{(m_0,m_1,m_2):{\displaystyle {\sum }_{j=0}^2{m}_j=m}}\left(\begin{array}{c}m\\ m_0{m}_1{m}_2\end{array}\right){\pi }_0^{m_0}{\pi }_1^{m_1}{a}^{m_2}v}\hfill \\ & \times (m_0,m_1,m_2,b)(m_0+m_1{e}^{{\beta }_0}+m_{2}b),\hfill \end{array}$$

where υ is a 2×2 symmetric matrix with the expression for the components,

$$\begin{array}{ccc}{v}_{\beta \beta }(m_0,m_1,m_2,b)& =\frac{m_1{e}^{{\beta }_0}(m_0+m_{2}b)}{{(m_0+m_1{e}^{{\beta }_0}+m_{2}b)}^2}& \\ v_{\beta \eta }(m_0,m_1,m_2,b)& =\frac{-m_1{m}_{2}b{e}^{{\beta }_0}}{{(m_0+m_1{e}^{{\beta }_0}+m_{2}b)}^2}& \\ v_{\eta \eta }(m_0,m_1,m_2,b)& =\frac{m_{2}b(m_0+m_1{e}^{{\beta }_0})}{{(m_0+m_1{e}^{{\beta }_0}+m_{2}b)}^2.}& .\end{array}$$

The full (no missing) data and CCA asymptotic Fisher information (AFI) for β are proportional to the β, β corners of Γ*(1, 0) and Γ*(q, 0), respectively. The SMI AFI for β is proportional to the inverse of the β, β corner of [Γ*(q, e^η0 )]⁻¹.

Now, consider 1:1 matching (m = 2) and the situation when X does not depend on M (MCAR situation) so that π₀ = (1 − π)(1 − q) and π₁ = π(1 − q). The AFI expressions simplify considerably and are proportional to

$$\begin{array}{cc}{\mathit{\text{AFI}}}_{\mathit{\text{full}}}\hfill & =\pi (1-\pi )e^{{\beta }_0}/(1+e^{{\beta }_0})\hfill \\ {\mathit{\text{AFI}}}_{\mathit{\text{CCA}}}\hfill & ={(1-q)}^2\pi (1-\pi )e^{{\beta }_0}/(1+e^{{\beta }_0})\hfill \\ {\mathit{\text{AFI}}}_{\mathit{\text{SMI}}}\hfill & =(1-q)\pi (1-\pi )\frac{e^{{\beta }_0}}{(1+e^{{\beta }_0})}\hfill \\ & \times \left\{1-q+\frac{{\mathit{\text{qe}}}^{{\eta }_0}(1+e^{{\beta }_0})}{e^{{\beta }_0}+(1-\pi )e^{{\eta }_0}+\pi e^{{\beta }_0+{\eta }_0}}\right\}.\hfill \end{array}$$

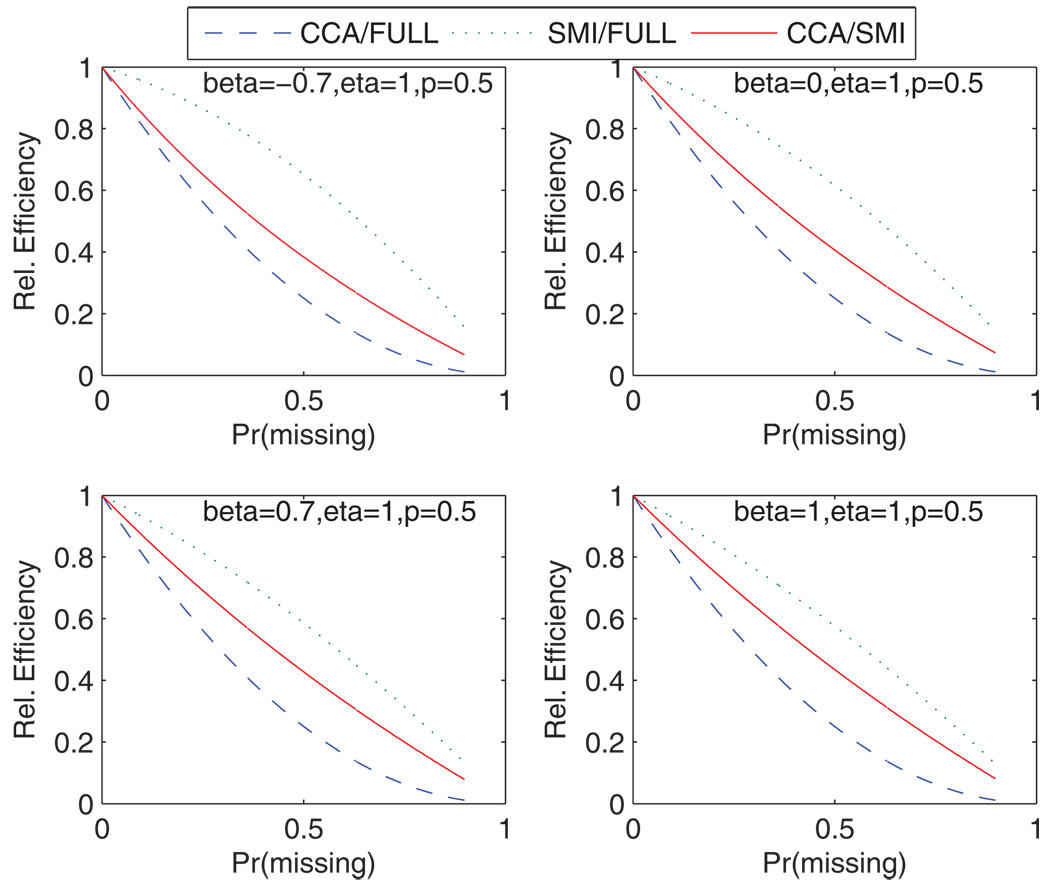
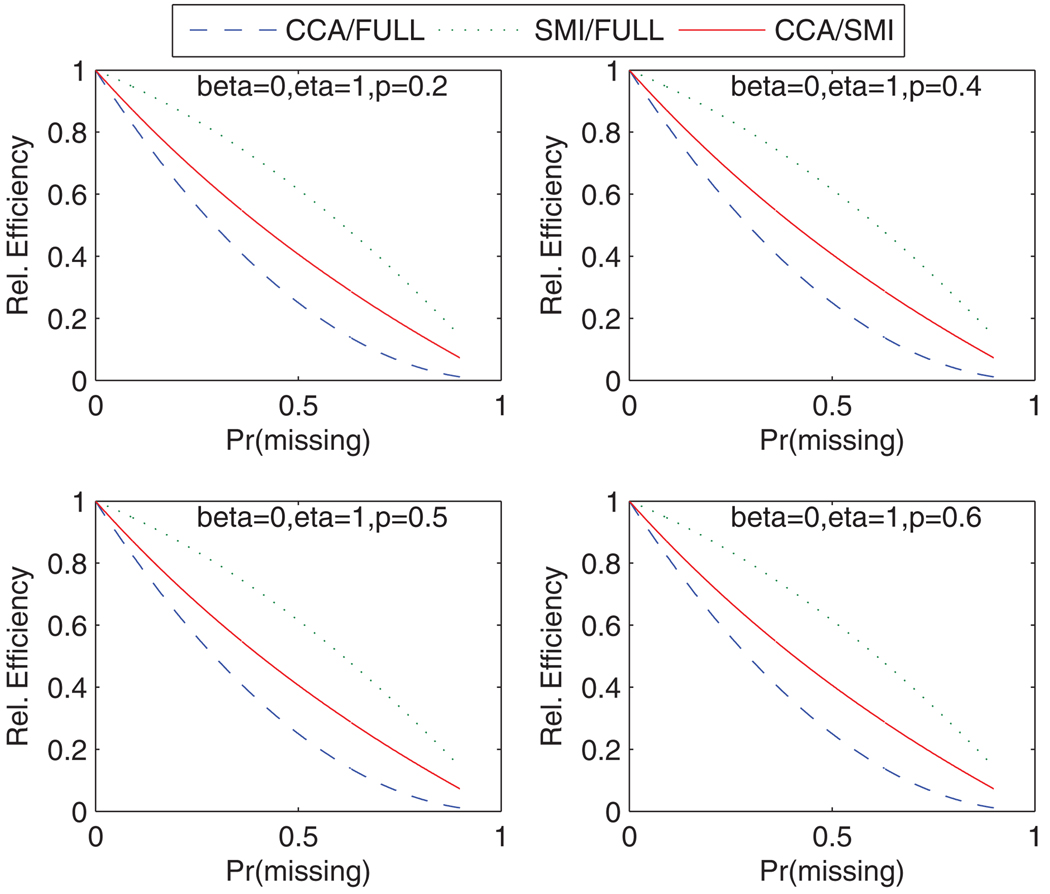
Based on these expressions, relative efficiencies, computed as the ratio of the AFI corresponding to the estimate from SMI or CCA to the AFI of the estimate from the full data analysis and the relative efficiency of SMI to CCA, are presented in Figure 1 and Figure 2. All the figures show that the relative efficiency of CCA and SMI are equivalent when q = 0, there is no missing data, and both CCA and SMI converge to the same efficiency performance as q approaches one. However, when X is partially missing, the figures show that the missing indicator method performed much better in terms of efficiency than CCA. It is easy to show analytically that AFI for SMI is always between the AFIs for the CCA and complete data.

Figure 1.

Relative efficiency of CCA and SMI estimates compared to full data analysis for varying β but fixed η and p(X = 1), 1:1 matched case–control data. This figure appears in color in the electronic version of this article.

Figure 2.

Relative efficiency of CCA and SMI estimates compared to full data analysis for varying p(X = 1) but fixed β and η. 1:1 matched case–control data. This figure appears in color in the electronic version of this article.

3. Simulation Study

The study group consists of individually matched case–control sets that were generated using the paradigm of risk set sampling from cohort data in continuous time (Thomas, 1977; Oakes, 1981; Langholz, 2007), which was implemented using SAS 9.1 (SAS Institute Inc., 2003). Typically, in this paradigm, a random sample of controls of fixed size (one or four in our studies) is sampled at each failure time of a cohort study independently from controls in each risk set. However, to evaluate the performance of estimators for a bias as well as efficiency, it is sufficient and simpler to generate “independent” risk sets rather than to generate failure time data and then form the risk sets (Langholz, 2007). This is valid because when sampling is independent across risk sets, the asymptotics only depend on the distribution of the covariates at each point in time, not on how the covariates are connected over time by the individuals in the cohort. First, a binary or continuous exposure X and a three level potential confounder Z were generated. Three correlation or association settings between Z and X, which correspond to independent, moderate association, and strong association between X and Z were fixed as follows: logit[pr(X = 1|Z)] = 0.5 − 0.69Z for moderate and logit[pr(X = 1|Z)] = 1.0 − 1.40Z for strong association. These would determine the confounding effect of Z on the association between X and the case indicator D since the generation of D depends on both X and Z. A single case was randomly chosen from the risk set based on probability proportional to r_i (β_X , β_Z) = exp(Z_iβ_Z + X_iβ_X ), which is the parametric component of the Cox model. These probabilities of failure or D = 1 were generated for exp(β_X ) values of 0.5, 1.0, 1.5, and 2.0 and exp(β_Z) = 1.42. These result in a fixed number of independent risk sets that form the cohort risk set data. Finally, one control was (or four controls were) randomly sampled from controls in each risk set. Case–control sets were generated in this way to create a case–control study of the desired size of 2n or 5n (Langholz, 2007). This process was repeated for each simulation replicate where new risk sets are generated for each replicate so that the joint distribution of (X,Z) varies across risk sets (code at http://hydra.usc.edu/timefactors).

3.1 Missing Data Generation and Analysis

Data sets with missing exposure X data were generated from the case–control study with a 20% or 50% missing proportion. We considered a wide range of missing scenarios broadly classified into MCAR, MAR, and NI types in the sense of Little and Rubin (2002). Further classification of the missing data mechanism was made based on the dependence of the probabilities of missing X on D. Given X and Z, if M is independent of D then the missing mechanism is classified as a predictable mechanism, but if M depends on D then it is classified as a nonpredictable missing mechanism. We made the assumption that the missingness model is logistic and is specified as

$$\text{logit}[\text{pr}(M=1|X,Z,D)]={\gamma }_0+{\gamma }_{d}D+{\gamma }_{x}X+{\gamma }_{z1}{Z}_1+{\gamma }_{z2}{Z}_2,$$

where M is the missing indicator, Z₁, Z₂ are dummy variables representing two of the three categories of Z, γ₀ determines the overall proportion of missingness and the other coefficients, γs are the corresponding log odds ratios (ORs) for missingness. Overall, five missing data mechanism scenarios, MCAR, MAR(Z), MAR(D), NI(X), and NI(X,Z) were considered. The values for the coefficients in the missingness model were γ_d = 2.2, γ_x = 2.2, γ_{z 1} = −1.6, γ_{z 2} = −0.8 and the value of the intercept γ₀ was determined depending on the desired overall missing data proportion desired in the case–control data set. For MCAR, all coefficients except γ₀ were set to zero, whereas for MAR(Z) all parameters except γ₀, γ_{z 1}, γ_{z 2} were zero. For the NI(X) scenario, where pr(M = 1| X,Z,D) = Pr(M = 1|X), γ₀ and γ_x took values as defined above but all other coefficients were set to zero. For NI(X,Z), only γ_d was set to zero whereas all other coefficients were set at the values given above.

The resulting data sets from each scenario were analyzed using the three special cases of the induced intensity method: CCA, a SMI, and MMI. We also compared the semi-parametric method to other missing data methods including MPI, WCL, and MI methods cited in the Introduction with the implementation described in Web Appendix D.

From 1,000 replicates, we computed the average coefficient values β̂_X, β̂_Z their corresponding empirical standard errors, the average of the estimated standard errors, empirical coverage probability of the 95% confidence interval, relative efficiency, and relevant statistics to assess the properties of each method and to assure the simulation study is performing as expected.

3.2 Results of Simulation Study

In each of Table 1–Table 3, the rows give the sampling design, missingness type, and confounding level, and the columns display the methods of analysis. The “no” panel of the table provides results when X and Z are independent, i.e., Z is not a confounder. The “strong” panel of the table provides results when _X and Z are strongly negatively correlated or associated, hence Z is a strong confounder, since Z is associated with D. We only present tabulated results for 1:1 matching when n = 400. Results from n = 200 and n = 400 for both the 1:1 and 1:4 matching scenarios were qualitatively similar to results from n = 100 for 1:2 matching except the magnitude of the power of the Wald test, 95% coverage and relative efficiency were smaller, as expected, in the n = 100 scenarios.

Table 1.

Percent relative bias (PRB) comparing complete-case analysis (CCA), single missing indicator (SMI), modeled missing indicator (MMI), and multiple imputation (MI) for 1:1 design, number of case–control sets = 400, exp(β_X ) = 2, exp(β_Z) = 1.42, pr(X = 1) = 0.5. PRB is computed as the ratio of the bias in the rate ratio estimate from SMI, MMI, or CCA to the true rate ratio. Based on 1000 trials.

		PRB in exp(β̂X)			PRB in exp(β̂Z)
	Missing
pr(M = 1)-Confounding	type	CCA	SMI	MMI	CCA	SMI	MMI
50%-no	MCAR	1.6	0.9	1.1	1.9	0.8	0.7
	MAR(Z)	1.8	0.7	0.9	2.1	0.8	0.5
	MAR(D)	3.0	2.3	2.6	2.4	0.6	0.5
	NI(X)	4.4	1.4	1.7	2.7	0.9	0.9
	NI(X,Z)	2.7	1.8	2.1	1.9	2.1	0.6
50%-strong	MCAR	2.6	−9.6	0.2	1.5	−11	0.7
	MAR(Z)	2.0	−7.9	1.1	1.0	−12	0.9
	MAR(D)	4.7	−8.2	1.9	2.8	−11	1.0
	NI(X)	3.7	−5.4	1.0	1.0	−7.5	0.0
	NI(X,Z)	3.9	−3.6	1.0	1.3	−7.4	−0.1
20%-no	MCAR	0.6	0.4	0.5	1.5	0.8	1.1
	MAR(Z)	0.5	0.5	0.6	1.2	0.9	1.1
	MAR(D)	0.2	0.2	0.2	0.9	0.6	0.7
	NI(X)	0.6	0.4	0.5	1.3	0.8	1.1
	NI(X,Z)	0.3	0.5	0.6	1.2	1.1	0.9
20%-strong	MCAR	1.7	−3.3	1.2	1.0	−4.5	0.9
	MAR(Z)	2.4	−3.4	1.4	0.9	−5.3	0.7
	MAR(D)	1.7	−1.3	1.5	0.7	−2.7	0.6
	NI(X)	0.4	−1.7	0.5	0.2	−2.1	0.4
	NI(X,Z)	1.2	0.9	1.0	0.5	−1.8	0.7

MCAR, missing at random unconditionally; MAR(D), missing at random conditional on D; MAR(Z), missing at random conditional on Z; NI(X), missing not at random conditional on X; NI(X,Z), missing not at random conditional on X,Z.

Table 3.

Ninety-five percent confidence coverage comparing complete-case analysis (CCA), single missing indicator (SMI), modeled missing indicator (MMI), and multiple imputation (MI) for 1:1 design, number of case–control sets = 400, exp(β_X ) = 2, exp(β_Z) = 1.42, pr(X = 1) = 0.5. Based on 1000 trials.

		In exp(β̂X)			In exp(β̂Z)
	Missing
pr(M = 1)-Confounding	type	CCA	SMI	MMI	CCA	SMI	MMI
50%-no	MCAR	96	97	96	95	95	96
	MAR(Z)	96	97	97	95	95	95
	MAR(D)	95	96	96	95	96	96
	NI(X)	97	96	96	97	95	97
	NI(X,Z)	95	96	96	95	95	96
50%-strong	MCAR	96	-	94	97	-	97
	MAR(Z)	95	-	93	95	-	97
	MAR(D)	96	-	95	95	-	95
	NI(X)	94	-	93	95	-	94
	NI(X,Z)	94	-	94	94	-	96
20%-no	MCAR	95	97	97	96	95	96
	MAR(Z)	96	97	97	96	95	96
	MAR(D)	96	96	96	97	96	95
	NI(X)	96	96	96	96	95	95
	NI(X,Z)	95	96	96	95	95	95
20%-strong	MCAR	93	-	93	95	-	95
	MAR(Z)	94	-	94	95	-	95
	MAR(D)	94	-	94	95	-	94
	NI(X)	95	-	94	93	-	95
	NI(X,Z)	95	-	94	94	-	95

MCAR, missing at random unconditionally; MAR(D), missing at random conditional on D; MAR(Z), missing at random conditional on Z; NI(X), missing not at random conditional on X; NI(X,Z), missing not at random conditional on X,Z.

The first three columns of Table 1 show percent relative bias in the rate ratio estimates of the effect of X for the 1:1 sampling design with 20% and 50% missing data proportions. For the same design when there was no missing data, the relative bias in the average rate ratio was 0.7% indicating that the estimates from full sample data were very close to the true value. But, when there was 20% or 50% missing data, as seen in the “strong” panel of the table, when X and Z were confounded the rate ratio estimates from the SMI were biased even under MCAR, which is in agreement with Li et al. (2004)’s observation. The inclusion of the linear missing indicator-Z interaction term controlled the confounding. Interestingly, as shown from the MAR(D) mechanism results, the assumption of predictable missingness has a big impact on CCA and SMI, whereas MMI seems to be robust. To further investigate the robustness to the assumption of predictable missing mechanism, limited simulations based on NI(X,D) mechanism showed that all the methods give highly biased results (not shown).

The last three columns of Table 1 show percent relative bias in the rate ratio estimates of the effect of Z for the 1:1 sampling design with 20% and 50% missing data proportions. Similarly for β_Z , SMI was biased when there was strong confounding even under MCAR. As in the previous tables, the magnitude of the bias in the 20% missing proportion scenario was lower than the 50% scenario, but the trend in bias was similar.

The empirical relative efficiency of CCA, SMI, and MMI compared to the full data estimate is summarized in Table 2 for situations in which the bias was small. The methods that were unbiased for β_X were more efficient than CCA, while the other estimators were of comparable efficiency. For estimation of β_Z , the CCA estimator was less efficient than MMI, which, in turn, was less efficient than SMI.

Table 2.

Relative efficiency (REff) comparing complete-case analysis (CCA), single missing indicator (SMI), modeled missing indicator (MMI), and multiple imputation (MI) for 1:1 design, number of case–control sets = 400, exp(β_X ) = 2, exp(β_Z) = 1.42, pr(X = 1) = 0.5. REff is computed as the ratio of the variance from the full data analysis to the variance of the estimate from the corresponding SMI or CCA. Based on 1000 trials.

		REff in exp(β̂X)			REff in exp(β̂Z )
	Missing
pr(M = 1)-Confounding	type	CCA	SMI	MMI	CCA	SMI	MMI
50%-no	MCAR	0.48	0.71	0.71	0.46	1.00	0.71
	MAR(Z)	0.48	0.77	0.77	0.42	1.00	0.59
	MAR(D)	0.40	0.53	0.53	0.42	0.77	0.53
	NI(X)	0.44	0.67	0.67	0.48	1.00	0.71
	NI(X,Z)	0.46	0.67	0.67	0.44	1.00	0.63
50%-strong	MCAR	0.50	-	0.71	0.53	-	0.71
	MAR(Z)	0.53	-	0.71	0.46	-	0.67
	MAR(D)	0.42	-	0.59	0.40	-	0.56
	NI(X)	0.42	-	0.63	0.56	-	0.71
	NI(X,Z)	0.48	-	0.71	0.50	-	0.71
20%-no	MCAR	0.91	1.00	1.00	0.91	1.00	1.00
	MAR(Z)	0.91	1.00	1.00	0.91	1.00	1.00
	MAR(D)	0.91	1.00	1.00	0.91	1.00	1.00
	NI(X)	0.91	1.00	1.00	0.91	1.00	1.00
	NI(X,Z)	0.91	1.00	1.00	0.91	1.00	1.00
20%-strong	MCAR	0.83	-	0.91	0.77	-	0.91
	MAR(Z)	0.83	-	0.91	0.77	-	0.91
	MAR(D)	0.77	-	0.83	0.77	-	0.83
	NI(X)	0.83	-	0.91	0.77	-	0.91
	NI(X,Z)	0.83	-	0.91	0.77	-	0.91

“-,” not applicable because the estimate is biased; MCAR, missing at random unconditionally; MAR(D), missing at random conditional on D; MAR(Z), missing at random conditional on Z; NI(X), missing not at random conditional on X; NI(X,Z), missing not at random conditional on X,Z.

Table 3 shows the empirical 95% confidence coverage for β̂_X and β̂_Z The coverage probabilities were close to the nominal value of 95% in all scenarios where the estimators were unbiased. To check the validity of the Wald’s tests, we performed a simulation study with β_X = 0 when β_Z = 0.35 and β_Z = 0 when β_X = 0.693 and the tests had test size close to the nominal 5% level (data not tabulated).

Bias and efficiency results of the semi-parametric induced intensity estimators with other missing data methods are given in Web Appendix D. While no method is superior in all respects, the SMI performed well in terms of efficiency when there is no confounding and the MMI estimator performed well in terms of unbiasedness when there was strong confounding. MI and MPI methods also performed well but were somewhat biased for β_Z when missingness depended on X and there was strong confounding with Z. We note that although the WCL method was unbiased in a wide range of situations, it exhibited poor efficiency that was comparable to the CCA.

We also investigated two other regression imputation methods, one based on imputing predicted values from f(X | Z,D) (Gibbons and Hosmer, 1991) and the other imputing from f(X |Z) (Caroll and Stefanski, 1990). As was found by Paik and Sacco (2000), the first is severely biased for all scenarios of missingness. The latter is unbiased except when missingness depends on D (results not tabulated).

4. Data Example

Our data example comes from collaborative work on a case–control study of the association between multiple myeloma risk and some polymorphisms in the IL-6 region. The details of the study are reported elsewhere (Cozen et al., 2006). Briefly, the 150 cases, the residents of Los Angeles County, were diagnosed with primary multiple myeloma or plasmacytoma (ICD-03 9731–9734) from October 1, 1999 through December 31, 2002, and were under the age of 75 at diagnosis. They were ascertained by the University of Southern California Cancer Surveillance Program (USC-CSP), the population-based cancer registry for Los Angeles County. The controls were family members (siblings and cousins) and consisted of 112 controls individually matched to each case on some age- and sex-based priority algorithm (Cozen et al., 2006). A second group of 126 controls consisted of population-controls who were frequency matched to an expected race-, age-, and sex-distribution and were identified by a random digit dialing. Additional variables were education level (≤12,13–15, ≥16), BMI (<25,25–29.9, ≥30 kg/m²), and continuous age. DNA was extracted from cases’ and controls’ samples and at least one single nucleotide polymorphism (SNP) was successfully genotyped from every subject in each group. Our analysis is limited to the case and relative-control comparison.

The distribution of the genotypes and the odds ratio (OR) estimates from CCA, SMI, and MMI are provided in Table 4. We also report MI results based on 10 imputations with all completely observed covariates and case–control status as predictors for the imputation model. Analysis using CCA led to a loss of about 40 case–control pairs as a result of missing values in IL-6rα, BMI, or education. The estimates from CCA were smaller than the others with relatively large asymptotic standard error (ASE). On the other hand, SMI resulted in large OR estimate with ASE = 0.174. MI and MMI resulted in similar OR estimates with ASE of 0.171 and 0.191, respectively. We presented two different scenarios of MMI. While MMI1 was based on modeling the interaction between the missing indicator and gender, MMI2 was based on modeling the interaction between missing indicator and race. The OR estimate from MMI2 had smaller standard error. Based on our observation from an unconditional logistic regression analysis of case–control status as an outcome and IL-6rα as a missing covariate after breaking the matching, compared to race adjusting for gender, had a smaller impact in changing the OR for IL-6rα. So, bias and efficiency trade-off considerations would imply that there is no need to consider MMI1. This is consistent with our simulation results that a larger confounding effect is needed before we see the impact of modeling the interaction between the missing indicator and completely observed confounding variables.

Table 4.

Genotype distribution and analysis results of the association between multiple myeloma and IL-6rα, Los-Angeles County, 1999–2002

Genotype distribution of IL-6rα, Los-Angeles County, 1999–2002
IL-6rα	Case	Relative-Control	Case/relative used for Cozen et al.
DD	55	50	36/39
DA+AA	55+11	37+14	46/43
Missing	29	11	68/30
Total	150	112	150/112
Odds Ratio estimates for the association of IL-6rα and the risk of multiple myeloma
Method	OR	ASE	95% CI
CCA	1.80	0.464	(0.70, 4.50)
SMI	2.95	0.174	(2.10, 4.16)
MMI1	1.92	0.219	(1.25, 2.95)
MMI2	2.14	0.191	(1.47, 3.42)
MI	2.08	0.171	(1.49, 2.91)

ASE, asymptotic standard error; CI, confidence interval; CCA, complete case analysis adjusted for education level, BMI, and age as in Cozen et al., 2006; SMI, single missing indicator; MMI, modeled missing indicator; MMI1, MMI with interaction between missing indicator and gender; MMI2, MMI with interaction between missing indicator and race (white/black); MI, multiple imputation.

Note: From the total of 112 pairs CCA uses 82 complete pairs

5. Discussion

In this article, we proposed a semi-parametric missing-data-induced approach to the analysis of individually matched case–control data when there is at least one covariate with missing values and the missing data mechanism does not depend on case–control status. Our work gives a rigorous theoretical development justifying the use of missing indicator methods that can be easily implemented using familiar modeling techniques and standard conditional logistic regression software. The relevance and application of the theory we developed is demonstrated using data from computer simulations and application to a real data example.

Let M be an indicator of whether X is missing or not. For SMI, the missing-data-induced model will have the terms (1 −M)X and M and the coefficient of the term (1 −M)X yields an estimator of the true coefficient of X when the missing data mechanism does not depend on case–control status. The SMI, M, can be replaced with multiple terms that include interactions between M and components of the vector of observed covariates Z based on standard modeling considerations. In our simulation results, concordant with other studies, we found that the SMI resulted in a biased estimation of either X or Z effects when the association between X and D was confounded by Z. The bias was significantly reduced when we added missing indicator terms that include interactions between M and Z. Thus, when the association between X and D is strongly confounded by Z, the variation in the rate ratio associated with the missing indicator needed to be modeled over values of the known covariates in the model to control for covariate-disease confounding using covariate-missing indicator interaction terms. However, in most settings, that is, modest amount of missing data and no strong confounding by other covariates, the SMI should be adequate.

Given that the derivation of some of the existing methods (Satten and Kupper, 1993; Lipsitz et al., 1998; Paik and Sacco, 2000; Satten and Carroll, 2000) including MI all rely on an MAR assumption, the finding that missing indicator methods do not require the MAR assumption is of a great practical value in case–control studies as MAR is likely to be violated. For instance, in the low birth weight data and smoking example used by several studies (Li et al., 2004; Sinha et al., 2004; Sinha et al., 2005; Sinha and Maiti, 2008) making the assumption of MAR may not be justifiable, since it is not unrealistic to think that smokers are more likely to leave a smoking question missing than nonsmokers. Thus, the biggest consideration should be whether missingness depends jointly on X and D. In many settings, covariate information is collected from sources compiled prior to the occurrence of disease in cases, and it may safely be assumed that missingness does not depend on a disease status. In these situations, missing indicator methods will provide a valid estimation. However, when information is collected after a disease occurrence, one needs to carefully assess whether missingness depends on both X and D.

Two general approaches that have been widely discussed in the missing covariate data literature and shown to lead to consistent inference under different sets of assumptions are modeling the missingness process (Lipsitz et al., 1998) and modeling the distribution of the missing covariate (Satten and Kupper, 1993; Paik and Sacco, 2000; Satten and Carroll, 2000). Rathouz et al. (2002) proposed a semi-parametric efficient approach that jointly uses both these approaches. Like this method, our proposed method makes use of the data on (D,Z) from the incomplete pairs leading to gain in efficiency over those methods that throw it away. The additional novelty in our approach is that the parameters in the distribution of X |Z in subjects for whom X is missing are accommodated in the induced intensity model instead of being estimated separately as done in other studies (Rathouz et al., 2002; Sinha et al., 2004). It will be of interest to compare the performance of all these different approaches, a topic for future work. Our simulation study indicated that, under the predictable missing data mechanism, the appropriate semi-parametric induced intensity estimators had smaller variance than the WCL (Lipsitz et al., 1998) estimator and were generally comparable to the MPI (Paik and Sacco, 2000) and MI methods (Rubin, 1987), but much simpler to implement.

Interestingly, other investigators have studied the performance of SMI under several analytic settings, such as in unmatched case–control data (Vach and Blettner, 1991; Greenland and Finkle, 1995) and individually matched case–control data (Huberman and Langholz, 1999; Li et al., 2004) and least squares regression (Jones, 1996) and found that it performed poorly. The bias observed in the individually matched studies may be attributable to the use of a single indicator when strong confounders of exposure are also in the model (Vach and Blettner, 1991; Li et al., 2004); a result concordant with our findings. Thus, while we have shown that missing indicator methods can be advantageous for individually matched data, others have not found a comparable gain in other data settings.

Our theoretical development builds on past theoretical work on case–control data resulting from a sampled risk set framework (Goldstein and Langholz, 1992; Borgan et al., 1995). This approach is especially convenient in that most studies are reasonably represented by the model and the process representation provides a nice analysis framework. Other models for matched case–control data are based on simple binary data. Our methods can be adapted to this model under a rare disease assumption. Let the odds of disease be given by λ(x, z) = α exp(β₁x + β₂z). Loosely, under a rare disease assumption, the probability of disease is then

$$p(x,z)=\frac{\alpha \text{exp}({\beta }_{1}x+{\beta }_{2}z)}{1+\alpha \text{exp}({\beta }_{1}x+{\beta }_{2}z)}\approx \alpha \text{exp}({\beta }_{1}x+{\beta }_{2}z).$$

The missing-data-induced probability can then be approximated as

$$p((1-m)x,m,z)\approx \alpha \text{exp}({\beta }_{1}x(1-m)+{\beta }_{2}z+\varphi (z)m),$$

where ϕ(z) = logE[exp(β₁X) | Z = z,M = 1] would be modeled as a function of the observable Z as ϕ(Z; η) which is described in Section 2. The conditional logistic likelihood contribution for individually matched data can then be derived as highly stratified data so that the probability of two events in a given stratum is exceedingly small (Breslow and Day, 1980) or by taking a retrospective approach with independent sampling of a case and m − 1 controls (Hosmer and Lemeshow 2000).