Abstract
Fluorescence correlation spectroscopy (FCS) is a robust method for the detection of intramolecular dynamics in proteins but is also susceptible to interference from other dynamic processes such as triplet kinetics and photobleaching. We describe an approach for detection of intramolecular dynamics in proteins labeled with a FRET dye pair based on global fitting to the two autocorrelation functions (green-green and red-red) and the two cross-correlation functions (green-red and red-green). We applied the method to detect intramolecular dynamics in the Ca2+ signaling protein calmodulin. Dynamics were detected on the 100-μs time scale in Ca2+-activated calmodulin, whereas in apocalmodulin dynamics were not detected on this time scale. Control measurements on a polyproline FRET construct (Gly-Pro15-Cys) demonstrate the reliability of the method for isolating intramolecular dynamics from other dynamic processes on the microsecond time scale and confirm the absence of intramolecular dynamics of polyproline. We further show the sensitivity of the initial amplitudes of the FCS auto and cross-correlation functions to the presence of multiple FRET states, static or dynamic. The FCS measurements also show that the diffusion of Ca2+-calmodulin is slower than that of apocalmodulin, indicating either a larger average hydrodynamic radius or shape effects resulting in a slower translational diffusion.
Keywords: calmodulin, fluorescence correlation spectroscopy (FCS), Förster resonance energy transfer (FRET), polyproline, protein dynamics
Introduction
Fluorescence correlation spectroscopy (FCS) reveals fluctuations in the fluorescence intensity of a small number of molecules as they pass through the probe volume. FCS detects both concentration fluctuations within the focal volume and kinetic or photophysical processes such as triplet population kinetics and fluorescence quenching. An early application of FCS was to chemical kinetics.1-2 For biological systems,3-7 important applications of FCS include reaction kinetics,2,8-11 conformational dynamics12-14 high-throughput assays,6,15-17 intracellular dynamics,18-19 and a host of others.
Introduction of donor and acceptor fluorophores into the same protein molecule brings in the possibility of fluctuations in the fluorescence intensity through Förster resonance energy transfer (FRET). FCS with FRET is a powerful combination for probing molecular conformations and dynamics, as illustrated by a number of recent publications.11,14,20-26 FRET states may be static, i.e. involving interchange between FRET states that is slow on the time scale of diffusion through the detection volume, or dynamic, leading to fluctuations in fluorescence on the time scale of the molecules transit through the focal region. Methods are needed to analyze FCS data in order to clearly and reliably distinguish FRET dynamics from other sources of fluctuations. Triplet-state dynamics, for example, often occur on the microsecond time scale, and their contribution must be clearly distinguishable from intramolecular dynamics.
In this paper we examine the relationship between FCS and FRET in two systems, one with dynamics on the time scale of transit through the focal region and another where dynamics occur on time scales much faster (or slower) than, but not on the time scale as transit through the focal region. In the first system, we expect contributions to FCS auto and cross-correlations from intramolecular dynamics. In the second (non-dynamic) system, we expect FRET states to be static on the FCS time scale. Satisfactory fitting of FCS curves for a non-dynamic system will serve as a control for FCS curves in cases where dynamics may be present.
A system with static FRET states on the microsecond time scale is polyproline with length ranging from 6-20 prolines.27-30 Using a polyproline sample labeled with donor and acceptor fluorophores, we show that the amplitudes of the FCS correlation functions, both autocorrelations and cross-correlations, are sensitive to the presence of multiple FRET states. Furthermore, analysis of the time dependence confirms the absence of dynamics on the time scale of transit through the focal region. We compare these results with FCS of calmodulin (CaM), a system where we have previously detected dynamics on the microsecond time scale.31 We compute the two autocorrelation functions, one for the green channel and one for the red channel, and the two cross-correlation functions. Our strategy for finding FRET dynamics in CaM is to fit the four functions globally, tying parameters (diffusion time, dynamics time constant, average molecule number, etc) across all four fits.
Materials and Methods
Sample Preparation
A synthetic peptide with the sequence Gly-(Pro)15-Cys was purchased from Sigma Genosys (St. Louis, MO). The amino terminal glycine and carboxyl terminal cysteine were positioned to allow conjugation of reactive fluorescent dyes to the respective sites. Lyophilized peptide was dissolved in 50-mM sodium phosphate buffer at pH 7.2 and labeled with Texas Red (TR) maleimide (Invitrogen Corp. Carlsbad, CA) as per manufacturer recommendations. The labeled peptide was purified on a Superdex Peptide HR 10/30 size exclusion column (GE Healthcare Life Sciences) with 20-mM sodium bicarbonate buffer at pH 7.5. The collected fractions were then concentrated to ∼0.25 mM and dialyzed into 100-mM sodium bicarbonate buffer at pH 7.5. Reaction of the amino terminus was carried out with Alexa Fluor 488 (AF488) succinimidyl ester (Invitrogen Corp. Carlsbad, CA) at room temperature for 90 minutes. The doubly labeled peptide was purified on the Superdex Peptide HR 10/30 size exclusion column as described above. Samples were verified to consist of pure donor-acceptor labeled peptide by mass spectrometry and UV-Vis absorbance measurements.
CaM with two threonine to cysteine mutations (T34C,T110C-CaM) was expressed and labeled with AF488 maleimide and TR maleimide as described previously.32 CaM doubly labeled with donor and acceptor was separated from other species (double-donor, double-acceptor, etc.) by HPLC as described previously.33
FCS Measurements
FCS measurements were performed on an inverted fluorescence microscope (Nikon TE200) adapted for two-color FCS measurements. Laser light at 488 nm from an argon ion laser source (JDS Uniphase) was made circularly polarized with a λ/4 waveplate and passed through a 488/10× excitation filter (Chroma Technology Corp. Rockingham, VT). The light was reflected into a 60× water-immersion objective (UPLSAPO, Olympus, Center Valley, PA) by a 500DCXR dichroic mirror (Chroma). For polyproline measurements, a sample of ∼30 μL of a 5 nM solution in pH 7.0 sodium phosphate buffer was placed on a cover slip treated with bovine serum albumin (BSA) to reduce sample loss due to adhesion of protein to the surface. For high-Ca2+ conditions CaM was added to a pH 7.4 buffer consisting of 10 mM HEPES, 0.1 M KCl, 1 mM MgCl2 and 0.1 mM CaCl2. The low Ca2+ buffer was prepared with 10 mM HEPES, 100 mM KCl, 1 mM MgCl2 and 3 mM EGTA and adjusted to pH 7.4. The concentration of each sample was adjusted to give correlation curves with initial amplitudes in the range of 0.2-1.0. This generally resulted in concentrations of 10-20 nM for each sample.
The laser focus was positioned 20 μm above the surface of the cover slip. Fluorescence was collected in an epifluorescence arrangement and passed through the dichroic mirror. The fluorescence was split into green and red components by a 565DCLP dichroic beam splitter (Chroma). Pinholes (75 μm) were placed in each of the beam paths at their image planes. Separate pinholes for each channel were necessary for optimum probe volume overlap in order to correct for chromatic aberrations in the microscope optics. The fluorescence transmitted through the pinholes was focused onto the active area of the single-photon counting modules (Perkin-Elmer SPCM AQR-14). Emission filters were placed in front of the green (HQ535/50M Chroma) and red (HQ620/75M Chroma) detectors. The resulting stream of photon counts was collected for approximately 5 minutes with a 6602-PCI counter timer card (National Instruments, Austin, TX) controlled with LabView software to tag photon arrival times of both channels using the on-board 80-MHz clock.
Correlation functions
Correlation functions were calculated from photon arrival times with a quasi-logarithmic time axis as described by previous workers.34-37 After-pulsing correction was applied by the method of Zhao et.al.38 Briefly, after-pulsing profiles were collected by focusing to the surface of a cover slip and collecting laser scatter at approximately a 1 kHz count rate for each channel for about 1 million photon counts. The after-pulsing files were correlated and converted to a probability distribution. The probability distributions were fit to a multiple exponential function chosen to accurately describe the shape of the after-pulse contribution starting at the peak of the after-pulse. The resulting fit parameters were then used to subtract the after-pulsing contribution from the collected data sets.
Autocorrelation functions were fit to equations of the form
| (1) |
where the subscript x denotes the green (G) or red (R) channel; Exx(τ) is the contribution from intramolecular dynamics (defined in greater detail below); GT (τ) is the triplet contribution given by39:
where fT is the amplitude for the triplet component and τT is the triplet time constant; Ntot is the average number of fluorescent molecules in the focal volume, Gdiff(τ) is given by:
| (2) |
The axial-radial ratio p was determined previously to equal 8 for our system31 and was fixed for data fitting. Cross-correlation functions were fit to a similar correlation decay function but without the triplet component:
| (3) |
where Ecc(τ) is the contribution to the cross-correlation from intramolecular dynamics. Global fits were carried in Microsoft Excel using the built-in solver to minimize the sum of χ2 values over the four data sets. To calculate the appropriate weighting to use in the fits, each data file for CaM FCS curves was split into eight equal sections.40 The correlations were calculated for each of the eight sections, and the variance σ2 for each correlation point was determined. In fits, each point in the correlation function was weighted by 1/σ2.
Theory
In this section we present a theoretical description of the FCS autocorrelation and cross-correlation functions generated by a system (static or dynamic) with multiple FRET states. Four correlation functions can be calculated from the green and red data streams:
| (4) |
where x and y are the green or red signal channels and 〈…〉 denotes the average over t. For green (G) and red (R) fluorescence channels, eq 4 gives two autocorrelation functions (xy = GG, RR) and two cross-correlation functions (xy = GR, RG).
Case of static FRET states
If the FRET efficiency is static on the FCS time scale (microseconds to milliseconds in this case), then the presence of multiple FRET states affects only the initial amplitudes but not the time dependence of the correlation functions. With fractional populations of FRET states fi (written here for i=1, 2), the initial amplitudes of the correlation functions (not including contributions from processes other than diffusion, such as triplet kinetics or photon antibunching) can be written41:
| (5) |
| (6) |
| (7) |
where Ntot is the average total number of molecules in the focal volume, Ei is the FRET efficiency for conformational state i, and γi = [βEi + (1 − Ei)α], where β is the brightness factor of the FRET-excited acceptor relative to the directly excited donor, and α is the fractional contribution of cross-talk of donor emission into the acceptor channel. Eqs 5-7 assume that the quantum yields of donor and acceptor are independent of the FRET state. (We have also assumed that there is no direct excitation of acceptor, although correction for it could easily be incorporated as well.) These expressions are readily extended to any number of static FRET states in an obvious way. Similar equations for a static FRET system were derived previously in the Gratton group for the case of a single FRET state in the presence of species labeled with donor only and acceptor only.42
Equations 5-7 predict the dependence of the initial amplitudes of correlation functions on the FRET efficiencies of the states present. If only a single FRET state exists (f1=1), the initial amplitudes predicted by eqs 5-7 are identical and given by 1/Ntot. The result (apart from other processes such as triplet kinetics) would be overlapping correlation decay curves. In the presence of two or more static FRET states the initial amplitudes are no longer equal. Thus, the initial amplitudes of the auto and cross-correlation functions for a FRET system can be used to diagnose the presence of multiple FRET states. If their FRET efficiencies are known in advance, the initial amplitudes can then be used to determine the populations of each of these states.
Case of dynamic FRET states
In the case of dynamic FRET states, the FRET efficiency can change while a molecule diffuses through the probe volume. The resulting fluorescence fluctuations lead to additional decay (for the autocorrelations) or rise (for cross-correlations) components. Expressions have been derived for correlation functions with dynamic interchange between FRET states. 25,42-46 For interchange between two FRET states with FRET efficiencies E1 and E2
the FCS correlation functions can be written14,25,42,44
| (8) |
| (9) |
| (10) |
where GT(τ) is the triplet contribution and τ1 = (k1+k-1)-1 is the kinetic relaxation time. We have assumed that both the quantum efficiencies of the fluorophores and the diffusion coefficients are the same in the two FRET states and therefore unchanged by conformational changes of the protein. We note that apart from the triplet contribution eqs 8-10 reduce to eqs 5-7 at τ=0.
Results
Probe volume overlap
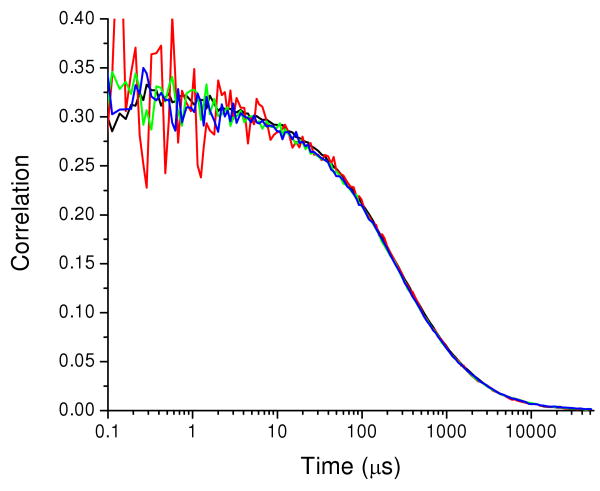
To correctly measure auto and cross-correlation functions, the two channels (green and red) must detect the same region of the sample. Overlap of the detection volumes probed in the green and red channels was verified with fluorescence from CaM-34-110 doubly labeled with AF488 (CaM-AF488-AF488), which was detected in both channels. The signal in the red channel arose from cross-talk of fluorescence into the red channel (about 15%). CaM-AF488-AF488 emission with cross-talk replicates a FRET system with a single FRET efficiency. The two autocorrelation functions, GGG(τ) and GRR(τ), and the two cross-correlation functions, GGR(τ) and GRG(τ), were calculated. Figure 1 shows the four correlation functions for CaM-AF488-AF488. The overlap of the four correlation curves demonstrates overlap of the probe volumes for the green and red channels.
Figure 1.
Correlations for CaM-AF488-AF488. GGG(τ) (black), GRR(τ) (red), GGR(τ) (green), and GRG(τ) (blue). Signal in the red channel arises from AF488 fluorescence detected in the red channel. The close overlap of all four correlation functions demonstrates proper alignment of the probe volumes for the two channels.
FCS of polyproline FRET pair
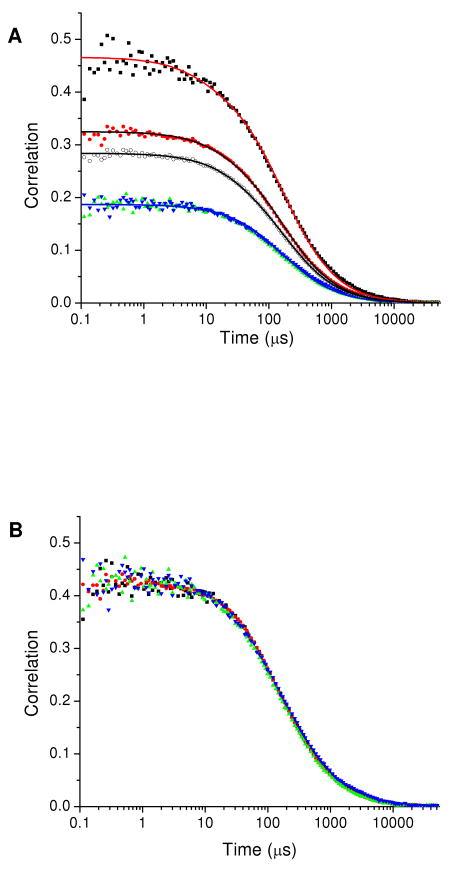
After verification of the probe volume overlap as described above, data were recorded for the peptide Gly-(Pro)15-Cys labeled with donor and acceptor fluorophores AF 488 and TR (polyproline-AF488-TR). The four correlation functions are shown in Figure 2. Unlike the correlation functions for CaM-AF488-AF488 in Figure 1, the correlation functions for polyproline-AF488-TR do not overlay each other. The two cross-correlations GGR(τ) and GRG(τ) overlap as expected but have an initial amplitude different from those of the two autocorrelations GGG(τ) and GRR(τ), which themselves have different amplitudes. The four correlation functions were fit globally to eq 1 or eq 3 without intramolecular dynamics with a total of eight fitting parameters (the triplet parameters fT and τT for green and red channels, the three initial amplitudes, and the diffusion time τd). The initial amplitudes Gxy(0) served as fitting parameters while the transit time was fit globally over all four correlation functions (Figure 2A). Triplet decay components were included in fits to the two autocorrelation functions but not in the fits to the cross-correlation functions. Table 1 shows the average values and standard errors for the fitting parameters from three separate data sets. Global fitting imposes significant constraints on the fitting parameters as suggested by the reproducibility of the fits across the three data sets.
Figure 2.
(A) Correlation functions for polyproline-AF488-TR: GGG(τ) (black squares), GRR(τ) (red circles), GGR(τ) (green triangles), and GRG(τ) (blue inverted triangles). The open circles show the correlation of the combined photon stream. The solid lines show a global fit where the transit times are linked (for GGG(τ), GGR(τ), and GRG(τ)) and the initial amplitudes are allowed to vary independently. Fitting parameters are in Table 1. (B) Correlation functions for polyproline-AF488-TR normalized to show overlap of the time dependence of the four correlation functions.
Table 1.
Global fit parameters for polyproline averaged from different days. The initial amplitudes were allowed to vary independently
| Average | Standard Errora | |
|---|---|---|
| fT (green) | 0.081 | 0.009 |
| τT (green) (μs) | 11.4 | 3.6 |
| fT (red) | 0.065 | 0.010 |
| τT (red) (μs) | 19.2 | 1.1 |
| GGG (0) | 0.403 | 0.015 |
| GRR (0) | 0.273 | 0.018 |
| GGR (0) and GRG (0) | 0.165 | 0.010 |
| τD (μs) | 158.2 | 6.0 |
| p (fixed) | 8 |
Standard deviation in the mean of 3 measurements
Our purpose in analyzing the correlation functions of polyproline-AF488-TR was to verify that the time dependences of the autocorrelation and cross-correlation functions are identical in FCS measurements for a molecule with no dynamics on the microsecond to millisecond time scales (after correction for after-pulsing and triplet contributions). Figure 2B shows the four correlations normalized to the same initial values. The normalization was performed by first dividing out the triplet contributions from the two autocorrelations and then using the initial amplitudes from the global fit to scale all of the correlations to the same initial value. The overlap demonstrates the identical time dependence of the four correlation functions and thus the absence of intramolecular dynamics on the microsecond to millisecond time scales. If there were fluctuations in the FRET efficiency on the microsecond to millisecond timescale, then two extra features would be present. First, the two autocorrelations would have an additional decay component due to another source of fluctuations in the fluorescence signal (eqs 8 and 9). Second, the cross-correlations would contain a rising component due to the anti-correlated nature of FRET fluctuations between the two channels (eq 10). FRET fluctuations would therefore result in the normalized curves not overlapping as they do in Figure 2. The successful fits to the polyproline correlation functions without an intramolecular dynamics component confirm the absence of dynamics on the microsecond time scale.
The different initial amplitudes of the correlation functions observed in Figure 2, even after correction for after-pulsing and triplet decay. The sample was known to consist of pure donor-acceptor labeled peptide, eliminating the possibility of a difference in initial amplitudes caused by a difference in the concentrations of the two fluorophores present. Thus the initial amplitudes demonstrate the presence of more than one FRET efficiency in the polyproline sample or of polyproline molecules without an active acceptor. Equations 5-7 provide the simplest model (two FRET states with the FRET parameters E1, E2, and f1 and the molecule number Ntot) to describe the initial amplitudes. The initial amplitudes constitute three constraints on these parameters. Thus, the initial amplitudes of the green autocorrelation GGG(0), the red autocorrelation GRR(0), and the two cross correlations GGR(0) and GRG(0), which have the same initial amplitude apart from experimental noise, can be used to determine three parameters. The absolute scale of the initial amplitudes is determined by the molecule number Ntot. The three FRET parameters E1, E2, and f1 determine the relative signal levels in the green and red channels and thus are associated with the relative values of the initial amplitudes. It follows that the three values of the initial amplitudes can be used to determine the molecule number Ntot and two of the FRET parameters. Eqs 5-7 thus yield the value of Ntot and ranges of values for E1, E2, and f1 consistent with the measured initial amplitudes. The following range of values are consistent with the initial amplitudes for polyproline in Table 1: 0.79 ≤ E1 ≤ 0.94; 0.04 ≤ E2 ≤ 0.37; 0.44 ≤ f1 ≤ 0.80.
The average molecule number Ntot can also be estimated from the combined photon stream from the two channels. For the case where the quantum yields and detection efficiencies of the two fluorophores are equal, the result is a data stream with the effect of FRET removed. In the present case the quantum yields and detection efficiencies differ by only 10% for the two dyes, so the effect of FRET should be largely absent from the autocorrelation function for the combined photon stream. The autocorrelation of the combined photon stream is included in Figure 2. The combined correlation was fit with a single diffusion time and a triplet component (eq 1). The average total number of particles in the focal volume Ntot was then determined from the initial amplitude of the fit and the value (4.2) is in very good agreement with the value determined from the individual correlation amplitudes.
Given the unequal initial amplitudes, we now address the question of the nature of the multiple FRET states. To identify FRET states that were detected by FCS, single-molecule burst measurements of the polyproline sample were carried out following methods described previously.47 The resulting histogram of the apparent FRET efficiencies displays a population with FRET efficiency greater than 0.7 and another with apparent FRET efficiency less than 0.2 (see Supplementary Information). The average FRET efficiency in the range E>0.4 was 0.82 (fraction 0.74), and the average FRET efficiency for E<0.4 was 0.12 with a fraction of 0.26. The burst measurements are consistent with parameters values obtained from solution of eqs 5-7. Thus, the initial amplitudes can be predicted from the FRET efficiencies of the states present. Furthermore, the initial amplitudes could be used to determine the FRET parameters or populations in appropriate systems. For example if the FRET efficiencies were known from independent measurements, the initial amplitudes of the four correlation functions could be used to find the fractional populations and the total number of molecules.
A population with a low apparent FRET efficiency was detected both in the burst distributions and by analysis of the FCS initial amplitudes. However, an apparent FRET efficiency of ca. 0.1 is inconsistent with the predicted FRET efficiency for a straight-chain polyproline conformation (end-to-end distance of ≤ 42 Å28 or FRET efficiency > 0.7) suggesting that this population was most likely a result of photobleaching of the acceptor molecule. Since molecules that pass through the focal volume have a significant probability of re-entry into the observation volume in FCS and burst measurements,48 photobleaching generates fluorescence bursts with a low apparent FRET efficiency. Thus we expect that the population with low apparent FRET efficiency arose from molecules with a photobleached acceptor fluorophore.
FCS of Calmodulin
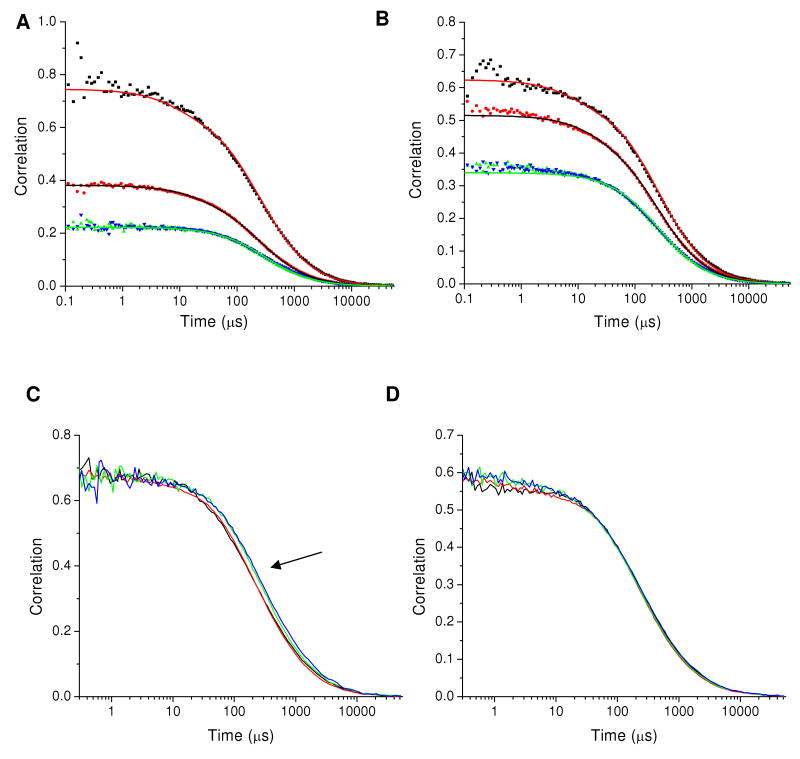
In contrast to polyproline, CaM is a molecule where dynamics are expected on the microsecond time scale.31 Correlation functions for CaM-34-110 labeled with AF488 and TR (CaM-AF488-TR) are shown in Figure 3 for high-Ca 2+ and low-Ca 2+ conditions. For both Ca2+-CaM and apoCaM it was necessary to include a static FRET component to describe the correlation decays. To model this data, the correlation functions for three interchanging FRET states were derived (see Supplementary Information). In the limit where one time constant is long compared to the transit time the intramolecular FRET fitting functions take the form:
Figure 3.
Correlation functions for CaM-AF488-TR. (A) CaM in high-Ca2+ buffer. GGG(τ) (black squares), GRR(τ) (red circles), GGR(τ) (green triangles), and GRG(τ) (blue inverted triangles). The solid lines show a global fit with a time constant for intramolecular dynamics of 92 μs plus a static FRET state. (B) CaM in low-Ca2+ buffer. The global fit in this case incorporates two static FRET states but no intramolecular dynamics. Fitting parameters are given in Table 2. (C) Normalized correlations (with triplet dynamics removed) for CaM-AF488-TR in high-Ca2+ buffer. GGG(τ), GRR(τ), GGR(τ), and GRG(τ) are shown as black, red, green, and blue lines, respectively. The arrow points to the shift between the auto-correlation and cross-correlation curves showing the presence of intramolecular dynamics. (D) Normalized correlations (with triplet dynamics removed) for CaM-AF488-TR in low-Ca2+ buffer. The close overlap between autocorrelation and cross-correlation decays shows that no intramolecular dynamics are detected for apoCaM.
| (11) |
where a and c are the amplitudes for dynamic FRET and b and d are the amplitudes for static FRET. These parameters can be defined in terms of the kinetic rate constants and FRET efficiencies of the FRET states (see Supplementary Information). The four correlation functions for Ca2+-CaM were fit globally with the eight fitting parameters in Table 2 plus the four amplitude parameters (a, b, c, and d) in eq 11. Of these fitting parameters, the triplet parameters were fixed to the values previously determined for polyproline, leaving eight adjustable parameters that were determined from the global fits over four correlation functions. For apoCaM the fitting parameters to describe dynamic FRET (a, c, and τ) were not needed. Transit times for both sets of correlations were linked for GGG(τ), GGR(τ), and GRG(τ), but a shorter transit time was used for GRR(τ) to account for a small contribution to the time dependence from photobleaching of the acceptor fluorophore.
Table 2.
Fitting parameters for CaM 34-110 in high and low Ca2+ buffers. All fits contained a static FRET component; fT is the triplet fraction; τT is the triplet time constant; τD is the transit time.
| Fit Parameter | High Ca2+c | Low Ca2+c | |
|---|---|---|---|
| 〈N〉 | 3.13 ± 0.02 | 2.37 ± 0.02 | |
| fT (green) | 0.1 | 0.1 | |
| τT (green) (μs) | 8 | 8 | |
| fT (red) | 0.09 | 0.09 | |
| τT (red) (μs) | 18 | 18 | |
| τD (μs)a | 281 ± 6 | 264 ± 6 | |
| τD RR (μs)b | 246 ± 5 | 247 ± 8 | |
| τ1 (μs) |
|
n.a. | |
| χ2 | 1.42 | 2.53 |
Transit time for GGG(τ), GGR(τ), and GRG(τ).
The transit time for GRR(τ) was allowed to vary independently to account for photobleaching of the acceptor during transit through the focal volume.
Uncertainties were calculated by the support plane method with confidence range 1 σ.
Table 2 lists the fitting parameters for each of the samples. The fits reveal a correlation time of ∼90 μs for intramolecular dynamics in Ca2+-CaM. FRET dynamics were not detectable for apoCaM. The triplet parameters τT and f for GGG(τ) were set to values obtained from CaM doubly labeled with AF 488 (CaM-AF488-AF488) and fixed during fitting. For Texas Red the triplet parameters were taken from fits to the polyproline GRR(τ) autocorrelation decays. The triplet parameter values depend on laser power and therefore were determined using the same laser powers used for the measurements of CaM. The time scale for dynamics is in agreement with the value previously reported from our laboratory,31 but the amplitude of the dynamics reported here is smaller. This appears to be a result, at least in part, of an irregular response in the control of the NI-6602 data collection card used for the previous measurements, which affected the cross-correlation functions. This problem was rectified for the present measurements. To aid in visualizing the presence or absence of dynamics, the correlations are also shown normalized (Figure 3C and 3D). The high Ca2+ CaM 34-110 correlations clearly show dynamics on the 100's of μs timescale whereas overlap of the curves for apoCaM shows that dynamics were not detected in the low Ca2+ buffer.
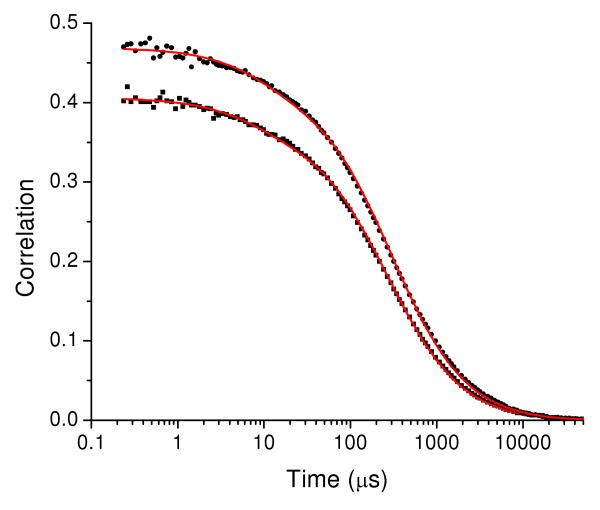
The parameters summarized in Table 2 indicate a longer transit time for Ca2+-CaM than for apoCaM. To check this result, the transit times were determined independently from the autocorrelation function for CaM-AF488-AF488, where the only dynamics contributions come from diffusion and triplet blinking. Figure 4 shows the correlation results for CaM-AF488-AF488. The transit times τd for CaM-AF488-AF488 differed in the high-Ca2+ (τd = 297 ± 10 μs) and low-Ca2+ (τd = 267 ± 8 μs) buffers, in agreement with the value for τd in Table 2. The difference in τd for the high and low Ca2+ buffers was reproducible and was not a result of changes to the buffer viscosity, as shown by the fact that the transit times of free AF488 dye was 65 ± 3 μs and 64 ± 3 μs for the high and low Ca2+ buffers respectively. The relative transit times of CaM at high and low Ca2+ corresponds to a roughly 10% higher hydrodynamic radius at high Ca2+. This difference was not resolved in our previous FCS measurements on CaM.31 However, shape differences could also contribute to the difference in transit time.
Figure 4.
CaM-AF488-AF488 autocorrelation functions in high-Ca2+ buffer (circles) and in low-Ca2+ buffer (squares). The red lines show fits to eq 2 with triplet correction with τD = 297 ± 10 μs, fT = 0.10 ± 0.02, and τT = 8 ± 3 μs in the high-Ca2+ buffer and τD = 267 ± 8 μs, fT = 0.10 ± 0.02, and τT = 8 ± 3 μs in the low Ca2+ buffer.
Discussion
The propensity of CaM to recognize and bind many different target peptide sequences49-51 suggests that CaM is a particularly flexibile and dynamic protein. Dynamics are necessary for protein function. Hence, we expect that CaM dynamics involved in Ca2+ binding or in recognition and binding to an enzyme target domain are manifested by CaM even when no target domain is present. Because CaM recognition of target polypeptides is controlled by Ca2+ binding, understanding the effect of Ca2+ on CaM conformational dynamics is necessary for a full understanding of CaM function. The dynamics observed in Ca2+-CaM thus support the notion that the motions required for CaM to function “pre-exist” even in the absence of a substrate.52-53
Functionally significant protein dynamics often occur on the microsecond time scale.54-57 Our goal here is to demonstrate the utility of FCS to detect dynamics on this time scale. Our approach is based on the combination of FCS and FRET. However, the sensitivity of FCS to other dynamic phenomena on this time scale (triplet dynamics, translational diffusion) means that reliable methods are needed to distinguish dynamic contributions to FCS. The contribution from intramolecular dynamics is distinguishable in FRET-FCS because dynamics contribute in a different manner to the autocorrelation and cross-correlation functions, appearing as a decay in the autocorrelations and a rise in the cross-correlations. We use global fitting of the four correlation functions (two autocorrelations and two cross-correlations) from two fluorophores to extract the intramolecular time constants. Control measurements on a system without microsecond dynamics (polyproline) are an important component of our approach. They confirm the validility of the method and, furthermore, allowed determination of triplet parameters that could then be fixed in fits for molecules with dynamics such as CaM. The results presented here also demonstrate the sensitivity of the initial amplitudes of the auto and cross-correlation functions to the presence of multiple FRET states.
FCS and FRET make a powerful combination as demonstrated in a number of previous investigations. FRET-FCS was applied to a fusion protein (called “cameleon”58) consisting of cyan fluroescent protein, calmodulin, and yellow fluorescent protein. Fitting of the cross-correlation curve yielded a time constant of 42 μs,59 consistent with the time constant for intramolecular dynamics reported in the present paper. Seidel and co-workers detected sub-millisecond intramolecular dynamics in a mutant of syntaxin 1 by first finding the diffusion parameters from a mutant that does not show FRET changes and then globally fitting the auto and cross-correlation curves for a syntaxin mutant exhibiting intramolecular dynamics.60 In our lab, we previously characterized dynamics in CaM by comparison of the cross-correlation funcion with the autocorrelation function for singly labeled CaM.20 Recently, in an analysis of intramolecular dynamics in nucleosomes, Torres and Levitus pointed out that intramolecular dynamics could be extracted in the ratio of auto and cross correlation functions.25,61 As an examination of eqs 8-10 shows, the diffusion contribution is thus eliminated and need not be characterized, and as a result this approach is clearly appealing. However, triplet contributions may also be present in the autocorrelation functions, and these are not elimiated by the ratio method and must therefore be taken into account. We therefore prefer to globally fit the four correlation functions as described in the present paper. Fits to a system without dynamics (polyproline) demonstrate the absence of artifacts and yield the triplet contributions. The global fitting approach has the further advantage of fitting the correlation functions directly, rather than fitting a ratio of two noisy data sets in which taking account of uncertainties in weighted fits could be problematic.
Polyproline
In the absence of intramolecular dynamics, the time dependence of the four correlation functions (after correction for triplet dynamics) is determined by diffusion through the probe volume. The overlap of the four scaled correlation functions in Figure 2 verifies the absence of dynamics and thus the absence of artificats that might be interpreted as dynamics. Thus the polyproline FRET system can serve as a control for detection of intramolecular dynamics by FRET in FCS measurements. In addition, we can also conclude that segmental motions of the fluorophores themselves, for example reorientations about their carbon chain linkers or interactions with the protein, do not lead to changes in FRET efficiency on the microsecond to millisecond time scales.
The initial amplitudes depend on the FRET efficiencies (Figure 2). It should be noted that if there is only one FRET efficiency species present in the sample, the initial amplitudes in eqs 5-7 simplify to 1/Ntot for all of the correlations. This leads to the conclusion that the difference in initial amplitudes demonstrates the presence of multiple FRET states present in the sample, as observed for both polyproline and CaM.
Calmodulin
Comparison of the autocorrelation and cross-correlation curves for CaM at 100 μM Ca2+ confirms a contribution from dynamics on the time scale of 100 μs. No contribution from dynamics was detected for CaM at low Ca2+ (apoCaM). Static FRET states were also present for both Ca2+-CaM and apoCaM, indicating that FRET states are present that interchange on a timescale longer than the transit time of CaM through the focal volume. We have previously observed FRET states of CaM that interchange on a timescale longer than the transit time.31,62 The observation of static FRET states may reflect the presence of these conformations.
The 100 μs time scale of dynamics detected by FCS is consistent with other investigations of the dynamics of CaM. Ca2+ dissociation in stopped-flow measurements occurs with rates of 240 s-1 and 24 s-1 (in the presence of 0.1 M KCl), for Ca2+ dissociation in the N-terminal and C-terminal domains of CaM, respectively.63 Nuclear magnetic resonance relaxation measurements of backbone dynamics64-65 revealed conformational exchange in the C-terminal domain with exchange rates of ∼3000 to 5000 s-1 for CaM at low Ca2+ occupancy and exchange contributions of ∼2 × 104 s-1 for select residues in apoCaM. However, none of these experimental methods has probed the conformational dynamics within Ca2+-CaM. In experiments with a fast micromixer used to measure the kinetics of Ca2+ binding to fluorescently labeled CaM, Ca2+ binding was detected on the ∼490 μs and ∼20 ms timescales and attributed to conformational transitions of the C- and N-terminal domains of the protein, respectively.66 Simulations also have been used to probe conformational dynamics of CaM.67-69 A study of the N-terminal domain67 predicted a transition from a closed to open form of the N-terminus with a rate of 4 × 104 s-1. The dynamics detected here by FCS for Ca2+-CaM are on a similar time scale and could be related to Ca2+ dissociation. However, the fact that dynamics were not detected for apoCaM is inconsistent with an assignment of the dynamics to opening and closing of the Ca2+-binding domains, since these motions are expected in the absence of Ca2+. This suggests that the dynamics detected here by FCS may rather be associated with motions of the N- and C-terminal domains of CaM about the flexible central linker, or with global motions within the N-terminal and/or C-terminal domains themselves.
Conclusions
This study presents a global-fitting approach to two-color FCS FRET data for both polyproline-AF488-TR and CaM-AF488-TR. The absence of overlap in the initial amplitudes of the four auto and cross-correlation functions is consistent with the presence of multiple FRET states in the polyproline sample. The overlap of the correlations when normalized to the sample initial amplitude (after correction for afterpulsing and triplet decays) indicated that there were no fluctuations in FRET efficiencies on the time scale of the molecular transit through the excitation volume. Analysis of the auto- and cross-correlation functions confirmed that the difference in initial amplitude is explained by the presence of multiple FRET states in the polyproline peptide.
In this work, FCS was used to measure the dynamics of CaM-AF488-TR with labels at residues 34 and 110. Because FCS-FRET experiments can be applied to detect intramolecular dynamics by FRET, our motivation was first to demonstrate that features or experimental artifacts that might be interpreted as originating from intramolecular dynamics are in fact absent for a system where intramolecular dynamics are not expected. We expect that a system such as polyproline-AF488-TR used here will be useful as a control in studies of intramolecular dynamics by FCS.
For CaM we detected dynamics with a correlation time of ∼90 μs in the presence of Ca2+. The existence of dynamics was demonstrated by the different time dependence of the autocorrelation and cross-correlation functions. Dynamics were not detected for apoCaM. Thus, Ca2+ activates CaM intramolecular dynamics. Such motions might be involved in target recognition or binding. The question of the nature of the dynamics requires further investigation by both experimental and computational approaches. The comparison of dynamics detected by FCS for different pairs of labeling sites may further characterize the dynamics and would provide experimental observations for comparison with molecular dynamics simulations.
Supplementary Material
Acknowledgments
This work was suppported by the National Science Foundation (CHE-0710515). ESP acknowledges support from the Pharmaceutical Aspects of Biotechnology NIH Training Grant (NIGMS 08359).
References
- 1.Elson EL, Magde D. Biopolymers. 1974;13:1. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 2.Magde D, Elson EL, Webb WW. Biopolymers. 1974;13:29. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 3.Rigler R, Widengren J. Bioscience. 1990;3:180. [Google Scholar]
- 4.Rigler R, Elson ES. Fluorescence Correlation Spectroscopy: Theory and Applications. Springer-Verlag; Berlin: 2001. [Google Scholar]
- 5.Hess ST, Huang S, Heikal AA, Webb WW. Biochemistry. 2002;41:697. doi: 10.1021/bi0118512. [DOI] [PubMed] [Google Scholar]
- 6.Eggeling C, Jager S, Winkler D, Kask P. Curr Pharm Biotechnol. 2005;6:351. doi: 10.2174/138920105774370571. [DOI] [PubMed] [Google Scholar]
- 7.Haustein E, Schwille P. Annu Rev Biophys Biomol Struct. 2007;36:151. doi: 10.1146/annurev.biophys.36.040306.132612. [DOI] [PubMed] [Google Scholar]
- 8.Widengren J, Dapprich J, Rigler R. Chem Phys. 1997;216:417. [Google Scholar]
- 9.Haupts U, Maiti S, Schwille P, Webb WW. Proc Natl Acad Sci U S A. 1998;95:13573. doi: 10.1073/pnas.95.23.13573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lamb DC, Schenk A, Rocker C, Scalfi-Happ C, Nienhaus GU. Biophys J. 2000;79:1129. doi: 10.1016/S0006-3495(00)76366-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hom EFY, Verkman AS. Biophys J. 2002;83:533. doi: 10.1016/S0006-3495(02)75189-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bonnet G, Krichevsky O, Libchaber A. Proc Natl Acad Sci U S A. 1998;95:8602. doi: 10.1073/pnas.95.15.8602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chattopadhyay K, Saffarian S, Elson EL, Frieden C. Proc Natl Acad Sci USA. 2002;99:14171. doi: 10.1073/pnas.172524899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Margittai M, Widengren J, Schweinberger E, Schroder GF, Felekyan S, Haustein E, Konig M, Fasshauer D, Grubmuller H, Jahn R, Seidel CAM. Proc Natl Acad Sci USA. 2003;100:15516. doi: 10.1073/pnas.2331232100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Koltermann A, Kettling U, Bieschke J, Winkler T, Eigen M. Proc Natl Acad Sci USA. 1998;95:1421. doi: 10.1073/pnas.95.4.1421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Matayoshi E, Swift K. Springer Ser Chem Phys. 2001;65:84. [Google Scholar]
- 17.Kohl T, Heinze KG, Kuhlemann R, Koltermann A, Schwille P. Proc Natl Acad Sci USA. 2002;99:12161. doi: 10.1073/pnas.192433499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kim SA, Heinze KG, Bacia K, Waxham MN, Schwille P. Biophys J. 2005;88:4319. doi: 10.1529/biophysj.104.055319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schwille P, Haupts U, Maiti S, Webb WW. Biophys J. 1999;77:2251. doi: 10.1016/S0006-3495(99)77065-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Slaughter BD, Allen MW, Unruh JR, Urbauer RJB, Johnson CK. J Phys Chem B. 2004;108:10388. [Google Scholar]
- 21.Laurence TA, Kapanidis AN, Kong X, Chemla DS, Weiss S. J Phys Chem B. 2004;108:3051. [Google Scholar]
- 22.Eggeling C, Kask P, Winkler D, Jaeger S. Biophys J. 2005;89:605. doi: 10.1529/biophysj.104.052753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Müller BK, Zaychikov E, Brauchle C, Lamb DC. Biophys J. 2005;89:3508. doi: 10.1529/biophysj.105.064766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ruetinger S, Macdonald R, Kramer B, Koberling F, Roos M, Hildt E. Journal of Biomedical Optics. 2006;11 doi: 10.1117/1.2187425. 024012/1. [DOI] [PubMed] [Google Scholar]
- 25.Torres T, Levitus M. J Phys Chem B. 2007;111:7392. doi: 10.1021/jp070659s. [DOI] [PubMed] [Google Scholar]
- 26.Nettels D, Hoffmann A, Schuler B. J Phys Chem B. 2008;112:6137. doi: 10.1021/jp076971j. [DOI] [PubMed] [Google Scholar]
- 27.Schuler B, Lipman EA, Eaton WA. Nature. 2002;419:743. doi: 10.1038/nature01060. [DOI] [PubMed] [Google Scholar]
- 28.Schuler B, Lipman EA, Steinbach PJ, Kumke M, Eaton WA. Proc Natl Acad Sci USA. 2005;102:2754. doi: 10.1073/pnas.0408164102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Watkins LP, Chang HY, Yang H. J Phys Chem A. 2006;110:5191. doi: 10.1021/jp055886d. [DOI] [PubMed] [Google Scholar]
- 30.Best RB, Merchant KA, Gopich IV, Schuler B, Bax A, Eaton WA. Proc Natl Acad Sci USA. 2007;104:18964. doi: 10.1073/pnas.0709567104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Slaughter BD, Allen MW, Unruh JR, Urbauer RJB, Johnson CK. J Phys Chem B. 2004;108:10388. [Google Scholar]
- 32.Allen MW, Bieber Urbauer RJ, Johnson CK. Anal Chem. 2004;76:3630. doi: 10.1021/ac0497656. [DOI] [PubMed] [Google Scholar]
- 33.Allen MW, Urbauer RJB, Zaidi A, Williams TD, Urbauer JL, Johnson CK. Anal Biochem. 2004;325:273. doi: 10.1016/j.ab.2003.10.045. [DOI] [PubMed] [Google Scholar]
- 34.Eid JS, Muller JD, Gratton E. Rev Sci Instrum. 2000;71:361. [Google Scholar]
- 35.Magatti D, Ferri F. Rev Sci Instrum. 2003;74:1135. [Google Scholar]
- 36.Wahl M, Gregor I, Patting M, Enderlein J. Opt Express. 2003;11:3583. doi: 10.1364/oe.11.003583. [DOI] [PubMed] [Google Scholar]
- 37.Felekyan S, Kuehnemuth R, Kudryavtsev V, Sandhagen C, Becker W, Seidel CAM. Rev Sci Instrum. 2005;76 083104/1. [Google Scholar]
- 38.Zhao M, Jin L, Chen B, Ding Y, Ma H, Chen DY. Appl Opt. 2003;42:4031. doi: 10.1364/ao.42.004031. [DOI] [PubMed] [Google Scholar]
- 39.Widengren J, Mets U, Rigler R. J Phys Chem. 1995;99:13368. [Google Scholar]
- 40.Wohland T, Rigler R, Vogel H. Biophys J. 2001;80:2987. doi: 10.1016/S0006-3495(01)76264-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Price ES. Single-Molecule Spectroscopic Tools for Measuring Microsecond and Millisecond Dynamics of Calmodulin. University of Kansas; 2009. [Google Scholar]
- 42.Eid JS. Ph D Thesis. University of Illinois; 2002. Two-Photon Dual Channel Fluctuation Correlation Spectroscopy: Theory and Application. [Google Scholar]
- 43.Magde D, Elson E, Webb WW. Phys Rev Lett. 1972;29:705. [Google Scholar]
- 44.Berne BJ, Pecora R. Dynamic Light Scattering. Wiley; New York: 1976. [Google Scholar]
- 45.Palmer AG, 3rd, Thompson NL. Biophys J. 1987;51:339. doi: 10.1016/S0006-3495(87)83340-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Widengren J, Mets Ü. Conceptual Basis of Fluorescence Correlation Spectroscopy and Related Techniques as Tools in Bioscience. In: Zander C, Enderlein J, Keller RA, editors. Single Molecule Detection in Solution. Wiley-VCH; Berlin: 2002. p. 69. [Google Scholar]
- 47.Slaughter BD, Unruh JR, Allen MW, Urbauer RJB, Johnson CK. Biochemistry. 2005;44:3694. doi: 10.1021/bi048595o. [DOI] [PubMed] [Google Scholar]
- 48.Földes-Papp Z. Exp Mol Path. 2007;82:147. doi: 10.1016/j.yexmp.2006.12.002. [DOI] [PubMed] [Google Scholar]
- 49.Means AR. Handbook of Cell Signaling. 2004;2:83. [Google Scholar]
- 50.Yamniuk AP, Vogel HJ. Mol Biotechnol. 2004;27:33. doi: 10.1385/MB:27:1:33. [DOI] [PubMed] [Google Scholar]
- 51.Berggård T, Arrigoni G, Olsson O, Fex M, Linse S, James P. J Proteome Res. 2006;5:669. doi: 10.1021/pr050421l. [DOI] [PubMed] [Google Scholar]
- 52.Eisenmesser EZ, Bosco DA, Akke M, Kern D. Science. 2002;295:1520. doi: 10.1126/science.1066176. [DOI] [PubMed] [Google Scholar]
- 53.Gsponer J, Christodoulou J, Cavalli A, Bui JM, Richter B, Dobson CM, Vendruscolo M. Structure. 2008;16:736. doi: 10.1016/j.str.2008.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Frauenfelder H, Sligar SG, Wolynes PG. Science. 1991;254:1598. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 55.Englander SW, Kallenbach NR. Q Rev Biophys. 1983;16:521. doi: 10.1017/s0033583500005217. [DOI] [PubMed] [Google Scholar]
- 56.Wand AJ. Nat Struct Biol. 2001;8:926. doi: 10.1038/nsb1101-926. [DOI] [PubMed] [Google Scholar]
- 57.Palmer AG., III Chem Rev. 2004;104:3623. doi: 10.1021/cr030413t. [DOI] [PubMed] [Google Scholar]
- 58.Miyawaki A, Llopis J, Heim R, McCaffery JM, Adams JA, Ikura M, Tsien RY. Nature. 1997;388:882. doi: 10.1038/42264. [DOI] [PubMed] [Google Scholar]
- 59.Eid JS. Two-photon Dual Channel Fluctuation Correlation Spectroscopy: Theory and Application. 2002 [Google Scholar]
- 60.Margittai M, Widengren J, Schweinberger E, Schroder GF, Felekyan S, Haustein E, Konig M, Fasshauer D, Grubmuller H, Jahn R, Seidel CA. Proc Natl Acad Sci U S A. 2003;100:15516. doi: 10.1073/pnas.2331232100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Gurunathan K, Levitus M. The Journal of Physical Chemistry B. 2009;114:980. doi: 10.1021/jp907390n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Slaughter BD, Bieber-Urbauer RJ, Johnson CK. J Phys Chem B. 2005;109:12658. doi: 10.1021/jp051666o. [DOI] [PubMed] [Google Scholar]
- 63.Martin SR, Andersson Teleman A, Bayley PM, Drakenberg T, Forsen S. Eur J Biochem. 1985;151:543. doi: 10.1111/j.1432-1033.1985.tb09137.x. [DOI] [PubMed] [Google Scholar]
- 64.Malmendal A, Evenas J, Forsen S, Akke M. J Mol Biol. 1999;293:883. doi: 10.1006/jmbi.1999.3188. [DOI] [PubMed] [Google Scholar]
- 65.Tjandra N, Kuboniwa H, Ren H, Bax A. Eur J Biochem. 1995;230:1014. doi: 10.1111/j.1432-1033.1995.tb20650.x. [DOI] [PubMed] [Google Scholar]
- 66.Park HY, Kim SA, Korlach J, Rhoades E, Kwok LW, Zipfel WR, Waxham MN, Webb WW, Pollack L. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:542. doi: 10.1073/pnas.0710810105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Tripathi S, Portman JJ. J Chem Phys. 2008;128:205104. doi: 10.1063/1.2928634. [DOI] [PubMed] [Google Scholar]
- 68.Tripathi S, Portman JJ. Proc Natl Acad Sci U S A. 2009;106:2104. doi: 10.1073/pnas.0806872106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Yang C, Jas GS, Kuczera K. Journal of Biomolecular Structure & Dynamics. 2001;19:247. doi: 10.1080/07391102.2001.10506736. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.