Abstract
Understanding the mechanisms of evolution requires information on the rate of appearance of new mutations and their effects at the molecular and phenotypic levels. Although procuring such data has been technically challenging, high-throughput genome sequencing is rapidly expanding knowledge in this area. With information on spontaneous mutations now available in a variety of organisms, general patterns have emerged for the scaling of the mutation rate with genome size and for the likely mechanisms driving this pattern. Support is presented for the hypothesis that natural selection pushes mutation rates down to a lower limit set by the power of random genetic drift rather than by intrinsic physiological limitations, and that this has resulted in reduced levels of replication, transcription, and translation fidelity in eukaryotes relative to prokaryotes.
Keywords: mutation, mutation rate, mutational spectrum, somatic mutation
The challenge of mutation rate estimation
Because mutation is the ultimate source of all variation, both adaptive and deleterious, a mechanistic understanding of the evolutionary process will be incomplete until a detailed account has been made of the rate of origin, molecular nature, and phenotypic consequences of spontaneous alterations for a diversity of organisms. Owing to the extreme rarity of mutational events and their frequent elimination by selection in natural environments, most prior insights into the molecular aspects of mutation have been derived from a few reporter constructs in a handful of model species (Drake 2006). This situation is now rapidly changing as the application of high-throughput genome sequencing to mutation accumulation experiments allows the identification of de novo mutations in an essentially unbiased manner.
At least two broad generalizations now seem possible. First, there is a dramatic reversal in the directional relationship between the mutation rate and genome size from viruses to cellular microbes to multicellular species, with prokaryotes having higher levels of fidelity than eukaryotes at the levels of replication, transcription, and translation. Second, in multicellular species, somatic mutation rates are notably higher than germline rates, whereas on a cell division basis the latter are not much different than rates observed in unicellular species. With these observations in hand, we are now in a better position to understand the causes and consequences of mutation rate evolution in various phylogenetic lineages.
Phylogenetic scaling of the mutation rate
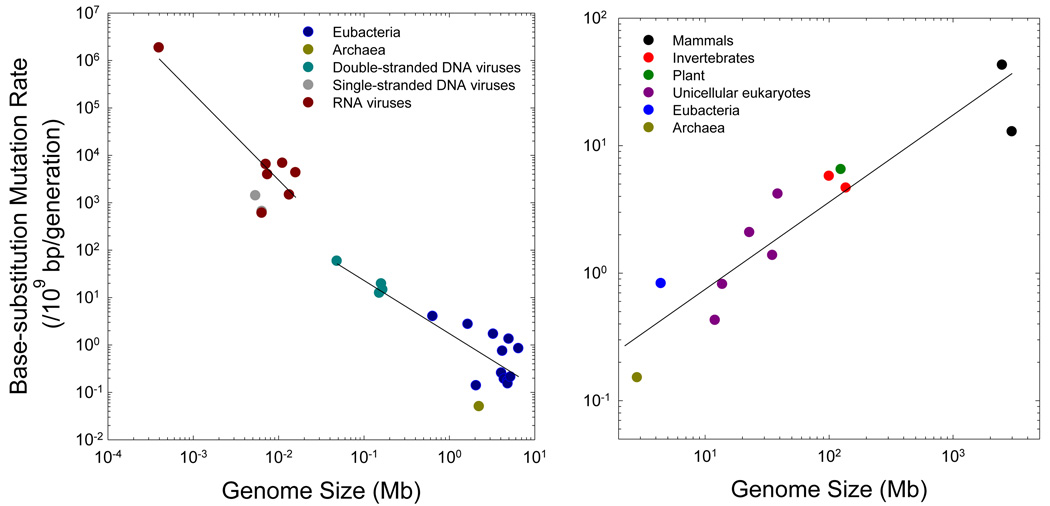
In one of the first attempts to understand the patterning of mutation rates across various organisms, Drake (1991) concluded that the mutation rate/nucleotide site/generation (u) scales inversely with genome size (G) in DNA-based microbes, which further implies that the mutation rate/genome/generation (uG) is essentially constant across all microbial life. Because this early analysis was based on just seven taxa, four of which were bacteriophage, there was room for skepticism over the initial findings, but additional mutation rate assays performed in recent years have allowed for a substantial extension of this previous analysis. Although most microbial mutation rate estimates still rely on single reporter constructs, the approaches advocated by Drake (1991) can be used to translate per locus rates to a per nucleotide site scale (Supplemental Material). The focus here will be on base substitution mutations alone, as considerably less work has been done on insertions and deletions.
For double-stranded DNA viruses and prokaryotes, strong support for Drake’s conjecture remains (Figure 1a), with the mutation rate/site/generation scaling with the −1.1 power of total genome size, although an obvious remaining concern is that the pattern is largely dependent on the inclusion of bacteriophage genomes. Mutation rates for RNA viruses are greater than those for double-stranded DNA genomes of comparable size, but the negative scaling is retained (although this is entirely dependent on a single data point). For the prokaryotic genomes for which data are available, the sampling error of the mutation rate is so large and the range in variation for genome size is so small that only a weak scaling of u with G can be discerned. To more clearly resolve this matter, whole genome mutation accumulation assays, like those now available for several eukaryotes (Lynch et al. 2008; Denver et al. 2009; Keightley et al. 2009; Ossowski et al. 2010), are desirable for a range of prokaryotes, particularly those with extreme genome sizes.
Figure 1.
The scaling of base substitution rate/nucleotide site/generation with genome size. Each data point represents the average estimate for a separate taxon, although the results for most microbes are based on just one or a few reporter constructs (and hence have high sampling error), whereas those for most multicellular taxa are based on very large data sets (in several cases, whole genome sequences). (a) For non-eukaryotes, two separate regressions are provided, one for RNA viruses alone, and one for the pooled data from double-stranded DNA viruses, eubacteria, and archaea. The respective regressions of the log10 plotted mutation rates are −0.17 – 1.83log10(G) and 0.24 – 1.12log10(G), with G denoting the genome size in megabases, and r2 = 0.78 and 0.72, respectively. (b) The regression for cellular organisms is −0.81 + 0.68log10(G), with r2 = 0.80. Here, the results for various eubacteria (excluding Buchnera, which has an unusually small genome) are averaged into a single point. The pattern is quite similar if prokaryotes are excluded (the slope = 0.59 and r2 = 0.83).
In striking contrast to the preceding pattern, when attention is confined to cellular species, mutation rates scale positively with genome size, with vertebrates having nearly 100× higher per generation rates than prokaryotes, and with the rates for unicellular eukaryotes, invertebrates, and land plants being intermediate (Figure 1b). Most of the eukaryotic estimates are based on surveys of substantial genomic regions (including complete genome sequences in four cases), which greatly reduces the sampling variance associated with locus-specific peculiarities, and a statistical scaling of u with the ~2/3rds power of genome size has very strong statistical support (Figure 1b). Note that on a per generation basis, the average mammalian mutation rate is nearly equal to that per replication in double-stranded DNA viruses.
Random genetic drift as the lower limit to DNA repair fidelity
Drake (1991) suggested that the constant rate of total genomic mutation in microbes “is likely to be determined by deep general forces, perhaps by a balance between the usually deleterious effects of mutation and the physiological costs of further reducing mutation rates.” The implicit assumption here is that organisms under strong selection for rapid replication cannot maximize the fidelity of DNA replacement without limiting the rate of DNA synthesis necessary for daughter cell production. This general idea has been promoted broadly (Kimura 1967; Kondrashov 1995; Dawson 1998, 1999; Drake et al. 1998; Sniegowski et al. 2000; André and Godelle 2006; Baer et al. 2007), and although it has not been the subject of empirical investigation, it is known that microbial systems can be improved (Quiñones and Piechocki 1985; Loh et al. 2010).
If the cost-of-repair hypothesis is correct, then we would infer a higher cost of replication in multicellular species (where mutation rates are high) than in prokaryotes. However, the time necessary for the replication of large eukaryotic genomes is compensated by the population of chromosomes with multiple origins of replication (in contrast to the single origin in most bacterial chromosomes). Moreover, as will be discussed below, the burden of somatic mutations imposes a downward selective pressure on mutation rates in multicellular species which is not shared by unicellular species. Thus, an alternative explanation must be sought for the elevated rates of mutation in eukaryotes.
One possibility is that the lower bound on the mutation rate is not set by physiological or biochemical limitations, but by the intrinsic inability of selection to push the rate any lower. The power of random genetic drift (1/2Ne for diploid organisms, where Ne is the genetic effective population size) ultimately constrains what natural selection can accomplish with any trait, and once the mutation rate is pushed to such a low level that any further incremental improvement conveys a fitness advantage smaller than the power of drift, selection will be incapable of reducing the rate any further. Therefore, a key to understanding mutation rate evolution is determining the degree to which evolved mutation rates approach the barriers imposed by drift.
By producing a correlated genetic load through the recurrent influx of deleterious mutations at linked and unlinked sites, even the weakest of mutator alleles suffer an indirect selective disadvantage associated with the excess mutational burden contained within the genomes of carrier individuals (Kimura 1967; Kondrashov 1995; Dawson 1999; Lynch 2008). This disadvantage can be quite small, however, having a maximum value equal to twice the product of the average deleterious effect of a heterozygous mutation (sd) and the diploid genome-wide reduction in the deleterious mutation rate (ΔU, where U is in the range of 0.01 to 1.0 per generation for multicellular eukaryotes, Lynch and Walsh 1998; Baer et al. 2007; and perhaps an order of magnitude lower in yeast, Wloch et al. 2001; Joseph and Hall 2004). The factor of two arises because most induced mutations arise on chromosomes unlinked to the mutator, retaining an association with the latter for an average of just two generations.
Two factors will reduce the selective advantage of an antimutator allele below 2sdΔU, where ΔU is now the genome-wide reduction in the deleterious mutation rate. First, the full long-term advantage of an antimutator is not realized until it has reached selection-mutation balance with respect to its reduced mutation load (Johnson 1999), thus making it more difficult for selection to initially promote such an allele towards fixation. Second, if there is any “cost of replication” associated with the antimutator (sr), the maximum selective advantage becomes 2sdΔU - sr. Thus, because allelic variants with selection coefficients much smaller than the power of random genetic drift evolve in an effectively neutral manner (Kimura 1983), an antimutator allele will be insensitive to selection unless the change in the genome-wide deleterious mutation rate is considerably greater than [1/(2Ne) + sr]/(2sd). Assuming that sd and sr are independent of Ne, this suggests that the mutation rate should scale negatively with Ne up to the point where U is so low that further incremental reductions cannot overcome the drift barrier.
Are eukaryotic mutation rates driven to such low levels? Although a definitive answer cannot yet be given, it is known that Ne is typically in the range of 105 to 106 for the nuclear genomes of multicellular species (Lynch 2007), and that the average value of sd generally ranges from 10−3 to 10−2 (Lynch and Walsh 1998). This implies that a selectable antimutator must reduce the deleterious genome-wide mutation rate in a multicellular lineage by an amount much greater than 10−4 to 10−2. Because these values are ~1% of the genome-wide deleterious mutation rates known for multicellular species, it follows that an antimutator allele would have to reduce U by much more than 1%, perhaps an order of magnitude more, to be promoted by selection. Although not impossible, given that DNA replication and repair are functions of dozens of loci, single amino acid altering mutations at such loci might only rarely have such large effects. Thus, the drift hypothesis appears to be quantitatively plausible.
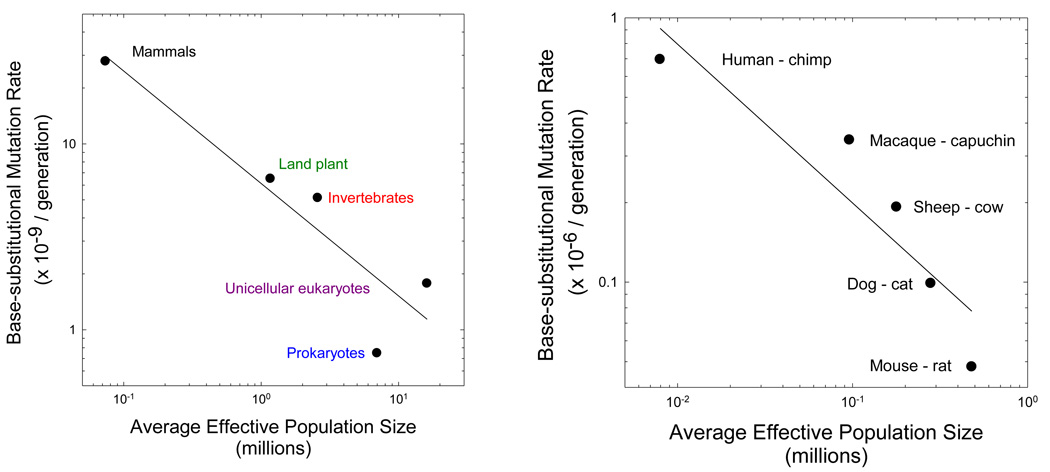
The drift hypothesis derives further support from the distribution of average Ne among phylogenetic lineages (Lynch 2006, 2007). Under the assumption that nucleotide diversity at silent sites in natural populations is effectively neutral (due to the lack of impact at the amino acid level), the equilibrium level of heterozygosity (πs) at such sites is ~4Neu in diploid species (and 2Neu in haploids), where u is the mutation rate per site. Using previously summarized data on πs from major phylogenetic groupings (Lynch 2006), and factoring out the average mutation rates provided in Figure 1, the average Ne in these groups can be approximated. One then finds a significant negative correlation between u and Ne in accordance with the drift hypothesis (Figure 2a).
Figure 2.
The scaling of the base substitution mutation rate per generation (u) and the effective number of genes per locus (2Ne for diploids, and Ne for haploids). (a) The slope of the log-log regression for the nuclear genome of major phylogenetic groupings is −0.60 (0.16), where the number in parentheses denotes the standard error, with r2 = 0.84, although if the estimated Ne for prokaryotes is assumed to be 10 times too low (Lynch 2007), the slope is modified to −0.52 (0.02) with r2 = 0.99. (b) The slope of the log-log regression for the mitochondrial genome of mammalian lineages is −0.60 (0.15), with r2 = 0.84. The data are the average estimates from analyses assuming fixed and variable substitution rates in Piganeau and Eyre-Walker (2009).
A similar pattern is found for mammalian mitochondrial genomes using data from Piganeau and Eyre-Walker (2009). Here, Ne is the effective number of females, as the mammalian mitochondrion is maternally inherited. The mutation rate was inferred indirectly from phylogenetic estimates of divergence at silent sites (assumed to be neutral), estimated times of divergence from the fossil record, and estimated mean generation times. Despite the greater degree of uncertainty in these data, the log-log regression of lineage-specific estimates of u on Ne has a slope identical to that for the nuclear data described above (Figure 2b).
Because the indirect estimates of Ne in both of these analyses are associated with a considerable (but unknown) degree of sampling error, the true scaling of u and Ne might be more extreme than the observed −0.6 power. Nevertheless, that two analyses based on different phylogenetic groups, types of data analysis, and genomic compartments yield essentially the same result provides strong support for the hypothesis that declines in Ne compromise the ability of selection to maintain high-fidelity replication and/or repair mechanisms. Still further support derives from a body of studies suggesting that several aspects of replication fidelity in eukaryotes are compromised relative to the situation in prokaryotes (Lynch 2008), although some aspects of DNA repair seem to be enhanced in mammals relative to microbes (Saparbaev et al. 2000).
These observations help explain a long-standing conundrum in evolutionary genetics – the near independence of nuclear molecular heterozygosity levels across phylogenetic groups with presumably large disparities in Ne. Lewontin (1974) dubbed this pattern “the paradox of variation,” although Nei (1983) later pointed out a weak positive correlation between levels of variation and Ne. We now see that the relative phylogenetic stability of πs across broad domains of life is not a reflection of relatively constant Ne, but of an inverse relationship between u and Ne. This inverse relationship appears also to be responsible for the relative invariance of πs in the mitochondrial genomes of diverse animals (Bazin et al. 2006; Nabholz et al. 2008, 2009)
The preceding arguments also provide a plausible explanation for the opposite scaling pattern of the mutation rate with genome size in viruses and prokaryotes. The case has been made that an upper-bound to Ne, in the neighborhood of 109 to 1011, might exist in cellular species, dictated by the physical (linked) nature of the genome (Lynch 2007). Assuming this upper bound is approximated in non-eukaryotic microbes, and the genome-wide deleterious mutation rate is driven to the lower limit compatible with the associated magnitude of drift, then because selection operates on the genome-wide deleterious mutation rate, any reduction in genome size would increase the lower limit of the achievable per site mutation rate by reducing the number of mutational targets, yielding the inverse scaling suggested by Drake. Such a response is quite notable in the endosymbiotic bacterium Buchnera aphidicola (Moran et al. 2009), which has a highly reduced genome size and the highest known mutation rate for a prokaryote (left-most eubacterial data point in Figure 1).
It also follows that if the average effect of a deleterious mutation (sd) were to increase, the lower limit to the achievable mutation rate would decrease. Drawing from observations that mutations that are benign at low temperatures often have elevated deleterious effects at high temperatures, Drake (2009) has argued that an elevation in sd has promoted the evolution of reduced base-substitution mutation rates in thermophilic bacteria.
Finally, it should be noted that despite the similar scaling of the per site mutation rate with Ne in both nuclear and mitochondrial genomes, the absolute values of u are much greater for mitochondria (Figure 2). Such a pattern is also in agreement with the expectations of the drift hypothesis, as the number of mutational targets in the animal mitochondrion (e.g., just 13 protein-coding genes) is far below the number in nuclear genomes. Thus, although it is often argued that elevated mitochondrial mutation rates in metazoans are an inevitable consequence of a highly oxidative mitochondrial environment, the drift hypothesis provides an explanation based purely on the efficiency of selection. Nonetheless, a remaining puzzle with respect to organelle mutation rates concerns the apparent ~ten-fold reduction in land plants relative to nuclear rates (Lynch 2007). Plant organelle genomes can be up to ten-fold larger than animal mitochondrial genomes, but they are still vastly smaller than nuclear genomes, and the effective population sizes of such organelles do not appear to be unusually large (Lynch 2007). Thus, to be consistent with the drift hypothesis, the average deleterious effects of organelle mutations in land plants must be unusually large, some aspects of the repair machinery must be driven by nuclear functions and/or there must be mechanisms for reducing plant organelle mutation rates in much smaller increments than in nuclear environments.
Somatic mutation
Along with the burden of deleterious germline mutations, multicellular species experience transient somatic mutations, which influence the reproductive output of parental genomes via the development of cancer, senescence, and a large number of other disorders. Although almost no theory exists on the consequences of somatic mutations for the evolution of the mutation rate, because the same basic repair pathway machinery appears to be deployed in all cells, there must be a direct connection between selection to reduce the somatic mutation rate and the evolution of the germline mutation rate, and vice versa (Lynch 2008).
To evaluate the evolutionary consequences of somatic mutations, it is first instructive to put things on an equal footing by standardizing the germline mutation rates of multicellular lineages to a per cell division basis. Such a comparison shows that although selection has been incapable of maintaining per generation germline mutation rates for base substitutions at the levels observed in microbes, the rates per cell division have been kept low, and in humans, perhaps even suppressed (Table 1). However, this degree of conservation seems not to apply to all forms of mutation, as germline mutations at microsatellite loci arise five times more frequently per cell division in Caenorhabditis elegans than in yeast or slime mold, with mammalian and land plant rates being ~14× those in C. elegans (Seyfert et al. 2008; Marriage et al. 2009).
Table 1.
Mutation rates per nucleotide site (× 10−9) in a variety of tissues.
| Mutation ratesb | ||||
|---|---|---|---|---|
| Species | Tissue | Cell divisions per generationa | Per generation | Per cell division |
| Homo sapiens | Germline | 216 | 12.85 | 0.06 |
| Retina | 55 | 54.45 | 0.99 | |
| Intestinal epithelium | 600 | 162.00 | 0.27 | |
| Fibroblast (culture) | 1.34 | |||
| Lymphocytes (culture) | 1.47 | |||
| Mus musculus | Male germline | 39 | 38.00 | 0.97 |
| Brain | 76.94 | |||
| Colon | 83.35 | |||
| Epidermis | 90.38 | |||
| Intestine | 117.69 | |||
| Liver | 237.88 | |||
| Lung | 166.83 | |||
| Spleen | 130.00 | |||
| Rattus norvegicus | Colon | 178.38 | ||
| Kidney | 167.45 | |||
| Liver | 179.92 | |||
| Lung | 223.22 | |||
| Mammary gland | 57.70 | |||
| Prostate | 448.90 | |||
| Spleen | 101.62 | |||
| Drosophila melanogaster | Germline | 36 | 4.65 | 0.13 |
| Whole body | 380.92 | |||
| Caenorhabditis elegans | Germline | 9 | 5.60 | 0.62 |
| Arabidopsis thaliana | Germline | 40 | 6.50 | 0.16 |
| Saccharomyces cerevisiae | 1 | 0.33 | 0.33 | |
| Escherichia coli | 1 | 0.26 | 0.26 | |
References to data on numbers of germline cell divisions: human (Crow 2000); D. melanogaster and mouse (Drost and Lee 1995); C. elegans (Wilkins 1992); and . A. thaliana (Hoffman et al. 2004). Numbers of cell divisions are unknown for the mouse and rat rates.
Mammalian tissue-specific rates are given only for tissues in which at least two independent estimates have been acquired. All data on human mutation rates are taken from Lynch (2010). Data for somatic mutation rates in mouse and rat are derived from references contained within the Supplementary Material. References to data on germline mutation rates: D. melanogaster (Keightley et al. 2009); C. elegans (Denver et al. 2009); A. thaliana (Ossowski et al. 2009); S. cerevisiae (Lynch et al. 2008); and E. coli (Lynch 2006).
Although the maintenance of somatic integrity is critical to germline transmission, metazoan somatic mutation rates are consistently greater than germline rates. In humans, the average mutation rate for four somatic cell types, 1.02 × 10−9/site/cell division (SE = 0.27 × 10−9), is 17× higher than the germline rate and 3.5× higher than the average for yeast and Escherichia coli (Lynch 2010). Assays of a wide range of tissue types in mouse and rat lines engineered to carry reporter constructs show that somatic cells accumulate two- to six-fold more mutations than do cells in the testes at the age of maturity, and considerably more later in life (Table 1). On an absolute time scale, somatic mutation rates are also higher than germline rates in the medaka fish (Winn et al. 2000), and in Drosophila melanogaster per generation somatic rates average ~80× those in the germline (Garcia et al. 2007; Edman et al. 2009). Thus, without the advantages of germline protection, the precise nature of which remains to be determined, the heritable per generation mutation rates for animal species would be several-fold higher.
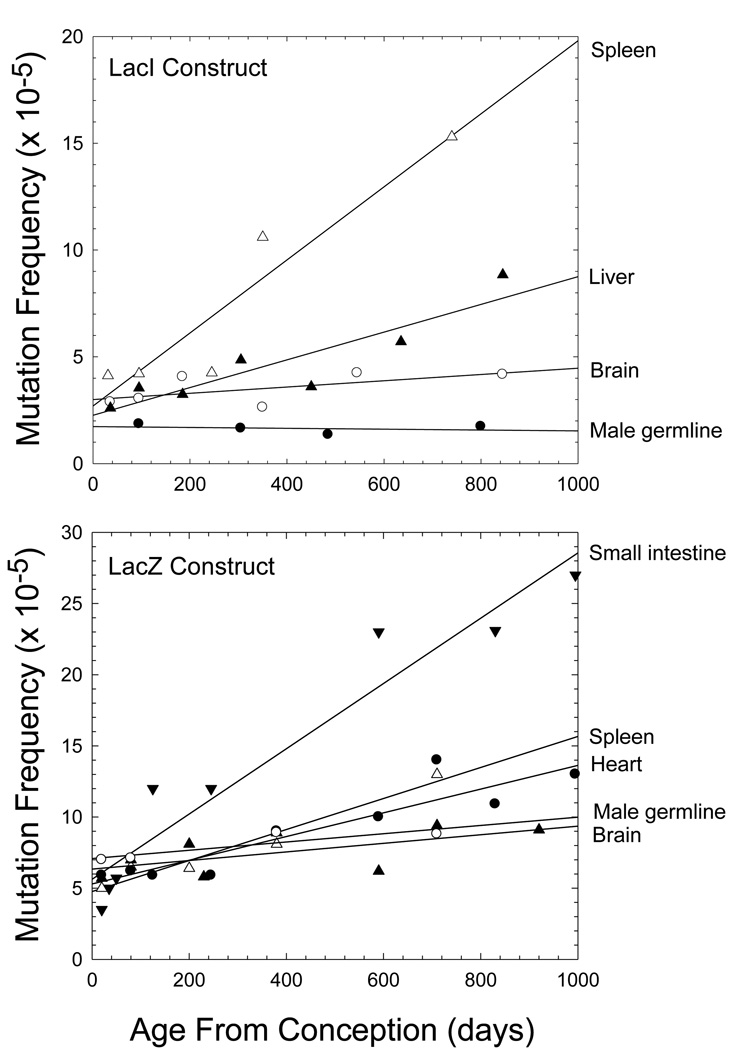
The enormity of the somatic mutation problem can be roughly estimated in humans, where the per generation rate of mutation for intestinal epithelium is ~13× that in the germline, and by extrapolation, that in fibroblasts and lymphocytes is likely to be ~5× higher again (Table 1). Thus, with a human germline mutation rate of ~10−8 base substitutions/site/generation, a site in a somatic nucleus will be mutated with a probability of 10−7 to 10−6 by the average age of reproduction, with the burden being higher in older individuals. With a diploid genome size of 6 × 109 sites and ~1013 cells per soma, the body of a middle-aged human might then contain >1016 mutations (not including insertions, deletions, or other larger scale mutations). Only about 1% of the human genome consists of coding DNA, so a substantial fraction of somatic mutations will be inconsequential, but even if just 1% of coding mutations had significant fitness effects, the total body burden of mutations would be of order 1012. Diploidy might mask the effects of many deleterious mutations, but most mutations with small effects act in a nearly additive fashion (Lynch and Walsh 1998), and although processes such as apoptosis might remove some cells with major mutational defects, it is unlikely that cells with incremental levels of incapacitation could be selectively eliminated. The net result is a progressive lifetime accumulation of somatic mutations, as clearly revealed in the mouse where the germline DNA remains relatively stable within an environment of degrading somatic cell genomes (Figure 3).
Figure 3.
Tissue-specific frequencies of mutations as a function of age in mouse lines carrying Lac reporter constructs. Results are averaged over multiple studies (Supplemental Material).
Without details on the absolute fitness effects of somatic mutations, only qualitative statements can be made on their consequences for the evolution of the germline mutation rate (Lynch 2008). One central question is the degree to which the efficiency of selection operating on the mutation rate via the consequences of somatic mutations changes with the level of multicellularity. At low levels of organismal complexity, the reduction in individual fitness associated with somatic mutations can be described roughly as the product of four factors, 2usTnss, where 2us is the diploid somatic mutation rate per nucleotide site per generation, T is the number of sites influencing fitness, n is the number of cells influencing fitness, and ss is the reduction in fitness per somatic mutation. (A more explicit form of this expression would not treat all cells equally, but sum over independent tissues; Lynch 2008).
Although T and n must increase with increasing levels of multicellularity, ss might decrease, depending on aspects of cellular surveillance and the buffering effects of multicellularity on individual mutant cells. By contrast, as noted in Figure 2, increased multicellularity is generally associated with a reduction in Ne, which in turn reduces the efficiency of selection. Thus, a key to understanding the degree to which the burden of somatic mutations impacts selection on the mutation rate itself is analogous to the situation noted above for germline mutations. If the increase in 1/(2Ne) with increasing multicellularity exceeds the increase in 2usTnss, the ability of selection to reduce the somatic mutation rate (and likely the correlated effect on the germline rate) will become progressively compromised.
Moreover, a scenario can be envisioned whereby a critical level of multicellularity is eventually reached, beyond which the ability of selection to reduce the somatic mutation rate begins to decline (Lynch 2008). Such behavior is expected because the strength of selection depends on relative rather than absolute fitness effects. Although the absolute negative consequences of somatic mutations might continue to increase indefinitely with increasing multicellularity, once a level has been reached at which the fraction of affected individuals approaches saturation, the relative selective disadvantage of a further increase in the mutation rate must begin to decline. It is unclear where organisms with various levels of multicellularity reside on this continuum. However, it is clear that if the somatic mutation load plays a role in the evolution of the germline mutation rate, it has generally been incapable of keeping the somatic rate at levels observed in unicellular species.
Transcription and translation fidelity
Although somatic nuclear mutations permanently influence a host cell and all of its descendants, two more transient forms of mutations are also of relevance – errors in transcription and translation. The average error rate estimate for RNA Polymerase II (the polymerase involved in transcription of coding mRNAs) in E. coli is 1 × 10−5 per base incorporation (Blank et al. 1986; Ninio 1991; Goldsmith and Tawfik 2009), whereas that for Saccharomyces cerevisiae is in the range of 2 × 10−6 to 3 × 10−4 (Shaw et al. 2002; Kireeva et al. 2008), and the single estimate for a multicellular species is 1 × 10−3 in wheat (de Mercoyrol et al. 1992). These rough estimates are based on a variety of methodologies and have a restricted phylogenetic range. Nevertheless, they indicate that transcription error rates per nucleotide transaction are orders of magnitude higher than the replicaton error rates noted above. They also suggest that transcriptional fidelity is reduced in eukaryotes, perhaps substantially so in multicellular lineages.
A similar pattern is observed for translation, with the overall level of fidelity appearing to be even lower than that for transcription. Although there can be considerable variation among codon types, the average translation error rate per codon in E. coli is 6 × 10−4 (Ortego et al. 2007; Kramer and Farabaugh 2007; Willensdorfer et al. 2007), whereas the average rates for yeast, rabbit reticulocytes, and mouse liver cells are, respectively, 2 × 10−3 (Stansfield et al. 1998; Salas-Marco and Bedwell 2005), 3 × 10−4 (Loftfield and Vanderjagt 1972), and 1 × 10−3 (Mori et al. 1985). Taken together, with an average protein length of ~300 amino acid residues (Lynch 2007), these observations suggest that, without removal by post-translational surveillance, >20% of individual proteins will contain at least one inappropriate amino acid (Drummond and Wilkie 2009).
Like DNA polymerases, RNA polymerases have a proof-reading capacity (Sydow and Cramer 2009), and there is no obvious reason why they (or the translational machinery) should be intrinsically constrained from operating at the level of efficiency of DNA polymerases. However, because individual loci generally produce multiple transcripts, and mRNAs and individual proteins have transient residence times within cells, transcriptional and translational errors are expected to have less severe effects on cell integrity than genome-level errors. Thus, the strength of selection operating on the transcriptional and translational machinery is likely to be less stringent, and consistent with the drift hypothesis, this might explain the greatly elevated error rates at these processes.
Concluding remarks
Germline mutation rate data provide a critical basis for interpreting patterns of molecular diversity within species and divergence among species. Indeed, inferences regarding selection have been historically derived by assuming certain classes of sites (e.g., synonymous coding-region positions) to be effectively neutral and hence to evolve at the mutation rate, hence providing clear predictions of evolutionary patterns expected in the absence of selection (Kimura 1983). However, the direct estimates of mutation rates and molecular spectra obtained in the studies reviewed herein are often substantially different from those derived by indirect inference from natural populations, at least in part because selection is more pervasive than formerly believed (e.g., Eöry et al. 2009). Thus, to be fully reliable, future molecular investigations with a goal of interpreting evolutionary mechanisms should take advantage of direct estimates of mutation rates. One might argue that laboratory estimates are subject to their own peculiar biases, but the consistent patterns noted above suggest that we are close to developing a general understanding of the rates at which base substitutions arise in various phylogenetic lineages.
Although there are strong scaling patterns between the mutation rate per generation and genome size, this pattern is not a function of direct causality, i.e., large eukaryotic genomes do not intrinsically engender low fidelity of DNA replication. Rather, because there is a general insertional bias in most eukaryotic genomes, as effective population sizes decline and the efficiency of selection against excess DNA is relaxed, genome size increases in a passive fashion (Lynch 2007), along with the mutation rate. By contrast, effective population sizes in viruses and prokaryotes might often be so close to their maxima that the lower limit to the evolvable genome-wide mutation rate has been reached. Once this point has been reached, any events that lead to a further reduction in genome size (e.g., loss of non-essential genes in endosymbionts and parasites) will generally increase the minimum evolvable per site mutation rate, as the product of the latter and the genome-wide number of selected sites is equal to the genome-wide deleterious rate. However, why the total genomic mutation rate for microbes converges on ~0.003 per cell division (Drake 1991) is a mystery that remains to be solved.
An additional unsolved problem concerns the long-term stability of the mutation rate in low-Ne lineages. Just as random genetic drift can inhibit the fixation of an antimutator with an insufficiently large effect on the genomic mutation rate, it can prevent the fixation of sufficiently mild mutator alleles. What then prevents the gradual accumulation of very mildly deleterious mutations at DNA repair loci and a slow but progressive increase in the mutation rate in multicellular lineages? Given the preceding arguments, it might be premature to assume that the mutation rate in such lineages has actually attained equilibrium.
Supplementary Material
Acknowledgements
This work was funded by NIH grant GM36827 and NSF grant EF-0827411, and by the MetaCyte program derived from Lilly Foundation funding to Indiana University. I am grateful to J. Drake for helpful comments.
Glossary
- Antimutator allele
denotes a mutant copy of any gene that confers a reduction (of arbitrary size) in the mutation rate.
- Equilibrium level of heterozygosity (πs)
approximately 4Neu in diploid species and 2Neu in haploids under neutrality. This result is simply obtained for diploids by noting that the mutational rate of origin of new heterozygosity at a homozygous site is 2u, whereas the fractional loss of existing heterozygosity by drift is 1/(2Ne), with the equilibrium being given by the ratio of these rates.
- Fitness
the relative reproductive capacity of an individual (also accounting for viability to maturity), scaled to fall between values of 0 and 1.
- G
genome size in number of nucleotides per haploid genome.
- Mutator allele
denotes a mutant copy of any gene that confers an increase in the mutation rate.
- Ne
genetic effective population size which measures the size of the population with respect to the stochastic behavior of allele frequencies relative to the situation for an ideal random-mating population. Technical details are reviewed in Lynch (2007) and Charlesworth (2009). A central point is that Ne is generally much smaller than the actual size of a population, as a consequence of variation in family size, non-random mating, sex-ratio bias, and many other aspects of population structure. At small population sizes, Ne might increase in parallel with the actual population size, but at very large population sizes Ne becomes largely limited by the structure of chromosomes, as simultaneously segregating mutations at linked loci interfere with each other, thereby reducing the efficiency of selection relative to the situation for independent loci. The latter factor might result in Ne eventually asymptoting at an upper limit, regardless of the actual population size.
- Random genetic drift
stochastic fluctuations in allele frequencies resulting from the sampling of a finite number of gametes in the establishment of each generation. For haploid and diploid species, the variance in allele frequency resulting from drift is proportional to 1/Ne and 1/(2Ne), respectively.
- sd
proportional reduction in fitness resulting from a heterozygous mutation.
- sr
proportional reduction in fitness resulting from the cost of replication associated with an antimutator allele.
- Selection-mutation balance
refers to the equilibrium frequencies of deleterious alleles that are reached when the input of new variants by mutation is balanced by the removal by natural selection.
- Silent site
a position in a protein-coding gene where nucleotide substitution has no influence on the protein sequence, owing to the redundancy in the genetic code.
- Somatic mutation
a mutation arising in a non-germline cell in a multicellular species, which can influence individual fitness, but is not inherited by offspring.
- u
mutation rate per nucleotide site per generation.
- U or uG
genome-wide mutation rate per generation.
- ΔU
the positive or negative change in the genome-wide mutation rate caused, respectively, by a mutat or or antimutator allele.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- André JB, Godelle B. The evolution of mutation rate in finite asexual populations. Genetics. 2006;172:611–626. doi: 10.1534/genetics.105.046680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baer CF, Miyamoto MM, Denver DR. Mutation rate variation in multicellular eukaryotes: causes and consequences. Nat. Rev. Genet. 2007;8:619–631. doi: 10.1038/nrg2158. [DOI] [PubMed] [Google Scholar]
- Bazin E, Glémin S, Galtier N. Population size does not influence mitochondrial genetic diversity in animals. Science. 2006;312:570–572. doi: 10.1126/science.1122033. [DOI] [PubMed] [Google Scholar]
- Blank A, Gallant JA, Burgess RR, Loeb LA. An RNA polymerase mutant with reduced accuracy of chain elongation. Biochemistry. 1986;25:5920–5928. doi: 10.1021/bi00368a013. [DOI] [PubMed] [Google Scholar]
- Charlesworth B. Fundamental concepts in genetics: effective population size and patterns of molecular evolution and variation. Nat. Rev. Genet. 2009;10:195–205. doi: 10.1038/nrg2526. [DOI] [PubMed] [Google Scholar]
- Dawson KJ. Evolutionarily stable mutation rates. J. Theor. Biol. 1998;194:143–157. doi: 10.1006/jtbi.1998.0752. [DOI] [PubMed] [Google Scholar]
- Dawson KJ. The dynamics of infinitesimally rare alleles, applied to the evolution of mutation rates and the expression of deleterious mutations. Theor. Popul. Biol. 1999;55:1–22. doi: 10.1006/tpbi.1998.1375. [DOI] [PubMed] [Google Scholar]
- de Mercoyrol L, Corda Y, Job C, Job D. Accuracy of wheat-germ RNA polymerase II. General enzymatic properties and effect of template conformational transition from right-handed B-DNA to left-handed Z-DNA. Eur. J. Biochem. 1992;206:49–58. doi: 10.1111/j.1432-1033.1992.tb16900.x. [DOI] [PubMed] [Google Scholar]
- Denver DR, Dolan PC, Wilhelm LJ, Sung W, Lucas-Lledó JI, Howe DK, Lewis SC, Okamoto K, Thomas WK, Lynch M, Baer CF. A genome-wide view of Caenorhabditis elegans base substitution mutation processes. Proc. Natl. Acad. Sci. USA. 2009;106:16310–16314. doi: 10.1073/pnas.0904895106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake JW. A constant rate of spontaneous mutation in DNA-based microbes. Proc. Natl. Acad. Sci. USA. 1991;88:7160–7164. doi: 10.1073/pnas.88.16.7160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake JW. Chaos and order in spontaneous mutation. Genetics. 2006;173:1–8. doi: 10.1093/genetics/173.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake JW. Avoiding dangerous missense: thermophiles display especially low mutation rates. PLoS Genet. 2009;5 doi: 10.1371/journal.pgen.1000520. e1000520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake JW, Charlesworth B, Charlesworth D, Crow JF. Rates of spontaneous mutation. Genetics. 1998;148:1667–1686. doi: 10.1093/genetics/148.4.1667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drost JB, Lee WR. Biological basis of germline mutation: comparisons of spontaneous germline mutation rates among Drosophila, mouse, and human. Environ. Mol. Mut., Suppl. 1995;26:48–64. doi: 10.1002/em.2850250609. [DOI] [PubMed] [Google Scholar]
- Drummond DA, Wilke CO. The evolutionary consequences of erroneous protein synthesis. Nat. Rev. Genet. 2009;10:715–724. doi: 10.1038/nrg2662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edman U, Garcia AM, Busuttil RA, Sorensen D, Lundell M, Kapahi P, Vijg J. Lifespan extension by dietary restriction is not linked to protection against somatic DNA damage in Drosophila melanogaster. Aging Cell. 2009;8:331–338. doi: 10.1111/j.1474-9726.2009.00480.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eöry L, Halligan DL, Keightley PD. Distributions of selectively constrained sites and deleterious mutation rates in the hominid and murid genomes. Mol. Biol. Evol. 2009;27:177–192. doi: 10.1093/molbev/msp219. [DOI] [PubMed] [Google Scholar]
- Garcia AM, Derventzi A, Busuttil R, Calder RB, Perez E, Jr, Chadwell L, Dollé ME, Lundell M, Vijg J. A model system for analyzing somatic mutations in Drosophila melanogaster. Nature Methods. 2007;4:401–403. doi: 10.1038/NMETH1027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldsmith M, Tawfik DS. Potential role of phenotypic mutations in the evolution of protein expression and stability. Proc. Natl. Acad. Sci. USA. 2009;106:6197–6202. doi: 10.1073/pnas.0809506106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman PD, Leonard JM, Lindberg GE, Bollmann SR, Hays JB. Rapid accumulation of mutations during seed-to-seed propagation of mismatch-repair-defective Arabidopsis. Genes Dev. 2004;18:2676–2685. doi: 10.1101/gad.1217204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson T. The approach to mutation-selection balance in an infinite asexual population, and the evolution of mutation rates. Proc. Biol. Sci. 1999;266:2389–2397. doi: 10.1098/rspb.1999.0936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joseph SB, Hall DW. Spontaneous mutations in diploid Saccharomyces cerevisiae: More beneficial than expected. Genetics. 2004;168:1817–1825. doi: 10.1534/genetics.104.033761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley PD, Trivedi U, Thomson M, Oliver F, Kumar S, Blaxter ML. Analysis of the genome sequences of three Drosophila melanogaster spontaneous mutation accumulation lines. Genome Res. 2009;19:1195–1201. doi: 10.1101/gr.091231.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M. On the evolutionary adjustment of spontaneous mutation rates. Genet. Res. 1967;9:23–34. [Google Scholar]
- Kimura M. The Neutral Theory of Molecular Evolution. Cambridge, UK: Cambridge Univ. Press; 1983. [Google Scholar]
- Kireeva ML, Nedialkov YA, Cremona GH, Purtov YA, Lubkowska L, Malagon F, Burton ZF, Strathern JN, Kashlev M. Transient reversal of RNA polymerase II active site closing controls fidelity of transcription elongation. Mol. Cell. 2008;30:557–566. doi: 10.1016/j.molcel.2008.04.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov AS. Modifiers of mutation-selection balance: general approach and the evolution of mutation rates. Genet. Res. 1995;66:53–70. [Google Scholar]
- Kramer EB, Farabaugh PJ. The frequency of translational misreading errors in E. coli is largely determined by tRNA competition. RNA. 2007;13:87–96. doi: 10.1261/rna.294907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewontin RC. The Genetic Basis of Evolutionary Change. New York, NY: Columbia Univ. Press; 1974. [Google Scholar]
- Loh E, Salk JJ, Loeb LA. Optimization of DNA polymerase mutation rates during bacterial evolution. Proc. Natl. Acad. Sci. USA. 2010;107:1154–1159. doi: 10.1073/pnas.0912451107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loftfield RB, Vanderjagt D. The frequency of errors in protein biosynthesis. Biochem. J. 1972;128:1353–1356. doi: 10.1042/bj1281353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M. The origins of eukaryotic gene structure. Mol. Biol. Evol. 2006;23:450–468. doi: 10.1093/molbev/msj050. [DOI] [PubMed] [Google Scholar]
- Lynch M. The Origins of Genome Architecture. Sunderland, MA: Sinauer Assocs., Inc.; 2007. [Google Scholar]
- Lynch M. The cellular, developmental, and population-genetic determinants of mutation-rate evolution. Genetics. 2008;180:933–943. doi: 10.1534/genetics.108.090456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M. The rate, molecular spectrum, and consequences of human mutation. Proc. Natl. Acad. Sci. USA. 2010;107:961–968. doi: 10.1073/pnas.0912629107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Sung W, Morris K, Crown N, Landry CR, Dopman EB, Dickinson WJ, Okamoto K, Kulkarni S, Hartl DL, Thomas WK. A genome-wide view of the spectrum of spontaneous mutations in yeast. Proc. Natl. Acad. Sci. USA. 2008;105:9272–9277. doi: 10.1073/pnas.0803466105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Walsh JB. Genetics and Analysis of Quantitative Traits. Sunderland, MA: Sinauer Assocs., Inc.; 1998. [Google Scholar]
- Marriage TN, Hudman S, Mort ME, Orive ME, Shaw RG, Kelly JK. Direct estimation of the mutation rate at dinucleotide microsatellite loci in Arabidopsis thaliana (Brassicaceae) Heredity. 2009;103:310–317. doi: 10.1038/hdy.2009.67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran NA, McLaughlin HJ, Sorek R. The dynamics and time scale of ongoing genomic erosion in symbiotic bacteria. Science. 2009;323:379–382. doi: 10.1126/science.1167140. [DOI] [PubMed] [Google Scholar]
- Mori N, Funatsu Y, Hiruta K, Goto S. Analysis of translational fidelity of ribosomes with protamine messenger RNA as a template. Biochemistry. 1985;24:1231–1239. doi: 10.1021/bi00326a027. [DOI] [PubMed] [Google Scholar]
- Nabholz B, Glémin S, Galtier N. The erratic mitochondrial clock: variations of mutation rate, not population size, affect mtDNA diversity across birds and mammals. BMC Evol. Biol. 2009;10:54. doi: 10.1186/1471-2148-9-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nabholz B, Mauffrey JF, Bazin E, Galtier N, Glemin S. Determination of mitochondrial genetic diversity in mammals. Genetics. 2008;178:351–361. doi: 10.1534/genetics.107.073346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei M. Genetic polymorphism and the role of mutation in evolution. In: Nei M, Koehn RK, editors. Evolution of Genes and Proteins. Sunderland, MA: Sinauer Assocs., Inc.; 1983. pp. 165–190. [Google Scholar]
- Ninio J. Transient mutators: a semiquantitative analysis of the influence of translation and transcription errors on mutation rates. Genetics. 1991;129:957–962. doi: 10.1093/genetics/129.3.957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ortego BC, Whittenton JJ, Li H, Tu SC, Willson RC. In vivo translational inaccuracy in Escherichia coli: missense reporting using extremely low activity mutants of Vibrio harveyi luciferase. Biochemistry. 2007;46:13864–13873. doi: 10.1021/bi602660s. [DOI] [PubMed] [Google Scholar]
- Ossowski S, Schneeberger K, Lucas-Lledó J, Warthmann N, Clark RM, Shaw RG, Weigel D, Lynch M. The rate and molecular spectrum of spontaneous mutations in Arabidopsis thaliana. Science. 2010;327:92–94. doi: 10.1126/science.1180677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piganeau G, Eyre-Walker A. Evidence for variation in the effective population size of animal mitochondrial DNA. PLoS One. 2009;4:e4396. doi: 10.1371/journal.pone.0004396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quiñones A, Piechocki R. Isolation and characterization of Escherichia coli antimutators: a new strategy to study the nature and origin of spontaneous mutations. Mol. Gen. Genet. 1985;201:315–322. doi: 10.1007/BF00425677. [DOI] [PubMed] [Google Scholar]
- Salas-Marco J, Bedwell DM. Discrimination between defects in elongation fidelity and termination efficiency provides mechanistic insights into translational readthrough. J. Mol. Biol. 2005;348:801–815. doi: 10.1016/j.jmb.2005.03.025. [DOI] [PubMed] [Google Scholar]
- Saparbaev M, Mani JC, Laval J. Interactions of the human, rat, Saccharomyces cerevisiae and Escherichia coli 3-methyladenine-DNA glycosylases with DNA containing dIMP residues. Nucleic Acids Res. 2000;28:1332–1339. doi: 10.1093/nar/28.6.1332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seyfert AL, Cristescu MEA, Frisse L, Schaack S, Thomas WK, Lynch M. The rate and spectrum of microsatellite mutation in Caenorhabditis elegans and Daphnia pulex. Genetics. 2008;178:2113–2121. doi: 10.1534/genetics.107.081927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw RJ, Bonawitz ND, Reines D. Use of an in vivo reporter assay to test for transcriptional and translational fidelity in yeast. J. Biol. Chem. 2002;277:24420–24426. doi: 10.1074/jbc.M202059200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stansfield I, Jones KM, Herbert P, Lewendon A, Shaw WV, Tuite MF. Missense translation errors in Saccharomyces cerevisiae. J. Mol. Biol. 1998;282:13–24. doi: 10.1006/jmbi.1998.1976. [DOI] [PubMed] [Google Scholar]
- Sniegowski PD, Gerrish PJ, Johnson T, Shaver A. The evolution of mutation rates: separating causes from consequences. Bioessays. 2000;22:1057–1066. doi: 10.1002/1521-1878(200012)22:12<1057::AID-BIES3>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- Sydow JF, Cramer P. RNA polymerase fidelity and transcriptional proofreading. Curr. Opin. Struct. Biol. 2009;19:732–739. doi: 10.1016/j.sbi.2009.10.009. [DOI] [PubMed] [Google Scholar]
- Wilkins AS. Genetic Analysis of Animal Development. Second Ed. NewYork: Wiley-Liss; 1992. [Google Scholar]
- Willensdorfer M, Bürger R, Nowak MA. Phenotypic mutation rates and the abundance of abnormal proteins in yeast. PLoS Comput. Biol. 2007;3:e203. doi: 10.1371/journal.pcbi.0030203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winn RN, Norris MB, Brayer KJ, Torres C, Muller SL. Detection of mutations in transgenic fish carrying a bacteriophage lambda cII transgene target. Proc. Natl. Acad. Sci. USA. 2000;97:12655–12660. doi: 10.1073/pnas.220428097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wloch D, Szafraniec MK, Borts RH, Korona R. Direct estimate of the mutation rate and the distribution of fitness effects in the yeast Saccharomyces cerevisiae. Genetics. 2001;159:441–452. doi: 10.1093/genetics/159.2.441. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.