Regularization Parameter Selections via Generalized Information Criterion

Abstract

We apply the nonconcave penalized likelihood approach to obtain variable selections as well as shrinkage estimators. This approach relies heavily on the choice of regularization parameter, which controls the model complexity. In this paper, we propose employing the generalized information criterion (GIC), encompassing the commonly used Akaike information criterion (AIC) and Bayesian information criterion (BIC), for selecting the regularization parameter. Our proposal makes a connection between the classical variable selection criteria and the regularization parameter selections for the nonconcave penalized likelihood approaches. We show that the BIC-type selector enables identification of the true model consistently, and the resulting estimator possesses the oracle property in the terminology of Fan and Li (2001). In contrast, however, the AIC-type selector tends to overfit with positive probability. We further show that the AIC-type selector is asymptotically loss efficient, while the BIC-type selector is not. Our simulation results confirm these theoretical findings, and an empirical example is presented. Some technical proofs are given in the online supplementary material.

1 Introduction

Using the penalized likelihood function to simultaneously select variables and estimate unknown parameters has received considerable attention in recent years. To avoid the instability of the classical subset selection procedure, Tibshirani (1996) proposed the Least Absolute Shrinkage and Selection Operator (LASSO). In the same spirit as LASSO, Fan and Li (2001) introduced a unified approach via a nonconcave penalized likelihood function, and demonstrated its usefulness for both linear and generalized linear models. Subsequently, Fan and Li (2002) employed the nonconcave penalized likelihood approach for Cox models, while Fan and Li (2004) used it on semiparametric regression models. In addition, Fan and Peng (2004) investigated the theoretical properties of the nonconcave penalized likelihood when the number of parameters tends to infinity as the sample size increases. Recently, more researchers applied penalized approaches to study variable selections (e.g., Park and Hastie, 2007; Wang and Leng, 2007; Yuan and Lin, 2007; Zhang and Lu, 2007; Li and Liang, 2008).

In employing the nonconcave penalized likelihood in regression analysis, we face two challenges. The first hurdle is to compute the nonconcave penalized likelihood estimate. This issue has been carefully studied in the recent literature: (i.) Fan and Li (2001) proposed the local quadratic approximation (LQA) algorithm, which was further analyzed by Hunter and Li (2005); (ii.) Efron, Hastie, Johnstone, and Tibshirani (2004) introduced the LARS algorithm, which can be used for the adaptive LASSO (Zou, 2006; Wang, Li, and Tsai, 2007a; Zhang and Lu, 2007). With the aid of local linear approximation (LLA) algorithm (Zou and Li, 2008), LARS can be adopted to solve optimization problems of nonconcave penalized likelihood functions. However, the above computational procedures rely on the regularization parameter. Hence, the selection of this parameter becomes the second challenge, and is therefore the primary aim of our paper.

In the literature, selection criteria are usually classified into two categories: consistent (e.g., the Bayesian information criterion BIC, Schwarz, 1978) and efficient (e.g., the Akaike information criterion AIC, Akaike, 1974; the generalized cross-validation GCV, Craven and Wahba, 1979). A consistent criterion identifies the true model with a probability that approaches 1 in large samples when a set of candidate models contains the true model. An efficient criterion selects the model so that its average squared error is asymptotically equivalent to the minimum offered by the candidate models when the true model is approximated by a family of candidate models. Detailed discussions on efficiency and consistency can be found in Shibata (1981, 1984), Li (1987), Shao (1997) and McQuarrie and Tsai (1998). In the context of linear and generalized linear models (GLIM) with a nonconcave penalized function, Fan and Li (2001) proposed applying GCV to choose the regularization parameter. Recently, Wang, Li, and Tsai (2007b) found that the resulting model selected by GCV tends to overfit, while BIC is able to identify the finite-dimensional true linear and partial linear models consistently. Wang et al. (2007b) also indicated that GCV is similar to AIC. However, they only studied the penalized least squares function with the smoothly clipped absolute deviation (SCAD) penalty. This motivated us to study the issues of regularization parameter selection for penalized likelihood-based models with a nonconcave penalized function.

In this paper, we adopt Nishii's (1984) generalized information criterion (GIC) to choose regularization parameters in nonconcave penalized likelihood functions. This criterion not only contains AIC and BIC as its special cases, but also bridges the connection between the classical variable selection criteria and the nonconcave penalized likelihood methodology. This connection provides more flexibility for practitioners to employ their own favored variable selection criteria in choosing desirable models. When the true model is among a set of candidate models with the GLIM structure, we show that the BIC-type tuning parameter selector enables us to identify the true model consistently, whereas the AIC-type selector tends to yield an overfitted model. On the other hand, if the true model is approximated by a set of candidate models with the linear structure, we demonstrate that the AIC-type tuning parameter selector is asymptotically loss efficient, while the BIC-type selector does not have this property in general. These findings are consistent with the features of AIC (see Shibata, 1981; Li, 1987) and BIC (see Shao, 1997) used in best subset variable selections.

The rest of the paper is organized as follows. Section 2 proposes the generalized information criterion under a general nonconcave penalized likelihood setting. Section 3 studies the consistent property of GIC for generalized linear models, while section 4 investigates the asymptotic loss efficiency of the AIC-type selector for linear regression models. Monte Carlo simulations and an empirical example are presented in section 5 to illustrate the use of the regularization parameter selectors. Section 6 provides discussions, and technical proofs are given in the Appendix.

2 Nonconcave penalized likelihood function

2.1 Penalized estimators and penalty conditions

Consider the data (x₁, y₁), · · · , (x_n, y_n) being collected identically and independently, where y_i is the response from the ith subject, and x_i is the associated d dimensional predictor variable. Let $\ell \left(\beta \right)$ be the log likelihood-based (or loss) function of d dimensional parameter vector $\beta ={({\beta }_1,\dots ,{\beta }_d)}^T$. Then, adopting Fan and Li's (2001) approach, we define a penalized likelihood to be

$$Q\left(\beta \right)=\ell \left(\beta \right)-n\sum _{j=1}^d{p}_{\lambda }\left(\mid {\beta }_j\mid \right),$$ (1)

where p_λ(·) is a penalty function with regularization parameter λ. Several penalty functions have been proposed in the literature. For example, the L_q (0 < q < 2) penalty, namely p_λ(|β|) = q^–1λ|β|^q, leads to the bridge regression (Frank and Friedman, 1993). In particular, the L₁ penalty yields the LASSO estimator (Tibshirani, 1996). Fan and Li (2001) proposed the nonconcave penalized likelihood method and advocated the use of the smoothly clipped absolute deviation (SCAD) penalty, whose first derivative is given by

$$p_{\lambda }^{\prime }\left(\mid {\beta }_j\mid \right)=\lambda \left\{I(\mid {\beta }_j\mid \le \lambda )+\frac{(a\lambda -\mid {\beta }_j\mid )+}{(a-1)\lambda }I(\mid {\beta }_j\mid >\lambda )\right\},$$

with a = 3.7 and p_λ(0) = 0. With properly chosen regularization parameter λ from 0 to its upper limit, λ_max, the resulting penalized estimator is sparse and therefore suitable for variable selections.

To investigate the asymptotic properties of the regularization parameter selectors, we present the penalty conditions given below.

• (C1) Assume that λ_max depends on n and satisfies λ_max → 0 as n → ∞.

• (C2) There exists a constant m such that the penalty p_λ(ζ) satisfies $p_{\lambda }^{\prime }\left(\zeta \right)=0$ for θ > mζ.

• (C3) If λ_n → 0 as n → ∞, then the penalty function satisfies

  $$\underset{n\to \infty }{\lim \inf }\underset{\zeta \to 0+}{\lim \inf }\sqrt{n}{p}_{\lambda n}^{\prime }\left(\zeta \right)\to \infty .$$

Condition (C1) indicates that a smaller regularization parameter is needed if the sample size is large. Condition (C2) assures that the resulting penalized likelihood estimate is asymptotically unbiased (Fan and Li, 2001). Both the SCAD and Zhang's (2007) minimax concave penalties (MCP) satisfy this condition. Condition (C3) is adapted from Fan and Li's (2001) Equation (3.5), which is used to study the oracle property.

Remark 1. Both the SCAD penalty and L_q penalty for 0 < q ≤ 1 are singular at the origin. Hence, it becomes challenging to maximize their corresponding penalized likelihood functions. Accordingly, Fan and Li (2001) proposed the LQA algorithm for finding the solution of the nonconcave penalized likelihood. In LQA, p_λ(|β|) is locally approximated by a quadratic function q_λ(|β|), whose first derivative is given by

$$q_{\lambda }^{\prime }\left(\mid {\beta }_j\mid \right)=\{p_{\lambda }^{\prime }\left(\mid {\beta }_j\mid \right)∕\mid {\beta }_j\mid \}{\beta }_j.$$

The above equation is evaluated at the (k + 1)-step iteration of the Newton-Raphson algorithm if ${\beta }_j^{\left(k\right)}$ is not very close to zero. Otherwise, the resulting parameter estimator of β_j is set to 0.

2.2 Generalized information criterion

Before introducing the generalized information criterion, we first define the candidate model, which is involved in variable selections.

Definition 1 (Candidate Model). We define α, a subset of $\stackrel{‒}{\alpha }=\{1,\dots ,d\}$, as a candidate model, meaning that the corresponding predictors labelled by α are included in the model. Accordingly, $\stackrel{‒}{\alpha }$ is the full model. In addition, we denote the size of model α (i.e., the number of nonzero parameters in α) and the coefficients associated with the predictors in model α by d_α and β_α, respectively. Moreover, we denote the collection of all candidate models by $\mathcal{A}$. For a penalized estimator ${\widehat{\beta }}_{\lambda }$ that minimizes the objective function (1), denote the model associated with ${\widehat{\beta }}_{\lambda }$ by α_λ.

In the normal linear regression model, $y_i+{\mathbf{x}}_i^T{\beta }_{\alpha }+e_i$ and e_i ~ N(0, σ²) for i = 1, · · · , n, Nishii (1984) proposed the generalized information criterion for classical variable selections. It is

$${\mathrm{GIC}}_{{\kappa }_n}\left(\alpha \right)=\log {\widehat{\sigma }}_{\alpha }^2+\frac{1}{n}{\kappa }_n{d}_{\alpha },$$

where β_α is the parameter of the candidate model α, ${\widehat{\sigma }}_{\alpha }^2$ is the maximum likelihood estimator of σ², and κ_n is a positive number that controls the properties of variable selection. Note that Nishii's GIC is different from the GIC proposed by Konishi and Kitagawa (1996). When κ_n = 2, GIC becomes AIC, while κ_n = log(n) leads to GIC being BIC. Because GIC contains a broad range of selection criteria, this motivates us to propose the following GIC-type regularization parameter selector,

$${\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)=\frac{1}{n}\{G(\mathbf{y},{\widehat{\beta }}_{\lambda })+{\kappa }_{n}d{f}_{\lambda }\},$$ (2)

where $G(\mathbf{y},{\widehat{\beta }}_{\lambda })$ measures the fitting of model α_λ, y = (y₁, · · · , y_n)^T, ${\widehat{\beta }}_{\lambda }$ is the penalized parameter estimator obtained by maximizing Equation (1) with respect to β, and df_λ is the degrees of freedom of model α_λ. For any given κ_n, we select λ that minimizes GIC_κn(λ). We can see that, the larger κ_n is, the higher the penalty for models with more variables. Therefore, for some given data, the size of the selected model decreases as κ_n increases.

Remark 2. For any given model α (including the penalized model α_λ and the full model $\stackrel{‒}{\alpha }$), we are able to obtain the non-penalized parameter estimator ${\widehat{\beta }}_{\alpha }^{\ast }$ by maximizing the log-likelihood function $\ell \left(\beta \right)$ in (1). Then, Equation (2) becomes

$${\mathrm{GIC}}_{{\kappa }_n}^{\ast }\left(\alpha \right)=\frac{1}{n}\{G(\mathbf{y},{\widehat{\beta }}_{\alpha }^{\ast })+{\kappa }_n{d}_{\alpha }\},$$ (3)

which can be used for classical variable selections. In addition, ${\mathrm{GIC}}_{{\kappa }_n}^{\ast }\left(\alpha \right)$ turns into Nishii's GIC_κn(α) if we replace $G(\mathbf{y},{\widehat{\beta }}_{\alpha }^{\ast })$ in (3) with the –2 log-likelihood function of the fitted normal regression model.

We next study the degrees of freedom used in the second term of GIC. In the selection of the regularization parameter, Fan and Li (2001, 2002) proposed that the degrees of freedom be the trace of the approximate linear projection matrix, i.e.

$$d{f}_L\left(\lambda \right)\triangleq tr\left\{{\left({\nabla }_{\lambda }^{\otimes 2}{Q}^{\ast }\left({\widehat{\beta }}_{\lambda }\right)\right)}^{-1}{\nabla }_{\lambda }^{\otimes 2}\ell \left({\widehat{\beta }}_{\lambda }\right)\right\},$$ (4)

where $Q^{\ast }\left(\beta \right)=\ell \left(\beta \right)-n{\sum }_{j=1}^d{q}_{\lambda }\left(\mid {\beta }_j\mid \right)$, ${\left[{\nabla }_{\lambda }^{\otimes 2}{Q}^{\ast }\left(\beta \right)\right]}_{j{j}^{\prime }}=\frac{{\partial }^2}{\partial {\beta }_j{\beta }_{j^{\prime }}}{Q}^{\ast }\left(\beta \right)$, and ${\left[{\nabla }_{\lambda }^{\otimes 2}\ell \left(\beta \right)\right]}_{j{j}^{\prime }}=\frac{{\partial }^2}{\partial {\beta }_j{\beta }_{j^{\prime }}}\ell \left(\beta \right)$ for j, j′ such that ${\widehat{\beta }}_j\ne 0$ and ${\widehat{\beta }}_{j^{\prime }}\ne 0$. To understand the large sample property of df_L(λ), we show its asymptotic behavior given below.

Proposition 1. Assume that the penalized likelihood estimator ${\widehat{\beta }}_{\lambda }$ is sparse (i.e., with probability tending to one, ${\widehat{\beta }}_{\lambda j}=0$ if the true value of β_j is 0) and consistent, where ${\widehat{\beta }}_{\lambda j}$ is the j-th component of ${\widehat{\beta }}_{\lambda }$. Under conditions (C1) and (C2), we have

$$P\{d{f}_L\left(\lambda \right)=d_{{\alpha }_{\lambda }}\}\to 1,$$

where d_αλ is the size of model α_λ.

Proof. After algebraic simplifications, $d{f}_L\left(\lambda \right)=tr\left\{{\left({\nabla }_{\lambda }^{\otimes 2}{\ell }_{{\alpha }_{\lambda }}\left({\widehat{\beta }}_{\lambda }\right)+n{\Sigma }_{\lambda }\right)}^{-1}{\nabla }_{\lambda }^{\otimes 2}\ell \left({\widehat{\beta }}_{\lambda }\right)\right\}$, where ${\Sigma }_{\lambda }={\mathrm{diag}}_{{\widehat{\beta }}_{\lambda j}\ne 0}\left\{p_{\lambda }^{\prime }\left(\mid {\widehat{\beta }}_{\lambda j}\mid \right)∕\mid {\widehat{\beta }}_{\lambda j}\mid \right\}$. Because of the consistency and sparsity of ${\widehat{\beta }}_{\lambda j}$, ${\widehat{\beta }}_{\lambda j}$ converges to β_j with probability tending to 1 for all j such that ${\widehat{\beta }}_{\lambda j}>0$. Hence, those ${\widehat{\beta }}_{\lambda j}$ are all bounded from 0. This result, together with conditions (C1) and (C2), implies that Σ_λ = 0 with probability tending to 1. Subsequently, using the fact that $n^{-1}{\nabla }_{\lambda }^{\otimes 2}\ell \left({\widehat{\beta }}_{\lambda }\right)=O_P\left(1\right)$, we complete the proof.

The above proposition suggests that the difference between df_L(λ) and the size of the model, d_αλ, is small. Because d_αλ is simple to calculate, we use it as the degrees of freedom df_λ in (2). In linear regression models, Efron et al. (2004) and Zou, Hastie, and Tibshirani (2007) also suggested using d_αλ as an estimator of the degrees of freedom for LASSO. Moreover, Zou et al. (2007) showed that d_αλ is an asymptotically unbiased estimator. In this article, our asymptotical results are valid without regard to the use of df_L(λ) or d_αλ as the degrees of freedom. When the sample size is small, however, df_L(λ) should be considered. In the following section, we explore the properties of GIC for the generalized linear models which have been widely used in various disciplines.

3 Consistency

In this section, we assume that the set of candidate models contains the unique true model, and that the number of parameters in the full model is finite. Under this assumption, we are able to study the asymptotic consistency of GIC by introducing the following definition and condition.

Definition 2 (Underfitted and Overfitted Models). We assume that there is a unique true model α₀ in $\mathcal{A}$, whose corresponding coefficients are nonzero. Therefore, any candidate model α ⊅ α₀, is referred to as an underfitted model, while any α ⊃ α₀ other than α₀ itself is referred to as an overfitted model.

Based on the above definitions, we partition the tuning parameter interval [0, λ_max] into the underfitted, true, and overfitted subsets, respectively,

$$\begin{array}{cc}\hfill {\Omega }_{-}& =\{\lambda :{\alpha }_{\lambda }\not\supset {\alpha }_0\},\hfill \\ \hfill {\Omega }_0& =\{\lambda :{\alpha }_{\lambda }={\alpha }_0\},\text{and}\hfill \\ \hfill {\Omega }_{+}& =\{\lambda :{\alpha }_{\lambda }\supset {\alpha }_0\text{and}{\alpha }_{\lambda }\ne {\alpha }_0\}.\hfill \end{array}$$

This partition allows us to assess the performance of regularization parameter selections.

To investigate the asymptotic properties of the regularization parameter selectors, we introduce the technical condition given below.

• (C4) For any candidate model $\alpha \in \mathcal{A}$, there exists c_α > 0 such that $\frac{1}{n}G(\mathbf{y},{\widehat{\beta }}_{\alpha }^{\ast })\stackrel{P}{\to }{c}_{\alpha }$. In addition, for any underfitted model α ⊅ α₀, c_α > c_α0, where c_α0 is the limit of $\frac{1}{n}G(\mathbf{y},{\beta }_{{\alpha }_0})$ and β_α0 is the parameter vector of the true model α₀.

The above condition assures that the underfitted model yields a larger measure of model fitting than that of the true model. We next explore the asymptotic consistency of GIC for the generalized linear models which have been used in various disciplines.

Consider the generalized linear model (GLIM, see McCullagh and Nelder, 1989), whose conditional density function of y_i given x_i is

$$f_i(y_i;{\theta }_i,\varphi )=\exp \{[y_i{\theta }_i-b\left({\theta }_i\right)]∕a\left(\varphi \right)+c(y_i,\varphi )\},$$ (5)

where a(·), b(·) and c(·, ·) are suitably chosen functions, θ_i is the canonical parameter, E(y_i|x_i) = μ_i = b′(θ_i), g(μ_i) = θ_i, g is a link function, and ϕ is a scale parameter. Throughout this paper, we assume that ϕ is known (such as in the logistic regression model and the Poisson log-linear model) or that it can be estimated by fitting the data with the full model (for instance, the normal linear model). In addition, we follow the classical regression approach to model θ_i by ${\mathbf{x}}_i^T\beta$. Based on (5), the log likelihood-based function in (1) is

$$\ell \left(\beta \right)=\ell (\mu ;\mathbf{y})=\ell \left(\theta \right)=\sum _{i=1}^n\log f_i(y_i;{\theta }_i,\varphi )=\sum _{i=1}^n[\{y_i{\mathbf{x}}_i^T\beta -b\left({\mathbf{x}}_i^T\beta \right)\}∕a\left(\varphi \right)+c(y_i,\varphi )],$$ (6)

where μ = (μ₁, · · · , μ_n)^T, y = (y₁, · · · , y_n)^T, and θ = (θ₁, · · · , θ_n)^T. Then, the resulting scaled deviance of a penalized estimate ${\widehat{\beta }}_{\lambda }$ is

$$D(\mathbf{y};{\widehat{\mu }}_{\lambda })=2\{\ell (\mathbf{y};\mathbf{y})-\ell ({\widehat{\mu }}_{\lambda };\mathbf{y})\},$$

where ${\widehat{\mu }}_{\lambda }={(g^{-1}\left({\mathbf{x}}_1^T{\widehat{\beta }}_{\lambda }\right),\cdots ,g^{-1}\left({\mathbf{x}}_n^T{\widehat{\beta }}_{\lambda }\right))}^T$.

For model α_λ, we employ the scaled deviance $D(\mathbf{y};{\widehat{\mu }}_{\lambda })$ as the goodness-of-fit measure, $G(\mathbf{y},{\widehat{\beta }}_{\lambda })$, in (2) so that the resulting generalized information criterion for GLIM is

$${\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)=\frac{1}{n}D(\mathbf{y};{\widehat{\mu }}_{\lambda })+\frac{1}{n}{\kappa }_{n}d{f}_{\lambda }.$$ (7)

In addition, when we fit the data with the non-penalized likelihood approach under model α, GIC becomes

$${\mathrm{GIC}}_{{\kappa }_n}^{\ast }\left(\alpha \right)=\frac{1}{n}D(\mathbf{y};{\widehat{\mu }}_{\alpha }^{\ast })+\frac{1}{n}{\kappa }_n{d}_{\alpha },$$ (8)

where ${\widehat{\mu }}_{\alpha }^{\ast }={(g^{-1}\left({\mathbf{x}}_1^T{\widehat{\beta }}_{\alpha }^{\ast }\right),\cdots ,g^{-1}\left({\mathbf{x}}_n^T{\widehat{\beta }}_{\alpha }^{\ast }\right))}^T$, and ${\widehat{\beta }}_{\alpha }^{\ast }$ is the non-penalized maximum likelihood estimator of β. Accordingly, GIC* can be used in classical variable selection (see Eq. (3.10) of McCullagh and Nelder, 1989). Next, we show the asymptotic performances of GIC.

Theorem 1. Suppose the density function of the generalized linear model satisfies Fan and Li's (2001) three regularity conditions (A)–(C) and that the technical condition (C4) holds.

1. If there exists a positive constant M such that κ_n < M, then the tuning parameter $\widehat{\lambda }$ selected by minimizing GIC_κn(λ) in (7) satisfies

   $$P\left\{\widehat{\lambda }\in {\Omega }_{-}\right\}\to 0,andP\left\{\widehat{\lambda }\in {\Omega }_{+}\right\}\ge \pi ,$$

   where π is a nonzero probability.

2. Suppose that conditions (C1)-(C3) are satisfied. If κ_n → ∞ and ${\kappa }_n∕\sqrt{n}\to 0$, then the tuning parameter $\widehat{\lambda }$ selected by minimizing GIC_κn(λ) in (7) satisfies $P\{{\alpha }_{\widehat{\lambda }}={\alpha }_0\}\to 1$.

The proof is given in Appendix A.

Theorem 1 provides guidance on the choice of the regularization parameter. Theorem 1(A) implies that the GIC selector with bounded κ_n tends to overfit without regard to which penalty function is being used. Analogous to the classical variable selection criterion AIC, we refer to GIC with κ_n = 2 as the AIC selector, while we name GIC with κ_n → 2 the AIC-type selector. In contrast, because κ_n = log(n) fulfills the conditions of Theorem 1(B), we call GIC with κ_n → ∞ and ${\kappa }_n∕\sqrt{n}\to 0$ the BIC-type selector.Theorem 1(B) indicates that the BIC-type selector identifies the true model consistently. Thus, the nonconcave penalized likelihood of the generalized linear model with the BIC-type selector possesses the oracle property.

Remark 3. In linear regression models, Fan and Li (2001) applied the GCV selector given below to choose the regularization parameter,

$${\mathrm{GCV}}^{\ast }\left(\lambda \right)=\frac{{\Vert \mathbf{y}-\mathbf{X}{\widehat{\beta }}_{\lambda }\Vert }^2}{n{\{1-d{f}_L\left(\lambda \right)∕n\}}^2},$$ (9)

where ∥ · ∥ denotes the Euclidean norm, $X={(x_1^T,\cdots ,x_n^T)}^T$, and df_L(λ) is defined in (4). To extend the application of GCV, we replace the residual sum of squares in (9) by $G(\mathbf{y},{\widehat{\beta }}_{\lambda })$, and then choose λ that minimizes

$$\mathrm{GCV}\left(\lambda \right)=\frac{G(\mathbf{y},{\widehat{\beta }}_{\lambda })}{n{\{1-d{f}_{\lambda }∕n\}}^2}.$$ (10)

Using the Taylor expansion, we further have that

$$\mathrm{GCV}\left(\lambda \right)\approx \frac{1}{n}\left\{G(\mathbf{y},{\widehat{\beta }}_{\lambda })+d{f}_{\lambda }\left[\frac{2G(\mathbf{y},{\widehat{\beta }}_{\lambda })}{n}\right]\right\}.$$

Because $G(\mathbf{y},{\widehat{\beta }}_{\lambda })∕n$ is bounded via Condition (C4), GCV yields an overfitted model with a positive probability. Therefore, the penalized partial likelihood with the GCV selector does not possess the oracle property.

Remark 4. In linear regression models, Wang et al. (2007b) demonstrated that Fan and Li's (2001) GCV-selector for the SCAD penalized least squares procedure cannot select the tuning parameter consistently. They further proposed the following BIC tuning parameter selector,

$${\mathrm{BIC}}^{\ast }\left(\lambda \right)=\log \left({\widehat{\sigma }}_{\lambda }^2\right)+\frac{1}{n}\log \left(n\right)d{f}_L\left(\lambda \right),$$

where ${\widehat{\sigma }}_{\lambda }^2={\sum }_{i=1}^n{(y_i-{\mathbf{x}}_i^T{\widehat{\beta }}_{\lambda })}^2∕\mathrm{n}$. Using the result that log(1 + t) ≈ t for small t, ${\mathrm{BIC}}_{\lambda }^{\ast }$ is approximately equal to

$${\mathrm{BIC}}^{\ast \ast }\left(\lambda \right)=\frac{1}{n}{D}^{\ast \ast }(\mathbf{y};{\widehat{\mu }}_{\lambda })+\frac{1}{n}\log \left(n\right)d{f}_L\left(\lambda \right),$$

where $D^{\ast \ast }(\mathbf{y};{\widehat{\mu }}_{\lambda })={\widehat{\sigma }}_{\lambda }^2∕{\widehat{\sigma }}_{\stackrel{‒}{\alpha }}^2$ is the scaled deviance of the normal distribution, and ${\widehat{\sigma }}_{\stackrel{‒}{\alpha }}^2$ is the dispersion parameter estimator computed from the full model. It can be seen that BIC** is a BIC-type selector. Under the conditions in Theorem 1(B), the SCAD penalized least squares procedure with the BIC** selector possesses the oracle property, which is consistent with the findings in Wang et al. (2007b).

4 Efficiency

Under the assumption that the true model is included in a family of candidate models, we established the consistency of BIC-type selectors. In practice, however, this assumption may not be valid, which motivates us to study the asymptotic efficiency of the AIC-type selector. In the literature, the L₂ norm has been commonly used to assess the efficiency of the classical AIC procedure (see Shibata, 1981, 1984 and Li, 1987) in linear regression models. Hence, we focus on the efficiency of linear regression model selections via L₂ norm.

Consider the following model

$$y_i={\mu }_i+{∊}_i,\text{for}i=1,\dots ,n,$$

where μ = (μ₁, ..., μ_n)^T is an unknown mean vector, and ε_i's are independent and identically distributed (i.i.d) random errors with mean 0 and variance σ². Furthermore, we assume that Xβ constitutes the nearest representation of the true mean vector μ, and hence the full model is not necessarily a correct model. Adapting the formulation of Li (1987), we allow d, the dimension of β, to tend to infinity with n, but d/n → 0.

For the given data set {(x_i, y_i) : i = 1, · · · , n}, we follow the formulation of (1) to define the penalized least squares function

$$Q^{LS}\left(\beta \right)=\sum _{i=1}^n{(y_i-{\mathbf{x}}_i^T\beta )}^2+n\sum _{j=1}^d{p}_{\lambda }\left(\mid {\beta }_j\mid \right).$$ (11)

The resulting penalized estimator of μ in model α_λ is ${\widehat{\mu }}_{\lambda }=\mathbf{X}{\widehat{\beta }}_{\lambda }$. In addition, the non-penalized estimator of μ in model α is ${\widehat{\mu }}_{\alpha }^{\ast }=\mathbf{X}{\widehat{\beta }}_{\alpha }^{\ast }$. It is noteworthy that ${\widehat{\beta }}_{\lambda }$ and ${\widehat{\beta }}_{\alpha }^{\ast }$ have been defined in Definition 1 and Remark 2, respectively. In practice, the tuning parameter λ is unknown and can be selected by minimizing

$${\mathrm{GIC}}_{{\kappa }_n}^{LS}\left(\lambda \right)=\frac{1}{n}\left\{\sum _{i=1}^n{(y_i-{\mathbf{x}}_i^T{\widehat{\beta }}_{\lambda })}^2+{\kappa }_n{\sigma }^2{d}_{{\alpha }_{\lambda }}\right\},$$ (12)

where σ² is assumed to be known, and the case with the unknown σ² will be discussed later. When ${\widehat{\beta }}_{\lambda }$ in (12) is replaced by the least squares estimator ${\widehat{\beta }}_{\alpha }^{\ast }$, ${\mathrm{GIC}}_{{\kappa }_n}^{LS}$ with κ_n = 2 becomes the Mallows’ C_p criterion that has been used for classical variable selections.

To assess the performance of the tuning parameter selector, we adopt the approach of Shibata (1981) (also see Li, 1987; Shao, 1997), and define the average squared loss (or the L₂ loss) associated with the estimator ${\widehat{\beta }}_{\lambda }$ to be

$$L\left({\widehat{\beta }}_{\lambda }\right)=\frac{1}{n}{\Vert \mu -{\widehat{\mu }}_{\lambda }\Vert }^2=\frac{1}{n}\sum _{i=1}^n{\left({\mu }_i-{\mathbf{x}}_i^T{\widehat{\beta }}_{\lambda }\right)}^2.$$ (13)

Accordingly, the risk function is $R\left(\widehat{\beta }\right)=E\left[L\left(\widehat{\beta }\right)\right]$.

Using the average squared loss measure, we further define the asymptotic loss efficiency.

Definition 3 (Asymptotically Loss Efficient). A tuning parameter selection procedure is said to be asymptotically loss efficient if

$$\frac{L\left({\widehat{\beta }}_{\widehat{\lambda }}\right)}{{\inf }_{\lambda \in [0,{\lambda }_{\max }]}L\left({\widehat{\beta }}_{\lambda }\right)}\to 1,$$ (14)

in probability, where ${\widehat{\beta }}_{\widehat{\lambda }}$ is associated with the tuning parameter $\widehat{\lambda }$ selected by this procedure. We also say ${\widehat{\beta }}_{\widehat{\lambda }}$ is asymptotically loss efficient if (14) holds.

Moreover, we introduce the following technical conditions for studying the asymptotic loss efficiency of the AIC-type selector in linear regression.

• (C5) ${\left(\frac{1}{n}{\mathbf{X}}^T\mathbf{X}\right)}^{-1}$ exists, and its largest eigenvalue is bounded by a constant number C.

• (C6) $E{∊}_1^{4q}<\infty$, for some positive integer q.

• (C7) The risks of the least squares estimators ${\widehat{\beta }}_{\alpha }^{\ast }$ for all $\alpha \in \mathcal{A}$ satisfy

  $$\sum _{\alpha \in \mathcal{A}}{\left[nR\left({\widehat{\beta }}_{\alpha }^{\ast }\right)\right]}^{-q}\to 0.$$
• (C8) Let b = (b₁, ..., b_d)^T, where $b_j=p_{\lambda }^{\prime }\left(\mid {\widehat{\beta }}_{\lambda j}\mid \right)\mathrm{sgn}\left({\widehat{\beta }}_{\lambda j}\right)$ for all j such that $\mid {\widehat{\beta }}_{\lambda j}\mid <0$, and b_j = 0 otherwise, and ${\widehat{\beta }}_{\lambda j}$ is the j-th component of the penalized estimator ${\widehat{\beta }}_{\lambda }$. In addition, let ${\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }$ be the least squares estimator of β obtained from model α_λ. Then, we assume that, in probability,

  $$\underset{\lambda \in [0,{\lambda }_{\max }]}{\sup }\frac{{\Vert \mathbf{b}\Vert }^2}{R\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)}\to 0.$$

Condition (C5) has been commonly considered in the literature. Conditions (C6) and (C7) are adopted from conditions (A.2) and (A.3), respectively, in Li (1987). It can be shown that if the true model is approximated by a set of the candidate models (e.g., the true model is of infinite dimension), then Condition (C7) holds. Condition (C8) ensures that the difference between the penalized mean function estimator and the corresponding least squares mean function estimator is small in comparison with the risk of the least squares estimator (see Lemma 3 in Appendix B). Sufficient conditions for (C8) are also given in Appendix C. We next show the asymptotic efficiency of the AIC-type selector.

Theorem 2. Assume conditions (C5)—(C8) hold. Then, the tuning parameter $\widehat{\lambda }$ selected by minimizing $GI{C}_{{\kappa }_n}^{LS}\left(\lambda \right)$ in (12) with κ_n → 2 yields an asymptotically loss efficient estimator, ${\widehat{\beta }}_{\widehat{\lambda }}$, in the sense of (14).

The proof is given in Appendix B.

Theorem 2 demonstrates that the AIC-type selector is asymptotically loss efficient. In addition, using the result that log(1 + t) ≈ t for small t, the AIC selector behaves similarly to the following AIC* selector,

$${\mathrm{AIC}}^{\ast }\left(\lambda \right)=\log \left({\widehat{\sigma }}_{\lambda }^2\right)+\frac{2{\sigma }^2{d}_{{\alpha }_{\lambda }}}{n}.$$

Accordingly, both AIC and AIC* selectors are asymptotically loss efficient.

Applying Lemma 4 and Equation (26) in Appendix B, we find that if ${\sup }_{\lambda \in [0,{\lambda }_{\max }]}\mid n^{-1}({\kappa }_n-2){\sigma }^2{d}_{{\alpha }_{\lambda }}∕R\left({\widehat{\beta }}_{\lambda }\right)\mid \to 0$ in probability, then ${\mathrm{GIC}}_{{\kappa }_n}^{LS}$ is asymptotically loss efficient. Note that it can be shown $n^{-1}{\sigma }^2{d}_{{\alpha }_{\lambda }}∕R\left({\widehat{\beta }}_{\lambda }\right)$ is bounded by 1. As a result, κ_n → 2 (including κ_n = 2) is critical in establishing the asymptotic loss efficiency. This finding is similar to the classical efficient criteria (see Shibata, 1980, Shao, 1997 and Yang, 2005). It is also not surprising that the BIC-type selectors do not possess asymptotic loss efficiency, which is consistent with the finding of classical variable selections (see Li, 1987 and Shao, 1997).

In practice, σ² is often unknown. It is natural to replace the σ² in ${\mathrm{GIC}}_2^{LS}$ by its consistent estimator (see Shao, 1997). The following corollary shows that the asymptotical property of GIC still holds.

Corollary 1. If the tuning parameter $\widehat{\lambda }$ is selected by minimizing ${\mathrm{GIC}}_{{\kappa }_n}^{LS}\left(\lambda \right)$ with κ_n → 2 and σ² being replaced by its consistent estimator ${\tilde{\sigma }}^2$, then the resulting procedure is also asymptotically loss efficient.

The proof is given in Appendix B.

Remark 5. As suggested by an anonymous reviewer, we study the asymptotic loss efficiency of the generalized linear model in (5). Following the spirit of the deviance measure commonly used in the GLIM, we adopt the Kullback-Leibler (KL) distance measure to define the KL loss of an estimate $\widehat{\beta }$ (either the maximum likelihood estimate ${\widehat{\beta }}_{\alpha }^{\ast }$ or the nonconcave penalized estimate ${\widehat{\beta }}_{\lambda }$), as

$$L_{KL}\left(\widehat{\beta }\right)=\frac{2}{n}{E}_0\left\{\ell \left({\theta }_0\right)-\ell \left(\widehat{\theta }\right)\right\},$$ (15)

where $\ell (\cdot )$ is defined in (6), θ₀ = (θ₀₁, · · · , θ_0n)^T is the true unknown canonical parameter, $\widehat{\theta }={({\widehat{\theta }}_1,\cdots ,{\widehat{\theta }}_n)}^T=\mathbf{X}\widehat{\beta }$ under canonical link function, and E₀ denotes the expectation under the true model (see McQuarrie and Tsai, 1998, for example). It can be shown that the KL loss is identical to the squared loss for normal linear regression models with known variance. To obtain the asymptotic loss efficiency for GLIM, however, it is necessary to employ the Taylor expansion to expand $b\left({\widehat{\theta }}_i\right)$ at the true value of θ_0i for i = 1, · · · , n. Accordingly, we need to impose some strong assumptions to establish the asymptotic loss efficiency for the nonconcave penalized estimate under the KL loss if the tuning parameter $\widehat{\lambda }$ is selected by minimizing GIC in (7) with κ_n → 2. To avoid considerably increasing the length of the paper, we do not present detailed discussions, justifications, and proofs here, but they are given in the online supplemental material available in JASA website.

5 Numerical studies

In this section, we present three examples comprised of two Monte Carlo experiments and one empirical example. It is noteworthy that Example 1 considers a setting in which the true model is in a set of candidate models with logistic regressions. This setting allows us to examine the finite sample performance of the consistent selection criterion, which is expected to perform well via Theorem 1. In contrast, Example 2 considers a setting in which the true model is not included in a set of candidate models with Gaussian regressions. This setting enables us to assess the finite sample performance of the efficient selection criterion, which is expected to perform well via Theorem 2.

Example 1. Adapting the model setting from Tibshirani (1996) and Fan and Li (2001), we simulate the data from the logistic regression model, y|x ~ Bernoulli{p(x^T β)}, where

$$p\left({\mathbf{x}}^T\beta \right)=\mu \left({\mathbf{x}}^T\beta \right)=\frac{\exp \left({\mathbf{x}}^T\beta \right)}{1+\exp \left({\mathbf{x}}^T\beta \right)}.$$

In addition, β = (3, 1.5, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0)^T, x is a 12-dimensional random vector, the first 9 components of x are multivariate normal with covariance matrix Σ = (σ_ij), in which σ_ij = 0.5^|i–j|, and the last 3 components of x are generated from an independent Bernoulli distribution with success probability 0.5. Moreover, we conduct 1000 realizations with the sample sizes n = 200 and 400.

To assess the finite sample performance of the proposed methods, we report the percentage of models correctly fitted, underfitted, and overfitted with 1, 2, 3, 4, 5 or more parameters by SCAD-AIC (i.e., κ_n = 2), SCAD-BIC (i.e., κ_n = log(n)), SCAD-GCV, AIC, and BIC selectors as well as via the oracle procedure (i.e., the simulated data were fitted with the true model). Their corresponding standard errors can be calculated by $\sqrt{\widehat{p}(1-\widehat{p})∕1000}$, where p̂ is the observed proportion in 1000 simulations. Moreover, we report the average number of zero coefficients that were correctly (C) and incorrectly (I) identified by different methods. To compare model fittings, we further calculate the following model error for the new observation (x, y),

$$\mathrm{ME}\left(\widehat{\beta }\right)=E_{\mathbf{x}}{\{\mu \left({\mathbf{x}}^T\beta \right)-\mu \left({\mathbf{x}}^T\widehat{\beta }\right)\}}^2,$$

where the expectation is taken with respect to the new observed covariate vector x, and μ(x^T β) = E(y|x). Then, we report the median of the relative model error (MRME), where the relative model error is defined as RME = ME/ME_full, and ME_full is the model error calculated by fitting the data with the full model.

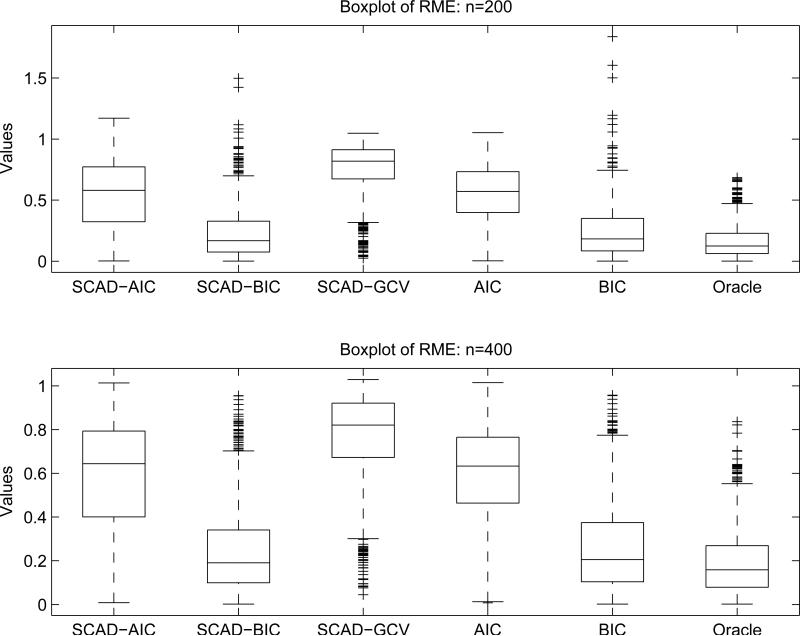
Table 1 shows that the MRME of SCAD-BIC is smaller than that of SCAD-AIC. As the sample size increases, the MRME of SCAD-BIC approaches that of the oracle estimator, whereas the MRME of SCAD-AIC remains at the same level. Hence, SCAD-BIC is superior to SCAD-AIC in terms of model error measures in this example. Moreover, Figure 1 presents the boxplots of RMEs, which lead to a similar conclusion.

Table 1.

Simulation results for the logistic regression model. MRME is the median relative model error; C denotes the average number of the nine true zero coefficients that were correctly identified as zero, while I denotes the average number of the three nonzero coefficients that were incorrectly identified as zero; the numbers in parentheses are standard errors; Under, Exact and Overfitted represent the proportions of corresponding models being selected in 1000 Monte Carlo realizations, respectively.

	MRME (%)	Zeros		Under (%)	Exact (%)	Overfitted (%)
Method		C	I			1	2	3	4	≥ 5
n = 200
SCAD-AIC	58.03	7.4 (1.6)	0.0 (0.0)	0.2	30.2	23.2	19.6	13.6	7.5	5.9
SCAD-BIC	16.90	8.8 (0.5)	0.0 (0.1)	0.7	83.7	13.2	2.4	0.4	0.0	0.0
SCAD-GCV	81.91	5.8 (1.9)	0.0 (0.0)	0.0	7.8	12.0	18.1	18.8	17.6	25.7
AIC	57.05	7.4 (1.2)	0.0 (0.0)	0.1	19.9	31.5	26.7	14.8	4.3	2.8
BIC	18.27	8.8 (0.5)	0.0 (0.1)	0.8	80.4	17.0	2.3	0.1	0.0	0.0
Oracle	12.49	9.0 (0.0)	0.0 (0.0)	0.0	100.0	0.0	0.0	0.0	0.0	0.0
n = 400
SCAD-AIC	64.45	7.4 (1.5)	0.0 (0.0)	0.0	29.4	21.9	21.0	15.1	8.5	4.1
SCAD-BIC	19.03	8.9 (0.4)	0.0 (0.0)	0.0	89.9	7.9	1.8	0.2	0.2	0.0
SCAD-GCV	82.13	6.0 (1.9)	0.0 (0.0)	0.0	9.2	14.7	18.6	19.8	15.9	21.8
AIC	63.17	7.4 (1.2)	0.0 (0.0)	0.0	21.7	29.2	27.3	14.6	5.5	1.7
BIC	20.46	8.8 (0.4)	0.0 (0.0)	0.0	86.3	12.1	1.4	0.2	0.0	0.0
Oracle	15.88	9.0 (0.0)	0.0 (0.0)	0.0	100.0	0.0	0.0	0.0	0.0	0.0

Figure 1.

Boxplot of relative model error (RME) with n=200 and n=400.

In model identifications, SCAD-BIC has a higher chance than SCAD-AIC of correctly setting the nine true zero coefficients to zero, while SCAD-BIC is slightly more prone than SCAD-AIC to incorrectly set the three nonzero coefficients to zero when the sample size is small. In addition, SCAD-BIC has a much higher possibility of correctly identifying the true model than that of SCAD-AIC. Moreover, among the overfitted models, the SCAD-BIC method is likely to include only one irrelevant variable, whereas the SCAD-AIC method often includes two or more. When the sample size increases, the SCAD-BIC method yields a lesser degree of overfitting, while the SCAD-AIC method still overfits quite seriously. These results are consistent with the theoretical findings presented in Theorem 1.

It is not surprising that SCAD-GCV performs similar to SCAD-AIC. Furthermore, the classical AIC and BIC selection criteria behave as SCAD-AIC and SCAD-BIC, respectively, in terms of model errors and identifications. It is of interest to note that SCAD-AIC usually suggests a sparser model than AIC. In sum, SCAD-BIC performs the best.

Example 2. In practice, it is plausible that the full model fails to include some important explanatory variable. This motivates us to mimic such a situation and then assess various selection procedures. Accordingly, we consider a linear regression model $y_i={\mathbf{x}}_i^T\beta +{∊}_i$, where x_i's are i.i.d. multivariate normal random variables with dimension 13, the correlation between x_i and x_j is 0.5^|i–j|, and ε_i's are i.i.d. N(0, σ²) with σ = 4. In addition, we partition $\mathbf{x}={({\mathbf{x}}_{\mathrm{full}}^T,{\mathbf{x}}_{\mathrm{exc}}^T)}^T$, where x_full contains d = 12 covariates of the full model and x_exc is the covariate excluded from model fittings. Accordingly, we partition $\beta ={({\beta }_{\mathrm{full}}^T,{\beta }_{\mathrm{exc}}^T)}^T$, where β_full is a 12 × 1 vector and β_exc is a scalar. To investigate the performance of the proposed methods under various parameter structures, we let ${\beta }_{\mathrm{full}}={\beta }_0+\gamma \delta ∕\sqrt{n}$, where β₀ = (3, 1.5, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0)^T, δ = (0, 0, 1.5, 1.5, 1, 1, 0, 0, 0, 0, 0.5, 0.5)^T, γ ranges from 0 to 10, and β_exc = 0.2. Because the candidate model is the subset of the full model that contains 12 covariates in x_full, the above model settings ensure that the true model is not included in the set of candidate models.

We simulate 1000 data sets with n = 400, 800, and 1600. To study the performance of selectors, we define the finite sample's loss efficiency,

$$\mathrm{LE}\left({\widehat{\beta }}_{\widehat{\lambda }}\right)=\frac{L\left({\widehat{\beta }}_{\widehat{\lambda }}\right)}{{\inf }_{\lambda }L\left({\widehat{\beta }}_{\lambda }\right)},$$

where $\widehat{\lambda }$ is chosen by SCAD-GCV, SCAD-AIC, and SCAD-BIC. It is noteworthy that β_full depends on the sample size and γ, a sensible approach to compare the loss efficiency of the selection criterion across different sample sizes is to compare the loss efficiency under the same value of β_full.

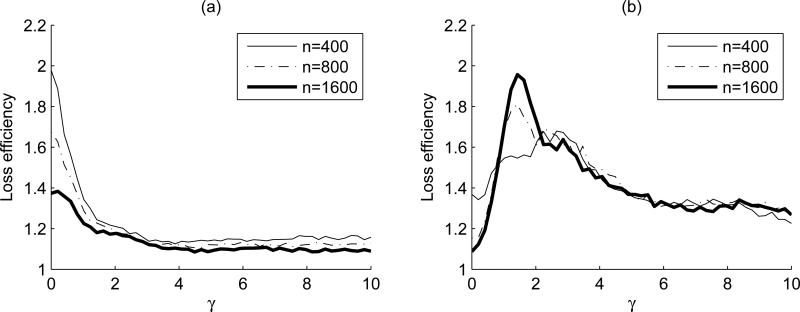
Because the performance of SCAD-GCV is very similar to that of SCAD-AIC, it is not reported here. Figure 2(a) and 2(b) depict the LEs of SCAD-AIC and SCAD-BIC, respectively, across various γ. Figure 2(a) clearly indicates that the loss efficiency of SCAD-AIC converges to 1 regardless of the value of γ, which corroborates the theoretical finding in Theorem 2. However, the loss efficiency of SCAD-BIC in Figure 2(b) does not show this tendency. Specifically, when γ is close to 0 (i.e., the model is nearly sparse), SCAD-BIC results in smaller loss due to its larger penalty function. As γ increases so that the full model contains the medium-sized coefficients, SCAD-BIC is likely to choose the model that is too sparse and hence increases the loss. When γ becomes large enough and the coefficient β_exc is dominated by the remaining coefficients in β_full, the consistent property of SCAD-BIC tends to have the smaller loss. In sum, Figure 2 shows that SCAD-AIC is efficient, whereas SCAD-BIC is not. Finally, we examine the efficiencies of AIC and BIC, and find that the performances of AIC and BIC are similar to those of SCAD-AIC and SCAD-BIC, respectively, and hence are omitted.

Figure 2.

(a) The loss efficiency of SCAD-AIC; (b) The loss efficiency of SCAD-BIC.

Example 3. (Mammographic mass data) Mammography is the most effective method for screening for the presence of breast cancer. However, mammogram interpretations yield approximately a 70% rate of unnecessary biopsies with benign outcomes. Hence, several computer-aided diagnosis (CAD) systems have been proposed to assist physicians in predicting breast biopsy outcomes from the findings of BI-RADS (Breast Imaging Reporting And Data System). To examine the capability of two novel CAD approaches, Elter, Schulz-Wendtland, and Wittenberg (2007) recently analyzed a data set containing 516 benign and 445 malignant instances. We downloaded this data set from UCI Machine Learning Repository, and excluded 131 missing values and 15 coding errors. As a result, we considered a total of 815 cases.

To study the severity (benign or malignant), Elter et al. (2007) considered the following three covariates: x₁-birads, BI-RADS assessment assigned in a double-review process by physicians (definitely benign=1 to highly suggestive of malignancy=5); x₂-age, patient's age in years; x₃-mass density, high=1, iso=2, low=3, fat-containing=4. In addition, we employ the dummy variables, x₄ to x₆, to represent the four mass shapes: round=1, oval=2, lobular=3, irregular=4, where “irregular” is used as the baseline. Analogously, we apply the dummy variables, x₇ to x₁₀, to represent the five mass margins: circumscribed=1, microlobulated=2, obscured=3, ill-defined=4, spiculated=5), where “spiculated” is used as the baseline.

To predict the value of the binary response, y = 0 (benign) or y = 1 (malignant), on the basis of the 10 explanatory variables, we fit the data with the following logistic regression model:

$$\log \frac{p\left({\mathbf{x}}^T\beta \right)}{1-p\left({\mathbf{x}}^T\beta \right)}={\beta }_0+\sum _{j=1}^{10}{x}_j{\beta }_j,$$

where x = (x₁, . . . , x₁₀)^T, β = (β₁, . . . , β₁₀)^T, and p(x^Tβ) is the probability of the case being classified as malignant. As a result, the tuning parameters selected by SCAD-AIC and SCAD-BIC are 0.0332 and 0.1512, respectively, and SCAD-GCV yields the same model as SCAD-AIC. Because the true model is unknown, we follow an anonymous referee's suggestion to include the models selected by the delete-one cross validation (delete-1 CV) and the 5-fold cross validation (5-fold CV). The detailed procedures for fitting those models can be obtained from the first author.

Because the model selected by the delete-1 CV is the same as SCAD-AIC, Table 2 only presents the non-penalized maximum likelihood estimates from the full-model as well as the SCAD-AIC, SCAD-BIC, and 5-fold CV estimates, together with their standard errors. It indicates that the non-penalized maximum likelihood approach fits five spurious variables (x₃, x₆, and x₈ to x₁₀), while SCAD-AIC and 5-fold CV include two variables (x₆ and x₉) and one variable (x₉), respectively, with insignificant effects at a level of 0.05. In contrast, all variables (x₁, x₂, x₄, x₅, and x₇) selected by SCAD-BIC are significant. Because the sample size n = 815 is large, these findings are consistent with Theorem 1 and the simulation results. In addition, the p-value of the deviance test for assessing the SCAD-BIC model against the full model is 0.41, and as a result, there is no evidence of lack of fit in the SCAD-BIC model.

Table 2.

Estimates for mammographic mass data with standard deviations in parentheses

	MLE	SCAD-AIC	SCAD-BIC	5-Fold CV
β 0	−11.04(1.48)	−11.17(1.13)	−11.16(1.07)	−11.49 (1.14)
BIRADS (x1)	2.18(0.23)	2.19(0.23)	2.25(0.23)	2.23 (0.23)
age (x2)	0.05(0.01)	0.04(0.01)	0.04(0.01)	0.05 (0.01)
density (x3)	−0.04(0.29)	0(-)	0(-)	0(-)
sRound (x4)	−0.98(0.37)	−0.99(0.37)	−0.80(0.34)	−0.81 (0.35)
sOval (x5)	−1.21(0.32)	−1.22(0.32)	−1.07(0.30)	−1.07 (0.30)
sLobular (x6)	−0.53(0.35)	−0.54(0.34)	0(-)	0(-)
mCircum (x7)	−1.05(0.42)	−0.98(0.32)	−1.01(0.30)	−1.07 (0.31)
mMicro (x8)	−0.03(0.65)	0(-)	0(-)	0(-)
mObscured (x9)	−0.48(0.39)	−0.42(0.30)	0(-)	−0.47 (0.30)
mIlldef (x10)	−0.09(0.33)	0(-)	0(-)	0(-)

Based on the model selected by SCAD-BIC, we conclude that a higher BI-RADS assessment or a greater age results in a higher chance for malignancy. In addition, the oval or round mass shape yields lower odds for malignance than does the irregular mass shape, while the odds for malignance designated by the lobular mass shape is not significantly different from that of the irregular mass shape. Moreover, the odds for malignance indicated by the microlobulated, obscured, and ill-defined mass margins are not significantly different from that of the spiculated mass margin. However, the circumscribed mass margin leads to lesser odds for malignance than that of the four other types of mass margins.

6 Discussion

In the context of variable selection, we propose the generalized information criterion to choose regularization parameters for nonconcave penalized likelihood functions. Furthermore, we study the theoretical properties of GIC. If we believe that the true model is contained in a set of candidate models with the GLIM structure, then the BIC-type selector identifies the true model with probability tending to 1, while the GIC selectors with bounded κ_n tends to overfit with positive probability. However, if the true model is approximated by a family of candidate models, the AIC-type selector is asymptotically loss efficient, whereas the BIC-type selector is not, in general. Simulation studies support the finite sample performance of the selection criteria.

Although we obtain the theoretical properties of GIC for GLIM, the application of GIC is not limited. For example, we could employ GIC to select the regularization parameter in Cox proportional hazard and quasi-likelihood models. We believe that these efforts would further enhance the usefulness of GIC in real data analysis.

Appendix A. Proof of Theorem 1

Before proving the theorem, we show the following two lemmas. Then, Theorems 1(A) and 1(B) follow from Lemmas 1 and 2, respectively. For the sake of convenience, we denote $D(\mathbf{y};{\widehat{\mu }}_{\lambda })$ in (7) and $D(\mathbf{y};{\widehat{\mu }}_{\alpha }^{\ast })$ in (8) by D(λ) and D*(α), respectively.

Lemma 1. Suppose the density function of the generalized linear model satisfies Fan and Li's (2001) three regularity conditions (A)—(C). Assume that there exists a positive constant M such that κ_n < M. Then under condition (C4), we have

$$P\left\{\underset{\lambda \in {\Omega }_{-}}{\inf }GI{C}_{{\kappa }_n}\left(\lambda \right)>GI{C}_{{\kappa }_n}^{\ast }\left(\stackrel{‒}{\alpha }\right)\right\}\to 1$$ (16)

and

$$\underset{n\to \infty }{\lim \inf }P\left\{\underset{\lambda \in {\Omega }_0}{\inf }GI{C}_{{\kappa }_n}\left(\lambda \right)>GI{C}_{{\kappa }_n}^{\ast }\left(\stackrel{‒}{\alpha }\right)\right\}\ge \pi .$$ (17)

as n → ∞.

Proof. For a given λ, the non-penalized maximum likelihood estimator, ${\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }$, maximizes $\ell \left(\beta \right)$ under model α_λ. This implies D(λ) ≥ D*(α_λ) for any given λ, which leads to

$${\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)=D\left(\lambda \right)∕n+{\kappa }_{n}d{f}_{\lambda }∕n>D^{\ast }\left({\alpha }_{\lambda }\right)∕n.$$ (18)

Then, we obtain that

$${\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)-{\mathrm{GIC}}_{{\kappa }_n}^{\ast }\left(\stackrel{‒}{\alpha }\right)>\frac{D^{\ast }\left({\alpha }_{\lambda }\right)}{n}-\frac{D^{\ast }\left(\stackrel{‒}{\alpha }\right)}{n}-\frac{{\kappa }_n{d}_{\stackrel{‒}{\alpha }}}{n},$$

holds true for any λ ∈ Ω_– = {λ : α_λ ⊅ α₀}. This together with condition (C4) and ${\kappa }_n{d}_{\stackrel{‒}{\alpha }}∕n=o_P\left(1\right)$ obtained from the fact of κ_n < M, we have

$$\begin{array}{cc}\hfill P\left\{\underset{\lambda \in {\Omega }_{-}}{\inf }{\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)-{\mathrm{GIC}}_{{\kappa }_n}^{\ast }\left(\stackrel{‒}{\alpha }\right)>0\right\}& \ge P\left\{\underset{\alpha \not\supset {\alpha }_0}{\min }\frac{D^{\ast }\left(\alpha \right)}{n}-\frac{D^{\ast }\left(\stackrel{‒}{\alpha }\right)}{n}-\frac{{\kappa }_n{d}_{\stackrel{‒}{\alpha }}}{n}>0\right\}\hfill \\ \hfill & =P\left\{\underset{\alpha \not\supset {\alpha }_0}{\min }{c}_{\alpha }-c_{\stackrel{‒}{\alpha }}+o_P\left(1\right)>0\right\}\to 1,\hfill \end{array}$$ (19)

as n → ∞. The last step uses the fact that the number of underfitting models is finite, hence min_α⊅α0 c_α is strictly greater than $c_{\stackrel{‒}{\alpha }}$ (i.e., c_α0) under condition (C4). The above equation yields (16) immediately.

Next we show that the model selected by the GIC selector with bounded κ_n is overfitted with probability bounded away from zero. For any λ ∈ Ω₀, α_λ = α₀. Then subtracting ${\mathrm{GIC}}_{{\kappa }_n}^{\ast }\left(\stackrel{‒}{\alpha }\right)$ from both sides of (18) and subsequently taking inf_λ∈Ω0 over GIC_κn(λ), we have

$$\underset{\lambda \in {\Omega }_0}{\inf }{\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)-{\mathrm{GIC}}_{{\kappa }_n}^{\ast }\left(\stackrel{‒}{\alpha }\right)>D^{\ast }\left({\alpha }_0\right)∕n-[D^{\ast }\left(\stackrel{‒}{\alpha }\right)∕n+{\kappa }_n{d}_{\stackrel{‒}{\alpha }}∕n].$$ (20)

Note that the right-hand side of the above equation does not involve λ.

$D^{\ast }\left({\alpha }_0\right)-D^{\ast }\left(\stackrel{‒}{\alpha }\right)=-2\left[\ell \left({\widehat{\beta }}_{{\alpha }_0}^{\ast }\right)-\ell \left({\widehat{\beta }}_{\stackrel{‒}{\alpha }}^{\ast }\right)\right]$, where ${\widehat{\beta }}_{{\alpha }_0}^{\ast }$ and ${\widehat{\beta }}_{\stackrel{‒}{\alpha }}^{\ast }$ are the non-penalized maximum likelihood estimators computed via the true and full models, respectively. Under regularity conditions (A)—(C) in Fan and Li (2001), it can be shown that ${\widehat{\beta }}_{{\alpha }_0}^{\ast }$ and ${\widehat{\beta }}_{\stackrel{‒}{\alpha }}^{\ast }$ are consistent and asymptotically normal. Hence, the likelihood ratio test statistic $-2\left[\ell \left({\widehat{\beta }}_{{\alpha }_0}^{\ast }\right)-\ell \left({\widehat{\beta }}_{\stackrel{‒}{\alpha }}^{\ast }\right)\right]\stackrel{\mathcal{L}}{\to }{\chi }_{d_{\stackrel{‒}{\alpha }}-d_{{\alpha }_0}}^2$. This result, together with κ_n < M and (20), yields

$$\begin{array}{cc}\hfill P\left\{\underset{\lambda \in {\Omega }_0}{\inf }{\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)-{\mathrm{GIC}}_{{\kappa }_n}^{\ast }\left(\stackrel{‒}{\alpha }\right)>0\right\}& \ge P\left\{-\frac{2}{n}\left[\ell \left({\widehat{\beta }}_{{\alpha }_0}^{\ast }\right)-\ell \left({\widehat{\beta }}_{\stackrel{‒}{\alpha }}^{\ast }\right)\right]-{\kappa }_n{d}_{\stackrel{‒}{\alpha }}∕n>0\right\}\hfill \\ \hfill & \ge P\left\{-2\left[\ell \left({\widehat{\beta }}_{{\alpha }_0}^{\ast }\right)-\ell \left({\widehat{\beta }}_{\stackrel{‒}{\alpha }}^{\ast }\right)\right]>d_{\stackrel{‒}{\alpha }}M\right\}\hfill \\ \hfill & \to P\left\{{\chi }_{d_{\stackrel{‒}{\alpha }}-d_{{\alpha }_0}}^2\ge d_{\stackrel{‒}{\alpha }}M\right\}\triangleq \pi .\hfill \end{array}$$

This implies (17), and we complete the proof of Lemma 1.

To prove Theorem 1(B), we present the following lemma.

Lemma 2. Suppose the density function of the generalized linear model satisfies Fan and Li's (2001) three regularity conditions (A)—(C). Assume conditions (C1)—(C4) hold, and let ${\lambda }_n={\kappa }_n∕\sqrt{n}$. If κ_n satisfies κ_n → ∞ and λ_n → 0 as n → ∞, then

$$P\{GI{C}_{{\kappa }_n}\left({\lambda }_n\right)=GI{C}_{{\kappa }_n}^{\ast }\left({\alpha }_0\right)\}\to 1,$$ (21)

and

$$P\left\{\underset{\lambda \in {\Omega }_{-}\cup {\Omega }_{+}}{\inf }GI{C}_{{\kappa }_n}\left(\lambda \right)>GI{C}_{{\kappa }_n}\left({\lambda }_n\right)\right\}\to 1.$$ (22)

Proof. Without loss of generality, we assume that the first d_α0 coefficients of β_α0 in the true model are nonzero and the rest are zeros. Note that the density function of the generalized linear model satisfies Fan and Li's (2001) three regularity conditions (A)—(C). These conditions, together with condition (C3) and the assumptions of κ_n stated in Lemma 2, allow us to apply Fan and Li's Theorems 1 and 2 to show that, with probability tending to 1, the last d – d_α0 components of ${\widehat{\beta }}_{{\lambda }_n}$ are zeros and the first d_α0 components of ${\widehat{\beta }}_{{\lambda }_n}$ satisfy the normal equations

$$\frac{\partial }{\partial {\beta }_j}\ell \left({\widehat{\beta }}_{{\lambda }_n}\right)+b_{{\lambda }_{n}j}=0forj=1,\dots ,d_{{\alpha }_0},$$ (23)

where $b_{{\lambda }_{n}j}=p_{{\lambda }_n}^{\prime }\left(\mid {\widehat{\beta }}_{{\lambda }_{n}j}\mid \right)\mathrm{sgn}\left({\widehat{\beta }}_{{\lambda }_{n}j}\right)$, and ${\widehat{\beta }}_{{\lambda }_{n}j}$ is the j-th component of ${\widehat{\beta }}_{{\lambda }_n}$.

Using the oracle property, we have $\mid {\widehat{\beta }}_{{\lambda }_{n}j}\mid \to \mid {\beta }_j\mid \ge {\min }_{1\le j\le d_{{\alpha }_0}}\mid {\beta }_j\mid$. Then, under conditions (C1) and (C2), there exists a constant m so that $p_{{\lambda }_n}^{\prime }\left(\mid {\widehat{\beta }}_{{\lambda }_{n}j}\mid \right)=0$ for min_1≤j≤dα0 |β_j| > mλ_n as n gets large. Accordingly, P(b_λnj = 0) → 1 for j = 1, ..., d_α0. This together with (23) implies that, with probability tending to 1, the first d_α0 components of ${\widehat{\beta }}_{{\lambda }_n}$ solve the normal equations

$$\frac{\partial }{\partial {\beta }_j}\ell \left({\widehat{\beta }}_{{\lambda }_n}\right)=0,j=1,\dots ,d_{{\alpha }_0},$$

and the remaining d – d_α0 components are zeros. This is exactly the same as the normal equation in solving the non-penalized maximum likelihood estimator ${\widehat{\beta }}_{{\alpha }_0}^{\ast }$. As a result, ${\widehat{\beta }}_{{\alpha }_0}^{\ast }={\widehat{\beta }}_{{\lambda }_n}$ with probability tending to 1. It follows that

$$P\{D\left({\lambda }_n\right)=D^{\ast }\left({\alpha }_0\right)\}=P\left\{\ell \left({\widehat{\beta }}_{{\lambda }_n}\right)=\ell \left({\widehat{\beta }}_{{\alpha }_0}^{\ast }\right)\right\}\to 1.$$

Moreover, using the result from Proposition 1, we have P{df_λn = d_α0} → 1. Consequently,

$$P\{{\mathrm{GIC}}_{{\kappa }_n}\left({\lambda }_n\right)={\mathrm{GIC}}_{{\kappa }_n}^{\ast }\left({\alpha }_0\right)\}=P\left\{\frac{1}{n}(D\left(\lambda \right)-D^{\ast }\left({\alpha }_0\right))+\frac{{\kappa }_n}{n}(d{f}_{{\lambda }_n}-d_{{\alpha }_0})=0\right\}\to 1.$$

The proof of (21) is complete.

We next show that, for any λ which cannot identify the true model, the resulting GIC_κn(λ) is consistently larger than GIC_κn(λ_n). To this end, we consider two cases, underfitting and overfitting.

Case 1: Underfitted model (i.e., λ ∈ Ω_– so that α_λ ⊅ α₀). Applying (18) and (21), we obtain that, with probability tending to 1,

$${\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)-{\mathrm{GIC}}_{{\kappa }_n}\left({\lambda }_n\right)>\frac{1}{n}{D}^{\ast }\left({\alpha }_{\lambda }\right)-\frac{1}{n}{D}^{\ast }\left({\alpha }_0\right)-\frac{{\kappa }_n}{n}{d}_{{\alpha }_0}.$$

Subsequently, take inf_λ∈Ω– of both sides of the above equation, which yields

$$\underset{\lambda \in {\Omega }_{-}}{\inf }{\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)-{\mathrm{GIC}}_{{\kappa }_n}\left({\lambda }_n\right)>\underset{\alpha \not\supset {\alpha }_0}{\min }\frac{1}{n}{D}^{\ast }\left(\alpha \right)-\frac{1}{n}{D}^{\ast }\left({\alpha }_0\right)-\frac{{\kappa }_n}{n}{d}_{{\alpha }_0}.$$ (24)

This, in conjunction with condition (C4) and the number of underfitted models being finite, leads to

$$P\left\{\underset{\alpha \not\supset {\alpha }_0}{\min }\frac{1}{n}{D}^{\ast }\left(\alpha \right)-\frac{1}{n}{D}^{\ast }\left({\alpha }_0\right)-\frac{{\kappa }_n}{n}{d}_{{\alpha }_0}>0\right\}=P\left\{\underset{\alpha \not\supset {\alpha }_0}{\min }{c}_{\alpha }-c_{{\alpha }_0}+o_P\left(1\right)>0\right\}\to 1,$$

as n → ∞. As a result,

$$P\left\{\underset{\lambda \in {\Omega }_{-}}{\inf }{\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)>{\mathrm{GIC}}_{{\kappa }_n}\left({\lambda }_n\right)\right\}\to 1.$$

Case 2: Overfitted model (i.e., λ ∈ Ω₊ so that ${\alpha }_{\lambda }⫌{\alpha }_0$. According to Lemma 1, with probability tending to 1, D(λ_n) = D*(α₀). In addition, Proposition 1 indicates that df_λ – df_λn > τ + O_P (1) for some τ > 0 and λ ∈ Ω₊. Moreover, as noticed in the proof of Lemma 1, D(λ) ≥ D*(α_λ). Therefore, with probability tending to 1,

$$\begin{array}{cc}\hfill n({\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)-{\mathrm{GIC}}_{{\kappa }_n}\left({\lambda }_n\right))& =D\left(\lambda \right)-D\left({\lambda }_n\right)+(d{f}_{\lambda }-d{f}_{{\lambda }_n}){\kappa }_n\hfill \\ \hfill & \ge D^{\ast }\left({\alpha }_{\lambda }\right)-D^{\ast }\left({\alpha }_0\right)+(\tau +o_P\left(1\right)){\kappa }_n.\hfill \end{array}$$

Because D*(α₀) – D*(α) follows a χ² distribution with d_α – d_α0 degrees of freedom asymptotically for any $\alpha ⫌{\alpha }_0$, it is of order O_P (1). Accordingly,

$$\underset{\lambda \in {\Omega }_{+}}{\inf }n({\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)-{\mathrm{GIC}}_{{\kappa }_n}\left({\lambda }_n\right))\ge \underset{\alpha ⫌{\alpha }_0}{\min }\{D^{\ast }\left({\alpha }_0\right)-D^{\ast }\left(\alpha \right)\}+(\tau +o_P\left(1\right)){\kappa }_n\approx \tau {\kappa }_n.$$ (25)

Using the fact that κ_n goes to infinity as n → ∞, the right-hand side of equation (25) goes to positive infinity, which guarantees that the left-hand side of equation (25) is positive as n → ∞. Hence, we finally have

$$P\left\{\underset{\lambda \in {\Omega }_{+}}{\inf }{\mathrm{GIC}}_{{\kappa }_n}\left(\lambda \right)>{\mathrm{GIC}}_{{\kappa }_n}\left({\lambda }_n\right)\right\}\to 1.$$

The results of Cases 1 and 2 complete the proof of (22).

Proofs of Theorem 1. Lemma 1 implies that GIC_κn(λ), which produces the underfitted model, is consistently larger than ${\mathrm{GIC}}_{{\kappa }_n}^{\ast }\left(\stackrel{‒}{\alpha }\right)$. Thus, the optimal model selected by minimizing the GIC_κn(λ) must contain all of the significant variables with probability tending to one. In addition, Lemma 1 indicates that there is a nonzero probability that the smallest value of GIC_κn(λ) for λ ∈ Ω₀ is larger than that of the full model. As a result, there is a positive probability that any λ associated with the true model cannot be selected by GIC_κn(λ) as the regularization parameter. Theorem 1(A) follows.

Lemma 2 indicates that the model identified by λ_n converges to the true model as the sample size gets large. In addition, it shows λ's that fail to identify the true model cannot be selected by GIC_κn(λ) asymptotically. Theorem 1(B) follows.

Appendix B. Proofs of Theorem 2 and Corollary 1

Before proving the theorem, we establish the following two lemmas. Lemma 3 evaluates the difference between a penalized mean estimator ${\widehat{\mu }}_{\lambda }$ and its corresponding least squares mean estimator ${\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }$, while Lemma 4 demonstrates that the losses of ${\widehat{\mu }}_{\lambda }$ and ${\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }$ are asymptotically equivalent.

Lemma 3. Under condition (C5),

$${\Vert {\widehat{\mu }}_{\lambda }-{\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }\Vert }^2\le nC{\Vert \mathbf{b}\Vert }^2,$$

where C is the constant number in condition (C5) and b is defined in condition (C8).

Proof. Without loss of generality, we assume that the first d_αλ components of ${\widehat{\beta }}_{\lambda }$ and ${\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }$ are nonzero, and denote them by ${\widehat{\beta }}_{\lambda }^{\left(1\right)}$ and ${\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast \left(1\right)}$, respectively. Thus, ${\widehat{\mu }}_{\lambda }=\mathbf{X}{\widehat{\beta }}_{\lambda }={\mathbf{X}}_{{\alpha }_{\lambda }}{\widehat{\beta }}_{\lambda }^{\left(1\right)}$ and ${\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }=\mathbf{X}{\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }={\mathbf{X}}_{{\alpha }_{\lambda }}{\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast \left(1\right)}$. From the proofs of Theorems 1 and 2 in Fan and Li (2001), with probability tending to 1, we have that ${\widehat{\beta }}_{\lambda }^{\left(1\right)}$ is the solution of the following equation,

$$\frac{1}{n}{\mathbf{X}}_{{\alpha }_{\lambda }}^T\left(\mathbf{y}-{\mathbf{X}}_{{\alpha }_{\lambda }}{\beta }_{\lambda }^{\left(1\right)}\right)+{\mathbf{b}}^{\left(1\right)}=0,$$

where b⁽¹⁾ is the subvector of b that corresponds to ${\widehat{\beta }}_{\lambda }^{\left(1\right)}$. Accordingly,

$${\widehat{\beta }}_{\lambda }^{\left(1\right)}={\left({\mathbf{X}}_{{\alpha }_{\lambda }}^T{\mathbf{X}}_{{\alpha }_{\lambda }}\right)}^{-1}{\mathbf{X}}_{{\alpha }_{\lambda }}^T\mathbf{y}+{\left(\frac{1}{n}{\mathbf{X}}_{{\alpha }_{\lambda }}^T{\mathbf{X}}_{{\alpha }_{\lambda }}\right)}^{-1}{\mathbf{b}}^{\left(1\right)}={\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast \left(1\right)}+{\mathbf{V}}_{{\alpha }_{\lambda }}{\mathbf{b}}^{\left(1\right)},$$

where ${\mathbf{V}}_{{\alpha }_{\lambda }}\triangleq {\left(\frac{1}{n}{\mathbf{X}}_{{\alpha }_{\lambda }}^T{\mathbf{X}}_{{\alpha }_{\lambda }}\right)}^{-1}$. In addition, the eigenvalues of V_αλ are bounded under condition (C5). Hence,

$${\Vert {\widehat{\mu }}_{\lambda }-{\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }\Vert }^2={\Vert {\mathbf{X}}_{{\alpha }_{\lambda }}({\widehat{\beta }}_{\lambda }^{\left(1\right)}-{\widehat{\beta }}_{\lambda }^{\ast \left(1\right)})\Vert }^2=n{\mathbf{b}}_1^T{\mathbf{V}}_{{\alpha }_{\lambda }}{\mathbf{b}}^{\left(1\right)}\le nC{\Vert \mathbf{b}\Vert }^2,$$

for some positive constant number C. This completes the proof.

Lemma 4. If conditions (C5)—(C8) hold, then

$$\underset{\lambda \in [0,{\lambda }_{\max }]}{\sup }\mid \frac{L\left({\widehat{\beta }}_{\lambda }\right)}{L\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)}-1\mid \to 0,$$

in probability.

Proof. After algebraic simplification, we have

$$L\left({\widehat{\beta }}_{\lambda }\right)-L\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)=\frac{{\Vert {\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }-{\widehat{\mu }}_{\lambda }\Vert }^2}{n}+\frac{2{(\mu -{\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast })}^T({\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }-{\widehat{\mu }}_{\lambda })}{n}=I_1+I_2.$$

Under conditions (C6) and (C7), Li (1987) showed that

$$\underset{\alpha \in \mathcal{A}}{\sup }\mid \frac{\lambda \left({\widehat{\beta }}_{\alpha }^{\ast }\right)}{R\left({\widehat{\beta }}_{\alpha }^{\ast }\right)}-1\mid \to 0.$$

This, together with condition (C8) and Lemma 3, implies

$$\underset{\lambda \in [0,{\lambda }_{\max }]}{\sup }\mid \frac{I_1}{L\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)}\mid =\underset{\lambda \in [0,{\lambda }_{\max }]}{\sup }\left\{\frac{{\Vert {\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }-{\widehat{\mu }}_{\lambda }\Vert }^2}{nR\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)}-\frac{{\Vert {\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }-{\widehat{\mu }}_{\lambda }\Vert }^2}{nL\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)}\left[\frac{L\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)}{R\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)}-1\right]\right\}\to 0.$$

Applying the Cauchy-Schwarz inequality, we next obtain

$$I_2\le \frac{2\Vert \mu -{\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }\Vert \cdot \Vert {\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }-{\widehat{\mu }}_{\lambda }\Vert }{n}=2\sqrt{L\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)}\cdot \frac{1}{\sqrt{n}}\Vert {\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }-{\widehat{\mu }}_{\lambda }\Vert .$$

As a result, ${\sup }_{\lambda \in [0,{\lambda }_{\max }]}\mid \frac{I_2}{L\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)}\mid \to 0$, and Lemma 4 follows immediately.

Proof of Theorem 2. To show the asymptotic efficiency of the AIC-type selector, it suffices to demonstrate that minimizing ${\mathrm{GIC}}_{{\kappa }_n}^{LS}\left(\lambda \right)$ with κ_n → 2 is the same as minimizing $L\left({\widehat{\beta }}_{\lambda }\right)$ asymptotically. To this end, we need to prove that, in probability,

$$\underset{\lambda \in [0,{\lambda }_{\max }]}{\sup }\mid \frac{{\mathrm{GIC}}_{{\kappa }_n}^{LS}\left(\lambda \right)-\frac{{\Vert ∊\Vert }^2}{n}-L\left({\widehat{\beta }}_{\lambda }\right)}{L\left({\widehat{\beta }}_{\lambda }\right)}\mid \to 0.$$ (26)

Let the projection matrix corresponding to the model α be ${\mathbf{H}}_{\alpha }={\mathbf{X}}_{\alpha }{\left({\mathbf{X}}_{\alpha }^T{\mathbf{X}}_{\alpha }\right)}^{-1}{\mathbf{X}}_{\alpha }^T$. Then,

$$\begin{array}{cc}\hfill {\mathrm{GIC}}_{{\kappa }_n}^{LS}\left(\lambda \right)=& \frac{{\Vert \mathbf{y}-\mathbf{X}{\widehat{\beta }}_{\lambda }\Vert }^2}{n}+\frac{{\kappa }_n{\sigma }^2{d}_{{\alpha }_{\lambda }}}{n}\hfill \\ \hfill =& \frac{{\Vert \mathbf{y}-{\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }\Vert }^2}{n}+\frac{{\Vert {\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }-{\widehat{\mu }}_{\lambda }\Vert }^2}{n}+\frac{{\kappa }_n{\sigma }^2{d}_{{\alpha }_{\lambda }}}{n}\hfill \\ \hfill =& \frac{{\Vert ∊\Vert }^2}{n}+L\left({\widehat{\beta }}_{\lambda }\right)+\left[L\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)-L\left({\widehat{\beta }}_{\lambda }\right)\right]+\frac{1}{n}{\Vert {\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }-{\widehat{\mu }}_{\lambda }\Vert }^2\hfill \\ \hfill & +\frac{2}{n}{∊}^T(\mathbf{I}-{\mathbf{H}}_{{\alpha }_{\lambda }})\mu +\frac{2}{n}({\sigma }^2{d}_{{\alpha }_{\lambda }}-{∊}^T{\mathbf{H}}_{{\alpha }_{\lambda }}∊)+\frac{1}{n}({\kappa }_n-2){\sigma }^2{d}_{{\alpha }_{\lambda }}.\hfill \end{array}$$ (27)

Let $J_1=L\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)-L\left({\widehat{\beta }}_{\lambda }\right),J_2={\Vert {\widehat{\mu }}_{{\alpha }_{\lambda }}^{\ast }-{\widehat{\mu }}_{\lambda }\Vert }^2∕n,J_3=2{\widehat{∊}}^T(\mathbf{I}-{\mathbf{H}}_{{\alpha }_{\lambda }})\mu ∕n,J_4=2({\sigma }^2{d}_{{\alpha }_{\lambda }}-{∊}^T{\mathbf{H}}_{{\alpha }_{\lambda }}∊)∕n$ and J₅ = (κ_n – 2)σ²d_αλ/n. Using Lemma 3, Lemma 4 and similar arguments used in Li (1987), we obtain that, in probability,

$$\underset{\lambda \in [0,{\lambda }_{\max }]}{\sup }\mid \frac{J_j}{L\left({\widehat{\beta }}_{\lambda }\right)}\mid \to 0,\text{for}j=1,\dots ,4.$$

Because κ_n – 2 and the fact that $n^{-1}{\sigma }^2{d}_{{\alpha }_{\lambda }}∕R\left({\widehat{\beta }}_{\lambda }\right)$ is bounded by 1, we can further show that ${\sup }_{\lambda \in [0,{\lambda }_{\max }]}\mid J_5∕L\left({\widehat{\beta }}_{\lambda }\right)\mid \to 0$ using Lemma 4 and condition (C7). Accordingly, (26) holds, which implies that the difference between ${\mathrm{GIC}}_{{\kappa }_n}^{LS}\left(\lambda \right)-\frac{{\Vert ∊\Vert }^2}{n}$ and $L\left({\widehat{\beta }}_{\lambda }\right)$ is negligible in comparison to $L\left({\widehat{\beta }}_{\lambda }\right)$. This completes the proof.

Proof of Corollary 1. When σ² is unknown, the ${\mathrm{GIC}}_{{\kappa }_n}^{LS}\left(\lambda \right)$ in (27) becomes

$${\mathrm{GIC}}_{{\kappa }_n}^{LS}\left(\lambda \right)=\frac{{\Vert ∊\Vert }^2}{n}+L\left({\widehat{\beta }}_{\lambda }\right)+J_1+J_2+J_3+J_4+J_5+\frac{2({\tilde{\sigma }}^2-{\sigma }^2)d_{{\alpha }_{\lambda }}}{n}.$$

Using Lemma 4 and condition (C7), we have

$$\underset{\lambda \in [0,{\lambda }_{\max }]}{\sup }\mid \frac{2({\tilde{\sigma }}^2-{\sigma }^2)d_{{\alpha }_{\lambda }}}{nL\left({\widehat{\beta }}_{\lambda }\right)}\mid \to 0$$

in probability, which completes the proof.

Appendix C. Sufficient conditions for (C8)

We first present three sufficient conditions for (C8).

• (S1) There exists a constant M₁ such that λ_max satisfies $\sqrt{n}{\lambda }_{\max }<M_1$ for all n.

• (S2) There exists a constant M₂ such that p_λ(θ) satisfies $p_{\lambda }^{\prime }\left(\theta \right)\le M_2\lambda$ for any θ.

• (S3) The average error of the full model $\stackrel{‒}{\alpha }$, i.e. ${\Delta }_{\stackrel{‒}{\alpha }}\triangleq {\Vert \mu -{\mathbf{H}}_{\stackrel{‒}{\alpha }}\mu \Vert }^2∕n$, satisfies $\frac{n{\Delta }_{\stackrel{‒}{\alpha }}}{d}\to \infty$, as n → ∞.

We next provide motivations for these conditions. Assume that the true model is ${\mathbf{x}}_i^T{\beta }_0={\sum }_{j=1}^d{x}_{ij}{\beta }_{j0}$ for i = 1, . . . , n, and then write $a_n={\max }_{1\le j\le d}\{p_{{\lambda }_n}^{\prime }\left(\mid {\beta }_{j0}\mid \right),{\beta }_{j0}\ne 0\}$. Under the condition d = O(n^ν) with ν < ¼, Fan and Peng (2004) proved that there exists a local maximum of the penalized least squares function, so that $\Vert \widehat{\beta }-{\beta }_0\Vert =O_P\left\{\sqrt{d}(n^{-1∕2}+a_n)\right\}$. Thus, conditions (S1) and (S2) ensure that the penalized estimator is $\sqrt{n∕d}\text{-consistent}$. As for condition (S3), consider a case where the full model misses an important variable x_exc that is orthogonal to the rest of the variables. Accordingly, ${\Delta }_{\stackrel{‒}{\alpha }}=n^{-1}{\sum }_{i=1}^n{x}_{\mathrm{exc};i}^2{\beta }_{\mathrm{exc}}^2$, and hence $n{\Delta }_{\stackrel{‒}{\alpha }}∕d$ is of the same order as $n{\beta }_{\mathrm{exc}}^2∕d$. Consequently, (S3) holds if the coefficient β_exc satisfies $\sqrt{n∕d}{\beta }_{\mathrm{exc}}\to \infty$, which is valid, for example, when β_exc is fixed.

In contrast to imposing condition (S3) on the error of the full model, an alternative condition (S3*) motivated by Fan and Peng (2004) is given below.

• (S3*) The proportion of penalized coefficients satisfies ${\sup }_{\lambda \in [0,{\lambda }_{\max }]}\frac{1}{d_{{\alpha }_{\lambda }}}{\sum }_{j=1}^{d}I(0<\mid {\widehat{\beta }}_{\lambda j}\mid \le m\lambda )\to 0$, as n → ∞, where m is defined in (C2).

Condition (S3*) means that the proportion of small or moderate size coefficients $(0<\sqrt{n}\mid {\widehat{\beta }}_{\lambda j}\mid \le m{M}_1)$ is vanishing. This condition is satisfied under the identifiability assumption of Fan and Peng (2004) (i.e., min_j:β0≠0 |β_0j|/λ → ∞, as n → ∞). As a byproduct, a similar condition can also be established for the adaptive LASSO, which employs data-driven penalties with $b_j=\lambda ∕{\left({\widehat{\beta }}_{\stackrel{‒}{\alpha }j}^{\ast }\right)}^k$ for some k > 0 to cope with the bias of LASSO. In sum, (S1) to (S3) (or S3*) are mild conditions, and two propositions given below demonstrate their sufficiency for condition (C8).

Proposition 2. Under (S1) to (S3), condition (C8) holds.

Proof. It is noteworthy that

$$R\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)={\Delta }_{{\alpha }_{\lambda }}+\frac{d_{{\alpha }_{\lambda }}{\sigma }^2}{n}\ge {\Delta }_{\stackrel{‒}{\alpha }}+\frac{d_{{\alpha }_{\lambda }}{\sigma }^2}{n}.$$ (28)

On the right-hand side of (28), the first term dominates the second term via condition (S3). From (S1), (S2), and (28), we have that

$$\frac{{\Vert \mathbf{b}\Vert }^2}{R\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)}\le \frac{M_2^2{\lambda }^2{d}_{{\alpha }_{\lambda }}}{R\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)}\le M_2^2\cdot n{\lambda }_{\max }^2\cdot \frac{1}{n{\Delta }_{\stackrel{‒}{\alpha }}∕d},$$

which goes to zero independently of λ. This completes the proof.

Proposition 3. Assume that the penalty function satisfies condition (C2). Under (S1) to (S3*), condition (C8) holds.

Proof. Under condition (C2), the components in b are zero except for those ${\widehat{\beta }}_{\lambda j}\le m\lambda$. Then, employing (S2) and (28), we obtain that

$$\frac{{\Vert \mathbf{b}\Vert }^2}{R\left({\widehat{\beta }}_{{\alpha }_{\lambda }}^{\ast }\right)}\le \frac{{\Vert \mathbf{b}\Vert }^2}{n^{-1}{d}_{{\alpha }_{\lambda }}{\sigma }^2}\le \frac{M_2^2}{{\sigma }^2}\cdot n{\lambda }_{\max }^2\cdot \frac{1}{d_{{\alpha }_{\lambda }}}\sum _{j=1}^{d}I(0<\mid {\widehat{\beta }}_{\lambda j}\mid \le m\lambda ).$$

On the right-hand side of the above equation, the first term is constant, the second term is bounded under (S1), and the third term goes to zero uniformly in λ under (S3*). This completes the proof.