Abstract
Force spectroscopy based on magnetic tweezers is a powerful technique to manipulate single biomolecules and study their interactions. The resolution in a magnetic probe displacement, however, needs to be commensurate with molecular sizes. To achieve the desirable sensitivity in tracking displacements of the magnetic probe, some recent approaches have combined magnetic tweezers with total internal reflection fluorescence microscopy. In this situation, a typical force probe is a polymer microsphere containing two types of optically active components – a pure absorber (magnetic nanoparticles for providing the pulling force) and a luminophore (semiconducting nanoparticles or organic dyes for fluorescent imaging). In order to fully assess the system’s capability for tracking the position of the force probe with sub-nanometer accuracy, we developed a body-of-revolution formulation of the method of auxiliary sources (BOR-MAS) to simulate absorption, scattering, and fluorescence of microscopic spheres in an evanescent electromagnetic field. The theoretical formulation uses the axial symmetry of the system to reduce the dimensionality of the modeling problem and produces excellent agreement with the reported experimental data on forward scattering intensity. Using the BOR-MAS numerical model, we investigated the probe detection sensitivity for a high numerical aperture objective. The analysis of both backscattering and fluorescence observation modes shows that the total intensity of the bead image decays exponentially with the distance from the surface (or the length of a biomolecule). Our investigations demonstrate that the decay lengths of observable optical power are smaller than the penetration depth of the unperturbed excitation evanescent wave. In addition, our numerical modeling results illustrate that the expected sensitivity for the decay length changes with the incident angle, tracking the theoretical penetration depth for a two-media model, and is sensitive to the bead size. The BOR-MAS methodology developed in this work for near field modeling of bead tracking experiments fully describes the fundamental photonic response of microscopic BOR probes at the sub-wavelength level and can be used for future improvements in the design of these probes or in the setup of bead tracking experiments.
Introduction
Single molecule force spectroscopy has developed into a powerful tool for manipulation of biological molecules and studies of their biophysics.1 Molecular recognition,2 protein unfolding,3 DNA-protein interactions,4 structural transitions in polysaccharides,5 formation of supramolecular structures6 or peeling of biopolymers from flat substrates7 have all been studied at the single molecule level using force spectroscopy. The use of mechanical force as an external control parameter, demonstrated in these experiments, has made it possible to envision single molecules as a component of a micro-analytical platform,8 in which high-resolution force spectroscopy can detect structural changes down to monomer resolution.
Optical tweezers and atomic force microscopy (AFM) are the most widely used techniques for practical implementation of force spectroscopy experiments.9 They provide both sub-nanoNewton sensitivity in measurements of applied forces and sub-nanometer sensitivity in molecular extensions. The drawback of these techniques is that they require advanced (and in the case of AFM, costly) instrumentation and achieve their high level of control usually in a serial, one-molecule-at-a-time manner. Application of force spectroscopy in routine micro-analytical devices should, instead, be easy to implement in a parallel format, with no expensive consumables. Magnetic tweezers hold a promise to be such a technique for broad application of force spectroscopy in bioanalysis.10 In magnetic tweezers, the forces are applied to molecules via superparamagnetic spherical probes using an external magnetic field. These probes, or magnetic beads, can be synthesized in bulk solutions and some are already available commercially. With such probes one can cover several orders of magnitude in forces (from femto-Newtons to tens of pico-Newtons), but a resolution in probe displacement commensurate with molecular sizes (sub-nm) is also required, especially for shorter biopolymers.
This level of sensitivity to movement of the probe can be achieved with analysis of interference fringes in optical images of the microscopic beads1,11 or, alternatively, by observing optical response of the probes placed in the evanescent field near the interface where biomolecules are anchored. Singh-Zocchi et al. achieved nanometer resolution in distance from the surface for the DNA-tethered beads using analysis of the scattering of the optical near field by the dielectric microspheres.12 Evanescent wave scattering or luminescence from colloids has become an established tool to map particle-surface potential energy profiles.13–14 Therefore, photometry applied to images of magnetic microspheres excited by the optical evanescent field can potentially be used for highly sensitive measurements of molecular extensions in magnetic tweezers (Figures 1A, 1B).15 In order to understand the fundamentals of the optical response of magnetic-fluorescent microspheres, we carried out numerical simulations of electromagnetic (EM) interactions of these probes with the optical near field. We developed a body-of-revolution formulation of the method of auxiliary sources (BOR-MAS) and used it to study the absorbance, scattering, and fluorescence in a typical force spectroscopy experiment. The numerical results presented here could serve as a guide for design and analysis of magnetic tweezers-based force spectroscopy experiments and establish the requirements for fabrication of the force probes.
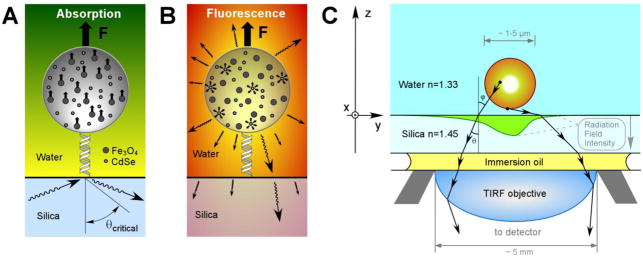
Figure 1.
(A) Absorption of evanescent EM radiation by a fluorescent magnetic bead in water. Evanescent EM field is created by a laser beam undergoing TIR at the silica-water interface. Polystyrene beads are pulled by a magnetic field with a total force F resulting from the interactions (small arrows) between magnetic moments induced in individual magnetite nanoparticles and the magnetic field gradient. (B) The detectable response from the bead fluorescent component – QDs that emit in all directions (arrows) – results from those photons that are transmitted through silica. (C) Geometry of the objective-silica-water-bead setting.
Approach
The evanescent EM field can be readily created in the vicinity of the solid-water interface in an optical microscope using either a prism or objective-based total internal reflection (TIR) setup (Figure 1). The penetration depth, or characteristic decay length, of the evanescent EM field will depend on the refractive indices of the solid support and buffer solution, the laser beam wavelength and its angle of incidence.16 In general, the penetration depth is in the range of 50–200 nm for visible light. One can use the measurement of the amplitude of electric field at a given location in water as a means to map the distance of this location from the TIR interface. A probe that is capable of interaction with an EM field (e.g. a fluorescent dye molecule or a nanoscopic scatterer) will effectively report its position with respect to the interface when it produces a measurable photonic response (such as fluorescence). The description of the measurement of molecular extension by bead tracking requires a rigorous numerical solution of vector electromagnetic field equations, since the critical dimensions (distance between the bead and solid support as well as, possibly, the size of the bead itself) are sub-wavelength scale.
For micron-size probes, the waist of the incident collimated laser beam is much greater than the bead diameter; therefore, the incident electromagnetic wave can be approximated as a plane wave. In addition, the numerical aperture of a typical TIR objective is 1.45 and is the same as the refractive index of quartz or fused silica (a frequently used material with low autofluorescence, nD=1.45) substrates, which guarantees that any incidence angle θ between critical and glancing angles (66.5° and 90°) is achievable in these substrates (Figure 1C). Notice that, use of common glass coverslips (nD=1.52) as substrates will limit the available range of incident angles, but will not significantly affect the outcome of the simulations within that range. Choice of an incident angle is important in considerations of the dynamic range and sensitivity. Small angles (close to the critical angle) have a small field gradient, while large angles (close to 90°) have too short a penetration depth. In this paper, we use the index of silica in order to cover the widest possible choice of conditions for incident light. The angles of 70, 75, 80 and 85 degrees are used in calculations to investigate the dependence of the decay length on the incident angle.
Practical implementation of magnetic tweezers for detection of the molecular extension using TIRFM (Total Internal Reflection Fluorescence Microscopy) relies on the use of probes that are several microns in diameter and contain a significant amount of magnetite (volumetric fraction > 20%) in order to approach a high force regime (>10 pN) in pulling experiments.1 A potential for long term exposure to laser radiation favors the use of luminescent components, such as semiconducting nanocrystals, that are more resistant to photobleaching than typical fluorescent organic dyes.17 The schematic diagram for such a bead tracking setup is shown in Figure 1. Part of the energy in the incident wave is absorbed by the conductive bead components (magnetite and quantum dots), while the rest is scattered either back into the TIRF objective or forward scattered away from the detector. This paper focuses primarily on the fluorescence detection scheme, because it is straightforward to implement with commercial TIRF microscopes and has an extremely favorable signal to noise ratio due to efficient filtering of the background radiation.16
The power absorbed by magnetite is dissipated, while the optical power deposited in the semiconducting quantum dots (or fluorescent organic dyes) is re-emitted at a longer wavelength. Thus two different physical processes take place: a) absorption and scattering, and b) fluorescence. To understand the underlying physics of each these processes, using the BOR-MAS model, we separate the interaction of light with the bead into two steps: (i) an absorption and scattering stage and (ii) a fluorescence stage. The strength of the fluorescent signal depends on the composition of the bead, material properties of each of the components, incident power, and the out-of-plane (z) position of the bead. At the fluorescent stage, the EM waves emitted by quantum dots (QDs) escape the bead, undergoing absorption by magnetite on their way, and are collected by the microscope objective to yield the final image. The premise behind this setup is that one can use the total intensity of this fluorescent image to determine the z-position of the bead and, therefore, the end-to-end extension of the biomolecule under a given force. The goal of the present work is to develop the formalism for analysis of this EM problem and quantify the interaction of the micron-sized beads with the optical near field as a function of the bead size, location in the field, and composition.
Dielectric constants of the microscopic probes
Synthesized beads consist of randomly oriented, complex-shaped nanoparticles of magnetite (Fe3O4) and CdSe QDs, resting in a base polystyrene dielectric. The rigorous solution of an EM wave scattering problem would account for shape, position and orientation of these particles – a process that requires enormous amounts of computational power and time. In fact, little insight would be gained from the exact solution of the EM problem at a high level of detail for any particular bead realization. Rather, of interest to us is the general behavior of the composite bead that depends only on a limited number of macroscopic properties (such as volumetric fraction of nanoscopic components and their EM properties). There have been several attempts to account analytically for random shape and position of small inclusions in a medium and derive the effective properties of the composite media,18 with variable rates of success. Comparison and description of these effective medium models is a separate active research topic19–20 and beyond the scope of this paper. Since, empirically, most of these models, none being exact, result in similar predictions of effective medium properties, it is sufficient to perform the entire analysis based on a single model.
For the purposes of this paper, we assume that for the majority of real-life scenarios the embedded conductive particles can be considered spherical and spread randomly in a linear isotropic medium. In this case, the Maxwell-Garnett20 model gives the following prediction of the effective dielectric permittivity εeff of the bead as a whole:
| (1) |
where fi is a volumetric fraction of the ith spherical inclusion, having a dielectric constant εi, in a base material of the dielectric constant εb (see sections 1 and 2 of Supporting Information for a discussion of the applicability of the Maxwell-Garnett model and calculation of the refractive indices).
The power per unit volume absorbed by the inclusions can be estimated from the calculated local field EL that excites the ith inclusion using the following expression:
| (2) |
Equation 2, derived under the same assumptions as Maxwell-Garnett formula (see section 3 of Supporting Information), can be used to determine the fraction of power absorbed by each of the components in the mixture. The fraction of power absorbed by QDs is emitted back as a fluorescent signal and weighted by both their volumetric fraction and conductivity. While we use CdSe QDs as specific luminophores in our system, the results are directly applicable to other emitters when the optical power is rescaled according to their volume fraction and conductivity.
Near field optics
We used the Method of Auxiliary Sources (MAS) to determine the near and far field responses of the lossy dielectric bead in the evanescent electromagnetic field.1 The MAS, that belongs to the generalized multiple technique family,21 is a numerical technique for a rigorous solution of Maxwell’s equations. The method is easy to implement and has been successfully applied to electromagnetic scattering and radiation problems.22–24 The backbone of the method is the idea of representing the field in the domains of interest by expanding it into a finite series of fields produced by elementary auxiliary sources located inside and outside of the boundaries of the physical object. These auxiliary sources are usually placed on surfaces conformal to the actual surface of the object and have a uniform distribution. Auxiliary sources outside of the object are responsible for the representation of the inner field, and vice versa, the sources inside the object boundary produce the field outside that boundary, thus, singularities are never encountered. Since the wave function of each of the auxiliary sources represents a solution of the wave equation, the only requirement imposed on these sources is to satisfy the boundary conditions, namely, the continuity of tangential components of electric and magnetic fields on both sides of the physical surfaces.
Shubitidze et al. described an effective optimization of the MAS for quasi-magnetostatic problems with cylindrical symmetry.23 By expanding the fields into Fourier series in the azimuthal direction (angle ϕ, Figure 2), one can significantly reduce the dimensionality of the problem. Instead of a 3-dimensional problem with unknown auxiliary sources distributed across surfaces, we now have a 2.5-dimensional problem, with unknowns distributed along a 2-dimensional line. The added cost, expressed effectively as an extra 0.5 dimension, is the need to perform a separate calculation for each of the spatial Fourier components in azimuthal direction in the incident field. In this paper, we extend the body of revolution formulation of the MAS for a general case of EM fields of arbitrary frequency.
Figure 2.
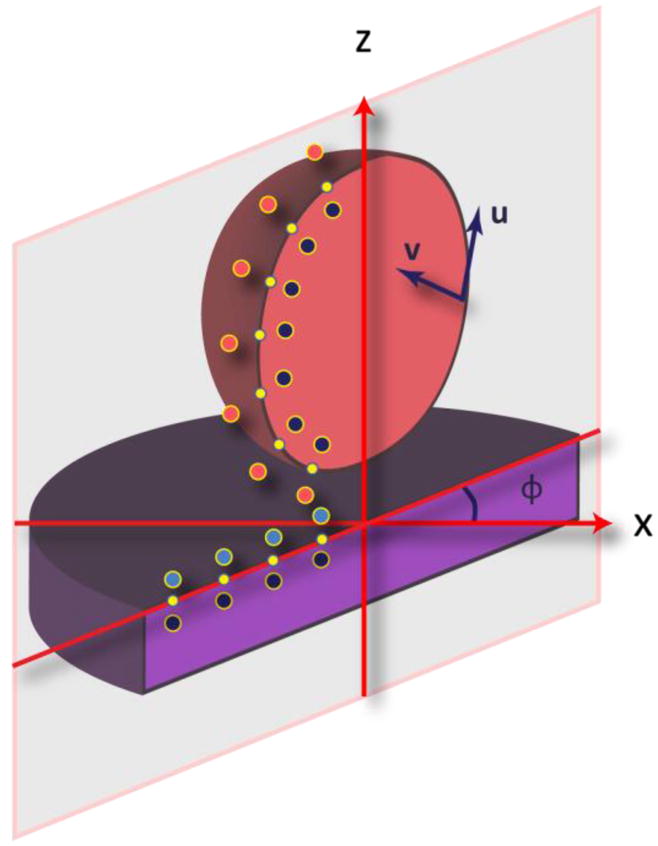
A cross-section of the body of revolution objects (the bead and semi-infinite half-space) with their boundary collocation points (small dots, yellow in color version), internal (black) and external (blue and red in color version) auxiliary sources and surface tangents (u and v) used for the boundary field projection and auxiliary source alignment.
According to the conventional MAS procedures, we first allocate a set of uniformly distributed collocation points on the surfaces of interest and define two conformal surfaces holding auxiliary sources – one inside and one outside of the object (Figure 2). Every point on the surface hosts two orthogonal auxiliary sources, whose wave functions already satisfy Maxwell’s equations (i.e. electric dipoles and magnetic dipoles). Auxiliary sources that describe EM fields in a certain region are located outside of that region, on a surface conformal to its boundary. Typically, the positions of auxiliary sources are obtained by sliding up and down along the surface normals at the boundary collocation points. Such placement helps avoid singularities in the solution, since the fields are always evaluated at a finite distance away from the source origin.
Let the index n=1, 2,…, N identify the collocation points on a belt hosting the origins of auxiliary sources, prior to their out-of-surface shifting. Let un (ϕ) and vn (ϕ) be the vectors, tangent to the object surface, used for both the auxiliary source alignment and the EM field projection. The fields Fid inside the object at point r are then represented as follows:
| (3) |
where are fields (electric or magnetic) generated by the independent sources in the domain id=[silica, water, bead] and GF (r, r0|τ) represents the electric (F = E) and magnetic (F = H) fields created at the point r by a unit elementary dipole, located at r0 and oriented along τ (= u or v):
| (4) |
| (5) |
where R = r−r0 is the relative distance of the target from the source, is the wave number, with k0 being that in free space, and {ε, μ} is the relative dielectric permittivity and magnetic permeability of the domain medium.
According to EM field boundary conditions, the following vector equations should be satisfied at every point of real object surfaces:
| (6a) |
| (6b) |
where n = v × u is the surface normal, and the corresponding field vectors are evaluated separately for the two domains bounded by the surface. Therefore, in order to solve the scattering problem and evaluate fields in the entire space, one has to solve a single system of linear equations for unknown amplitudes of auxiliary sources, arising from boundary conditions (6).
For the body of revolution (BoR) problems, we can account for the ϕ dependence of incident fields and amplitudes of auxiliary sources by expanding the fields into a Fourier series in the azimuthal direction:
| (7a) |
| (7b) |
where r = r(ρ, z, ϕ) is in the cylindrical system of coordinates, are Fourier coefficients for incident fields in the domain id, while are Fourier coefficients for amplitudes of the auxiliary sources, and L is the spatial mode in the azimuthal direction. Since the spatial distribution of the currents induced in the system depends on the behavior of the driving external EM field, the substitution of Fourier expansions (Equation 7) into boundary conditions (Equation 6), evaluated at a set of uniformly distributed collocation points along the object boundaries, will yield 2L+1 independent systems of 4×N linear equations for the unknown Fourier amplitudes of auxiliary sources (one system of equations for each of cos (Lϕ) and sin (Lϕ) modes along with that for the 0th mode). Once these amplitudes are found, any other EM parameter of interest (power flow, near and far fields, distribution of excited volumetric currents inside lossy objects, etc.) can be derived through the superposition of fields created by real and auxiliary sources. This scheme also provides an easy way of monitoring the accuracy of the numerical solution by inspecting the mismatch of boundary conditions resulting from inner and outer auxiliary sources.
The benefit of the MAS formalism is that, besides the original source of radiation (the incident EM wave), it allows for consideration of any number of additional EM field sources both inside and outside of the object of interest, thus making modeling of the fluorescence straightforward. Since the wave fields of each of the auxiliary sources satisfy the wave equation exactly, the only source of error arises from the imperfect satisfaction of the boundary conditions, due to the discretization of the distribution of auxiliary sources. The major obstacle to efficiency of the method arises from the large number of auxiliary sources needed to precisely identify the fields inside and outside of the microsphere and the unknown deviations of auxiliary surfaces from real geometry. Using the BoR approximation reduces the number of unknown auxiliary source amplitudes from 4N×M to 4N (where M is the average number of collocation points required to cover object surfaces in azimuthal direction for each of the N belts), significantly decreasing the size of the system of linear equations. This reduction, however, comes at the expense of the requirement to solve the EM problem separately for each of the spatial Fourier components in the azimuthal direction (L=0, 1, …, Lmax, where Lmax is the highest mode number, whose value depends on the specific character of the incident field).
The major advantage of BoR with respect to the full 3D model becomes obvious when the full complexity of the problem, mimicking a potential experimental application, is considered: namely, in order to account for the presence of the nearby interfaces (e.g. multilayered substrates) and other material layers (e.g. core-shell structure of the probes), it is necessary to place a large number of auxiliary EM field sources across these interfaces. BoR approximation, by reducing the problem dimensionality, makes it possible to use a reasonable number of auxiliary sources and provides an accurate solution within reasonable time limits (approximately 3–5 hours per case on a present-day desktop PC).
Results and Discussion
Calculation of the absorbed, scattered, and fluorescently emitted power
The MAS approach allows efficient computation of energy transfer through surfaces of the bead or silica by numerically evaluating the integral of the Poynting vector flux across these surfaces:
| (8) |
where E is the electric field and H* is a complex conjugate of the magnetic field phasor. On the one hand, during the absorption stage, since there are no EM field sources inside the bead, the integration across the bead surface will yield the total power absorbed inside the bead. On the other hand, during the fluorescence stage, this integral yields the total power emitted by quantum dots.
Of more interest, however, is the part of the observable radiation, i.e. either the incident power scattered by the bead or the part of the power re-emitted by the fluorophores that reaches the microscope objective after passing through the silica substrate. For incident rays leaving the objective, the numerical aperture is (Figure 1) NA = nsolid · sin(θmax) = nwater · sin(ϕmax), where θmax and ϕmax are beam propagation angles in solid substrate and water, respectively. If NA = nsilica = 1.45, then, essentially, any incidence angle in silica, i.e. any value of θ from 0° to 90°, is achievable. According to the reciprocity theorem, and taking into the account that the entrance pupil of the objective is much greater than the area of interest (millimeter vs. micrometer scales respectively), it is also true that any ray entering the silica through water-silica interface ends up in the objective. Therefore, to find the total energy transformed into the image of the bead, we integrate the Poynting vector flux (Equation 8) across the water-silica interface within the finite area directly underneath the bead. The re-radiated field decays quickly with distance, and the area 10λ in radius is usually sufficient to capture the total flux through silica with a high accuracy. In general, however, for objectives having a smaller NA, one would have to limit the area of integration to be consistent with the numerical aperture of the microscope objective.
Two separate MAS simulations are required in order to account for the underlying two-stage physical processes of the described experiments. At the first stage, the bead, having effective medium properties, is excited by the incident evanescent electromagnetic field and the volumetric distribution of currents inside the bead is calculated. At the second stage, these volumetric currents are re-scaled according to Equation 2, in order to account for power deposited in quantum dots only, and used further as excitation to simulate bead fluorescence at a higher wavelength (see section 4 of Supporting Information for discussion of the issue of dealing with the phase distribution of bead volumetric currents).
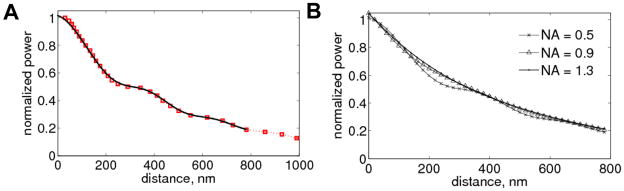
To verify the accuracy of our numerical simulations, we compared the forward scattering simulations on pure polystyrene beads to published experimental data.25 In these experiments, the scattered fields were observed far away above the bead, in the positive z-direction (Figure 1), after passing through a linear polarizer, using an objective with NA of 0.5.26 To simulate truncation of the scattered waves by the objective, we calculated far field distributions in polar coordinates and integrated optical power over angles captured by the 0.5-NA-objective. We found an excellent agreement with the existing data (Figure 3A). Our simulations also show that for high-NA objectives the power-distance relation is approaching exponential. This change in behavior is illustrated in the Figure 3B, where the far field pattern of the scattered field is integrated within the spherical angles corresponding to objectives with NA=0.5, 0.9 and 1.3. The accuracy of our MAS simulations was further confirmed by excellent matching of boundary conditions on bead and silica surfaces for both absorption and fluorescence stages (see section 5 of Supporting Information).
Figure 3.
Intensity of 658 nm light forward scattered from a 1.35 μm diameter polystyrene bead in water (nwater=1.333) versus distance from the glass substrate (nglass=1.515). TIR wave penetration depth δp = 500 nm (θ=62.0°). (A) Solid line indicates results of our simulations, while dotted line with square markers (red in online version) represents experimental data.25 (B) Simulations of optical power observed by objectives with varying NA. Power is normalized to the maximum intensity observed when the bead is effectively in contact with the surface.
Field and power distributions
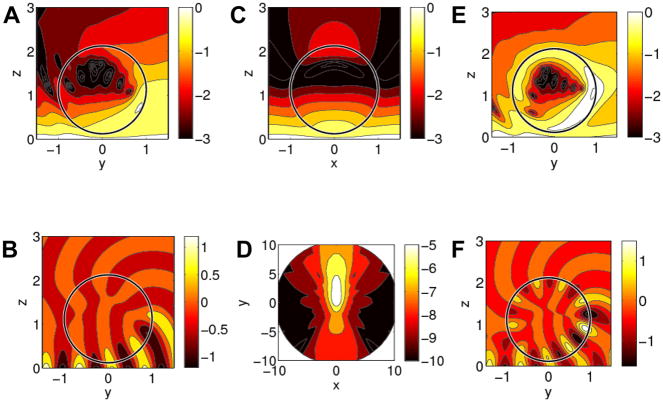
Figure 4A and C show two-dimensional electric field distributions in the planes containing the center of the bead for TE polarization (see section 6 of Supporting Information for TM polarization). Each distribution has the expected evanescent character with field amplitude around the sphere decaying away from the silica-water interface, although the presence of the bead noticeably perturbs the original field distribution, which is laterally uniform.
Figure 4.
Electric field, phase, and power distribution for a 1μm diameter bead containing 20% Fe3O4 and 5% (A–D) or 40% (E–F) CdSe QDs positioned 60 nm away from the silica-water interface, illuminated by a TE polarized 532 nm beam incident at 75°. All coordinates are in units of bead radius, the color scale in A, C, D, and E is logarithmic, and |Einc| =1 for the incident field. (A) Absolute E field distribution in the yz plane; (B) Ex phase distribution in the yz plane; (C) absolute field distribution in the xz plane; (D) distribution of power scattered through silica in the xy plane; (E) absolute E field distribution in the yz plane on a log scale; (F) Ex phase distribution in the yz plane.
There is a significant increase in optical field intensity in the bead itself due to waveguiding: since the refractive index of the bead is higher than that of water, the traveling wave can be formed in both y and z directions inside the bead, and as a result, the field intensity wraps around polymer-water interface along the bead circumference. Figure 4A, C indicate that most of the incident power will be deposited in the quantum dots closest to the silica-water interface, since electric fields are highest in the vicinity of the interface. The area with the least power absorption is in the middle of the bead. Qualitatively, the fields are similar for both TE and TM excitation polarizations, although the detectable fluorescence power in TE is greater by ~50% than that in TM polarization (compare Figure 4B and Figure S5B in Supporting Information). Figure 4D, showing the power flux across the water-silica interface, indicates a significant power drop with distance from the bead along the silica surface (a ten-fold decrease occurs about 2 μm away from the bead). This observation supports the assumption that, for a high NA objective, to find the total power transmitted by the light that forms the image of the bead, it is sufficient to integrate the Poynting vector flux over the appropriate finite area on the silica surface.
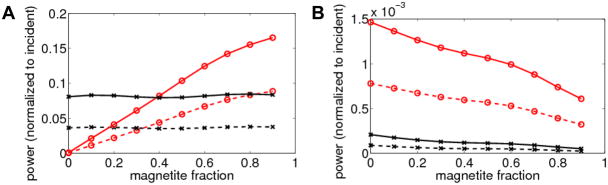
Power as a function of bead composition
The amount of power absorbed in a microsphere and emitted back is nonlinear with changes in the bead composition and distance from the surface, as shown in Figures 5A and 5B for TE polarized excitation (see section 6 of Supporting Information for TM polarization). Only at small loads of magnetite and QDs does the power absorbed change approximately linearly with the amount of the two nanoscopic components. Since practical considerations call for high magnetite content (to achieve high force sensitivity), but requires relatively modest amount of fluorescent material for adequate detection, the behavior of the beads containing 10–40% (volume) of magnetite and 5% (volume) QDs is considered as representative of the probes designed for magnetic tweezers. For a bead with 5% luminescent inclusions, we observed that, while the absorbed power indeed increased approximately linearly with the amount of magnetite, the scattered intensity remained approximately constant (Figure 5A). In spite of more power being absorbed by the bead when the concentration of magnetite increased, the amount of fluorescence has steadily decreased (Figure 5B), consistent with the expectation that most of the increase in absorption is due to absorption by magnetite only. The increased amount of magnetite also resulted in screening of the fluorescence from the quantum dots; however, the overall reduction was moderate – an increase in the amount of magnetite from 0% to 50% resulted in reduction of the fluorescence by only 25% from its initial value in the non-screened case. Data in Figure 5 indicates that these general trends are true for various bead-silica distances and incident TIR wave polarizations. The further the bead is from the silica surface the less amount of power is absorbed, scattered, and re-emitted.
Figure 5.
(A) Power deposited in the bead (o) and scattered through silica substrate (×) during the absorption stage (TE polarization, λ=532 nm). (B) Total fluorescent power leaving the bead (o) and detectable fluorescent power (×) (λ=597 nm). All power is plotted as a function of bead magnetite concentration (QD volume fraction is constant at 5%, angle of incidence θ=75°, bead diameter is 1.0 μm). Solid and dotted lines correspond to beads positioned 30 nm and 90 nm away from silica. The powers are normalized by the total power available from the incident beam in the silica substrate (for the circular cross-sectional area with a radius equal to the bead radius).
As seen from Figure 5, for a typical probe with a 0.1–0.3 volume fraction of magnetite less than 7% of the total incident power is absorbed and 3% of the absorbed power is re-emitted as fluorescence, with 10–15% of the total fluorescence eventually reaching the detector. Since then the total efficiency of conversion of the incident optical power to fluorescence for a micron-sized sphere is around 10−4, it is clear that the signal to noise ratio in bead tracking can be significantly improved by reducing undesired absorbance (by magnetite) or improvements in fluorescent properties. Significant input of power dissipated as heat can also potentially lead to undesirable local heating of the probe. Interestingly, scattered intensity changes little with magnetite composition and can direct a significant amount (~8 %) of the incident power to the detector.
We have also surveyed the changes in photonic response of the probes over the entire range of compositions by varying the volume fraction between 0 and 1 for both magnetic and luminescent components. The results of such a global calculation for a 1.0 μm diameter bead shown in Figure 6 demonstrate that, while the overall absorption and fluorescence scale as expected with the amount of optically active materials, the observable scattering and fluorescence experience relatively moderate changes (within a factor of 2) for a wide range of compositions.
Figure 6.
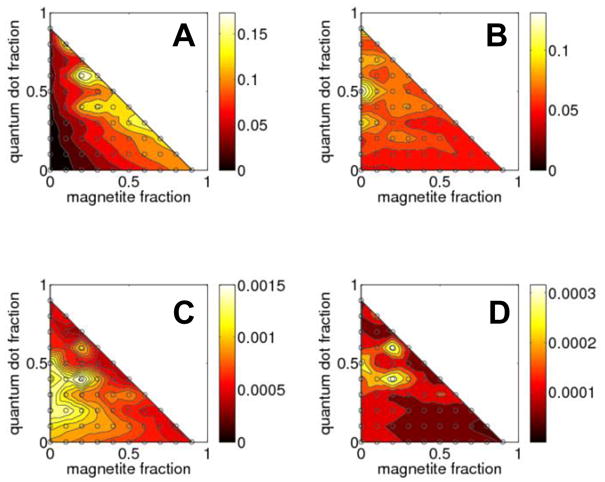
Power deposited in sphere (A) and scattered through silica (B) at the absorption stage; power emitted from the sphere (C) and transmitted through silica (D) at the fluorescence stage. All power is plotted as a function of magnetite and QD volume fractions. (TE polarization, θ=75°, bead diameter is 1.0 μm, the distance from silica is 60 nm, incident λ=532 nm, fluorescence λ=597 nm).
As illustrated by Figure 6B, the amount of power at the original wavelength of incident light scattered by the bead and traveling back to the objective is significant. The power emitted during the fluorescent stage, although several orders of magnitude lower than the elastically scattered power, can be effectively filtered out from the illuminating and scattered power and readily detected using commercial TIRF microscopes.
A substantial increase in the fluorescence is apparent in Figures 6C and 6D for a bead containing approximately 20% magnetite and 40% quantum dots compared to most other compositions. The field distribution for this case is shown in Figure 4E: although qualitatively it is similar to distributions shown in Figure 4A (i.e. highest field is observed inside the part of the bead that is closest the TIR interface), a certain resonance clearly takes place -- a relatively high field is present inside an entire bead near its surface. This resonance condition leads to efficient coupling of the optical power from the incident beam into waveguided modes of the bead (whispering gallery modes), which results in more power being absorbed and emitted by the bead. While this particular bead composition having high quantum dots content is hardly practical, such distribution of near fields concentrating close to the surface of the bead may be useful in layered structures. The beads consisting of a magnetic core surrounded by a layer of fluorescent material would effectively guide and store the incident waves solely in the fluorescent components, eliminating the unnecessary energy losses in the magnetic material.
Intensity of the probe image
Since the brightness of the fluorescing microsphere is used as a quantitative measure of its distance from the silica-water interface (i.e. molecular extension), an understanding of how various experimental factors influence this signal-distance dependence is important for bead tracking experiments. An exponential drop in a far-field image intensity, consistent with a standard two-media TIR model, is expected for a point-like probe; however, with finite size probes, due to a presence of multiple interfaces, the exact nature of changes in the decay length for both scattering and fluorescence is hard to predict without numerical solutions. As Figure 4 demonstrates, the electric field distribution in and around the bead is perturbed so significantly from the exponentially decaying field distribution in the case of planar interface that estimates based on a simple TIR model should not be viewed as reliable a priori. For a given probe of a fixed composition, the size of the probe could potentially change the characteristic decay length even for the same angle of incidence.
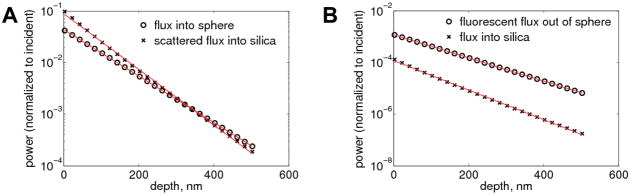
Figure 7A shows the results of the calculation of absorbed and observed scattered power for a 1 μm diameter bead as a function of the bead displacement (depth) from the point of contact with the surface. Both types of curves display an exponential dependence with the same decay constants: 96.7 nm for absorbance and 80.0 nm for scattering at the incident angle of 75°.
Figure 7.
Distance calibration curves of intensity versus bead position (symbols – simulations, lines – fits to exponentials): (A) optical power deposited in the bead and scattered through silica at the absorption stage; (B) total fluorescent power leaving the bead along with detectable power passing through silica; all power is shown as a function of the bead-surface distance. (20% Fe3O4 and 5% CdSe, θ=75°, bead diameter is 1.0 μm)
The characteristic penetration depth for unperturbed EM field intensity is equal to 96.5 nm. The total fluorescent output from the bead and part of the fluorescence detectable as the probe image (flux through silica-water interface) also scales exponentially with the separation from the surface of the sample (Figure 7B). These two curves have decay constants that mimic those for absorption and scattering. The effective decay length for observed fluorescence is noticeably smaller than the penetration depth of the evanescent field. These observations confirm the intuitive notion that the total intensity of a microsphere image (in either scattering or fluorescence modes) can serve as an unambiguous measure of the position of a microsphere with respect to the silica surface. One has to avoid, however, a direct use of the penetration depth of the evanescent field, calculated using simple models, in these intensity versus distance relations without experimental verification of such calibration curves.
A higher incident angle will lead to a steeper attenuation of the field in the transmission medium and we expect to see a decrease in the decay length for bead intensity versus distance from the surface as the incident angle increases. Calculations for a 1 μm diameter bead confirm this dependence (Table 1); the decay length for observed fluorescence dropped from 98.2 nm to 59.9 nm when the incident angle increased from 70° to 85°. Overall, the change in the decay length was consistent with predictions of the simple analytical TIR model; however, the observed effective penetration depth was only two thirds of the value for the unperturbed case. The overall intensity of the bead also decreased dramatically because the field was confined to a narrowing volume in the vicinity of the silica surface as the angle increased. A smaller excitation volume at high angles resulted in a lower image intensity compared to angles of incidence that were closer to the critical angle.
Table 1.
Effective decay lengths (nm) for different TIR incidence angles (λ=532 nm, TE-polarization, bead diameter is 1 μm).
| TIR angle of incidence θ | Unperturbed δp | Absorption stage | Fluorescence stage | ||
|---|---|---|---|---|---|
| Sphere absorption | Scatter into silica | Sphere fluorescence | Transmission into silica | ||
| 70° | 143.0 | 141.0 | 104.4 | 141.5 | 98.2 |
| 75° | 96.5 | 96.7 | 80.0 | 96.4 | 75.5 |
| 80° | 81.5 | 81.3 | 66.4 | 80.9 | 63.0 |
| 85° | 75.0 | 74.9 | 62.9 | 74.8 | 59.9 |
At a fixed angle of incidence, the change in the size of the probes could also lead to changes in the excitation volume and observed integrated intensity of the bead (Table 2). The total optical power absorbed and re-emitted by the beads in the size range we studied (diameter D=0.2–1.4 μm) scales approximately as D2.2. Observed total scattered or fluorescent power, on the other hand, scales approximately linearly with the bead size, with the intensity of fluorescence showing a saturation for D>0.8 μm. The results for beads of different sizes compiled in Table 2 illustrate the effect of the probe size on observed decay length and show that, while the overall intensity grows rapidly with the increase in the bead diameter, the decay length varies slowly. This approximate constancy of the decay length is important because it provides a natural way to deal with limited polydispersity in a typical sample of such beads. If the intensity of the probe images is normalized to their intensity at the point of contact, then these normalized images for all microspheres in a given sample should be representative of their position with a single decay length (within 1–2 %) as long as the polydispersity is limited to about ±10%.
Table 2.
Effective decay length and optical power as a function of the bead diameter (λ=532 nm, TE-polarization, θ=75, bead composition: 5% QDs and 20% magnetite). Fluorescent power is scaled up by a factor of 100 for ease of comparison.
| Diameter |
200 nm | 400 nm | 600 nm | 800 nm | 1000 nm | 1400 nm |
|---|---|---|---|---|---|---|
| Process | ||||||
| Decay length (nm) | ||||||
| Sphere absorption | 96.0 | 96.2 | 96.1 | 96.0 | 96.7 | 96.3 |
| Observed scattering | 84.2 | 84.0 | 80.8 | 78.5 | 80.0 | 76.1 |
| Sphere fluorescence | 96.5 | 96.5 | 96.2 | 96.1 | 96.4 | 94.9 |
| Transmitted fluorescence | 83.9 | 82.9 | 78.8 | 76.6 | 75.5 | 68.2 |
| Maximum optical power (probe at z=2 nm) | ||||||
| Sphere absorption | 0.011 | 0.052 | 0.117 | 0.203 | 0.317 | 0.699 |
| Observed scattering | 0.020 | 0.181 | 0.386 | 0.553 | 0.707 | 1.00 |
| Sphere fluorescence (×102) | 0.005 | 0.078 | 0.235 | 0.499 | 0.780 | 1.45 |
| Transmitted fluorescence (×102) | 0.003 | 0.034 | 0.068 | 0.102 | 0.103 | 0.108 |
Conclusions
Use of magnetic-fluorescent force probes illuminated in the near field regime in magnetic tweezers is a promising approach to measure molecular dimensions. The MAS can uncover fundamentals of the photonic response at the sub-wavelength level of detail in these bead tracking experiments using TIRFM. We used cylindrical symmetry of the system to reduce the dimensionality of the problem and enable efficient and accurate calculation with minimal computational resources (desktop PC). Our studies demonstrated that for high NA objectives the total intensity of the bead image, due to either backscattering or fluorescence transmitted into silica, showed an exponential decay with increased distance from the surface. Decay lengths of powers absorbed and reemitted from the bead are similar to penetration depth of evanescent waves at a given incidence angle. On the other hand, the decay length of observable power, i.e. scattered or fluorescent radiation transmitted through silica-water interface, is smaller (by as much as 20–30 %) than the penetration depth of the excitation evanescent wave. The discrepancy between penetration depth of the evanescent field and effective decay length observable with TIRFM setup, as well as variations in decay length due to changes in bead size, emphasize the need for calibration of every representative probe used in the experiment, if quantitative information on the bead position is required.
We believe that the new body-of-revolution formulation of the method of auxiliary sources described here can be used further in (i) exhaustive simulations of complex multilayered systems (both beads and surfaces) and (ii) can help guide efforts in design and fabrication of optimized probes or in improvements to experimental configurations for bead tracking and single molecule manipulation experiments. The BOR-MAS method should be useful in analysis of similar problems involving near field and sub-wavelength sized objects, for example, in simulations of light transmission through sub-wavelength holes in metal films or excitation of individual emitters in such wells.
Supplementary Material
Acknowledgments
This work was supported by NIH grant R21 HG004141.
Footnotes
A copy of the program can be obtained by contacting the authors
Supporting information available: Limitations of the effective medium (Maxwell-Garnett) model; refractive indices of optically active component materials – magnetite (Fe3O4) and quantum dots (CdSe); separation of optical power absorbed in magnetite and quantum dots; numerical simulation of fluorescence; verification of solution accuracy through boundary conditions; distributions of electric field and optical power for TM polarization of the incident beam. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Neuman KC, Lionnet T, Allemand JF. Ann Rev Mater Res. 2007;37:33. [Google Scholar]
- 2.Stroh C, Wang H, Bash R, Ashcroft B, Nelson J, Gruber H, Lohr D, Lindsay SM, Hinterdorfer P. Proc Natl Acad Sci U S A. 2004;101:12503. doi: 10.1073/pnas.0403538101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rief M, Gautel M, Oesterhelt F, Fernandez JM, Gaub HE. Science. 1997;276:1109. doi: 10.1126/science.276.5315.1109. [DOI] [PubMed] [Google Scholar]
- 4.Ros R, Eckel R, Bartels F, Sischka A, Baumgarth B, Wilking SD, Puhler A, Sewald N, Becker A, Anselmetti D. J Biotech. 2004;112:5. doi: 10.1016/j.jbiotec.2004.04.029. [DOI] [PubMed] [Google Scholar]
- 5.Marszalek PE, Li HB, Fernandez JM. Nature Biotech. 2001;19:258. doi: 10.1038/85712. [DOI] [PubMed] [Google Scholar]
- 6.Embrechts A, Schonherr H, Vancso GJ. J Phys Chem B. 2008;112:7359. doi: 10.1021/jp803260n. [DOI] [PubMed] [Google Scholar]
- 7.Manohar S, Mantz AR, Bancroft KE, Hui CY, Jagota A, Vezenov DV. Nano Lett. 2008;8:4365. doi: 10.1021/nl8022143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Albrecht C, Blank K, Lalic-Multhaler M, Hirler S, Mai T, Gilbert I, Schiffmann S, Bayer T, Clausen-Schaumann H, Gaub HE. Science. 2003;301:367. doi: 10.1126/science.1084713. [DOI] [PubMed] [Google Scholar]
- 9.Neuman KC, Nagy A. Nature Methods. 2008;5:491. doi: 10.1038/nmeth.1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Assi F, Jenks R, Yang J, Love C, Prentiss M. J Appl Phys. 2002;92:5584. [Google Scholar]
- 11.Noy A, editor. Handbook of Molecular Force Spectroscopy. Springer; 2008. [Google Scholar]
- 12.Singh-Zocchi M, Dixit S, Ivanov V, Zocchi G. Proc Natl Acad Sci U S A. 2003;100:7605. doi: 10.1073/pnas.1337215100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wu HJ, Shah S, Beckham R, Meissner KE, Bevan MA. Langmuir. 2008;24:13790. doi: 10.1021/la8025655. [DOI] [PubMed] [Google Scholar]
- 14.Everett WN, Beckham RE, Meissner K, Bevan MA. Langmuir. 2007;23:8950. doi: 10.1021/la701012j. [DOI] [PubMed] [Google Scholar]
- 15.Liu RC, Garcia-Manyes S, Sarkar A, Badilla CL, Fernandez JM. Biophys J. 2009;96:3810. doi: 10.1016/j.bpj.2009.01.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wazawa T, Ueda M. Microscopy Techniques. 2005;95:77. doi: 10.1007/b102211. [DOI] [PubMed] [Google Scholar]
- 17.Sapsford KE, Pons T, Medintz IL, Mattoussi H. Sensors. 2006;6:925. [Google Scholar]
- 18.Sihvola AH, Kong JA. ITGRS. 1988;26:420. [Google Scholar]
- 19.Zhou PH, Deng LJ, Wu BI, Kong JA. Prog Electromag Res. 2008;85:69. [Google Scholar]
- 20.Sihvola A. Subsurface Sen Tech Appl. 2000;1:393. [Google Scholar]
- 21.Wriedt T. Generalized multipole techniques for electromagnetic and light scattering. 1. Elsevier; Amsterdam; New York: 1999. [Google Scholar]
- 22.Shubitidze F, Anastassiu HT, Kaklamani DI. IEEE T Antenn Propag. 2004;52:302. [Google Scholar]
- 23.Shubitidze F, O’Neill K, Haider SA, Sun K, Paulsen KD. IEEE T Geosci Remote. 2002;40:928. [Google Scholar]
- 24.Shubitidze F, O’Neill K, Sun K, Shamatava I, Paulsen KD. Appl Comput Electrom. 2004;19:112. [Google Scholar]
- 25.Hertlein C, Riefler N, Eremina E, Wriedt T, Eremin Y, Helden L, Bechinger C. Langmuir. 2008;24:1. doi: 10.1021/la703322d. [DOI] [PubMed] [Google Scholar]
- 26.Riefler N, Eremina E, Hertlein C, Helden L, Eremin Y, Wriedt T, Bechinger C. J Quant Spectrosc Ra. 2007;106:464. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.