Polymer Partitioning and Ion Selectivity Suggest Asymmetrical Shape for the Membrane Pore Formed by Epsilon Toxin

Abstract

Using poly-(ethylene glycol)s of different molecular weights, we probe the channels formed in planar lipid bilayers by epsilon toxin secreted by the anaerobic bacterium Clostridium perfringens. We find that the pore is highly asymmetric. The cutoff size of polymers entering the pore through its opening from the cis side, the side of toxin addition, is ∼500 Da, whereas the cutoff size for the polymers entering from the trans side is ∼2300 Da. Comparing these characteristic molecular weights with those reported earlier for OmpF porin and the α-Hemolysin channel, we estimate the radii of cis and trans openings as 0.4 nm and 1.0 nm, respectively. The simplest geometry corresponding to these findings is that of a truncated cone. The asymmetry of the pore is also confirmed by measurements of the reversal potential at oppositely directed salt gradients. The moderate anionic selectivity of the channel is salted-out more efficiently when the salt concentration is higher at the trans side of the pore.

Introduction

Epsilon toxin (ETX) (for review, see (1–3)) is the major virulence factor secreted by Gram-positive, spore-forming anaerobic bacteria Clostridium perfringens types B and D (4). ETX is responsible for a rapidly fatal enterotoxaemia in herbivores when their gastrointestinal tracts are colonized by this bacterium leading to in situ toxin production (1,5,6). ETX is secreted in a poorly active form called prototoxin (7) and is activated into a highly potent toxin by proteolytic removal of 11 or 13 N-terminal and 29 C-terminal amino acid residues (8). The β-sheet-rich, ∼31 kDa ETX shows 20–27% sequence homology with the Mtx2 and Mtx3 toxins of Bacillus sphaericus and with c53 protein of Bacillus thuringiensis (3). The ETX structure (9) has a similarity to the large lobe of aerolysin, a 100-fold less potent (8) pore-forming protein produced by the Gram-negative pathogen Aeromonas hydrophila. ETX consists of three structural domains: i), N-terminal domain I, which may be involved in receptor binding; ii), domain II, which is thought to contain a transmembrane stem involved in pore formation and probably also participates in oligomer formation; iii), C-terminal domain III, which likely helps to mediate ETX insertion into membranes.

ETX activation triggers its oligomerization in the synaptosomal membrane within the detergent-insoluble microdomains (lipid rafts) of MDCK cells (10,11). ETX was reported to form aerolysinlike (9) β-barrel heptameric (10–12) transmembrane pores that increase cell permeability to small molecules and ions (1,13–15). In vitro, only a few cell lines such as MDCK, mouse kidney cells, and human renal leiomyoblastoma G-402 cells were found to retain susceptibility to ETX (12,14) due to the presence of specific ETX-binding receptors. No receptors are needed for ETX incorporation into artificial lipid bilayers (16,17) or liposomes (18). In bilayer lipid membranes, ETX was reported to form wide, slightly anion-selective general diffusion pores with a single-channel conductance in the range of 440–640 pS in 1 M KCl (16,17). Based on the structural and functional similarities with oligomeric aerolysin of Aeromonas hydrophila and α-Hemolysin of Staphylococcus aureus, ETX was supposed to be permeable to solutes up to a molecular mass of at least 1 kDa (16). Petit et al. (16) estimated the diameter of the transmembrane ETX channel to be ∼2 nm based on experiments on competitive entry of propidium iodide and osmotic uncharged compounds (i.e., glucose, sucrose, poly(ethylene) glycol (PEG) 1000, PEG 3350, and PEG 6000) with different hydrodynamic radii into MDCK cells. However, the authors pointed out that the data were not highly reliable because of PEG 1000 cytotoxicity (16).

Activated ETX is one of the most potent bacterial toxins after botulinum and tetanus neurotoxins (2,19); an estimated lethal human dose is 7 μg via the intravenous route (6). Due to ETX's high potency and lethality, it has been classified as a CDC category B agent. Driven by the idea of designing a small-molecule blocker of the ETX pore similarly to the cyclodextrin-based potent inhibitors discovered earlier for the anthrax PA₆₃ (20) and α-Hemolysin (21) pores, we start with the study of the pore's physical properties.

First, we use the polymer partitioning approach under conditions of PEG asymmetrical addition to access the pore's functional shape and size (22–26). This approach explores the ability of polymers to reduce channel conductance in a molecular-weight-dependent way (27–38), while reducing solution conductivity based only on their monomer concentration (39). We find that PEGs' partitioning is highly asymmetric. The trans opening of the ETX pore allows the penetration of much larger polymer molecules than its cis opening. The partitioning data are suggestive of an asymmetrical, e.g., conical shape of the pore with the tentative radii of the openings of 0.4 nm and 1.0 nm on the cis and trans sides, respectively.

Second, we explore the ionic selectivity of the pore by measuring reversal potentials in the oppositely directed gradients of potassium chloride aqueous solutions. As it was shown previously (40), such measurements allow one to judge upon the charge distribution along the channel axis. Interestingly, we find that the asymmetry of the reversal potential in the salt gradient is opposite to what is reported for the conical nanopores with a uniformly spread surface charge (41,42). In the case of the ETX pore, the selectivity is salted-out more easily from the wide trans opening of the channel. This suggests that the residues carrying the positive charge responsible for the anionic selectivity of the ETX pore (16,17) are not localized at its cis opening but are shifted toward the trans side.

Material and Methods

Reagents

ETX was obtained from Dr. Bruce A. McClane, University of Pittsburgh and activated by incubation with trypsin as described (18) with some modifications. An aliquot of the ɛ-prototoxin was treated with trypsin (8 μg trypsin/1 μg toxin) and incubated at room temperature for 30 min. Next, an equal volume of a trypsin inhibitor bead suspension was added, and the mixture was incubated at room temperature for additional 30 min. The mixture then was centrifuged for 10 min at 13,000 RPM and the pellet/beads were discarded. The activated ETX was checked by protein gel electrophoresis, then aliquoted and stored at −80°C for future experiments.

The following chemical reagents were used: KCl, KOH, and HCl; MES; “purum” hexadecane (Fluka, Buchs, Switzerland); diphytanoyl phosphatidylcholine (Avanti Polar Lipids, Alabaster, AL); pentane (Burdick and Jackson, Muskegon, MI), and agarose (Bethesda Research Laboratory, Gaithersburg, MD). The poly(ethylene glycol)s (PEGs) of different molecular weights: diethylene glycol 106.12, PEG 200, PEG 300, PEG 400, PEG 600, PEG 1000, PEG 1500, PEG 2000, PEG 3400, PEG 4600, PEG 8000, PEG 20,000, and PEG 35,000 were purchased from Sigma (St. Louis, MO) and used in a 15% w/w concentration. The polymers were added to a 1 M KCl water solution. Doubly distilled and deionized water was used to prepare the solutions. All solutions were purified by filtration through a 0.45-μm filter.

Channel reconstitution

To form solvent-free planar lipid bilayers with the lipid monolayer opposition technique (43), we used a 5 mg/mL stock solution of diphytanoyl phosphatidylcholine in pentane. Bilayers were formed on a 60-μm-diameter aperture in a 15-μm-thick Teflon film that separated two compartments as described elsewhere (44). The 1 M aqueous solutions of KCl were buffered by 5 mM MES at pH 6. All measurements were performed on single ETX channels at room temperature (23 ± 0.5)°C. Channels were formed by adding 0.2–0.5 μL of ETX 0.15 mg/mL stock solution to the 1.5 mL aqueous phase in the cis half of the chamber while stirring. Under this protocol, ETX insertion was always directional, as judged by channel conductance asymmetry in the applied transmembrane voltage. For asymmetrical experiments, PEGs of varied molecular weights were added from one side of the membrane, while the impermeant PEG 8000 was on the other side. The electrical potential difference across the lipid bilayer was applied with a pair of Ag-AgCl electrodes in 2 M KCl, 1.5% agarose bridges. The applied potential is defined as positive if it is higher at the side of protein addition.

Conductance and selectivity measurements were performed using an Axopatch 200B amplifier (Axon Instruments, Foster City, CA) in the voltage-clamp mode. Signals were filtered by a low-pass 8-pole Butterworth filter (Model 9002; Frequency Devices, Haverhill, MA) at 15 kHz, and directly saved into the computer memory with a sampling frequency of 50 kHz. The reversal potentials were obtained as described (40,45).

Results and Discussion

A typical ionic current record illustrating spontaneous events of channel formation by ETX is given in Fig. 1 A. At 100 mV of applied transmembrane voltage, the formation of the first channel is seen as a current jump of ∼48 pA, followed by the second channel of approximately equal conductance. The conductance value, 480 pS, is in good agreement with earlier reported ETX conductance (16). The variation of conductance from channel to channel was typical for that of some of β-barrel channels (46). At very high voltages (exceeding 150 mV), we also observed voltage-dependent closures (data not shown) reported for other β-barrel channels (47,48) such as anthrax's PA₆₃ channel (49), OmpF (50), α-Hemolysin (51), and VDAC (52). The current through the open channels is noisy, displaying switching between well-resolved conductance substates. The characteristic time of this switching is in the range of several seconds as is illustrated by the inset in Fig. 1 A and the power spectral density of current fluctuations in Fig. 1 B. The slopes of the parts of the spectra below 3 Hz are close to −2, suggesting that they represent the tails of low-frequency Lorentzians. We never observed this kind of noise in the absence of the ETX channel's main conductance while the occurrence of these substates significantly varied from channel to channel.

Figure 1.

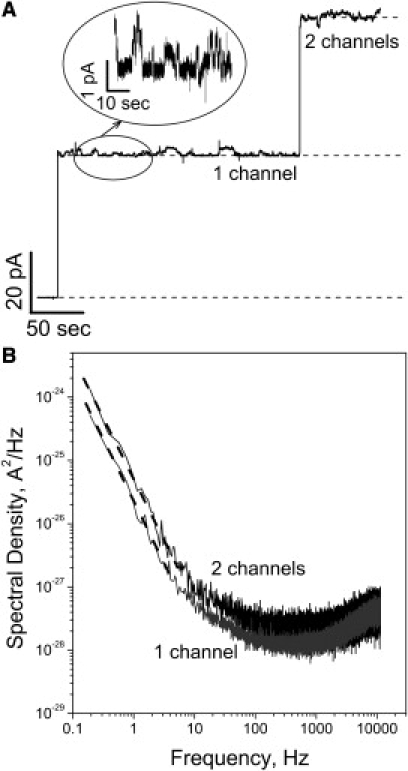
(A) Typical ion current recordings obtained after addition of ∼30 ng of the activated ETX to 1.5 mL of the aqueous phase in the cis compartment of the bilayer chamber. Applied voltage was 100 mV; aqueous solution of 1 M KCl was buffered at pH 6 with 5 mM MES. Two consecutive insertions of independent single channels are seen. The time resolution was 50 ms. (Inset) Characteristic low-frequency switching between several conductance substates of the open ETX channel at 10-ms time resolution. (B) Power spectral density of the current noise of one (shaded spectrum) and two (solid spectrum) ETX channels shown in panel A. Power spectra at low frequencies 0.1–3 Hz are approximated by a linear fit (dashed lines) with a slope of ∼−1.8.

Addition of PEG to the membrane-bathing aqueous solution of KCl changed channel conductance in a polymer-weight-dependent manner. The records of ionic current taken at 0.1-ms resolution are shown in Fig. 2 for PEGs of different molecular weights in comparison with the record in polymer-free solution. The upper set (Fig. 2 A) shows the effect of symmetrical polymer addition when PEGs are added to both sides of the membrane in equal concentration. It is seen that small polymers, such as PEG 300, decrease the average conductance of the channel without any significant fluctuations at this time resolution. Larger polymers, PEG 1500 and PEG 2000, decrease the average conductance and produce vigorous current fluctuations. Still larger PEG 8000 does not produce significant fluctuations and slightly increases the average current. The current track in the absence of PEG (Fig. 2 A, left) lacks the characteristic switching between conductance substates seen in the inset of Fig. 1 for the reason that here we present very short, 20-ms fragments of the recordings.

Figure 2.

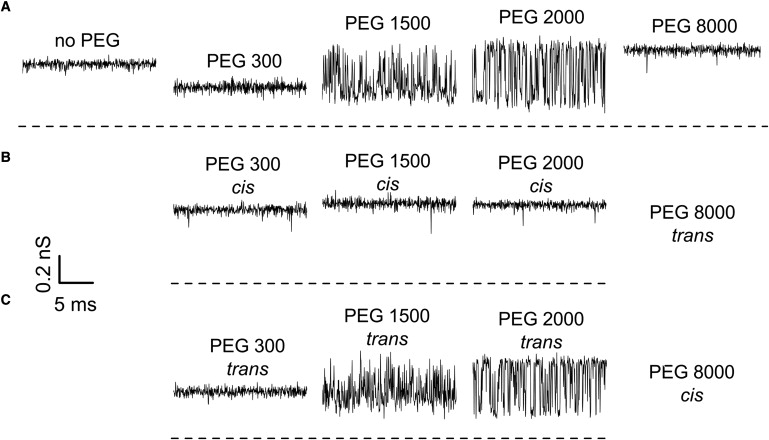
(A) The effect of symmetrical PEG addition (15% w/w) on the conductance of a single ETX channel. It is seen that PEGs not only change the average conductance but, depending on molecular weight, induce significant fluctuations. Experiments performed under asymmetrical PEG additions (B and C) demonstrate that these fluctuations are mostly caused by permeant PEGs added to the trans side of the membrane (C). Time resolution was 0.1 ms, transmembrane voltage −100 mV.

Fig. 2 B shows the consequences of asymmetrical polymer addition when PEGs of different molecular weights are added to the cis side of the membrane, while the trans side contains PEG 8000 in the same 15% concentration to (partially) offset the osmotic gradient across the membrane. It is seen that the PEG effect in this case is quite different from the effect of symmetrical addition shown in Fig. 2 A. The conductance of the channel is significantly less sensitive to polymer addition compared with the symmetrical case. Finally, Fig. 2 C demonstrates that the asymmetrical polymer addition, wherein PEGs of varying molecular weights are added from the trans side and PEG 8000 is at the cis side, gives results similar to those obtained for the symmetrical conditions of Fig. 2 A. The increase in channel conductance in the presence of excluded polymers (e.g., rightmost trace in Fig. 2 A) above that of the control in the absence of polymer (leftmost trace) is partially related to the PEG-induced increase in salt activity (see discussion in (29)). A similar effect was reported for other channels (23,31,37). However, for reasons that are not clear at the time of this writing, the increase in the ETX channel conductance is ∼10% higher than that expected based on salt activity increase (29).

The effect of polymer is voltage-dependent (see also (27,37,53,54)). Fig. 3 illustrates this point by showing the average conductance of the channel at symmetric application of polymers as a function of transmembrane voltage in comparison with the channel conductance in polymer-free solution (open circles). It is seen that while the relative effect of small and large PEGs, i.e., polymer-induced decrease or increase in conductance, is not significantly changed by the applied voltage, the action of PEG of intermediate sizes can reverse in sign. Indeed, both PEG 1500 and PEG 2000 decrease the averaged channel conductance at −100 mV but increase it at +100 mV. As this happens under symmetrical conditions in which both the concentration and molecular weight of applied polymers are the same on both sides of the membrane, the observed asymmetry must come from the asymmetric structure of the ETX channel either via field-sign-dependent interactions of polymers with the channel or voltage dependence of the channel structure itself.

Figure 3.

Average conductance of the channel in the presence of PEG shows dependence on the applied voltage that is different from the dependence in polymer-free solution (open circles). The sensitivity to voltage can be opposite for different PEG molecular weights, as in the case for PEG 1500 and PEG 8000. PEGs were added symmetrically, to both sides of the membrane at 15% concentration.

To escape these additional difficulties in the interpretation of polymer partitioning experiments, we have chosen to apply quantitative analysis only to equilibrium data. We interpolated data points similar to those illustrated in Fig. 3 to zero applied voltage and plotted the results as functions of polymer molecular weight. Fig. 4 shows three sets of measurements. Open circles give the average channel conductance for symmetrical polymer addition (see Fig. 2 A), triangles stand for the results obtained in the asymmetrical set of experiments with PEGs of varied molecular weight at the trans side of the membrane (Fig. 2 C), and open boxes for the opposite asymmetrical addition (Fig. 2 B). It is seen that all three sets are different, with the symmetrical PEG application producing the most profound change in the average channel conductance.

Figure 4.

The relative change in ETX channel conductance as a function of PEG molecular weight at V = 0 mV. (Solid triangles and open squares) The trans- and cis-side application of polymers of varying molecular weights, respectively. The impermeant PEG 8000 was on the opposite side of the membrane. (Open circles) Symmetrical addition of PEG. (Dotted line) Starting at 0.6, this corresponds to the ratio of bulk solution conductivities with and without polymers. Conductance data at 0 mV voltages were directly obtained from G-V curves shown in Fig. 3 or similar by interpolation of the data points to zero voltages. (Error bars) Root-mean-square deviations of estimates obtained from three-to-seven independent measurements.

While the qualitative description of polymer partitioning leading to the conductance change shown in Fig. 4 is relatively simple, its quantitative description is still elusive. Qualitatively speaking, in the case of symmetrical (open circles) and trans (solid triangles) PEG application, a characteristic molecular weight of ∼2000 Da separates the regime of penetration of smaller PEGs from the regime of exclusion of larger PEGs. Small polymers enter the channel and reduce its ionic conductance. Large polymers stay away from the channel pore and increase its conductance above that in PEG-free solution because the presence of PEG increases KCl activity (29). In the case of cis addition (open boxes), the regime of exclusion shifts toward smaller polymers, suggesting that the size of the channel opening on this side is significantly smaller than on trans side.

Quantitatively, polymer partitioning into the ETX channel, as well as into a number of other channels of different origins, cannot be satisfactorily described by the available polymer theories. This holds true even for the case of equilibrium partitioning, an example of which is given in Fig. 4 by the open circles corresponding to a symmetrical polymer solution composition and zero applied voltage. For this reason, here we use an empirical approach suggested in Bezrukov et al. (31) and Rostovtseva et al. (34). We characterize partitioning using two main parameters—the characteristic polymer molecular weight w₀, which defines the position of the penetration-to-exclusion transition, and parameter α, which characterizes the steepness of this transition,

$$g\left(w\right)/g_{noPEG}=g{\left(w\right)}_{\text{max}}/g_{noPEG}-\chi \text{exp}\left(-{\left(w/w_0\right)}^{\alpha }\right),$$ (1)

where g(w)/g_noPEG is the ratio of the channel conductance in the presence and in the absence of PEG with molecular weight w and χ is the parameter characterizing the relative amplitude of the change in the channel conductance between the regimes of complete exclusion and full penetration,

$$\chi =\left(g{\left(w\right)}_{\max }-g{\left(w\right)}_{\min }\right)/g_{noPEG}.$$

Fitting Eq. 1 to both equilibrium and nonequilibrium data in Fig. 4, we obtained the following parameters: for symmetrical PEG application w₀ = 2300 Da, α = 1.4; for PEG of a varying molecular weight from the trans side w₀ = 2300 Da, α = 2.1; and for PEG of a varying molecular weight from the cis side w₀ = 480 Da, α = 1.3. Note that the steepness parameter α depends on the conditions of polymer addition. Though a comprehensive theory of the partitioning does not yet exist, it is clear that the steepness reflects interactions between the polymer and pore; therefore, the difference between values of α could be related to the fact that at different modes of addition, polymers probe different regions of the channel.

As the next step, we compare the obtained w₀ values with those found in the OmpF and α-Hemolysin study (see Figs. 8 and 9 in (34)) where the characteristic molecular weights were related to the radii of these channels found by x-ray crystallography. To estimate the radii, we use the 3/5 power scaling between the polymer size and its molecular weight (55). For the effective radius of the channel, we have

$$r_{ch}=r_{OmpF}{\left(w_0/w_{OmpF}\right)}^{\frac{3}{5}},$$ (2)

where r_OmpF is the effective radius of the OmpF channel (0.7 nm) and w_OmpF is the characteristic PEG molecular weight (1360 Da) found for that channel. Applying Eq. 2 to the w₀ value obtained in the equilibrium experiment, we find the following estimate for the effective radius of the ETX channel: r_{ch eq} = 0.96 nm. For the data at asymmetrical addition, we arrive at r_{ch cis} = 0.37 nm and r_{ch trans} = 0.96 nm. Multiple obvious complications in the interpretation of partitioning data at asymmetric polymer addition were recently discussed in a study with the syringomycin E channel (26). The asymmetry in polymer molecular weights at the two openings of the channel leads to nonequilibrium conditions even if the applied voltage is zero, creating directional flux and complex distribution of polymers along the channel axis. Nevertheless, we anticipate that the empirical approach based on Eqs. 1 and 2 captures some of the important features of the channel structure.

We have also studied the dynamics of polymer exchange between the channel pore and the membrane-bathing solution by measuring the power spectral density of PEG-induced conductance fluctuations. Fig. 5 A gives results for the symmetrical application of PEG 2000 at three different transmembrane voltages. It is seen that the power spectral density, similarly to the polymer effect on channel conductance illustrated in Fig. 3, depends not only on the applied potential but also on its sign.

Figure 5.

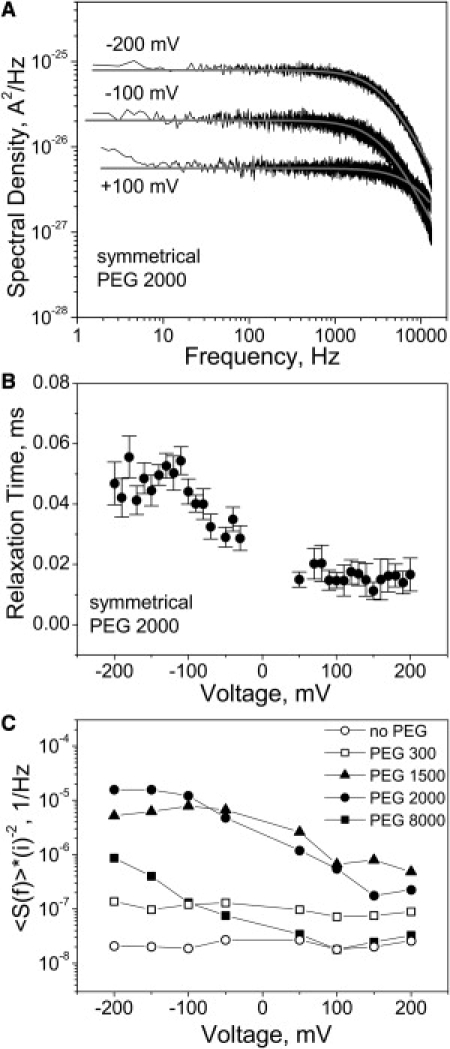
(A) Power spectral densities of the current noise of a single channel with the symmetrical addition of PEG 2000 obtained at 100 mV, −100 mV, and −200 mV of applied transmembrane voltage. Shaded curves represent single Lorentzian fits to the data. Note that these spectra do not contain the characteristic low-frequency part (<10 Hz) shown in Fig. 1B for the reason that here we analyzed rather short (free from the low-frequency switching) fragments (∼1 s). (B) Relaxation time of PEG 2000 induced fluctuations as a function of voltage. Error bars show root-mean-square deviations of estimates obtained from three different fragments of the current record. (C) Normalized low-frequency spectral density 〈S(f)〉/〈i〉² as a function of voltage with S(f) averaged over a 80–200 Hz interval. We chose this frequency interval because, at the lower frequencies, especially at low voltages and for PEGs showing weaker interactions, spectral analyses did not allow us to obtain spectral densities of the excess PEG-induced noise reliably enough.

The spectra in Fig. 5 A could be approximated by single Lorentzians of the form

$$S\left(f\right)=S\left(0\right)/\left(1+{\left(f/f_c\right)}^2\right),$$

where f is frequency and f_c is the characteristic corner frequency. The best fits are shown as smooth shaded lines through the data. The characteristic corner frequency allows one to obtain the relaxation time of polymer exchange according to τ = 1/2πf_c. This time for PEG 2000 as a function of transmembrane voltage is shown in Fig. 5 B. It changes from ∼50 μs at −200 mV to ∼15 μs at +200 mV. At equilibrium conditions (zero applied voltage and identical polymer solutions on both sides of the membrane), the relaxation time for this polymer is ∼20 μs. This relaxation time is orders-of-magnitude larger than the time expected for freely diffusing particles in the channel with a length of several nanometers (56) suggesting strong attractive interactions between the polymer and the channel pore.

The power spectral density of current noise shown in Fig. 5 A is supposed to be voltage-dependent even if the fluctuations in channel conductance that cause this noise are voltage-independent. In the system under study, the conductance fluctuations depend on the applied voltage: the spectral density is sign-sensitive and its corner frequency changes with voltage. Thus, the dynamics of polymers in the channel that produce the conductance reduction are voltage-dependent. This is made clear by Fig. 5 C showing the normalized low-frequency spectral density, 〈S(f)〉/〈i〉². For a linear system with voltage-independent conductance fluctuations, this quantity should be constant in voltage. The data for PEG 1500, PEG 2000, and PEG 8000 plotted in Fig. 5 C display an order-of-magnitude change of the normalized spectral densities as functions of voltage.

The dependence of PEG-induced fluctuations in the form of the spectral density 〈S(f)〉 on the PEG molecular weight is given in Fig. 6 for all polymer weights used in the study. It shows a pronounced maximum for PEG 2000 (see also (57)). Qualitative interpretation of this result is rather straightforward. Larger polymers produce larger effects on channel conductance with each visit to the channel pore and their exchange between the channel and the bulk is slower than for smaller polymers. Therefore, the low-frequency conductance noise increases with polymer size. However, for polymers that are too large to partition into the pore, the probability of entering the pore is reduced, thus reducing not only their effect on the average channel conductance but also on its fluctuations.

Figure 6.

Averaged low-frequency power spectral density 〈S(f)〉 of channel current noise as a function of PEG molecular weight obtained under symmetrical and asymmetrical PEG additions at −100 mV. (Solid triangles and open squares) The trans- and cis-side application of polymers of varying molecular weight, respectively. The impermeant PEG 8000 was on the opposite side of the membrane. (Open circles) Symmetrical PEG addition. Note that spectral density values over the whole range of studied polymer weights are practically the same for symmetrical and trans-side addition of polymers of varying molecular weights. Error bars show root-mean-square deviations of estimates obtained from three-to-seven independent measurements.

Finally, we probed channel ionic selectivity using the opposite salt concentration gradients. As was shown previously (40), these measurements provide information about charge distribution in the channel. Fig. 7 shows the reversal potential of the ETX channel obtained in two sets of experiments. In one of them, represented by solid circles, the concentration of the cis side membrane-bathing solution was kept constant and equal to 0.1 M KCl, while the concentration on the trans side was varied from 0.01 M KCl to 3 M KCl. In the other, represented by open boxes, the protocol was inversed: the trans side was the side with the constant salt concentration. It is seen that the reversal potential is sensitive to the direction of the salt gradient. The higher concentration on the trans side salts-out channel selectivity more efficiently.

Figure 7.

Channel reversal potential as a function of the concentration ratio for two series of measurements with oppositely directed gradients. (Solid circles) E_rev obtained in the series where c_cis was kept constant at 0.1 M KCl and c_trans was varied from 0.01 M KCl to 3 M KCl. (Open squares) −E_rev for the reversed gradient where c_trans = 0.1 M KCl and c_cis was changed from 0.01 M KCl to 3 M KCl. The channel is asymmetric: the absolute value of the reversal potential is smaller when the more concentrated solution is on the trans side of the membrane. (Open triangles) Difference. Error bars show root-mean-square deviations of estimates obtained from three-to-five independent measurements.

This observation suggests structural asymmetry and can be explained by the asymmetry of the ETX channel found in polymer-partitioning experiments (Fig. 4). Indeed, if the charged residues that are responsible for the channel's ionic selectivity are located in the depth of the pore, close to the channel center for example, and the trans opening of the pore is wider, the residues are more accessible for salt screening from the trans side. The salt concentration near the charged residues is expected to be higher if it is higher at the trans side than at the inversed concentration arrangement. Interestingly, the effect of the gradient inversion found here with the ETX channel is opposite of that reported for synthetic conical pores, where the more efficient salting-out happens when the higher salt concentration is applied at the narrow opening of the pore (41,42). This happens because in synthetic pores the uniformly spread surface charge creates an effective selectivity filter at the narrowest part of the pore. Such a selectivity filter is screened more effectively when directly exposed to the higher salt concentration.

Although we suggest a conical shape for the ETX pore, our findings are also compatible with more complex geometries wherein, for example, one of the openings of a cylindrical channel is partially blocked by protruding peptide loops. More fanciful geometries of the pore (e.g., irregular funnel-, bottle-, or mushroom-like) are also realistic. The proposed geometry of a circular truncated cone is just the simplest asymmetric shape that can be described by three parameters only: the length of the pore and the two radii of its openings.

To conclude, our PEG partitioning and ion selectivity studies reveal a pronounced asymmetry of the Clostridium perfringens ETX channel with the estimated cis opening of 0.4-nm radius being much narrower than the trans opening of 1-nm radius, wherein the positively charged residues, producing a moderate anionic selectivity, are hidden inside the pore. These structural features are important in our search for the prospective small-molecule compounds that would block the ETX pore similarly to anthrax's PA₆₃ pore inhibition by positively charged cyclodextrins derivatives (20). Using an analogy with other bacterial toxins, we assume that ETX incorporation into the lipid bilayers mimics its incorporation occurring in vivo. According to our observations, ETX added to the cis side of the membrane inserts strictly unidirectionally, so that the narrow cis-opening of the channel would correspond to the extracellular side of the membrane. However, it is worth noting here that the role of the specific membrane receptors for ETX binding in most of the situations in vivo is not clear in this respect. Additional studies may need to be designed to reveal the pore orientation in the membranes of target cells.