Uncovering Specific Electrostatic Interactions in the Denatured States of Proteins

Abstract

The stability and folding of proteins are modulated by energetically significant interactions in the denatured state that is in equilibrium with the native state. These interactions remain largely invisible to current experimental techniques, however, due to the sparse population and conformational heterogeneity of the denatured-state ensemble under folding conditions. Molecular dynamics simulations using physics-based force fields can in principle offer atomistic details of the denatured state. However, practical applications are plagued with the lack of rigorous means to validate microscopic information and deficiencies in force fields and solvent models. This study presents a method based on coupled titration and molecular dynamics sampling of the denatured state starting from the extended sequence under native conditions. The resulting denatured-state pK_as allow for the prediction of experimental observables such as pH- and mutation-induced stability changes. I show the capability and use of the method by investigating the electrostatic interactions in the denatured states of wild-type and K12M mutant of NTL9 protein. This study shows that the major errors in electrostatics can be identified by validating the titration properties of the fragment peptides derived from the sequence of the intact protein. Consistent with experimental evidence, our simulations show a significantly depressed pK_a for Asp⁸ in the denatured state of wild-type, which is due to a nonnative interaction between Asp⁸ and Lys¹². Interestingly, the simulation also shows a nonnative interaction between Asp⁸ and Glu⁴⁸ in the denatured state of the mutant. I believe the presented method is general and can be applied to extract and validate microscopic electrostatics of the entire folding energy landscape.

Introduction

I am interested in the denatured state that is in equilibrium with the native state under physiological conditions, D^phys (1). D^phys provides the thermodynamic reference for the stability of a protein, e.g., the free energy of unfolding, ΔG_unf. Thus, molecular interactions in D_phys may perturb the denatured-state energy thereby modulating thermodynamic stability and kinetic barrier for folding. Direct structural characterization of D^phys is challenging, because it is sparsely populated for stable proteins under folding conditions. Most experimental data published so far have been collected under denaturing conditions or by using mutants that have destabilized native states. Nonetheless, increasing lines of evidence suggest that D^phys ranges from being expanded to compact and it may contain native or nonnative secondary structures, hydrophobic and electrostatic interactions, as well as long-range structural orders. See recent reviews (2,3).

One approach that can provide clues about the presence of energetically significant electrostatic interactions in the denatured state is to compare measured pH-dependent unfolding free energies with calculations based on the Wyman-Tanford linkage equation (4,5).

$$\partial \Delta G_{\text{unf}}/\partial \text{pH}=2.303RT\left(Q^D-Q^N\right).$$ (1)

Here Q^N and Q^D are the total net charges of the native and denatured states, respectively. While Q^N can be experimentally determined, Q^D can be calculated using the pK_as of model compounds, if D^phys is random-coil like, e.g., charged groups in the denatured state are fully exposed to solvent and not subject to net electrostatic effects. Consequently, a discrepancy between the measured and calculated stability data offers evidence for energetically significant electrostatic interactions in D^phys. Applications of this approach have shown significant deviations between measured and calculated pH-dependent stability profiles for several proteins (6–12).

In the attempt to explain the aforementioned deviations, several theoretical models have been proposed for representing denatured states. The most notable examples are perhaps the native-like model in which the protein adopts expanded states (13), and the Gaussian-chain model that treats charge-charge interactions as Gaussian distributions (14). Although these models contradict each other, both were able to reproduce the experimental pH-dependent stability data for several proteins, which is a clear indication of the problem of underdetermination. Most recently, calculations of pH-dependent stabilities for staphylococcal nuclease using theoretical models that differ in the amount of disorder in the denatured state showed significant differences (15). Although the native-like and Gaussian-chain models have offered valuable insights into features of denatured states, it is clear that more sophisticated methods are needed to capture sequence-dependent residual structures such as native and nonnative interactions (2). More recently, methods have been developed that use distance information derived by nuclear Overhauser effect or paramagnetic relaxation enhancement as restraints in molecular dynamics/Monte-Carlo simulations or as criteria for assigning weights to a pregenerated pool of conformations (16,17). However, these empirical approaches are also subject to under- or overdetermination in addition to the large uncertainty of the distances derived by the nuclear Overhauser effect and paramagnetic relaxation enhancement (17).

Given converged conformational sampling and accurate physics-based force fields, atomistic information of denatured states can be obtained from molecular dynamics simulations without resorting to specific structural models. The most direct approach to study denatured states is to establish the thermodynamic equilibrium between folded and unfolded states through repeated folding events in ab initio all-atom folding simulations. However, with the current CPU speed and simulation methods, folding studies are limited to peptides and ultra fast folding miniproteins (18,19). So far multiple folding events have only been observed for small peptides (20). Thus, alternative strategies have to be deployed. One such strategy is to carry out high-temperature simulations (21). However, the drawback is that the high-temperature conformations may not represent those populated at low temperatures due to temperature-dependent hydrophobic and intramolecular hydrogen bonding effects (22,23). Another alternative is to sample the denatured-state ensemble at room temperature by conducting simulations initiated from the extended sequence. The feasibility of this approach is supported by the growing amount of NMR data that indicate that the conformational space of the denatured state is restricted (16,24,25). Ab initio folding simulations of peptides and miniproteins have also shown that only a fraction of possible denatured conformations are populated under physiological conditions (19,20). Aided by distributed computing and other enhanced sampling protocols, folding of denatured states has been applied by several groups in the past (22,26,27). A similar approach will be adopted in this study.

Although simulation-based approaches have provided valuable information about denatured states, they do not address the issue of how microscopic data can be rigorously validated. The latter however is critical because current force fields underlying atomistic simulations have been developed targeting native-state properties and the accuracy for modeling denatured states is largely unknown. Recent studies on unstructured peptides reveal that most force fields have a bias in sampling backbone torsion angles, which results in overstabilization of α-helical relative to extended states (28,29). This problem can become exacerbated in simulations using generalized Born implicit-solvent models (30). This study presents an approach based on coupled titration and molecular dynamics simulations of denatured states at room temperature starting from the extended sequence. The coexistence of charged and uncharged populations allows for the extraction of denatured-state pK_a values, which can be used to calculate pH- and mutation-induced stability changes. This study illustrates the approach using a model system, the N-terminal domain of ribosomal protein L9 (NLT9), which was suggested to have significant electrostatic interactions in the denatured state because of the large deviation between the measured pH-dependent stability data and calculation based on pK_as of model compound or fragment peptides (11,31,32). The deviation, however, is largely abolished for the K12M mutant, which is more stable than WT by 1.9 kcal/mol but maintains a nearly identical native structure (32). This study applies replica-exchange continuous constant pH molecular dynamics (REX-CPHMD) simulations (33–35) to generate putative denatured states of WT and K12M NTL9. The excellent agreement with measured pH- and mutation-induced stability data encourages us to examine the microscopic electrostatic environment in the denatured states of WT and K12M NTL9 and test the hypothesis regarding a nonnative interaction between Asp⁸ and Lys¹².

Methods

Calculation of pH-dependent stability changes

Integrating the Wyman-Tanford linkage equation (Eq. 1) and substituting the total charges by the native- and denature-state pK_as through the generalized Henderson-Hasselbalch equation, I obtain the relative free energy of unfolding as a function of pH.

$$\Delta G\left(\text{pH}\right)-\Delta G\left({\text{pH}}^{\text{ref}}\right)=RT\sum _{i}ln\frac{{\left(1+{10}^{n{\left(i\right)}^N\left(p{K}_a^N\left(i\right)-\text{pH}\right)}\right)}^{1/n{\left(i\right)}^N}{\left(1+{10}^{n{\left(i\right)}^D(p{K}_a^D\left(i\right)-{\text{pH}}^{\text{ref}})}\right)}^{1/n{\left(i\right)}^D}}{{\left(1+{10}^{n{\left(i\right)}^D(p{K}_a^D\left(i\right)-\text{pH})}\right)}^{1/n{\left(i\right)}^D}{\left(1+{10}^{n{\left(i\right)}^N\left(p{K}_a^N\left(i\right)-{\text{pH}}^{\text{ref}}\right)}\right)}^{1/n{\left(i\right)}^N}}.$$ (2)

Here pH^ref is a reference pH and the summation runs over all residues titrable in the range of pH and pH^ref. The superscripts N and D denote the native and denatured states, respectively. n refers to the Hill coefficient. Because the degree of cooperativity for ionization of multiple groups is typically small, replacing the Hill coefficients by 1 does not result in noticeable change in the calculated free energy (31). Thus the Hill coefficients are replaced by 1 in our calculations and following discussions. Equation 2 offers a way to break down the total change in stability into residue-based electrostatic contributions. Because pH^ref is arbitrary, one can choose it to be much higher than the native and denatured-state pK_as of residue i. Thus, $1+{10}^{\left(p{K}_a^D\left(i\right)-{\text{pH}}^{\text{ref}}\right)}\approx 1$ and $1+{10}^{\left(p{K}_a^N\left(i\right)-{\text{pH}}^{\text{ref}}\right)}\approx 1$. If pH is much lower than the native- and denatured-state pK_as of residue i, e.g., residue i becomes protonated, the above equation can be further reduced to

$$\Delta \Delta G_i^{\text{ele}}=2.303RT\left(p{K}_a^N\left(i\right)-p{K}_a^D\left(i\right)\right).$$ (3)

This is the maximum electrostatic contribution from residue i to the total stability. It is the free energy change associated with titration of residue i in the absence of changes in the pK_as of other titratable residues in the native and denatured states. This quantity represents the major electrostatic contribution to the stability change due to a charge-neutralizing mutation that does not significantly perturb the structures of native and denatured states.

Simulation details

This study describes briefly the simulation details. The complete simulation protocols are given in the Supporting Material. Details of REX-CPHMD titration and folding simulations have also been described elsewhere (36–38). For the denatured states of WT and K12M NTL9, simulations were carried out at pH 4 and 100 mM salt starting from 20 replicas in the extended conformations with different initial velocity seeds. Sampling of each replica lasted 65 ns resulting in an aggregated simulation time of 1.3 μs. Unless otherwise noted, data from the first 15 ns was discarded in the analysis. Simulations for the native states of WT and K12M NTL9 were carried out at pH 2, 3, and 4 starting from the crystal structures for WT (residues 1–52, PDB ID: 2HBB) and K12M mutant (PDB ID: 2HBA, sequence 1–52) as well as the NMR model for WT (residues 1–56, PDB ID: 1CQU) and the corresponding computationally mutated model for the mutant. The simulation time was 2 ns per replica. Data from the first 500 ps was discarded in the pK_a calculations. REX-CPHMD simulations for the fragment peptides were carried out at pH 4 and 100 mM salt concentration starting from eight replicas in the extended conformations. The sequences were taken from the experimental work (31): 1–11, 12–23, 21–27, 35–42, 40–56. The simulation length for each replica was 40 ns, resulting in an aggregated time of 320 ns. Data from the last 20 ns simulation was used for pK_a calculations.

Results and Discussion

Native states of WT and K12M NTL9 are almost identical

NTL9 is a 56-residue basic protein with 2 Asp, 4 Glu, 11 Lys, and 1 Arg side chains (Fig. 1). Crystal structures of the truncated wild-type (residues 1–52) and K12M mutant (residues 1–51) are nearly identical, with an RMS deviation of 0.75 Å for identical Cα atoms. NMR chemical shifts data indicates no change in the local environment of position 12 due to replacement of lysine by methionine (32).

Figure 1.

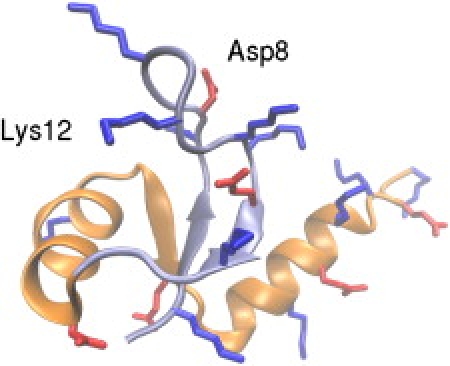
Native structure of NTL9. Segment A (residues 1–22) and segment B (residues 23–56) are shown in ice blue and orange, respectively. All acidic and basic side chains are shown in stick representation and colored red and blue, respectively. Residues Asp⁸ and Lys¹² are labeled.

This study examines the NMR titration data for WT and K12M NTL9. As expected, the differences in pK_as for the acidic residues in WT and K12M are very small, with the largest deviation being 0.12 pH units on Glu¹⁷ (Table 1). All pK_as are shifted down relative to the model values indicating that the native state is electrostatically stabilized (Table 1). Asp⁸ and Asp²³ show the largest pK_a shifts (−1 unit). The depressed pK_a of Asp⁸ is a result of the interaction with a highly charged loop, ¹⁰K-G-K-G-K-K-G¹⁶ (N-loop1), which connects the first two β strands. N-loop1 is well ordered and contains two absolutely conserved residues, Gly¹³ and Gly¹⁶ (39,40). Among all loop lysines, Lys¹⁴ forms the strongest interaction with Asp⁸. The Asp⁸-Lys¹⁴ distance is 6.5 Å in the crystal structure. In contrast, the interaction between Lys¹² and Asp⁸ is minimum as the distance between them is >15 Å (Fig. 1). I will return to the discussion of Asp⁸-Lys¹² and Asp⁸-Lys¹⁴ interactions later.

Table 1.

Summary of pK_a values for the native states of WT and K12M NTL9

Residue	WT			K12M			Pert§
	X-ray∗	NMR†	Expt‡	X-ray∗	NMR†	Expt‡
Asp8	2.80	1.83	2.99	2.80	2.45	2.94	−0.05
Glu17	3.57	3.84	3.57	3.70	3.62	3.69	0.12
Asp23	3.30	2.09	3.05	3.47	2.14	3.06	0.01
Glu38	4.50	3.74	4.04	4.42	3.73	4.04	0.00
Glu48	4.06	3.79	4.21	3.97	3.62	4.21	0.00
Glu54	–	3.63	4.21	–	3.38	4.17	−0.04
RMSD	0.26	0.66		0.28	0.51

^∗Calculations based the crystal structures of WT (PDB ID: 2HBB, sequence 1–51) and K12M NTL9 (PDB ID: 2HBA, sequence 1–52).

^†Calculations based on the NMR model for WT (PDB ID: 1CQU, sequence 1–56) and the corresponding computationally mutated model for K12M. Model pK_a values for Asp and Glu residues used in the calculations are 4.0 and 4.4, respectively.

^‡NMR titration data obtained with the full-sequence NTL9 (31,32).

^§Measured changes in pK_a values due to mutation.

The native-state pK_as of WT and K12M NTL9 were calculated using REX-CPHMD titration simulations based on the crystal structures (Table 1). Because the crystal structures lack of a few C-terminal residues, I repeated the simulations based on the full-length NMR model of WT and the corresponding mutant structure generated through computational mutation. The NMR model deviates significantly from the crystal structure. The root mean-square deviation (RMSD) for identical Cα atoms is 2.2 Å and for N-loop1 is 3.0 Å. Thus, it is not surprising that the pK_as calculated based on the NMR model show a larger RMSD from the NMR titration data (0.66 for WT and 0.51 for mutant) as compared to those based on the crystal structure (0.26 for WT and 0.28 for mutant). For this reason I will focus on calculations based on the crystal structures in the remainder of this study. Consistent with experiment, the calculated pK_as for WT and mutant are very similar. The calculation errors for most residues are within the statistical uncertainty of the REX-CPHMD method, which was estimated to be 0.16 pH units in converged simulations (34). The exception is Glu³⁸, where the calculation predicts a small positive pK_a shift of 0.1 units for WT, whereas the experiment gives a negative shift of about −0.4 units. I will come back to the discussion of the electrostatic environment of Glu³⁸.

Denatured basins of WT and K12M NTL9 are different

REX-CPHMD simulations were initiated from the extended conformations of the full-length WT and K12M NTL9 for a total of 1.3 μs (or 65 ns per replica). To facilitate conformational analysis, I partitioned the protein into two segments. Segment A, residues 1–22, encompasses the first two β-strands connected by a loop, whereas segment B, residues 23–56, encompasses the second helix, the third β-strand, and the C-terminal helix (Fig. 1). I examined the time series of radius of gyration (R_g), RMSD of segment A and B with respect to the native structure, and fraction of native contacts (Q). Within 1 ns, R_g decreased to ∼11 Å, a value similar to the native state. The RMSD of segment A and B quickly settled to the range of 6–8 and 8–10 Å, respectively, and remained stable in the remaining simulations (Fig. S1). Interestingly, the K12M mutant forms a smaller number of native contacts but is a little more compact than WT (Fig. S1, see later discussions). Examination of conformational snapshots shows that, although partial helix formation occurred in residues 1–11, 12–23, and 40–56, occasional β-bridges also appeared between the two N-terminal β-strands.

To test the convergence of the conformational ensembles, I calculated the distance distributions for the attractive interactions Asp⁸-Lys¹² and Glu¹⁷-Lys¹² as well as the repulsive interaction between Asp⁸ and Glu⁴⁸, as these interactions represent the most significant electrostatic effects in the denatured states of WT and K12M NTL9 (see later discussions). The probability distributions for these distances are well converged in the last 15 ns simulations (Fig. S2, Fig. S3, and Fig. S4). I also tested convergence of the calculated denatured-state pK_as. For both WT and K12M, the fluctuations in the pK_as are within 0.1 pH units in the last 10 ns simulations (Table S2 and Table S3). These fluctuations are below the statistical uncertainty of 0.16 pH units as found in previous studies (34). Note that the random noise in REX-CPHMD simulations can be further reduced by allowing exchanges of the pH biasing potential, which is a topic of our future work (J. A. Wallace and J. K. Shen, unpublished data). Because the total energy, order parameters, distance distributions, and pK_as are plateaued but the total simulation time (1.3 μs) remains two orders of magnitude below the estimated half life of NTL9, which is ∼0.34 ms at 69°C (40), I suggest that significant sampling of the denatured basins is reached with the simulation length of 65 ns per replica. Further evidence for sufficient sampling is provided by the most recent single-molecule Förster resonance energy transfer data that shows that the global reconfiguration time for the unfolded 66-residue cold shock protein Csp is ∼50 ns (41). Sampling of conformational space is faster in our Langevin dynamics simulations in implicit solvent because I used friction coefficient of 5 ps⁻¹, which is one order of magnitude smaller than that of water, which was estimated to be 50 ps⁻¹ (42).

This study characterized the denatured basins of WT and K12M NTL9 using the free energy surface along two order parameters, R_g and RMSD of segment A or B (Fig. 2). For WT, both free energy surfaces, ΔG(R_g, RMSD_A) and ΔG(R_g, RMSD_B) show one minimum region with R_g centered at round 11 Å. (Fig. 2, left). Thus, the denatured state of WT can be represented by a conformational cluster D1 defined as 6.0 < RMSD_A < 8.0 and 8.0 < RMSD_B < 10.0. For K12M, the free energy surface ΔG(R_g, RMSD_A) contains one minimum centered at 10.7 Å, whereas ΔG(R_g, RMSD_B) contains two minima centered at 9.7 and 10.9 Å (Fig. 2, right). Thus, the denatured basin of K12M can be represented by two conformational clusters. This study defined the first cluster D1 as 6.5 < RMSD_A < 7.5 and 9.0 < RMSD_B < 10.0, and the second cluster D2 as 6.5 < RMSD_A < 7.5 and 10.2 < RMSD_B < 11.2. D2 contains more compact conformations than D1. The presence of more compact conformations in the denatured state of K12M is also evident in the time series of R_g (Fig. S1).

Figure 2.

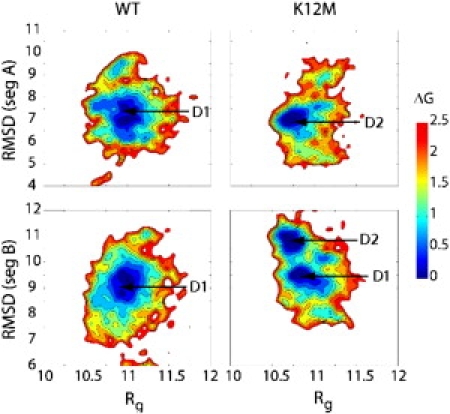
Free energy surfaces for the denatured basins of WT and K12M NTL9 at pH 4. Relative free energies (ΔG in kcal/mol) were calculated as a function of radius of gyration R_g (Å) and Cα RMSD (Å) of segment A (top) and segment B (bottom) with respect to the first entry in the NMR structure ensemble (PDB ID: 1CQU).

Denatured state of WT is electrostatically more stabilized than K12M NTL9

To characterize the electrostatic properties of the denatured states of WT and K12M NTL9 pK_as was calculated (Table 2). First compare pK_as of WT and K12M calculated using all denatured conformations (D). Except for Asp²³ all pK_as in the denatured state of WT are more depressed than those in the mutant suggesting that the denatured state of WT is more stabilized. The largest difference is seen at Asp⁸, where the pK_a in WT is lower than the mutant by ∼0.6 pH units. As mentioned earlier, the conformations in the D2 cluster of K12M NTL9 is more compact than those in D1. The pK_as calculated based on these two clusters also show significant differences. In going from the cluster D1 to D2, the pK_a of Asp⁸ is down by ∼0.8 units whereas that of Glu⁴⁸ is down by ∼0.4 units. Asp⁸ experiences a small net electrostatic repulsive force in cluster D1 whereas it becomes stabilized in cluster D2. For Glu⁴⁸ the net electrostatic repulsive force is weakened in D2. Taken together, these data suggest that the denatured-state electrostatic environment in WT is different from that in the K12M mutant. Specifically, Asp⁸ is significantly stabilized in the denatured state of WT but not the mutant. Glu⁴⁸ is not perturbed by net electrostatic effects in the denatured state of WT but it is significantly destabilized in the mutant.

Table 2.

Summary of pK_a values for the denatured states of WT and K12M NTL9

Residue	Frag∗	WT		K12M
		D†	D1	D†	D1	D2
Asp8	3.84	3.22	3.18	3.80	4.23	3.42
Glu17	4.11	3.93	3.88	4.11	4.11	4.20
Asp23	4.11	3.95	4.02	3.91	3.87	4.04
Glu38	4.63	3.86	3.79	4.11	4.11	4.15
Glu48	4.31	4.50	4.48	4.74	4.99	4.58
Glu54	4.32	4.16	4.16	4.25	4.29	4.23

Conformational clusters D1 and D2 are defined in the main text.

^∗Measured pK_a for the fragment peptides (31,32), which were used to calibrate the denatured-state pK_a (see main text and Table S1). Based on our earlier work (34), I estimated a SD of 0.16 pH units for the calculated pK_a.

^†All conformations sampled from the last 50 ns simulations.

Comparison to pH-dependent stability measurements

To validate the electrostatic features of the denatured states emerged from the simulation data, the pH-dependent stability profiles of WT and K12M were calculated using Eq. 2, where the denatured-state pK_as were obtained from the REX-CPHMD simulations. The calculations were repeated using the pK_as of the fragment peptides to represent the denatured-state electrostatics. The latter results capture the effects due to sequence-local interactions. I refer to them as the model curves.

I first discuss the results derived from the measured pK_as for the native state and the calculated pK_as for the denatured state (Fig. 3, top two plots). Consistent with experiment, the calculated stability profile for WT, using either all denatured conformations or the cluster D1, deviates substantially from the model curve, which is a proof for the presence of significant nonlocal electrostatic interactions in the denatured state. Nevertheless, the deviation from the model curve is overestimated as compared to experiment, which suggests that at least one of the denatured-state pK_as is underestimated (see later discussions). The calculated stability profile for K12M based on all denatured conformations is in quantitative agreement with experiment, showing a significantly reduced deviation from the model curve, which suggests that Lys¹² is involved in nonlocal electrostatic interactions in the denatured state of WT NTL9. The fact that mutation K12M does not completely abolish the deviation from the model curve indicates possible denatured-state electrostatic interactions that do not involve Lys¹². Because the denatured state of K12M shows two distinct populations (Fig. 2), the pH-dependent stabilities were also calculated based on two population clusters. Cluster D2 gives smaller stability decreases at low pH values as compared to cluster D1, which is the result of the much lower pK_a value for Asp⁸ calculated using the D2 cluster (Table 2). This is also consistent with the D2 conformations being more compact (smaller R_g, see Fig. 2). Finally, I discuss the results based on the calculated native- and denatured-state pK_as (Fig. 3, bottom two plots). Although all ΔΔG values are shifted up, the deviations between the model curves and calculated stability profiles remain approximately the same for both WT and mutant.

Figure 3.

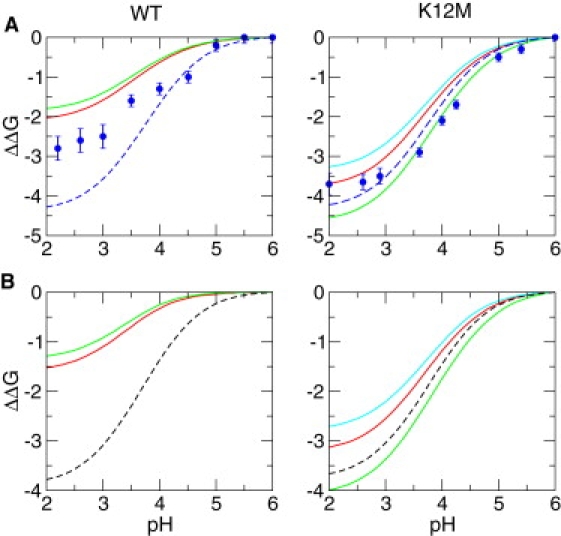
Calculated and measured stabilities of WT and K12M NTL9 relative to pH 6. Curves are obtained using Eq. 2 based on the denatured- and native-state pK_a values. Experimental data adapted from Cho and Raleigh (11) are displayed as solid blue circles with error bars. For the native-state pK_as, either the (A) measured or (B) calculated values (based on the crystal structures) were used. The denatured-state pK_as were taken from the NMR titration data of fragment peptides (dashed curves) or simulations (solid curves). Calculations based on all denatured-state conformations (D) are shown in red whereas those based on clusters D1 and D2 are in green and cyan, respectively.

Comparison to stability changes on mutations

To further validate the denatured-state electrostatics of WT NTL9 at the residue level, this study compares the maximum residue-based electrostatic contribution to stability (ΔΔG_i^ele) with the stability change on mutation (ΔΔG_i^tot) that replaces a charged side chain with a neutral one such as Asp → Asn and Glu → Gln. In the absence of significant structural perturbation, ΔΔG_i^tot can be broken down into the electrostatic and nonelectrostatic contributions. The electrostatic contribution is mainly captured by ΔΔG_i^ele, which is related to the difference between the denatured- and native-state pK_as through Eq. 3. Thus, for residues that have a significant difference between pK_i^D and pK_i^N, ΔΔG_i^ele is large and dominates the total stability change ΔΔG_i^tot. In this case, a comparison between ΔΔG_i^ele and the measured value of ΔΔG_i^tot offers an estimate for the accuracy of the calculated pK_i^D.

Fig. 4 shows ΔΔG_i^ele calculated using the denatured-state pK_as (dotted bars) and the pK_as of fragment peptides as pK_i^D (open bars) in comparison to the measured stability changes. Except for E38Q and E48Q the calculations using the denatured-state pK_as are closer to the mutation-induced stability changes. For E38Q the calculated ΔΔG_i^ele has an opposite sign as the stability change, which suggests that the denatured-state pK_a for Glu³⁸ is significantly underestimated in the simulation. In this case, the pK_a of the fragment offers a better estimate for pK_i^D. Curiously, note that Glu³⁸ is the only residue that has an upfield pK_a shift (relative to the model value) in the fragment peptide according to experiment. Our simulation, however, gives in a downfield pK_a shift. This qualitative difference suggests that the major inaccuracy in the simulation data may involve the microscopic electrostatics surrounding Glu³⁸. The underestimation of pK_i^D for Glu³⁸ is likely the major cause for the discrepancy between the calculated and measured pH-dependent stability changes. For E48Q the calculated ΔΔG_i^ele using the fragment pK_a value (4.31) for Glu⁴⁸ is closer to the measured stability change, which suggests that the calculated pK_i^D of 4.50 is too high and the fragment pK_a may offer a better estimate. The second largest deviation between ΔΔG_i^ele and ΔΔG_i^tot is for D23N, where the former is larger by ∼0.6 kcal/mol. Given that the nonelectrostatic contribution is most likely much smaller, this difference suggests that pK_i^D for Asp²³ should be shifted down relative to the model value whereas our simulation predicts no shift.

Figure 4.

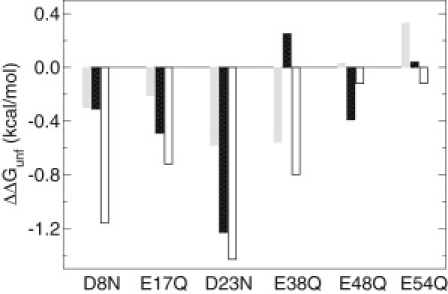
Comparison between the maximum residue-based electrostatic contributions to stability (ΔΔG_i^ele) and measured stability changes on mutations. Gray bars give the measured stability changes of NTL9 on mutations (11). Black bars give the calculated ΔΔG_i^ele based on Eq. 3 using the calculated pK_as for the denatured state and experimental pK_as for the native state. Open bars give the calculated ΔΔG_i^ele using the measured pK_as of the fragment peptides for the denatured state. Using Eq. 3 and an error of 0.16 pH units for the denatured-state pK_as (34), a maximum error of 0.22 kcal/mol for the residue-based electrostatic contribution is estimated.

Specific electrostatic interactions in the denatured states of WT and K12M NTL9

This study focuses on the electrostatic environment around Lys¹² and Asp⁸ in the denatured states of WT and K12M NTL9. I was curious to see whether the denatured-state electrostatic interactions involving Lys¹² are any different than other lysines in N-loop1. I computed the radial distribution function (RDF) for a loop lysine and an acidic residue in the denatured state of WT NTL9 (Fig. 5 A). Remarkably, the RDF for Lys¹² shows the highest peak at short distances, which suggests that Lys¹² experiences the strongest attraction from acidic groups as compared to other lysines in the loop. To examine the repulsive interactions, I also computed the RDF for a loop lysine and another basic residue in the denatured state of WT NTL9 (Fig. 5 B). The resulting RDFs show that Lys¹² behaves similarly as other loop lysines in the destabilizing electrostatic interactions.

Figure 5.

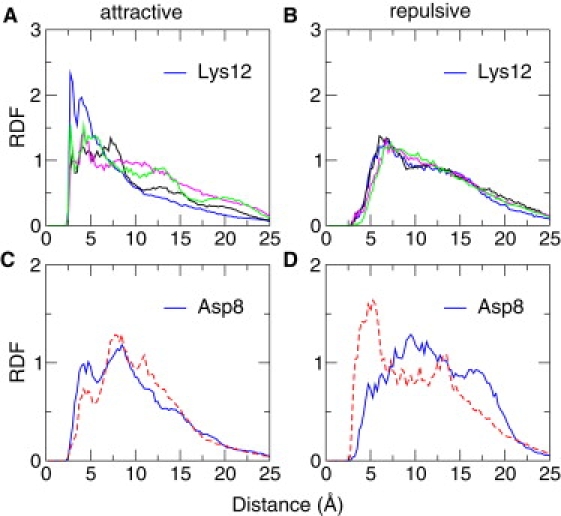
RDF for attractive or repulsive charge pairs in the denatured states of WT and K12M NTL9 at pH 4. (A) RDF for a loop lysine and an acidic residue in the denatured state of WT NTL9. (B) RDF for a loop lysine and another basic residue. RDFs corresponding to Lys¹² are shown in blue. (C) RDF for Asp⁸ and a basic residue in the denatured state of WT (blue) and K12M NTL9 (dashed red). (D) RDF for Asp⁸ and another acidic residue in the denatured state of WT (blue) and K12M NTL9 (dashed red). In RDF calculations the distances between charge centers of titratable residues were used. A charge center is defined as one of the amino nitrogen atoms in basic groups or one of the carboxylate oxygen atoms in acidic groups.

To explore the microscopic origin of the negative pK_a shift of Asp⁸ in the denatured state of WT relative to that in the K12M mutant, I compared the RDFs for the attractive and repulsive interactions involving Asp⁸ in the denatured states of WT and K12M. Fig. 5, C and D, show that although the attractive interactions involving Asp⁸ in the denatured state of K12M are significantly weakened, the electrostatic repulsions are significantly strengthened. To test the hypothesis that Asp⁸ forms a specific interaction with Lys¹² in the denatured state of WT NTL9, I calculated the probability distribution for the distance between Asp⁸ and all basic residues except for the sequence neighbors, Lys⁷ and Lys¹⁰ (Fig. 6 A). Interestingly, Asp⁸ forms the strongest interaction with Lys¹² followed by Lys¹⁴. The most probable distance between Asp⁸ and Lys¹² is ∼8 Å, although a sizable population shows a salt-bridge like interaction with a distance <5 Å. Considering that the distances for Asp⁸-Lys¹⁴ and Asp⁸-Lys¹² are 6.5 Å and 15 Å respectively in the native state, the denatured state contains both the native interaction, Asp⁸-Lys¹⁴, and the nonnative interaction, Asp⁸-Lys¹².

Figure 6.

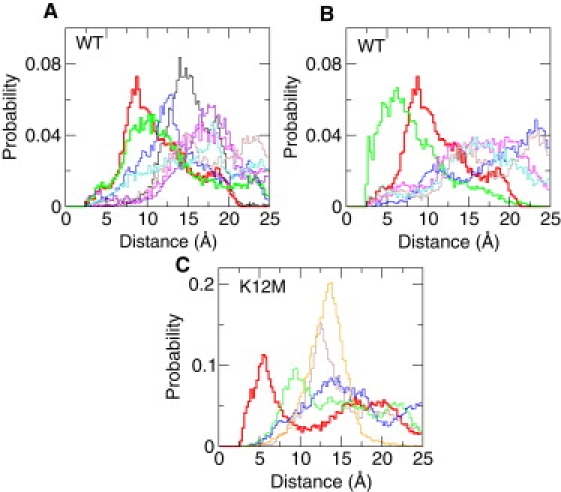
Probability distributions for attractive and repulsive interactions in the denatured states of WT and K12M NTL9 at pH 4. (A) Between Asp⁸ and a basic residue (except for Lys⁷ and Lys¹⁰) in the denatured state of WT. The distributions for Asp⁸-Lys¹² and Asp⁸-Lys¹⁴ are shown in red and green, respectively. (B) Between Lys¹² and an acidic residue in the denatured state of WT. The distribution for Asp⁸-Lys¹² and Glu¹⁷-Lys¹² are shown in red and green, respectively. (C) Between a pair of acidic residues in the denatured state of mutant K12M. The distribution for Asp⁸-Glu⁴⁸ is shown in red. Histograms were made in the range between 0 to 25 Å with a bin width of 0.25 Å.

Next, the attractive interactions involving Lys¹² in the denatured state of WT NTL9 were probed. Lys¹² forms the strongest interactions with Glu¹⁷ followed by Asp⁸ (Fig. 6 B). The former interaction is also seen in the simulation of the fragment peptide (12–23) maybe an antifact due to overstabilization of local electrostatics as evident from the underestimation of the pK_a of Glu¹⁷ in the fragment peptide. As expected, the distribution for Asp⁸-Lys¹² is identical to the one seen in Fig. 6 A. Finally, this study explored the repulsive interactions in the denatured state of K12M. To explore the microscopic origin for the positive pK_a shift of Glu⁴⁸ in the denatured state of K12M, this study examined the probability distribution of the distance between Glu⁴⁸ and other acidic residues (Fig. 6 C). Remarkably, Glu⁴⁸ and Asp⁸ form the strongest repulsion, which explains not only the pK_a shift of Glu⁴⁸ but also the significant repulsion experienced by Asp⁸ as shown in Fig. 5 D.

Conclusions

This study has presented what I believe to be a new approach to study microscopic electrostatic interactions in the denatured states of proteins. In this approach, constant pH molecular dynamics simulations with REX-CPHMD are carried out at room temperature starting from the extended sequence of the protein to generate the pH-modulated denatured-state ensemble under folding conditions. The latter results in a set of denatured-state pK_as that can be used to predict experimental observables such as the pH-dependent relative free energies of unfolding and to estimate the stability changes due to mutations of charged residues. Thus, the presented approach offers a means to validate microscopic electrostatics, which is not possible with conventional simulation-based approaches. To address the second limitation, which is related to the conformational bias as a result of deficiencies in current force fields and solvent models, I propose to use as benchmarks the conformational and titration properties of fragment peptides derived from the sequence of the intact protein of interest.

This study illustrated the approach using the NTL9 protein. I conducted REX-CPHMD folding simulations for the fragment peptides and found that the pK_as for all acidic side chains are overly depressed relative to experimental values. The deviations were later used to calibrate the denatured-state pK_as. I carried out REX-CPHMD simulations for WT and K12M mutant of NTL9 starting from the extended sequences to generate the putative denatured states. The data reveals one conformational ensemble for WT but two distinct conformational clusters for the K12M mutant that differ in terms of compaction and deviation from the native structure. To test the microscopic electrostatics in the putative denatured states, the pH-dependent relative stabilities of WT and K12M NTL9 were calculated based on the calibrated denatured-state pK_as. This study also obtained the residue-based electrostatic contributions to the stability of NTL9, which were used to estimate the stability changes due to charge-neutralizing mutations. The agreement of these calculations with experiment validates the microscopic picture of the denatured state, in which the charged state of Asp⁸ is stabilized significantly by a nonnative electrostatic interaction with Lys¹², consistent with experimental evidence (11). Moreover, simulations predict that mutation K12M results in the formation of a nonnative interaction between Asp⁸ and Glu⁴⁸ that destabilizes the charged state of Glu⁴⁸ in the K12M mutant. This hypothesis can be tested experimentally by measuring the stability of a double mutant K12M/E48Q. The comparison to the mutation-induced stability changes also allowed us to identify the inaccuracies in the microscopic description of electrostatics. For example, this study found that the denatured-state pK_a of Glu³⁸ is underestimated whereas that of Asp²³ is overestimated. Nevertheless, a more precise assessment of the simulation accuracy awaits the experimental data of denatured-state pK_as. Work has begun to address this issue (43). A theoretical means to estimate the nonelectrostatic contributions to stability changes on mutations would also be helpful.

The case study of NTL9 shows that both specificity and nonnative interactions are important in the determination of denatured-state energetics. Hence, Gaussian-chain or native-like models are not sufficient in revealing the microscopic origins of the deviation between the pH-dependent stability measurement and calculations assuming random-coil electrostatics. The distinct electrostatic features of the denatured-state ensembles emerged from our simulations and the agreement with macroscopic observables lend support to the notion that the relevant conformational space of denatured states is rather restricted (20,44). Thus, direct sampling of the denatured basin may offer a viable route to gaining insights into structural and energetic properties of the denatured state (22,26,27) in the absence of a thermodynamic equilibrium with the native state. Such a strategy is advantageous in practice because multiple folding events for even small fast folding proteins can not be sampled with current simulation methods and computational resources.

A major issue in studying denatured states is related to the deficiencies in the force field and solvent model. Because force fields have been traditionally developed by targeting native-state properties, the accuracy for describing the energetics in denatured states remains to be established. Nevertheless, limited published data points toward a major problem involving the backbone torsional bias in commonly used force fields (28–30,45). Overstabilization of helical segments and local electrostatic interactions as revealed by our data may be a major reason for overcompaction of denatured states as observed in previous implicit-solvent simulation studies (45,46). Although work is under way to address this issue (M. Feig, Michigan State University, A. MacKerell, University of Maryland, and R. Best, Cambridge University, personal communication, 2010), I believe the data presented in this study shows that the major inaccuracy in modeling denatured-state electrostatics can be identified at the local level by examining the conformational and electrostatic properties of fragment peptides. The latter suggests a useful strategy for the development of improved force fields and solvent models, and it also offers a means to study local interactions in the denatured state of the intact protein. This work used a set of peptides that have the sequences of the helical and β-strand segments of NTL9 to take advantage of the published experimental data (31,32). Because the choice of fragment peptides is not unique, however, the study based on one set of fragments may not uncover all the sequence-local interactions that are present in the denatured state of the intact protein. Future work will address this issue and examine whether the nonnative interaction between Asp⁸ and Lys¹² can be seen in a different fragment peptide. Finally, I believe the work presented in this study shows that constant pH molecular dynamics is a powerful tool for studying residue-specific electrostatic interactions in the denatured states of proteins. Coupled with first principles folding simulations it can be used to unravel and validate microscopic electrostatics of the entire folding energy landscape.