Abstract
Microscopy-based fluorescence resonance energy transfer (FRET) experiments measure donor and acceptor intensities by isolating these signals with a series of optical elements. Because this filtering discards portions of the spectrum, the observed FRET efficiency is dependent on the set of filters in use. Similarly, observed FRET efficiency is also affected by differences in fluorophore quantum yield. Recovering the absolute FRET efficiency requires normalization for these effects to account for differences between the donor and acceptor fluorophores in their quantum yield and detection efficiency. Without this correction, FRET is consistent across multiple experiments only if the photophysical and instrument properties remain unchanged. Here we present what is, to our knowledge, the first systematic study of methods to recover the true FRET efficiency using DNA rulers with known fluorophore separations. We varied optical elements to purposefully alter observed FRET and examined protein samples to achieve quantum yields distinct from those in the DNA samples. Correction for calculated instrument transmission reduced FRET deviations, which can facilitate comparison of results from different instruments. Empirical normalization was more effective but required significant effort. Normalization based on single-molecule photobleaching was the most effective depending on how it is applied. Surprisingly, per-molecule γ-normalization reduced the peak width in the DNA FRET distribution because anomalous γ-values correspond to FRET outliers. Thus, molecule-to-molecule variation in gamma has an unrecognized effect on the FRET distribution that must be considered to extract information on sample dynamics from the distribution width.
Introduction
Fluorescence resonance energy transfer (FRET) is widely thought of as a spectroscopic ruler on the nanometer scale (1,2). Many biological phenomena occur on this scale, making FRET a popular tool in biology. The efficiency of energy transfer (E) between two fluorescent dyes is related to the fluorophore separation (r) by
| (1) |
where R0 is the Förster radius (3), which encompasses parameters such as spectral overlap, donor quantum yield, and the orientation of the transition dipoles.
FRET efficiency is used as a marker for colocalization and interaction, to study the magnitude of conformational changes and to calculate absolute distances. Measuring FRET using microscopy comes with a unique set of technical challenges to recover biologically relevant information. Microscopy experiments measure the donor and acceptor intensity by passing the emission through a series of optical elements to avalanche photodiode detectors or a sensitive digital camera (commonly an electron multiplied charge-coupled device (EMCCD)). The observed FRET efficiency has been called the relative proximity ratio (EPR) because it is internally consistent as long as the photophysical and instrumental properties remain unchanged (4). EPR is determined from the measured intensities (I) of the donor (D) and acceptor (A):
| (2) |
Because EPR varies with fluorophore separation, it is useful for drawing conclusions about the timescale and magnitude of structural changes and molecular associations. However, it is often desirable to recover the true FRET efficiency (E) separated from instrument and photophysical effects. The measured intensity values must be corrected as
| (3) |
where βID corrects for leakage of donor emission into the acceptor channel (5). The parameter γ accounts for differences between the donor and acceptor in detection efficiency (η) and quantum yield (φ) (6,7):
| (4) |
Thus, normalization by γ adjusts for differences between the donor and acceptor dyes in their probability of photon emission upon excitation and the probability that emitted photons will be detected. Because FRET is a ratio, the effect of γ-normalization is not a constant but rather varies as a function of the true FRET efficiency. The values of β and γ can be manipulated by the investigator through the choice of optical elements. This must be balanced with considerations of the signal/noise ratio. Filter sets can be chosen to bring ηA/D near to one but this does not account for φA/D making it difficult to maintain control over the magnitude of these corrections.
In single-molecule FRET (smFRET) microscopy, methods of γ determination vary depending on experimental methodology. Measurements on diffusing molecules have relied on empirical measurement of the individual parameters in Eq. 4 for quantum yield and detector efficiency (8–10). A related approach to γ-determination for diffusing molecules also relies on a linear relationship between EPR and the stoichiometry (5). For immobilized single molecules, γ has been obtained from the change in intensities before (Pre) and after (Post) acceptor photobleaching (7) as
| (5) |
Photobleaching is a hallmark of smFRET, so this method of γ determination does not require additional experiments. Molecules where acceptor photobleaching precedes that of the donor provide the needed information. The value γ can also be obtained from the difference in FRET efficiencies calculated from fluorescence intensity and fluorescence lifetime but this requires specialized instrumentation (11).
Methods of γ-determination are chosen largely due to experimental constraints. In diffusing molecule experiments, motion out of the detection volume is typically faster than photobleaching making empirical determination of γ necessary (5,10). Similarly, the ease of recovering γ using Eq. 5 when measuring immobilized single molecules removes the need for empirical determination of γ. Although not all FRET studies report γ-normalization, various forms of normalization have been used for more than a decade. Despite the large effect γ can have on measured FRET, the efficacy of γEmpirical and γPhotobleach have never been compared. We present here the first systematic comparison of γ-normalization methods using a series of FRET microscopy measurements on duplex DNA samples with known donor and acceptor fluorophore separations.
To demonstrate the dependence of EPR on the choice of optical elements, we recorded smFRET distributions using different optical paths. To examine the effect of photophysical properties on EPR, we also used dye-labeled protein samples with differing quantum yield. We tested the efficacy of methods for correcting the smFRET efficiency. We compared:
-
1.
A simplified normalization using the filter transmission properties.
-
2.
γEmpirical determined from control experiments.
-
3.
γPhotobleach.
Our results show that molecule-to-molecule variations in γ are an unrecognized contribution to the width of the smFRET distribution that can only be corrected using per molecule γ normalization with γPhotobleach.
Materials and Methods
DNA constructs
Fluorescently-labeled, HPLC-purified oligonucleotides (some biotinylated) were purchased from Integrated DNA Technologies (Coralville, IA) (see Fig. 1 for sequences and position of modifications). Equimolar donor- and acceptor-labeled complementary strands were combined in a microfuge tube at 1 μM in 10 mM Tris·HCl, 50 mM NaCl, and 1 mM EDTA, pH 8.0. Duplexes were annealed by placing the samples in 1 L water that had been brought to a boil and was allowed to cool spontaneously to 4°C. For ensemble measurements, donor and acceptor strands were annealed to complementary DNA strands lacking biotin and dye.
Figure 1.
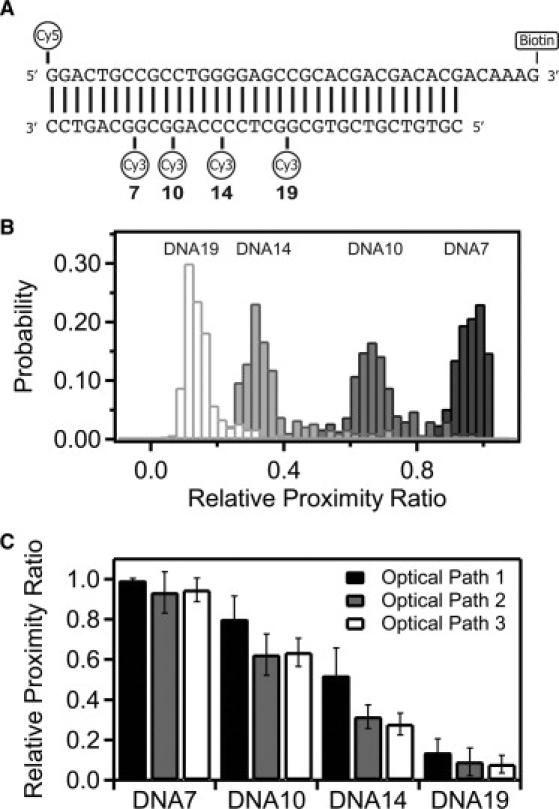
DNA duplexes used as FRET standards. (A) DNA oligonucleotides used to form the FRET standards. The acceptor strand has a 5′ terminal Cy5 dye and a 3′ biotin TEG moiety for tethering the DNA. Four different DNA constructs were generated by annealing this top strand with one of four complimentary strands each containing an internal Cy3 dye at the position indicated. The numbering refers to the basepair preceding the internal Cy3. (B) Raw FRET histograms show the relative proximity ratio (EPR) for each of the DNA constructs as labeled above their distribution: DNA19 (19 bp), DNA14 (14 bp), DNA10 (10 bp), and DNA7 (7 bp). Separate measurements are shown for each DNA duplex under optical path 3. (C) Relative proximity ratio for the four DNA duplexes measured under optical path 1 (solid), optical path 2 (shaded), and optical path 3 (open). Panel shows the mean value with the error bars indicating the width from a Gaussian fit.
Distances within the DNA crystal structure were measured using PyMol (DeLano Scientific, South San Francisco, CA).
Fluorescence microscopy
Images were collected with a 60×, 1.2 NA water immersion objective (Olympus, Center Valley, PA). Total internal reflection was achieved with a home-built prism illuminator. Laser excitation was at 532 nm and 633 nm for donor and acceptor, respectively. Images were recorded with an iXon EMCCD camera (Andor Technologies, Belfast, UK) or a Cascade 512B (Roper Scientific, Tucson, AZ). Glucose oxidase and catalase in 1% glucose were used as an oxygen scavenging system and triplet state quenchers (Trolox for DNA and cyclooctatetraene for protein) were included (Sigma-Aldrich, St. Louis, MO).
Optical path 1 contained a 550 LP filter (Chroma Technology, Rockingham, VT), a 593-nm dichroic mirror (Semrock, Rochester, NY), a 562/40 BP filter (Semrock) and a 670/30 BP filter (Semrock) with the Andor camera. Optical path 2 is a separate instrument that uses a 645-nm dichroic mirror (Chroma), a 585/70 BP filter (Chroma), and a 700/75 BP filter (Chroma) with the Cascade camera. Optical path 3 is the same instrument as optical path 1 but contained a 550 LP filter (Chroma), a 645-nm dichroic mirror (Chroma), a 585/70 BP filter (Chroma), and a 670/30 BP filter (Semrock) with the Andor camera. See Table 1 and Fig. 2 A.
Table 1.
Wavelength cutoffs of the optical elements in the microscopy filter sets
| Optical path | Long pass filter | Dichroic mirror cutoff | Bandpass filter (donor) | Bandpass filter (acceptor) | EMCCD camera | Theoretical ηA/D | Empirical ηA/D |
|---|---|---|---|---|---|---|---|
| 1 | 550 nm | 593 nm | 562/40 | 670/30 | Andor iXON | 1.41 | 0.79 |
| 2 | None | 645 nm | 585/70 | 700/75 | Cascade 512B | 0.78 | N/D |
| 3 | 550 nm | 645 nm | 585/70 | 670/30 | Andor iXON | 1.08 | 0.46 |
Figure 2.
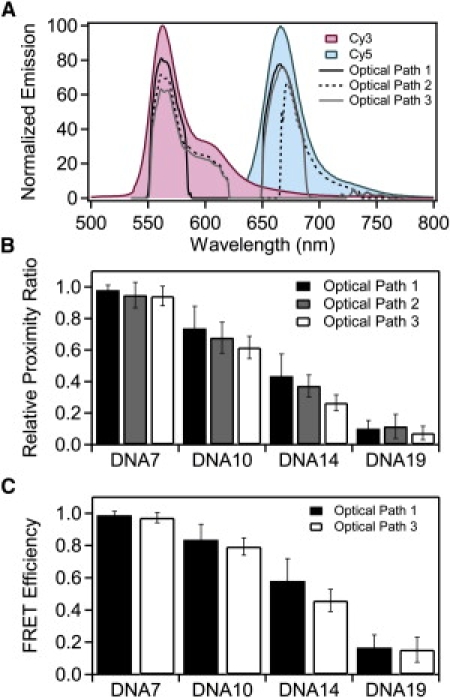
Normalizing the relative proximity ratio using calculated ηA/D. (A) Measured emission spectra of Cy3 (red) and Cy5 (blue) normalized to the emission maxima. The transmitted spectrum for each dye was calculated from the emission spectrum and the transmission spectrum for each element in the optical path and the camera response curve. Calculated transmission is shown for optical path 1 (solid line), optical path 2 (dashed line), and optical path 3 (shaded line). (B) Normalized relative proximity ratios for DNA under optical path 1 (solid), optical path 2 (shaded), and optical path 3 (open). EPR was adjusted using the theoretical ηA/D, calculated as shown in panel A. Panel shows the mean value with the error bars indicating the width from a Gaussian fit. (C) FRET efficiencies for DNA recorded under optical path 1 (black) and optical path 3 (white) normalized using calculated γEmpirical values specific to the indicated sample and filter set. Mean FRET efficiencies are shown with error bars indicating the width from a Gaussian fit.
Data analysis
Images were analyzed using MATLAB (The MathWorks, Natick, MA). See Supporting Material for details. Single molecules were verified by selecting only events showing single-step photobleaching to baseline. The raw EPR values are corrected for background and leakage of the donor into the acceptor channel but not normalized by γ. Acceptable events for calculating γ, where the acceptor photobleaches before the donor (Fig. 3 A), typically make up <50% of otherwise acceptable FRET events. The value γ was calculated based upon the average donor and acceptor intensities for the 20 frames immediately before and after the manually selected photobleaching event.
Figure 3.
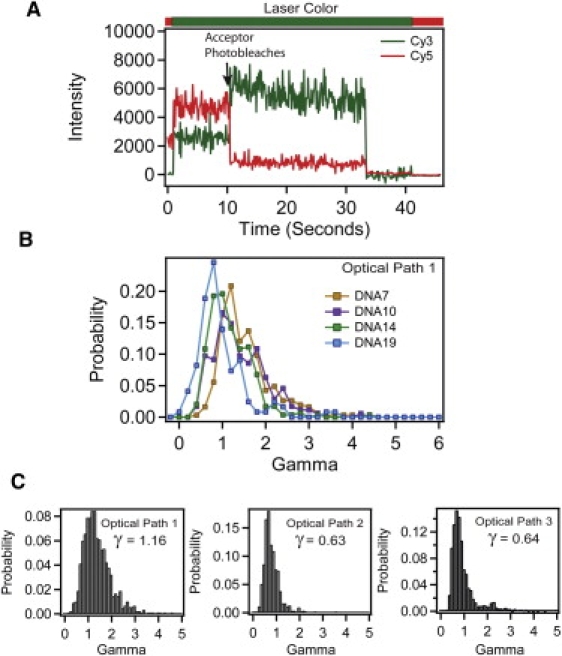
Measuring γ from anti-correlated photobleaching events. (A) Example trace (DNA10) showing a molecule from which γ can be calculated based upon the anti-correlated change in acceptor (red) and donor (green) intensity. Acceptor photobleaching is indicated with arrow. The bar above the panel shows the alternating laser colors during acquisition. The γPhotobleach can only be calculated from molecules where acceptor photobleaching precedes donor photobleaching. (B) Histogram of individual γPhotobleach values for each DNA molecule recorded under optical path 1 for DNA7 (orange), DNA10 (purple), DNA14 (green), and DNA19 (blue). (C) Cumulative histogram showing universal γPhotobleach for DNA duplexes measured under optical path 1 (left), optical path 2 (middle), and optical path 3 (right).
Protein constructs
The cDNA for rat PSD-95 was cloned into pet28a and expressed using Rosetta cells (EMD Chemicals, Gibbstown, NJ) according to the manufacturer's instructions. Labeling with maleimide derivatives of Alexa dyes (Invitrogen, Carlsbad, CA) was done in 25 mM HEPES, 300 mM NaCl, and 0.5 mM TCEP, pH 7.4. Free dye was removed by desalting using Sephadex G50 resin (GE Healthcare, Piscataway, NJ). Labeling efficiency was >90% as determined from absorbance measurements using calculated extinction coefficients and the corrected ratio of absorbance at 280 nm to 556 nm and 651 nm for Alexa 555 and Alexa 647, respectively. Protein was encapsulated into 100-nm vesicles by extrusion (Avanti Polar Lipids, Alabaster, AL) (12).
Results
Correcting for optical elements as a means of standardizing smFRET instrumentation
DNA oligonucleotides are one of the mostly widely measured systems in smFRET (4,5,13–19). Because it adopts well-defined structures, DNA has served as a molecular standard to investigate accuracy, effects of anisotropy, and the impact of instrumentation and data processing on smFRET measurements. In line with these previous studies, we used short, duplex DNA samples to examine methods of standardizing different instruments and for recovering a true FRET efficiency from measured single-molecule intensities. To this end, we used a series of 34-basepair duplex oligonucleotides containing a Cy5 acceptor dye attached to the 5′ end of one strand and an internal Cy3 donor attached at a variable position along the other strand in the duplex (Fig. 1 A). We created four duplexes containing donor-acceptor separations of 7 basepairs (DNA7), 10 basepairs (DNA10), 14 basepairs (DNA14), and 19 basepairs (DNA19).
The raw FRET efficiency (relative proximity ratio, EPR) decreased with increasing fluorophore separation as expected (Fig. 1 B and Table S1 in the Supporting Material). We measured this DNA ladder under the same conditions on two separate instruments with different EMCCD cameras using a total of three different optical paths, which resulted in differing values for EPR (Fig. 1 C and Table S1). The variation between measurements is greatest at EPR values near the Förster radius, where the distance dependence is most sensitive, with much less variation in EPR for samples with high or low FRET.
In this study, donor and acceptor emission interacts with three spectrally dependent optical elements before reaching the camera. The transmission properties of the filters limit how much of the spectrum of fluorescence emission is collected, which affects the measured intensity (Fig. 2 A and Table 1) and thus changes EPR (Fig. 1 C). Despite this, changing the optical path has a minimal effect on EPR for samples with FRET near zero or one. In these cases, the donor or acceptor intensity is near zero, so FRET is less sensitive to changes in the fraction transmitted. For this reason, the accuracy of FRET measurements may be diminished at the extreme ends of the FRET scale. The sensitivity of FRET to changes in distance also drops sharply in these regions, so such values can be of limited quantitative value. As such, we will focus our attention on correcting for the large deviation in samples with FRET values near the Förster radius. Given that the samples were identical, the structure of the duplex DNA is the same for all measurements. This leaves the terms composing γ as the expected cause of the differences in EPR. The true FRET efficiency is independent of the optical elements so we wanted to measure how well we remove the artifacts introduced by changing the filters. We compared the mean FRET values for a given DNA sample measured under the three optical paths. To assess convergence of the mean FRET, we calculated the standard deviation of the mean FRET values after normalization. Thus, reduced standard deviation of the means corresponds to closer agreement in EPR between different measurements. Convergence of the mean directly reveals our ability to correct for the optical changes we have made to the instrument. The accuracy of the corrected FRET efficiency when used for distance calculations is discussed separately below.
A straightforward method of γ-normalization is to use only the transmission properties of the optical filters and detector efficiencies of the EMCCD cameras as provided by the manufacturers. We calculated the theoretical ηA/D by multiplying the emission spectra of the donor and acceptor fluorophores by the spectrally dependent transmission and detection efficiencies of the optical elements in the microscope and taking the ratio of the transmitted intensity of the donor and acceptor. To calculate FRET, the donor intensity was normalized according to Eq. 3 using a γ-factor equal to the theoretical ηA/D. The values for the theoretical ηA/D are shown in Table 1. Normalization with the theoretical ηA/D values reduced the mean standard deviation for all DNA samples by 35% as compared to the raw EPR values (Fig. 2 B and Table 2). The normalized EPR values for the DNA ladder measured on different instruments or using different optical paths could be brought into closer agreement (Table S2). Differences in EPR are still pronounced. Also, although normalization for detection efficiency increased convergence for FRET measured under varying optical conditions, the resultant value should still be considered EPR rather than the true FRET efficiency because this is only a partial correction. According to Eqs. 3 and 4, we still must account for differences in quantum yield.
Table 2.
Effect of γ-normalization methodology on the convergence of DNA FRET values recorded under different optical paths
| Normalization method | Average standard deviation of the mean |
|---|---|
| Raw | 0.0724 |
| ηA/D (Theoretical) | 0.0470 |
| ηA/D (Empirical) | 0.0340 |
| γEmpirical | 0.0362 |
| Universal γPhotobleach | 0.0220 |
| Global γPhotobleach | 0.0198 |
| Individual γPhotobleach | 0.0082 |
Empirical determination of the parameters composing γ
In studies of diffusing single molecules, γ has been determined empirically (γEmpirical) by making a series of experimental measurements of the individual parameters: the relative instrument response, ηA/D, and relative quantum yield, φA/D, and then calculating γEmpirical using Eq. 4 (8–10). To our knowledge, an equivalent empirical calibration has not been published for wide-field observation of immobilized single molecules, so we determined γEmpirical for our EMCCD-based total internal reflection fluorescence microscope. As control samples, we used oligonucleotides with either the 5′ Cy5 acceptor or the internal Cy3 donor (from DNA19), which were annealed with an unlabeled complimentary oligonucleotide to form the singly-labeled control DNA duplexes.
In studies of diffusing molecules, detection efficiency was determined by measuring the avalanche photodiode detector count rate as a function of the concentration of singly-labeled control samples (8–10). In this experimental configuration, the number of molecules in the focal volume varies with time but the average intensity scales with solution concentration. For immobilized samples, a single molecule can be unambiguously identified from the photobleaching decay. Variation in FRET efficiency arises from different emission rates from a single dye. Thus, detection efficiency for immobilized molecules depends on the sensitivity to different rates of single dye emission. To examine this directly, we varied the rate of photon emission from a single molecule by increasing the excitation laser power rather than increasing the number of molecules emitting photons.
DNA samples singly-labeled with either Cy3 or Cy5 were both excited at 532 nm and the mean emission intensity was determined at a series of laser powers. To examine how effectively empirically measured detection efficiency corrects for variations in optical elements, we measured the power dependence under optical paths 1 and 3, which gave different values for ηA/D (Fig. S1 A and Table 1).
Using the same singly-labeled DNA, we measured the dependence of the integrated ensemble fluorescence emission of each fluorophore as a function of concentration (Fig. S1 A, bottom panel). Because the ensemble measurements collected the entire emission spectra of the fluorophores, we used this value to normalize the single-molecule response as described by Ferreon et al. (8):
| (6) |
Here mSM is the slope of single-molecule laser-power dependence and mEnsemble is the ensemble concentration dependence. The values for the empirical ηA/D are shown in Table 1. Although our determined values for empirical ηA/D trend with the theoretical ηA/D, the magnitudes were significantly different. Similar values for the empirical ηA/D were obtained for protein samples singly-labeled with either Alexa 555 or Alexa 647 encapsulated within lipid vesicles due to the similarity of the emission spectra with respect to the emission bands passed (Fig. S1 B).
Using empirical values of ηA/D to correct the EPR of the DNA samples resulted in a 53% reduction in mean standard deviation for all DNA samples measured under these two optical paths as compared to the raw EPR values (Table 2 and Table S3). Empirical ηA/D normalization reduced the mean standard deviation by ∼45% relative to the theoretical ηA/D for measurements made under optical paths 1 and 3 (Table 2), which suggests that the theoretical transmission of the optical elements alone are insufficient to determine the instrument response. Even though normalization by empirical ηA/D improved convergence, it does not normalize for φA/D and thus is still technically considered EPR (see Eqs. 3 and 4).
To recover the true FRET efficiency, we determined the ensemble quantum yield of the acceptor and each donor in singly-labeled DNA duplexes (20). There was little variation in donor φ as a function of labeling site, so φA/D was similar for all DNA constructs (Table S4). The EPR distribution for each of the DNA samples was corrected using γEmpirical calculated from the empirical φA/D for that DNA duplex and the empirical ηA/D for the optical path. Thus eight values of γEmpirical were calculated one for each DNA duplex under optical paths 1 and 3 (Table S5). The use of γEmpirical yielded no additional improvement in the convergence of the mean FRET values when compared to using the empirical ηA/D alone (Fig. 2 C and Table S6). Incorporating φA/D recovers the true FRET efficiency but the convergence relative to the raw EPR values was slightly worse than not using the quantum yield information (Table 2). The failure of γEmpirical suggests that the ensemble measurements may not be yielding accurate quantum yield values, but single-molecule intensity measurements confirmed that there was little variation in emission levels between the duplexes (Fig. S2).
Determination of γ from photobleaching
We also measured γ for immobilized single molecules from the magnitude of the anticorrelated intensity change of the intensities upon acceptor bleaching using Eq. 5 (7). An example of such a photobleaching event is shown in Fig. 3 A. As described previously, the value of γ varies among molecules within a given sample (Fig. 3 B) (6,16). The majority of values were normally distributed about a mean but there were always outliers that displayed values severalfold higher than the mean γ-value (Fig. 3, B and C). To correct EPR, the predominant peak in the γ-distribution was fit to a Gaussian function and the center value was used as γPhotobleach for each sample. Across all three optical paths, γPhotobleach decreased as the distance between donor and acceptor increased (Table S5). Thus, γPhotobleach appeared to correlate with the FRET efficiency. There was reasonable agreement between γPhotobleach and γEmpirical for the shortest interfluorophore separation (DNA7) but the values diverge at larger separations because γEmpirical did not show distance dependence (Table S5).
Optimal application of γ-normalization
Variability in γ and the presence of γ-outliers raise questions as to how normalization should be applied to recover FRET efficiency effectively. γPhotobleach can be measured once and applied as a universal normalization to all measurements using the same dyes and optical path. This method does not account for the sample-to-sample variation in γ that we observed. One could normalize an individual data set using the data set specific mean or global γ-factor. This does not account for variation within a data set or the outliers with γ-values significantly different from the mean. To account for these outliers, one would have to normalize each molecule with an individual γ-factor. These approaches have all been previously reported but never compared (6,7,21–23).
To determine the optimal method for normalization, we compared results of applying each approach to the DNA data sets (Table S7). The universal γ-factor was taken as the value at the center of a Gaussian fit to a combined γ distribution containing all four DNA constructs. The universal γPhotobleach was determined separately for each optical path resulting in three values for γ (Fig. 3 C). The global γPhotobleach was determined from the γ-distribution of each combination of DNA and optical path and gave rise to 12 values for γ (Table S5). Calculating the individual γPhotobleach gave rise to hundreds of values for γ, equal to the total number of molecules.
Because FRET is minimally sensitive to optical path at extreme FRET values, we focus our comparison of effectiveness on DNA10 and DNA14, which showed midrange FRET. Normalization of donor intensity by γPhotobleach resulted in convergence of the mean FRET values across optical paths compared to raw EPR albeit with some variation in effectiveness depending on the application (Fig. 4 A and Table 2). Applying a universal normalization resulted in a 70% decrease in standard deviation relative to the raw EPR values for all samples under the three optical paths (Table 2). In contrast, global normalization resulted in a 73% decrease whereas individual γ-normalization resulted in an 89% decrease (Table 2). Thus all γPhotobleach normalization methods largely corrected the apparent FRET for the changes made to the optical path, but individual normalization showed the greatest convergence (Fig. 4 A). Raw EPR distributions showed wide FRET peaks, and normalization methods that utilized a single γ-value per sample had no effect on the peak width (Fig. 4 B). In contrast, individual γ-normalization resulted in a decrease in peak width for DNA10 and DNA14 (Fig. 4 B). The reason for this effect becomes apparent when we plot the distribution of γ within the FRET peak (Fig. 5). We calculated the mean γ for all the molecules within each bin of the FRET histogram and colored every bin in the histogram according to its mean γ-value. In the raw data, γ increases with FRET efficiency such that molecules at the high or low edge of the peak have correspondingly high or low γ (Fig. 5 A). Per-molecule normalization reduced the γ-bias such that γ is more uniformly distributed across the peak (Fig. 5 B). This reduced the peak width by bringing outlying FRET values closer to the mean. Thus, individually normalized DNA samples have very narrow FRET peaks as would be expected for molecules with little conformational variability.
Figure 4.
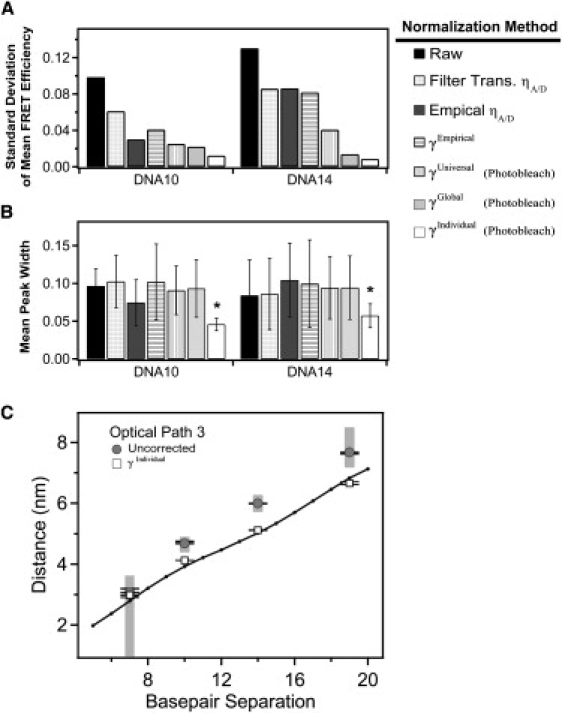
Comparison of methods for normalization of DNA FRET using γPhotobleach. Effectiveness of the normalization methodology was assessed by comparing the mean and width from Gaussian fits to the histogram of a given DNA construct under each of the three different optical paths. (A) The standard deviation in the corrected mean FRET efficiency of each DNA construct measured under the three different optical paths after the indicated method of γ-normalization. Reduced standard deviation indicates convergence of the mean FRET efficiency after γ-normalization is applied. (B) The mean peak width for each DNA duplex under the three optical paths. A reduced mean width indicates narrower peaks after γ-normalization. Error bars indicate the standard deviation between the mean widths measured under different filter sets after the indicated method of γ-normalization. Smaller error bars indicate convergence in the γ-normalized width between the different optical paths. Asterisk denotes statistical significance (p < 0.001), Student's one-tailed t-test. (C) Raw relative proximity ratios (shaded) and γIndividual normalized (open) DNA samples measured under path 3 were converted to distances assuming κ2 = 2/3 and using a Förster's radius of 5.1 nm. The crystal structure of Rhodamine 6G terminally attached to the 5′ end of a DNA double helix (PDB ID: 2V3L) was used as a reference. Using PyMol, distances between the phosphate backbone and the oxygen atom of the central xanthene chromophore were calculated as a function of basepair separation. Error bars indicate the standard deviation for replicate measurements made under the same optical path. The shaded regions correspond to distances calculated from the raw EPR histogram peak widths. In this simple analysis, which does not take into account dye positioning or orientation, γ-normalization results in FRET efficiencies in closer agreement to existing data.
Figure 5.
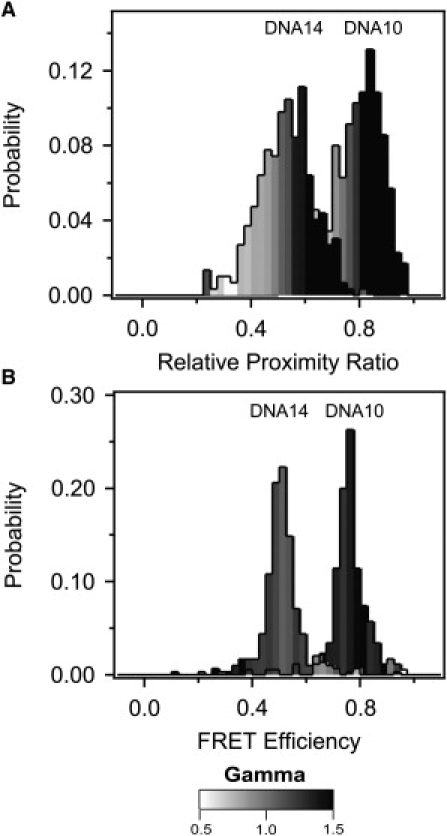
Distribution of γ within the FRET peak for DNA. (A) The mean γ-value for all molecules within each bin of the uncorrected relative proximity ratio histogram for DNA10 and DNA14 measured under optical path 1. The value of mean γ for each bin of the FRET histogram is colored according to the scale bar shown beneath the panels. An increasing relative proximity ratio correlated with increased γ for uncorrected measurements. (B) The mean γ-value for all molecules within each bin of the corrected FRET efficiency histogram for DNA10 and DNA14 after γIndividual normalization. The γ-values are more evenly distributed in the FRET histogram but γ-outliers still show outlying FRET values.
Effect of γ-normalization on structural calculations using FRET values
To confirm that the different γ-normalization methods are producing the true FRET efficiency, we performed some basic structural calculations using Eq. 1 to convert FRET efficiencies measured from the DNA rulers into dye-separation distances. A major challenge in calculating distances from FRET data is accounting for the relative orientations of the transition dipoles of the donor and acceptor (24). This effect is captured in a parameter termed κ in common calculations of the Förster radius. A widely used assumption is that the dyes are freely rotating on the measurement timescale, which gives a value of κ2 = 2/3. Limits can be placed on κ through measurement of the anisotropy, but this does not remove uncertainty regarding the dye orientation (25). Despite this uncertainty, distance calculations using κ2 = 2/3 have been repeatedly confirmed by high resolution methods (26,27). The intricacies of structural calculation are beyond the scope of this study so we have used the published Förster radius (R0 = 5.1 nm) that includes the assumption of κ2 = 2/3. In comparing our values (derived from FRET measurements) to distances measured from the crystal structure of 5′ fluorescently-labeled DNA (28), we find that normalization improves the agreement between smFRET and high-resolution structural data (Fig. 4 C).
Application of γ-normalization to protein samples
The different DNA samples showed little difference in φA/D. To demonstrate the effects of γ-normalization on samples with different quantum yields, we measured intramolecular smFRET data from two doubly-labeled proteins. Because the protein surface is chemically variable, the quantum yield of protein-attached dyes can be greatly affected by the local environment. We used the synaptic scaffold protein PSD-95, which contains tandem N-terminal PDZ domains connected by a short linker. We created a series of constructs containing a single cysteine within each domain for fluorescent labeling. We introduced the mutation Y236C in PDZ2 and paired this with one of two mutations in PDZ1: E135C (PSD21) or S142C (PSD20). The protein numbering is arbitrary and does not relate to the fluorophore separation, as the protein structure is not known. The dye separations for these two labeling site combinations were expected to be similar. The constructs differ at only one of the labeling sites in which the dye position was moved by only seven residues in the primary sequence. Despite the proximity of the labeling site positions, the ensemble quantum yield measurements showed that donor φ varied with the labeling position, thus changing φA/D (Table S4). The mean EPR values determined using optical path 1 for each of the protein samples were also divergent (Fig. 6 A and Table S8). Differences in γPhotobleach agreed with the measured differences in φA/D, which predict higher γ for PSD 20 (Fig. 6 B and Table S5). Normalization by γ showed that the two samples had similar true FRET efficiency despite differing in apparent EPR. This confirmed that differences in raw EPR were the result of changes in the photophysical properties of the dye molecules, rather than underlying fluorophore separation.
Figure 6.
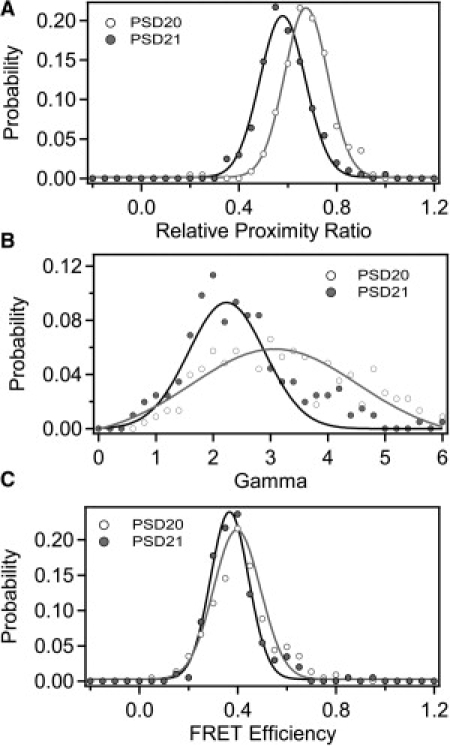
Application of γ normalization to protein samples. Two different PSD-95 mutants are shown: PSD20 contained the mutations S142C-Y236C (open); PSD21 contained the mutations E135C-Y236C (shaded). Proteins were randomly labeled with a mixture of Alexa 555 and Alexa 647. Data shown was measured under optical path 1. (A) Histogram of EPR for PSD20 (open) and PSD21 (shaded). Data points are shown as solid circles with the Gaussian fit shown as a solid line. (B) Histogram of γ-values compiled from individual photobleaching events. (C) Histograms of FRET efficiency normalized with γIndividual. Because of differences in γ, samples with similar FRET display differing EPR.
Altering the optical path has the same effect on protein EPR as was observed in DNA (Table S8 and Fig. S3 A). Normalization by γEmpirical, γGlobal, and γIndividual all proved effective at reducing the effect of optical path manipulations with 77%, 89%, and 95% reductions in mean standard deviation, respectively (Table S8 and Fig. S3 D). Thus, γ-normalization is similarly effective in achieving convergence of the mean FRET values for protein and DNA. Interestingly, applying individual γ-normalization to protein FRET histograms did not result in the same magnitude reduction in peak width observed in the DNA FRET histograms (Fig. S3 E). Examination of the γ-distribution within the FRET peak shows a similar dependence of γ on EPR that is removed upon γ-normalization, but this was not accompanied by a similar width reduction (Fig. S4). This suggests that factors other than γ-variability, such as dynamic molecular properties, are limiting factors in the distribution width.
Discussion
When γ is near 1, normalization has a small impact on the FRET efficiency. It is reasonably straightforward to set the relative detection efficiency (ηA/D) equal to one, but the quantum yields of dyes conjugated to biological molecules are more difficult to control. Quantitative interpretation of FRET microscopy experiments requires normalizations for these effects to allow comparisons between different instruments, different optical paths, or between samples with different dye quantum yields. Accurate conversion of FRET efficiency to dye separations also requires proper normalization of the donor intensity by γ.
Simple normalization using the manufacturer's transmission data for the optical elements facilitates comparison to results on other instruments (Fig. 2 B and Table 2). Empirical measurement of transmission further improved convergence, which suggests that factors other than the optical filters contribute to the detection efficiency (Fig. 2 C and Table 2).
Accounting for detection efficiency is insufficient to get the true FRET efficiency (see Eqs. 3 and 4) which requires normalization for the quantum yield (φ). Despite successful cross-validation of two quantum yield standards, normalization by γEmpirical did not improve convergence. This suggests that some other parameter is affecting the single-molecule FRET measurements beyond fluorophore quantum yield.
Normalization using γPhotobleach was the most effective at achieving convergence of the EPR values (Fig. 4 A). Our results show that the global γ-factor was sufficient to correct the mean FRET efficiency (Fig. 4 A and Table 2). A universal γ-factor was less effective because it fails to account for actual variability in γ between samples (Fig. 2 B and Fig. 4 A). However, only normalization with individual γ-factors for each molecule resulted a narrowing of width of smFRET distributions (Fig. 4 B).
Both systematic factors, including instrumental or photophysical effects as well as dynamic molecular motion, can contribute to broadening the widths of FRET efficiency distribution peaks in smFRET experiments (4,11,29). Here we show for the first time, to our knowledge, that γ-variability also contributes to broadening FRET histogram widths. Molecules with FRET values near the edges of the FRET distribution also commonly had outlying γ-values and per-molecule γ-normalization brings these values closer to the mean (Fig. 5 and Fig. S4).
Applying γ-normalization has less effect on convergence at low and high FRET where EPR is minimally sensitive to changes in the optical path. This artifact occurs because calculations are being made with either the donor or acceptor emission near zero. At these regions, even alterations in the optical path did not produce a large divergence of the raw EPR. Despite poor performance on convergence, γ-normalization still improves the accuracy of structural calculations when γ is not near 1 (Fig. 4 C). This may arise because molecules that, due to background subtraction, appear below FRET = 0 or above FRET = 1, can be shifted away from these erroneous FRET values.
Most molecules have γ-values distributed normally about the mean, but outliers can differ by more than a factor of two at exclusively higher γ-values (Fig. 3, B and C). Single-molecule intensity distributions lack equivalent outliers varying by severalfold from the mean (Fig. S2 and data not shown). Thus, γ-outliers are not explained by anomalous single-molecule quantum yield. To rule out the possibility that a bleached acceptor alters the donor emission and thereby affects γ, we compared the donor intensity measured from a singly-labeled protein sample to donor intensity using the same site on a doubly-labeled sample after the acceptor was intentionally photobleached. Donor emission is affected by acceptor photobleaching-intermediates at very small fluorophore separations (30), but we found no affect at the fluorophore separations used here (data not shown).
Examination of the shape of the diffraction-limited image spot for molecules with outlying γ-values showed deviation from a symmetric two-dimensional Gaussian (data not shown). In microscope images, γ-outliers commonly localize to the image periphery (data not shown), consistent with the finding for diffusing single molecules that γ depends on the position in the focal spot (6). Focus and channel mapping of the donor and acceptor images is less effective at the image periphery (data not shown). The focal plane differs for the donor and acceptor because of differences in wavelength. Adjustment of either of these factors changes the measured intensity, affecting γ and FRET. Because each recording requires new alignment and focus, which is typically carried out manually, additional γ-variability may be introduced.
Therefore, the γ-outliers may be due to artifactual differences in detection efficiency introduced during image recording or processing. In agreement with this notion, it has been noted that one can change the value of γ by misaligning the detectors when measuring diffusing single molecules (4,5). Empirical measurements of the terms composing γ cannot account for aberration this of kind. As a consequence of the fact that γ outliers are not representative of the population, applying a γ-cutoff as a means of selecting accepted molecules could further affect peak width and shape.
Acknowledgments
The authors thank Stuart McLaughlin for technical assistance and helpful discussions and Axel Brunger and Celia Marshik for comments on the manuscript.
The authors acknowledge the National Institutes of Mental Health for funding to M.E.B. (grant No. MH081923) and a CASI award from the Burroughs Wellcome Fund to K.W.
Supporting Material
References
- 1.Stryer L., Haugland R.P. Energy transfer: a spectroscopic ruler. Proc. Natl. Acad. Sci. USA. 1967;58:719–726. doi: 10.1073/pnas.58.2.719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Stryer L. Fluorescence energy transfer as a spectroscopic ruler. Annu. Rev. Biochem. 1978;47:819–846. doi: 10.1146/annurev.bi.47.070178.004131. [DOI] [PubMed] [Google Scholar]
- 3.Lakowicz J.R. Springer; New York: 2006. Principles of Fluorescence Spectroscopy. [Google Scholar]
- 4.Nir E., Michalet X., Weiss S. Shot-noise limited single-molecule FRET histograms: comparison between theory and experiments. J. Phys. Chem. B. 2006;110:22103–22124. doi: 10.1021/jp063483n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lee N.K., Kapanidis A.N., Weiss S. Accurate FRET measurements within single diffusing biomolecules using alternating-laser excitation. Biophys. J. 2005;88:2939–2953. doi: 10.1529/biophysj.104.054114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dahan M., Deniz A.A., Weiss S. Ratiometric measurement and identification of single diffusing molecules. Chem. Phys. 1999;247:85–106. [Google Scholar]
- 7.Ha T., Ting A.Y., Weiss S. Single-molecule fluorescence spectroscopy of enzyme conformational dynamics and cleavage mechanism. Proc. Natl. Acad. Sci. USA. 1999;96:893–898. doi: 10.1073/pnas.96.3.893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ferreon A.C.M., Gambin Y., Deniz A.A. Interplay of α-synuclein binding and conformational switching probed by single-molecule fluorescence. Proc. Natl. Acad. Sci. USA. 2009;106:5645–5650. doi: 10.1073/pnas.0809232106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schuler B., Lipman E.A., Eaton W.A. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature. 2002;419:743–747. doi: 10.1038/nature01060. [DOI] [PubMed] [Google Scholar]
- 10.Best R.B., Merchant K.A., Eaton W.A. Effect of flexibility and cis residues in single-molecule FRET studies of polyproline. Proc. Natl. Acad. Sci. USA. 2007;104:18964–18969. doi: 10.1073/pnas.0709567104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Merchant K.A., Best R.B., Eaton W.A. Characterizing the unfolded states of proteins using single-molecule FRET spectroscopy and molecular simulations. Proc. Natl. Acad. Sci. USA. 2007;104:1528–1533. doi: 10.1073/pnas.0607097104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Boukobza E., Sonnenfeld A., Haran G. Immobilization in surface-tethered lipid vesicles as a new tool for single biomolecule spectroscopy. J. Phys. Chem. B. 2001;105:12165–12170. [Google Scholar]
- 13.Ha T., Enderle T., Weiss S. Probing the interaction between two single molecules: fluorescence resonance energy transfer between a single donor and a single acceptor. Proc. Natl. Acad. Sci. USA. 1996;93:6264–6268. doi: 10.1073/pnas.93.13.6264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Deniz A.A., Dahan M., Schultz P.G. Single-pair fluorescence resonance energy transfer on freely diffusing molecules: observation of Förster distance dependence and subpopulations. Proc. Natl. Acad. Sci. USA. 1999;96:3670–3675. doi: 10.1073/pnas.96.7.3670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dietrich A., Buschmann V., Sauer M. Fluorescence resonance energy transfer (FRET) and competing processes in donor-acceptor substituted DNA strands: a comparative study of ensemble and single-molecule data. Rev. Mol. Biotechnol. 2002;82:211–231. doi: 10.1016/s1389-0352(01)00039-3. [DOI] [PubMed] [Google Scholar]
- 16.Sabanayagam C.R., Eid J.S., Meller A. Using fluorescence resonance energy transfer to measure distances along individual DNA molecules: corrections due to nonideal transfer. J. Chem. Phys. 2005;122:061103–061105. doi: 10.1063/1.1854120. [DOI] [PubMed] [Google Scholar]
- 17.Iqbal A., Arslan S., Lilley D.M. Orientation dependence in fluorescent energy transfer between Cy3 and Cy5 terminally attached to double-stranded nucleic acids. Proc. Natl. Acad. Sci. USA. 2008;105:11176–11181. doi: 10.1073/pnas.0801707105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Woźniak A.K., Schröder G.F., Oesterhelt F. Single-molecule FRET measures bends and kinks in DNA. Proc. Natl. Acad. Sci. USA. 2008;105:18337–18342. doi: 10.1073/pnas.0800977105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ranjit S., Gurunathan K., Levitus M. Photophysics of backbone fluorescent DNA modifications: reducing uncertainties in FRET. J. Phys. Chem. B. 2009;113:7861–7866. doi: 10.1021/jp810842u. [DOI] [PubMed] [Google Scholar]
- 20.Karstens T., Kobs K. Rhodamine B and rhodamine 101 as reference substances for fluorescence quantum yield measurements. J. Phys. Chem. 1980;84:1871–1872. [Google Scholar]
- 21.Ha T., Ting A.Y., Weiss S. Temporal fluctuations of fluorescence resonance energy transfer between two dyes conjugated to a single protein. Chem. Phys. 1999;247:107–118. [Google Scholar]
- 22.Roy R., Kozlov A.G., Ha T. Dynamic structural rearrangements between DNA binding modes of E. coli SSB protein. J. Mol. Biol. 2007;369:1244–1257. doi: 10.1016/j.jmb.2007.03.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Watkins L.P., Chang H., Yang H. Quantitative single-molecule conformational distributions: a case study with poly-(L-proline) J. Phys. Chem. A. 2006;110:5191–5203. doi: 10.1021/jp055886d. [DOI] [PubMed] [Google Scholar]
- 24.van der Meer B.W. Kappa-squared: from nuisance to new sense. Rev. Mol. Biotechnol. 2002;82:181–196. doi: 10.1016/s1389-0352(01)00037-x. [DOI] [PubMed] [Google Scholar]
- 25.Muschielok A., Andrecka J., Michaelis J. A nano-positioning system for macromolecular structural analysis. Nat. Methods. 2008;5:965–971. doi: 10.1038/nmeth.1259. [DOI] [PubMed] [Google Scholar]
- 26.dos Remedios C.G., Moens P.D.J. Fluorescence resonance energy transfer spectroscopy is a reliable “ruler” for measuring structural changes in proteins. Dispelling the problem of the unknown orientation factor. J. Struct. Biol. 1995;115:175–185. doi: 10.1006/jsbi.1995.1042. [DOI] [PubMed] [Google Scholar]
- 27.Weiss S. Measuring conformational dynamics of biomolecules by single molecule fluorescence spectroscopy. Nat. Struct. Mol. Biol. 2000;7:724–729. doi: 10.1038/78941. [DOI] [PubMed] [Google Scholar]
- 28.Neubauer H., Gaiko N., Volkmer A. Orientational and dynamical heterogeneity of rhodamine 6G terminally attached to a DNA helix revealed by NMR and single-molecule fluorescence spectroscopy. J. Am. Chem. Soc. 2007;129:12746–12755. doi: 10.1021/ja0722574. [DOI] [PubMed] [Google Scholar]
- 29.Cherny D.I., Eperon I.C., Bagshaw C.R. Probing complexes with single fluorophores: factors contributing to dispersion of FRET in DNA/RNA duplexes. Eur. Biophys. J. 2009;38:395–405. doi: 10.1007/s00249-008-0383-z. [DOI] [PubMed] [Google Scholar]
- 30.Ha T., Xu J. Photodestruction intermediates probed by an adjacent reporter molecule. Phys. Rev. Lett. 2003;90:223002. doi: 10.1103/PhysRevLett.90.223002. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


