Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2010 Apr 16;26(11):1409–1415. doi: 10.1093/bioinformatics/btq159

HIV classification using the coalescent theory

Ingo Bulla 1,*, Anne-Kathrin Schultz 1, Fabian Schreiber 1, Ming Zhang 2, Thomas Leitner 2, Bette Korber 2,3, Burkhard Morgenstern 1, Mario Stanke 1
PMCID: PMC2913666  PMID: 20400454

Abstract

Motivation: Existing coalescent models and phylogenetic tools based on them are not designed for studying the genealogy of sequences like those of HIV, since in HIV recombinants with multiple cross-over points between the parental strains frequently arise. Hence, ambiguous cases in the classification of HIV sequences into subtypes and circulating recombinant forms (CRFs) have been treated with ad hoc methods in lack of tools based on a comprehensive coalescent model accounting for complex recombination patterns.

Results: We developed the program ARGUS that scores classifications of sequences into subtypes and recombinant forms. It reconstructs ancestral recombination graphs (ARGs) that reflect the genealogy of the input sequences given a classification hypothesis. An ARG with maximal probability is approximated using a Markov chain Monte Carlo approach. ARGUS was able to distinguish the correct classification with a low error rate from plausible alternative classifications in simulation studies with realistic parameters. We applied our algorithm to decide between two recently debated alternatives in the classification of CRF02 of HIV-1 and find that CRF02 is indeed a recombinant of Subtypes A and G.

Availability: ARGUS is implemented in C++ and the source code is available at http://gobics.de/software

Contact: ibulla@uni-goettingen.de

Supplementary Information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

A coalescent model incorporating recombination was first introduced by Hudson (1983). In the presence of recombination, the genealogy of a set of sequences can be represented as a so-called ancestral recombination graph (ARG) rather than a tree (Griffiths and Marjoram, 1997). In human immunodeficiency virus (HIV) recombination is frequent and recombinant forms of the virus that spread are called circulating recombinant forms (CRFs). In current nomenclature, sequences of the epidemiologically most relevant clade, HIV-1 Group M, are classified into 9 subtypes and 43 CRFs [see Los Alamos National Lab (LANL)-database; http://www.hiv.lanl.gov]. The CRFs have (usually multiple) recombination breakpoints between unrecombined segments of the ‘pure’ parental subtypes.

Algorithms for subtype classification and breakpoint detection of HIV-1 sequences are based on the classification system of HIV-1 (Robertson et al., 2000). Hence, their quality highly depend on this system. But due to the evolution of HIV-1 nomenclature, developed in real time in conjunction with emerging knowledge of the global diversity of the virus, the current nomenclature has anomalies. E.g. the phylogenetic distance between Subtypes B and D is relatively small compared to that of other pairs of subtypes. In fact, it is more like the distance of a pair of subsubtypes (Robertson et al., 2000).

Furthermore, several questions about the current classification system of sequences are unanswered or debated: There are 8 complete and over 400 partial HIV-1 Group M genomes in the LANL-database, which are ‘undefined’, i.e. belong neither to a subtype nor to a CRF (this is due to many reasons, e.g. parental sequences have not been identified yet). Additionally, in the nomenclature system CRF02 is considered to be a recombinant of subtype A and G, but recently some evidence has been presented in the literature suggesting that CRF02 would actually be better described as a subtype and subtype G as a recombinant (Abecasis et al., 2007; Lemey et al., 2009). A few years ago it was also debated whether CRF01 is in fact a pure subtype (Anderson et al., 2000).

Moreover, assignments in the database are reflected on diverse classification strategies employed by different investigators in the primary literature. Therefore, it is desirable to have tools for classifying the HIV sequence set systematically based on a comprehensive coalescent model accounting for complex recombination patterns.

While the problem of recombination has been well documented in HIV-1, recombination also occurs in the other lentiviruses. Moreover, intra-segmental recombination has been reported from a large variety of other viruses, e.g. coronaviruses, flaviviruses, alphaviruses, rotaviruses, influenzaviruses, hantaviruses, arenaviruses and avian oncoviruses (Bergmann et al., 1992; Charrel et al., 2001; Hahn et al., 1988; Jarvis and Kirkegaard, 1992; Lai, 1992; Leitner, 2002; Orlich et al., 1994; Shaikh et al., 1978; Sibold et al., 1999; Worobey et al., 1999). Furthermore, recombination plays also a role in other species, such as bacteria (Feil and Spratt, 2001; Goss et al., 2005). Thus, it is possible that many virus systems would benefit from a systematic classification that explicitly includes recombination (Foley and Fauquet, 2008).

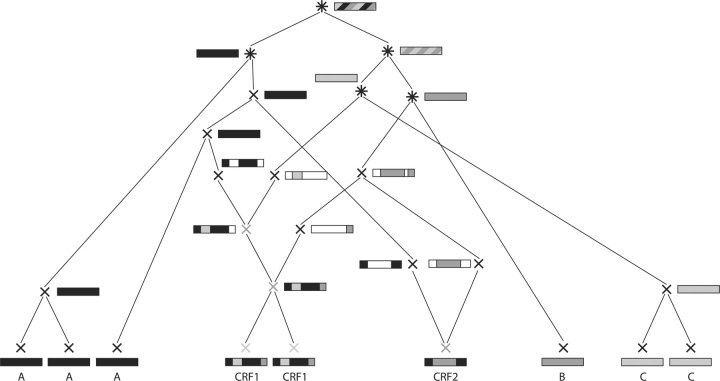
Our work addresses the simpler subproblem to score classifications of given input sequences of some virus species. ‘Classification’ here denotes a partitioning of the input sequences into several subtypes and, if applicable, CRFs. To score a classification, we reconstruct ARGs of the input sequences under restrictions determined by the classification (see Fig. 2 for an example or Supplementary Fig. 12 for a colored version). These restrictions are imposed in order to ensure that the reconstructed ARGs do not contradict the classification under consideration. Then, we find the ARG with maximal likelihood by means of Markov chain Monte Carlo (MCMC) methods. The likelihood of the most likely ARG is interpreted as a score for the classification.

Fig. 2.

Fig. 2.

Open in a new tab

A legal ARG corresponding to the classification given in Figure 1. At the bottom, the nine input (tip) sequences with their classification are shown. The tip sequences are defined to be generated at time zero. Looking from bottom to top (i.e. into the past), two nodes coalescing to one (parental) node, represent the event of these two nodes finding their most recent common ancestor. A node splitting into two parental nodes represents a recombination event. Single-color boxes show the subtype of the node. Horizontally segmented boxes show for a recombinant sequence the parental subtypes of each segment. Diagonally shaded boxes show the different subtypes the node belongs to. White parts in boxes indicate positions not contributing to the tip sequences and, hence, of which we do not keep track. For recombination events, they also illustrate the positions of the recombination breakpoints. For further details, see Section 2.3.

Finally, we apply ARGUS, the implementation of our algorithm, to decide between the two main hypotheses regarding CRF02.

Although up to now ∼50 tools for classification of HIV-1 genomes, identification of recombinants and precise breakpoint detection have been developed—e.g. Recombinant Identification Program (RIP) (http://www.hiv.lanl.gov/content/sequence/RIP/RIP.html), REGA HIV-1 Subtyping Tool (referring to the Rega Institute for Medical Research) (de Oliveira et al., 2005) and Recco (Maydt and Lengauer, 2006)—, to our knowledge, our particular problem fits only roughly into the scope of one algorithm (VisRD, described in Lemey et al., 2009). A comparison with respect to performance and scope between our algorithm and VisRD is carried out in Section 3.3.

Moreover, the software package Lamarc (Kuhner et al., 2000) allows for sampling ARGs, but it assumes that recombination events only involve one breakpoint. However, HIV recombinants usually have more than one breakpoint. Moreover, Lamarc does not perform an explicit breakpoint detection, but tries to find them by chance. Although this approach is suitable for most situations, it will not lead to satisfying results in case of highly recombining viruses with multiple breakpoints.

Up to now, researchers confronted with the task to classify genome sequence data strongly affected by recombination with multiple crossovers normally segmented the aligned genomes in recombination-free parts [Simplot (Lole et al., 1999) is a widespread tool for this task] and analyzed these parts with traditional phylogenetic tools. The information stemming from different parts of the genome had to be assembled by ad hoc methods (Abecasis et al., 2007; Bailes et al., 2003; Lukashev et al., 2005).

2 METHODS

A classification is a partition of the input sequences {s1,…, sn} into disjoint sets P1,…, Pmp and R1,…, Rmr, where each set Pi contains the sequences belonging to the i-th (pure) subtype and each set Ri contains the ones belonging to the i-th CRF. An example of a classification is given in the upper part of Figure 1 (see Supplementary Fig. 11). The algorithm takes the input sequences and a hypothesis classification and scores the classification by constructing a likely ARG for the sequences under this classification.

Fig. 1.

Fig. 1.

Open in a new tab

Example of a classification of nine sequences into three subtypes (A–C) and two CRFs (CRF1, CRF2). At the bottom the recombinants have been segmented and the segments assigned a subtype by jpHMM.

Notice that CRFs (in our notation) are allowed to be composed of less than three epidemiologically independent sequences violating the definition of a CRF (Robertson et al., 2000). Nevertheless, we will use the word ‘CRF’ as this is the most typical application.

2.1 Preparing step

All input sequences are aligned and only positions composed entirely of non-gaps are further considered. Then, the breakpoints of the input sequences designated as recombinants are identified and the subtypes of the resulting segments are classified by jumping profile hidden Markov model (jpHMM), introduced by Schultz et al. (2006) and Zhang et al. (2006). An example of this step is shown in the lower part of Figure 1. We use jpHMM for breakpoint detection since we need a fully automatically working tool.

jpHMM is a probabilistic generalization of the jumping-alignment approach introduced by Spang et al. (2002). Given a partition of the aligned input sequence family into known sequence subtypes (in our case P1,…, Pmp), this model can jump between states corresponding to these different subtypes, depending on which subtype is locally most similar to a query sequence. Jumps between different subtypes are indicative of intersubtype recombinations.

More strictly, assume the subtypes occurring in the considered classification are denoted by S1,…, Smp and the length of an alleged recombinant sequence is ℓ. Then, jpHMM provides a mapping f : ℕℓ → {S1,…, Smp}, i.e. f assigns a subtype to each position of the query sequence. This mapping will also be called the segmentation of the query sequence.

For each CRF, a single segmentation is calculated by applying jpHMM to one of the sequences of the CRF. See Supplementary Section 3.1 for additional details.

2.2 Coalescent model

The non-recombinant coalescent genealogy was introduced by Kingman (1982a, b) and extended to the recombinant case by Hudson (1983). Apart from Hudson's back-in-time algorithm, the spatial algorithm of Wiuf and Hein (1999) allows for constructing the coalescent with the recombination process. We apply a formulation of the recombinant genealogy similar to the one introduced in Kuhner et al. (2000). Like Kuhner et al. (2000), we discard lineages not contributing at least one site to the sample and we discard recombination events that do not separate at least two sites contributing to the sample. The difference of our formulation consists in allowing for multiple breakpoints. I.e., the probability of a recombination event taking place is the same as in Hudson (1990) and Kuhner et al. (2000), but multiple breakpoints can occur due to the recombination event. Adapting the framework of Hudson (1990) and Kuhner et al. (2000) to our setting is a simplification, but justified by the fact that the affected quantities play a very minor role in our algorithm. Using jpHMM with a sufficiently low jump probability to predict the breakpoints prevents the recombination events from yielding too many breakpoints, which would lead to strongly fragmented sequences. As customary (Hein et al., 2005; Wakeley, 2008), we call a recombinant genealogy an ARG.

The likelihood of an ARG G is the product of the probability of the (sequence) data D with respect to the ARG, P(D|G), and the probability of the ARG given the evolution parameters, P(G|Θ, r). Here, Θ = 2Nμ and r = C/μ, where N is the effective population size, C the per-site recombination rate and μ the per-site neutral mutation rate. See Supplementary Section 3.2 for additional details.

2.3 Restrictions to the genealogy

We approximate the most likely ARG G of the input HIV sequences, where we impose restrictions to the approximating ARG Ĝ according to the classification to be scored. The score of the classification is then given by P(D|Ĝ). In detail, the restrictions are given in the following (see Fig. 2 and Supplementary Fig. 12 for the symbols).

In the lower part of the ARG, sequences of subtypes that are composed of more than one sequence or are present in the genome of a CRF are only allowed to coalesce and only with sequences of the same subtype. Sequences of multi-sequence CRFs (light gray ‘×’ in Fig. 2 and orange ‘×’ in the Supplementary Fig. 12) are only allowed to coalesce and only with sequences of the same CRF. Sequences from different subtypes can only coalesce if they are the only sequence of their subtype left ((black ‘*’ in Fig. 2, brown ‘*’ in the Supplementary Fig. 12)). Furthermore, coalescing sequences of the same subtype (black ‘×’ in both figures) generate a sequence belonging to the same subtype as their children.

The last (or only) sequence of a CRF (gray ‘×’ in Fig. 2, purple ‘×’ in the Supplementary Fig. 12) is obliged to recombine. Breakpoints (multiple) have to be chosen such that the parental subtypes get separated and recombination events have to take place until all parental subtypes are separated. The final sequences generated by this process only contain one subtype. This subtype is interpreted as the subtype of these (final) sequences. They are allowed to coalesce with other sequences of the same subtype. No sequence of their subtype is allowed to coalesce with a sequence of another subtype before having coalesced with these sequences.

This set of restriction rules (a more formal description is given in Supplementary Section 1) is imposed in order to enforce ARGs, which are plausible under the condition that the underlying classification is a reasonable one. This would not be the case, e.g. if Subtype A sequences coalesced with Subtype C sequences before coalescing within their respective subtype or the two CRF1 sequences recombined independently of each other without coalescing first.

These rules imply the assumption that intra-subtype recombinations and the recombinations occurring before the subtypes were formed are negligible. The negligence of the first type of recombination simply means that we do not aim to obtain a classification resolving finer than the level of subtypes. Neglecting the second type can be justified by the HIV subtypes being separated by founder effects (Rambaut et al., 2004). Since alternative methods are restricted by far stronger assumptions, we refrain from analyzing our simplifications in more detail.

2.4 MCMC

After having constructed an initial ARG, the likelihood of the ARG is iteratively maximized using MCMC methods. More precisely, in a first step an initial ARG G1 is sampled from the conditional coalescent distribution. Thereafter, by modifying the ARG slightly and accepting or rejecting these modifications based on how they affect the likelihood of the ARG, a Markov chain {Gi}i∈ℕ is generated. If no significant improvement of the likelihood seems achievable any more, the chain is stopped at the current chain position n and the probability of the data D given the most likely ARG

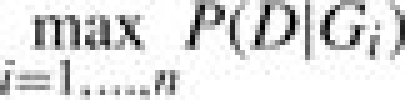graphic file with name btq159m1.jpg (1)

is interpreted as a score for the classification (see Supplementary Section 3.3 for details). We stop the MCMC algorithm at step n > M if

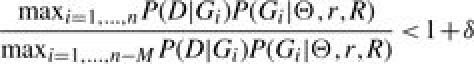graphic file with name btq159um1.jpg

with M = 1000 and δ = 10−8 (chosen by rule of thumb). Here, P(G|Θ, r, R) denotes the probability of the ARG G given the parameters Θ and r, and restricted to our rules R. Due to the small influence of this quantity, we used P(G|Θ, r) instead of P(G|Θ, r, R) for the sake of simplicity where appropriate. Normally, the MCMC algorithm is carried out several times for different initial ARGs. Details about the MCMC algorithm are explained in the Supplementary Material (Section 2). The parameter Θ was estimated with Lamarc 2.1.3 (Kuhner, 2006).

2.5 Extension to unknown subtypes

In the genome of several CRFs, segments are commonly classified to belong to an unknown subtype. To address classification problems involving unknown subtypes, we have to adapt our algorithm appropriately as described in Supplementary Section 3.6.

3 RESULTS

Test settings:

to test ARGUS, three different settings are tested:

  • T1 a representative selection of 40 HIV-1 Group M sequences from Subtypes A to K (presented in Supplementary Section 5.1)

  • T2 a classification involving all features offered by ARGUS except unknown subtypes

  • T3 two classifications corresponding to the situations that

    • CRF02 is a CRF and G a subtype or

    • CRF02 is a subtype and G a CRF,

The first test setting is intended to show the ability of ARGUS to construct a phylogenetic tree (without recombination). This is a subproblem also arising when reconstructing an ARG and, hence, must be accomplishable by ARGUS. The second setting demonstrates the ability of ARGUS to differentiate between similar classifications of real-world complexity. We refrain from incorporating unknown subtypes, since this would prohibit performing the test fully automatically. Finally, the last setting shows the applicability of ARGUS to the task of further analyzing subtype G and CRF02, to determine whether they are more likely to be recombinants or ancestral subtypes; this question was raised by earlier analysis in Abecasis et al. (2007) and Lemey et al. (2009).

Parameter estimation:

the model uses two different mutation rates since increasing their number does not improve the results, whereas a constant mutation rate performs considerably worse (data not shown). The per-site recombination rate C is set to 10−4 (Zhuang et al., 2002). The parameter Θ is estimated by applying Lamarc 2.1.3 to 10 randomly chosen HIV-1 Group M sequences, classified as pure subtypes in the LANL HIV sequence database. Disabling recombination and growth, Lamarc yields Θ = 1.25. The gamma distribution parameter of the General Time-Reversible (GTR) model is estimated to be α = 0.416 by Findmodel. The length of the simulated sequences is 8500 bp, which is approximately the length of the HIV-1 Group M sequences used in the application in Section 3.2 (after removal of gap-affected positions).

3.1 Simulation studies

3.1.1 T2—with recombination

This test setting is composed of two parts, for each we choose an original classification and a number of alternative classifications for testing. Then, we perform the following steps for each part:

  1. Simulate an ARG according to the original classification;

  2. Simulate the mutation process on the ARG (from the root downwards), thereby obtain simulated tip sequences;

  3. Score both the original as well as one or more plausible alternative classifications using the simulated tip sequences.

When the original classification scores higher than the test classifications, this indicates that ARGUS works for the analyzed setting.

The details are given in Supplementary Section 5.2. In short, we obtain the following results:

  • In the first part, we compare nine classifications (including the original classification), in the second one 6. In both parts, 15 sequences are to be classified.

  • Simulating nine ARGs and the mutation process five times per ARG (in both parts), our algorithms succeeds to rate the original classification highest in 43, respectively, 44 out of 45 cases.

3.1.2 T3—simulation of CRF02 case

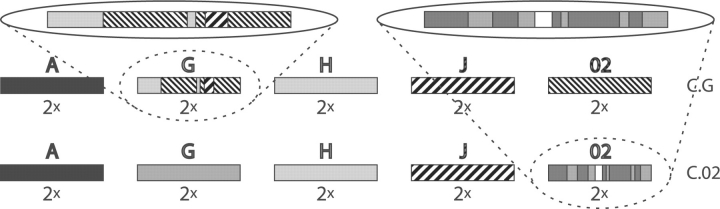
In Section 3.2, we will apply ARGUS to the question whether Subtype G is actually a pure subtype and CRF02 is a recombinant form (like assumed in Robertson et al., 2000) or G is a recombinant form and CRF02 is a pure subtype (like claimed in Abecasis et al., 2007). The classification systems that best describe the genealogical situation assumed in Robertson et al. (2000) and Abecasis et al. (2007), respectively, are given in Figure 3 (see Supplementary Fig. 13). We choose to use two sequences per subtype and CRF, respectively, since at the time of the beginning of our project, only two full-length sequences of Subtype J were available and jpHMM occasionally experience difficulties in case of varying number of sequences per subtype or CRF, respectively.

Fig. 3.

Fig. 3.

Open in a new tab

Classifications used in Section 3.2 for deciding whether Subtype G or CRF02 (=02) is a pure subtype or a recombinant form, respectively. The white segment in the lower segmentation of CRF02, indicates a part of the genome designated to stem from an unknown subtype. Above the classifications, the segmentation of the alleged CRFs is shown magnified.

To verify whether ARGUS can theoretically distinguish between these two concrete classifications, we first simulate the data and apply the same testing method as in Section 3.1.1. This simulation test is in preparation to the application using the real sequences in Section 3.2. More precisely, our test is composed of two parts: in the first one, C.02 is the original classification, whereas in the second one C.G is the original classification. For both parts C.02 as well as C.G are used as test classifications. We generate 10 ARGs and simulate 5 sets of tip sequences for each ARG (for both parts).

When C.02 is scored in the first part, the position of the segment belonging to the unknown subtype has to be provided manually. Of course, this implies that ARGUS is provided with a part of the true classification instead of having to estimate it, which facilitates its task. Nevertheless, the introduced bias is most likely small as the unknown region is only short.

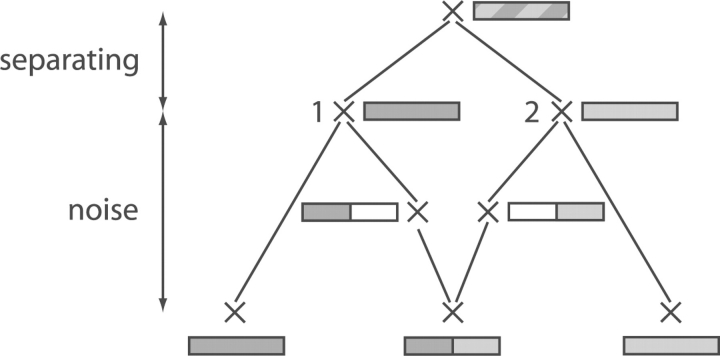
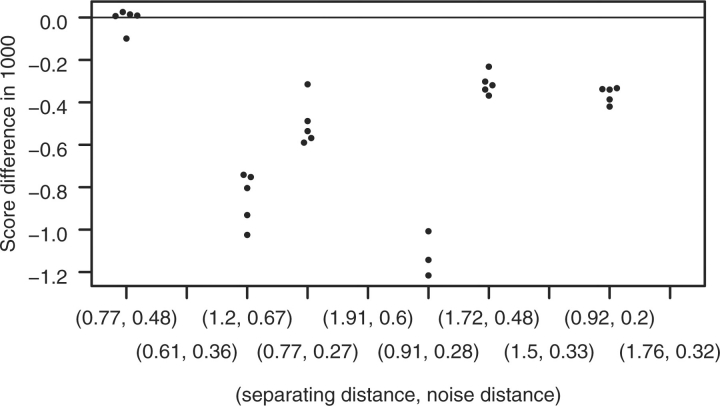
To characterize the ARGs with respect to how feasible the task is to decide which classification is the original one, we introduce two simple measures, explained in Figure 4 (separating and noise distance).

Fig. 4.

Fig. 4.

Open in a new tab

ARG illustrating the ‘separating distance’ and the ‘noise distance’. To be able to detect the recombination event, the nodes labeled 1 and 2 have to be sufficiently different. That is, the ‘separating distance’ needs to be large enough. Contrariwise, the larger the ‘noise distance’, the less precisely the sequences of Nodes 1 and 2 can be reconstructed from the tip sequences. That is, the ‘noise distance’ should be small. The definition of the separating and noise distance is given in Supplementary Section 4. For details about the symbolism used in the ARG, see Figure 2.

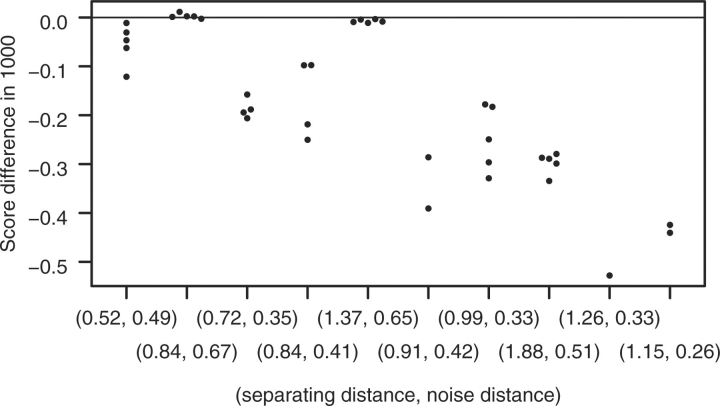
The results are shown in Figures 5 and 6. Apparently our theoretical considerations about the explanatory power of the ratio of separating and noise distance is supported by these testing results: In the first part (C.02 being the original classification), ARGUS fails for 1 out of 10 simulated ARGs to always (i.e. for all simulated tip sequences sets) score the original classification highest (applying ARGUS to C.G, for 4 ARGs jpHMM does not predict any recombination in Subtype G for any simulated tip sequences set). The ARG yielding misclassifications is the one with the lowest distance ratio. For this ARG, ARGUS fails for four tip sequences sets with the wrong classification scoring at most 26 points better than the original one.

Fig. 5.

Fig. 5.

Open in a new tab

Results for the test setting preparing for the application with C.02 being the original classification. On the vertical axis, log(P(D|GT)−logP(D|GO))·10−3 is given, with GT the most likely ARG for the test classification C.G and GO the most likely reconstructed ARG for the original classification C.02. On the horizontal axis, the separating and noise distance is given for each of the 10 generated ARGs. The ARGs are sorted by their ratio of separating to noise distance (increasing from left to right). All points on a vertical represent tests conducted for the same ARG with different tip sequence data (for clarity, points with very similar y-values were shifted slightly horizontally). In case jpHMM was not able to detect the CRF in C.G (i.e. the alleged CRF was diagnosed to belong to a pure subtype), the test results are omitted. For the MCMC algorithm, 20 different initial ARGs were used.

Fig. 6.

Fig. 6.

Open in a new tab

Results for the test setting preparing for the application with C.G being the original classification. On the vertical axis, (logP(D|GT)−logP(D|GO))·10−3 is given, with GT and GO, respectively, the most likely (reconstructed) ARG for C.02 and C.G, respectively. For more details (with the role of C.G and C.02 switched), see Figure 5.

In the second part (C.G being the original classification), ARGUS also fails for 1 out of 10 simulated ARGs to always score the original classification highest. The ARG yielding misclassifications is the one with the second lowest distance ratio, with the ones with the lowest and the fifth lowest ratio being quite close to failing. For the second ARG, ARGUS fails for four tip sequences sets with the wrong classification scoring at most 11 points better than the original one. For both parts, jpHMM always succeeds in detecting breakpoints in the alleged CRF of the original classification.

It should be stated that for the setting presented in Section 3.1.1, no significant relation between separating and noise distance and the reliability of ARGUS was observable (data not shown). Due to the simplicity of these distance measures and their obvious shortcomings, it has to be expected that they fail their purpose for some settings.

3.2 Empirical data

To decide which classification from Figure 3 describes the real situation better, we randomly choose two full-length sequences from Subtype A, G, H and J and from CRF02. Applying ARGUS to them (performing 30 runs of the MCMC algorithm for each classification), yields a maximum score of −33 513 for C.02 and −33 714 for C.G. During the tests in Section 3.1.2, we saw that—even under worse circumstances—the difference between the score of the wrong classification and the score of the right one never exceeded 26 (in case of a misclassification). Since the score of C.02 is higher than the one of C.G by more than 200, ARGUS indicates that the classification currently in use is the preferable one. We, therefore, conclude that the sequences of CRF02 are indeed recombinants of the Subtypes A and G rather than the sequences of Subtype G being recombinants of the ‘Subtypes’ H, J and CRF02.

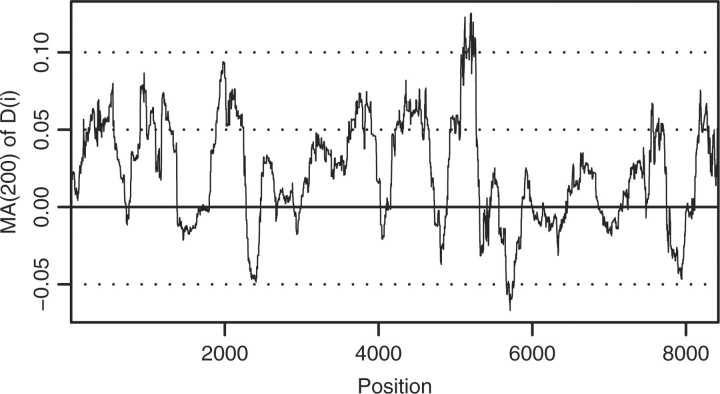
Since P(D|G) = ∏iP(Di|G) where Di is the tip sequence data at position i, we can easily analyze which part of the genome supports which classification better. To this end, we plot log P(Di|G)−log P(Di|G′) with G and G′ the most likely reconstructed ARGs of the two considered classifications (Fig. 7). Moreover, ARGUS provides the option to visualize the most likely ARG found by the MCMC algorithm using Graphviz (http://www.graphviz.org). For C.02, this visualization is shown in Supplementary Figure 10 in a processed form.

Fig. 7.

Fig. 7.

Open in a new tab

Moving average of D(i)≔logP(Di|G)−logP(Di|G′) with an averaging period of 200 positions. Here, G and G′ are the most likely reconstructed ARGs of the classifications C.02 and C.G, respectively. (see Fig. 3 for the classifications). At position i, the average of position i until i + 199 is given.

Abecasis et al. (2007) applied monophyly rules to determine whether G or CRF02 is a subtype. They obtained conclusive results for the region corresponding to positions 4393–4802 in HXB2, favoring CRF02 to be a subtype. This region corresponds to positions 3494–3928 in our analysis. Figure 7 shows that our results do not support this conclusion. One has to keep in mind that our method strongly differs from the one used by Abecasis et al. (2007). Moreover, on the one hand, Abecasis' method makes use only of a small part of the available information and applies a model of low complexity. On the other hand, our method is only able to test two alternative classifications fitting into the framework of ARGUS. In particular, the genome of CRFs is not allowed to be composed of other CRFs but only subtypes and no recombination events near to the root of the ARG are allowed. Both simplifying assumptions are violated in the real evolutionary history of HIV-1.

3.3 Comparison

We restrict our comparison to the version 3.0 of VisRD since, to our knowledge, VisRD is the only software tool that is suitable to address the task carried out by ARGUS. For the comparison, we use the first five ARGs generated according to classification C1.1 in Section 3.1.1. Due to the fact that VisRD has to be operated interactively, we restrict ourselves to a smaller test setting than the ones used in Section 3.1. For each ARG, we simulate three sets of tip sequences with a genome length of 8500 bp, using the simpler Jukes–Cantor model since VisRD does not allow for a GTR model. We apply the taxon ranking analysis of VisRD to these 15 sets of simulated tip sequences (with default windows and step size and—using Random Shuffling—default number of generated replicate datasets per set). VisRD finds no recombination at all. Moreover, the sequence triple VisRD determines to be the most likely to be a recombinant is not one of the two recombinant triplets for 11 out of 15 sets of simulated tip sequences.

3.4 Running time

For the test settings discussed in Section 3.1.1 and 3.1.2 of the article, the running time (on a Dell PowerEdge 2650 2, 80GHz/512 KB Xeon) of the MCMC algorithm lies between 6.9 and 394 min with a mean of 45 min and quartiles of 26, 37 and 55 min. The running time moderately depends on the data: considering all tested pairs of original and test classifications separately, the minimal mean of the running time is 28 min, the maximal 61 min. See Supplementary Section 3.5 for further details on the running time of ARGUS.

The running time of jpHMM is described in Schultz et al. (2006).

4 DISCUSSION

We presented ARGUS, a classification tool for recombining viruses, particularly HIV. Up to now, researchers intending to classify sequences of strongly recombining viruses had to analyze the sequences separately by segmenting their genome in recombination-free parts and applying traditional phylogenetic tools to them. The information stemming from different parts of the genome had to be assembled by ad hoc methods (if even possible at all). Here, ARGUS offers an alternative by applying sophisticated coalescent theory and MCMC-based methods and incorporating much larger parts of the available information in an integrated and model-based way.

The recently developed version 3.0 of VisRD does not perform well on the datasets analyzed in this article. Nevertheless, one has to keep in mind that the approach used by VisRD is in principle not adequate for a small number of sequence groups. In fact our test setting is the smallest possible for which the taxon ranking of VisRD can be applied. Since applying ARGUS on a very large number of sequence groups is prohibitive with respect to running time (at least in the current implementation), we can conclude that the scopes of VisRD and ARGUS are roughly exclusive.

Moreover, the application range of ARGUS is limited in two directions: first, ARGUS is not designed to rank different classifications not containing any recombinants. This is due to the fact that the two classifications assigning the same subtype to all sequences and assigning a different subtype to each sequence, respectively, achieve the highest likelihood among all CRF-free classifications by definition. Second, when applying ARGUS one has to keep in mind that there might be very plausible classifications that do not fit into the framework of ARGUS, i.e. classifications incorporating intra-subtype recombination and recombination events in the early history of the ARG.

In this study, we first verified in different test settings that ARGUS possesses the ability to reliably identify the most appropriate classification in most investigated cases. Due to the character of the test method, we can conclude that for input sequences stemming from (sub-)species well separated by founder effects—such as HIV-1—ARGUS classifies correctly with very high probability. Afterwards, we applied ARGUS to real-world HIV-1 Group M data in order to address the intensively debated question whether CRF02 is truly a CRF or rather the alleged Subtype G is one. Our results show that the former classification explains the data better.

The fact that we had to run the MCMC algorithm with up to 50 initial ARGs to achieve satisfying results, shows that the MCMC algorithm is not often able to find the global maximum directly, very probably due to getting trapped in a local maximum. We plan to overcome this problem by applying Metropolis-coupled MCMC (MC3) methods (Altekar et al., 2004).

A standard task after sequencing a new HIV genome is subtyping as performed by jpHMM and other tools: The genome is segmented into regions that are each related to one known pure subtype of HIV. A future application of ARGUS will be to vote between the results of several subtyping tools in case they disagree on the correct classification of the query sequence (easily carried out by replacing the recombination prediction of jpHMM by the ones of the other subtyping tools). This application is a special case for the model in which two or more classifications are compared that differ only in the recombination pattern of one sequence, the other sequences all being pure subtypes. While ARGUS does not search for a recombination pattern itself, its comprehensive model is well suited to compare such patterns.

In the near future, we plan to incorporate additional rules (such as intra-subtype recombination and recombination near to the root) into ARGUS and allow for growth of the population and temporally spaced sequence data. In the long run, we will generalize our approach and perform an unconstrained search of the space of ARGs without requiring prior classification of the input sequences into subtypes and recombinant forms.

We would like to encourage users to contact us for assistance in assessing running time and suitability of ARGUS for their purposes.

Funding: Deutsche Forschungsgemeinschaft (STA 1009/5-1 to B.M. and M.S.); National Institutes of Health-Department of Energy interagency agreement (Y1-AI-8309 to B.K. and T.L.).

Conflict of Interest: none declared.

Supplementary Material

[Supplementary Data]
btq159_index.html (591B, html)

REFERENCES

  1. Abecasis AB, et al. Recombination confounds the early evolutionary history of human immunodeficiency virus type 1: subtype G is a circulating recombinant form. J. Virol. 2007;81:8543–8551. doi: 10.1128/JVI.00463-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Altekar G, et al. Parallel Metropolis coupled Markov chain Monte Carlo for Bayesian phylogenetic inference. Bioinformatics. 2004;20:407–415. doi: 10.1093/bioinformatics/btg427. [DOI] [PubMed] [Google Scholar]
  3. Anderson JP, et al. Testing the hypothesis of a recombinant origin of human immunodeficiency virus type 1 subtype E. J. Virol. 2000;74:10752–10765. doi: 10.1128/jvi.74.22.10752-10765.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bailes E, et al. Hybrid origin of SIV in chimpanzees. Science. 2003;300:1713. doi: 10.1126/science.1080657. [DOI] [PubMed] [Google Scholar]
  5. Bergmann M, et al. Transfection-mediated recombination of influenza A virus. J. Virol. 1992;66:7576–7580. doi: 10.1128/jvi.66.12.7576-7580.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Charrel RN, et al. The Whitewater Arroyo virus: natural evidence for genetic recombination among Tacaribe serocomplex viruses (family Arenaviridae) Virology. 2001;283:161–166. doi: 10.1006/viro.2001.0874. [DOI] [PubMed] [Google Scholar]
  7. de Oliveira T, et al. An automated genotyping system for analysis of HIV-1 and other microbial sequences. Bioinformatics. 2005;21:3797–3800. doi: 10.1093/bioinformatics/bti607. [DOI] [PubMed] [Google Scholar]
  8. Feil EJ, Spratt BG. Recombination and the population structures of bacterial pathogens. Annu. Rev. Microbiol. 2001;55:561–590. doi: 10.1146/annurev.micro.55.1.561. [DOI] [PubMed] [Google Scholar]
  9. Foley B, Fauquet C. 15th International HIV Dynamics & Evolution meeting. Santa Fe, NM: 2008. We're not as confused as we may think we are: HIV nomenclature and classification in comparison to the nomenclature and classification of other viruses and bacteria. [Google Scholar]
  10. Goss EM, et al. Genetic diversity, recombination and cryptic clades in Pseudomonas viridiflava infecting natural populations of Arabidopsis thaliana. Genetics. 2005;169:21–35. doi: 10.1534/genetics.104.031351. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Griffiths RC, Marjoram P. An ancestral recombination graph. In: Donnelly P, Tavaré S, editors. Progress in Population Genetics and Human Evolution. New York: Springer; 1997. pp. 257–270. [Google Scholar]
  12. Hahn CS, et al. Western equine encephalitis virus is a recombinant virus. Proc. Natl Acad. Sci. USA. 1988;85:5997–6001. doi: 10.1073/pnas.85.16.5997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hein J, et al. Gene Genealogies, Variation and Evolution: A Primer in Coalescent Theory. USA: Oxford University Press; 2005. [Google Scholar]
  14. Hudson RR. Properties of a neutral allele model with intragenic recombination. Theor. Popul. Biol. 1983;23:183–201. doi: 10.1016/0040-5809(83)90013-8. [DOI] [PubMed] [Google Scholar]
  15. Hudson RR. Gene genealogies and the coalescent process. In: Futuyama J.AD, editor. Oxford Surveys in Evolutionary Biology. Vol. 7. Oxford: Oxford University Press; 1990. pp. 1–44. [Google Scholar]
  16. Jarvis TC, Kirkegaard K. Poliovirus RNA recombination: mechanistic studies in the absence of selection. Virology. 1992;11:3135–3145. doi: 10.1002/j.1460-2075.1992.tb05386.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kingman J.FC. The coalescent. Stoch. Proc. Appl. 1982a;13:235–248. [Google Scholar]
  18. Kingman J.FC. On the genealogy of large populations. J. Appl. Probab. 1982b;19A:27–43. [Google Scholar]
  19. Kuhner MK. LAMARC 2.0: maximum likelihood and Bayesian estimation of population parameters. Bioinformatics. 2006;22:768–770. doi: 10.1093/bioinformatics/btk051. [DOI] [PubMed] [Google Scholar]
  20. Kuhner MK, et al. Maximum likelihood estimation of recombination rates from population data. Genetics. 2000;156:1393–1401. doi: 10.1093/genetics/156.3.1393. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lai MM. RNA recombination in animal and plant viruses. Microbiol. Mol. Biol. Rev. 1992;56:61–79. doi: 10.1128/mr.56.1.61-79.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Leitner T. The molecular epidemiology of human viruses. Norwell, MA: Kluwer Academic publishers; 2002. [Google Scholar]
  23. Lemey P, et al. Identifying recombinants in human and primate immunodeficiency virus sequence alignments using quartet scanning. BMC Bioinformatics. 2009;10:126. doi: 10.1186/1471-2105-10-126. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lole KS, et al. Full-length human immunodeficiency virus type 1 genomes from subtype C-infected seroconverters in India, with evidence of intersubtype recombination. J. Virology. 1999;73:152–160. doi: 10.1128/jvi.73.1.152-160.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lukashev AN, et al. Recombination in circulating Human enterovirus B: independent evolution of structural and non-structural genome regions. J. Gen. Virol. 2005;86:3281–3290. doi: 10.1099/vir.0.81264-0. [DOI] [PubMed] [Google Scholar]
  26. Maydt J, Lengauer T. Recco: recombination analysis using cost optimization. Bioinformatics. 2006;22:1064–1071. doi: 10.1093/bioinformatics/btl057. [DOI] [PubMed] [Google Scholar]
  27. Orlich M, et al. Nonhomologous recombination between the hemagglutinin gene and the nucleoprotein gene of an influenza virus. Virology. 1994;204:462–465. doi: 10.1006/viro.1994.1555. [DOI] [PubMed] [Google Scholar]
  28. Rambaut A, et al. The causes and consequences of HIV evolution. Nat. Rev. Genet. 2004;5:52–61. doi: 10.1038/nrg1246. [DOI] [PubMed] [Google Scholar]
  29. Robertson DL, et al. HIV-1 nomenclature proposal. Science. 2000;288:55–57. doi: 10.1126/science.288.5463.55d. [DOI] [PubMed] [Google Scholar]
  30. Schultz A.-K, et al. A jumping profile hidden Markov model and applications to recombination sites in HIV and HCV genomes. BMC Bioinformatics. 2006;7:265. doi: 10.1186/1471-2105-7-265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Shaikh R, et al. Recombinant avian oncoviruses I. Alterations in the precursor to the internal structural proteins. Virology. 1978;87:326–338. doi: 10.1016/0042-6822(78)90138-1. [DOI] [PubMed] [Google Scholar]
  32. Sibold C, et al. Recombination in Tula hantavirus evolution: analysis of genetic lineages from Slovakia. J. Virol. 1999;73:667–675. doi: 10.1128/jvi.73.1.667-675.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Spang R, et al. A novel approach to remote homology detection: jumping alignments. J. Comput. Biol. 2002;9:747–760. doi: 10.1089/106652702761034172. [DOI] [PubMed] [Google Scholar]
  34. Wakeley J. Coalescent Theory: An Introduction. USA: Roberts & Company Publishers; 2008. [Google Scholar]
  35. Wiuf C, Hein J. Recombination as a point process along sequences. Theor. Popul. Biol. 1999;55:248–259. doi: 10.1006/tpbi.1998.1403. [DOI] [PubMed] [Google Scholar]
  36. Worobey M, et al. Widespread intra-serotype recombination in natural populations of dengue virus. Proc. Natl Acad. Sci. USA. 1999;96:7352–7357. doi: 10.1073/pnas.96.13.7352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Zhang M, et al. jpHMM at GOBICS: a web server to detect genomic recombinations in HIV-1. Nucleic Acids Res. 2006;34:W463–W465. doi: 10.1093/nar/gkl255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Zhuang J, et al. Human immunodeficiency virus type 1 recombination: rate, fidelity, and putative hot spots. J. Virol. 2002;76:11273–11282. doi: 10.1128/JVI.76.22.11273-11282.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
btq159_index.html (591B, html)
btq159_1.pdf (273.1KB, pdf)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES