A Bayesian Discovery Procedure

Summary

We discuss a Bayesian discovery procedure for multiple comparison problems. We show that under a coherent decision theoretic framework, a loss function combining true positive and false positive counts leads to a decision rule based on a threshold of the posterior probability of the alternative. Under a semi-parametric model for the data, we show that the Bayes rule can be approximated by the optimal discovery procedure (ODP), recently introduced by Storey (2007a). Improving the approximation leads us to a Bayesian discovery procedure (BDP), which exploits the multiple shrinkage in clusters implied by the assumed nonparametric model. We compare the BDP and the ODP estimates in a simple simulation study and in an assessment of differential gene expression based on microarray data from tumor samples. We extend the setting of the ODP by discussing modifications of the loss function that lead to different single thresholding statistics. Finally, we provide an application of the previous arguments to dependent (spatial) data.

1. Introduction

A number of different approaches have been introduced in the recent literature to address the multiple comparison problem. Most focus on controlling some error rate. For example, the control of the familywise error rate (FWER) guarantees a bound on the probability of a false rejection among all tests. Benjamini and Hochberg (1995) developed a simple procedure, based on the ordered p-values that controls the false discovery rate (FDR), defined as the expected proportion of rejected null hypotheses which are erroneously rejected. A decision-theoretic approach to the multiple comparison problem requires the explicit statement of a loss function, which weights the relative importance of the different outcomes according to the preferences and inferential focus of the investigators. Cohen and Sackrowitz (2007) prove the inadmissibility of the Benjamini and Hochberg procedure under any loss that is a linear combination of false discoveries and false acceptances and under several sampling models, including the general one-parameter exponential family. Müller et al. (2004, 2007) undertake a decision theoretic approach to multiple testing and discuss several loss functions that lead to the use of FDR-based rules. More recently, Bogdan et al. (2008) compared the Benjamini-Hochberg procedure with several Bayesian rules for multiple testing. They show that whenever the proportion of true nulls is small, the misclassification error of the Benjamini-Hochberg procedure is close to optimal, in the sense of matching a Bayesian oracle. This property is shown to be shared by some of the Bayesian procedures they consider. In addition, through simulations, they show that Bayes rules generally perform better for large or moderate proportions.

The general multiple comparison problem is stated as follows. Assume we observe data sets x₁,…,x_m, where x_i = {x_1i,…,x_nii}, and for each x_i we consider a test of a null hypothesis H_0i. Often the data is reduced to a statistic z_i with z_i ~ f (z_i; μ_i), for some distribution f, indexed by an unknown parameter μ_i, i = 1,…,m. Assume we wish to test H_0i : μ_i ∈ A vs. H_1i : μ_i ∉ A for i = 1,…,m. We discuss the multiple comparison problem in a Bayesian decision theoretic framework. A Bayesian decision problem is characterized by a sampling model, f (z_i; μ_i) in this case, a prior and a loss function which represents the utility preferences associated with possible outcomes.

Specifically, we use a prior model that includes a random effects distribution G for the μ_i. Instead of a parametric model for G, we consider G as an unknown random probability measure (RPM). A prior probability model for an RPM is known as a nonparametric Bayesian model. We assume a Dirichlet process (DP) prior, one of the most popular nonparametric Bayesian models.

For sufficiently large m and a small total mass parameter of the DP prior, the posterior RPM can be approximated by the empirical distribution of the maximum likelihood estimates μ̂_i. The result is an approximate Bayes rule that is closely related to Storey’s optimal discovery procedure (ODP, Storey, 2007a).

The ODP is based on a thresholding statistic,

$$S_{\text{ODP}}(z_i)=\frac{{\displaystyle {\sum }_{{\mu }_j\notin A}f(z_i;{\mu }_j)}}{{\displaystyle {\sum }_{{\mu }_j\in A}f(z_i;{\mu }_j)}}.$$ (1)

The null hypothesis H_0i is rejected if S_ODP(z_i) ≥ λ, for some 0 ≤ λ < ∞. Let d_i^ODP = I (S_ODP (z_i) ≥ λ). Storey proves that d^ODP maximizes the expected number of true positives (ETP) among all procedures with equal or smaller expected number of false positives (EFP). For a point null, A = {0}, the test reduces to thresholding S_ODP (z_i) = ∑_{μj ∉ A} f (z_i; μ_j)/f (z_i; 0). As stated, the threshold function S_ODP involves the unknown parameters μ_j, j = 1,…,m. In practice, S_ODP (·) has to be estimated. For a point null, i.e., A = {0}, the ODP is evaluated as

$${\widehat{S}}_{\text{ODP}}(z)=\frac{{\displaystyle {\sum }_{j=1}^{m}f(z;{\widehat{\mu }}_j)}}{f(z;0)},$$ (2)

where μ̂_j is a point estimate for μ_j (e.g., the maximum likelihood estimate). It is shown that the performance of Ŝ_ODP is comparable to the theoretically optimal discovery procedure based on S_ODP.

For general A the ODP proceeds with the thresholding function

$${\widehat{S}}_{\text{ODP}}(z)=\frac{{\displaystyle {\sum }_{j=1}^{m}f(z;{\widehat{\mu }}_j)}}{{\displaystyle {\sum }_{j=1}^m{w}_{j}f(z;{\widehat{\mu }}_j)}},$$ (3)

where w_j are suitable weights, chosen to estimate the true status of each hypothesis. For example, w_j = 1 for all comparisons that are estimated (by some preliminary test) to be null, and w_j = 0 otherwise. Storey et al. (2007b) show that (3) outperforms many procedures commonly used in testing a large number of genes for differential expression.

We show that the ODP statistic can be recognized as an approximate Bayes rule under the proposed nonparametric prior model for μ_i. This result is in accordance with Ferguson’s (1973) observation that nonparametric Bayesian inference often yields results that are comparable to corresponding classical inference. The expectation in Storey’s optimality statement for d^ODP is under the (frequentist) repeated sampling model. The expectation in the Bayes rule is under the posterior distribution for a given outcome z. Maximization of the conditional expectation for each z implies maximization of the marginal expectation across repeated sampling. A similar argument can be made about the constraint on the expected number of false positives. A bound on the conditional expectation, conditional on each outcome z implies the same bound on the marginal expectation. We conclude that the Bayes rule under the nonparametric prior approximately satisfies the optimality property of the ODP procedure. By the same arguments we show that thresholding the marginal posterior probability amounts to controlling the positive FDR (Storey, 2002; Storey and Tibshirani, 2003).

Once we have established the utility function and the probability model leading to the ODP we can proceed with generalizations in two directions. First, we will consider variations of the ODP to improve the approximation. We show that the resulting rules lead to small improvement in inference. More importantly, once we recognize the ODP as a Bayes rule we can modify the procedure to adapt to variations in the loss function. We provide specific examples, including a study of exceedance regions of a spatial process and the detection of neurodegenerative patterns in MRI scans.

DP priors in the context of multiple hypotheses testing have been considered before by Gopalan and Berry (1993). More recently, Dahl and Newton (2007) have proposed a DP mixture model (BEMMA) for testing correlated hypotheses and showed that the induced clustering information leads to an improved testing power. Unrelated to a discussion of Storey’s ODP, Bogdan et al. (2008) proposed the same semiparametric model we introduce in section 3 and used it for the comparison of misclassification rates among several competing models. The distinction between the previous approaches and ours is that here the DP prior is part of a decision theoretic setup. Besides, both Gopalan and Berry (1993) and Dahl and Newton (2007) restrict inference to hypotheses concerning the configuration of ties among the parameters of interest. A Bayesian implementation of the ODP procedure has been recently considered also by Cao et al. (2009). They develop a parametric Bayes hierarchical mixture model that achieves shrinkage of the gene-specific sampling variances. The resulting posterior means are then plugged in the ODP statistic and this is shown to outperform the original ODP and many widely used competing procedures. The discussion in Cao et al. (2009) is purely empirical, without reference to a decision theoretic setup.

The format of the paper is as follows. In section 2, we introduce the decision problem and the resulting Bayes rule. In section 3 we introduce the nonparametric (NP) probability model and we detail the algorithm for posterior inference. In section 4 we finally discuss the interpretation of the ODP as an approximate Bayes rule and introduce the corresponding BDP statistics. In section 5 we compare the behavior of the ODP and the BDP with simulated data and a microarray dataset. We show that the BDP provides at least some improvement over the frequentist optimal procedure. In section 6 we discuss some extensions of the previous settings for multigroup experiments, different loss functions and different inferential purposes. In particular, we consider a spatially dependent NP model and apply the Bayesian multicomparison decision rule to a simplified MRI dataset.

2. The Decision Problem

For a formal definition of the multiple comparison problem we need some notation and minimal assumptions on the sampling model. Assume that the data are z_i | μ_i ~ f (z_i; μ_i), independently across i, i = 1,…,m. The competing hypotheses are formalized as

$$H_{0i}:{\mu }_i\in A\text{vs}.H_{1i}:{\mu }_i\notin A,$$

using, for example, A = (−∊+ ∊) or A = {0}. Let G denote the distribution of μ_i, obtained by marginalizing over the two competing hypotheses and let π₀ denote the prior probability of the null hypothesis, i.e., π₀ ≡ G(A) = p(H_0i). Let G(μ | A) ∝ G(μ) I(μ ∈ A) denote G conditional on A. The model can be written as a mixture prior,

$$p({\mu }_i|G)={\pi }_{0}G({\mu }_i|A)+(1-{\pi }_0)G({\mu }_i|A^c),$$

where A^c denote the complement set of A. Alternatively, the model can be defined as a hierarchical model by means of a latent indicator parameter r_i ∈ {0, 1}, which is interpreted as the (unknown) truth of the i-th comparison.

$$p({\mu }_i|r_i)=\{\begin{array}{cc}G({\mu }_i|A)\hfill & \text{if}{r}_i=0\hfill \\ G({\mu }_i|A^c)\hfill & \text{if}{r}_i=1,\hfill \end{array}\text{and}\mathit{\text{Pr}}(r_i=0)={\pi }_0.$$ (4)

We will use z = (z₁,…,z_m) and θ = (G, r_i, μ_i, i = 1,…,m) to refer generically to the data and parameters in model (4).

In addition to a probability model, a Bayesian decision theoretic approach is characterized by a set of actions (decisions) and a loss function corresponding to all possible outcomes of the experiment. Let d_i ∈ {0, 1} denote the decision for the i-th hypothesis, with d_i = 1 indicating a decision against H_0i, and let d = (d₁,…,d_m). To define an optimal rule for d_i we introduce a loss function L(d, θ, z). The optimal rule $d_i^{*}(z)$ is defined by minimizing L in expectation with respect to the posterior model p(θ | z). Formally,

$$d^{*}=\underset{d}{\text{arg}\text{min}}{\displaystyle \int L(d,\theta ,z)p(\theta |z)}\mathrm{d}\theta .$$

We use a loss function that combines the true positive count, TP = ∑ d_i r_i, and false positive count, FP = ∑ d_i(1 − r_i),

$$L(d,\theta ,z)=-{\displaystyle \sum d_i{r}_i+\mathrm{\lambda }{\displaystyle \sum d_i(1-r_i)=-\text{TP}}+\mathrm{\lambda }\text{FP}}$$ (5)

The loss (5) can be interpreted as the Lagrangian for maximizing TP subject to a given bound on FP. It is a multiple comparison equivalent of the loss function underlying the Neyman-Pearson paradigm for a simple test.

Let v_i = E(r_i | z) denote the marginal posterior probability for the i-th alternative hypothesis. It is straightforward to show that the optimal rule under (5) is a threshold on v_i,

$$d_i^{*}=I(v_i>t)=I\left(\frac{v_i}{1-v_i}>t_2\right).$$ (6)

Alternatively, the threshold on v_i can be written as a threshold on the posterior odds v_i/(1 − v_i). The statement is true for any probability model (subject only to the stated quantities having meaningful interpretations). Moreover rules based on thresholding the marginal posterior probability imply control of the frequentist positive FDR (Storey, 2002; Storey and Tibshirani, 2003):

PROPOSITION 1

Consider m hypothesis tests H_0i : μ_i ∈ A vs H_1i : μi ∈ A^c, data z₁,…,z_m, where z_i | μ_i ~ f (z_i; μ_i), independently across i, i = 1,…,m, and a prior probability model p(μ_i | G) = π₀ G(μ_i | A) + (1 − π₀) G(μ_i | A^c) for some distribution G and probabilty π₀ = p(H_0i) = p(r_i = 0). Let the rejection region be determined by (6), i.e. $d_i^{*}=I(v_i>t)$. Let $D={\displaystyle {\sum }_{i=1}^m{d}_i}$. Then,

$$\mathit{\text{pFDR}}=E\left(\frac{\mathit{\text{FP}}}{D}|D>0\right)<1-t.$$

PROOF

See appendix.

The only substantial assumption in Proposition 1 is that $d_i^{*}$ is a threshold on the gene-specific posterior probabilities of differential expression. Bogdan et al. (2008) proved a similar result for loss functions that are a linear combination of FN and FP counts.

Note that rule (6) is different from rules based on local FDR. Local FDR is defined as the posterior probability of the null given that we have observed a certain value z_i, and given assumed known sampling models under the null and alternative hypotheses (Efron et al., 2001). In contrast, v_i is defined conditionally on the observed values of z across all tests. Hence, the local FDR provides a measure of significance local to z_i, while v_i is a global measure of significance.

3. A Nonparametric Bayes Decision Rule

3.1. A Semiparametric Bayesian Model

We complete the sampling model (4) with a prior model for G. Prior probability models for unknown distributions, G in this case, are traditionally known as non-parametric (NP) Bayesian models. One of the most commonly used NP Bayesian priors is the DP model. We write G ~ DP (G*,α) to indicate a DP for a random probability measure G. See Ferguson (1973, 1974) for a definition and important properties of the DP model. The model requires the specification of two parameters, the base measure G* and the total mass parameter α. The base measure G* is the prior mean, E(G) = G*. The total mass parameter determines, among other important properties, the variation of the random measure around the prior mean. Small values of α imply high uncertainty. In the following discussion we exploit two key properties of the DP. A random measure G with DP prior is a.s. discrete. This allows us to write G as a mixture of point masses, G = ∑w_h δ_mh. Another important property is the conjugate nature of the DP prior under random sampling. Assume μ_i ~ G, i = 1,…,m, are an i.i.d. sample from a random measure G with DP prior, p(G) = DP(G*, α). Then, the posterior probability model is $p(G|\mu )=\mathit{\text{DP}}(G_1^{*},\alpha +m),\text{for}{G}_1^{*}\propto \alpha G^{*}+m{F}_m$. Here, F_m = 1/m ∑ δ_μi (·) is the empirical distribution of the realized μ_i’s.

We use a DP prior on G to complete model (4)

$${\mu }_i|G~GG~\text{DP}(G^{*},\alpha ).$$ (7)

Model (7) implies that the prior for the null hypothesis p₀ = G(A) is Beta, p₀ ~ Be (αG* (A), α[1 − G* (A)]).

3.2. A semiparametric Bayes Rule for Multiple Testing

Many approaches have been proposed in the literature to implement posterior Monte Carlo simulation for DP mixture models. See, for example, Neal (2000) for a review. We outline how these methods can be adapted to compute the posterior probabilities v_i.

Let z_i, i = 1,⋯,m denote the observed data (or a summary statistic) for test i. We assume

$$z_i|{\mu }_i\stackrel{\mathit{\text{ind}}}{~}f(z_i;{\mu }_i),i=1,\cdots ,m.$$ (8)

For example, f (z_i; μ_i) ≡ N (z_i; μ_i, σ), a normal distribution with mean μ_i and and variance σ². We complete the model with a non-parametric prior

$$\begin{array}{c}{\mu }_i|G\stackrel{\mathit{\text{iid}}}{~}G\hfill \\ G~\text{DP}(G^{*},\alpha )\text{with}{G}^{*}(·)~{\pi }_0{h}_A(·)+(1-{\pi }_0)h_{A^c}(·),\hfill \end{array}$$ (9)

where h_A(·) and h_A^c (·) are distributions with support, respectively, on A and A^c. Equations (8) and (9) define a DP mixture model where G* itself is a mixture of two terms. Unrelated to a discussion of the ODP, Bogdan et al. (2008) proposed the same model for multiple comparison problems. They compare misclassification rates using inference based on pFDR and FDR.

Algorithms for posterior Monte Carlo simulation in DP process mixture models can easily be modified to adapt to the mixture in G*. We will focus on the case A = {0} and outline the necessary changes for general A. We set h_A(·) = δ₀(·), i.e. a point mass at 0. Also, we choose h_A^c(·) to be continuous, e.g. N(0, σ²) and will denote it simply by h(·). The a.s. discrete nature of a DP random probability measure implies a positive probability for ties in a sample from G. The ties naturally define a partition of observations into clusters with common values μ_j. We introduce latent cluster membership indicators s_i to describe this partition by s_i = s_k if μ_i = μ_k. We reserve the label s_i = 1 for the null distribution, i.e. we set s_i = 1 if and only if μ_i = 0. Let z_−i and s_−i denote the set of observations and the indicators excluding the i-th one. Also, let L be the number of clusters defined by ties (an unmatched single observation counts as a singleton cluster), m_s be the size of cluster s, and m_{− i,s} be the size of cluster s without observation i. Finally, let Γ_s = {i : s_i = s} denote the s-th cluster, and let ${\mu }_s^{*}={\mu }_i,i\in {\mathrm{\Gamma }}_s$ denote the common value of μ_i for cluster s. Then, the i-th observation falls in one of the existing clusters or forms a new cluster according to the following modified Pólya urn scheme,

$$P(s_i=s|s_{-i},z)\propto \{\begin{array}{cc}\frac{m_{-i,1}+{\pi }_0\alpha }{m-1+\alpha }f(z_i|{\mu }_{s_i}^{*}=0)\hfill & \text{if}s=1\hfill \\ \frac{m_{-i,s}}{m-1+\alpha }{\displaystyle \int f(z_i|{\mu }_s^{*})h({\mu }_s^{*}|z_{-i,s})d{\mu }_s^{*},}\hfill & \text{if}2\le s\le L\hfill \\ \frac{(1-{\pi }_0)\alpha }{m-1+\alpha }{\displaystyle \int f(z_i|{\mu }_s^{*})h({\mu }_s^{*})d{\mu }_s^{*},}\hfill & \text{if}s=L+1\hfill \end{array}$$

Here, $h({\mu }_s^{*}|z_{-i,s})$ denotes the posterior distribution of ${\mu }_s^{*}$ based on the prior h(·) and all observations z_h, h ∈ Γ_s/{i}. Note that the posterior of ${\mu }_1^{*}$ given all the observations in cluster 1 is still a point mass δ₀(·). We described the algorithm for a particular choice of A and G*. But it can be easily extended to more general A and G*. In the general case, clusters are formed either by samples from h_A(·) or h_A^c (·). The algorithm is greatly simplified when A is an interval, h_A(μ) ∝ h(μ) I_A(μ), h_A^c (μ) ∝ h(μ) I_A^c (μ), for some continuous distribution h(μ) and π₀ = G*(A). Then, equations (8) and (9) describe a traditional DP mixture of normals model with Gaussian base measure G*. The usual Pólya urn scheme for DP mixtures may be used.

Once we have a posterior Monte Carlo sample of the model parameters it is easy to evaluate the decision rule. Assume we have B posterior Monte Carlo samples of random partitions, $s^{(b)}=(s_1^{(b)},\dots ,s_m^{(b)})$, b = 1,…,B. We evaluate v_i = E(r_i | z) numerically as ${\overline{v}}_i=1-{\displaystyle {\sum }_{b=1}^{B}I(s_i^{(b)}=1)/B.}$ We evaluate $d_i^{*}$ by substituting v̄_i in (6)

$$S_{\mathit{\text{NP}}}=I(\frac{{\overline{v}}_i}{1-{\overline{v}}_i}>t).$$ (10)

In the next section we show that S_NP can be approximated by a single threshold statistic similar to (1).

4. The Bayesian Discovery Procedure (BDP)

4.1. The ODP as approximate Bayes Rule

We show that, under a DP prior model, d* ≈ d^ODP, that is the ODP is an approximate Bayes Rule. We start by writing the marginal posterior probability as expectation of conditional posterior probabilities,

$$v_i=E[p(r_i=1|G,z)|z]=E\left[\frac{{\displaystyle {\int }_{A^c}f(z_i;\mu )\mathit{\text{dG}}(\mu )}}{{\displaystyle {\int }_{A\cup A^c}f(z_i;\mu )\mathit{\text{dG}}(\mu )}}|z\right],$$

and proceed with an approximation of the conditional posterior distribution p(G | z). The conjugate nature of the DP prior under random sampling implies $E(G|\mu ,z)=G_1^{*}\propto \alpha G^{*}+{\displaystyle \sum {\delta }_{{\mu }_i}}.$. Recall that F_m ∝ ∑ δ_μ̂i is the empirical distribution of the maximum likelihood estimates μ̂_i. For large m, small α, and an informative sampling model f(z_i; μ), E(G | z) ≈ F_m. Further, for large m, the uncertainty of the posterior DP, $p(G|\mu ,z)=\mathit{\text{DP}}(G_1^{*},m+\alpha )$ is negligible, allowing us to approximate the posterior on the random probability measure G with a degenerate distribution at $F_m,p(G|z)\approx {\delta }_{F_m}(G),\text{i.e.}G\approx \frac{1}{m}{\displaystyle \sum {\delta }_{{\widehat{\mu }}_i}.}$. Therefore,

$$v_i\approx \frac{{\displaystyle {\int }_{A^c}f(z;\mu ){\mathit{\text{dF}}}_m(\mu )}}{{\displaystyle \int f(z;\mu ){\mathit{\text{dF}}}_m(\mu )}}=\frac{{\displaystyle {\sum }_{{\widehat{\mu }}_j\in A^c}f(z_i;{\widehat{\mu }}_j)}}{{\displaystyle {\sum }_{j=i}^{m}f(z_i;{\widehat{\mu }}_j)}}.$$ (11)

The connection with the ODP rule is apparent by computing the posterior odds, $v_i/(1-v_i)\approx {\displaystyle {\sum }_{{\widehat{\mu }}_j\in A^c}f(z_i;{\widehat{\mu }}_j)/}{\displaystyle {\sum }_{{\widehat{\mu }}_j\in A}f(z_i;{\widehat{\mu }}_j).}$. Finally, thresholding v_i/(1− v_i) is equivalent to thresholding

$$\frac{v_i}{1-v_i}+1\approx \frac{{\displaystyle {\sum }_{j=1}^{m}f(z_i;{\widehat{\mu }}_j)}}{{\displaystyle {\sum }_{{\widehat{\mu }}_{j\in A}}f(z_i;{\widehat{\mu }}_j)}}.$$

This is (3) with w_j = I(μ̂_j ∈ A).

Recognizing the ODP as an approximate Bayes rule opens two important directions of generalization. First, we can sharpen the approximation to define a slightly improved procedure, at no cost beyond moderate computational effort. We will do this in sections 4.2 and 4.3. Second, we can improve the ODP by making it more relevant to the decision problem at hand by modifying features of the underlying loss function; we will do this in Section 6.

4.2. The BDP statistic

We can improve the approximation in (11) by conditioning on a cluster configuration s and using cluster specific point estimates ${\widehat{\mu }}_j^{*}$. Given model (8)–(9), we can approximate the posterior probability v_i by

$$S_{\text{BDP}}(z_i)=\frac{{\displaystyle {\sum }_{j=1}^{m}f(z_i;{\widehat{\mu }}_j)}}{{\displaystyle {\sum }_{{\widehat{\mu }}_j\in A}f(z_i;{\widehat{\mu }}_j)}}.$$ (12)

The μ̂_j are point estimates based on (9). For example, one could use the posterior means μ̂_j = E(μ_j | z). Short of posterior means, we propose to use a partition s^(b) to evaluate cluster-specific point estimates ${\widehat{\mu }}_i={\widehat{\mu }}_{s_i}^{*}$, using maximum likelihood estimation within each cluster. The choice of the specific partition s^(b) is not critical. Finally, we report test i significant if S_BDP(z_i) > t, for some threshold t. Substituting ${\widehat{\mu }}_{s_i}^{*}$ in (12) the S_BDP can be interpreted as a multiple shrinkage version of the S_ODP statistic. For later reference we note that thresholding S_BDP is equivalent to thresholding

$${\widehat{v}}_i\equiv {\displaystyle \sum _{{\widehat{\mu }}_j^{*}\in A^c}{m}_j/mf(z_i;{\widehat{\mu }}_j^{*}})/{\displaystyle \sum _j{m}_j/mf(z_i;{\widehat{\mu }}_j^{*}}).$$ (13)

By the earlier argument v̂_i ≈ v_i.

The nature of the approximation (12) is further clarified and formalized by the following result, which justifies the replacement of μ_i by the cluster specific mle’s ${\widehat{\mu }}_j^{*}$. Proving asymptotic results of this kind for the DP is generally not easy. One has to establish that the posterior mass for the random G is concentrated on a set of RPM’s with a small number of discontinuities relative to m. See, for example, Arratia et al. (2003) and Coram and Lalley (2006) for recent discussions. In particular, Coram and Lalley (2006) address the problem from the perspective of “overfitting” for NP Bayes procedures. They conjecture that in a variety of problems, the critical determinant of the consistency of Bayes procedures are the rate functions in associated large deviations problems. We avoid the technical difficulties by proving the result for a finite dimensional Dirichlet prior, that is a random probability measure G_k such that

$$G_k(A)={\displaystyle \sum _{j=1}^k{p}_j{\delta }_{{\mu }_j^o}(·),}$$ (14)

with (p₁,…,p_k) ~ D(α/k,…,α/k), and ${\mu }_j^o~G^{*}$ as in (9). Inference under the DP prior and (14) is comparable, since any integrable functional of the Dirichlet Process can be approximated by corresponding functionals of G_k for sufficiently large k (see Iswharan and Zarepour, 2002). Also Rodriguez et al. (2009) discuss the approximation of inference under a DP prior by results under G_k.

THEOREM 2

Assume $z_i|{\mu }_i\stackrel{\mathit{\text{ind}}}{~}f(z_i;{\mu }_i)$, i = 1,…,m and a random effects distribution p(μ_i | G_k) = G_k as in (9), with G_k defined in (14). Assume f, h_A(·), and h_A^c (·) satisfy the conditions for the Laplace approximation for an open set A (see Schervish, 1995, chapter 7.4.3). Then

$$\underset{m\to +\infty }{\text{lim}}p(r_i=1|z_1,\dots ,z_m)=\frac{E({\displaystyle {\sum }_{j:{\widehat{\mu }}_j^{*}\in A^c}\frac{m_j}{m}f(z_i;{\widehat{\mu }}_j^{*})}|z)}{E({\displaystyle {\sum }_j\frac{m_j}{m}f(z_i;{\widehat{\mu }}_j^{*})}|z)}.$$

The expectation is with respect to the posterior distribution over all possible partitions of {1,…,m} with at most k clusters and ${\widehat{\mu }}_j^{*}$ is the cluster-specific m.l.e.

PROOF

See appendix.

4.3. Multigroup comparisons

The definition of the BDP can easily be extended to the general k samples comparison problem. We assume that data for experimental units i, i = 1,…,m, are arranged by k distinct groups, and we wish to test if the k groups share a common sampling model. Let x_i = {x_i1,…,x_in} be a vector of measurements across k experimental conditions, i = 1,…,m. We denote the subset of data from each condition by $x_i^l,l=1,\dots ,k,i=1,\dots ,m$. Alternatively, data in each group may be reduced to statistics $z_i^l~f(z_i^l;{\mu }_i^l)$, and we can write z = {z₁,…,z_m}, $z_i=\{z_i^1,\dots ,z_i^k\}$, with similar notation for μ and μ_i. For notational simplicity, we proceed with the case k = 2. But the arguments hold for general k. The competing hypothesis are $H_0:({\mu }_i^1,{\mu }_i^2)\in A$ against $H_1:({\mu }_i^1,{\mu }_i^2)\notin A$. Typically $A=({\mu }_i^1={\mu }_i^2)$. Under the loss (5) and the NP model

$$\begin{array}{c}\hfill z_i^l|{\mu }_i^l\stackrel{\mathit{\text{ind}}}{~}f(z_i^l;{\mu }_i^l),l=1,2,i=1,\dots ,m\\ {\mu }_i=\{{\mu }_i^1,{\mu }_i^2\}|G\stackrel{i.i.d}{~}G,\text{with}G~\mathit{\text{DP}}(\alpha ,G_0)\hfill \end{array}$$

we can proceed as in section 2.3 and approximate the posterior odds for the i-th comparison by

$$\frac{v_i}{1-v_i}\approx \frac{{\displaystyle {\int }_{A^c}f(z;\mu ){\mathit{\text{dF}}}_m(\mu )}}{{\displaystyle {\int }_{A}f(z;\mu ){\mathit{\text{dF}}}_m(\mu )}}=\frac{{\displaystyle {\sum }_{i:({\widehat{\mu }}_i^1,{\widehat{\mu }}_i^2)\in A^c}f(z_i^1|{\widehat{\mu }}_i^1)f(z_i^2|}{\widehat{\mu }}_i^2)}{{\displaystyle {\sum }_{i:({\widehat{\mu }}_i^1,{\widehat{\mu }}_i^2)\in A}f(z;{\widehat{\mu }}_i)}},$$ (15)

where ${\widehat{\mu }}_i^1,{\widehat{\mu }}_i^2$ and μ̂_i are appropriate estimates of the relevant parameters within and across conditions. Expression (15) is an estimated ODP statistics for the multicomparison problem, as discussed in Storey et al. (2007b). As before, substituting cluster-specific estimates ${\widehat{\mu }}_{s_i}^{*}$ for a selected partition s defines the corresponding BDP rule.

5. Comparison of S_ODP versus S_BDP

5.1. A Simulation Study

We conduct a simulation study to compare the ODP with the NP Bayesian approximation outlined in the previous sections. We assume m = 2000 tests of H₀ : μ_i = 0 versus H₁ : μ ≠ 0 based on a single observation z_i ~ N(μ_i, 1) for each test. The simulation truth is such that half of the observations are drawn from the null, while the other half are sampled from the following probability distribution:

μi	−4	−3	−2	−1.5	1.2	2	3	4.5	5.8
pi	0.02	0.08	0.01	0.01	0.27	0.02	0.08	0.005	0.005

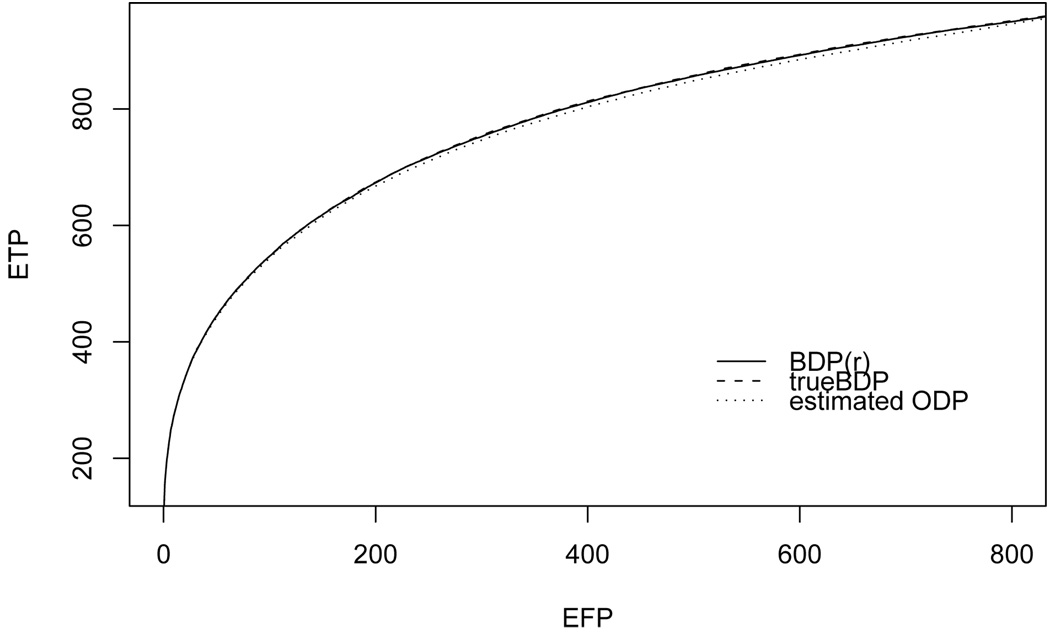
The distribution mimicks the observed distribution of the t-scores in the microarray data example considered in section 5.2, as shown in Figure 1. We use A = {0}, and h_A^c (·) = N (0, 1). We simulated 1000 datasets. For each simulated data set we ran 2000 iterations of a posterior MCMC sampler (with 1000 iterations burn in). The results confirm the obervation in Storey et al. (2007b) that the S_ODP outperforms the UMP unbiased procedure in all cases where the alternative means are not arranged in a perfectly symmetric fashion around zero. The S_BDP further improves on the S_ODP by borrowing strength across comparisons with the multiple shrinkage induced by the DP clustering. Figure 2 shows that for any threshold of expected FP, the expected TP is comparable and slightly better under the S_BDP than under the S_ODP. Expectations are over repeated simulations, i.e., the comparison is by the criterion that is being optimized by the oracle version (1) of the ODP. The curves for the S_BDP are computed with a random (last) configuration; the true BDP curve refers to the BDP statistics computed based on the (known) true configuration. The differences in Figure 2 are small. However, for many applications with massive multiple comparisons the number of comparisons is much larger, leading to correspondingly larger differences in true positives. Most importantly, the improvements come at no additional experimental cost.

Fig. 1.

The scores z_i for the simulation example in 5.1 (left panel) and the the data z_i for the BRCA mutation microarray data in section 5.2 (right panel).

Fig. 2.

ETP = E(TP) versus EFP = E(TP) for Ŝ_ODP and S_BDP. BDP(r) refers to S_BDP computed for a random configuration (we use the last configuration in the MCMC simulation). TrueBDP refers to the BDP statistics computed on the basis of the simulation truth. The three curves are almost undistinguishable. See 5.1 for details.

We also considered a similar comparison using (12) with posterior means substituted for μ̂_i, and using A = (−ε, ε), for several (small) values of ε, instead of the point null. The plot (not shown) of expected TP versus FP showed no substantial differences to Figure 2.

5.2. A Microarray Data Example

We first compare the Ŝ_ODP versus the S_BDP test by analyzing a microarray dataset obtained from breast cancer tumor tissues. The data have been analyzed, among others, in Hedenfalk et al (2001), Storey and Tibshirani (2003) and Storey et al. (2007b) and can be downloaded from http://research.nhgri.nih.gov/microarray/NEJM_Supplement/. The data consist of 3,226 gene expression measurements on n₁ = 7 BRCA1 arrays and n₂ = 8 BRCA2 arrays (a third “sporadic” group was not used for this analysis). Following Storey and Tibshirani (2003), genes with one or more measurement exceeding 20 were eliminated from the data set, leaving m = 3, 169 genes.

Let x_ij be the log₂ expression measurement for gene i on array j, i = 1,…,m, j = 1,…,n. For illustration purposes, we test differential expression between BRCA1 and BRCA2 mutation genes using the two samples t statistics $z_i=({\overline{x}}_{i1}-{\overline{x}}_{i2})/\sqrt{(}{s}_{i1}^2/n_1+s_{i2}^2/n_2)$, where x̄_i,k and $s_{\mathit{\text{ik}}}^2$ are respectively the sample mean and sample variance for gene i with respect to the arrays in group k, k = 1, 2. We assume model (8) and (9) with f(z_i; μ_i) = N(μ_i, σ) and test H_0i : μ_i = 0. For simplicity, we fix σ = 1. A model extension with a prior on unknown σ is straightforward. The results remain almost unchanged (not shown).

We assess the relative performance of the estimated Ŝ_ODP versus approximation (12) of the NP Bayes rule. For a fair comparison, we evaluate the S_BDP as a frequentist rule with rejection region {S_BDP ≥ c}. The power of the test is evaluated in terms of the FDR and the q-value. See Storey (2002) and Storey et al. (2007b) for more discussion of the q-value and its evaluation.

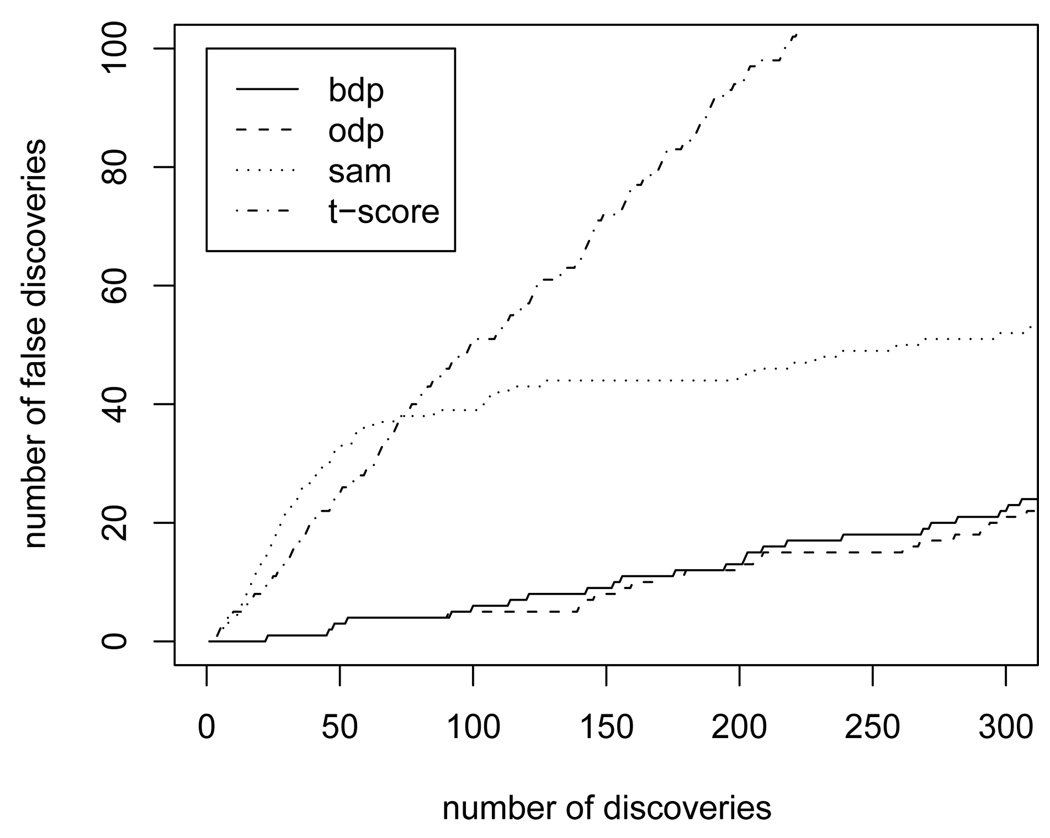
The evaluation of S_BDP is based on 2000 iterations of a posterior MCMC sampler (1000 burn in). The number of significant genes detected at each q-value is shown in Figure 3. We report the S_BDP as computed on the basis of the cluster configuration of a single iteration of the MCMC sampling scheme. We use the partition from a random iteration and from MAP (maximum a posteriori) partition. Other choices are possible. However, our experience does not suggest significantly different conclusions using alternative choices. In Figure 3 we see that in both cases the S_BDP achieves larger numbers of significant genes at the same q-value than the S_ODP. The result leads us to recommend the S_BDP as a useful tool in multicomparison problems where a natural clustering of the tests is expected. In Table 1, we report the percentage of genes that are flagged by both tests for some choices of q-values. For most q-values of practical interest the S_BDP procedure identifies all genes that were flagged by the S_ODP, plus additional discoveries. For example, at q = 0.05, the BDP reveals 98 significant genes, against 87 revealed by the ODP and 47 by the standard FDR procedure devised by Benjamini and Hochberg (1995). Out of the 11 additional genes, 7 had been previously reported in the literature as significant in distinguishing BRCA1 and BRCA2 mutations (see Hedenfalk et al. 2001). The additionally identified genes come at no extra cost beyond moderate computational effort. No additional experimental effort is required, and no trade off in error rates is involved.

Fig. 3.

A comparison of S_BDP and S_ODP for identifying differentially expressed genes (see section 5.2). The BDP(h) curve is is based on the MAP configuration; BDP(r) refers to S_BDP computed under the (random) last configuration imputed in the MCMC simulation.

Table 1.

The intersection between the decisions with the ODP and the BDP procedures.

q-value	ODP	BDP	BDP⋂ODP
0.05	87	98	100%
0.06	124	148	100%
0.07	163	176	100%
0.08	202	217	100%
0.09	234	241	99.5%
0.10	272	270	98.14%
0.11	293	298	98.63%
0.12	318	341	98.11%

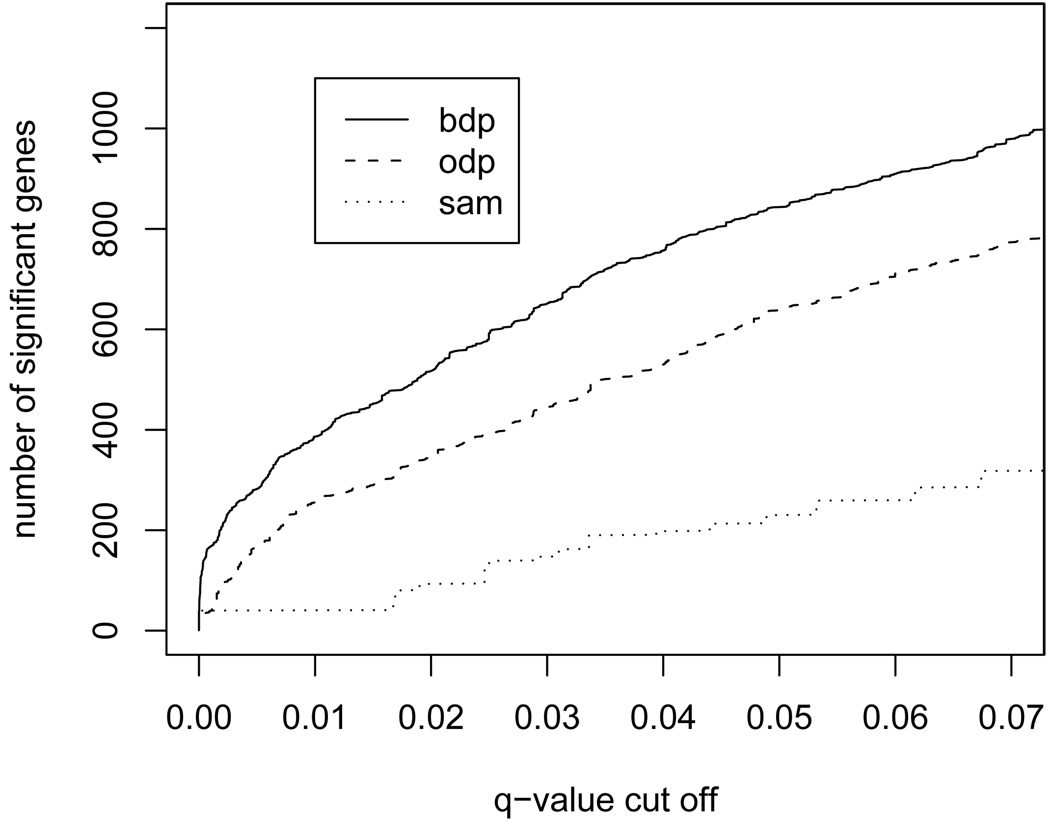
For an alternative comparison we consider the “Golden Spike” data of Choe et al. (2005). They describe an Affymetrix GeneChip experiment, where 1309 individual cRNAs have been “spiked in” at known relative concentrations between the two samples (spike-in and control). We implemented the BDP and ODP as described above. For comparison, we also include alternative comparisons using the SAM procedure (Tusher et al., 2001; Storey, 2002) and independent two-sample t-tests. We used the reduced Golden Spike dataset provided in the R package st. The dataset reports 11,475 genes with 3 replicates per group, including 1,331 genes with known differential expression. Figure 4 shows the results of a comparison of BDP, ODP, SAM and independent t-tests. To compute the SAM statistic we used the samr package in R and alternatively the SAM software from http://www-stat.stanford.edu/~tibs/SAM/. Both implementations give practically identical results.

Fig. 4.

Golden Spike data. A comparison of S_BDP, S_ODP, SAM and independent two-sample t-tests.

Both comparisons, in Figures 3 and 5, are for the ODP and BDP test based on data with a single gene-specific summary statistic z_i per gene. The restriction to a single summary statistic in the definition of ODP and BDP was purely for presentation, and can easily be relaxed. Let x_ijk denote the expression measurement for gene i, sample j and condition k. For simplicity, we still assume only two conditions. Group k = 0 is assumed to be a control/reference group. Let ${\widehat{\mu }}_{i0}={\displaystyle {\sum }_{l=1}^{n_0}{x}_{\mathit{\text{il}}}/n_0}$ be the gene specific mean of the observations in group 0. We define z_ijk = x_ijk − μ̂_i0, k = 0, 1, and assume $z_{{\mathit{\text{ij}}}_k}|{\mu }_{\mathit{\text{ik}}},{\sigma }_i^2~N({\mu }_{\mathit{\text{ik}}},{\sigma }_i^2)$, with μ_i0 ≡ 0. The hypothesis testing problem becomes:

$$H_{0i}:{\mu }_{i1}=0\text{vs}{H}_{1i}:{\mu }_{i1}\ne 0,i=1,\dots ,m.$$

Fig. 5.

Hedenfalk data: Comparison of S_BDP, S_ODP and SAM under model (16).

Similar to before we define a random effects distribution G for ${\theta }_i=({\mu }_{i1},{\sigma }_i^2)$ and assume a NP Bayesian prior on G,

$${\theta }_i|G~G\text{and}G~\mathit{\text{DP}}(\alpha ,G_0),i=1,\dots ,m.$$ (16)

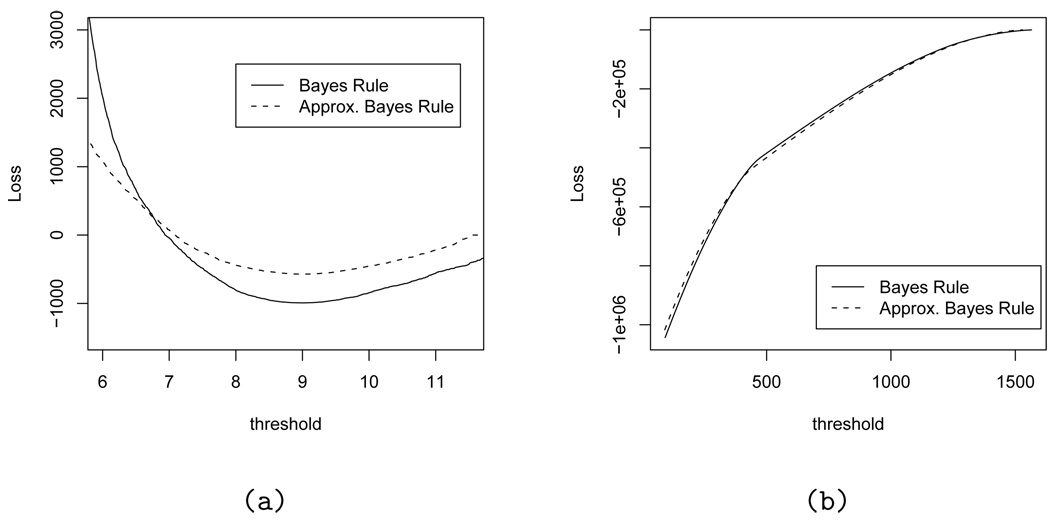
For the DP base measure we use a conjugate normal-inverse χ² distribution $G_0=\left[{\pi }_0{\delta }_0+(1-{\pi }_0)N(0,\frac{{\sigma }_i^2}{k_0})\right]\times \text{Inv}-{\chi }^2({\sigma }_i^2;{\nu }_0,{\sigma }_0^{2*})$. We can then proceed as in section 4.3 to define the ODP and BDP statistic, respectively. Figure 6 summarizes the results.

Fig. 6.

Expected loss under the exact Bayes rules d^m* (left panel) and d^p* (right panel) plotted against the cutoff t (solid lines). The dashed lines show the expected loss under the ODP rules based on $S_{\text{BDP}}^m$ (left panel) and $S_{\text{BDP}}^p$ (right panel).

6. Extensions of the ODP and BDP

6.1. Weighted Loss Functions

Once the optimality criterion and the probability model that lead to the ODP are identified, it is easy to modify the procedure to better accomodate preferences and losses other than (5). Often some discoveries might be considered more important than others. For example if A = {μ_i = 0} one might be more interested in large deviations from 0. In this case the loss function should include an explicit reward for detecting true signals as a function of some (monotone) function of μ_i. Scott and Berger (2003) describe a decision theoretic approach based on separate loss functions for false positives and false negatives. Similarly, we consider the following loss function,

$$L(d,\theta ,z)=-{\displaystyle \sum d_{i}t({\mu }_i)+\mathrm{\lambda }{\displaystyle \sum d_i(1-r_i)},}$$ (17)

where t(μ_i) is a known function of the mean, e.g. t(μ_i) = ||μ_i||, ||·|| being some norm of μ_i. Let $\overline{t({\mu }_i)}=E(t({\mu }_i)|z)$. The posterior expected loss is $E(L|z)=-{\displaystyle \sum d_i[\overline{t({\mu }_i)}+\mathrm{\lambda }{v}_i]+{\displaystyle \sum d_i}}$. The Bayes rule is easily shown to be

$$d_i^{m*}=I(\mathrm{\lambda }{v}_i+\overline{t({\mu }_i)}>t),$$ (18)

for some threshold t. Although the nature of the rule has changed, we can still proceed as before and define a modified S_ODP statistics that approximates the Bayes rule. Let $\overline{t({\mu }_i)}\approx {\displaystyle {\sum }_{j=1}^{m}t({\widehat{\mu }}_j)}f(z_i;{\widehat{\mu }}_j)/{\displaystyle {\sum }_{j=1}^{m}f(z_i;{\widehat{\mu }}_j)}$ be an empirical Bayes estimate of $\overline{t({\mu }_i)}$, justified similarly to the approximation in (11). As before the point estimates μ̂_i are cluster-specific m.l.e.’s ${\widehat{\mu }}_{s_i}^{*}$ for some partition s. By an argument similar to before we can justify the following single thresholding statistic as an approximation of (18):

$$S_{\text{BDP}}^m(z_i)=\frac{\mathrm{\lambda }{\displaystyle {\sum }_{{\widehat{\mu }}_j\notin A}f(z_i;{\widehat{\mu }}_j)+{\displaystyle {\sum }_{j}t({\widehat{\mu }}_j)f(z_i;{\widehat{\mu }}_j)}}}{{\displaystyle {\sum }_{j}f(z_i;{\widehat{\mu }}_j)}}.$$ (19)

We use $S_{\text{BDP}}^m(y_i)$ as a single thresholding function for the multiple comparison test in lieu of the S_ODP.

Any loss function that is written as a sum of comparison-specific terms leads to similar approximations and modifications of the ODP. For example, consider a loss function that involves a stylized description of a follow-up experiment. The loss function is motivated by the following scenario. Many microarray group comparison experiments are carried out as a screening experiment. Genes that are flagged in the microarray experiment are chosen for a follow-up experiment to verify the possible discovery with an alternative experimental platform. For example, Abruzzo et al. (2005) describe a setup where RT-PCR (reverse transcription polymerase chain reaction) experiments are carried out to confirm discoveries proposed by an initial microarray group comparison. Abruzzo et al. (2005) report specific values for correlations across the platforms, error variances etc. On the basis of this setup Müller et al. (2007) consider a loss function that formalizes the consequences of this follow-up experiment. The loss function includes a sampling cost for the RT-PCR experiment and a reward that is realized if the RT-PCR experiment concludes with a significant outcome. The sample size is determined by a traditional power argument for a two-sample comparison, assuming a simple z-test for the difference of two population means. The probability of a significant outcome is the posterior predictive probability of the test statistic in the follow-up experiment falling in the rejection region. Let (μ̄_i, s_i) denote the posterior mean and standard deviation of the difference in mean expression for gene i between the two experimental groups. Let ρ̄, ρ*, p_ρ denote known parameters of the joint distribution of the microarray gene expression and the outcome of the RT-PCR experiment for the same gene. Details of the sampling model (see Müller et al., 2007) are not required for the following argument. Finally, let q_α define the (1 − α) quantile of a standard normal distribution. For a given signficance level α and a desired power (1 − β) at the alternative ${\mu }_i^A=\overline{\rho }({\overline{\mu }}_i-s_i)$, we find a minimum sample size for the follow up experiment

$$n_i(z_i)=2{[(q_{\alpha }+q_{\beta })/{\mu }_i^A]}^2.$$

Let Φ(z) denote the standard normal c.d.f. The posterior predictive probability for a significant outcome of the follow-up experiment is approximately

$${\pi }_i(z_i)=(1-p_{\rho })\alpha +p_{\rho }\mathrm{\Phi }\left[\frac{{\rho }^{*}{\overline{\mu }}_i\sqrt{n_i/2}-q_{\alpha }}{\sqrt{1+n_i/2{\rho }^{*2}{s}_i^2}}\right].$$

We formalize the goal of maximizing the probability of success for the follow-up experiment while controlling the sampling cost by the loss function

$$L(d,\theta ,z)={\displaystyle \sum _{d_i=1}[-c_1{\pi }_i(z_i)+n_i(z_i)]}+c_2{\displaystyle \sum d_i}.$$

Here c₂ is a fixed cost per gene for setting up a follow-up experiment, c₁ is the (large) reward for a significant outcome in the follow-up experiment, and c₃ ≡ 1 is the sampling cost per gene and experiment. The Bayes rule is $d_i^{p*}=I(c_1{\pi }_i-n_i\ge c_2)$. As before we can use ${\overline{\mu }}_i\approx {\displaystyle {\sum }_{j=1}^m{\widehat{\mu }}_{j}f(z_i;{\widehat{\mu }}_j)/}{\displaystyle {\sum }_{j=1}^{m}f(z_i;{\widehat{\mu }}_j)}\text{and}{s}_i^2\approx {\displaystyle {\sum }_{j=1}^m{({\overline{\mu }}_i-{\widehat{\mu }}_j)}^{2}f(z_i|{\widehat{\mu }}_j)/}{\displaystyle {\sum }_{j=1}^{m}f(z_i;{\widehat{\mu }}_j)}$ and approximate the Bayes rule by a modified ODP style statistic. Let π̂_i and n̂_i denote π_i and n_i evaluated with the approximations for μ̄_i and $s_i^2$. We consider the modified ODP threshold statistic

$$S_{\text{BDP}}^p(z_i)=c_1{\widehat{\pi }}_i(z_i)-{\widehat{n}}_i$$

Figure 6 compares the exact Bayes rules (18) and $d_i^{p*}=I(c_1{\pi }_i-n_i\ge c_2)$ with the tests based on the approximate ODP statistic $S_{\text{BDP}}^m$ and $S_{\text{BDP}}^p$, respectively.

6.2. Spatial Dependence

The nature of the ODP as an approximate Bayes rule was based on the semi-parametric model (7). However, the Bayes rules (6) or (18) remain meaningful under any probability model, as long as v_i and $\overline{t({\mu }_i)}$ have meaningful interpretations. For example, in geostatistical applications, we may be interested in isolating the exceedance regions of a spatial process, i.e. where the process has values above a given threshold (Zhang et al., 2008). Similarly, in the analysis of fMRI data, we aim to detect region specific activations of the brain. See Pacifico et al. (2004) and Flandin and Penny (2007) for two recent Bayesian solutions to the problem. In particular, Friston and Penny (2003) propose an empirical Bayes approach to build posterior probability maps of site specific signals. These approaches do not make use of an explicitely defined optimality criterion to support the proposed decision rules.

We consider a variation of the ODP that is suitable for spatial inference problems, using a specific spatial probability model as an example. We use the spatial model proposed by Gelfand et al. (2005). Let {Y (s), s ∈ D} be a random field, where D ⊂ R^d, d ≥ 2. Let s⁽ⁿ⁾ = (s₁,…,s_n) be the specific distinct locations in D where observations are collected. Assume that we have replicate observations at each location so that the full data set consists of the collection of vectors Y_i = {Y_i(s₁),…,Y_i(s_n)}^T, i = 1,…,m. We assume

$$Y_i|{\theta }_i\stackrel{\mathit{\text{ind}}}{~}f(y_i|\mu +{\theta }_i),i=1,\dots ,m$$ (20)

where f is some multivariate distribution, μ is a (not necessarily constant across s) regressive term and θ_i = {θ_i(s₁),…,θ_i(s_n)}^T is a spatial random effect, such that

$${\theta }_i|G\stackrel{\mathit{\text{iid}}}{~}Gi=1,\dots ,m\text{with}G~\mathit{\text{DP}}(\alpha ,G_0),$$ (21)

for some base measure G₀. See Gelfand et al. (2005) for details. The assumption of the DP prior in the model is unrelated to the DP that we used to justify the nature of the ODP as approximate Bayes rule. In this setting, the inferential problem might be quite general, as it may involve subsets of sites and replicates.

For simplicity, we consider a null hypothesis specific to each location s and replicate i: H_0si: θ_i ∈ A_si, A_si = {θ_i(s) > b}. For a fixed replicate i, let d_j = d(s_j) be the decision at site s_j, j = 1,…,n. Analogously, let r_j = r(s_j) denote the unknown truth at s_j. We could now proceed as before and consider the loss (5) and the rule, $d_j^{*}=I(v_j>t)$, where v_j is the posterior probability of the event A under the chosen probability model. For m sufficiently large and under model (20)–(21), it is possible to use the asymptotic arguments detailed in section 4 and define a BDP statistics for the spatial testing problem.

The loss function (5) is usually not an adequate representation of the investigator’s preferences in a spatial setting. Posterior probability maps may show very irregular patterns that could lead to, for example, flagging very irregular sets of pixels for exceedance θ_i(s) > b. We may explicitly include into the loss function a penalty for such irregularities, i.e.

$$L(d,\mathit{\theta },\mathit{y})=-{\displaystyle \sum d_j{r}_j+\mathrm{\lambda }{\displaystyle \sum d_j(1-r_j)}+\mathrm{\gamma }\mathit{\text{PI}},}$$ (22)

where PI is a penalization for irregularities. For example, PI could be the number of connected regions. See the example below. The decision rule corresponding to (22) is

$$d^{*}(D)=\underset{\{d(s),s\in D\}}{\text{arg}\text{min}}L(d(s),\theta (s),y(s)).$$

Finding d* requires numerical optimization.

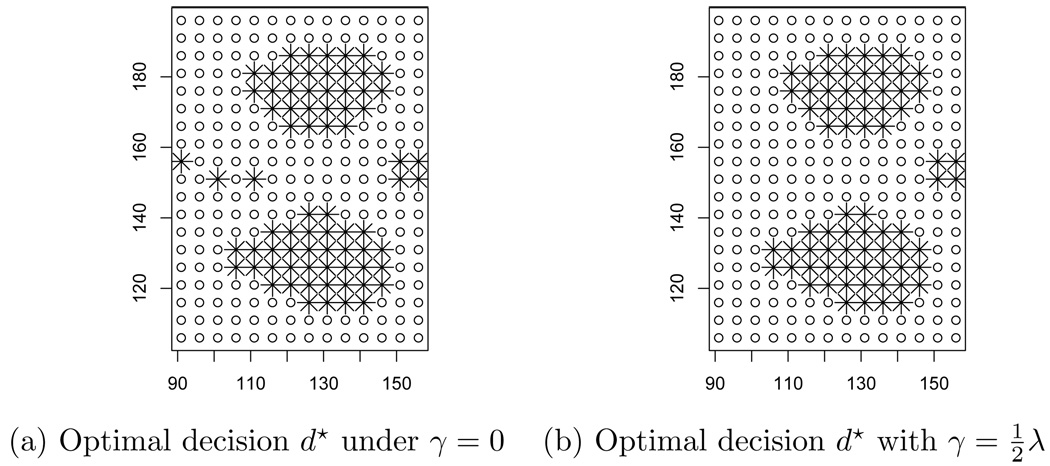
We illustrate the approach with a dataset of 18 individuals who underwent an MRI scan to detect signals of neurodegenerative patterns typical of the Alzheimer’s disease (Ashburner et al., 2003). The data have been provided by the Laboratory of Epidemiology and Neuroimaging, IRCSS, Centro San Giovanni di Dio, Brescia, Italy and have been previously normalized with the freely available SPM5 sowftare (http://www.fil.ion.ucl.ac.uk/spm/, see Friston et al. (1995) and Worsley and Friston (1995)). For simplicity, the dataset is restricted to gray density matter intensity values collected on a regular two-dimensional grid of 14 × 19 pixels encompassing the hippocampus and are treated as continuous. The data have been analyzed in Petrone et al. (2009) before, although with a different inferential aim.

We assume the random effect model (20)–(21), where f is a multivariate gaussian, with mean μ + θ and covariance matrix τ²I_n. The base measure G₀ is a zero-mean stationary Gaussian process with variance σ² and correlation ρ(s, s′) = exp(−φ||s − s′||), for some range parameter φ. Vague inverse gamma prior distributions on τ² and σ², and a vague gamma prior for φ complete the model. Hence, (20)–(21) defines a DP mixture of spatial processes (Gelfand et al., 2005). The model is sufficiently flexible to account for most of the spatial dependence observed in each individual. However, it is known that one of the marks of the Alzheimer’s disease is local hippocampal atrophy. Low grey matter intensity observed in normal neuroanatomical structures of the brain should not be reported as a signal. This consideration may lead to introduce several kinds of penalties into (22) to penalize for detections in non-interesting regions. Local atrophy is a condition that typically affects clusters of sites at the same time. This leads us to consider a penalty PI for the number of isolated signals on D. Specifically, PI is the number of interconnected regions and isolated points for which d_i(s) = 1. We use a numerical procedures to explore the action space and minimize (22). We find the optimal decision d* by a random search, initialized with the optimal rule under γ = 0.

Figure 7 shows the resulting optimal rule for one individual in the MRI dataset. We are interested in detecting regions of low gray matter intensity in the MRI scans. Hence we consider A = {θ(s) < b}, where b is a fixed constant, corresponding to the first decile of the dataset. The activation threshold for the posterior probability is t = 0.8. Figure 7 shows the activation map for an individual with recognizable signs of hypoccampal atrophy for γ = 0 (panel (a)) and for $\mathrm{\gamma }=\frac{1}{2}\mathrm{\lambda }$ (panel (b)). The additional penalty term provided a principled and coherent means of removing the singleton clusters that would otherwise be reported.

Fig. 7.

The effect of a loss function disfavoring isolated signals on the decisions taken according to loss (5). See 6.2 for details.

7. Conclusions and Summary

Starting from a decision theoretic framework, we provided an interpretation of the ODP as an approximate Bayes rule and introduced two directions of generalizations. First we improved the rule by sharpening the approximation. In a simulation example and a data analysis example we showed improved performance of the resulting BDP rule, even by the frequentist operating characteristics that are optimized by the oracle version of the ODP. Second, we considered generalizations of the ODP by replacing the original generic loss function by loss functions that better reflect the goals of the specific analysis. For loss functions with similar additive structure as the original loss function the resulting rule can still be approximated by a single thresholding statistic similar to the ODP.

The use of a decision theoretic framework provides a convenient assurance of coherent inference for the proposed approach. However, it also inherits the limitations of any decision theoretic procedure. The optimality is always with respect to an assumed probability model and loss function. The stated loss function is usually a stylized version of the actual inference goals. Often that is sufficient to obtain a reasonable rule. But we still caution to critically validate and if necessary revise the inference in the light of evaluations such as frequentist operating characteristics. Also, the proposed methods are more computation intensive than the original ODP procedure. In the simplest case we require some additional simulation to find a clustering of comparisons to compute cluster-specific m.l.e.’s.

The main strengths of the proposed approach are the generality and the assurance of coherent inference. The approach is general in the sense that the proposed methods are meaningful for any underlying probability model, and in principle for arbitrary loss functions. The approach is coherent in the sense that it derives from minimizing expected loss under a well defined probability model. From a data analysis perspective, an important strength of the proposed approach is the need and the opportunity to explicitely think about the inference goals and formalize them in the loss function. A practical strength is the opportunity for improved inference at no additional experimental cost, and only moderate additional computational cost.

Appendix

Proof of Preposition 1

The proof follows closely the proof of Theorem 1 in Storey and Tibshirani (2003). First, rewrite

$$\text{pFDR}=E\left(\frac{\mathit{\text{FP}}}{D}|D>0\right)=E\left(\frac{{\displaystyle {\sum }_{i=1}^n{d}_i(1-r_i)}}{{\displaystyle {\sum }_{i=1}^n{d}_i}}|D>0\right).$$ (23)

The expectation is with respect to the distribution of (z₁,…,z_m), conditionally on the event that some of the comparisons are significant. Hence,

$$\text{pFDR}=E_{Z_1,\dots ,Z_m|D>0}\left[E\left(\frac{{\displaystyle {\sum }_{i=1}^n{d}_i(1-r_i)}}{{\displaystyle {\sum }_{i=1}^n{d}_i}}|z_1,\dots ,z_m\right)\right].$$

Since d_i is a function of the sample z₁,…,z_m, the inner expectation is just

$$E\left(\frac{{\displaystyle {\sum }_{i=1}^n{d}_i(1-r_i)}}{{\displaystyle {\sum }_{i=1}^n{d}_i}}|z_1,\dots ,z_m\right)=\frac{{\displaystyle {\sum }_{i=1}^n{d}_i(1-v_i)}}{{\displaystyle {\sum }_{i=1}^n{d}_i}},$$

and since $d_i^{*}=I(v_i>t)$,

$${\text{pFDR}<E}_{z_1,\dots ,z_m|D>0}\left(\frac{{\displaystyle {\sum }_{i=1}^n{d}_i(1-t)}}{{\displaystyle {\sum }_{i=1}^n{d}_i}}\right)=1-t$$

Proof of Theorem 2

Because of the exchangeability of samples from a Pólya Urn, without loss of generality, we may consider v_m = p(r_m = 1|z₁,…,z_m). First, note that

$$\begin{array}{cc}{v}_m\hfill & ={\displaystyle \int p(r_m=1|G_k,z_1,\dots ,z_m)p(d{G}_k|z_1,\dots ,z_m)}={\displaystyle \int G_k(A^c)p(d{G}_k|z_1,\dots ,z_m)}\hfill \\ \hfill & =\frac{{\displaystyle \int {\displaystyle {\int }_{A^c}p(z_m|{\mu }_m)}{G}_k(d{\mu }_m)p(d{G}_k|z_1,\dots ,z_{m-1})}}{p(z_m|z_1,\dots ,z_{m-1})}\hfill \end{array}$$

Both numerator and denominator take the form of

$$E\left({\displaystyle {\int }_{B}p(z_m|{\mu }_m)G_k(d{\mu }_m)|z_1,\dots ,z_m}\right)={\displaystyle {\int }_{𝒫}{\displaystyle {\int }_{B}p(z_m|{\mu }_m)G_k(d{\mu }_m)p(d{G}_k|z_1,\dots ,z_m)},}$$

for a Borel set B. Let s^o(m) be a vector of cluster indicators, that is $s_i^o=j\text{ iff }{\mu }_i={\mu }_j^o$, i = 1,…,m, j = 1,…,k.

For any fixed m, let {s^o(m)} denote the set of all partitions of {1,…,m} into at most k clusters. From the discussions in Ferguson (1983), Lo (1984), Ishwaran and James (2003), it follows that

$$E\left({\displaystyle {\int }_{B}p(Z_m|{\mu }_m)G_k(d{\mu }_m)|z_1,\dots ,Z_{m-1}}\right)=\frac{m}{\alpha +m}{\displaystyle \sum _{s^{(m-1)}}p(s^{(m-1)}|z_1,\dots ,z_{m-1})}\times \times {\displaystyle \sum _{j=1}^k\frac{\frac{\alpha }{K}+m_j^o}{m}}{\displaystyle {\int }_{B}p(z_m|{\mu }_j^o)p(d{\mu }_j^o|z_i:s_i=j,i=1,\dots ,m-1),}$$ (24)

where $m_j^o=\mathit{\text{card}}\{s_i^o:s_i^o=j,i=1,\dots ,m-1\}$ is the number of elements in cluster j. If $m_j^o=0,\text{then}p(d{\mu }_j^o|z_i:s_i=j)\equiv G^{*}(d{\mu }_j^o)$. Expression (24) highlights that any partition of {1,…,m} can be obtained from a corresponding partition of {1,…,m−1} by adding the m-th observation to any of the previous cluster or by forming a new one.

Now, note that for each j = 1,…,k, either $\frac{m_j^o}{m}=o(1)\text{ or }\frac{m_j^o}{m}=O(1)$. If $\frac{m_j^o}{m}=o(1),(\alpha /k+m_j^o)/m\to 0;\text{if}\frac{m_j^o}{m}=O(1)$, we can use Laplace approximation arguments (see Schervish, 1995, chapter 7.4.3 or Ghosh et al., 2006, pag. 115) to obtain

$${\displaystyle {\int }_{B}p(z_m|{\mu }_j^o)p(d{\mu }_j^o|z_i:s_i^o=j)\approx p(z_m|{\widehat{\mu }}_j^o)\mathrm{\Phi }({\widehat{\mu }}_j^o\in B)[1+O(m_j^{o-2})]},$$

where ${\widehat{\mu }}_j^o$ is the MLE estimate computed in cluster j, j = 1,…k, obtained by solving $\frac{\partial }{\partial \mu }{\displaystyle {\sum }_{i:s_i=j}f(z_i;\mu )+}\frac{\partial }{\partial \mu }f(z_m;\mu )=0$ and Φ(·) denotes a standard gaussian probability distribution.

Next we relabel the non-empty clusters by identifying the set $\{{\mu }_j^o;m_j^o>0\}$ as the set of unique values $\{{\mu }_j^{*},j=1,\dots ,L\}$.

The proof is completed after noting that, since $\frac{m_j^o}{m}=O(1)$, and because of the asymptotic consistency of posterior distributions, as m → ∞, Φ(μ̂_j ∈ B) → I_B(μ̂_j).