A Simple Approach to the Estimation of Incidence Rate Difference

Abstract

The incidence rate difference (IRD) is a parameter of interest in many medical studies. For example, in vaccine studies, it is interpreted as the vaccine-attributable reduction in disease incidence. This is an important parameter, because it shows the public health impact of an intervention. The IRD is difficult to estimate for various reasons, especially when there are quantitative covariates or the duration of follow-up is variable. In this paper, the authors propose an approach based on weighted least-squares regression for estimating the IRD. It is very easy to implement because it boils down to performing ordinary least-squares regression analysis of transformed variables. Furthermore, if the outcome events are repeatable, the authors propose that data on all events be analyzed instead of first events only. Four versions of the Huber-White robust standard error are considered for statistical inference. Simulation studies are used to examine the performance of the proposed method. In a variety of scenarios simulated, the method provides an unbiased estimate for the IRD, and the empirical coverage proportion of the 95% confidence interval is very close to the nominal level. The method is illustrated with data from a vaccine trial carried out in the Gambia in 2001–2004.

The relative merits of the odds ratio, risk ratio, and risk difference and procedures for estimating them have been discussed by many epidemiologists and statisticians (1–3). The usage and relative merits of the incidence rate ratio (IRR) and the incidence rate difference (IRD) have received much less attention. Both IRR and IRD are commonly used in reporting results from vaccine trials. In vaccine trials, vaccine efficacy is estimated by 1 – (incidence rate in vaccine group/incidence rate in control group), or 1 – IRR, and vaccine-attributable reduction in incidence is estimated by (incidence rate in control group – incidence rate in vaccine group), or IRD (4, 5). Vaccine-attributable reduction represents the reduction in disease burden and is a useful measure of the public health importance of a vaccine. Furthermore, the inverse of vaccine-attributable reduction (or IRD) has the useful interpretation of “number needed to treat” in order to prevent 1 episode of disease per person-year (6). The impact of vaccines may also be studied in observational (nonrandomized) studies in which the evaluation can be subject to confounding, thus requiring statistical adjustment. The same concepts apply to the evaluation of other interventions or exposures. Hence, in this article, the generic term incidence rate difference is used instead of vaccine-attributable reduction, and it refers to the incidence rate in the control (unexposed) group minus that in the intervention (exposed) group.

There are 3 issues to consider when estimating IRD and IRR. Firstly, if the outcome events are repeatable, should one use data on time to first events only or all events? In the context of vaccine research, this issue has been the topic of recent debate (7, 8). A meeting convened by the World Health Organization in 2008 recommended that data on all events should be included in the evaluation of vaccine efficacy for malaria vaccines (8). It appears that the bias in estimating IRD by using first events only has been somewhat neglected (see Web Appendix 1, available on the Journal’s Web site (http://aje.oxfordjournals.org/), for an illustration).

Secondly, statistical estimation of IRD is more difficult than that of IRR. For a simple 2-group comparison without adjustment for covariates, there are established methods for estimating IRD on the basis of the Poisson distribution (first event) and the negative binomial distribution (all events) (9, 10). For analysis of a single quantitative exposure variable or multiple exposure variables, generalized linear models readily deal with estimation of the IRR by using the log of follow-up time as an “offset” term in the log(incidence) equation. However, unless follow-up time is equal for every participant, which is not true in many studies, it is not clear how well the generalized linear models estimate the IRD. Even in the simple case of equal follow-up time, the iterations for Poisson and negative binomial regression models with a quantitative exposure variable may not always converge (3). One possible option for multivariable analysis of IRD is standardization (11, 12), but this cannot accommodate quantitative exposure variables, and it becomes difficult in practice as the number of (categorical) exposure variables increases.

Thirdly, valid statistical inference for data on repeatable (or recurrent) events needs to avoid underestimation of variance and inflation of type 1 error rates due to correlated events within the same person.

In this article, we aim to provide a simple method based on a weighted least-squares regression approach and a robust standard error estimator for estimating IRD. The proposed method easily controls for unequal follow-up time and quantitative or multiple covariates. The method is general in that it is applicable to analysis of first events and all events. When there is only 1 binary exposure variable, the method will reduce to the one proposed by Stukel et al. (11) and Glynn and Buring (10) under mild conditions.

METHODS

Notations and model

Suppose there are n subjects in a study. For subject i (i = 1, …, n), for the analysis of recurrent-event data, Y_i is the total number of events recorded and Z_i is the total length of follow-up time, referring to the time from recruitment into the cohort to either loss to follow-up, which is random, or study closure, which is determined by the investigators. Moreover, X_i = (X_i0, X_i1, …, X_ik) is the covariate vector for subject i. β = (β₀, β₁, …, β_k) is the unknown regression coefficient vector associated with X_i. Let X_i0 = 1 be the intercept of the design matrix, X_i1 be an indicator of the exposure status, and X_i2–X_ik be the other covariates. The estimate of the incidence rate for subject i is Y_i/Z_i. The observed incidence rate using data on all events in the unexposed (X_i1 = 0) group is

whereas the observed IRD between groups is

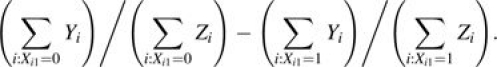The gist of our proposed method, which will be elaborated below, is to generate new variables 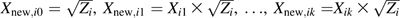and to perform ordinary least-squares regression without an intercept for the regression equation

(1)

Note that IRD = −β₁ by definition, and we will show below that the estimator 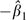is unbiased. If a less conventional data coding scheme is used—for example, if the exposed (unexposed) group is indicated by X_i1 = 0 (X_i1 = 1)—then IRD = β₁.

To accommodate possible unobserved heterogeneity in the event rates among subjects, a frailty term υ_i is introduced. Therefore, the incidence rate for subject i can be modeled as

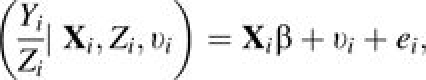(2)

where the e_i’s are the independent individual residuals, with E(e_i) = 0, Var(e_i) = σ²/Z_i, and Cov(e_i, e_j) = 0 if i ≠ j. υ_i is uncorrelated with X_i, Z_i, and e_i, and follows an arbitrary distribution with E(υ_i) = ν and Var(υ_i) = ϱ.

Estimation

Following model 2 (equation 2), the conditional mean and variance for the incidence rate of subject i are

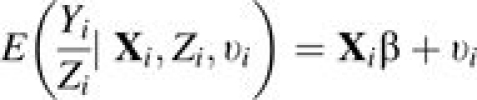(3)

and

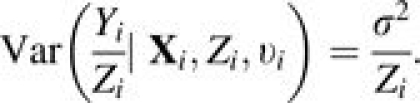(4)

Consequently, for any distribution of Y_i, the marginal mean and variance of Y_i/Z_i are

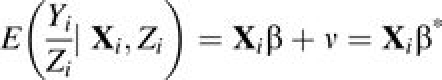(5)

and

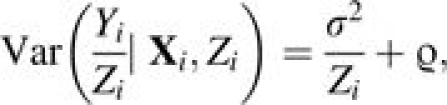(6)

respectively. β^* = (β₀ + ν, β₁, …, β_k), where the mean of the possible unobserved heterogeneity becomes part of the intercept. Since the primary interest is to estimate β from β₁ (or equivalently, –IRD) to β_k and subsequently make inference about β₁,… β_k, no further attention is paid to β₀^*.

Throughout this article, models and expectations are conditional on υ_i or marginal with respect to υ_i, while for each situation they are always conditional on X_i and Z_i.

Note that equations 2–6 apply to recurrent-events data. When analysis is limited to the first events, Z_i is subject to being censored by the first event. Moreover, the frailty υ_i is not required, and model 2 reduces to the linear probability model with a binary response variable. Nonetheless, the following estimation procedure still applies, but it is unbiased only if there is no heterogeneity (see Web Appendix 1 for an illustration).

We propose to estimate β^* using the following estimation equation:

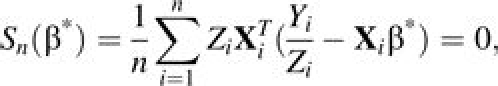(7)

which is a special case of generalized estimating equations (13). Using the conditional variance in equation 4 instead of the marginal variance in equation 6 in the estimating equation gives an explicit solution that allows one to incorporate some existing estimation methods. A robust variance estimator is used to correct for the misspecification of the working variance. By the general theory of generalized estimating equations (13), the resulting estimator of β^* is consistent and asymptotically normal as long as equation 5 holds true.

For notational simplicity, let Y = (Y₁, …, Y_n)^T, Z = (Z₁, …, Z_n)^T, X = (X₁^T,…,X_n^T)^T, and W = diag(Z₁, …, Z_n). Following equation 7,

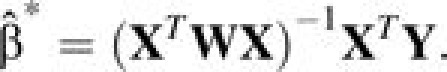(8)

Moreover, it can be shown, in the case of time-varying regression coefficients, that 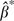is estimating the average of the covariates’ effects over the total number of person-years studied using data on all of the events (the mathematical proof and simulation evidence are part of our ongoing work).

In the simplest case in which X_i = (1, X_i1), where X_i1 = 0 or 1 and β^* = (β₀^*,β₁)^T, equation 8 yields

and

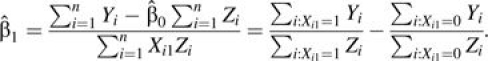Therefore, 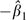is the observed IRD in the sample.

In the presence of L strata in the sample defined by 1 or more categorical confounders, using equation 8, 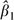reduces to

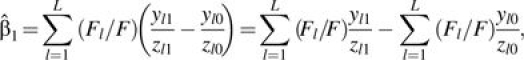where y_lj and z_lj are the total number of events and the total follow-up time, respectively, for all subjects in the lth (l = 1, …, L) stratum in the unexposed group (j = 0) and the exposed group (j = 1). F_l = 1/(1/z_l0 + 1/z_l1) and F = ∑_{l = 1}^LF_l. This agrees with the estimator proposed by Stukel et al. (11), which is a weighted average of the IRD between the exposed (j = 1) and the unexposed (j = 0) across the L strata.

Note that equation 8 can be equivalently estimated via an ordinary least-squares regression on the transformed variables Y and X—that is, Y_new = W^–1/2Y and X_new = W^1/2X, as introduced above. Therefore, the robust variance estimator (14) for is

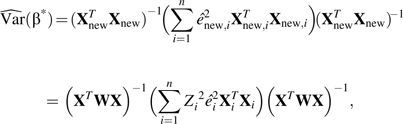(9)

where 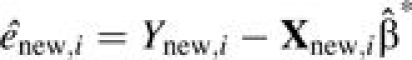and

For the simplest case in which X_i = (1, X_i1) and X_i1 = 0 or 1, the robust variance estimator for 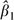can be simplified as

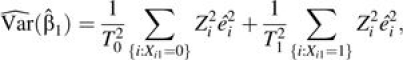(10)

where T_g = ∑_{{i:Xi1 = g}}Z_i and g = 0 or 1. It can be shown that the variance estimator in equation 10 is consistent with that given by Stukel et al. (11), provided that the residuals are independently and identically distributed within each group defined by X_i1 (see Web Appendix 2).

Small-sample adjustment

Equation 9 gives the asymptotic, or large-sample, version of the robust variance, which we name HC_r. Three versions of adjustment for a small sample size have been proposed (15), conventionally named HC₁, HC₂, and HC₃. The small-sample adjustment involves multiplying the ith summand in the middle term of HC_r in equation 9 by a correction factor n/(n – k), 1/(1 – h_i), or 1/(1 – h_i)² to obtain HC₁, HC₂, or HC₃, respectively, where h_i is the ith diagonal element in the matrix H:

The adjustment is smallest for HC₁ and largest for HC₃, and the 4 variance estimators are asymptotically the same.

SIMULATION STUDIES

The proposed method is general, but this work is motivated by our research in pediatric infectious diseases. The simulation scenarios will follow realistic situations seen in the studies of acute otitis media and radiologically confirmed pneumonia, representing diseases with relatively high and low incidence rates in young children (16, 17).

Data on first events and on all events will be used to estimate β^*, and the differences in the estimates will be examined. The performance of the proposed estimator and robust variance estimator will be evaluated in various scenarios, using the average of parameter estimates, the average of the robust standard error estimates, the empirical standard deviation, and the 95% coverage proportion based on the robust standard error estimates. The variance estimate proposed by Stukel et al. (11) will also be calculated in the scenarios with only 1 binary exposure variable for comparison.

Simulation parameter configurations and data generation processes are described in detail in Web Appendix 3. For each scenario, 10,000 replications were simulated.

Table 1 shows the simulation results with n = 1,000 in the absence of confounding. It can be seen that the average of parameter estimates using all events was close to the true parameter value (β₁ = −0.5 in high-incidence scenarios and β₁ = −0.025 in low-incidence scenarios), regardless of whether the binary exposure variable X_i1 (X_i1 ∼ Bernoulli(p)) was evenly (p = 0.5) or unevenly (p = 0.7) distributed and regardless of heterogeneity (ν_i). However, the presence of heterogeneity resulted in biased estimates for β₁ using first events for high-incidence scenarios (the averages of parameter estimates were –0.5151 and –0.5073 under 2 forms of heterogeneity, respectively), though little bias was observed for low-incidence scenarios (the averages of parameter estimates were very close to –0.025). Secondly, the 95% coverage proportions based on the robust standard error estimates were very close to their nominal level. When using data on all events, the inferences derived using robust standard errors were practically identical to those of the Stukel et al. (11) approach in terms of the average of parameter estimates and the 95% coverage proportion based on the robust standard error estimates. Moreover, regardless of whether data on first events or all events were used, the average of the robust standard error estimates and the empirical standard deviation agreed very well. Since this is also true in other simulation scenarios, we suppressed the display of empirical standard deviations in subsequent tables in the interest of space. Similar findings were observed for the cases with n = 200 (Web Table 1).

Table 1.

Simulation Results on the Estimates for β₁ in the Absence of Confounding (n = 1,000)

p and β1	υi	First Events				All Events
		Proposed Method				Average Estimatea	ESD	Proposed Method		Stukel et al. (11)
		Average Estimatea	ESD	Average SErb	CPrc			Average SErb	CPrc	Average SEd	CPe
p = 0.5
β1 = −0.5	0	−0.5011	0.0537	0.0539	95.1	−0.4999	0.0348	0.0347	95.0	0.0347	95.0
	±0.25	−0.5151	0.0520	0.0525	94.7	−0.5001	0.0380	0.0381	95.2	0.0381	95.2
	γ	−0.5073	0.0605	0.0599	94.6	−0.5001	0.0408	0.0406	94.8	0.0406	94.8
β1 = −0.025	0	−0.0250	0.0080	0.0080	94.9	−0.0250	0.0077	0.0077	95.0	0.0077	95.0
	±0.025	−0.0251	0.0078	0.0079	95.3	−0.0250	0.0077	0.0078	95.4	0.0078	95.3
	γ	−0.0250	0.0086	0.0086	95.0	−0.0249	0.0083	0.0084	94.9	0.0084	94.9
p = 0.7
β1 = −0.5	0	−0.5030	0.0648	0.0646	94.9	−0.5005	0.0399	0.0402	94.9	0.0402	95.0
	±0.25	−0.5158	0.0689	0.0698	95.4	−0.5004	0.0455	0.0454	95.0	0.0454	94.9
	γ	−0.5074	0.0702	0.0703	95.0	−0.4998	0.0459	0.0455	94.9	0.0455	94.9
β1 = −0.025	0	−0.0250	0.0093	0.0093	94.7	−0.0249	0.0091	0.0090	94.5	0.0090	94.6
	±0.025	−0.0251	0.0098	0.0098	94.9	−0.0250	0.0096	0.0095	94.7	0.0095	94.7
	γ	−0.0250	0.0097	0.0098	95.0	−0.0249	0.0094	0.0095	94.9	0.0095	95.0

Abbreviations: CP, coverage proportion; ESD, empirical standard deviation; SE, standard error.

^aAverage of the parameter estimates.

^bAverage of the robust standard error estimates.

^c95% coverage proportion based on the robust standard error estimates.

^dAverage of the standard error estimates using the method proposed by Stukel et al. (11).

^e95% coverage proportion based on the standard error estimates using the method proposed by Stukel et al. (11).

Table 2 shows the simulation results when the intervention effect was confounded by a quantitative variable X_i2 which was slightly skewed. The analysis simultaneously included X_i1 and X_i2 in the regression model. The proposed method using all events performed very well for high-incidence scenarios, that is, (β₁, β₂) = (–0.5, 0.05). Regardless of the distribution of X_i1 (p = 0.5 or 0.7), the degree of collinearity, or the presence of heterogeneity, the mean estimates for β₁ and β₂ were always close to the targeted values. The 95% coverage proportions based on the robust standard error estimates were also very close to the nominal level. In the low-incidence scenarios with (β₁, β₂) = (–0.025, 0.005), the proposed method gave a mean estimate for β₂ somewhat different from the true value. Nevertheless, the 95% coverage proportion based on the robust standard error estimates was still close to the nominal level. In only 1 case did the 95% coverage proportion based on the robust standard error estimates deviate from 95% by more than 0.5% (94.3% at p = 0.7, β₁ = –0.025, υ_i = 0, and moderate collinearity). Results were very similar when n = 200 (Web Table 2).

Table 2.

Simulation Results on the Estimates for (β₁,β₂) With n = 1,000 and X₂ Slightly Skewed

p and β	υi	Moderate Collinearity						Strong Collinearity
		First Events			All Events			First Events			All Events
		Average Estimatea	Average SErb	CPrc	Average Estimate	Average SEr	CPr	Average Estimate	Average SEr	CPr	Average Estimate	Average SEr	CPr
p = 0.5
β1 = −0.5	0	−0.5000	0.0637	94.7	−0.4994	0.0393	94.9	−0.5019	0.0727	94.8	−0.5004	0.0450	94.7
	±0.25	−0.5124	0.0623	95.1	−0.4993	0.0426	95.0	−0.5145	0.0712	94.3	−0.5003	0.0487	94.9
	γ	−0.5058	0.0699	95.3	−0.4993	0.0451	95.0	−0.5077	0.0804	94.7	−0.5001	0.0515	94.9
β2 = 0.05	0	0.0501	0.0404	94.8	0.0499	0.0265	95.1	0.0505	0.0449	94.8	0.0507	0.0288	94.9
	±0.25	0.0506	0.0394	94.3	0.0496	0.0287	94.9	0.0519	0.0439	94.7	0.0505	0.0311	94.8
	γ	0.0503	0.0449	95.2	0.0499	0.0303	95.0	0.0511	0.0497	94.8	0.0499	0.0328	94.8
β1 = −0.025	0	−0.0251	0.0084	94.9	−0.0251	0.0081	94.8	−0.0250	0.0095	94.8	−0.0249	0.0093	94.6
	±0.025	−0.0251	0.0084	94.8	−0.0251	0.0082	94.9	−0.0251	0.0095	95.0	−0.0251	0.0093	94.8
	γ	−0.0249	0.0090	95.1	−0.0249	0.0088	95.0	−0.0251	0.0103	95.1	−0.0251	0.0100	95.0
β2 = 0.005	0	0.0057	0.1129	95.3	0.0056	0.1098	95.1	0.0042	0.1231	95.2	0.0039	0.1196	95.0
	±0.025	0.0043	0.1126	94.8	0.0044	0.1104	94.8	0.0056	0.1227	95.5	0.0059	0.1200	95.1
	γ	0.0043	0.1218	95.2	0.0049	0.1188	94.9	0.0048	0.1323	95.3	0.0046	0.1288	95.1
p = 0.7
β1 = −0.5	0	−0.5041	0.0744	95.0	−0.5001	0.0446	94.9	−0.5023	0.0816	95.2	−0.4995	0.0497	94.8
	±0.25	−0.5160	0.0800	94.8	−0.4997	0.0496	94.9	−0.5159	0.0878	94.5	−0.4998	0.0553	94.8
	γ	−0.5086	0.0807	94.9	−0.5000	0.0497	95.1	−0.5093	0.0885	95.1	−0.5002	0.0555	94.9
β2 = 0.05	0	0.0503	0.0374	94.8	0.0505	0.0254	94.8	0.0498	0.0429	95.1	0.0498	0.0287	95.1
	±0.25	0.0514	0.0407	94.9	0.0500	0.0289	95.1	0.0506	0.0466	95.1	0.0498	0.0323	94.7
	γ	0.0508	0.0411	94.9	0.0502	0.0289	95.2	0.0513	0.0470	94.7	0.0507	0.0324	94.9
β1 = −0.025	0	−0.0250	0.0096	94.3	−0.0249	0.0093	94.3	−0.0253	0.0106	94.8	−0.0251	0.0103	94.6
	±0.025	−0.0251	0.0102	94.5	−0.0251	0.0099	94.7	−0.0251	0.0113	95.0	−0.0250	0.0109	94.7
	γ	−0.0251	0.0103	94.9	−0.0250	0.0099	94.6	−0.0248	0.0113	94.8	−0.0248	0.0109	94.5
β2 = 0.005	0	0.0068	0.1070	95.2	0.0071	0.1043	95.0	0.0067	0.1206	95.1	0.0065	0.1174	95.0
	±0.025	0.0049	0.1149	95.3	0.0051	0.1124	95.1	0.0046	0.1290	95.3	0.0049	0.1259	95.0
	γ	0.0045	0.1151	95.2	0.0041	0.1126	94.9	0.0048	0.1293	95.1	0.0051	0.1263	95.0

Abbreviations: CP, coverage proportion; SE, standard error.

^aAverage of the parameter estimates.

^bAverage of the robust standard error estimates.

^c95% coverage proportion based on the robust standard error estimates.

Table 3 shows the simulation results obtained when the intervention effect was confounded by a quantitative variable X_i2 which was highly skewed. The results were very similar to those reported for the slightly skewed data series in Table 2. Again, results were very similar when n = 200 (Web Table 3).

Table 3.

Simulation Results on the Estimates for (β₁, β₂) With n = 1,000 and X₂ Highly Skewed

p and β	υi	Moderate Collinearity						Strong Collinearity
		First Events			All Events			First Events			All Events
		Average Estimatea	Average SErb	CPrc	Average Estimate	Average SEr	CPr	Average Estimate	Average SEr	CPr	Average Estimate	Average SEr	CPr
p = 0.5
β1 = −0.5	0	−0.5006	0.0678	95.0	−0.4993	0.0410	94.9	−0.5024	0.0767	95.1	−0.5004	0.0459	95.0
	±0.25	−0.5148	0.0665	94.6	−0.5006	0.0443	94.8	−0.5139	0.0754	94.4	−0.5002	0.0494	95.2
	γ	−0.5078	0.0745	94.6	−0.5006	0.0468	94.7	−0.5069	0.0841	94.4	−0.5003	0.0520	95.0
β2 = 0.05	0	0.0499	0.0308	95.3	0.0500	0.0199	95.2	0.0499	0.0367	94.9	0.0501	0.0227	94.7
	±0.25	0.0509	0.0303	94.8	0.0497	0.0210	94.9	0.0504	0.0363	94.2	0.0501	0.0239	94.9
	γ	0.0501	0.0341	94.9	0.0497	0.0222	95.0	0.0501	0.0404	95.0	0.0501	0.0251	94.9
β1 = −0.025	0	−0.0250	0.0085	94.7	−0.0250	0.0083	94.8	−0.0251	0.0095	94.5	−0.0250	0.0092	94.6
	±0.025	−0.0250	0.0085	94.8	−0.0250	0.0083	94.8	−0.0250	0.0095	94.9	−0.0249	0.0093	94.7
	γ	−0.0250	0.0092	94.9	−0.0250	0.0090	95.0	−0.0250	0.0102	94.9	−0.0249	0.0100	94.6
β2 = 0.005	0	0.0050	0.0836	95.1	0.0055	0.0812	94.7	0.0048	0.0964	94.9	0.0050	0.0931	94.8
	±0.025	0.0044	0.0835	94.8	0.0049	0.0815	94.6	0.0037	0.0961	95.0	0.0040	0.0934	94.8
	γ	0.0033	0.0898	95.0	0.0035	0.0873	94.9	0.0042	0.1028	95.0	0.0042	0.0997	94.9
p = 0.7
β1 = −0.5	0	−0.5024	0.0785	94.9	−0.5001	0.0464	95.1	−0.5026	0.0880	94.9	−0.4996	0.0521	94.7
	±0.25	−0.5155	0.0844	94.7	−0.5003	0.0514	95.2	−0.5154	0.0946	94.8	−0.5003	0.0576	94.9
	γ	−0.5095	0.0848	94.7	−0.5006	0.0516	94.8	−0.5080	0.0950	94.5	−0.4994	0.0577	94.8
β2 = 0.05	0	0.0497	0.0303	94.7	0.0498	0.0200	95.1	0.0490	0.0397	94.8	0.0500	0.0249	95.2
	±0.25	0.0509	0.0328	94.4	0.0499	0.0225	94.8	0.0494	0.0429	94.7	0.0496	0.0278	95.0
	γ	0.0498	0.0331	95.3	0.0501	0.0225	95.0	0.0500	0.0431	94.7	0.0503	0.0278	94.7
β1 = −0.025	0	−0.0252	0.0098	95.1	−0.0251	0.0095	94.9	−0.0252	0.0109	94.9	−0.0251	0.0106	94.7
	±0.25	−0.0252	0.0104	94.8	−0.0251	0.0101	94.6	−0.0249	0.0115	95.0	−0.0248	0.0112	94.7
	γ	−0.0252	0.0104	94.7	−0.0251	0.0101	94.7	−0.0252	0.0116	94.5	−0.0251	0.0112	94.2
β2 = 0.005	0	0.0065	0.0842	95.3	0.0066	0.0819	95.0	0.0033	0.1065	95.0	0.0039	0.1030	94.9
	±0.025	0.0043	0.0899	95.2	0.0049	0.0877	94.9	0.0026	0.1129	94.8	0.0031	0.1094	94.3
	γ	0.0048	0.0902	94.6	0.0051	0.0880	94.5	0.0038	0.1131	95.0	0.0040	0.1096	94.8

Abbreviations: CP, coverage proportion; SE, standard error.

^aAverage of the parameter estimates.

^bAverage of the robust standard error estimates.

^c95% coverage proportion based on the robust standard error estimates.

Furthermore, under all of the simulation scenarios, the variances were underestimated if the naive variance estimator was used, and consequently the coverage proportions were smaller than expected (details not shown).

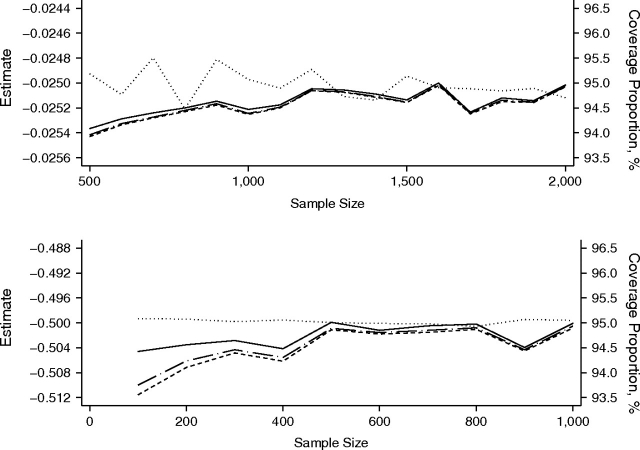
Figure 1 focuses on the performance of the asymptotic and small-sample versions of the robust variance estimator for the regression estimates using all events. Data were simulated under the unfavorable setup of unbalanced group size (p = 0.7), with a quantitative confounder X_i2 following a highly skewed distribution and being strongly correlated with the intervention status as previously described. The simulation replications for each scenario were 20,000. Because of the similarities between the 95% coverage proportions obtained using HC_r and those obtained using HC₁ as n/(n – k) ≈ 1, only the 95% coverage proportions obtained using HC_r, HC₂, and HC₃ are shown in Figure 1. Mean estimates for β₁ are also presented. For the low-incidence scenario with β₁ = –0.025, the mean estimate for β₁ fluctuated within 0.8% of the true value −0.025, and the 95% coverage proportion obtained using HC_r was, at most, 1% different from the intended 95% coverage proportion when n was greater than 500. For the high-incidence scenario with β₁ = –0.5, the estimate for β₁ fluctuated within 0.1% of the true value –0.5, and the difference between the 95% coverage proportion obtained using HC_r and the intended 95% coverage proportion was less than 1% when n was greater than 200. The 95% coverage proportion obtained using HC₃ was always closer to the intended 95% level than the 95% coverage proportions obtained using HC_r and HC₂, but the differences were important only if n was less than or equal to 500.

Figure 1.

Average estimates and coverage proportions of 3 variance estimators for β₁ using all events data in the scenario of γ random effects. X₁ ∼ Bernoulli(0.7). X₂ is highly skewed and highly correlated with X₁. Dotted line, estimate; dashed line, 95% coverage proportion using robust variance estimator HC_r; long-dashed-and-dotted line, 95% coverage proportion using HC₂; solid line, 95% coverage proportion using HC₃. There were 20,000 replications. Upper panel: β₁ = –0.025; lower panel: β₁ = –0.5.

CASE STUDY

Data from a randomized, double-blinded, placebo-controlled trial of a 9-valent pneumococcal conjugate vaccine conducted in the Gambia (17) were reanalyzed. Our purpose was 2-fold: firstly, to illustrate the proposed method and compare the analysis of first events with the analysis of all events in estimating the IRD; and secondly, to examine whether there was any ethnic difference in disease incidence. Details on the trial and the vaccine efficacy estimated using only first events can be found in the paper by Cutts et al. (17). Briefly, approximately 17,000 children aged 6–51 weeks were randomly allocated to one of the 2 regimens: receipt of either 3 doses of the vaccine or 3 doses of the placebo. Radiologically confirmed pneumonia was the primary endpoint. A disease episode was considered to be new only if at least 30 days had elapsed since the child's previous episode (18), and the 30 days were not counted in the person-time exposed. Following the method of Cutts et al. (17), we performed a per-protocol analysis and used time from 14 days after the third dose or placebo as the time scale. Permission to use the data for the present study was given by the Medical Research Council–Gambian Government Joint Ethics Committee.

Covariates included in the analyses were district (Bansang, Basse, or other), age at enrollment, gender, and ethnicity (Mandinka, Fula, Serahule, Wolof, or others). The placebo and vaccine groups were well balanced in terms of baseline covariates. In the study area, each of the 3 major ethnic groups (Mandinka, Fula, and Serahule) comprised approximately 30% of the local population. Moreover, across the 5 different ethnic groups, it was noted that: 1) the proportions of males were comparable; 2) the median ages were also comparable, but there were some differences at the upper percentiles (e.g., the 90th percentiles ranged from 0.44 to 0.50); and 3) the geographic distributions of ethnic groups varied considerably. For example, 27.5% of the Wolof participants lived in Bansang, where the disease incidence was the highest (see Table 4). This percentage was notably higher than percentages in the other ethnic groups (Mandinka, 5.0%; Fula, 11.3%; Serahule, 0.1%; and others, 14.1%). On the other hand, 3.9% of the Wolof participants lived in Basse, as compared with 36.0%, 26.9%, 31.8%, and 46.1% of the Mandinka, Fula, Serahule, and others, respectively.

Table 4.

Incidence Rate of Radiologically Confirmed Pneumonia in the Placebo Group and Incidence Rate Difference per Child-Year, by Ethnicity and District, the Gambia, 2001–2004

	First Events			All Events
Variable	Placeboa	Incidence Rate Differenceb		Placebo	Incidence Rate Differenceb
		Estimate	95% CI		Estimate	95% CI
Ethnicity
Mandinka	0.0512	−0.0239	−0.0329, −0.0149	0.0549	−0.0253	−0.0352, −0.0155
Fulla	0.0391	−0.0154	−0.0233, −0.0076	0.0416	−0.0163	−0.0248, −0.0078
Serahule	0.0329	−0.0076	−0.0156, 0.0005	0.0358	−0.0098	−0.0185, −0.0012
Wolof	0.0425	−0.0108	−0.0262, 0.0046	0.0453	−0.0109	−0.0279, 0.0061
Others	0.0216	0.0026	−0.0249, 0.0301	0.0211	0.0105	−0.0220, 0.0430
District
Bansang	0.0951	−0.0410	−0.0663, −0.0156	0.1027	−0.0451	−0.0724, −0.0178
Basse	0.0459	−0.0141	−0.0230, −0.0052	0.0506	−0.0176	−0.0274, −0.0078
Others	0.0324	−0.0125	−0.0176, −0.0074	0.0338	−0.0122	−0.0177, −0.0067

Abbreviation: CI, confidence interval.

^aIncidence rate in the placebo group.

^bIncidence rate in the vaccine group minus incidence rate in the control group.

Of the 929 radiologically confirmed pneumonia episodes detected in the 16,340 children during the trial period, 567 were from the placebo group and 362 were from the vaccine group. The total numbers of child-years were 12,914 and 13,070 in the placebo and vaccine groups, respectively. Approximately 95% of the children had no episodes of pneumonia detected throughout this period, while 772 children had 1 episode, 65 children had 2, and 9 children had 3; 846 (91.1%) of the episodes were first episodes.

Without consideration of potential confounders, the IRD 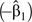attributable to the vaccine was 0.0150 per child-year (95% confidence interval: 0.0104, 0.0195) using first episodes only and 0.0162 per child-year (95% confidence interval: 0.0113, 0.0211) using all episodes. Analysis of first events and all events did not make a big difference, as was seen in the simulation studies for low-incidence scenarios. The estimates for the incidence rate in the placebo group and the IRD in different ethnic groups and districts are shown in Table 4. Results suggested that regardless of whether first episodes only or all episodes were used, among the 5 ethnic groups, 1) persons of Mandinka ethnicity had the highest placebo-group incidence rate and Wolof the second-highest, and 2) the IRDs between the vaccine and placebo groups were higher in Mandinka and Fula than in the other ethnic groups, but their 95% confidence intervals mostly overlapped. When the analysis was based on first episodes only, the vaccine was found to have a significant protective effect only in Mandinka and Fula. When all of the episodes were used, the protective effect was also found to be significant among persons of Serahule ethnicity.

Table 5 shows the results of the multivariable analyses (STATA codes (Stata Corporation, College Station, Texas) are available in Web Appendix 4). In correspondence with the results in Table 4, this multivariable analysis suggested that Mandinka had a higher incidence rate than all of the other ethnic groups, although the difference with Wolof was not statistically significant. The covariate-adjusted difference between Wolof and Mandinka was similar to the unadjusted difference, showing that there was no major confounding by district. Moreover, a joint test of the 4 ethnic contrasts showed no difference among Fula, Serahule, Wolof, and others.

Table 5.

Multivariable Regression Analysis of the Incidence of Radiologically Confirmed Pneumonia per Child-Year, by Ethnicity and District, the Gambia, 2001–2004

Variable	First Events			All Events
	Estimate	Robust SE	95% CI	Estimate	Robust SE	95% CI
Ethnicity (referent: Mandinka)
Fulla	−0.0085	0.0030	−0.0145, −0.0026	−0.0097	0.0033	−0.0161, −0.0032
Serahule	−0.0072	0.0031	−0.0132, −0.0011	−0.0083	0.0034	−0.0149, −0.0017
Wolof	−0.0078	0.0045	−0.0167, 0.0011	−0.0089	0.0049	−0.0186, 0.0007
Others	−0.0207	0.0075	−0.0353, −0.0061	−0.0205	0.0089	−0.0378, −0.0031
Vaccine	−0.0151	0.0023	−0.0196, −0.0105	−0.0163	0.0025	−0.0212, −0.0113
District (referent: others)
Bansang	0.0477	0.0066	0.0348, 0.0606	0.0518	0.0071	0.0379, 0.0656
Basse	0.0105	0.0027	0.0052, 0.0158	0.0116	0.0029	0.0059, 0.0174
Age, years	−0.0398	0.0072	−0.0540, −0.0257	−0.0442	0.0076	−0.0590, −0.0294
Male gender	0.0037	0.0023	−0.0009, 0.0082	0.0036	0.0025	−0.0013, 0.0085
Intercept	0.0484	0.0036	0.0413, 0.0556	0.0525	0.0039	0.0449, 0.0602

Abbreviations: CI, confidence interval; SE, standard error.

DISCUSSION

Statistical methods and software for estimation of the IRR are widely available. Much less attention has been given to the estimation of IRD. The IRD is an important parameter in medical research. It shows the public health impact of an intervention. We demonstrated here, using a hypothetical example (Web Appendix 1) and by simulation, that in the presence of unobserved heterogeneity, limiting the analysis of incidence rates for repeatable disease episodes to the first events results in bias. The severity of this bias depends on the disease incidence rate and on the degree and distribution of heterogeneity, which is usually unknown. The analysis of multiple events per person is more difficult than analysis of single events. The negative binomial regression model is an intuitive alternative for consideration. However, even in the simplest case in which the negative binomial model is fitted with an intercept only for a single group together with an “offset” term of log(follow-up time) in the log(incidence) equation, the point estimate does not necessarily agree with the observed disease incidence rate, such as when adopting the commonly used mean-variance relation that variance = mean + mean² × dispersion parameter, which is usually called the “NB2” parameterization (19). This is counterintuitive. For example, applying the NB2 approach to all of the radiologically confirmed pneumonia episodes as described above in the Case Study section, the parameter estimates on the logarithmic scale for the intercepts are –3.1020 and –3.5636 for the placebo and vaccine groups, respectively. The corresponding estimates for the incidence rates in the placebo and vaccine groups were 0.0450 and 0.0283, respectively, for an IRD estimate of 0.0167. However, the observed incidence rates in the placebo and vaccine groups were 0.0439 and 0.0277, respectively, and the observed IRD was 0.0162. It is not clear how a negative binomial model can be parameterized to produce an IRD estimate that agrees with the observed IRD.

Furthermore, similar to the regression analysis of risk difference, the iterations for the Poisson and negative binomial regression models with an identity link function do not always converge (3) because of their implicit positiveness constraints on the value of the link function. In contrast, the proposed least-squares method has an analytic solution, but it may predict negative incidence rates for some persons. We agree with Spiegelman and Hertzmark (20) that in epidemiology and public health, it is usually more important to estimate a parameter of interest than to fit the data. In our case, the parameters of interest are at the group level instead of at the individual level, so we do not see a problem in the application. If the research purpose were to develop a prognostic model for application to individuals, then the present method would be undesirable, because it can give implausible individual-level parameter values.

We have proposed a simple yet flexible approach to estimating the IRD for analysis of first events or all events. The proposed method has several merits. Firstly, it boils down to ordinary least-squares regression of transformed variables, together with a robust variance estimator for inference. It can easily handle quantitative covariates and has an explicit solution for the parameter estimates. Many popular statistical software packages, such as STATA (21), can perform the proposed analysis without additional programming. Secondly, the proposed estimator is unbiased. Thirdly, the proposed method includes other existing methods as special cases, such as that of Stukel et al. (11) and Glynn and Buring (10). As with these methods, when comparing 2 groups without covariate adjustment, our estimate for IRD has the desirable property that it agrees with the observed IRD. Moreover, it can be shown (our ongoing work) that in the case of time-varying covariates’ effects, the estimates are measuring the average of the covariates’ effects over the total number of person-years using data on all of the events. A limitation of the present proposal is that the method does not model the time-varying IRD, which may be needed in some research situations. Further methodological development is needed.

We have also compared the asymptotic and small-sample versions of the robust sandwich estimator. The differences among them are fairly minor, especially when the sample size is larger than 500. However, there is no harm in always using the HC₃ estimator. Interestingly, even HC₃ tends to have a coverage proportion slightly lower than the nominal level, although the undercoverage is small in many realistic situations. This issue has been raised by other researchers in the context of analysis of recurrent events, but there remains no explanation (22).

Glossary

Abbreviations

IRD

incidence rate difference

IRR

incidence rate ratio