Influence of the semi-permeable membrane on the performance of dynamic field gradient focusing

Abstract

This paper is part of our continued effort to understand the underlying principles of dynamic field gradient focusing. In this investigation, we examined three problems associated with the use of a semi-permeable membrane. First, the influence of steric and ionic exclusion of current carrying ions through the membrane was examined. It was found that resistance to the transport of ions across the membrane resulted in a shallowing of the electric field profile and an increase in the size of the defocusing zone, which is where the slope of the electric field is reversed so that it disperses rather than concentrates solutes. These problems could be reduced by using a membrane with large pores relative to the size of the buffering ions and completely void of fixed charges. Next, a numerical simulation was used to investigate concentration polarization of protein onto the surface of the membrane. Due to the presence of a transverse electric field, species were pulled toward the membrane. If the membrane is restrictive to those species, a concentrated, polarized layer will form on the surface. The simulation showed that by decreasing the channel to a depth of 20 μm, the concentrated region next to the membrane could be reduced. Finally, it was found that changes in column volume due to loss of membrane structural integrity could be mitigated by including a porous ceramic support. The variation in peak elution times was decreased from greater than 20% to less than 3%.

1 Introduction

Electric field gradient focusing (EFGF) is an equilibrium gradient method [1] in which an electric field gradient and a hydrodynamic flow counteract to focus charged species to discrete axial positions. Because of its ability to perform simultaneous, inline separations, EFGF techniques have been used in a wide range of studies which include: (i) focusing of proteins [2–12], small molecules [13], peptides [14], and DNA [13], (ii) separation of enatiomers [15], (iii) removal of salts and unwanted buffer components [8, 9], (iv) preconcentration [8, 16–18], and (v) selective removal of high-abundance species [8].

One of the key challenges in designing an EFGF device is the generation of the electric field gradient. The x-component of the electric field, E_x, can be described by [19]

$$Ex=-\frac{\text{d}V}{\text{d}x}=\frac{I_x}{A_s{\sigma }_{\text{ionic}}}$$ (1)

where V is the potential, I_x is the current density, A_s is the cross-sectional area and σ_ionic is the ionic conductivity. Equation (1) shows that an electric field gradient can be created in three manners: (i) varying the cross-sectional area, (ii) generating a conductivity gradient, or (iii) varying the potential (or current).

In 1996, Koegler and Ivory [7, 20] introduced a preparative-scale EFGF device that formed the electric field gradient by varying the cross-sectional area through which the electrical current flows. While the experimental apparatus was a success, it gave low-resolution results and proved to be awkward and difficult to assemble. Humble et al. [6] improved on the cumbersome design of Koegler and Ivory by introducing the use of an ionically conductive acrylic polymer to form the shaped channel. They were able to concentrate green fluorescent protein 10 000 fold. Kelly et al. [14] were able to miniaturize the EFGF design by moving to sacrificial materials and channels imprinted in PMMA. Using this method they were able to construct 3 cm long trapezoidal channels that were only 30 μm deep.

The first attempt at using conductivity gradients to perform EFGF was done by Greenlee and Ivory [4]. The device used a flat dialysis membrane and mismatched buffers to create an axial conductivity gradient along the length of the separation channel. Initial experiments performed in free solution showed only mediocre results because the proteins tended to form contiguous bands. The addition of a chromatographic packing to the separation channel decreased Taylor dispersion and led to better resolution. Wang et al. [12] were able to eliminate the need for a stationary phase by moving to a 250 μm id hollow fiber dialysis membrane.

In 2002, Ross and Locascio [13] introduced a conductivity gradient-based EFGF system, known as temperature gradient focusing, which does not require the use of a dialysis membrane. In this system, a temperature gradient is applied along the length of the separation channel. Buffers having temperature dependent ionic strengths are used to create a conductivity gradient, which ultimately gives rise to a gradient in the electric field. Temperature gradient focusing has been successfully used in a wide range of applications, which include separation of proteins [13, 21], small molecules [13, 21–23], DNA [24], enantiomers [15], and amino acids [25, 26].

In 1999, Huang and Ivory [5] introduced an EFGF device known as dynamic field gradient focusing (DFGF) that uses a computer-controlled array to vary the potential of up to 50 electrodes. Dynamic control of the electrode array allows for manipulation of the electric field profile during the course of an experiment to increase peak resolution, migrate analytes to off-take ports, or to systematically elute individual species. Unlike other EFGF devices, this system is not limited to a fixed electric field profile, but instead can operate with any number of versatile electric field profiles, including nonlinear, stair-stepped, and reversed polarity.

Myers and Bartle [27] introduced a miniaturized DFGF apparatus consisting of only five electrodes with each electrode controlled by a separate power supply. Petsev et al. [10] introduced a simpler DFGF device that consisted of a 200 μm separation channel placed at right angles to two, 200 μm side-channels. The side-channels were each connected to a separate power supply. This apparatus though simple in its design showed a successful separation of phycoerythrin and FITC-BSA in which each species focused at a different side-channel intersection.

More recently, Tracy and Ivory [11, 28–30] published a series of papers describing the development of a preparative scale DFGF apparatus capable of processing tens to hundreds of milligrams of protein. Unlike previous DFGF designs, Tracy and Ivory were able to mitigate the need for a stationary phase by basing their design on that of a vortex-stabilized electrophoresis apparatus [31]. In this case, an annulus is turned within a stationary cylinder, introducing counter-rotating vortex pairs that reduce axial dispersion along the length of the separation channel at the expense of radial dispersion [11]. Using this design, they were able to separate 7mg each of hemoglobin and FITC-BSA.

Although advances in the design and operation of EFGF devices have made it a promising and potentially powerful analytical- and preparative-scale separation technique, to date, very little has been published on reproducibility [32], likely due to the difficulty in achieving consistent results. However, several groups have published articles detailing attempts to improve EFGF performance. Sun et al. described the use of PEG-functionalized EFGF devices, which showed minimal protein adsorption and no detectable EOF. The development of this device was important because it has been shown that the presence of EOF within EFGF devices leads to reproducibility problems and increased band broadening [33]. In addition, the use of a PEG functionalized hydrogel allowed for easy cross-linking of a monolith. The monolith helped to reduce dispersion caused by laminar flow, resulting in tighter bands. In addition, other groups have examined buffer composition [34, 35] and elution strategies [2, 3] in an attempt to optimize experimental conditions.

A recent publication out of our group [3], geared to towards solving some of the reproducibility issues, examined the phenomenon of voltage degradation, which refers to the difference between the voltage applied to the electrodes and the voltage measured in the separation channel. A numerical simulation was used to show how changes in the design of the focusing apparatus could be made to minimize the effects of voltage degradation and its impact on the shape of the electric field profile [3].

This paper, a continuation on our efforts to eliminate the bottlenecks that have been deleterious to EFGF techniques, examines the influence of the semi-permeable membrane on system performance. The semi-permeable membrane in EFGF devices plays a critical role in the overall performance of the system because it is responsible not only for allowing the passage of current carrying ions but also is integral in providing and maintaining the structure of the separation channel. Numerous membrane designs have been used in EFGF devices including flat dialysis membranes [3–5], hollow fiber dialysis membranes [12], conductive polymers [6], porous glass Vycor [27], and in situ fabricated conductive membranes [14, 36], but to date a comprehensive examination of the underlying problems encountered when using semi-permeable membranes, and how one should determine which membrane is best suited, has not been published.

Using a 2-D nonlinear numerical simulation constructed in Comsol v3.4 along with supporting experiments, this paper addresses these issues and the steps that can be taken to alleviate or minimize them. In addition to results obtained in our lab, this paper pulls together work from other groups to provide a complete overview on this topic. Though specifically aimed at our DFGF apparatus, the conclusions drawn is this paper are applicable to all electrofocusing techniques that utilize a semi-permeable membrane.

2 Materials and methods

2.1 Reagents

All buffer chemicals and cytochrome c were obtained through Sigma-Aldrich (St. Louis, MO, USA). R-phycoerythrin and allophycocyanin (APC) were purchased from Invitrogen (Carlsbad, CA, USA).

2.2 DFGF apparatus

The DFGF chamber and voltage controller used in this paper were described previously [3]. Briefly, the focusing chamber is constructed from two 10.2 cm×5.1 cm×1.2 cm pieces of acrylic. The top piece, which contains the separation column, has a 5.7 cm×0.1 cm×200 μm channel machined into the surface. The bottom block contains a 6.5 cm×0.1 cm×0.3 cm trough, which serves both as a housing for the 21 controllable platinum electrodes and as a purge channel to remove joule heat and electrolysis products (Fig. 1). A syringe pump (KD Scientific, Holliston, MA, USA) fitted with a 500 μL glass Hamilton syringe (Hamilton, Reno, NV, USA) controls the flow of a 20mM Tris Acetate, pH 8.5, running buffer through the separation column. Electropherograms are collected by eluting focused peaks through a UV-Vis detector (model: Linear 206 PHD).

Figure 1.

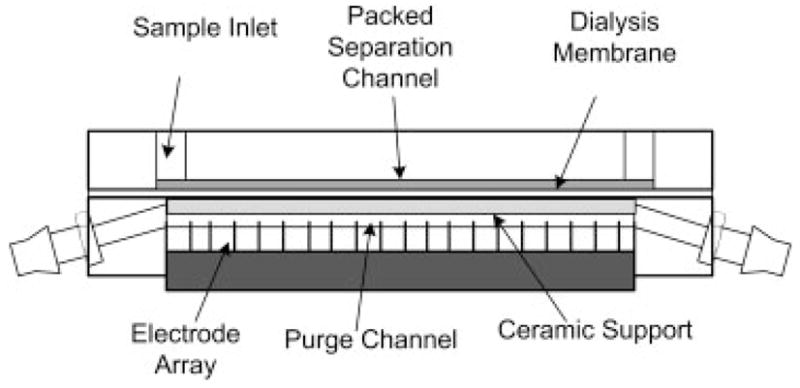
Schematic of DFGF apparatus. A ceramic support has been place directly below the dialysis membrane to ensure that to membrane does not “balloon” into the purge channel. This guarantees that the volume of the separation channel does not change during operation of the DFGF device.

3 Theory

The theory [20, 37] and development of the numerical simulation [3] has been described in detail elsewhere. Briefly, the Nernst-Planck application mode built into Comsol Multiphysics v3.4 is used to describe the flux of each species, N_i, in response to an applied electric field according to

$${\mathbf{N}}_i=-z_i{u}_{i}F{c}_i\nabla \mathrm{\Phi }-D_i\nabla c_i+\mathbf{v}{c}_i$$ (2)

where, z_i is the charge, u_i is the absolute mobility, F is Faraday’s constant, c_i is the concentration of each species i, Φ is the electric potential, D_i is the diffusion coefficient, and v is the hydrodynamic velocity vector. The transient problem is then

$$\frac{\partial c_i}{\partial t}=-\nabla ·{\mathbf{N}}_i+R_i$$ (3)

where R_i accounts for the buffering reactions of the supporting electrolyte, Tris Acetate, pH 8.5. The Nernst-Planck equation is used to describe the transport of the buffering ions (Tris, ${\text{CH}}_3{\text{CO}}_2^{-}$, CH₃CO₂ H, H⁺, OH⁻) and one simulated protein, P1. The concentration of the counterion, Tris⁺, is found by applying the electroneutrality constraint:

$$\sum _i{z}_i{c}_i=0$$ (4)

Constant concentration boundary conditions for each species are specified at the inlets, as well as, on the electrodes. A convective flux boundary condition, n · N_i=c_i (v · n), is set on the outlets and all other boundaries are assumed to be insulating, −n·N_i = 0, where n is the normal vector. An initial protein load of 2 μg was used.

The Brinkman application mode in Comsol Multiphysics v3.4 is used to solve for the convective velocity, v, for flow through a porous medium according to Brinkman’s equation [38]

$$\rho \frac{\partial \mathbf{v}}{\partial t}-\nabla ·(\eta (\nabla \mathbf{v}+{(\nabla \mathbf{v})}^{\text{T}}))+(\frac{\eta }{k}\mathbf{v}+\nabla p-\mathbf{F})=0$$ (5)

and the continuity equation

$$\nabla ·\mathbf{v}=0$$ (6)

where ρ is the fluid density, which is assumed to be constant for this simulation, η is the dynamic viscosity, p the pressure, and k denotes the permeability of the porous structure.

For our system, the packed separation channel and the membrane are described by flow through a porous medium and the purge chamber is described by free flow. By using Brinkman’s equation, a single equation can be solved for the flow over all subdomains, reducing computational requirements. Setting the permeability to a small number (<0.6) causes the viscous term in Eq. (5) to dominate, thus describing porous flow. A large permeability (~1) decreases the contribution from the Darcy term, reducing Eq. (5) to a form of the Navier–Stokes equation for free flow [39].

The boundary condition at the inlet to the separation channel is set to a flow velocity of 5.5×10⁻⁵ m/s and in the purge channel to 0.02 m/s. The outlets are set to zero pressure. All other boundaries and electrodes are assumed to be no-slip.

4 Results and discussion

4.1 Membrane resistance

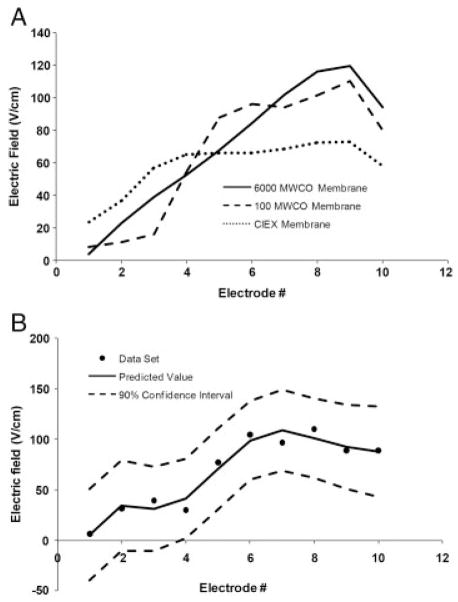
In EFGF devices, membranes serve to isolate the separation channel from the electrodes by allowing for the passage of current carrying ions while at the same time retaining the species being investigated within the separation channel. When using a 6000 molecular weight cutoff (MWCO) membrane (Fisher Scientific), all small ions (20mM tris acetate) are free to pass across the membrane with little or no resistance to transport. For instance, if a linear electric field profile is specified on the electrodes, then the field detected in the separation channel is very close to the expected electric field profile (Fig. 2A) reaching a maximum of 120 V/cm, and the defocusing region, which is where the slope of the electric field is reversed so that is disperses rather than focuses solutes, is limited to a small section of the separation channel. This is important because in the defocusing region the electric field and the flow are acting in the same direction. Bands that enter this region will become broadened and forced out of the separation channel. As a result, it is important to ensure that this region is minimized so as not to negatively affect the performance of the system.

Figure 2.

(A) Influence of the type of membrane on the shape of the experimentally measured electric field profile. The presence of steric exclusion (100 MWCO membrane) or ionic exclusion (CIEX membrane) causes distortions in the shape of the electric field profile. The results for each of the membranes shown here are the predicted values of the electric field based on calculating the 90% confidence intervals for a set of three experiments. The 90% confidence intervals for the 6000 MWCO membrane, 100 MWCO membrane, and CIEX membrane were ~ +/− 6.4, +/− 29.8, and +/−10.0 V/cm, respectively. (B) Shape of the electric field with 100 MWCO membrane and the addition of 5mM KCl. The KCl should be able to move freely through the membrane. If this were the case, the electric field profile would be the same as for the 6000 MWCO membrane in (A); however, instead, the electric field is distorted, implying that the K⁺ and Cl⁻ are experiencing some resistance through the membrane.

When analyzing small molecules, membranes with small pores must be used; however, the ability of the membrane to segregate target molecules from the current carrying ions becomes more difficult. For a 100 MWCO cellulose ester membrane (Spectrum Laboratories, Rancho Dominguez, CA), the current carrying ions, tris (121.1 g/mol) and acetate (59 g/mol), experience resistance to transport across the membrane. Due to differences in their molecular weights, their transference numbers across the membrane will be different.

The transference number, t_j, is defined as the fraction of current carried by each species, j, according to [19]:

$$t_j=\frac{z_j^2{u}_j{c}_j}{{\mathrm{\sum }}_i{z}_i^2{u}_i{c}_i}$$ (7)

Humble et al. [40] used a numerical simulation to show that when the transference numbers of the ionic species differed, concentration gradients would form in the separation channel. This resulted in distortions to the predicted electric field, which led to reproducibility problems and decreased performance. The effect of this is seen experimentally in Fig. 2A. With a 100 MWCO membrane, the current carrying ions experience resistance across the membrane when compared with using a 6000 MWCO membrane. In this case, even though a linear field was applied to the electrodes, the electric field measured in the separation channel is distorted with more defocusing (negative slope) regions.

When operating using a linear electric field, the entire channel can be used to perform the separation, allowing for higher peak capacity. However, when the field becomes distorted, as with the case of the 100 MWCO membrane, the electric field over most of the separation channel will act to disperse focused bands, leading to a system with very poor performance and low peak capacity.

A recent publication by Sun et al. [34] found that the addition of KCl improved reproducibility and gave a linear electric field distribution that agreed with theoretical predictions. With the use of KCl, resistance to transport across the membrane was minimized and the transference numbers for the K⁺ and Cl⁻ were nearly the same. For a membrane with larger pores this approach works; however, when using membranes with smaller pores (i.e. 100 MWCO), the addition of KCl to the running buffer has a minimal effect on the shape of the electric field profile (Fig. 2B) because the pores are nearly the same size as the ions. Even though the ions should be able to pass through the membrane, they experience a small amount of resistance due to steric exclusion, which is sufficient to cause distortions to the electric field, making the system unusable for performing separations. Since it is not possible to eliminate steric exclusion when analyzing small molecules, EFGF devices that utilize a porous membrane should be limited to the analysis of large molecular weight species.

Increased resistance across the membrane can also occur through ionic exclusion in which fixed charges within the membrane restrict the movement of ions of like charge. As with steric exclusion, ionic exclusion caused by using, e.g. a Nafion cation exchange membrane (The Electrosynthesis), gives rise to misshapen electric field profiles with broader defocusing regions (Fig. 2A). In particular, the electric field over most of the separation channel becomes shallow. This leads to broader peaks which are overly resolved.

As with steric exclusion, ionic exclusion present in the membrane will give rise to decreased performance and low peak capacity. A similar result was observed by Humble et al. [40]. They found that acidic impurities within their hydrogel membrane led to problems in the electric field profile. By eliminating the acidic (charged) residues, which imparted ionic exclusion to the buffer ions, they were able to achieve better reproducibility and improved resolution. As a result, when performing EFGF, care should be taken to operate with membranes free of fixed charges

4.2 Membrane polarization

Polarization of protein onto the surface of the semi-permeable membrane occurs because charged analytes are pulled down to the membrane by a transverse component of the electric field. Figure 3 shows a binary mixture of 4 μg of APC and 50 μg cytochrome c separated and focused using a high-end electric field strength of 227 V/cm and a flow rate of 0.25 μL/min. Looking through the front of the device, the cytochrome c band is barely noticeable and the APC peak cannot be seen. However, if we examine the backside of the DFGF device (Fig. 3B), by looking through the membrane, both the cytochrome c and APC are clearly visible. This indicates that the two proteins have been pulled down to the surface of the membrane and have formed a polarized layer analogous to that in ultrafiltration.

Figure 3.

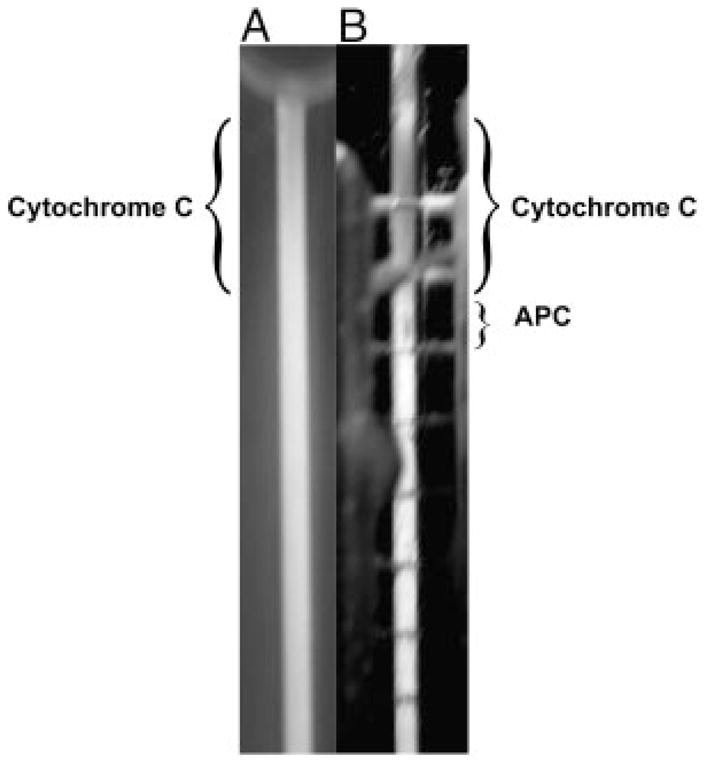
Picture showing the separation of Cytochrome c and APC, which illustrates the polarization of protein onto the surface of the membrane. (A) Picture through the front of the separation channel. The Cytochrome c is difficult to see and the APC cannot be seen at all. (B) Picture through the rear of the separation channel looking through the purge channel (containing the electrodes) and the membrane (Note: the horizontal lines are the individual platinum electrodes). The protein species are much more visible while looking through the back of the chamber, which implies that the proteins have formed a polarized layer on the surface of the membrane.

Though it is unlikely that concentrations will increase to the point of gel layer formation, the occurrence of polarization in EFGF devices is problematic. The first problem is that at artificially increased concentrations there is a higher likelihood of precipitation of the analyte. Secondly, increased peak concentrations can lead to local distortion of the electric field [20]. This distortion can act as a “well” that can pull two closely focused analytes together, leading to losses in resolution. Finally, a mass transfer limited situation can develop during elution in which protein in the less concentrated portion of the band will begin to migrate while species in the polarized layer must first diffuse away from the concentrated region near the membrane into the bulk flow, leading to a peak with a broad tail. Under focusing conditions, the band will recover if given time. However, during an automated elution protocol that is designed for fast elution, the peaks may not recover completely before they are collected.

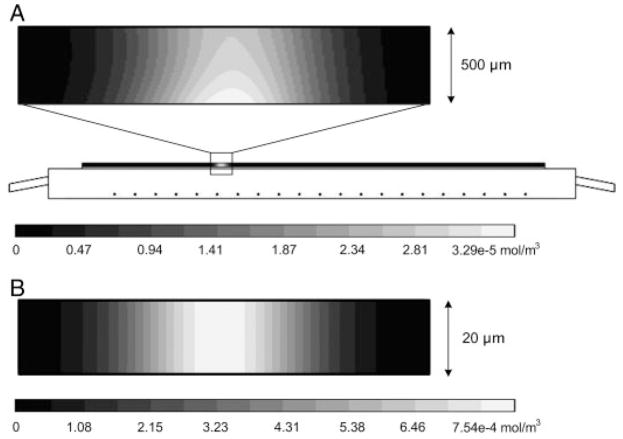
To further investigate membrane polarization, the nonlinear simulation described above was used. Figure 4A shows the simulation result assuming a 500 μm thick separation channel. As with the experimental result shown in Fig. 3, the simulation predicts the presence of concentration polarization on the surface of the membrane with the lower surface concentration ~20% greater than the concentration near the upper surface.

Figure 4.

(A) Schematic of domain solved for using Comsol v3.4. The expanded view illustrates the polarization of the simulated protein onto the surface of the membrane occurring in a 500 μm channel. (B) Illustration showing that using a 20 μm channel the polarization onto the membrane can be eliminated. In this case, the contour lines a vertical, which implies that the concentration is constant across the thickness of the separation channel.

To quantitate the degree of polarization, we can use the simulation to look at the ratio of the electrophoretic migration of the protein towards the membrane to the back diffusion of the protein away from the membrane. This so-called electrophoretic Peclet number, Pe_Ey, can be determined using the following equation

$$P{e}_{E_y}=\frac{{\mu }_P{E}_{y}H}{D_P}$$ (8)

where μ_P is the electrophoretic mobility of the protein (2×10⁻¹⁴m²/V s), E_y is the y-component of the electric field (270 V/m), D_p is the diffusion coefficient of the protein (5×10⁻¹¹m²/s), and H, the characteristic length, is chosen to be the height of the separation channel. For a channel thickness of 500 μm, the Pe_Ey is 24.1, implying that the membrane is highly polarized.

To eliminate membrane polarization, the electromigration towards the membrane should be balanced by back diffusion, resulting in a Pe_Ey approximately equal to or less than 1. According to Eq. (8), there are several ways that this can be accomplished. The first, which is a common technique in ultrafiltration, is to increase depolarize by inducing transverse mixing. Several different strategies in ultrafiltration have been investigated [41] including increased flow, pulsating flow, pulsating pressure, generation of vortices, flow through baffles, and externally applied electric fields. The introduction of vortices was shown by Tracy and Ivory [29] in a preparative scale DFGF apparatus. However, implementation of this or any of the other strategies into our DFGF design would either be deleterious to performance (i.e. pulsating pressures or flows) or difficult to achieve (i.e. vortices).

A better alternative for depolarization is to decrease the separation channel thickness, H. Using the model above, it was found that decreasing the channel thickness to 20 μm resulted in a Pe_Ey=1. Examination of the same simulated protein for a 20 μm channel shows that the concentration is the same over the entire thickness of the separation channel (Fig. 4B). This technique can be used during the design process to determine the appropriate thickness of the separation channel. For separations of large molecules, such as proteins, thinner channels are needed whereas with smaller molecules, which have higher diffusion coefficients, e.g. on the order of 5×10⁻¹⁰m²/s, channel thicknesses of up to 200 μm can be used while still maintaining a Pe_Ey of less than 1. Also, as the electric field is increased, the separation channel will have to be decreased in order to maintain a favorable Pe_Ey.

In addition to the commonly acknowledged advantages of smaller channels, such as increased heat dissipation and decreased sample size, Fig. 4 illustrates that for the same mass load and linear flow velocity more highly concentrated peaks can be obtained in narrower channels. To further investigate this phenomenon, the numerical simulation was run for a range of separation channel thicknesses and then moment analysis was performed on the focused peak.

The n^th spatial moment, m_n, along the x-axis can be calculated from

$$m_n={\int }_{A}C(x,y)x^n\text{d}x\text{d}y$$ (9)

where A is the area of the separation channel, C(x,y) is the concentration of the species and x and y are the axial and radial coordinates, respectively. The zero^th moment, which provides information on the total mass load, is determined using

$$m_0={\int }_{A}C(x,y)\text{d}x\text{d}y$$ (10)

The axial position of the center of mass of the peak, x_p, is given by the first absolute moment, m₁, normalized to m₀

$$x_p=\frac{m_1}{m_0}$$ (11)

and the variance, σ², is calculated by

$${\sigma }^2=\frac{m_2}{m_0}-{\left(\frac{m_1}{m_0}\right)}^2$$ (12)

where m₂ is the second spatial moment. We can now calculate the average concentration of the peak, c_avg, based on the standard deviation of the peak, σ, and the height of the separation channel, H:

$$c_{\text{avg}}=\frac{m_0}{4\sigma H}$$ (13)

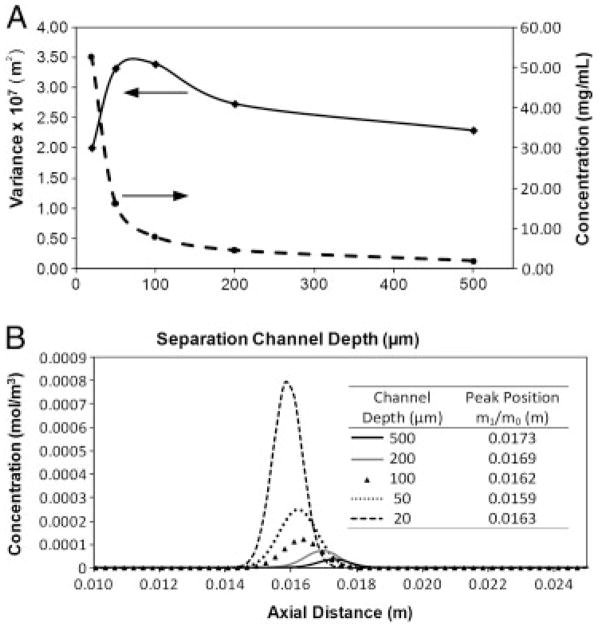
The results of the moment analysis are shown in Fig. 5. The advantages of going to a smaller separation channel are clearly visible in the increases in concentration that can be achieved (Fig. 5A). By decreasing the channel thickness from 500 to 20 μm, a 26.7-fold increase in peak concentration is obtained. This is further illustrated by looking at the peak profiles calculated at a height of 1 μm above the surface of the membrane (Fig. 5B). It should be noted that the difference in the peak areas arises from the fact that for smaller channels more protein is present in the region closer to the membrane. Nevertheless, Fig. 4B shows that significant improvements in peak concentration can be achieved without sacrificing peak width. In fact, a comparison of the peak variance, σ², as a function of channel depth (Fig. 5A) shows that smaller peak widths can be obtained in thinner channels.

Figure 5.

Moment analysis results. (A) Simulation results showing the effect of separation channel thickness on the average peak concentration and on the peak variance. At thinner separation channel thicknesses higher concentration peaks with smaller variance are achieved. A maximum in the peak variance is obtained in channels with a thickness of about 100 μm. (B) Simulated peak profiles calculated at a distance of 1 μm above the surface of the separation channel. At thinner channels, higher concentration peaks can be obtained for the same protein load.

4.3 Membrane stability

When choosing a semi-permeable membrane, consideration should be taken based not only on ion-exchange capabilities or MWCO, but also on the stability of the membrane and its ability to maintain the integrity of the separation channel. When using an unsupported, flexible membrane under sustained pressure, the membrane will gradually lose structural integrity. This will allow the membrane to “balloon” out into the purge channel, leading to changes in bed volume and packing efficiency, which results in decreased performance and problems with reproducibility.

To examine changes in the packed bed, a technique that is analogous to determining the extra-particle void volume in size-exclusion chromatography was employed. A sample of 1.5 μg of R-phycoerythrin, which has a molecular weight of ~240 kDa [42] and is too large to enter the pores of the stationary phase, was injected and allowed to focus at the top of the separation channel under no-flow conditions. After 1 h, the electric field was turned off and the flow rate was set to 0.25 μL/min. The focused peak was no longer under the influence of the electric field and was able to elute out of the bottom of the column. Two experimental sets consisting of 22 and 25 runs, respectively, were performed (Fig. 6A). Each experimental set was run in a DFGF apparatus assembled using a new dialysis membrane and fresh packing medium. Moment analysis was performed on the eluted peaks to determine the peak variance [43].

Figure 6.

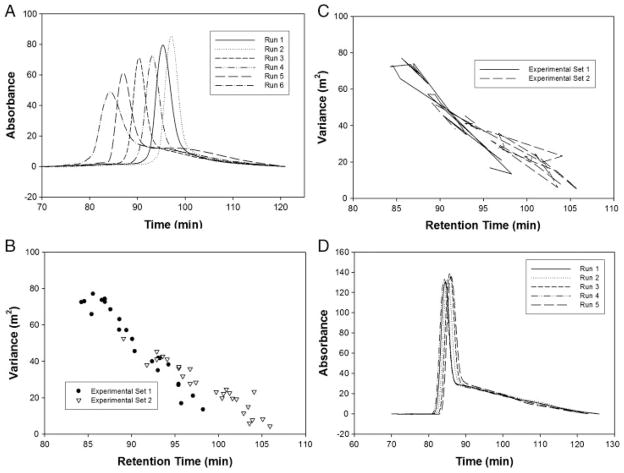
(A) Elution profiles performed under no electric field conditions illustrating run-to-run variation. The changes in peak retention time and peak shape are caused by changes in the volume of the packed separation channel. (B) The trend for variance plotted against retention time. As the variance increases, the retention time decreases. (C) This plot shows the same data as in (B) except that the data points have been connected to illustrate that the trend does not proceed in a chronological fashion. (D) Elution profiles performed under no electric field conditions illustrating the decrease in run-to-run variation provided by the insertion of a ceramic support behind the flexible dialysis membrane. The peak tails can be attributed to adsorption of the protein onto the surface of the stationary phase and the interaction with stagnant flow regions within the packed bead.

Peaks that eluted sooner tended to have greater tailing than peaks that eluted later (Fig. 6A). This is further illustrated in Fig. 6B. Here the peak variation is plotted against the retention time. A nearly linear trend exists, which seems to suggest an increase in the retention time with each subsequent run. Such a trend would be expected if the volume of the separation channel was simply increasing in a continuous manner. This, however, is not the case. Peak broadening is not happening in a sequential manner corresponding to the run number, but instead in an almost random fashion (Fig. 6C), implying that, though the volume of the separation channel is continuously increasing due to membrane bowing, other mechanisms are occurring, which give the impression of both positive and negative fluctuations in the total volume.

The apparent changes in the total volume of the separation channel are due to the fact that, as the membrane bows, the soft biogels expand to help fill the increased volume. Bio-Rad P2 is composed of polyacrylamide and is easily compressed when packed under pressure. As the membrane bows, the compressed packing will be allowed to expand causing one of three potential problems. The first is the presence of channeling. The formation of channels could allow a portion of the peak to move more quickly through the column while a smaller amount takes a more uniform route. In this case, a peak with a faster retention time and a broad tail would be expected. Secondly, the presence of dead-water regions could occur which would give rise to longer retention times. In addition, as the eluting peak encounters more stagnant regions the contributions of each becomes increasingly more important and the overall curve approaches that of a Gaussian peak [44]. Finally, changes in the packing efficiency could occur, which would lead to changes in the void volume, and hence the apparent volume, of the separation channel. These changes in the void volume, both increases and decreases, would lead to significant changes in the retention time of the peak. Changes in the packing efficiency are also assumed to be the reason for the observed differences between experimental sets 1 and 2.

To alleviate the problem of membrane bowing, other groups have used rigid membranes such as porous Vycor glass [27] or conductive polymer membranes [6]. These have properties that would maintain the integrity of the separation channel, but require time in terms of development and setup. For our application, it was easier to use a ceramic support to keep the flat dialysis membrane from bowing. This gave us the option to easily switch between any number of commercially available or in-house constructed membranes based on the need for a certain MWCO or on the surface chemistry of the membrane. The ceramic support was chosen based on its ability to pass current and on its heat transfer properties. A piece of porous alumina ceramic (Kerafol, Germany) was inserted into the purge channel in such a manner that it lay flat against the membrane (Fig. 1). An experimental set of five runs was conducted (Fig. 6D).

The addition of a ceramic support significantly improved our reproducibility (Fig. 6D), resulting in peak retention times which agree within 3%, compared with greater than 20% variation for the unsupported case. The peak tailing observed in Fig. 6D can be explained by a multi-compartment model in which some of the analyte is held back [44], likely due to adsorption on to the surface of the beads or the presence of stagnant regions.

5 Concluding remarks

The semi-permeable membrane plays three important roles in EFGF devices: (i) isolating the separation channel from the electrodes, (ii) restricting movement of solutes of interest, and (iii) allowing the passage of current carrying ions. When choosing a membrane, each of these aspects of the membrane must be considered to ensure optimum system performance.

The ability of the membrane to restrict the movement of specific species while allowing the passage of current carrying ions is paramount to the success of any EFGF separation. When the relative molecular weights of the species of interest to the current carrying ions are large, a membrane can easily be chosen, which does not adversely affect the shape of the electric field gradient. However, as the species being analyzed become smaller, approaching the size of the current carrying ions, a membrane with a smaller pore size must be chosen. Under these conditions, the membrane resistance increases as the ions now experience some steric exclusion, resulting in a deleterious change to the shape of the electric field profile. Based on these results, we have concluded that membrane-based devices should be limited to the analysis of large molecular weight species.

In addition, since the membrane is specifically designed to restrict the movement of target solutes, polarization onto the surface of the membrane needs to be considered. Using a numerical simulation, it was found that devices containing large separation channels (i.e. 500 μm) suffered substantially from membrane polarization. In this case, most of the protein polarized onto the surface of the membrane with a small amount spread transversely across the thickness of the channel. By decreasing the channel to 20 μm, the concentration gradients could be eliminated. The smaller separation channels were also shown to give rise to more highly concentrated peaks with smaller variance.

Finally, we have shown that under normal system operation the membrane, if unsupported, will give rise to large changes in the total volume of the separation channel. These changes influence not only performance but also the reproducibility of the system. By including a porous ceramic support, we were able to decrease the difference in retention time from greater than 20% to less than 3%.

Abbreviations

APC

allophycocyanin

DFGF

dynamic field gradient focusing

EFGF

electric field gradient focusing

MWCO

molecular weight cutoff