Modeling Smooth Muscle Myosin's Two Heads: Long-Lived Enzymatic Roles and Phosphorylation-Dependent Equilibria

Abstract

Smooth muscle myosin has two heads, each capable of interacting with actin to generate force and/or motion as it hydrolyzes ATP. These heads are inhibited when their associated regulatory light chain is unphosphorylated (0P), becoming active and hydrolyzing ATP maximally when phosphorylated (2P). Interestingly, with only one of the two regulatory light chains phosphorylated (1P), smooth muscle myosin is active but its ATPase rate is <2P. To explain published 1P single ATP turnover and steady-state ATPase activities, we propose a kinetic model in which 1P myosin exists in an equilibrium between being fully active (2P) and inhibited (0P). Based on the single ATP turnover data, we also propose that each 2P head adopts a hydrolytic role distinct from its partner at any point in time, i.e., one head strongly binds actin and hydrolyzes ATP at its actin-activated rate while the other weakly binds actin. Surprisingly, the heads switch roles slowly (<0.1 s⁻¹), suggesting that their activities are not independent. The phosphorylation-dependent equilibrium between active and inhibited states and the hydrolytic role that each head adopts during its interaction with actin may have implications for understanding regulation and mechanical performance of other members of the myosin family of molecular motors.

Introduction

Smooth muscle, as with all muscle, contracts by cyclic interactions between myosin thick filaments and actin-containing thin filaments. During these interactions, myosin undergoes a multistep cycle in which chemical energy in the form of ATP is converted into force or mechanical work (see Fig. 1). Specifically, the amino terminal head domain of myosin (M) binds weakly to actin (A) when ATP (T) or the hydrolysis products (ADP (D), P_i) are in the active site. Concomitant with P_i release, myosin strongly binds actin and undergoes a conformational change (i.e., a powerstroke) that generates force and/or motion. Smooth muscle myosin has two heads, each capable of actin binding and ATP hydrolysis (1,2). How this two-headed structure relates to myosin's regulation and functional performance continues to be debated.

Figure 1.

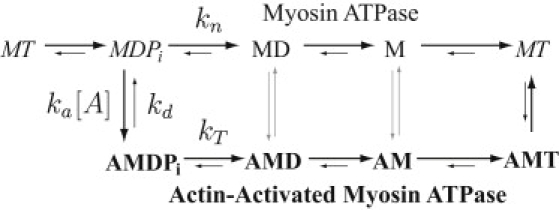
The kinetic mechanism of Lymn and Taylor (21), demonstrating myosin's inherent ATPase (top path, regular type) and its actin-activated ATPase (bottom path, bold). States common to both ATPase pathways are in italics. Myosin's ATPase is rate-limited by k_n, while the rate-limiting step for myosin's actin-activated ATPase depends on actin concentration ([A]). The actin-activated ATPase is rate-limited by k_a[A] at low actin concentrations, and by k_T at high actin concentrations.

Smooth muscle myosin is regulated by covalent phosphorylation of the regulatory light chain (RLC) associated with each of the two heads. A calcium-calmodulin-dependent myosin light-chain kinase phosphorylates the RLC. When neither RLC is phosphorylated (0P), the isolated molecule is compact and inactive; when both RLCs are phosphorylated (2P), the molecule is extended and active, having >1000 times the ATPase activity of 0P myosin in the presence of actin (3–6). High-resolution electron microscopy revealed that the two heads of 0P myosin interact directly to inhibit each other (7–9). Specifically, the actin binding domain of one head (i.e., the blocked head) associates with the converter domain of the other head (i.e., the free head), preventing the blocked head from binding actin and limiting the free head to weak actin binding. With 2P myosin, RLC phosphorylation presumably provides sufficient charged repulsive force to abolish these head-head interactions, freeing the heads to interact with actin and to rapidly hydrolyze ATP and generate mechanical work. In contrast, the enzymatic and mechanical activities of smooth muscle myosin with only one of its RLCs phosphorylated (1P) remain enigmatic. Characterizing these activities is critical to understanding how smooth muscle tissue can maintain isometric force with intermediate levels of RLC phosphorylation (i.e., the latch state (10)) where 1P myosin is likely to be the dominant species (11–13).

Only recently have pure preparations of 1P smooth muscle heavy meromyosin (HMM-1P; a double-headed myosin fragment) been expressed in and isolated from Sf9 cells (14–16). The enzymatic and mechanical properties of HMM-1P suggest that phosphorylation of a single RLC is sufficient to activate the molecule. However, the level of activity is preparation-dependent: in vitro light-chain exchange of the endogenous RLC with a mutant RLC produces an HMM-1P that generates less than half the hydrolytic and mechanical activity of doubly-phosphorylated HMM (HMM-2P) (15,17), while coexpression of mutant RLC and smooth muscle HMM in Sf9 cells, with subsequent affinity purification, results in HMM-1P having equal to or more than half the hydrolytic and mechanical activity of HMM-2P (14,16).

Regardless of its precise activity, is this 1P active molecule a new structural/functional conformation? Alternatively, the enzymatic and mechanical properties of the 1P might be described with a model that incorporates the known head-head interactions responsible for regulation and the apparent differential characteristics of the two heads in the 2P molecule. Specifically, based on 2P single ATPase turnover measurements (14,17,18) and single molecule biophysical measurements in the laser trap (19,20), it appears that, at any point in time, smooth muscle myosin's two heads are not functionally independent and that only one head strongly binds to actin, hydrolyzing ATP and generating force and motion, while the other weakly binds. Based on single ATP turnover data, these distinct functional roles must be maintained for a period greater than the hydrolysis lifetime. We incorporate this surprising phenomenon into a model that describes the slow kinetics of role switching (at a rate <0.1 s⁻¹) for each HMM-2P head even in the absence of actin. We then combine this model with a simple inactive-to-active-state transition associated with RLC phosphorylation to explain the HMM-1P ATP single turnover and steady-state hydrolytic activities. These models show that a new smooth muscle myosin conformation is not necessary to explain HMM-1P activity; rather, we propose that the molecule exists in a phosphorylation-dependent equilibrium between a folded (inactive) and an extended (active) conformation.

Modeling of Smooth Muscle HMM Enzymatic Data

We propose a kinetic model that can explain how phosphorylation of a single RLC results in an active smooth muscle HMM-1P molecule having an effective hydrolytic rate that is less than that of a fully phosphorylated (HMM-2P) molecule. The enzymatic data to be modeled are the steady-state actin-activated myosin ATPase and single ATP turnover data reported by two laboratories for HMM-2P, -1P, and -0P, using two different preparative techniques (14,17,18). These enzymatic data and our mathematical fits to these data determine the two most critical results of our modeling:

• 1.The two heads of HMM-2P are functionally distinct while hydrolyzing ATP, and
• 2.RLC phosphorylation modulates the equilibrium between inactive and active states and thus HMM's effective hydrolytic activity.

Here we provide a brief description of the experiments and the data (see the original articles for detailed methods (14,17,18)). Steady-state HMM ATPase activity in solution is determined by measuring the rate of P_i release as a function of actin concentration (see Fig. 3, top). At a given actin concentration, this rate reflects the ATP hydrolysis rate for the entire population of HMM molecules and cannot distinguish among HMM within the population that have inherently different ATPase activities. Thus, the steady-state ATPase is a weighted average of the entire population. In contrast, ATP hydrolysis measured one head at a time can be determined in a stopped-flow apparatus by monitoring single fluorescent ATP turnovers. For these experiments, fluorescent ATP (i.e., mant-dATP or a similar chemical species, FTP), an ATP analog that is fluorescent only when in the HMM nucleotide-binding pocket, is incubated with HMM in the absence of actin sufficiently long so that each head binds a fluorescent ATP. Then, HMM is rapidly mixed with known concentrations of actin and excess non-fluorescent ATP. Upon actin binding, the fluorescent ATP hydrolysis products are released from each head, with subsequent binding of a nonfluorescent ATP. As the fluorescent ATP products are released, the fluorescent signal of the population decays over time and provides a measurement of the number of individual myosin heads that have yet to release their fluorescent ATP hydrolysis products. It is important to note that, although a large ensemble of myosin is used, this experiment measures the ATP hydrolysis rate of individual myosin heads and can thus distinguish among populations of HMM heads that may hydrolyze ATP at inherently different rates.

Figure 3.

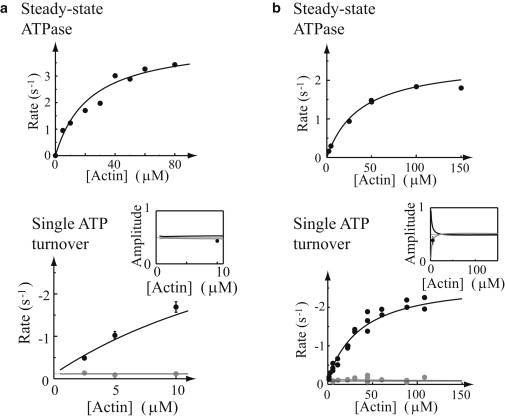
The model for doubly-phosphorylated (2P) myosin fits both single ATP turnover and steady-state ATPase data (p > 0.05), but requires a very slow role-switching rate, k_s. (Top) Steady-state ATPase and (bottom) ATP turnover rate (solid, faster actin-dependent rate; shaded, slower actin-independent rate) and (inset) amplitudes. (a) (Dots) Data from Rovner et al. (14). (b) (Dots, top and bottom) Data from Ellison et al. ((17,18), respectively).

Model of fully activated, doubly-phosphorylated myosin (2P): distinct hydrolytic roles for each head

Before we consider how phosphorylation of only one RLC may modulate the hydrolytic activity of smooth muscle HMM, we begin by modeling the hydrolytic activity for each head in a myosin molecule having both RLCs phosphorylated. We assume a Lymn and Taylor (21) multistep kinetic scheme for ATP hydrolysis for each of smooth muscle myosin's two heads both in the absence and presence of actin (see Fig. 1). In the absence of actin, each head hydrolizes ATP at its basal rate, k_n. In the presence of actin, myosin (MDP_i) can weakly bind actin at a rate k_a[A], where k_a is a pseudo first-order association rate and [A] is the actin concentration. At this point, myosin either dissociates with rate constant k_d or transitions to the strongly bound state upon P_i release with rate constant k_T. The subsequent actin-bound steps associated with ADP release and ATP binding are faster than k_T under the conditions of these experiments (i.e., 1 mM ATP and no added ADP) and thus k_T is the rate-limiting step for actin-activated hydrolysis.

Our first critical assumption, based on the results of single myosin molecule laser trap experiments (19,20) and the single ATP turnover data (14,18) (see Supporting Material), is that only one of myosin's two heads (see head A or B in shading in Fig. 2 a) is capable of strong actin binding at a time. Thus, each head is not independent of the other and adopts a distinct functional role during hydrolysis, even in the absence of actin. In our model for HMM-2P hydrolytic activity, we define these roles as one head being able to strongly bind to actin and hydrolyze its ATP through the actin-dependent pathway at rate k_T, while the other is delegated to (at most) weak actin-binding and will thus hydrolyze its ATP at the basal rate k_n (see Figs. 1 and 2). We assume that once a head adopts a specific role, in subsequent interactions, these roles can switch at a rate k_s and that role-switching occurs only when myosin is unbound from actin (see Fig. 2). In the Supporting Material, we justify these assumptions in greater detail (e.g., we show that neither models with double-headed binding, nor models where actin is necessary to define the functional roles of the two heads can fit the data, while a model with role switching during weak binding provides nearly identical results as the model presented here).

Figure 2.

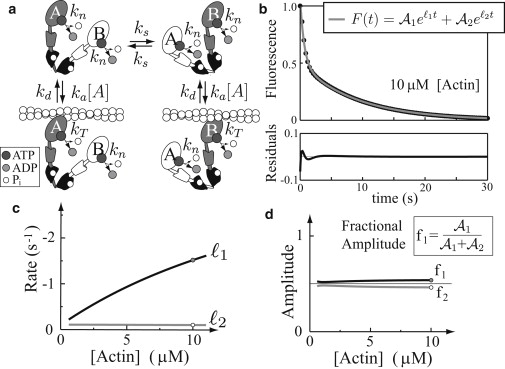
A model for doubly-phosphorylated (2P) myosin, and a simulated single ATP turnover experiment. (a) The kinetic model for 2P myosin. Each head is labeled “A” or “B.” The darker head adopts an actin-dependent role and after binding actin, may hydrolyze ATP through the actin-dependent pathway (k_T); the lighter head adopts a non- or weak-binding role, and must hydrolyze ATP at its basal rate (k_n). The heads switch roles at rate k_s. (b) The model predicts the fluorescence decay for a single ATP turnover experiment, where fluorescence is proportional to the number of heads that have yet to hydrolyze an ATP molecule. Experimentally, this curve is fit by the sum of two exponentials. The difference between the fit and the exact curve is the residual plotted at bottom (compare to Fig. 4a of (14)). (c) The two rates of the exponentials may be plotted as a function of actin concentration. (d) The two amplitudes of the exponentials may be plotted as a function of actin concentration.

Fitting the HMM-2P model to single turnover and steady-state ATPase data

We use the model in Fig. 2 a to fit the single ATP turnover and steady-state ATPase data (see Fig. 3) reported by Rovner et al. (14) and Ellison et al. (17,18). For the single ATP turnover experiments, this kinetic model predicts that fluorescence decays as the sum of four exponentials

$$F\left(t\right)=A_1{e}^{{\lambda }_{1}t}+A_2{e}^{{\lambda }_{2}t}+A_3{e}^{{\lambda }_{3}t}+A_4{e}^{{\lambda }_{4}t},$$ (1)

where the variables A_i and λ_i depend on the rate constants k_T, k_n, k_d, k_s, and k_a as well as actin concentration. The exact relationship between these variables cannot be written in closed form; however, given particular values of the rate constants and actin concentration, we may use numerical methods to determine the amplitudes (A_i) and exponential rates (λ_i), and therefore the fluorescence decay. While this theoretical curve is the sum of four exponentials, the experimental fluorescence decay is fit by two exponentials (14,17). To compare our model with these data, we used a numerical optimization procedure to determine the best-fit (in a least-squared sense) of the modeled fluorescence decay to two exponentials with amplitudes (${\mathcal{A}}_1$, ${\mathcal{A}}_2$) and rates (ℓ₁, ℓ₂) at various known actin concentrations, of the form

$$F\left(t\right)={\mathcal{A}}_1{e}^{{\ell }_{1}t}+{\mathcal{A}}_2{e}^{{\ell }_{2}t}.$$ (2)

We compare these rates and amplitudes to those measured experimentally (see Supporting Material for details of this fitting procedure and derivation of Eq. 1).

The same kinetic parameters (i.e., k_T, k_n, k_d, k_s, and k_a) used to predict the single ATP turnover were then used to model the ATPase (V_ATP) as a function of actin concentration (Fig. 3). In particular, we find

$$V_{\text{ATP}}\left(\left[A\right]\right)=k_n+\frac{k_T\left[A\right]+k_n{K}_m}{K_m+\left[A\right]},$$ (3)

where

$$K_m=\left(k_T+k_d\right)/k_a$$

(see Supporting Material for a full derivation). We then globally fit the HMM-2P single turnover and steady-state ATPase activities with the parameter set (k_T, k_n, k_d, k_s, and k_a) that minimizes the χ-squared error between the literature and model-predicted activities (we find p > 0.05, χ-square test; see Fig. 3). The best-fit parameters for the two HMM-2P preparations reported by Rovner et al. (14) and Ellison et al. (17,18) are summarized in Table 1, with the fits to their data shown as solid lines (Fig. 3). Note that the model is insensitive to the values of k_d and k_a, so we instead report the parameter K_m. Details of the sensitivity analysis and reasons for why the model is insensitive to these parameters are presented in the Supporting Material.

Table 1.

2P model parameter values

Optimized parameter values
Parameter	Rovner et al. (14)	Ellison et al. (17,18)
ks(s−1)	1 × 10−4 + 0.1	0.063 ± 0.02
kT(s−1)	4.5 ± 0.4	2.6 ± 0.4
kn(s−1)	0.11 ± 0.04	0.11 ± 0.02
Km(μM)	24 ± 4	44 ± 8

The model predicts the single turnover data and all its subtleties (Fig. 3). Specifically, the model predicts two rates of approximately equal amplitude, one dependent on actin concentration and the other independent of actin and an order-of-magnitude slower. However, for the model to adequately predict these data, the rate constant for role switching, k_s, must be small (see Table 1; k_s = 1 × 10⁻⁴ + 0.1 s⁻¹ and k_s = 0.063 ± 0.02 s⁻¹ for the two data sets) when compared to the ≥2 s⁻¹ actin-activated ATPase rate. If this were not the case, then the single ATP turnover should have been described by a single exponential, without any evidence of the slow, actin-independent myosin ATPase rate that comprises ≈50% of the fluorescence decay signal (see Supporting Material for further discussion of this point, and other aspects of the data that necessitate slow switching). The implications of such a slow rate are presented in the Discussion.

Model of singly-phosphorylated myosin (1P): a simple equilibrium between the inactive and active conformations

The HMM-2P model described above serves as the foundation for understanding the reduced biochemical and mechanical activity observed for expressed HMM-1P (14,16). We limit the model to predicting the single ATP turnover and steady-state ATPase data for the HMM-1P expressed construct described by Rovner et al. (14) (see Fig. 4), and most recently characterized by ourselves in the motility and laser trap assays (16). Rovner et al. (14) observed that the HMM-1P single turnover fluorescence decay, as with the HMM-2P, was best described by two exponentials, one actin-dependent and the other not. However, the ATPase rate of the HMM-1P actin-dependent component was less than that of the HMM-2P (Fig. 4 b). In addition, the actin-activated steady-state ATPase rate for the HMM-1P was similarly depressed compared to the HMM-2P (Fig. 4 b). Here, we demonstrate that the reduced HMM-1P activities can be explained by HMM-1P existing in an equilibrium between the fully inhibited (folded) and fully active (extended) states. We assume that this equilibrium may occur when the HMM-1P is detached or weakly-bound to actin, with k₂, $k_2^{\prime }$, k₃, and $k_3^{\prime }$ defining the rates of transition between the inhibited and active states (Fig. 4 a). When inhibited, the HMM-1P does not contribute to any measurable ATPase activity (22). We assume that, as for the HMM-2P above, while in the active state the two HMM-1P heads slowly switch between the non/weak-binding and actin-activated strong-binding roles. We also assume that transitions between the inhibited and active states may occur regardless of the role the heads adopt.

Figure 4.

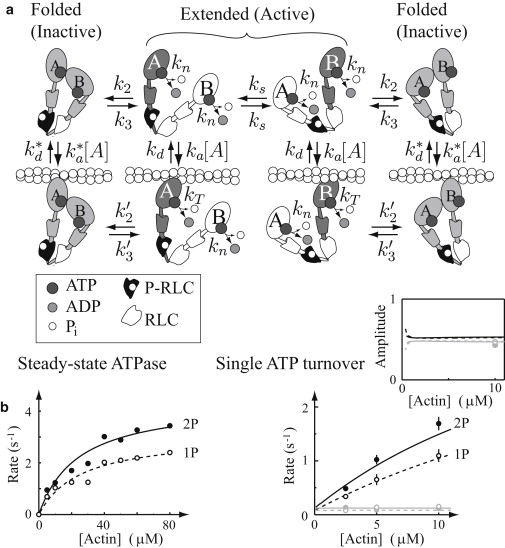
The model for singly phosphorylated (1P) myosin that assumes an equilibrium between the extended, active conformation and the folded, inactive conformation fits the single ATP turnover and steady-state ATPase data (p > 0.05). The same parameters in the model for doubly-phosphorylated (2P) myosin fit the single ATP turnover and steady-state ATPase data. (a) The model, showing an equilibrium between the folded and extended state. Note that the middle four states (the extended conformations) are the 2P model. (b) (Left) Steady-state ATPase and single ATP turnover rates and amplitudes (inset). The 2P and 1P models are shown (solid and dashed lines, respectively). (Right) (Shaded representation) The slower actin-independent rates and (solid representation) the faster actin-dependent rates in the single turnover plots. The data (2P, solid dots and 1P, circles) are from Rovner et al. (14).

As described, the kinetic scheme appears symmetrical (see Fig. 4 a). Note that the rate constants are not all independent, because energy/mass must be conserved, which gives us the relation

$$\frac{k_2^{\prime }{k}_a{k}_3}{k_3^{\prime }{k}_d{k}_2}=\frac{k_a{K}_{23}^{\prime }}{k_d{K}_{23}}=\frac{k_a^{\ast }}{k_d^{\ast }},$$ (4)

where the various rate constants are defined in Fig. 4 a.

Fitting the HMM-1P model to single turnover and steady-state ATPase data

The basic optimization techniques described above and in the Supporting Material for fitting the HMM-2P model to the single-turnover and steady-state ATPase data apply to the HMM-1P model as well. One difference is that when the HMM-1P is in the active state, the rate constants that specify its hydrolytic activity (k_T, k_n, k_d, k_s, and k_a) are that of the HMM-2P. Thus, when fitting the HMM-1P data, we must simultaneously fit the HMM-2P data. To fit both the HMM-1P and -2P data, we implicitly assume that the HMM-2P is fully active so that

$$k_2\to 0,k_2^{\prime }\to 0\text{and}/\text{or}{k}_3\to \infty ,k_3^{\prime }\to \mathrm{\infty }$$

(thereby recovering the HMM-2P model in Fig. 2).

Like the HMM-2P model described above, the HMM-1P model predicts the single ATP turnover fluorescence decays as a multiexponential function:

$$F^{1P}\left(t\right)=\sum _{i=1}^8{A}_i^{1P}{e}^{{\lambda }_i^{1P}t}.$$ (5)

Because the HMM-1P single ATP turnover data are fit by two exponentials (14), we first generate the predicted HMM-1P fluorescence decay curves at various actin concentrations and then use a numerical optimization procedure to determine the best-fit (in a least-squared sense) of the modeled fluorescence decay to two exponentials, as with the HMM-2P, of the form

$$F^{1P}\left(t\right)={\mathcal{A}}_1^{1P}{e}^{{\ell }_1^{1P}t}+{\mathcal{A}}_2^{1P}{e}^{{\ell }_2^{1P}t}.$$ (6)

To determine the best-fit set of rate constants, i.e.,

$$k_{T,}{k}_{n,}{k}_{d,}{k}_{s,}{k}_{a,}{k}_{2,}{k}_{3,}{k}_2^{\prime },k_3^{\prime },k_d^{\ast }\text{and}{k}_a^{\ast },$$

we globally fit the single turnover and steady-state ATPase rate ($V_{\text{ATP}}^{1P}$, see Supporting Material for a derivation).

HMM-1P exists in an equilibrium between active and inhibited states

The expanded kinetic model for HMM-1P fits both HMM-1P and HMM-2P single-turnover and steady-state ATPase data (p > 0.05, χ-square test; see Fig. 4). The best-fit parameters are summarized in Table 2. Note that, as with the parameters of the HMM-2P model, the fit was insensitive to some parameters as evidenced by the large estimated range for a given parameter that results in a good fit (p > 0.05, χ-square test). This insensitivity arises because the model depends more on particular combinations of parameters than the individual parameters themselves (see Supporting Material for an explanation of this result).

Table 2.

1P model parameter values

Optimized parameter values
Parameters	Optimized values
ks (s−1)	1 × 10−4 + 0.09
kT (s−1)	4.5 ± 0.4
kn (s−1)	0.12 ± 0.05
a1 (1/(1 + k2/k3))	0.67 ± 0.14
a2 (1/(1 + $k_2^{\prime }$/$k_3^{\prime }$))	0.71 ± 0.14
Km (μM)	24 ± 7
Km1P (μM)	26 ± 9

A critical assumption in the model is that the HMM-1P molecule can transition between the inactive and active states. It is the equilibrium between these two states that effectively modulates the hydrolytic activity of the HMM-1P molecule. In fact, the probability of an HMM-1P molecule being in the active state is ≈a₁ = 1/(1 + k₂/k₃) while detached, and a₂ = 1/(1 + $k_2^{\prime }$/$k_3^{\prime }$) while weakly bound to myosin. The best-fit values for these probabilities are a₁ = 0.67 ± 0.14 and a₂ = 0.71 ± 0.14, suggesting that an HMM-1P molecule spends ≈70% of its lifetime in the active state (in the conditions investigated in these experiments). This simple calculation provides a basis for the reduced steady-state and actin-dependent single-turnover ATPase activity for the HMM-1P compared to the HMM-2P (see Supporting Material for a more rigorous argument).

Results and Discussion

Smooth muscle myosin is only one of several class II myosins. The ease with which smooth muscle may be expressed in vitro has allowed investigators to test aspects of myosin molecular structure and function not easily addressable in other systems. Through structural mutagenesis of smooth muscle myosin, investigators have studied two basic physiological questions, specifically:

• 1.Do the two heads of myosin act independently of each other?
• 2.How does RLC phosphorylation both regulate and modulate smooth muscle myosin's enzymatic and mechanical properties?

Based on the models described here, we propose that the two heads are not independent; in particular, only one head is capable of interacting productively with actin at any point in time. Further, we propose that regulation of smooth muscle myosin by RLC phosphorylation involves modulating the equilibrium between inhibited and active conformations of the molecule.

The roles each head plays in smooth muscle myosin hydrolysis and mechanics

Since the discovery that skeletal muscle myosin has two heads (1), investigators have speculated whether or not the heads are independent of each other. For the most part, under steady-state conditions, there has been overwhelming evidence that each head contributes equally to enzymatic and mechanical activities. For example, early in vitro studies of actomyosin threads suggested that single-headed skeletal muscle myosin generates only half the force of double-headed myosin (23). In addition, the ATPase activity of double-headed HMM is twice that of the single headed, S1-fragment (2) (however, note that more recent experiments with smooth muscle find that some single-headed fragments have less than half the activity of fully phosphorylated double-headed HMM-2P (24–26)). These results can simply be interpreted as the activity scaling in proportion to the number of heads. However, at the single molecule level in the laser trap, Tyska et al. (19) showed that single-headed myosin, whether it be smooth or skeletal, generates half the displacement and unitary force of double-headed myosin. Based on this result, they proposed that only one head productively interacts with actin whereas the second head weakly interacts, optimizing the mechanical performance of its partner head. To test this hypothesis, Kad et al. (20) studied the displacement generated by a mutant, heterodimeric smooth muscle HMM construct having one normal head and the other head mutated to only weakly interact with actin. Interestingly, in support of the hypothesis of Tyska et al. (19), this heterodimer generated the same displacement as a normal double-headed myosin (20). Thus, only one head is required for force and motion generation while the other head is necessary to optimize the mechanical performance of the working head. These data suggest that functionally the two heads are not equivalent and that they each adopt separate, critical roles in myosin's force/work production.

Our model of fully active, doubly-phosphorylated smooth muscle myosin (2P) also suggests that the molecule adopts a functional conformation such that each head is nonequivalent. Specifically, one head, the actin-activated head, is capable of strong actin binding and a productive interaction (i.e., actin-activated ATP hydrolysis and force and/or mechanical work), while the other head can only weakly bind to actin at any point in time. Furthermore, the model suggests that this conformation is maintained for a considerable period of time so that each head assumes its particular role over many ATP hydrolysis cycles. Thus, once a particular head binds productively to actin, it is much more likely than its partner to do so again. Admittedly, we find this result counterintuitive, because we are unaware of any structural basis for differentiating the two heads in the absence of actin. A test of this concept is not trivial, but one could express a heterodimeric myosin in which the heads are both active but nonequivalent, each having a different hydrolytic activity or step size. Such heterodimers exist in nature, for example the two isoforms of cardiac myosin form heterodimers in vivo (27,28), and humans that are heterozygous for genetic forms of hypertrophic cardiomyopathy are expected to express heterodimeric myosin (29).

RLC phosphorylation and its modulation of smooth muscle myosin activity

Smooth muscle myosin, as with several other class II myosins, is regulated by RLC phosphorylation (30). During the activation and relaxation process in smooth muscle tissue, myosin will exist in various states of phosphorylation, where none, one, or both RLCs are phosphorylated. However, during sustained isometric contractions, the level of RLC phosphorylation decreases and the tissue enters the latch state where force is maintained with little energy expenditure (10). During this contractile phase, the population of myosin molecules with only one phosphorylated RLC (1P) can be substantial, suggesting that these myosin contribute to the latch state. Early biochemical studies used mixtures of 2P, 1P, and 0P myosin to infer the activity of 1P myosin based on assumptions about phosphorylation and the known activities of 2P and 0P myosin. Some studies concluded that 1P myosin has approximately half the activity of 2P myosin (31,32), while others concluded that 1P myosin has less than half the activity of 2P myosin (33,34). We propose that under all levels of phosphorylation (0P, 1P, and 2P), smooth muscle myosin may form the inhibited conformation, but does so with greater difficulty as the number of phosphorylated RLCs increases (Fig. 5). This proposal seems consistent with a mechanism proposed by Houdusse and Cohen (35) based on the structure of scallop muscle, and more recently described in a model by Tama et al. (36), who propose that the main difference between doubly-phosphorylated and unphosphorylated myosin is the stiffness of the lever arm in the region of the RLC. They suggest that phosphorylation increases lever arm stiffness, and thus gives a larger energetic cost to the strain that they propose is needed to form the head-head interactions of the inhibited conformation.

Figure 5.

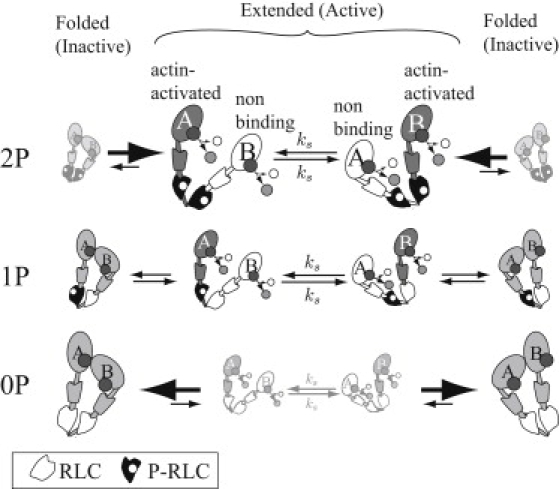
A cartoon of how light-chain phosphorylation modulates activity. Each head adopts either an actin-activated role, where it may strongly bind actin and hydrolyze ATP through the actin-activated pathway, or a non/weak-binding role where it may only (at most) weakly bind actin. The heads switch these roles slowly, at a rate k_s < 0.1 s⁻¹. The molecule is in a phosphorylation-dependent equilibrium between the active, extended state and the inactive, folded state. We represent the relative probability of being in each state by its size. In the doubly-phosphorylated (2P) state (top), the equilibrium lies toward the extended state, so the molecule is mostly active. In the unphosphorylated state (0P) state (bottom), the equilibrium lies toward the folded state, so the molecule is mostly inactive. In the singly phosphorylated state (middle), both the extended and folded states are present, so the molecule has intermediate activity. The shading and symbols are the same as in Fig. 4.

Based on our HMM-1P model, the equilibrium constant for the inhibited to active state transformation is ≈0.5 (i.e., k₂/k₃ and $k_2^{\prime }$/$k_3^{\prime }$). Thus, the HMM-1P molecule spends approximately one-third of its lifetime inhibited and the other two-thirds fully active. Implicit in this conclusion is the assumption that when the HMM-1P adopts the active state, the HMM-1P enzymatic and mechanical behavior are indistinguishable from that of the HMM-2P. Data to support this assumption were recently obtained in the laser trap, where single HMM-1P molecules generate step sizes and attached lifetimes identical to those of an HMM-2P molecule (16). In addition, actin filament velocities in the motility assay are equivalent for the HMM-1P and HMM-2P at saturating myosin surface densities (14,16).

The inactive/active equilibrium may also explain the observed reduction in duty ratio (α_1P) for HMM-1P compared to the HMM-2P (α_2P), i.e., α_1P/α_2P = 0.6 ± 0.2 (16). Myosin's duty ratio is defined as the fraction of the ATPase cycle that myosin is strongly bound to actin, α = t_on/(t_on + t_off), where t_on is the mean strong-binding lifetime and t_off is the mean time myosin spends detached from actin. The total cycle time, t_cycle, equals t_on + t_off, which is the reciprocal of the maximal ATPase rate (1/max(V_ATP)). In the motility assay at saturating myosin surface densities, actin filament speed, V_mot, is approximately equal to myosin's unitary step size d divided by t_on (V_mot = d/t_on) (e.g., (37)). Because there is no significant difference in V_mot or d between HMM-2P and HMM-1P (14,16), then t_on is the same for HMM-1P and -2P. Therefore, by substitution,

$${\alpha }_{1P}/{\alpha }_{2P}=\max \left(V_{\text{ATP}}^{1\mathit{P}}\right)/\max \left(V_{\text{ATP}}\right).$$

From our model, we may estimate these values as k_T and a₂k_T for the HMM-2P and -1P, respectively (see Supporting Material), so that α_1P/α_2P = a₂. The best fit value of a₂ = 0.71 ± 0.14, as measured from the fits to the single ATP turnover and steady-state ATPase data of Rovner et al. (14), is not significantly different (Student's t-test) from the relative duty ratios measured from HMM-1P and -2P, α_1P/α_2P = 0.6 ± 0.2 from the motility assay (16). Therefore, both the apparent reduction in ATPase activity and duty ratio for the HMM-1P can be explained by the HMM-1P spending only a fraction of its lifetime in the active state compared to the HMM-2P being active at all times.

Although the HMM-1P model presented above adequately describes the biochemical data, we must consider at least one alternative model. This model is similar to the one described above, but differs by assuming that the unphosphorylated head behaves differently from the phosphorylated head. For example, the light-chain binding domain associated with the unphosphorylated RLC may be more flexible than that of the phosphorylated RLC (36). If so, as the heads within the HMM-1P molecule switch their actin-binding roles, it is conceivable that when the unphosphorylated head is in the nonbinding role then it is capable of being in equilibrium with the inhibited state but not when the unphosphorylated head is in the actin-dependent role. This type of model would predict that the HMM-1P would behave effectively as if one head was fully active while the other was partially active. The partial activity would arise from one conformation of the HMM-1P being able to form the inhibited, folded conformation. This model fits the biochemical data almost as well as the model described above and is described in detail in the Supporting Material. Note that these two models, one where both heads are equally able to form the inhibited state, and the other where only one head is able to form the inhibited conformation, represent two extremes of a continuum of models where each head has a different ability to form the inhibited conformation. As both of these extremes fit the data, it is reasonable to assume that any of the intermediate models would fit the data too. With recent advances in single molecule fluorescent techniques and biophysical measurements, experiments may be designed to distinguish between these models.

Conclusions

The models we propose may also be applicable to other muscle myosins as well as other classes of myosin. For example, the head-head interactions that are critical for the inhibited state in smooth muscle myosin may in fact be a general property of all myosin II (38,39), even when the molecule exists within a myosin filament. Light-chain phosphorylation has been implicated in twitch potentiation in skeletal muscle (40), whereby unphosphorylated skeletal muscle may also exist, though to a lesser extent than smooth muscle myosin, in an equilibrium between an inactive an active conformation that can be modulated by the extent of RLC phosphorylation. Molluscan muscle myosin, which is activated by calcium binding to the essential light chain, is thought to be activated by a calcium-dependent equilibrium between an active and inactive state (41–43), and the absence of regulation in single-headed molluscan myosin (44) suggests a calcium-dependent folded-unfolded equilibrium. The unconventional myosin V, a processive intracellular cargo transporter, is regulated by its cargo-binding domain folding down to interact with the two heads, thus inhibiting the molecule (45). These examples and our models here suggest that a mechanism for modulating myosin's activity, and thus a graded response in vivo, is to simply alter the equilibrium between the inhibited (folded) and active (extended) state, which smooth muscle myosin has accomplished by varying the extent of RLC phosphorylation.

The most surprising aspect of our modeling efforts is that the two heads in a fully active smooth muscle myosin molecule are not independent and that the heads adopt non/weak-binding and actin-dependent roles and switch between these roles slowly. It must be emphasized that this conclusion, though counterintuitive, is strongly dictated by the double-exponential nature of the single ATP turnover data obtained with smooth muscle HMM (14,17,18). Whether this mechanism is common to all muscle myosins has yet to be determined.