Hydrodynamics of Sperm Cells near Surfaces

Abstract

Sperm are propelled by an actively beating tail, and display a wide variety of swimming patterns. When confined between two parallel walls, sperm swim either in circles or on curvilinear trajectories close to the walls. We employ mesoscale hydrodynamics simulations in combination with a mechanical sperm model to study the swimming behavior near walls. The simulations show that sperm become captured at the wall due to the hydrodynamic flow fields which are generated by the flagellar beat. The circular trajectories are determined by the chiral asymmetry of the sperm shape. For strong (weak) chirality, sperm swim in tight (wide) circles, with the beating plane of the flagellum oriented perpendicular (parallel) to the wall. For comparison, we also perform simulations based on a local anisotropic friction of the flagellum. In this resistive force approximation, surface adhesion and circular swimming patterns are obtained as well. However, the adhesion mechanism is now due to steric repulsion, and the orientation of the beating plane is different. Our model provides a theoretical framework that explains several distinct swimming behaviors of sperm near and far from a wall. Moreover, the model suggests a mechanism by which sperm navigate in a chemical gradient via a change of their shape.

Introduction

Sperm from different species display a variety of swimming behaviors. Freely swimming sperm (e.g., from sea urchin (1), mouse, and chinchilla (2)) move on helical trajectories (3). However, when spatially confined to a shallow recording chamber, sperm swim on circular or curvilinear trajectories at the fluid-wall interface (2,4–9). The helical swimming behavior is important for external fertilizers that release their gametes into the water. Curvilinear or circular trajectories close to a surface are relevant for the movement on the epithelial layer that lines the oviduct, and when sperm reach the surface of the much larger egg. For example, many fish eggs on their surface possess a small orifice, called the pylum, which must be reached by the sperm for successful fertilization. Moreover, the swimming behavior is modulated by chemoattractants that guide sperm to the egg (10,11). In a chemical gradient, sperm swim on drifting circles (5,8,12) toward the egg.

The swimming behavior near surfaces has been studied for sperm of bull (13), human (14), sea urchin (15), mouse, rat, and chinchilla (2). All experiments reveal circular or curvilinear trajectories close to the surface. For sea urchin sperm, portions of the tail are outside the focus plane of the microscope (15), suggesting an out-of-plane component of the beating pattern. Mouse sperm, which are characterized by a strongly curved midpiece, adhere to the wall only when the left side of the head faces the glass surface (2). Chinchilla sperm undergo a rolling motion as they move along the surface, thereby touching the wall with different parts of their head (2).

Several explanations have been proposed to account for the capture of sperm near a surface (2,13,15). In his pioneering study of bull sperm near surfaces, Rothschild concluded that hydrodynamic interaction is the most likely origin of this effect (13). For rodent sperm, two mechanisms have been proposed (2). For sperm that exhibit a three-dimensional beating pattern and display a rolling motion as they progress (like chinchilla sperm), it was argued that the conical shape of the flagellar envelope establishes a thrust toward the surface. Alternatively, for sperm that exhibit a two-dimensional beating pattern (like mouse sperm), the discoidal shape of the sperm head, which is slightly tilted with respect to the plane of the flagellar beat, may act as a hydrofoil (2).

Theoretical treatments of sperm motion in the presence of boundaries are based on numerical solutions of the Navier-Stokes equations for the fluid, coupled to the active beating motion of the sperm tail. Simulations of sperm in a two-dimensional fluid in a narrow channel (equivalent to a swimming sheet in a three-dimensional fluid) showed a tendency of the sperm to move toward the boundary (16). In these simulations, a generic sperm model of a circular head and a symmetrically beating tail was employed. A more detailed analysis was performed recently for a model of human sperm in a three-dimensional fluid (17). Much care has been taken to construct a realistic model of the head; both planar and helicoid beating patterns were considered. A stable trajectory parallel to the wall is found when the wave length of the oscillations of the flagellar beat becomes smaller than the tail length. In this case, the distance from the wall is ∼25% of the tail length, and sperm are slightly tilted away from the surface. The numerical method used in Smith et al. (17) breaks down when sperm come too close to the wall.

The approach we pursue in this article is different. Because surface capture is observed for sperm of many different species, which have different head shapes and wave forms of the tail beat, we construct a simple, generic sperm model. This model, consisting of a spherical head, a passive midpiece, and an actively beating tail, is embedded in a three-dimensional particle-based mesoscale fluid to describe the hydrodynamic interaction with the wall. This mesoscale hydrodynamics approach has the advantage that it is unconditionally stable and includes fluctuations, at the cost of not reaching quite the same accuracy as computational fluid dynamics methods. For comparison, we also employ a Brownian-Dynamics-type model, in which the sperm tail interacts by an anisotropic friction with the embedding medium. This allows us to distinguish steric effects (like the conical shape of the flagellar envelope suggested in Woolley (2)) from the effect of hydrodynamic interactions (2,13).

Our simulations show that hydrodynamic forces are sufficient to attract swimming sperm to a wall, such that the head essentially touches the wall. Furthermore, swimming trajectories both in the bulk and at a surface are controlled by the sperm shape. The principal parameters of our model are the average spontaneous (or preferred) curvature, c₀, of the flagellum and the chirality of the overall shape. For symmetrical shapes, sperm move on a straight path, both in the bulk and at the surface. The chirality induces helical motion in the bulk (1) and circular or curvilinear motion at the surface. Therefore, by changing their shape, sperm are able to navigate in a chemical gradient.

Sperm Model and Simulation Methods

Mechanical sperm model

The structure of sperm from many species is universal, consisting of a head and a thin flagellum. The flagellum is divided into a midpiece and a beating principal piece. For simplicity, the principal piece is denoted the tail. Bending of the tail is generated by motor proteins that move along microtubules and, thereby, generate a local bending moment (11,18).

We mimic this sperm structure by a spherical head of radius r_h and a flexible flagellum of length L_f. The flagellum is modeled by three semiflexible rods, each consisting of N_f = 100 monomers; the monomers are connected by bonds of length ℓ_b and are arranged in a filamentous structure with a triangular cross section (for details, see Appendix). The flagellum is divided into a passive midpiece of length L_m and an actively beating tail (Fig. 1 a). We model the force generation on the mesoscopic scale by imposing locally a preferred curvature c₀(t;s) of the tail at time t, where 0 < s < L_f is a measure of the contour length along the flagellum. Propulsion is induced by a sinusoidal propagating wave

$$c_0\left(t;s\right)=\left(A/L_f\right)\text{sin}\left(qs-\omega t\right)$$ (1)

along the tail, with L_m < s < L_f. This wave generates an approximately sinusoidal planar beat. Analysis of the flagellar beat of bull sperm showed that 95% of the power consumption is contributed by the first Fourier mode (19), suggesting that a sine wave describes the beat pattern fairly well.

Figure 1.

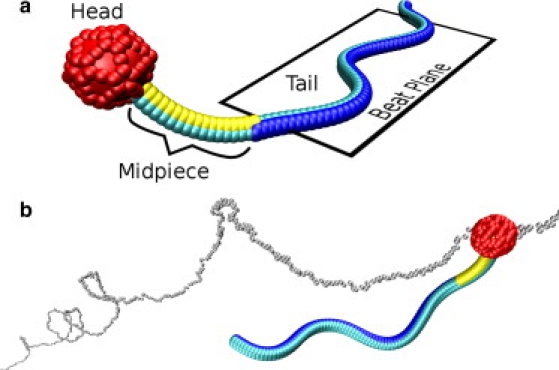
(a) The sperm structure consists of a spherical head (red), a curved midpiece (yellow to light blue), and a beating tail (dark blue to light blue). A traveling sinusoidal deformation of the tail generates a forward thrust. The curvature plane of the midpiece is tilted by an angle π/3 with respect to the beating plane. (b) Snapshot of a sperm with preferred curvature c₀^(m)L_m = 1 of the midpiece (MCE model), moving along a helical trajectory. The trajectory is indicated by the small gray spheres. See also Movie S1, which is published as Supporting Material on the Biophysical Journal web site. Visualization using VMD (24).

The parameters are chosen such that the beat pattern of sea urchin sperm is roughly reproduced. The sea urchin sperm is 50 μm long and has a beating amplitude of 4 μm. At a given time, ∼1.5 waves are present on the flagellum. Therefore, we chose A = 11.5 and qL_t = 12, such that the beating amplitude is ∼0.05L_f and 1.5 waves are present on the tail (3).

A helical swimming trajectory (1,3,20–23) requires not only asymmetry of the average sperm shape, i.e., the sperm shape averaged over a beat period, but also chirality. Sperm that are asymmetric only within the beating plane or a plane orthogonal to the beating plane would move on circles in that plane. A chiral structure implies that the beating plane rotates around the sperm axis (1).

To elucidate the impact of various shapes and beating modes on the swimming pattern of sperm from different species, we study two classes of chiral sperm models. The average flagellar shape is determined by the preferred curvature c₀ = 1/R₀, where R₀ is the local radius of curvature. The models differ by the distribution of the preferred curvature c₀ along the flagellum.

In the first class of models, the midpiece is curved, but the tail is straight. The curvature plane of the midpiece is tilted with respect to the beating plane by an angle π/3 (Fig. 1 a). Moreover, the flagellum is either elastic or stiff. While the bending rigidity is similar for elastic and stiff flagellum, the torsional rigidity is much larger for the stiff flagellum. This difference has consequences for the dynamic distortion of the flagellum during beating and, thereby, swimming behavior. We denote these two models the “midpiece curved elastic” (MCE) and the “midpiece curved stiff” (MCS).

A second class of model is characterized by a preferred curvature c₀ along the entire flagellum, not just the midpiece. The curvature plane of the tail is tilted with respect to the local beating plane by an angle π/3, which provides chirality. This model is denoted the “tail curved stiff” (TCS).

Mesoscale hydrodynamics

Microscopic swimmers like bacteria or sperm are characterized by low-Reynolds-number hydrodynamics (25). The model sperm are embedded in a particle-based mesoscale fluid. We employ the multiparticle collision dynamics (MPC) technique (26–28), which provides a good description of hydrodynamics at low Reynolds numbers (29).

The dynamics of the particles in an MPC fluid proceeds in two alternating steps. In the streaming step, the motion of the fluid particles of mass m is ballistic, whereas the motion of the monomers is determined by the forces exerted by the bonds within the sperm model. In the collision step, after a time interval Δt, all particles are sorted into the cells of a cubic lattice with lattice constant a. The collision of particles within a cell is described by a rotation of their relative momenta (with respect to the center-of-mass momentum of the cell) by an angle α around a randomly chosen axis. The low Reynolds numbers and large Schmidt numbers characteristic of viscous fluids are achieved by choosing small time steps Δt, which—at fixed temperature—correspond to a small mean-free path λ of the fluid particles (29).

Appropriate length- and timescales of the sperm motion and of the MPC fluid have to be chosen to achieve low-Reynolds-number hydrodynamics, slow diffusion compared to swimming, and good computational efficiency. In our simulations, we use λ/a = 0.05, α = 130°, and particle density ρa³ = 10. With a short bond length ℓ_b = 0.5 a, the flagellum, embedded in the MPC fluid, behaves hydrodynamically like a slender rod (30). For a beat frequency

$$\omega =0.1\sqrt{k_{\text{B}}T/m{a}^2},$$

the swimming velocity is found to be

$$v\simeq 0.0034\omega L_f=0.017\sqrt{k_{\text{B}}T/m}\text{.}$$

With these parameters, the time needed to swim a distance L_f/2 is approximately three-orders-of-magnitude less than that needed by diffusion. More simulation details are provided in the Supporting Material.

There are several sources of noise, such as fluctuations in the activity of motor proteins or in the signaling system, which affect the motion of real sperm (31,32). This noise leads to rotational diffusion of the sperm axis. We mimic these fluctuations by the noise inherited from the thermal fluctuations of the MPC fluid. The presence of fluctuations implies that our results are robust with respect to small perturbations.

Anisotropic-friction model

The effect of hydrodynamics on sperm motion can be separated into two parts: The first is a local anisotropic hydrodynamic friction of slender bodies in a fluid, which is responsible for the sperm propulsion (3). The second part involves long-range flow fields that mediate a hydrodynamic interaction between moving bodies.

To study the importance of long-range hydrodynamic interactions, we also performed simulations with local anisotropic friction only, which is commonly known as resistive-force theory. A slender rod slides through a fluid more easily along its long axis than perpendicular to it. This property is characterized by anisotropic friction coefficients, γ_‖ and γ_⊥, with γ_‖ < γ_⊥. The friction force

$$\mathbf{F}=-{\gamma }_{\perp }{\mathbf{v}}_{\perp }-{\gamma }_{\left|\right|}{\mathbf{v}}_{\Vert }$$ (2)

on a monomer in the flagellum is determined by the local orientation of the flagellum and its velocity

$$\mathbf{v}={\mathbf{v}}_{\perp }+{\mathbf{v}}_{\Vert }\text{.}$$

For comparison of the results of MPC simulations and resistive force theory, we employ a friction anisotropy γ_⊥/γ_‖ = 1.5 and a friction coefficient

$${\gamma }_{\perp }=10\sqrt{k_{\text{B}}Tm/a^2}$$

per monomer (for details, see Supporting Material). The friction of the head monomers was estimated by dividing the friction coefficient 6πηr_h of a sphere of radius r_h by the number of monomers. This implies

$$\mathbf{F}=-\gamma \mathbf{v}\text{with}\gamma =3\sqrt{k_{\text{B}}Tm/a^2}$$

for the head monomers.

Results

Sperm motion in the bulk with mesoscale hydrodynamics

The simulation of MCE sperm with significant asymmetry (midpiece curvature c₀^(m)L_m = 1) produces a pronounced helical trajectory, with the tail pointing away from the helical axis (Fig. 1 b). We analyzed three characteristic parameters of the helical motion of sperm: the curvature C of the trajectory, the tangential velocity v, and the rotation frequency Ω_b of the beating plane around the flagellar axis. The tangential velocity is fairly constant (v ≃ 0.0034ωL_f) across all sperm models and preferred curvatures c₀; it decreases by ∼30% for strongly asymmetric sperm.

The curvature C of the trajectory, however, strongly depends on the sperm model and the preferred curvature c₀ of the flagellum (Fig. 2). For weakly asymmetric shapes, the curvature C is small and, due to small fluctuations in the direction of motion, the helical trajectories are difficult to distinguish from the almost straight trajectories of symmetric sperm. For MCS sperm, the helicity of the trajectory is small for all c₀^(m) values. In contrast, strongly asymmetric sperm swim on pronounced helical trajectories. For sperm with a stiff tail (MCS, TCS), the curvature C of the trajectory increases linearly with the preferred curvature c₀, both for curved midpiece and curved tail (Fig. 2). However, because the tail is much longer than the midpiece, the impact of c₀ on the trajectory is stronger for sperm with a curved tail. For the TCS model, the curvature C of the trajectory and the preferred curvature c₀^(t) are nearly identical (Fig. 2), because the shape of the tail almost perfectly tracks the trajectory of the sperm head.

Figure 2.

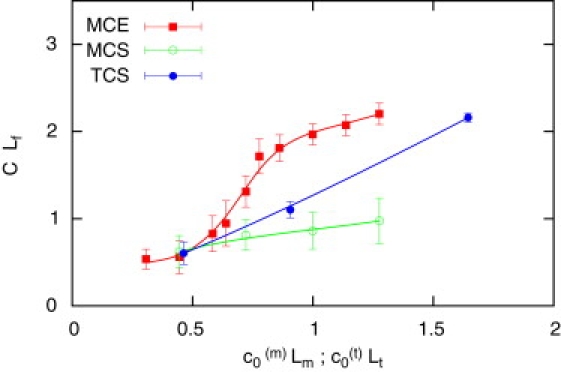
Scaled curvature CL_f of a helical trajectory as a function of the preferred curvature c₀ of the flagellum (scaled with L_m for MCS and MCE, and with L_t for TCS sperm models). The stiff, curved tail of the TCS model (•, blue line) produces a curvature of the trajectory which is nearly identical to the preferred curvature c₀^(t). The MCS sperm (•, green line) follow a trajectory with very little curvature. The MCE model (■, red line) shows a elastic deformation of the flagellum for c₀^(m)L_m ≳ 0.7, which increases the curvature of the tail. The curvature C of the trajectory is scaled by the flagellar length L_f, and the preferred curvature c₀ is scaled either by the length L_m of the midpiece (for MCE and MCS sperm) or the length L_t of the tail (for TCS), to facilitate comparison of simulations and experiments.

In contrast to the linear relationship between C and c₀^(m) of sperm with stiff flagellum (MCS, TCS), sperm with an elastic flagellum (MCE) show a highly nonlinear dependence (Fig. 2). This nonlinearity originates from the deformation of the tail for c₀^(m)L_m ≳ 0.5: the flagellum twists and bends due to the forward thrust of the tail and the hydrodynamic friction of the head (Fig. 1 b), which leads to a larger curvature of the trajectory than expected from c₀^(m) alone (Fig. 2).

Our simulations show that the rotation frequency Ω_b equals the pitch frequency—as expected for any swimmer with helical trajectory (1). For stiff sperm (MCS and TCS), Ω_b increases monotonically with c₀^(m) (Fig. 3). In contrast, elastic MCE sperm display a more complex behavior: in the low-curvature regime, the beating plane rotates faster than in stiff MCS sperm; initially, Ω_b rises steeply, reaches a maximum at $c_0^{\left(m\right)}{L}_m\simeq 0.35$, then decreases again, and for c₀^(m)L_m ≥ 0.7 even becomes smaller than Ω_b for a stiff flagellum (Fig. 3). Again, this behavior is due to the deformation of the elastic flagellum. At small c₀^(m), the flagellum twists, thereby increasing the chirality and consequently the rotation frequency Ω_b. For c₀^(m)L_m > 0.7, the enhanced tail curvature due to elastic deformation predominates over the preferred curvature, and leads to a behavior similar to the TCS model.

Figure 3.

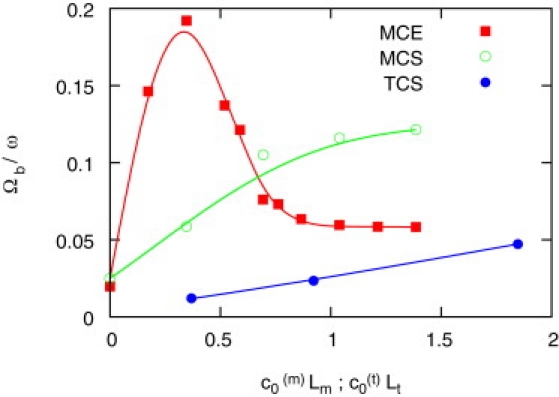
Rotation frequency Ω_b of the beating plane around the flagellar axis, scaled with the beat frequency ω, as a function of the preferred curvature c₀ of the flagellum. In the elastic MCE model, the rotation frequency increases with increasing chirality for small c₀^(m); however, for c₀^(m)L_m > 0.7, where curvature of the tail is generated by elastic deformation, rotation slows down.

We examined the MCE model at higher viscosity η and lower beat frequency ω. In the regime of low Reynolds numbers, theory predicts that—at fixed beat frequency and amplitude—the swimming velocity is independent of the viscosity (3). We observe that a 2.5-fold increase of η decreases the velocity by ∼20% and the rotation frequency by ∼30%. This small decrease is primarily due to a smaller beat amplitude, because larger viscous forces prevent the tail from fully attaining the local preferred curvature c₀(t;s) (Eq. 1). The curvature of the trajectory is not significantly affected by the higher viscosity. When the beat frequency ω is reduced twofold, the swimming velocity also decreases approximately twofold, as predicted by Stokes theory, i.e., for low Reynolds numbers (3). In this case, the dependence of C on c₀ of MCE sperm becomes similar to that of MCS sperm at the original beat frequency. This result is consistent with the conclusion that, in the MCE model, the tail for c₀^(m)L_m ≥ 0.7 is deformed; the deformation increases with propulsive force, i.e., with increasing ω.

Sperm motion confined between parallel walls

Sperm motion is often studied in confined geometries. Surfaces give rise to new phenomena, such as capture and circular swimming at the surface. To study these phenomena, we simulate the behavior of sperm between two planar walls, separated by a distance d = L_f, with no-slip boundary conditions. A short-range, purely repulsive Lennard-Jones interaction (with a range much smaller than the head diameter) prevents direct sperm-wall contact. A measure of capturing is an average distance between sperm head and surface less than the head diameter.

Both symmetrically and asymmetrically beating sperm display strong surface capture over the whole range 0 ≤ c₀^(m)L_m ≤ π/2 of preferred curvatures. Once the head hits the wall, the flagellum is almost parallel, but slightly tilted toward the wall (Fig. 4). We emphasize that the tail rarely comes within reach of the Lennard-Jones repulsion of the wall. Together these observations suggest that hydrodynamic interactions and directional self-propulsion are responsible for capturing. Adhesion persists in the presence of fluctuations and for a wide range of preferred flagellar curvatures, implying that it is very robust.

Figure 4.

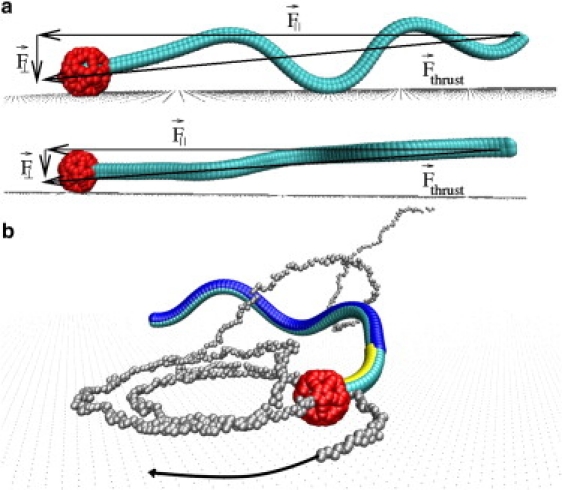
(a) Sketch of forces responsible for the adhesion of sperm at a surface. (Top) Without hydrodynamic interactions, the beating-plane of adhering sperm is oriented perpendicular to the surface. (Bottom) With hydrodynamic interactions, the beating-plane is oriented parallel to the surface. (b) Sperm (MCE model) with large preferred curvature (c₀^(m)L_m = 1) at a surface. The head touches the wall and blocks further rotation. The beating plane is approximately perpendicular to the surface. See also Movie S2 and Movie S3, which are published as Supporting Material on the Biophysical Journal web site.

We first analyze wall adhesion for the simpler case of symmetric sperm, and then describe wall adhesion and circular motion of chiral sperm.

Wall adhesion of symmetric sperm

To elucidate the hydrodynamic mechanism of attraction of symmetric sperm, we consider the flow field of the fluid in the vicinity of sperm. In the bulk, the flow field of self-propelled particles, which push themselves through a fluid (i.e., the pushers), is characterized by two vortex rings near the head and the tail (33,34). The vortices are generated by fluid that is dragged forward by the head and pushed backward by the tail. This generates a region of low pressure near the midpiece. As a consequence, fluid is streaming onto the pusher from the sides. Fig. 5 shows the flow field of a moving sperm near the surface, resulting from our simulations. The influx of fluid in the midpiece region becomes asymmetrical near the surface: the flow onto the midpiece from above relative to flow from below is greatly enhanced due to the presence of the wall (Fig. 5 a). This imbalance of fluxes generates an attraction to the wall in the midpiece region, in qualitative agreement with the predictions by a force-dipole approximation for large distances from the wall (35). The flow field near the end of the tail also has a component toward the wall (Fig. 5 a); this component is responsible for a hydrodynamic repulsion of the tail from the wall, which induces a tilt of the sperm axis toward the surface (Fig. 4). Furthermore, due to the no-slip boundary conditions, the flow in the plane parallel to the wall is strongly screened (Fig. 5 b).

Figure 5.

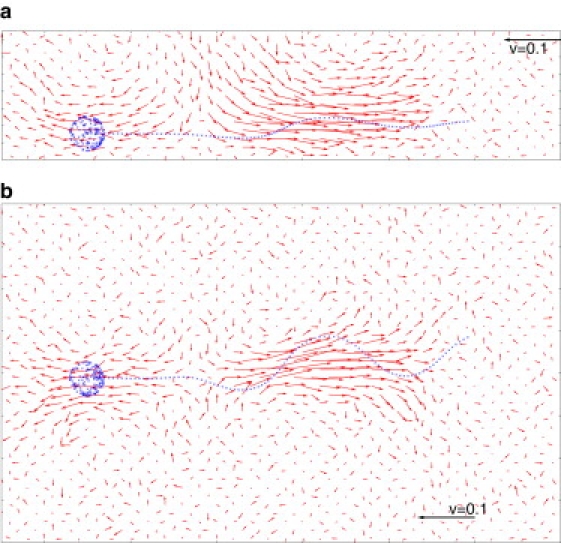
Averaged flow field in the vicinity of a sperm cell adhering to a wall. (a) Plane perpendicular to the wall (with wall at bottom of figure), and (b) plane parallel to the wall, with both planes containing the average sperm shape. A snapshot of a sperm is superimposed. The flow field generated by the beating tail is directed away from the sperm along their swimming direction and toward the sperm along its side.

Thus, we propose as a general adhesion mechanism for sperm a combination of

• 1.a hydrodynamic attraction due to the low-pressure region at the midpiece, and
• 2.a hydrodynamic repulsion of the tail from the surface, which induces a tilt of the sperm axis and thereby a thrust of the head toward the surface (Fig. 4).

The system adopts a stable state, where small fluctuations are quickly undone. However, large fluctuations can push the head far away from the wall, thereby sperm detach. This mechanism is supported by the observation that, at lower beat frequency (which increases the importance of fluctuations relative to the propulsive forces), sperm detach more frequently from the wall. The adhesion mechanism is also supported by the sperm orientation: sperm are oriented toward the wall with their beating plane parallel to the wall—in agreement with experimental observations for sea urchin sperm (5,8).

Wall adhesion and circular motion of chiral sperm

In the simulations, asymmetric sperm swim on circles at the surface—in agreement with experimental observations for sea urchin sperm (5,6,8). Here, we focus on the MCE model. The circular motion depends on the chirality of the sperm shape. We distinguish three different regimes. MCE sperm with large midpiece curvature (c₀^(m)L_m > 0.8) display a pronounced circular motion (Fig. 4 b). The origin of these circles is a hindered helical motion. When the head hits the surface, due to the repulsive force of the wall, the beating plane stops to rotate (Fig. 4 b); this generates a torque that forces sperm to swim on a circular trajectory. We emphasize, however, that the circular trajectory does not correspond to a simple projection of the helix circumference onto the surface.

In contrast, for small midpiece curvature (c₀^(m)L_m ≲ 0.5), the beating plane continues to rotate around the flagellar axis at the surface. How is rotation maintained close to the surface? The head touches the wall periodically for a short time; thereby, a small torque is generated that forces the sperm onto a circular trajectory. Subsequently, the head slips and sperm move on a straight line for another short time interval before the head hits again the surface. As a consequence, the curvature of the trajectory is significantly smaller than in the case of large c₀^(m)L_m (Fig. 6). Finally, at intermediate curvatures 0.5 < c₀^(m)L_m < 0.8, the head gets stuck for longer times until fluctuations cause it to slip, occasioning an erratic behavior, where a radius of curvature is difficult to define (Fig. 6).

Figure 6.

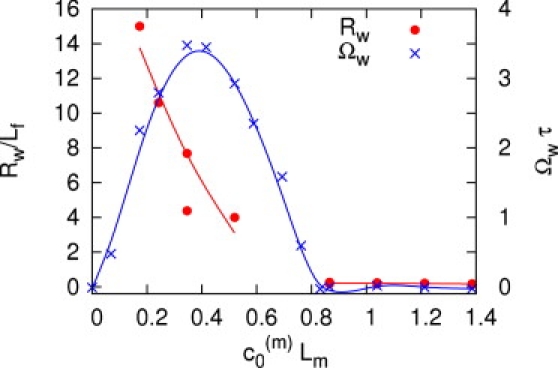
Radius R_w of circular motion and rotation frequency Ω_w of MCE sperm at the wall, as a function of scaled midpiece curvature c₀^(m)L_m. Irregular motion in the transition region is ignored. Only sperm with moderate preferred curvature c₀^(m) roll at the wall. Ω_w vanishes for c₀^(m) = 0 for symmetry reasons. Sperm with c₀^(m)L_m > 0.8 cannot rotate due to head-wall repulsion.

The two types of surface motion are clearly set apart by the dependence of the circle radius R_w on c₀ (Fig. 6). Sperm with weakly curved midpiece swim on significantly larger circles (R_w ≥ 2L_f) at the wall than sperm with strongly curved midpiece (R_w ≤ L_f). Sperm with weakly curved midpiece roll at the surface; the rotation frequency Ω_w increases with c₀^(m)L_m until it reaches a maximum at $c_0^{\left(m\right)}{L}_m\simeq 0.35$ (Fig. 6). For c₀^(m)L_m > 0.35, the head gets stuck at the surface for short periods of time, thereby slowing down the rotation. Sperm with c₀^(m)L_m > 0.8 swim in tight circles and do not roll, because the rotation around the tail axis becomes difficult for highly chiral shapes.

The orientation of the beating plane with respect to the wall is determined by the interplay between the blockage of the rotation by the wall-head interaction, the asymmetric shape of the sperm, and the hydrodynamic interaction between tail and wall. For symmetric or weakly curved sperm, where the beating plane is parallel to the surface, the distribution of orientation angles ϕ (between the beating plane and the surface) has two peaks at ϕ = 0° and ϕ = 180° (Fig. 7). For c₀^(m) = c₀^(t) = 0, the sperm shape is perfectly symmetric, implying that the distribution also becomes symmetric with respect to ϕ = 0° and ϕ = 90°, i.e., the two orientations ϕ = 0° and ϕ = 180° of the beating plane are equivalent. However, for chiral sperm, the two orientations are not equivalent; for ϕ = 0°, the head points away from the surface, whereas for ϕ = 180° it points toward the surface.

Figure 7.

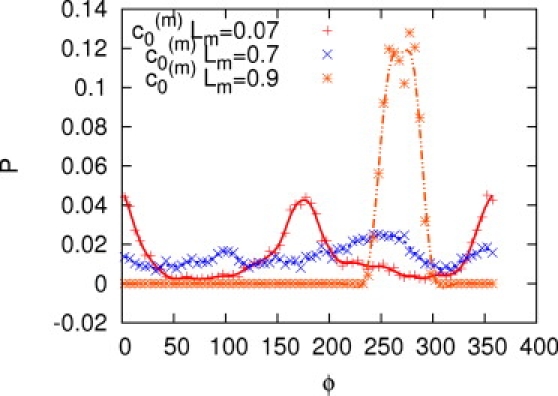
Probability distribution P of the rotation angle ϕ of the beating plane around the flagellar axis, where ϕ = 0° corresponds to parallel orientation to the wall. Data are shown for MCE sperm with small (c₀^(m)L_m = 0.07; pluses), medium (c₀^(m)L_m = 0.7; crosses), and large (c₀^(m)L_m = 0.9; stars) preferred midpiece curvatures. The distribution for c₀ = 0 is symmetric at ∼ϕ = 90° and ϕ = 180°.

For sperm with a moderately curved midpiece (0.3 ≤ c₀^(m)L_m ≤ 0.7), the distribution of orientations becomes significantly broader due to rolling. A broad peak at ϕ ≃ 250° indicates that the head, when it touches the surface, gets stuck for a short time. For c₀^(m)L_m ≥ 0.8, a prominent peak at ϕ ≃ 270° dominates the distribution; this peak corresponds to an almost perpendicular orientation of the beating plane. Obviously, the peak value of ϕ not only depends on the midpiece curvature, but also on the other parameters of the sperm shape, e.g., on the angle between the beating plane and the plane of midpiece curvature.

Wall adhesion—the stiff versus the elastic flagellum

In the elastic MCE model, the twist generated by an elastic deformation of the tail plays an important role for the bulk motion (Figs. 2 and 3). To study how the tail elasticity affects the wall capture and sperm motion, we also consider models with stiff flagellum. Stiff sperm adhere to a wall, but the adhesion behavior depends on the location of the curvature along the flagellum. While the trajectories of symmetric sperm are only little affected, the trajectories of chiral sperm show a pronounced dependence on tail stiffness. The TCS model—with uniform preferred curvature along the flagellum—shows strong adhesion and roughly circular trajectories. The dependence of R_w on the preferred flagellar curvature is much smoother than for MCE sperm, because the sudden change of R_w due to elastic distortion of the flagellum (Fig. 6) is absent.

Surprisingly, MCS sperm show much weaker surface adhesion than MCE sperm. Fig. 8 shows the z component (perpendicular to the wall) of some typical trajectories. MCS sperm for c₀^(m)L_m = 0.7 are still attracted to the wall with a few larger excursions. In contrast, MCS sperm with c₀^(m)L_m = 0.35 move back and forth between the walls. We conclude that elasticity of the flagellum enables sperm to adopt an optimal shape for adhesion.

Figure 8.

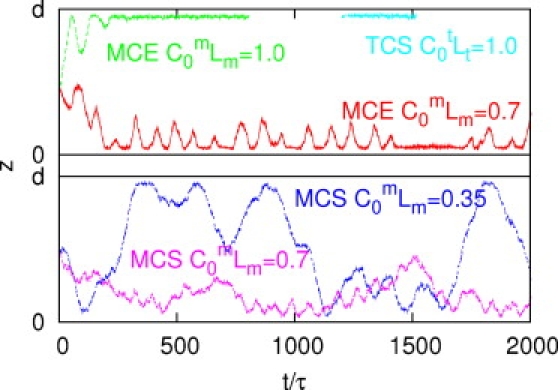
The z component (perpendicular to the wall) of characteristic trajectories of sperm with elastic (MCE) and stiff (MCS,TCS) tails and various flagellar curvatures, as indicated. MCE and TCS sperm adhere strongly to the wall. MCS sperm with moderate preferred curvature c₀^(m)L_m = 0.7 show weak surface capture, with oscillations caused by hindered rolling motion. MCS sperm with small preferred curvature c₀^(m)L_m = 0.35 do not adhere.

Anisotropic friction

The swimming behavior of sperm changes significantly without hydrodynamic interactions, i.e. with anisotropic friction coefficients only. Symmetric sperm also adhere to the wall, but with the beating plane perpendicular to the surface. In this case, the repulsion of the tail is provided by steric hindrance of the beating tail by the wall. This is consistent with the mechanism proposed in Cosson et al. (15). The difference of the sperm conformations is illustrated by the snapshots in Fig. 4.

Similarly, chiral sperm in the absence of hydrodynamic interactions adhere to a wall and swim on circles. Here, it is mainly the motion of elastic MCE sperm which is significantly affected. With anisotropic friction only, the elastic deformation of the tail occurs at much lower preferred curvature c₀^(m), which implies larger helical curvature and smaller rotation frequency. Also, the wall radius R_w is significantly smaller (Fig. 9) than with hydrodynamic interactions (Fig. 6).

Figure 9.

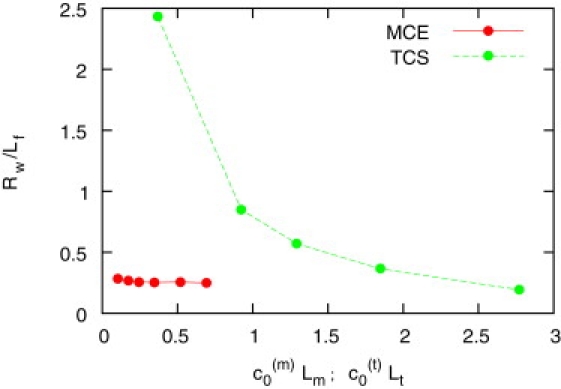
Radius R_w of circular motion of MCE and TCS sperm at the wall for anisotropic friction, as a function of scaled midpiece curvature c₀^(m)L_m (MCE sperm) and scaled tail curvature c₀^(t)L_t (TCS sperm), respectively. No rolling motion is observed.

In contrast, stiff sperm show an intriguingly similar behavior with and without hydrodynamic interactions; only the velocity increases by ∼25%. For the TCS model, where the curvature of the trajectory nearly equals the preferred curvature c₀^(t), the dependence of R_w on c₀^(t) is almost identical with and without hydrodynamic interactions. Also, R_w is very similar to that of MCE sperm with hydrodynamic interactions (Fig. 6).

An important difference between hydrodynamic interactions and anisotropic friction only is that no rolling occurs in the absence of hydrodynamic interactions and fluctuations.

Summary and Conclusions

We have shown that sperm adhere to walls for different sperm models and a broad range of flagellar curvatures—with some notable exceptions. Attraction is caused by the hydrodynamic interactions between tail and wall, in combination with the forward thrust of the flagellar beat. The models predict a close contact between the sperm head and the wall that is much smaller than the sperm length; moreover, a small but finite angle exists between sperm axis and the wall. Sperm with chiral shapes swim on helical trajectories in the bulk; the trajectories become circular at the surface. For small preferred curvatures of the flagellum, sperm undergo a rolling motion and swim on large circles, whereas for larger preferred curvatures, rolling stops and sperm move on smaller circles.

The proposed mechanism of adhesion is related to previously suggested mechanisms as follows. A highly simplified model for sperm is a self-propelled rod. Self-propelled rods (both with and without hydrodynamic interactions) also show surface accumulation due to steric alignment of the rod axis with the wall. However, the attraction is much weaker, and the rods detach from the wall after a characteristic time determined by the rod length and the swimming velocity (36). In contrast, sperm approach the wall and stay there (for the longest simulation times of up to 2000 beats).

One aspect of the attraction mechanism described here is qualitatively similar to the long-range hydrodynamic interaction predicted by the dipole approximation (valid for distances much larger than the sperm length), which leads to a torque that aligns the swimmer parallel to the wall, and a force that attracts the swimmer to the wall (35,37). We find that at short distances, hydrodynamics also leads to a tail repulsion, which implies an additional thrust of the head toward the wall.

With a numerical technique to solve the Stokes equation, weak attraction of human sperm with a distance from the wall of ∼25% of the sperm length and a sperm axis pointing away from the wall is predicted (17). Our simulation provides no evidence for swimming at such intermediate distances from the wall. Most likely, such a state is only marginally stable, and is absent due to fluctuations inherent to our simulations. Conversely, swimming very close to a wall is not accessible by the technique of Smith et al. (17), which becomes numerically unstable at short distances.

Our results have important ramifications for the navigation of sperm in a chemical gradient during chemotaxis. When confined to planar swimming at a surface, in a gradient of chemoattractant, sea urchin sperm swim on spirallike trajectories that resemble drifting circles (5,8,12). Within the framework of our model, these trajectories can be readily accounted for by periodic changes in the chirality of the sperm shape. Furthermore, our simulations apply for both the unrestricted sperm that swim on helical paths as well as the sperm that swim on circular trajectories near a surface. Moreover, our model accounts for sperm that swim in circles, like sperm from sea urchin, and sperm that swim on almost straight or curvilinear trajectories, like human sperm (10). Our generic model provides a general framework for different sperm shapes and swimming behaviors that proceeds from specific structures and beat patterns of individual species. We anticipate that our results will be useful for experimental studies to reconstruct the precise three-dimensional shape of sperm during swimming in bulk and near surfaces.

Further theoretical studies of sperm dynamics near walls would be interesting in several directions. For example, an important question concerns the role of the head shape on the swimming motion. Another example is the interplay of several sperm adhering to a wall at higher density.

Appendix: Flagellum Model

The flagellum is modeled as a cranelike structure (Fig. 10). Three semiflexible rods, each consisting of N_f = 100 monomers of mass M, are arranged in a filamentous structure with a triangular cross section. The bond length ℓ_b between neighboring monomers and the distance between the parallel filaments are identical. The filament length and the distance between filaments is kept nearly constant by harmonic bond potentials between nearest-neighbor (bond length ℓ_b, spring constant K₁) and next-nearest-neighbor (bond length ${\ell }_c=\sqrt{2}{\ell }_b$, spring constant K₂) monomers. All spring constants are chosen to be much larger than the thermal energy k_BT, so that the mean-squared thermal fluctuations of the bond length are much smaller than the bond length itself. A curvature potential is included for each filament to control the bending rigidity of the flagellum. Our model flagellum is characterized by an effective bending rigidity of κ/L_f ≈ 130 k_BT and a torsional rigidity J ≃ 10 k_BT to J ≃ 100 k_BT for elastic and stiff tails, respectively. More details about the flagellum model are provided in the Supporting Material.

Figure 10.

The flagellum is modeled as three semiflexible filaments that are connected by harmonic springs of length ℓ_b (nearest neighbors) and ℓ_c (next-nearest neighbors) to form a cranelike structure. Bond lengths on the top filament (red) are varied to induce both dynamic and static bending.

The bending rigidity of a flagellum has not yet been determined experimentally. However, we can estimate the rigidity from the structure of the axoneme, which consists of a two microtubules in the center, surrounded by nine double microtubules. The persistence length ξ_p of a single microtubule is ∼1 mm (38), which is related to the bending rigidity by κ₀ = k_BTξ_p. For a bundle of 20 microtubules of length L_f = 50 μm, this implies κ/L_f ≃ 400 k_BT. This is the same order of magnitude as the bending rigidity that we employ in the simulations.

The spherical sperm head, which is attached at its center to the flagellum, is constructed from N_h = 163 monomers. The head has a radius r_h = 4 ℓ_b and is held together by springs. The flagellum has a length L_f = (N_f − 1)ℓ_b, with N_f = 100, where 4 ℓ_b connect the center of the head to its surface (for stable anchoring), followed by a passive midpiece of length L_m = 15ℓ_b and an active principal piece (tail) of length L_t = 80ℓ_b.

We mimic force generation in the flagellum by changing the length of bonds in one of the semiflexible filaments (Fig. 1 a and Fig. 10). A length change (ℓ₀(t, s) – ℓ_b) of a bond generates a local spontaneous curvature

$$c_0\left(t,s\right)=\frac{{\ell }_0\left(t,s\right)-{\ell }_b}{{\ell }_b^2\sin \left(\pi /3\right)}\text{.}$$ (3)

A sinusoidal variation of the bond length as a function of contour length and time then generates the sinusoidal propagating wave of c₀(t, s) in Eq. 1. An additional permanent shortening of bonds in one of the rods generates a preferred curvature (Fig. 1 a).

This description is similar to but not identical with the sinusoidal beat pattern used in previous models, where the time-dependent flagellar shape is prescribed (3).