Collective motion and density fluctuations in bacterial colonies

Abstract

Flocking birds, fish schools, and insect swarms are familiar examples of collective motion that plays a role in a range of problems, such as spreading of diseases. Models have provided a qualitative understanding of the collective motion, but progress has been hindered by the lack of detailed experimental data. Here we report simultaneous measurements of the positions, velocities, and orientations as a function of time for up to a thousand wild-type Bacillus subtilis bacteria in a colony. The bacteria spontaneously form closely packed dynamic clusters within which they move cooperatively. The number of bacteria in a cluster exhibits a power-law distribution truncated by an exponential tail. The probability of finding clusters with large numbers of bacteria grows markedly as the bacterial density increases. The number of bacteria per unit area exhibits fluctuations far larger than those for populations in thermal equilibrium. Such “giant number fluctuations” have been found in models and in experiments on inert systems but not observed previously in a biological system. Our results demonstrate that bacteria are an excellent system to study the general phenomenon of collective motion.

Despite differences in the length scales and the cognitive abilities of constituent individuals, collective motion in systems as diverse as bird flocks, mammal herds, swarming bacteria, and vibrating granular particles (1–8) produces similar patterns of extended spatiotemporal coherence, suggesting general principles of collective motion. One approach to unveil these principles has been to model individuals as interacting self-propelled particles, which align their motions with neighbors (8–13). Some models also include repulsive and attractive interactions between particles in addition to the local alignment of velocities. With empirically chosen parameters such as the range over which the local alignment occurs, self-propelled particle models produce motions qualitatively similar to the observations. For example, within certain parameter regimes, models (8, 13) predict that collectively moving individuals form dynamic clusters, as often seen in fish schools or mammal herds (1); these clusters lead to large fluctuations in population density. Quantitatively, analytic theories based on liquid crystal physics (14–16) have predicted that these density fluctuations should scale with system size differently from fluctuations in thermal equilibrium systems.

In contrast to numerical models and analytical theories, quantitative experiments have been limited (2–8), though decisive experiments are urgently needed to test the theoretical assumptions, determine sensitive modeling parameters, and verify theoretical predictions. The lack of experimental data is mainly due to technical difficulties. In conventional macroscopic systems, such as bird flocks, it is exceedingly challenging to track individual motions of a large population over long periods of time, and studies with systematic parameter variation are rarely possible.

Recent studies (17–22) have shown that concentrated swimming bacteria, which can be considered as self-propelled polar microrods, under well-controlled conditions exhibit collective motion. These studies suggest that bacterial systems can serve as a promising alternative to the macroscopic systems to investigate general phenomena of collective motion. However, in previous studies, bacteria were so closely packed that it has not been possible to identify and simultaneously track many individual bacteria in collective motion for a long period of time.

In this article, we investigate collective bacterial motion in wild-type Bacillus subtilis colonies growing on agar substrates. Inside colonies, bacteria swim in a micrometer-thick film of liquid on the agar surface (23, 24); the bacteria are not observed to swim over one another. By tracking many individual bacteria, we quantify the correlations among bacteria, statistical properties of dynamic clusters, and the scaling of density fluctuations.

Results

Spatial Correlations.

Movies of bacterial motion are recorded at various bacterial densities. Each movie contains 6,000 consecutive images in which bacteria appear as white elongated objects. From the movies, we extract center-of-mass , instantaneous velocity , and cell body orientation for 95% of all bacteria in the imaging window (A = 90 × 90 μm²). Typical instantaneous configurations at two densities are shown in Fig. 1.

Fig. 1.

Instantaneous configurations at two densities with the average total number of bacteria in the imaging window N_total = 343 (A) and N_total = 718 (B). Velocity vectors are overlayed on the raw images of bacteria. The length of the arrows corresponds to bacterial speed, and nearby bacteria with arrows of the same color belong to the same dynamic cluster. (A Inset) A laboratory coordinate frame () and a local frame () are defined. The cell body and flagella of the ith bacterium are shown by solid and dashed lines, respectively (the flagella are not visible in our images); the local frame is centered at the center of mass , with and pointing at the transverse and longitudinal axes respectively. See Movies S1 and S2 for temporal evolution of the system.

Bacteria aggregate in clusters and move collectively as shown in Fig. 1 (also Movies S1 and S2). To quantify the local correlation of individual motions, we compute spatial correlation functions (18–20, 25–27) in a “local coordinate frame” with axes along () and perpendicular () to the cell body, as defined in the inset of Fig. 1A. The two-dimensional correlation functions, defined in Materials and Methods, for two densities are shown in Fig. 2 A–F, and their transverse profiles along y = 0 are shown in Fig. 2 G–I.

Fig. 2.

Two-dimensional pair correlation (A and D), orientational correlation (B and E), and velocity correlation (C and F) functions at two bacterial densities: N_total = 343 (A–C) and N_total = 718 (D–F). The dashed gray lines in A–F near the origin mark the border of the excluded volume. Transverse profiles, g(x,y = 0), are shown in G–I, where black and red lines correspond to N_total = 343 and N_total = 718, respectively.

The pair correlation function g(x,y) quantifies the probability per unit area (normalized by the area density ρ) of finding another bacterium at the location (x,y) away from the reference bacterium. The transverse profiles of the pair correlation function g(x,y = 0) in Fig. 2G show strong peaks at x = 1.44 μm for N_total = 343 and x = 1.08 μm for N_total = 718; thus bacteria in a cluster are positioned very close to a nearest neighbor. Peaks corresponding to the second and third nearest neighbors are also discernible for N_total = 718. As shown in Fig. 2 A and D, such bacterial aggregation in the flank extends in the longitudinal direction up to y ≈ 3.8 μm, which is roughly the length of the excluded volume. Close neighbors have similar orientation and velocity as the reference bacterium, as evidenced by the high correlation in orientation (Fig. 1 B, E, and H) and velocity (Fig. 1 C, F, and I). The positional, velocity, and orientational correlations are evident, for example, in the cluster at (20 μm, 30 μm) in Fig. 1B.

The strong correlations shown in Fig. 2 confirm the core assumption of local alignment in self-propelled particle models (8–13) and demonstrate that short-range correlations extending to the third nearest neighbor are sufficient to produce collective motion. The spatial correlations observed in our system originate from hydrodynamic (25–29) and excluded-volume (29–31) interactions between bacteria, and from physical intertwining of flagella of neighboring bacteria (20, 32–34). It has been shown that both excluded-volume (35) and hydrodynamic (28) interactions can lead to local orientational order. Physical intertwining of flagella has been directly demonstrated with fluorescent imaging (33, 34), but the interaction due to intertwining has not been quantified in experiments. Such an interaction also needs to be added to current models, and its role needs to be explored. The interactions between bacteria differ from the cognitive coordination of animals and birds, yet these systems all exhibit collective motions.

Dynamic Clusters.

The two-dimensional pair correlation functions in Fig. 2 A and D show no bacterial aggregation along the cell body () direction beyond y ≈ 3.8 μm. However, the velocity correlation function at N_total = 718 (see Fig. 2F) exhibits high correlation along the () direction over a distance up to y ≈ 8 μm. Such along-body velocity correlation is due to the formation of dynamic clusters, which are illustrated by color coding in Fig. 1. Clusters are long-lived (see Movies S1 and S2). Large clusters can cruise through the imaging window while maintaining their integrity, which prevents us from accurately measuring their lifetimes. Dynamic clusters continuously evolve, merge with others and split into smaller ones. This leads to a wide range of cluster sizes n, defined as the number of bacteria in a cluster. Representative configurations of clusters with various sizes n can be found in Fig. S1. We find the average speed of isolated bacteria in colonies is 15 μm/s. The speed increases with increasing cluster size, saturating at 40 μm/s for bacteria in clusters with more than 20 bacteria.

Bacterial motion within a cluster is strongly correlated. To characterize these intracluster correlations, we first compute spatial correlation functions within each cluster and then average these intracluster correlation functions over the ensemble of clusters within a given size range. In Fig. 3 A–C, we show cluster-size-dependent pair correlation g(x,y,n), orientational correlation C_θ(x,y,n), and velocity correlation C_v(x,y,n) functions for the cluster size ranges 81 ≤ n ≤ 110 obtained under the density condition N_total = 718. To measure the physical dimensions of clusters, we identify the contour of g(x,y,n) = 0.1 as the “statistical” edge of a cluster and extract longitudinal (λ_y) and transverse (λ_x) dimensions (see Fig. 3A). In Fig. 3D, λ_x and λ_y are plotted as a function of cluster sizes n. Clusters are elongated in the longitudinal direction: λ_y ≃ 1.4λ_x. Both λ_y and λ_x scale with a cluster’s size as n^0.5, which means the packing density within a cluster depends weakly on its size. As N_total increases from 513 to 718, the physical dimensions of a cluster with a given size decrease slightly; this is consistent with the shift of peaks in pair correlation functions (Fig. 2G). Cluster-size-dependent velocity C_v(x,y,n) and orientation C_θ(x,y,n) correlation functions show a high level of coherence within a cluster. Their numerical values at a point on the edge of clusters, plotted in Fig. 3E, decrease slightly from 0.85 to 0.7 as n increases from 3 to 125.5. Furthermore, correlation functions computed in clusters of the same size exhibit little dependence on N_total, as shown by data with different colors in Fig. 3E.

Fig. 3.

Statistical properties of dynamic clusters. (A) Cluster-size-dependent pair correlation g(x,y,n), (B) orientational correlation C_θ(x,y,n), and (C) velocity correlation C_v(x,y,n) functions. In A, the black line is the contour for g(x,y,n) = 0.1, which intersects the x and y axes at (λ_x,0) and (0,λ_y). Longitudinal λ_y and transverse λ_x lengthscales are plotted in D as functions of the cluster size n. The black dashed lines in D are fits of . In E, values of velocity and orientational correlation at (0,λ_y) are plotted against n. In D and E, data in blue and red are from N_total = 718 and N_total = 513, respectively. More cluster-size-dependent correlation functions computed at various conditions can be found in Figs. S2 and S3B.

The probability to find a cluster with size n is described by the cluster size distribution function, P(n), as shown in Fig. 4 for three density conditions. P(n) first decays as a power law (see Inset), then evolves into an exponential tail (main plot). Quantitatively, P(n) is well described by

[1]

where the cutoff size n_c characterizes the transition from power law to exponential behavior. We treat b and n_c as fitting parameters, and prefactor A is determined by a normalization condition: , where the summation over n runs from 1 to the size of the largest cluster observed. We find that the exponent b is independent of bacterial density (b = 1.85), whereas n_c increases with bacterial density, n_c = 6.5 for N_total = 343 and n_c = 75 for N_total = 718. The rapid increase of the cutoff size n_c with N_total means that the probability of finding large clusters grows markedly as the density of bacteria increases, which is presumably the reason for the larger correlation length in Fig. 1 for N_total = 718. The prefactor A decreases from A = 0.75 for N_total = 343 to A = 0.57 for N_total = 718; the change in A value is small enough that we can rescale and collapse all data onto a single curve as shown in the inset of Fig. 4. Beyond our system, the cluster size distribution described by Eq. 1 has been observed in fish schools and buffalo herds (8, 36, 37), which suggests general principles of collective motion across many length scales.

Fig. 4.

Size distribution of bacterial clusters for three bacterial densities: N_total = 343 (squares), N_total = 539 (circles), and N_total = 718 (triangles). Solid lines are fits to Eq. 1. (Inset) All data collapse onto a master curve by rescaling and are plotted in a log-log frame with a solid line showing the rescaled fit.

Density Fluctuations.

Bacteria in clusters are closely packed, which leads to high local density. Clusters are mobile and they often leave empty space in regions they just pass; this leads to low density in those regions. Consequently, mobile clusters cause large density fluctuations, as shown by a temporal record of the total number of bacteria in the whole imaging window in Fig. 5A. This record exhibits a maximum about twice as large as the minimum and has a standard deviation ΔN = 71 about 10% of the mean. Besides being large in amplitude, these density fluctuations scale with the mean differently from fluctuations in systems in thermodynamic equilibrium (7, 12–14, 16, 35, 38). For systems in thermal equilibrium where fluctuations obey the central limit theorem, ΔN is proportional to ; therefore should be a constant for all N. However, Fig. 5B shows that, for N_total = 343, where the cluster sizes remain small, initially increases, then saturates. For higher density (N_total = 718), the data show anomalous density fluctuations, sometimes called giant number fluctuations (7, 13). Here, the standard deviation ΔN grows more rapidly than and scales as ΔN ∝ N^0.75±0.03. Such anomalous density fluctuations have been observed in a numerical model of self-propelled polar particles that move unidirectionally like bacteria but interact differently according to phenomenological rules (13). The scaling exponent 0.8 found in the simulations is close to 0.75 ± 0.03 measured for bacteria, which suggests that general statistical properties of collective motion might be independent of the details of microscopic interactions. Systems of apolar (bidirectionally moving) particles also exhibit anomalous density fluctuations but with a scaling exponent closer to 1, as found in theory (16), numerics (12), and experiments (7, 38). Thus the scaling exponent seems to depend on the mode of motion of the individual particles.

Fig. 5.

Anomalous density fluctuations in collectively moving bacteria. (A) Total number of bacteria in the field of view as a function of time. Two snapshots, corresponding to minimal and maximal instantaneous bacteria density, are shown as insets. (B) The magnitude of the density fluctuations (quantified by the ratio of ΔN to ) against the mean bacterial number N, for interrogation areas of various sizes. Results from three conditions are shown: N_total = 343 (squares), N_total = 539 (circles), and N_total = 718 (triangles). The solid line in B has a slope of 0.25. To obtain the data in B, we define a series of interrogation areas centered at the imaging window with increasing sizes from A_i = 5.4 × 5.4 μm² to 90 × 90 μm². We then construct a temporal record of the number of bacteria in each interrogation area A_i (similar to the one in A). From these temporal records, we compute the standard deviation ΔN(A_i) and the mean N(A_i) for each A_i.

Discussion

Though bacteria have no central nervous system and are orders of magnitude smaller in physical dimension than macroscopic animals such as birds or fish (1–6), they locally align their individual motions like their macroscopic counterparts. Local alignment, which can arise from different interactions in different systems, is the essential ingredient responsible for collective motion according to models (8–13) and theories (14–16) designed to capture general principles of collective motion in a wide range of systems. Locally aligned bacteria move collectively in dynamic clusters with distinct statistical properties. These clusters lead to large fluctuations in population density, which exhibit an anomalous scaling with system sizes.

Our results demonstrate that bacteria are an excellent model system for studying general principles of collective motion. Their dynamics can be accurately quantified from the individual to the population level in the lab, their physical environment can be systematically controlled, and biological characteristics such as individual motility can be changed through genetic manipulations (17, 21, 23).

Materials and Methods

Bacteria Strain and Colony Growth.

Wild-type B. subtilis strain 3610 is a Gram-positive bacterium with a rod-shaped body and multiple flagella, which generate a propelling force in the direction of its body (21, 22). They swim with a mean speed about 40 μm/s in a thin liquid film on the substrate (24). In our experiments, the bacteria have mean dimensions of 0.72 μm × 7.4 μm (see Fig. S4 E and F).

Colonies grow on soft (0.5%) LB agar substrates. For inoculation, 5 μL of B. subtilis overnight culture (OD₆₅₀ = 1) is placed on the agar. The inoculated gel is stored in an incubator at 30 °C and 90% humidity. After a lag time of 2 h, a colony starts to expand outward isotropically with a speed 1.4 cm/hour (23).

Imaging Procedure.

After growing for 1.5 h, the colony (2.1 cm in radius) is placed under an optical microscope (Olympus IX50 with an LD 60X Phase contrast PH2 objective) for measurements. The imaging window (90 × 90 μm²) is positioned initially at the edge of the colony, and its position in the laboratory reference frame is left unchanged throughout the experiments. As the colony expands, the observed density of bacteria increases as a function of time due to a gradient of bacterial density from the edge to the interior of the colony. As shown in Fig. S5, the total number of bacteria N_total increases from 340 to 720 in 35 min, and then N_total saturates. The radius of a colony increases for 0.82 cm in 35 min, from which we estimate the density gradient near the colony edge is 465/cm. This means the spatial density variation within the imaging window is negligible.

At each density condition, we record 60 frame/s for 100 s, during which the increase in N_total is not significant (about 3%), and the system is in a quasisteady state. As shown in Figs. S6 and S7, the correlation times of density, velocity, and orientation fluctuations are about 0.2–0.4 s. Therefore, the number of statistically independent configurations sampled within 100 s is large enough to yield good statistics.

Image Analysis and Bacteria Tracking.

A typical raw image (1,000 × 1,000 pixels) is shown in Fig. S4A. The closely packed bacteria are in such close proximity in the image that simple procedures such as edge detection and intensity thresholding cannot separate them. In order to “isolate” a bacterium, we first obtain a background image by smoothing the original image with a moving Hamming window (7 × 7 pixels), and then the background is subtracted from the original image. A background-removed image is shown in Fig. S4B. Then a gradient-based edge-detection algorithm is applied to extract the edges of a bacterium. A binary image, as shown in Fig. S4C, is constructed such that only pixels inside the extracted edges are set to be white. Properties of the resultant white objects, such as center of mass, orientations, and sizes, are extracted by Matlab functions bwlabel and regionprops. White objects other than bacteria in binary images (cf. Fig. S4C) are eliminated by requiring each object to be elongated with an aspect ratio greater than 4. The final results are plotted on top of the original image in Fig. S4D, where the centers of mass of the bacteria are shown by red crosses and edges of the bacteria by blue lines.

To construct bacteria trajectories, we use a standard particle-tracking algorithm based on a minimum distance criterion between bacteria in successive frames. From the trajectories, we compute instantaneous velocities, 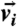. Because flagella are not resolved in our experiments, we cannot distinguish cell “head” from “tail” (where flagella connect to cell body) from static images. In order to determine the orientation vector uniquely, we assume the angle difference between 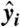and velocity is less than π/2. All image analysis and tracking programs are developed in Matlab.

Cluster Identification.

First, two bacteria are identified to be connected if the distance between their center of masses is less than R_d = 5.4 μm and the difference in their directions of motion is less than A_d = 20 degrees. We then define clusters recursively: A bacterium belongs to a cluster if it is connected to any other bacterium belonging to a cluster. Nine representative configurations of clusters are shown in Fig. S1. The majority of the clusters are elongated along the direction of motion.

The two parameters R_d = 5.4 μm and A_d = 20 degrees used to identify clusters are empirically chosen, based on correlation functions and instantaneous fields. We find that, around the chosen values (R_d = 5.4 μm and A_d = 20 degrees), the end results depend only weakly on the particular values of R_d and A_d. As shown in Fig. S3A, the cluster size distributions extracted under five sets of R_d and A_d are nearly indistinguishable. Higher values for R_d and A_d lead to slightly greater numbers of large clusters. Further, the cluster-size-dependent correlation functions (for 81 ≤ n ≤ 110) computed for different parameters in Fig. S3B also exhibit little difference. Lower values of R_d and A_d naturally lead to slightly higher correlations for velocity and orientation (first row in Fig. S3B).

Definition of Spatial Correlation Functions.

The two-dimensional pair correlation is defined as

[2]

where δ is a Dirac function, ρ = N_total/A is the area density, 〈…〉_i represents average over all reference bacteria i, and the position difference is expressed in ith local frame, as defined in the inset of Fig. 1A. The orientation correlation function and velocity correlation function are defined as

[3]

and

[4]

where 〈…〉_ij represents average over all possible pairs.