Phenotypic impact of regulatory noise in cellular stress-response pathways

Abstract

Recent studies indicate that intrinsic promoter-mediated gene expression noise can confer a selective advantage under acute environmental stress by providing beneficial phenotypic diversity within cell populations. To investigate how extrinsic gene expression noise impacts the fitness of cell populations under stress, we engineered two nearly isogenic budding yeast strains; one carrying a two-step regulatory cascade that allows for precise control of the noise transmitted from a transcriptional regulator to a downstream stress-inducing gene, and one carrying a network with low constant upstream noise. The fitness and gene expression of these strains were compared under acute and prolonged stress exposure. Using a phenomenological modeling approach, we predicted that increased noise should confer a fitness advantage under high stress conditions, but reciprocally reduce the resistance of the population to low stress. The model also predicted that extrinsic noise might serve as a basis for phenotypic plasticity whereby gene expression distributions are modulated in response to prolonged stress. Experimentally, we confirmed the predicted differential fitness advantage of extrinsic noise under acute stress, as well as the predicted modulation of gene expression under prolonged stress. However, contrary to model predictions, strains with low and high extrinsic noise showed very similar adaptive responses to prolonged stress. This suggests that while phenotypic heterogeneity generated by noise in regulatory signals can confer increased robustness to acute stress, it is not a requirement for the observed long-term phenotypic plasticity.

Introduction

Stochastic fluctuations in the activity of regulatory factors impose a fundamental limit on the precision of gene expression and cellular control mechanisms (Becskei and Serrano 2000; Louis and Becskei 2002; Blake et al. 2003; Rosenfeld et al. 2005; Dublanche et al. 2006). As a result, variability in gene regulatory signals (extrinsic noise) and fluctuations generated during the process of gene expression (intrinsic noise) are often viewed as detrimental and subject to minimization (Ozbudak et al. 2002; Fraser et al. 2004; Kærn et al. 2005; Batada and Hurst 2007; Barkai and Shilo 2007; Tanase-Nicola and ten Wolde 2008; Raj and van Oudenaarden 2008; Lehner 2008). However, gene expression noise can also be exploited to generate a fitness advantage under stress (Booth 2002; Avery 2006; Smits et al. 2006; Lopez-Maury et al. 2008; Losick and Desplan 2008; Fraser and Kærn 2009). For example, large-scale proteomic studies in budding yeast Saccharomyces cerevisiae have shown that genes associated with stress response pathways have elevated levels of intrinsic noise (Newman et al. 2006; Bar-Even et al. 2006). It has also been shown that severe stress causes a global increase in gene expression noise in Escherichia coli (Guido et al. 2007), and that increased extrinsic noise in Bacillus subtilis is used to trigger phenotypic switching in response to stress (Maamar et al. 2007). These observations suggest two possible stress-response mechanisms where high extrinsic noise plays a constructive role; one where it generates phenotypic diversity by increasing the variability in downstream gene expression, and one where it serves as a stochastic trigger of stress response programs.

Synthetic gene networks provide a framework for studying the origins and the consequences of noise in gene regulation under controlled conditions. Notable examples include single-cell measurements of fluctuations in gene expression rate as a function of transcription factor abundance (Rosenfeld et al. 2005), and measurements of the propagation of gene expression noise in transcriptional cascades (Blake et al. 2003; Hooshangi et al. 2005; Pedraza and van Oudenaarden 2005). Recently, a synthetic circuit was used to investigate the phenotypic consequences of promoter-generated gene expression noise in budding yeast exposed to acute antibiotic stress (Blake et al. 2006). Based on the predictions of a molecular-level model, the authors introduced targeted mutations in order to modulate the level of intrinsic noise in the expression of a gene providing antibiotic resistance. When cells were exposed to high doses of antibiotic, a strain with high intrinsic noise was observed to have higher viability than a strain with low intrinsic noise. On the other hand, the study also documented that increased intrinsic noise might be disadvantageous since the strain with low expression noise had higher viability than the high-noise strain when exposed to low doses of antibiotic.

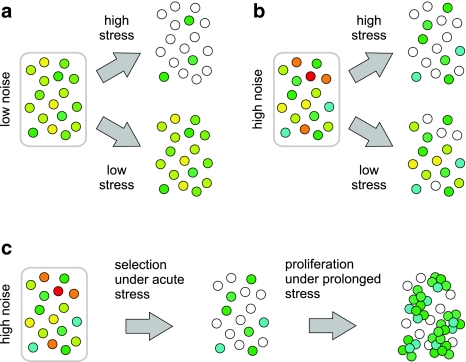
The advantages and disadvantages of gene expression noise can be explained by comparing the effects of acute stress on cell populations with low or high variability in the expression of a gene conferring stress resistance (Fig. 1). Figure 1a depicts the impact of low or high acute stress on a relatively homogenous, low noise population. While most of the cells within this population are resistant to low stress, only a few express the resistance gene at levels required to survive in high stress conditions. As a result, the population is unaffected by low stress but has limited resistance to high stress. In contrast, Fig. 1b considers a population with more variable gene expression. Here, elevated gene expression noise enables a higher number of cells to express at levels required for survival under high stress. Equally, however, an increased number of cells express at such low levels that they are susceptible even to low stress. Consequently, while gene expression noise can ensure increased viability at high stress, the effect is associated with a reciprocal disadvantage at low stress. Interestingly, these effects of gene expression noise are not limited to microorganisms. Brock et al. (2009) recently proposed that heterogeneity in gene expression might contribute to the development of drug-resistant somatic tumors. The model proposed by the authors in this context (Fig. 1c) is essentially an extension of the model in Fig. 1b to account for the effects on population dynamics of prolonged stress. In this model, only a small fraction of cells express a drug-resistance gene at sufficient levels to survive exposure to high drug doses. However, a tumor consisting of a drug-resistant cell population may form under prolonged drug treatment if these cells can produce offspring that also express the resistance gene at high levels.

Fig. 1.

Qualitative model explaining how noise in the expression of a stress-resistance gene impacts cell proliferation. a The effects of acute, high or low stress on a relatively homogenous, low noise cell population. While all cells can survive exposure to low stress, only a few have sufficiently high expression to endure high stress. b The effects of acute, high or low stress on a heterogeneous, high noise cell population. Increased noise increases the number of cells that express at high levels (cyan and dark green) and can survive high stress. It also increases the number of cells expressing at very low levels (orange and red) and fewer cells survive exposure to low stress. c A model for the emergence of a stress-resistant cell population under prolonged exposure. As in (b), increased noise enables a number of cells to survive high stress. These cells can then form a stress-resistant population if daughter cells inherit the high gene expression levels of their mothers

Here, we use a previously proposed phenomenological model (Fraser and Kærn 2009; Zhang et al. 2009) to make general predictions about the impact of extrinsic gene expression noise under acute and prolonged stress, respectively (see “Modeling heterogeneous population dynamics”). In the case of acute stress, the model predicts that the magnitude of the fitness advantage under high stress conditions increases with the level of gene expression noise, and that this is associated with a disadvantage of reciprocal magnitude under low stress conditions. In the case of prolonged stress, it predicts that drug-induced stress may result in substantial changes in gene expression distributions without requiring dedicated response mechanisms, and that increased noise should enhance the potential as well as the rate of this spontaneous, adaptive response. To explore the validity of these predictions, we designed a synthetic gene regulatory network allowing precise control of population variability in the expression of a stress-related gene by tuning the level of extrinsic noise in an upstream transcriptional regulator. This noise modulation circuit is described and characterized in “Synthetic network characterization”. In “Impact of noise under acute stress” and “Impact of noise under prolonged stress”, we present results obtained under acute and prolonged stress, respectively. In these experiments, we systematically varied the level of stress imposed on cell populations with different levels of extrinsic noise. Our results confirm the predicted reciprocal relationship between the advantages and disadvantages associated with gene expression noise under acute stress, as well as the predicted adaptive response of populations experiencing prolonged stress. However, contrary to model predictions, increased extrinsic noise did not have a significant impact on adaptation to long-term drug-induced stress. In fact, a strain engineered to have low extrinsic noise appeared to respond slightly faster than a strain with high extrinsic noise. Nevertheless, while regulatory noise seems not to be a requirement, our results provide support for the hypothesis by Brock et al. (2009) that a stress-resistant cell population can develop under prolonged drug treatment as a result of phenotypic selection and stable inheritance of beneficial expression states.

Methods and materials

Theoretical models and simulations

The impact of acute stress on the fitness W of a cell population can be calculated theoretically by evaluating the integral:

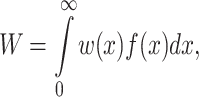1

where w(x) is the relative reproductive rate of cells expressing a stress-related gene at a level given by x, and f(x) describes the population distribution of gene expression when cells are exposed to stress. In a previous study (Fraser and Kærn 2009), this distribution was approximated by the lognormal distribution:

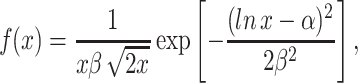2

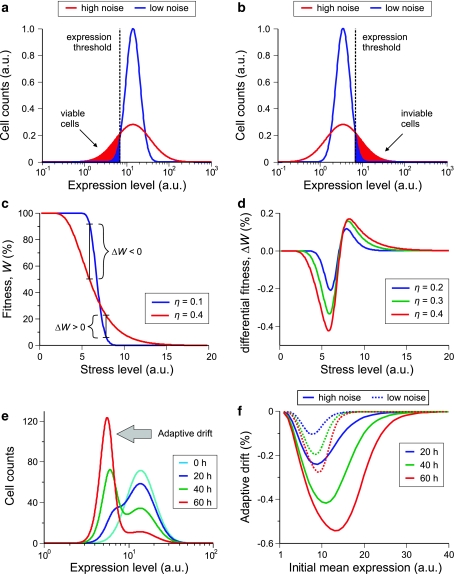
where α and β are defined by the average gene expression level μ and gene expression noise η through the relationships β ² = ln(1 + η ²) and α = ln(μ)−0.5β. The distributions in Fig. 2a and b were obtained for η = 0.4 and η = 1.2, respectively. Moreover, the impact of acute stress was approximated by a step function such that cells expressing a stress-resistance gene below a certain threshold have a reproductive rate of zero, i.e., fitness w(x) = 0 for x < s _thr, and are otherwise unaffected, i.e., w(x) = 1 for x ≥ s _thr.

Fig. 2.

Modeling the effects of noise in the expression of a stress-inducing gene. a High noise is beneficial when most cells express the stress-inducing gene at levels above a certain threshold. b Low noise is beneficial when most cells express below the threshold. c The effect of varying the stress level on fitness for a low and a high noise cell population. The stress level is calculated as the mode of the gene expression distributions (see “Methods”). Stress levels where noise is beneficial and disadvantageous are defined by a positive and negative value of the differential fitness ΔW, respectively. d Differential fitness at varying stress levels for three populations with elevated noise relative to a low noise (η ₀ = 0.1) reference population. e Changes in gene expression distributions predicted by during prolonged stress exposure. The change in the population mean is used to define the adaptive drift. f Adaptive drifts over time for a high noise (full curves) and a low noise (broken curves) population

The present study investigates a negative selection scheme where cells with high expression of a stress-inducing gene have low fitness, and cells with low expression have high fitness. We assumed that the level of stress s experienced by the population is related to the most likely level of gene expression. The stress level is then given by s = μ/(1 + η ²)^2/3, corresponding to the mode of the distribution in Eq. (2), and the α parameter can be written as α = ln[s(1 + η ²)]. Correspondingly, in a threshold model, the noise-dependency of population fitness in Eq. (1) is then given by an error function (erf) describing the cumulative lognormal distribution as:

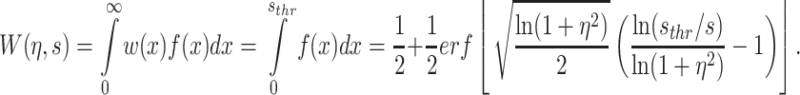3

Equation (3) was used to calculate the fitness curves displayed in Fig. 2c using s _thr = 6.91 and η = 0.1 or η = 0.4 for the low and high noise populations, respectively. Correspondingly, the differential fitness curves displayed in Fig. 2d were obtained by evaluating the quantity ΔW(η,s) = W(η,s) − W(η ₀,s) where W(η,s) is the fitness of a population with variable high noise (η = 0.2, 0.3 or 0.4) and W(η ₀,s) is a reference population with low noise (η ₀ = 0.1).

A more realistic description of the relationship between cellular fitness w(x) and gene expression level x is a sigmoid function of the form:

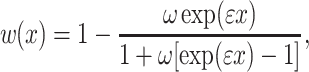4

where the ω and ε are phenomenological parameters with values ω = 0.001 and ε = 1. Using these parameters, a 50% reduction in fitness is achieved when x ≈ 6.91, which was chosen for the value of s _thr = 6.91 in all calculations.

To simulate the effects of prolonged stress, we assumed that the number of cells expressing at a given level x follows a standard exponential growth law:

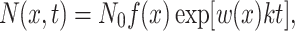5

where N(x,t) is the number of cells, N ₀ is the initial number of cells in the population and k is the growth rate in the absence of stress. The cell count histograms in Fig. 2c were obtained by solving Eq. (5) for t = 0, 20, 40 and 60 h using N ₀ = 10,000, k = 0.11 h⁻¹, and using Eqs. (2) and (4) to describe f(x) and w(x), respectively. The solution was rescaled to maintain a constant total number of cells at different times after stress was applied.

The adaptive phenotypic response of cell populations experiencing prolonged stress was quantified by calculating their adaptive drift, defined as the change in the population-averaged gene expression level over time. It is given by the equation:

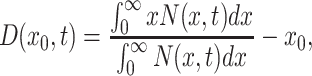6

where x ₀ is the initial population-averaged expression level. The adaptive drifts shown in Fig. 2f were obtained by systematically evaluating how stress modulates the mean of gene expression distributions over time as illustrated in Fig. 2e.

Molecular cloning and strain construction

The URA3 and yeast-enhanced green fluorescent protein (GFP) genes used in this study originated from pRS406 (Stratagene) and pEGFP3 (B. Cormack, Johns Hopkins University), respectively. The URA3 ^GFP fusion gene was constructed by PCR extension with overlapping primers and cloned into pRS403 (Stratagene), downstream of a tetracycline responsive element promoter (P _TRE) comprising the minimal CMV promoter containing seven tetracycline responsive elements, which originated from pCM179 (Euroscarf). The M2-variant of rtTA (Urlinger et al. 2000) was isolated by PCR from pUHrT16-16 (kind gift of C. Berens, Friedrich-Alexander Universität Erlangen-Nürnberg) and fused to a ~1 kb DNA fragment containing the GAL1 (P _GAL1) or the MYO2 (P _MYO2) promoter region, each isolated by PCR from genomic DNA of BY4741 (Open Biosystems). Strains used specifically to characterize the upstream component of the cascade (Fig. 2a) were obtained by replacing rtTA with GFP.

Vectors carrying the two variants of the full-length cascades were obtained by subcloning a DNA fragment containing the P _GAL1-rtTA or the P _MYO2-rtTA into the pRS406 derivative carrying P _TRE-URA3 ^GFP. Control vectors containing URA3 or GFP instead of URA3 ^GFP were obtained analogously to the P _GAL1-rtTA/P _TRE-URA3 ^GFP vector. All constructs were integrated into the ade2 locus of BY4741 by PCR-mediated gene disruption using the yeast HIS3 gene for auxotrophic selection. Proper gene disruption and expression cassette insertion was confirmed by visual inspection of colony pigmentation and by PCR. Cross-comparison of growth and fluorescence of strains expressing GFP, URA3 or URA3 ^GFP, in media containing different concentrations of doxycycline, galactose and FOA indicates full functionality of the URA3 ^GFP fusion gene (data not shown).

Media and growth conditions

Cells were grown in minimal synthetic dropout medium without histidine supplemented with 49 mg/l adenine, 2% raffinose (Sigma–Aldrich), and varying concentrations of galactose (gal) and doxycycline (dox) (Sigma–Aldrich). Media containing gal and dox were inoculated using an overnight culture grown in the absence of gal and dox. After ~6–8 h of induction with gal and dox, optical density (OD) was quantified at 600 nm using a Perkin-Elmer Victor3V plate reader and the cultures diluted to an OD of ~0.1 using fresh media with the appropriate concentrations of gal and dox. The stress-inducing drug 5-fluoroorotic acid (FOA), obtained from Toronto Research Chemicals, was subsequently added at a final concentration of 500 μg/ml. All cultures were incubated at 30°C with shaking (250 rpm). Cell cultures were diluted into fresh media every 18–22 h in experiments involving long-term FOA exposure.

Quantitative assays

Fitness profiling was conducted by measuring OD at regular intervals by spectrophotometry. The OD values were used to estimate the absolute cell count per unit volume based a correlation curve estimated by flow cytometry using Flow-Count Fluorospheres (Beckman-Coulter). Doubling times T were calculated from the equation T(t) = t ln(2)/[ln(CC _t)−ln(CC ₀)] where CC ₀ and CC _t are the initial cell count and the cell count at time t, respectively.

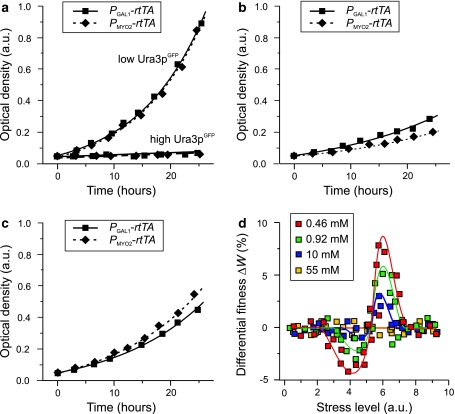
We defined fitness as the doubling time of URA3 ^GFP expressing strains relative to otherwise isogenic control strains that express GFP instead of URA3 ^GFP, under identical conditions. The level of stress s experienced by URA3 ^GFP expressing strains was estimated by the mode of cell count distributions of Ura3p^GFP abundance, assayed by flow cytometry. Specifically, the stress level was calculated as s = μ/(1 + η ²)^2/3, where μ is the mean fluorescence signal and η the coefficient of variation (noise). The differential fitness between strains carrying P _GAL1-rtTA/P _TRE-URA3 ^GFP and P _MYO2-rtTA/P _TRE-URA3 ^GFP (Fig. 5d) was evaluated for comparable levels of stress such that s deviated by less than 5%.

Fig. 5.

Impact of elevated extrinsic noise at different levels of stress. a–c Growth curves for the P _GAL1-rtTA strain (high noise) and the P _MYO2-rtTA reference strain (low noise). Both strains were grown in synthetic minimal media containing 0.46 mM gal and 500 μg/ml FOA with variable dox concentrations to achieve similar mean URA3 ^GFP expression levels. Solid curves were obtained from estimated doubling times. a Growth curves when expression is very high or very low, corresponding to severe and no stress, respectively. b Growth curves when expression is relatively high (high stress). c Growth curves when expression is relatively low (low stress). d Differential fitness calculated from measurements of strain doubling times for four different gal concentrations and varying levels of URA3 ^GFP expression (see text). Solid curves highlight trends in the data

Flow cytometry was carried out on a Beckman-Coulter FC500 MPL equipped with a 488 nm laser and calibrated using PeakFlow FC Reference Beads (Molecular Probes). Cells were typically gated to capture 70–80% of the population by autogating in the FS/SS plane. The mean fluorescence and coefficient of variation were calculated for GFP emission levels in the FL1 channel (510–540 nm filter) using the CXP Analysis 2.1 package (Applied Cytometry Systems), for populations typically of 20,000 cells. Staining with Trypan Blue (Fluka) was done as described (Martegani et al. 1993). Viable cells were distinguished from non-viable cells by gating in the SS/FL4 (740–770 nm filter) plane.

Microscopy was performed with a Zeiss Axioscope 2 instrument using Nothern Eclipse analyzing software (Empix Imaging Inc). Viable and inviable cells were separated using a 590 nm excitation/615 nm emission filter set. Ura3p^GFP fluorescence was quantified using a 490 nm excitation/525 nm emission filter set.

Results and discussion

Modeling heterogeneous population dynamics

We previously proposed a general phenomenological model to quantify the differential phenotypic impact of noise in the expression of a stress-resistance gene (Fraser and Kærn 2009). In this model, the effect of acute stress is determined solely by the distribution of gene product expressed within the cell population when stress is applied, and is independent of the intrinsic or extrinsic mechanisms that give rise to variability in gene expression.

In the present study, we analyzed a model describing the phenotypic impact of noise in the expression of a stress-inducing gene. The basic principle of the model is illustrated in Fig. 2a and b. The only difference between this model and the model analyzed by Fraser and Kærn (2009) is that cells expressing below a certain threshold are viable while those expressing above it are unable to reproduce. Figure 2a compares low and high noise gene expression distributions under severe stress where most cells are unable to reproduce owing to their high levels of gene expression. In this case, the high noise population has a higher number of viable cells than the low noise population as more cells express the stress-inducing gene at low levels. Increased noise thus provides a fitness advantage. In contrast, in Fig. 2b, most cells express at relatively low levels and the stress experienced by the two populations is fairly low. Here, only a small fraction of cells are unable to reproduce. However, this fraction is greater in the high noise population, and the population with low gene expression noise has a fitness advantage. The impact of varying stress levels on the fitness of low (η = 0.1) and high (η = 0.4) noise populations is further quantified in Fig. 2c, where the stress level is defined by the most likely level of gene expression within the population (see “Methods”). In this plot, the differential fitness ΔW is defined as the difference in fitness between the high and the low noise populations. Gene expression noise is advantageous at stress levels where ΔW > 0 and disadvantageous at stress levels where ΔW < 0.

The model predicts that the magnitude of the advantage afforded by noise under high stress is directly related to the magnitude of the noise. This is illustrated in Fig. 2d, which shows differential fitness ΔW as a function of the level of stress imposed on populations with highly variable gene expression noise (given by η = 0.2, 0.3 and 0.4) relative to a reference strain with low, constant noise (given by η ₀ = 0.1). Quantitatively, this plot reiterates that noise-dependent fitness advantages are potentially associated with a cost; while increasing noise amplifies the fitness advantage at high stress, it simultaneously lowers the resistance of the population to low stress, resulting in a fitness disadvantage of increased magnitude.

To explore the potential effects of gene expression noise on the phenotypic plasticity of cell populations under prolonged stress, we extended the model to incorporate population dynamics. This was achieved by allowing cells with advantageous gene expression levels to proliferate, and by assuming that daughter cells inherit the expression level of their mother. The model predicts that a significant modulation of the expression distribution of the stress-inducing gene will occur under prolonged, intermediate levels of stress. An example is given in Fig. 2e, which illustrates how an initial population distribution with relatively high gene expression changes over time following stress exposure. The distributions displayed were calculated from Eq. (5) at different time points with an initial distribution given by Eq. (2) using a mean expression of μ = 15 (arbitrary units) and noise of η = 0.40. Under these conditions, prolonged stress exposure causes a transient bimodal population response whereby a low expressing subpopulation gradually emerges and ultimately dominates the population. In contrast, very low or very high levels of stress are predicted not to change the initial population distribution (data not shown) since cells are either unaffected or unable to reproduce, respectively.

To evaluate the adaptive population response illustrated in Fig. 2e in a more systematic manner, we defined the adaptive drift as the change in mean expression over time. This drift is defined in Eq. (6). In Fig. 2f, we illustrate the adaptive drift calculated at different time points after stress exposure for a low (η = 0.10) and a high noise (η = 0.40) population. The curves indicate significant differences in phenotypic plasticity between the low and the high noise populations. Specifically, the high noise population adapts to the stress significantly faster than that of the low noise population, over a significantly broader range of initial expression levels. Thus, the model predicts that increased expression noise of a stress-related gene should increase the adaptive potential of an organism exposed to drug-induced stress over long time periods.

Synthetic network characterization

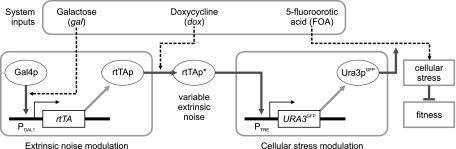
To explore the validity of the model predictions in “Modeling heterogeneous population dynamics”, we constructed a two-step gene regulatory cascade (Fig. 3) to control the level of extrinsic noise transmitted to the expression of a stress-inducing gene. In this cascade, the doxycycline (dox) inducible transcriptional activator rtTAp controlled the expression of a fluorescently labeled orotidine-5′-phosphate decarboxylase (Ura3p^GFP) from the P _TRE promoter (Gari et al. 1997; Urlinger et al. 2000). The Ura3p^GFP enzyme converts 5-fluoroorotic acid (FOA) to 5-fluorouracil, which is a highly effective toxin causing significant cellular stress and inhibiting cell division in a dose-dependent manner. Hence, in the presence of FOA, cells expressing Ura3p^GFP at high levels will grow slower than cells expressing the enzyme at low levels.

Fig. 3.

Synthetic circuit used to control extrinsic regulatory noise and the level of cellular stress in the presence of FOA. Noise in rtTA expression is modulated by gal, which induces the Gal4p-regulated P _GAL1 promoter, and by dox, which binds to and activates rtTAp. The activated regulator (rtTAp*) in turn induces transcription of the URA3 ^GFP gene from the P _TRE promoter. The Ura3p^GFP protein converts FOA into a toxin that causes stress and reduces fitness

To study the impact of gene regulatory noise transmitted to the URA3 ^GFP gene, we created two nearly isogenic yeast strains; a test strain with variable extrinsic noise and a reference strain with constant low extrinsic noise. These strains differ only in the upstream cascade component, namely the promoter driving the expression of the rtTA regulator of URA3 ^GFP expression. For the test strain with high extrinsic noise, we chose to express rtTA from the P _GAL1 promoter since the noise generated by this promoter has previously been shown to be quite high and to change significantly when the extracellular galactose (gal) concentration is varied (Blake et al. 2003, 2006; Raser and O’Shea 2004). For the reference strain with low, constant extrinsic noise, we chose to express rtTA from the P _MYO2 promoter since this promoter has been associated with relatively low noise (Becskei et al. 2005).

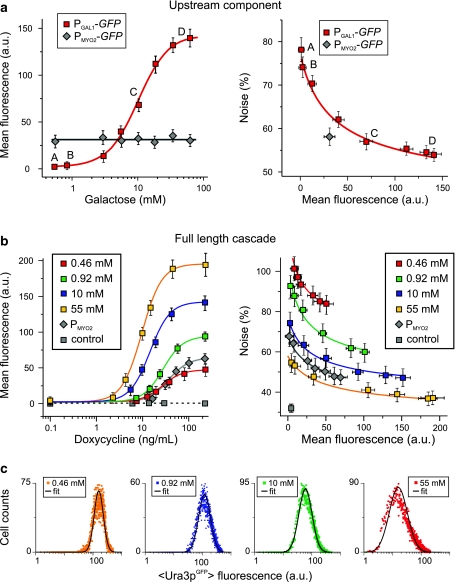
As a preamble, we characterized the expression from the P _GAL1 or P _MYO2 in experiments where the two promoters were used to drive the expression of GFP only. Fluorescence was measured for strains carrying P _GAL1-GFP or P _MYO2-GFP, grown in media containing different concentrations of gal (Fig. 4a). These experiments were used to identify four experimental conditions suitable for generating different levels of noise in rtTA expression in the full-length P _GAL1-rtTA/P _TRE-URA3 ^GFP cascade. Specifically, as illustrated in Fig. 4a, growth in media containing 0.46 or 0.92 mM gal gave rise to low P _GAL1-mediated expression with high noise (conditions A and B), whereas growth in media containing 10 or 55 mM gal was associated with high P _GAL1-mediated expression and relatively low noise (conditions C and D). The expression from P _MYO2 was not affected by changes in the gal concentration.

Fig. 4.

Characterization of the synthetic gene circuit. a Statistical characteristics of the upstream part of the cascade comprising the P _GAL1 or the P _MYO2 promoter. Error bars indicate the standard deviation (N = 3). Left: GFP expression at varying levels of gal. Right: Noise in GFP expression as a function of its mean expression level. Labels refer to gal concentrations used in subsequent experiments (A: 0.46 mM; B: 0.92 mM; C: 10 mM and D: 55 mM). b Statistical characteristics of the full-length cascade. Left: URA3 ^GFP expression at varying levels of dox at the indicated concentrations of gal. Right: Noise in URA3 ^GFP expression as a function of its mean expression level. Solid curves, obtained by fitting to Hill-type equations in the case of mean expression 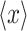and to the equation 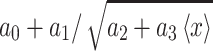in the case of noise, highlight the general trends in the data. c Cell count distributions of URA3 ^GFP expression, measured for four different gal concentrations and dox = 250 ng/ml, fitted to lognormal distributions

The effects of expressing rtTA from P _GAL1 or P _MYO2 on the expression of URA3 ^GFP expression in the full-length cascade are illustrated in Fig. 4b. In these experiments, two strains, carrying P _GAL1-rtTA/P _TRE-URA3 ^GFP and P _MYO2-rtTA/P _TRE-URA3 ^GFP, respectively, were grown in the four different concentrations of gal (identified in Fig. 4a) with variable concentrations of dox. As expected, increased expression of rtTA by induction of the P _GAL1 promoter with gal was associated with an increased sensitivity to dox induction. This increased sensitivity is manifested as a shift in the dox dose–response curves (Fig. 4b, left panel) whereby an increase in gal causes an increase in the URA3 ^GFP expression for a given level of dox. Also as expected, the mean expression of URA3 ^GFP was indepdent of the gal concentration when rtTA was expressed from P _MYO2.

Inspection of the combined effects of gal and dox induction on Ura3p^GFP expression noise (Fig. 4b, right panel) demonstrates contributions to population heterogeneity arising from both intrinsic noise, originating from the processes of URA3 ^GFP expression, and extrinsic noise, originating from variability in rtTA expression. In both strains, URA3 ^GFP expression noise was inversely correlated with the mean level of URA3 ^GFP expression, which is consistent with the expectation that intrinsic noise in URA3 ^GFP expression decreases as the number of Ura3p^GFP-encoding mRNA templates increases. While it is challenging to separate the contribution of noise in rtTA expression to overall population variability in URA3 ^GFP expression, the effects of elevated extrinsic noise are apparent when comparing Ura3p^GFP expression distributions measured when the strains are grown under conditions where P _GAL1 or P _MYO2 generates similar mean rtTAp levels, but different levels of rtTA expression noise. Specifically, similar Ura3p^GFP/dox dose–response curves were obtained for the P _GAL1-rtTA and P _MYO2-rtTA containing strains when grown in 0.46 mM gal (Fig. 4b, left panel). Nevertheless, the variability in Ura3p^GFP expression is ~50% lower in the P _MYO2-rtTA strain when compared to the P _GAL1-rtTA strain (Fig. 4b, right panel). Since the only difference between the two strains is the upstream promoter, we attributed this change in overall noise to differences in extrinsic noise associated with rtTA expression. In the following sections, we refer to the strains expressing rtTA from P _MYO2 and from P _GAL1 as the low and high noise strains, respectively.

Impact of noise under acute stress

In order to determine the impact of increased extrinsic gene expression noise under acute stress, we measured the fitness of the low and high noise strains the presence of FOA. These experiments were conducted at the four concentrations of gal associated with different levels of gene regulatory noise in the P _GAL1-rtTA strain, and by varying the concentrations of dox to modulate the level of FOA-dependent stress associated with URA3 ^GFP expression. All experiments used a constant concentration of FOA (see “Methods”). Fine-tuning of Ura3p^GFP expression distributions using dox was required to achieve compatibility in terms of the stress experienced by the two strains under otherwise identical growth conditions. The dox concentration used, typically between 1 and 50 ng/ml, had no impact on population fitness in the absence of FOA (data not shown). A gal concentration of 0.92 mM was used to generate high extrinsic noise in the P _GAL1-rtTA unless otherwise stated.

To quantify fitness, we systematically measured the optical density (OD) of cell cultures grown for up to 24 h at regular intervals. Representative growth curves are illustrated in Fig. 5a–c. These curves were obtained at similar initial ODs and mean Ura3p^GFP expression levels, allowing for direct comparison of growth of the low and high noise strains in the presence of FOA. While cell death may complicate the interpretation of OD-based growth curves, time-resolved microfluidics experiments indicated that acute FOA stress is primarily associated with delayed cell division and does not cause significant cell death (data not shown). In Fig. 5a, Ura3p^GFP expression is very high (high stress) or very low (low stress), and the growth curves for the low and high noise strains are indistinguishable. Hence, under these stress conditions, elevated extrinsic noise does not appear to have a significant effect on fitness. However, marked differences in the growth kinetics of the two strains can be observed at intermediate levels of URA3 ^GFP expression (Fig. 5b, c). On one hand, at high but permissive levels of stress (Fig. 5b), the high noise strain grows significantly faster than the low noise strain. This indicates there is a fitness advantage attributable to the increased extrinsic noise in the expression of rtTA from the P _GAL1 promoter. On the other hand, at relatively low levels of stress, the low noise strain grows faster indicating that the increased extrinsic noise associated with expression of rtTA from the P _GAL1 promoter imposes a fitness disadvantage (Fig. 5c).

To quantify the fitness impact attributable to the change in extrinsic noise, we calculated the difference in fitness between the high noise and low noise strains (Fig. 5d). This differential fitness ΔW was measured when the two strains were grown in 0.46, 0.92, 10 or 55 mM gal and variable concentrations of dox. To ensure comparable levels of URA3 ^GFP-induced stress, ΔW was calculated for conditions where different levels of dox yielded comparable initial expression distributions for specific gal concentrations. Moreover, to ensure that the different levels of dox did not introduce a bias in the results, the fitness of URA3 ^GFP-expressing strains was normalized to those of control strains in which URA3 ^GFP was replaced with GFP grown in identical conditions.

By plotting differential fitness (Fig. 5d), we confirmed that the fitness impact induced by increased noise in rtTA expression is dependent on the level of stress imposed by URA3 ^GFP expression. Indeed, the general shape of the differential fitness curves in Fig. 5d compares qualitatively with those predicted by the theoretical model (Fig. 2d). In the four gal concentrations tested, elevated extrinsic noise provides a selective advantage when the level of stress is above a certain threshold (~5 a.u.), yet poses a disadvantage below this threshold. Moreover, as predicted (Fig. 2d), the magnitude of these fitness effects correlates with the magnitude of the added extrinsic noise. Hence, increasing the level of noise not only increases the fitness advantage at high stress, but also increases the fitness disadvantage observed at low stress.

Impact of noise under prolonged stress

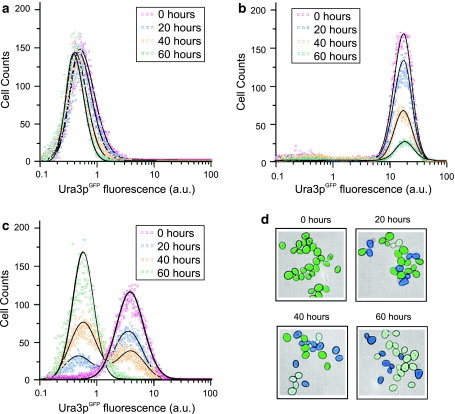
To experimentally characterize how extrinsic gene expression noise impacts adaptation to prolonged stress, we quantified how long-term exposure to FOA modified the population distribution of URA3 ^GFP expression. In these experiments, we combined the quantification of cell count distributions by flow cytometry with a cell viability assay to discriminate viable from inviable cells (see “Methods”). This was necessary since long-term FOA exposure, in contrast to its acute effect, is associated with significant rates of cell death. Representative cell count distributions obtained for the high noise strain at 0, 20, 40 and 60 h of FOA exposure are displayed in Fig. 6a–c. In Fig. 6a, URA3 ^GFP expression is relatively low, the vast majority of cells are viable, and there is little change in the cell count distribution over time. In Fig. 6b, URA3 ^GFP expression is relatively high, corresponding to all cells being subjected to a high level of stress. Here, the high level of stress causes massive cell death and a rapid decline in the number of viable cells over time. Nevertheless, URA3 ^GFP-expression within the surviving cells remains high. The observation of invariant expression distributions at both low and high levels of stress is consistent with the predictions by the theoretical model (see “Modeling heterogeneous population dynamics”).

Fig. 6.

Population dynamics under prolonged stress. a–c Cell count distributions of URA3 ^GFP expression within viable cells obtained by low cytometry for a low, b high and c intermediate initial levels of expression. The distributions were obtained for the high noise P _GAL1-rtTA strain after 0, 20, 40 and 60 h of exposure to 500 μg/ml FOA. Cells were grown in 0.92 mM gal and the initial expression level was modulated by varying the dox concentration. Solid curves are fits to Eq. (5). d Microscopy images illustrating the changes in single-cell expression during the response in (c)

In contrast to the invariant gene expression observed under low and high stress, prolonged exposure to moderate stress causes a dramatic change in the distribution of Ura3p^GFP over time. An example of this is given in Fig. 6c, which shows cell count distributions for the high noise strain after 0, 20, 40 and 60 h of FOA exposure. The observed adaptive phenotypic response is in remarkable resemblance of that predicted by the theoretical model for moderate prolonged stress (Fig. 2e). Specifically, the cell population undergoes a bimodal transition in which an initial distribution with relatively high URA3 ^GFP expression gradually diminishes, and a low URA3 ^GFP expressing subpopulation emerges. Ultimately, the population becomes indistinguishable from that observed under low stress conditions (Fig. 6a). The transient appearance of a mixed population containing both low and high URA3 ^GFP expressing cells was confirmed by microscopy (Fig. 6d). Interestingly, in parallel experiments (data not shown), the low noise strain was observed to display an adaptive response resembling that of the high noise strain.

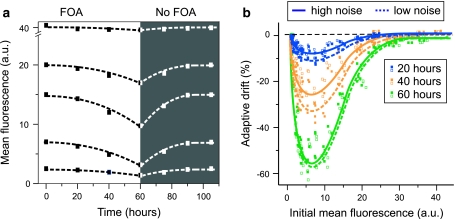
To characterize in further detail how elevated extrinsic noise contributes to the adaptive population response to prolonged FOA exposure, we first confirmed that the response is not due to spontaneous or FOA-induced mutagenesis. This was accomplished by demonstrating that the effect is FOA-dependent and reversible (Fig. 7a). We then systematically characterized the adaptive drift in URA3 ^GFP expression over time for the low and high noise strains. We defined the adaptive drift as the change in mean URA3 ^GFP expression relative to that of otherwise isogenic control strains expressing GFP instead of URA3 ^GFP, under identical growth conditions. These experiments were designed specifically to explore if increased population variability endows cell populations with increased adaptive potential and phenotypic plasticity, as predicted by the theoretical model (Fig. 2f). The observations for the high noise strain are in excellent agreement with the model predictions (Fig. 7b); a rapid and profound adaptive drift is observed when the initial mean URA3 ^GFP expression levels assume intermediate values. However, in contrast to the predictions of the model, the adaptive drifts measured for the low noise strain were very similar to those measured for the high noise strain, and thus no significant difference between the strains could be observed in terms of their ability to adapt to the imposed stress. In fact, the shift in mean expression may occur slightly faster in the low noise strain.

Fig. 7.

Adaptive population dynamics. a Changes in mean Ura3p^GFP expression following the addition and removal of 500 μg/ml FOA. Data was generated for the P _GAL1-rtTA strain using different concentrations of dox and fixed gal as described in Fig. 6. b Dependency between the initial mean Ura3p^GFP expression and the adaptive drift for the high noise P _GAL1-rtTA strain (open squared) and the low noise P _MYO2-rtTA strain (closed squares). Solid and broken curves highlight trends in the data

Conclusion

We have experimentally characterized how noise in a gene regulatory signal impacts the fitness of cell populations under acute and prolonged stress. Under acute stress conditions, our experiments confirm the prediction of a general, phenomenological model (Fraser and Kærn 2009; Zhang et al. 2009), that extrinsic gene expression noise provides a fitness advantage when cells are exposed to severe stress. This is consistent with the results reported for promoter-mediated, intrinsic noise by Blake et al. (2006), suggesting that several mechanisms could be targeted during evolution to optimize the population-variability in the expression of stress-related genes. Our experiments also confirmed a predicted tradeoff between the benefits and the costs of noise in the expression of stress-related genes; while increased noise increases the magnitude of the fitness advantage afforded under high stress condition, it also increases the magnitude of a fitness disadvantage under low stress conditions.

We extended the theoretical model to account for the effects of prolonged stress by assuming that beneficial expression levels can be stably inherited and maintained over successive cell generations. Experimentally, we observed alterations in gene expression distributions consistent with this model. Specifically, under prolonged, intermediate levels of stress, cell populations displayed profound phenotypic plasticity, which manifested as a change in their gene expression distribution towards expression levels supporting optimal fitness. In this case, the result of the prolonged stress was the emergence of a population with increased stress-resistance. While the mechanisms contributing to the observed phenotypic plasticity remain elusive, one possibility is that a slowly varying, inheritable epigenetic factor plays a key role in determining the level of gene expression in individual cells. In our model, such a factor is necessary to ensure that beneficial levels of gene expression are stably transmitted over one or more cell generations and the emergence of a stress-resistant cell population. This would also be consistent with the model recently proposed to account for the development of drug-resistant tumours in cancer progression (Brock et al. 2009). Further research is required to explore this hypothesis in detail.