Estimating the Parameters of Selection on Nonsynonymous Mutations in Drosophila pseudoobscura and D. miranda

Abstract

We present the results of surveys of diversity in sets of >40 X-linked and autosomal loci in samples from natural populations of Drosophila miranda and D. pseudoobscura, together with their sequence divergence from D. affinis. Mean silent site diversity in D. miranda is approximately one-quarter of that in D. pseudoobscura; mean X-linked silent diversity is about three-quarters of that for the autosomes in both species. Estimates of the distribution of selection coefficients against heterozygous, deleterious nonsynonymous mutations from two different methods suggest a wide distribution, with coefficients of variation greater than one, and with the average segregating amino acid mutation being subject to only very weak selection. Only a small fraction of new amino acid mutations behave as effectively neutral, however. A large fraction of amino acid differences between D. pseudoobscura and D. affinis appear to have been fixed by positive natural selection, using three different methods of estimation; estimates between D. miranda and D. affinis are more equivocal. Sources of bias in the estimates, especially those arising from selection on synonymous mutations and from the choice of genes, are discussed and corrections for these applied. Overall, the results show that both purifying selection and positive selection on nonsynonymous mutations are pervasive.

SURVEYS of DNA sequence diversity and divergence are shedding light on a number of questions in evolutionary genetics (for recent reviews, see Akey 2009; Sella et al. 2009). Two of the most important questions of this kind concern the distribution of selection coefficients against deleterious mutations affecting protein sequences and the proportion of amino acid sequence differences between related species that have been fixed by positive selection. Several different methods have been proposed for studying each of these questions, using different features of data on polymorphism and divergence at nonsynonymous and silent sites.

For example, the parameters of the distribution of selection coefficients against deleterious amino acid mutations have been estimated by contrasting the numbers of nonsynonymous and silent within-species polymorphisms and fixed differences between species (Sawyer and Hartl 1992; Bustamante et al. 2002; Piganeau and Eyre-Walker 2003; Sawyer et al. 2007); by fitting the frequency spectra of nonsynonymous and silent variants to models of selection, mutation, and drift (Akashi 1999; Eyre-Walker et al. 2006; Keightley and Eyre-Walker 2007; Kryukov et al. 2007; Boyko et al. 2008; Eyre-Walker and Keightley 2009); or by comparing levels of nonsynonymous and silent diversities between species with different population sizes (Loewe and Charlesworth 2006; Loewe et al. 2006). The results of these different approaches generally agree in suggesting that there is a wide distribution of selection coefficients against nonsynonymous mutations and that the mean selection coefficient against heterozygous carriers of such mutations is very small. The results imply that a typical individual from a human population carries several hundred weakly deleterious mutations (Eyre-Walker et al. 2006; Kryukov et al. 2007; Boyko et al. 2008); for a typical Drosophila population, with its much higher level of variability, the number is probably an order of magnitude greater (Loewe et al. 2006; Keightley and Eyre-Walker 2007).

The presence of this large load of slightly deleterious mutations in human and natural populations, most of which are held at low frequencies by natural selection, has many implications. From the point of view of understanding human genetic disease, it means that we have to face the likelihood that susceptibility to a disease can be influenced by variants at many loci, each with small effects (Kryukov et al. 2007). The pervasive presence of deleterious mutations throughout the genome contributes to inbreeding depression (Charlesworth and Willis 2009) and may mean that the effective population size is reduced by background selection effects, even in regions of the genome with normal levels of genetic recombination (Loewe and Charlesworth 2007). Their presence may contribute so strongly to Hill–Robertson effects (Hill and Robertson 1966; Felsenstein 1974) that they cause severely reduced levels of diversity and adaptation in low-recombination regions of the genome (Charlesworth et al. 2010) and create a selective advantage to maintaining nonzero levels of recombination (Keightley and Otto 2006; Charlesworth et al. 2010). In addition, having an estimate of the distribution of selection coefficients against deleterious nonsynonymous mutations allows their contribution to between-species divergence to be predicted, providing a way of estimating the fraction of fixed nonsynonymous differences caused by positive selection (Loewe et al. 2006; Boyko et al. 2008; Eyre-Walker and Keightley 2009).

It is thus important to collect data that shed light on the properties of selection against nonsynonymous mutations in a wide range of systems and also to compare the results from different methods of estimation, since they are subject to different sources of difficulty and biases. In a previous study, we proposed the use of a comparison between two related species with different effective population sizes for this purpose (Loewe and Charlesworth 2006; Loewe et al. 2006), using Drosophila miranda and D. pseudoobscura as material. These are well suited for this type of study, as they are closely related, live together in similar habitats, and yet have very different levels of silent nucleotide diversity, indicating different effective population sizes (N_e). This study was hampered by our inability to compare the same set of loci across the two species and by the small number of loci that could be used. We here present the results of a much larger study of DNA variation at X-linked and autosomal loci for these two species, using D. affinis as a basis for estimating divergence. We compare the results, applying the method of Loewe et al. (2006) with that of Eyre-Walker and Keightley (2009) for estimating the distribution of deleterious selection coefficients and with McDonald–Kreitman test-based methods for estimating the proportion of nonsynonymous differences fixed by positive selection. While broadly confirming the conclusions from earlier studies, we note some possible sources of bias and describe methods for minimizing their effects.

MATERIALS AND METHODS

Fly stocks:

The following 16 lines each of D. miranda and D. pseudoobscura (with collection locations) were used (Bartolomé and Charlesworth 2006): D. miranda 0101.3, 0101.4, 0101.5, 0101.7 (Port Coquitlam, BC, Canada), 0101.9, MA28, MA32, MA03.1, MA03.3, MA03.4, MA03.5, MA03.6 (Mather, CA), SP138, SP235, SP295 (Spray, OR), and MSH22 (Mt. St. Helena, CA); and D. pseudoobscura MV1, MV2, MV5, MV6, MV7, MV8, MV10, MV11, MV15, MV18, MV19, MV21, MV23, MV25, MV28, and MV32 (collected from Mesa Verde National Park, Mesa Verde, CO, in July 2005 and kindly provided by Stephen Schaeffer). A single D. affinis line was also used as an outgroup (no. 0141.2, Drosophila Species Resource Center).

Gene selection and primer design:

Polymorphism data were collected from both D. miranda and D. pseudoobscura for a total of 82 coding regions, including 41 loci on chromosome XL (homologous to the X chromosome in D. melanogaster) and 41 loci on chromosome 4 (homologous to chromosome 2L in D. melanogaster). Of these, 37 X-linked and 39 autosomal loci were also sequenced from the single D. affinis line. The D. melanogaster genome (http://flybase.org, Release 5.1) was used to identify coding regions containing an exon of at least 1 kb in length, for which the homologous D. pseudoobscura was identified using BLAST (http://flybase.org/blast/). Following the procedure of Vicoso et al. (2008), primers were designed in regions conserved between D. melanogaster and D. pseudoobscura using the Primer3 program (Rozen and Skaletsky 2000), to amplify between 400 and 650 bp. Details of all 82 loci can be found in supporting information, File S1.

DNA extraction, PCR, and sequencing:

Genomic DNA was extracted from a single male fly from each line using the Puregene DNA extraction kit (Qiagen, Crawley, West Sussex, UK). The polymerase chain reaction was used to amplify each region, and primers and unincorporated nucleotides were then removed using exonuclease I and shrimp alkaline phosphatase. Fragments were directly sequenced on both strands, using the Big Dye cycle sequencing kit (Version 3.0; Applied Biosystems, Foster City, CA), and run on an ABI 3730 capillary sequencer. Sequence trace files were edited using Sequencher (Gene Codes Corporation, Ann Arbor, MI). For the autosomal data, heterozygotes were identified from double peaks in the sequencing traces, and one allele was randomly discarded. For the polymorphism data on each locus, sequences from each ingroup species were aligned by eye, along with one randomly selected sequence from the other ingroup species and the single D. affinis sequence, where available. These alignments were then realigned using MUSCLE (http://www.drive5.com/muscle), with adjustments to preserve reading frames.

Population subdivision in D. miranda:

Given that the D. miranda lines sampled come from three geographic locations, tests for subdivision between different populations were carried out. For each locus, two different population differentiation statistics were calculated: Hudson's (2000) nearest neighbor statistic (S_nn) and K*_ST (Hudson et al. 1992), both calculated using DnaSP version 5 (Librado and Rozas 2009). Significance values for each statistic were obtained by permutation tests with 1000 replicates. This analysis was carried out with the lines divided into two groups [British Columbia (BC) and Oregon (OR) lines in one group and California (CA) lines in one group] and three groups (BC, OR, and CA lines separately) for comparison.

Polymorphism and divergence analysis:

The estimated number of synonymous and nonsynonymous sites, average pairwise diversity (Nei 1987, p. 256), average divergence from D. affinis, counts of the number of segregating polymorphisms, and the statistic Tajima's D (Tajima 1989) were calculated using a library of Perl scripts (“polyMORPHOrama”) written by Doris Bachtrog and Peter Andolfatto (Haddrill et al. 2008). An alternative measure of nucleotide diversity, θ_W, based on the number of segregating polymorphisms in a sample (Watterson 1975), was also calculated. The numbers of synonymous and nonsynonymous sites were estimated using the method of Nei and Gojobori (1986), and divergence estimates were corrected for multiple hits using a Jukes–Cantor correction (Jukes and Cantor 1969) and Kimura's two-parameter method (Kimura 1980). There was little difference between the results from these two different methods. To test for heterogeneity in levels of polymorphism relative to divergence at synonymous sites among loci, we carried out multilocus HKA tests (Hudson et al. 1987), using Jody Hey's program (http://genfaculty.rutgers.edu/hey/software#HKA). This program was also used to test the significance of Tajima's D values at synonymous sites via coalescent simulations, although it should be noted that this is conservative, since the simulations do not incorporate recombination.

Estimating the distribution of mutational effects and proportion of adaptive substitutions using the Loewe et al. method:

We estimated the strength of purifying selection and the fraction of positively selected amino acid substitutions using the method of Loewe et al. (2006). The method estimates the parameters of the probability distribution, φ(s), of heterozygous selection coefficients against deleterious nonsynonymous mutations using DNA sequence diversity data from two species with different N_e values. Full details are given in the original article. Combining the estimates of φ(s) with the observed long-term average K_A/K_S between D. miranda and D. affinis, together with an assumed ancestral N_e, allows us to estimate the fraction (α) of nonsynonymous substitutions that are not explained by the flux of mutations at sites subject to purifying selection; these are probably caused by the fixation of advantageous mutations. As previously, the statistical error of our estimates was assessed by the conservative procedure of bootstrapping across genes.

We assumed two different forms for φ(s), both of which allow for the possibility of a highly leptokurtic distribution of selection coefficients. The first is the lognormal distribution

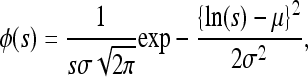(1)

where μ and σ are the arithmetic mean and standard deviation of the natural logarithm of s. We report the location parameter μ_g (the geometric mean of s = median = exp μ) and the shape parameter σ_g (exp σ), which give the limits of 68% of the probability mass by multiplying or dividing μ_g by σ_g. The arithmetic mean and standard deviation of s can be found from μ and σ by standard formulas, but are not shown here, because the truncation procedure described below implies that they are not very meaningful.

We also used the gamma distribution

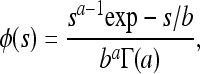(2)

where a and b are the shape and location parameters of the gamma distribution and Γ(a) is the gamma integral. The arithmetic mean of s is given by ab and the variance by ab².

For both types of distribution, we changed values of s that exceed 1 down to 1, so that they are classed as dominant lethals, since selection coefficients >1 are not biologically meaningful. All the distributional parameters are reported for the truncated distributions.

This method critically depends on the existence of significant differences in N_e between species, as estimated from synonymous site diversity, to estimate φ(s). Approximate mutation–selection–drift equilibrium in the contemporary populations and independence among polymorphisms at different sites are assumed. For this reason, for all three methods for estimating selection parameters that we used, we removed genes that showed unusually high or low synonymous diversities in either of the two species on the basis of the HKA test; using the D. pseudoobscura gene designations, these were GA15909, GA17538, GA21767, GA13913, GA12872, and GA14306 on the X chromosome and GA21851, GA10957, and GA13976 on the autosome. For the results shown in Table 3, we also removed genes where there was synonymous site diversity in D. miranda but not in D. pseudoobscura, since this also suggests the occurrence of a gross violation of equilibrium in the latter species. These genes are GA14705 on the X chromosome and GA17553, GA19427, GA19649, GA12147, GA12722, and GA20117 on the autosome. Following Loewe and Charlesworth (2006), we also eliminated all bootstraps where the ratio of mean nonsynonymous to mean synonymous diversity was lower for D. miranda than D. pseudoobscura, since meaningful parameter estimates cannot be generated in these cases.

TABLE 3.

Distributional statistics and estimates of α from the LCBN method

Model/fit	Shape	Location	Species Ne (×103)	Nes (am)	Nes (hm)	Nes (5%)	Nes (95%)	CV	cne%	αmir%, αpse%	α0.2 M%, α1 M%
X
Lognor 67.9%	49.8 (4.50/734)	0.00165 (3.83 × 10−5/0.19)	mir: 292 (215/379)	27,500 (36.7/142,000)	14.4 (5.08/28.3)	2.31 (1.12/7.01)	292,000 (141/346,000)	2.62 (0.968/7.91)	4.03 (1.71/5.71)	33.9 (2.54/66.5)	19.3 (−13.7/44.6)
			pse: 1,200 (1,010/1,440)	111,000 (153/562,000)	25.3 (14.7/42.8)	5.46 (3.00/16.2)	999,000 (1,810/2,190,000)	2.66 (0.983/8.03)	1.75 (1.24/2.98)	71.1 (51.8/96.3)	67.6 (48.9/94.7)
Gamma 83.6%	0.513 (0.153/1.43)	0.00137 (2.64 × 10−5/4,300)	mir: 292 (210/372)	213 (12.0/220,000)	13.6 (4.98/69.6)	2.48 (1.27/95.5)	819 (32.6/301,000)	1.36 (0.525/1.73)	3.75 (1.47/5.51)	38.4 (11.0/69.6)	25.2 (1.04/52.3)
			pse: 1,200 (1,000/1,440)	860 (48.4/854,000)	27.0 (15.8/88.9)	6.44 (3.83/225)	3,360 (126/1,190,000)	1.38 (0.534/1.76)	1.81 (0.207/3.65)	70.4 (42.2/95.3)	67.5 (40.5/93.9)
A
Lognor 57.1%	4.03 (2.24/49.3)	2.72 × 10−5 (1.34 × 10−5/0.00157)	mir: 380 (290/462)	27.7 (7.13/32,200)	4.92 (3.45/14.6)	1.20 (1.00/2.55)	106 (19.4/313,000)	2.42 (0.955/8.45)	1.67 (0.386/4.55)	53.9 (−10.5/79.0)	−15.3 (−81.4/27.7)
			pse: 1,800 (1,530/2,020)	129 (34.4/151,000)	19.1 (14.3/30.5)	4.81 (3.26/8.53)	502 (90.4/1,480,000)	2.44 (0.957/8.56)	0.061 (0.001/1.59)	97.6 (64.8/99.9)	91.6 (50.4/99.2)
Gamma 65.4%	1.60 (0.470/2.86)	1.64 × 10−5 (5.55 × 10−6/0.00255)	mir: 380 (287/470)	10.1 (5.77/513)	4.85 (3.50/17.6)	1.48 (1.15/3.62)	26.4 (12.3/2,030)	0.78 (0.587/1.39)	1.31 (0.318/4.27)	65.1 (5.08/87.5)	10.1 (−53.2/51.4)
			pse: 1,800 (1,540/2,050)	47.3 (29.1/2,130)	19.6 (14.7/38.1)	6.04 (4.08/12.3)	125 (62.7/8,450)	0.79 (0.592/1.41)	1.11 (0.004/1.84)	96.9 (60.1/99.8)	92.2 (46.3/98.9)

The computations assume an effective mutation rate of 4 × 10⁻⁹/site/generation, a mutational bias of κ = 2, the absence of completely neutral mutations, and N_es = 0.5 as the border with effective neutrality (Loewe et al. 2006). The values are point estimates for genes in the curated data set for D. miranda (mir) and D. pseudoobscura (pse); parentheses give the lower 5th percentiles and the upper 5th percentiles from the bootstraps that could be fitted. The left-hand column indicates the type of distribution fitted, and the percentage of 1000 bootstraps that could be fitted. N_e gives the estimated current N_e in thousands for the corresponding species; N_es (am), (hm), (5%), and (95%) are the arithmetic mean, the harmonic means, and the lower and upper 5th percentiles of distribution of the product of N_e and s for effectively deleterious but nonlethal selection coefficients; CV is the corresponding coefficient of variation (ratio of standard deviation to mean) of the truncated distribution; c_ne is the fraction of effectively neutral nonsynonymous mutations; and α is the estimated proportion of nonsynonymous substitutions between the two focal species and D. affinis that were fixed by positive selection, where mir and pse indicate estimates using the N_e estimates for the two species, and 0.2 M and 1 M fix N_e at 200,000 and 1,000,000, respectively.

There is a technical point about the estimation of N_es values for X-linked loci that should be noted. For the semidominant selection model assumed here, the rate of change of the frequency of a deleterious X-linked allele (with equal homozygous and hemizygous selection coefficients in females and males, respectively) is given by Δx_X = −4sx(1 − x)/3, whereas the autosomal equation is Δx_A = −sx(1 − x) (Vicoso and Charlesworth 2009). The program for estimating s assumes the latter expression for both X-linked and autosomal loci. The estimates of N_e for the X and the autosome are based on the infinite-sites equation for expected nucleotide site diversity, π = 4N_eμ (Kimura 1971), assuming the same mutation rate (μ) for males and females. Since the effective sizes for the X in both species on this basis are found to be nonsignificantly different from three-quarters of the autosomal values (see results), the N_es values for the X chromosome can be regarded as being measured on the same scale as for the autosomes. The same applies to the method of Eyre-Walker and Keightley (2009), which we now describe briefly.

Estimating the distribution of fitness effects and proportion of adaptive substitutions using the Eyre–Walker/Keightley method:

We also used the method of Eyre-Walker and Keightley (2009), an extension of the method of Keightley and Eyre-Walker (2007), to estimate the distribution of fitness effects of new amino acid mutations. The method uses a maximum-likelihood approach based on transition matrix calculations of population trajectories. It estimates the parameters of the distribution of selection coefficients, while simultaneously estimating the parameters of a demographic model that allows a population size change at some time in the past. This is done using the allele frequency distributions for selected (zerofold) and putatively neutrally evolving sites (fourfold degenerate synonymous sites in this case), taken across loci. It should be noted that Keightley and Eyre-Walker (2007) define s as the selection coefficient against homozygotes for the deleterious allele; this value is therefore one-half the value for the Loewe et al. (2006) method, since both methods assume semidominance. We use the latter definition here.

With this method, nonsynonymous mutations are assumed to have unconditionally deleterious effects and are drawn from a gamma distribution, the parameters of which are estimated along with the demographic parameters reflecting the relative difference between ancestral and current population sizes and the number of generations since the estimated change. These parameters are then used to estimate the average fixation probability of a selected mutation. This can be combined with an estimate of the mutation rate per site (proportional to the divergence at neutrally evolving sites) to estimate the expected divergence at selected sites due to the fixation of deleterious mutations, in the absence of the fixation of advantageous mutations. The proportion of adaptive substitutions (α) can then be estimated from the difference between the observed and expected between-species divergence at selected sites. We estimated 95% confidence intervals on all parameters by bootstrapping by locus 1000 times.

Estimating the proportion of adaptive substitutions using the Fay, Wyckoff, and Wu method:

For comparison, we also estimated α using the method of Fay et al. (2002), an extension of the McDonald–Kreitman approach (Mcdonald and Kreitman 1991) that uses the ratio of the number of polymorphic and divergent sites summed across loci, for putatively neutral (synonymous) and putatively selected (nonsynonymous) sites. The number of divergent sites at a locus was corrected for multiple hits using the Jukes–Cantor correction (Jukes and Cantor 1969), and 90% confidence intervals for α were estimated using a nonparametric bootstrapping method, with resampling by site (Haddrill et al. 2008). We calculated α after excluding singleton polymorphisms, since these are likely to reflect weakly deleterious mutations segregating in the population, which cause a downward bias in estimates of α (Fay et al. 2002; Charlesworth and Eyre-Walker 2008). We also calculated α using a subset of synonymous changes: those involving changes from preferred to preferred or unpreferred to unpreferred codons, using codon preferences for D. pseudoobscura, as classified in polyMORPHOrama.

RESULTS

Population subdivision in D. miranda:

The results of the population subdivision analyses are shown in File S2 and Figure S1. Although a small number of loci show some evidence for low-level population subdivision, only one locus (GA10135) exhibits significant levels of differentiation when the number of comparisons is taken into account. We can therefore conclude that the departures from neutral expectations detailed below cannot be explained by population subdivision within the D. miranda sample, in line with previous results for this species (Yi et al. 2003).

Polymorphism and divergence data:

Table 1 shows the unweighted means and standard errors for the polymorphism and divergence statistics for all the loci for which we obtained data on polymorphism in D. pseudoobscura and D. miranda, together with a single sequence from D. affinis. We found several loci that yielded ostensibly significant departures from neutrality in one or the other of the two species on the basis of the HKA test (see materials and methods). Table 2 shows detailed polymorphism and divergence statistics for these loci individually. Since these loci are candidates for departure from equilibrium, our subsequent analyses are based on data sets from which they were removed, reducing the data set to 33 X-linked loci and 34 autosomal loci. These outlier genes will form the subject of a separate study.

TABLE 1.

Polymorphism and divergence statistics for X chromosomal and autosomal loci in D. pseudoobscura and D. miranda

	πA (%)	πS (%)	πA/πS	KA (%)	KS (%)	KA/KS	Tajima's D (Nonsyn)	Tajima's D (Syn)
X (n = 39)
mir	0.034 (0.011)	0.662 (0.161)	0.051 (0.021)	1.519 (0.233)	24.827 (1.231)	0.061 (0.010)	−0.503 (0.286)	−0.608 (0.163)
pse	0.066 (0.015)	1.779 (0.256)	0.037 (0.100)	1.486 (0.222)	25.458 (1.264)	0.058 (0.010)	−0.824 (0.129)	−0.775 (0.113)
A (n = 37)
mir	0.072 (0.017)	0.664 (0.125)	0.108 (0.034)	1.464 (0.260)	28.297 (1.356)	0.052 (0.010)	−0.598 (0.203)	−0.470 (0.155)
pse	0.066 (0.013)	2.265 (0.214)	0.029 (0.006)	1.510 (0.275)	29.288 (1.449)	0.052 (0.010)	−0.881 (0.158)	−0.862 (0.101)

Means with standard errors in parentheses were calculated directly in all cases except for the standard errors of the ratios π_A/π_S and K_A/K_S, which were calculated using the delta method (Bulmer 1980, p. 83). mir and pse refer to data for D. miranda and D. pseudoobscura, respectively. Nonsyn and Syn refer to statistics calculated for nonsynonymous and synonymous sites, respectively. π is pairwise nucleotide diversity (Nei 1987, p. 256). Nonsynonymous (K_A) and synonymous (K_S) divergence was estimated using the Jukes–Cantor correction for multiple hits (Jukes and Cantor 1969). The data are not corrected for within-species diversity.

TABLE 2.

Polymorphism and divergence statistics for X chromosomal and autosomal outlier loci excluded from the main analyses

	πA (%)	πS (%)	πA/πS	KA (%)	KS (%)	KA/KS	Tajima's D (Nonsyn/Syn)	Fay and Wu's H (Nonsyn/Syn)
X
GA15909
mir	0.000	1.878	0.000	1.883	24.981	0.075	NA/−1.223	0.000/−7.483
pse	0.058	5.670	0.010	1.414	24.534	0.058	−1.498/−0.531	−1.633/−11.167
GA17538
mir	0.084	3.726	0.022	1.219	31.579	0.039	−1.038/0.850	0.317/−5.850
pse	0.000	1.561	0.000	1.177	31.311	0.038	NA/−1.213	0.000/−3.209
GA21767
mir	0.138	3.700	0.037	0.955	35.472	0.027	1.066/0.321	0.242/−3.303
pse	0.337	7.605	0.044	1.525	39.134	0.039	−0.178/-0.681	−0.248/−6.419
GA13913
mir	0.000	0.000	NA	0.274	46.657	0.006	NA/NA	0.000/0.000
pse	0.000	0.000	NA	0.274	48.108	0.006	NA/NA	0.000/0.000
GA12872
mir	0.000	0.621	0.000	2.199	16.457	0.134	NA/−0.414	0.000/0.617
pse	0.069	4.390	0.016	2.233	16.717	0.134	−1.481/−0.726	0.264/3.077
GA14306
mir	0.000	3.106	0.000	1.596	20.236	0.079	NA/−0.099	0.000/−6.400
pse	0.000	1.121	0.000	1.914	17.068	0.112	NA/−1.849	0.000/−2.762
A
GA21851
mir	0.094	2.744	0.034	1.102	34.104	0.032	−1.038/−0.120	0.317/−0.833
pse	0.000	0.851	0.000	1.325	35.784	0.037	NA/−1.409	0.000/−4.495
GA10957
mir	0.000	0.000	NA	1.492	47.224	0.032	NA/NA	0.000/0.000
pse	0.000	0.353	0.000	1.194	48.728	0.024	NA/−1.697	0.000/−1.517
GA13976
mir	0.040	3.303	0.012	2.171	19.360	0.112	−1.159/1.076	0.124/−0.162
pse	0.184	3.771	0.049	2.250	17.002	0.132	−1.550/−0.992	0.550/2.950

Abbreviations and definitions are defined in Table 1. NA, statistic cannot be calculated due to lack of polymorphic sites.

There are several patterns in the polymorphism and divergence data that are worth noting before we describe the main results. First, the synonymous diversity on the X chromosome for the full data set is substantially lower than on the autosome in D. pseudoobscura and is slightly less than the autosomal value in D. miranda. The significance of this difference between X and autosomal diversities was tested on the reduced data set used in the further analyses (after removing loci with significantly high or low diversities; see materials and methods) by the method of Bartolomé et al. (2005), using inverse variance-weighted estimates of π_S. For D. pseudoobscura, the means (with standard errors) of the weighted π_S values in percentages were 1.49 ± 0.18 and 2.30 ± 0.21 for the X and autosome, respectively, with an X/autosome ratio of 0.634 ± 0.098. Using bootstrapping across genes for the data set after removal of significant outliers on the basis of the HKA test (see materials and methods), the mean difference in weighted values between the X and the autosome was significant at the 1% level. Very similar results were obtained using unweighted diversity estimates. If the X chromosome diversities are multiplied by 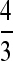, to adjust for the fact that the effective population size for the X chromosome is three-quarters of that for the autosomes with random variation in offspring number in both sexes (Wright 1931), the mean for the X becomes 1.99% and there is no significant difference from the autosomal value. For D. miranda, the weighted π_S values in percentages were 0.387 ± 0.096 and 0.540 ± 0.085 for the X and the autosome, respectively. While these are not significantly different from each other, weighting the X chromosome diversities by 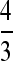yields a mean of 0.529, which is extremely close to the autosomal value.

However, there is also an apparent difference in synonymous site divergence between the X and the autosome for D. pseudoobscura vs. D. affinis, with means in percentages for the reduced data set (weighting each gene by its number of synonymous sites) of 25.3 ± 1.08 and 28.9 ± 1.39, respectively. K_S for the X is thus ∼88% of the value for the autosome. This difference is borderline significant at the P < 0.05 level on a two-tailed t-test or by bootstrap resampling. If the effect were real, and caused by a lower mutation rate on the X (Vicoso and Charlesworth 2006), we should use a weight of 4/(3 × 0.88) = 1.52 as an adjustment for X-linked diversity instead of 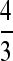. This brings the adjusted X mean weighted synonymous diversities up to 2.26 and 0.603% for D. pseudoobscura and D. miranda, respectively.

There is thus no evidence in either species for an elevation of the effective population size of the X chromosome above three-quarters of the autosomal value, in contrast to what was proposed previously on the basis of smaller data sets (Yi et al. 2003; Bartolomé et al. 2005) and that has been found in the Zimbabwe population of D. melanogaster (Andolfatto 2001; Hutter et al. 2007), but is in agreement with the results of Bachtrog and Andolfatto (2006) for D. miranda. Mean synonymous diversity is much higher for D. pseudoobscura than for D. miranda, with a D. pseudoobscura/D. miranda ratio of 3.75 for the X chromosome and 4.26 for the autosome, in agreement with previous results (Yi et al. 2003; Loewe et al. 2006).

In contrast, weighted mean nonsynonymous diversities for the reduced data set are similar for the X chromosome and the autosome in D. pseudoobscura (percentage values of 0.064 ± 0.015 and 0.064 ± 0.013, respectively). They are smaller, but not significantly so, for the X chromosome vs. the autosome in D. miranda (values of 0.033 ± 0.012 and 0.074 ± 0.018, respectively). The differences in π_A values between the two species are not significant in either case.

There is no difference in K_A between the X and the autosome for nonsynonymous divergence between D. pseudoobscura and D. affinis (the means of the percentage values for the reduced data set, weighted by numbers of nonsynonymous sites, are 1.51 ± 0.26 and 1.47 ± 2.95, respectively). The ratios of weighted mean K_A to mean K_S for the X and autosomes are also very similar (5.97 and 5.12%, respectively), so that there is no evidence for a faster-X effect of the type that has been much discussed in the literature (Mank et al. 2010). Other aspects of the polymorphism and divergence data will be discussed elsewhere.

Estimates of φ(s) and α from the Loewe et al. method:

The results of applying the method of Loewe and Charlesworth (2006) and Loewe et al. (2006) (referred to as the LCBN method from now on) for estimating α and the parameters of φ(s), described in materials and methods, are shown in Table 3. We also estimated the fraction of mutations that are effectively lethal (s ≥ 1); the point estimates of this are generally close to zero. A significant proportion of the bootstrapped values of the proportion of lethals were implausibly high, when compared with the estimates for the fraction of effectively lethal dominant mutations given by Loewe and Charlesworth (2006), but we did not exclude these cases from our bootstraps.

As in our previous work, some of the parameters are estimated quite precisely, and others have high statistical error. Among the former is the fraction of nonlethal mutations that are effectively neutral with respect to their behavior as polymorphic variants (c_ne), i.e., for which N_es ≤ 0.5, whose upper 5th percentiles are mostly <5%. The rationale for choosing this cutoff is that this intensity of selection yields equilibrium levels of nucleotide site diversity and rates of evolution that are at least 90 and 75% of the neutral value, given plausible mutational parameters (McVean and Charlesworth 1999). As expected from its larger N_e, the point estimates and upper percentiles of c_ne for D. pseudoobscura are lower than for D. miranda. This is in general agreement with the previous results for these species, but we now have more precise and lower overall point estimates for c_ne compared with Loewe and Charlesworth (2006). Most new amino acid mutations fall into the range in which selection significantly affects their behavior while they are segregating in the population.

Another parameter that is reasonably precisely estimated is the harmonic mean of N_es, equivalent to the product of N_e and the harmonic mean of s, s_h. Since φ(s) is assumed to be the same for both species, the differences between species in N_es_h mainly reflect the differences in the estimates of N_e. The point estimates and upper and lower percentile values for D. pseudoobscura are thus larger than for D. miranda. The bootstraps indicate that values <3 for D. miranda and 14 for D. pseudoobscura are unlikely to be valid, and values as high as 30 cannot be ruled out for D. pseudoobscura. The gamma and lognormal estimates are quite similar, and there are no obvious differences between the X and the autosome. These results also imply that the typical polymorphic, nonsynonymous mutation is under significant, although weak, selection.

Similarly, the results support the conclusion that there is a wide spread of selection coefficients among new amino acid mutations, although the confidence intervals on measures of this spread, such as the shape parameters of the two types of distribution and the coefficients of variation of s for nonlethal and nonneutral mutations, are fairly wide. For the autosomal loci, the distribution is apparently somewhat tighter than for the X-linked loci, although their bootstrap distributions overlap. The very noisy estimates of the arithmetic mean values of N_es for new mutations are also ostensibly lower for the autosome than for the X chromosome and for the gamma distribution than for the lognormal, but it is unclear whether these differences are meaningful.

We also used our data to estimate the proportion, α, of amino acid substitutions distinguishing the two focal species from D. affinis that were fixed by positive selection. This method uses the difference between the observed K_A/K_S and that predicted from the fraction of mutations subject to the distribution φ(s) that become fixed as a result of selection and/or genetic drift, so that the results are therefore very sensitive to assumptions about past effective population sizes (Loewe et al. 2006). For this reason, we used four different assumptions about ancestral N_e: they are equal to the point estimate for D. miranda, the point estimate for D. pseudoobscura (with different values for the X and the autosome), 2 × 10⁵, or 10⁶. As would be expected from the fact that more slightly deleterious mutations become fixed when N_e is low, the α-estimates are lower for the lower N_e values than for the higher ones. The diversity data show that D. miranda has a low N_e compared with most Drosophila species. In addition, the large negative Tajima's D values for synonymous sites in D. pseudoobscura (Table 1) strongly suggest a recent population expansion (see also the next section). An N_e of 10⁶ may represent a reasonable compromise among the various possibilities for the ancestor of both species. If this is correct, there is quite strong support for a high proportion of amino acid mutations having been fixed by positive selection, with point estimates of α for both the X and the autosomal data of between 70 and 90%, depending on the model for φ(s). The confidence intervals on these estimates are, however, large.

These results can be compared with those obtained from the less realistic but much simpler model proposed by Loewe et al. (2006), in which a fraction c_n of nonsynonymous mutations is assumed to be neutral in both species, and the rest are sufficiently strongly selected that they obey deterministic equations for their frequencies within populations (their Equations 1–4). For the X chromosome, this method yields estimates of N_es_h (where N_e is the value for D. miranda) of 19.9 (with lower and upper 5th percentiles of 9.62 and infinity) and of α of 0.656 (lower and upper 5th percentiles of 0.311 and 0.921); for the autosome, N_es_h = 8.80 (lower and upper 5th percentiles of 5.60 and 16.70) and α = 1 (lower and upper 5th percentiles of 0.786 and 1.34). In both cases, the estimates of c_n for D. miranda do not differ significantly from zero and have upper 5th percentiles of 0.045 and 0.011, for the X and the autosome, respectively. The results are thus in fairly good agreement with those obtained with the more complex method, consistent with the low values of the fraction of effectively neutral mutations, c_ne, estimated by this method.

Estimates of the distribution of fitness effects and α using the Eyre–Walker and Keightley method:

The results from the method of Eyre-Walker and Keightley (2009) (referred to from now on as EWK) are shown in Table 4, including the estimated demographic model, the proportion of mutations with effects in different N_es categories, and the estimates of α, the fraction of adaptive substitutions.

TABLE 4.

Estimates of the distribution of fitness effects and the fraction of adaptive substitutions using the EWK method

		Shape parameter (b)	Location parameter (mean/b)	Proportion of mutations in different Nes categories				α (fraction adaptive)
	N2/N1			0–0.5	0.5–5	5–50	50–∞
X
mir	10 (0.41/10)	0.102 (0.057/99.998)	−9.7 × 108	0.062 (0.000/0.221)	0.017 (0.000/0.156)	0.021 (0.000/0.811)	0.900 (0.011/0.999)	0.138 (−1.718/1.000)
pse	10 (3.38/10)	0.319 (0.114/0.855)	−180.906	0.024 (0.003/0.049)	0.026 (0.009/0.049)	0.053 (0.013/0.217)	0.898 (0.730/0.955)	0.704 (0.379/0.945)
A
mir	3.72 (1.74/10)	0.081 (0.065/0.644)	−1.2 × 109	0.118 (0.019/0.179)	0.024 (0.018/0.134)	0.029 (0.022/0.352)	0.829 (0.413/0.891)	−1.116 (−2.734/0.509)
pse	6.60 (4.09/10)	0.538 (0.221/1.022)	−32.727	0.005 (3 × 10−4/0.019)	0.013 (0.003/0.021)	0.044 (0.017/0.083)	0.938 (0.892/0.972)	0.872 (0.630/0.985)

Ninety-five percent confidence intervals are in parentheses. mir and pse refer to data for D. miranda and D. pseudoobscura, respectively. N2/N1 is the estimated demographic model (relative difference between current and ancestral population size).

As above, while some parameters are precisely estimated, some have large statistical error, particularly in the case of the D. miranda data. For both types of chromosome in both species, a population size expansion is inferred. The demographic model was estimated on the basis of the frequency distribution of fourfold synonymous site polymorphisms; a population size expansion would result in an excess of low-frequency variants, assuming that such variants are selectively neutral. We report the shape parameter estimated for the gamma distribution, for comparison with the LCBN method above. In all cases the shape parameter is <1, indicating that the distribution is strongly leptokurtic, although this is poorly estimated for the D. miranda X chromosome data. This is broadly in agreement with the results for the gamma distribution using the LCBN method, and the differences between the estimates using the two methods are not large enough to be statistically meaningful.

Table 4 also shows the estimated proportions of nonsynonymous mutations with fitness effects in different N_es categories (note that these are not truncated, as was done for the LCBN method); s here is the heterozygous selection coefficient, as described in materials and methods. For the X chromosome data in both species, and the D. pseudoobscura autosomal data set, 92–98% of mutations are estimated to be strongly deleterious (defined as having N_es ≥ 5, implying a near-zero chance of fixation by drift). For the D. miranda autosomal data, ∼85% of mutations are strongly deleterious, consistent with the estimates for the Zimbabwe population of D. melanogaster (Eyre-Walker and Keightley 2009).

Finally, we used this method to estimate α for amino acid substitutions between each species and D. affinis. For both data sets from D. miranda, estimates of α were low or negative and nonsignificantly different from zero, with very large confidence intervals (see Table 4). This differs somewhat from the results from the LCBN method (see above) and may reflect a lack of statistical power due to low polymorphism levels. With D. pseudoobscura, however, there is evidence that a very large fraction of the divergence from D. affinis has been driven to fixation by positive selection, with α-estimates of 70% for the X chromosome data and 87% for the autosomal data, both with reasonably tight confidence intervals. These values are broadly consistent with results using the LCBN method (see above) and are considerably higher than previous estimates for D. melanogaster (52%: Eyre-Walker and Keightley 2009), wild mice (57%: Halligan et al. 2010), and humans (0–6%: Eyre-Walker and Keightley 2009) from this method.

Estimates of α from the Fay, Wyckoff, and Wu method:

Estimates of α calculated using the method of Fay et al. (2002) are shown in Table 5. We present only estimates calculated with singleton polymorphisms removed, since these are not significantly different from estimates with singletons included. We calculated α for the full data set, including those genes that showed departures from neutrality on the basis of the HKA test, since there is no biologically meaningful reason for excluding these genes from this analysis. However, for comparison to our other estimates, we also calculated α for the reduced data set. Exclusion of these genes has little effect on results, although estimates of α are somewhat lower for the X chromosome data in both species; the difference between the two estimates is not significant in either case, however.

TABLE 5.

Estimates of the fraction of adaptive substitutions using the Fay, Wyckoff, and Wu method

	D. miranda		D. pseudoobscura
	X chromosome	Autosome	X chromosome	Autosome
All synonymous changes
Full data set	0.326 (−0.088/0.639)	−0.788 (−1.775/−0.119)	0.438 (0.207/0.628)	0.588 (0.365/0.764)
Reduced data set	−0.168 (−0.961/0.423)	−1.317 (−2.771/−0.380)	0.325 (0.007/0.584)	0.592 (0.372/0.764)
Neutral synonymous changes
Full dataset	0.123 (−1.018/0.584)	−2.263 (−8.120/−0.508)	0.526 (0.232/0.714)	0.680 (0.460/0.828)
Reduced dataset	−0.701 (−4.589/0.442)	−2.853 (−12.538/−0.578)	0.470 (0.129/0.694)	0.654 (0.412/0.818)

Ninety percent confidence intervals are in parentheses. Neutral synonymous changes estimates include only preferred to preferred and unpreferred to unpreferred synonymous changes as the neutral standard.

In agreement with the above results, estimates of the fraction of adaptive substitutions between D. miranda and D. affinis are low or negative with large confidence intervals and not significantly greater than zero [although the estimates for the autosomal data are significantly less than zero, indicating an excess of nonsynonymous polymorphisms; this is consistent with the neutrality index (Rand and Kann 1996) of 2.08 in this case]. However, in D. pseudoobscura there is evidence that a statistically significant fraction of the nonsynonymous divergence from D. affinis is caused by positive selection, with α-estimates of ∼40% for the X chromosome data and ∼60% for the autosomal data. Although these estimates are ∼20% lower than those reported with the more complex methods (above), the confidence intervals for all estimates overlap, and the general patterns are qualitatively very similar.

DISCUSSION

Purifying selection on nonsynonymous mutations:

In agreement with other recent studies of Drosophila populations (Fay et al. 2002; Loewe and Charlesworth 2006; Loewe et al. 2006; Keightley and Eyre-Walker 2007; Shapiro et al. 2007; Eyre-Walker and Keightley 2009), our data provide firm evidence that only a small proportion (c_ne) of new amino acid mutations are sufficiently weakly selected that they can be treated as nearly neutral (i.e., they have N_es ≤ 0.5, where s is the selection coefficient against a heterozygous mutation).

The point estimates and confidence intervals for the proportion of nonsynonymous mutations that fall below this threshold depend on both the model for the distribution of mutational effects (lognormal vs. gamma) and the method of estimation (comparison of D. miranda and D. pseudoobscura diversity statistics, LCBN method, vs. the frequency spectra of segregating nonsynonymous mutations for each species, EWK method). The estimates from the EWK method are much less precise for D. miranda than for D. pseudoobscura, reflecting the smaller number of polymorphisms in this species. The estimated autosomal N_e for D. pseudoobscura of 1.8 million (Table 3) is much closer to the published values for most other Drosophila species than the value of 380,000 for D. miranda, so that the D. pseudoobscura value is more comparable with the estimates from D. melanogaster. We therefore place more confidence in the estimates for D. pseudoobscura than for D. miranda.

The upper confidence limit for c_ne for the D. pseudoobscura autosome is of the order of 2% at the most, with a slightly higher value of ∼3% for the X chromosome. The point estimates of c_ne for both X and autosome from the EWK method are much larger for D. miranda than for D. pseudoobscura. Taking these results together with those for the same method for D. melanogaster (6%: Eyre-Walker and Keightley 2009), wild mice (10%: Halligan et al. 2010), and humans (29–38%: Eyre-Walker and Keightley 2009), this suggests that the differences between species in the relative proportions of very weakly selected mutations reflect differences in their effective population sizes, although larger data sets will probably be needed to establish this with certainty.

The conclusion that most amino acid variants are under significant purifying selection is also supported by the estimates of other parameters of the probability distribution of N_es values. Table 3 shows that the product of N_e and the harmonic mean (s_h) of s is likely to be at least 3 for D. miranda and 15 for D. pseudoobscura for mutations with 2N_es > 1; s_h is close to the mean selection coefficient against segregating amino acid variants with deleterious fitness effects (Sunyaev et al. 2001). These are somewhat higher than the lower bounds previously estimated by Loewe et al. (2006). The results imply an s_h that lies between ∼8 × 10⁻⁶ and 2 × 10⁻⁵ for autosomal mutations, which have the tighter confidence interval.

The estimates of the numbers of mutations in different N_es categories from the EWK method suggest that >90% of new amino acid mutations in D. pseudoobscura have negligible probabilities of fixation; i.e., they have N_es ≥ 5 [note that N_e here is an estimate of the effective size that is relevant to currently segregating variants and is intermediate between the final and initial population sizes inferred from the maximum-likelihood procedure (Eyre-Walker and Keightley 2009)]. The majority of these have N_es > 50, implying that their frequencies in the population are deterministically controlled. These proportions are somewhat higher than estimates obtained by this procedure for D. melanogaster (87%: Eyre-Walker and Keightley 2009) and wild mice (79%: Halligan et al. 2010) and much higher than in humans [44–66%, depending on the data set (Eyre-Walker and Keightley 2009)].

Both methods imply a wide, leptokurtic distribution of s values. The shape parameter of the gamma distribution is poorly estimated for D. miranda by the EWK method (Table 4), but has a reasonably tight confidence interval for X-linked mutations in D. pseudoobscura, with an upper confidence limit of 0.85. This implies a much wider spread of selection coefficients than under an exponential distribution. The interval estimates from the LCBN method are much wider, but overlap those from the EWK method (Table 3); they are also somewhat wider than those estimated by Loewe et al. (2006). The inference of a wide distribution of selection coefficients is reinforced by the estimates of the order of 2 for the coefficients of variation of the distribution of s for nonlethal mutations, given by the LCBN method (Table 3).

Neither method returns very precise estimates of the arithmetic mean of N_es for newly arising amino acid mutations, in common with other methods that use polymorphism data. As discussed by Eyre-Walker et al. (2006), the mutations found segregating in populations are those that have survived elimination by selection, so the properties of the upper tail of strongly selected mutations are an extrapolation from those for much more weakly selected mutations. If a gamma distribution is assumed (which gives the tightest confidence intervals), the LCBN method for D. pseudoobscura autosomal loci returns a lower 5th percentile value of 29, corresponding to a mean selection coefficient of 1.6 × 10⁻⁵, and an upper 5th percentile value of 2130, corresponding to a mean s of 1.2 × 10⁻³. The point estimates for the LCBN and EWK methods are 47 and 4500, respectively, corresponding to s = 1.6 × 10⁻⁵ and 2.5 × 10⁻³.

These results allow us to estimate the mean load of deleterious nonsynonymous mutations carried by a typical individual. The mean π_A averaged over the X and the autosome, and over D. miranda and D. pseudoobscura, is ∼5.9 × 10⁻⁴. The mean number of nonsynonymous sites per gene is ∼1.3 × 10³ (Loewe and Charlesworth 2007), yielding a mean number of heterozygous amino acid mutations per individual of 0.77 per gene. With ∼14,000 genes, this implies that the typical fly is heterozygous for ∼10,800 nonsynonymous mutations. Table 3 gives an estimate of 1.1% for c_ne in D. pseudoobscura. With a mutation rate of 4 × 10⁻⁹ per nucleotide site, as assumed here, and with N_e = 1.8 × 10⁶, the contribution of effectively neutral mutations to nonsynonymous diversity is 3.2 × 10⁻⁴, 54% of the estimate of π_A of 5.9 × 10⁻⁴. This yields a value of 0.46 × 10,800 ≈ 5000 deleterious amino acid mutations per individual, with an estimated mean selection coefficient (s_h) of ∼1.1 × 10⁻⁵. This estimate of the mean number of heterozygous deleterious mutations per fly is much larger than comparable estimates for humans, but the mean selection coefficient against segregating amino acid mutations is also apparently much larger in humans, of the order of 2 × 10⁻⁴ (Eyre-Walker et al. 2006). This difference may in part reflect the much smaller effective population size of humans, so that many fewer nonsynonymous mutations remain polymorphic, and their persistence time relative to neutrality is larger. Consistent with this difference in N_e, the ratio π_A/π_S for humans is ∼40% (Cargill et al. 1999), compared with a value of ∼10% for the D. miranda autosome and 3% for the D. pseudoobscura autosome.

The effect of nonneutrality of synonymous mutations on estimates of the intensity of purifying selection on nonsynonymous mutations:

A bias is created by selection on the synonymous sites that are assumed to be neutral, reflecting selection on codon usage (Hershberg and Petrov 2008). Approximately 65% of synonymous polymorphisms in our data set involve changes from preferred to unpreferred codons; if we assume that the remainder is neutral, then the predicted equilibrium π-values for synonymous mutations can be approximated by regarding 35% of the synonymous diversity as coming from neutral mutations and 65% from preferred vs. unpreferred codons. We have estimated γ = 4N_es for the latter for our reduced D. miranda and D. pseudoobscura data sets (P. R. Haddrill, K. Zeng and B. Charlesworth, unpublished results), using the method of Zeng and Charlesworth (2009), which also fits a model of population growth and estimates the mutational bias, κ, in favor of unpreferred codons vs. preferred codons. The estimate of κ was between 2 and 3; D. miranda showed no evidence for population expansion for autosomal loci and only relatively weak evidence for X-linked loci, whereas D. pseudoobscura gave a very strong signal of a recent expansion for both the autosome and the X chromosome, consistent with its larger negative Tajima's D estimates (Table 1). γ for selection on codon usage was poorly estimated for D. miranda, but had a value of 1.9 for D. pseudoobscura for both the X and the autosome, yielding a net value for all synonymous mutations of ∼1.5.

If we assume that the D. miranda value of γ is about one-third of the value for D. pseudoobscura, in line with the observed difference in their level of synonymous diversities, and substitute these parameter estimates into Equation 15 of McVean and Charlesworth (1999) for the equilibrium diversity at sites under selection, the ratios of expected synonymous diversities to the neutral values for D. miranda and D. pseudoobscura are 1.058 and 1.089, respectively, assuming that κ = 2, which is the value commonly found for Drosophila (Zeng and Charlesworth 2009); this reflects the effect of mutational bias in causing weakly selected variants to have slightly higher levels of diversity than neutral ones (McVean and Charlesworth 1999). These differences imply that the ratio of effective population size for D. miranda relative to D. pseudoobscura is likely to be underestimated by a factor of 1.058/1.089 = 0.971, leading to a very slight overestimation of the strength of purifying selection from the LCBN method.

In the presence of selection on synonymous sites, the EWK method will overestimate the change in population size and underestimate the strength of purifying selection on nonsynonymous mutations, because of the similar effects of population expansion and selection on variant frequencies. It is, indeed, hard to believe that D. miranda has undergone a population expansion, given its rarity in nature, low silent diversity, and evidence for a relaxation of selection on codon usage (Bartolomé and Charlesworth 2006; Bachtrog 2007), so that it is more plausible that the evidence for expansion in D. miranda comes mainly from selection on synonymous sites.

Positive selection on nonsynonymous mutations:

In line with other studies of polymorphism and divergence in several Drosophila species (Fay et al. 2002; Smith and Eyre-Walker 2002; Bierne and Eyre-Walker 2004; Pröschel et al. 2006; Welch 2006; Shapiro et al. 2007; Bachtrog 2008; Baines et al. 2008; Eyre-Walker and Keightley 2009), all three methods that we used show a substantial fraction of amino acid differences between D. pseudoobscura and D. affinis (Tables 3–5) have been fixed by positive selection. The evidence from D. miranda is more equivocal, with only the LCBN method showing significant evidence for nonzero α-values; it is likely that this difference may in part reflect the noise introduced by the low polymorphism levels in D. miranda. The results of Bachtrog (2008) for ∼90 X-linked loci in D. miranda gave evidence for values of α that are reasonably close to our D. pseudoobscura values and the X-linked D. miranda estimates from the LCBN method, but with wide confidence intervals. Given that we are using D. affinis as the outgroup, there is no reason to suspect a real difference between the results for D. miranda and D. pseudoobscura, since most of the evolution takes place along the branch between their common ancestor and D. affinis.

There are two main potential sources of bias in these estimates, which may lead to an overestimation of α. The first, which has been previously discussed in the literature (Akashi 1996; Eyre-Walker 2002), is the effect of population expansion; a rapid expansion in population size will have little effect on divergence due to the fixation by drift of weakly selected mutations, but may well cause a greater increase in the numbers of segregating neutral mutations compared with deleterious mutations. The results in Table 4 include corrections for the effect of population expansion, as discussed by Eyre-Walker and Keightley (2009). Less rigorous corrections, using different assumed values of ancestral N_e in the LCBN method, are given in Table 3.

The second, which has been much less widely discussed except in the context of the McDonald–Kreitman (MK) test (McDonald and Kreitman 1991), is the effect of weak selection on synonymous mutations, which are usually assumed to be neutral. As pointed out by Akashi (1995), this may bias McDonald–Kreitman tests in favor of the spurious detection of positive selection, since the ratio of synonymous divergence to synonymous diversity is reduced by selection on synonymous variants. It is reasonable, however, to assume that purifying selection is much stronger on most amino acid variants than on synonymous variants, consistent with the evidence discussed in the previous section. If anything, therefore, the operation of purifying selection on both classes of site will cause α-estimates to be downwardly biased. For the MK-based results in Table 5, we removed singletons from both the nonsynonymous and the synonymous sites, which has been widely used as a way of minimizing the effects of purifying selection (Fay et al. 2002; Charlesworth and Eyre-Walker 2008). This has been shown to be only partially effective when synonymous variants are neutral (Charlesworth and Eyre-Walker 2008), but its effectiveness when both classes of site are selected (but at different intensities) has not been investigated. It is also worth mentioning that, as pointed out by Eyre-Walker (2002), the effect of selection on synonymous sites may work against the biases caused by population expansion, since variability at synonymous sites changes less in response to a change in population size than variability at neutral sites, although more than variability at more strongly selected sites.

One way to deal with the potential bias in estimates of α caused by weak selection on synonymous sites is to remove the major effect of selection against unpreferred codons (Haddrill et al. 2008). This can be achieved by using only a subset of synonymous changes that, under a model of selection for codon usage bias, are predicted to be neutral, i.e., changes from preferred to preferred or unpreferred to unpreferred codons (Bulmer 1991; Akashi 1995). Table 5 shows the estimates of α calculated using only this subset of synonymous changes as the neutral reference class. The estimates agree reasonably well with, and are not significantly different from, the results using all synonymous changes. In D. pseudoobscura, estimates of α are slightly higher than estimates using all synonymous changes, whereas in D. miranda they are slightly lower and have substantially wider confidence intervals. This is perhaps not surprising given that use of this subset of synonymous changes results in the removal of >80% of synonymous polymorphisms, reducing the amount of data considerably, especially in D. miranda. In general, however, the agreement between the two sets of α-estimates suggests that weak selection on synonymous sites is not introducing significant bias into our estimates of the fraction of adaptive substitutions.

The problem of bias from this source is potentially more serious for the other two methods. Both use the same procedure of estimating the rate of substitution for nonsynonymous sites by using the rate for synonymous sites, multiplied by a factor that represents the predicted rate of substitution of nonsynonymous mutations, estimated from the analyses of purifying selection on the assumption that synonymous sites are neutral. Clearly, if synonymous sites are subject to purifying selection, the estimate of α will be biased upward. An expression to correct for this effect is derived in the appendix (Equation A3).

Using the parameters that we estimated for the selection intensity on synonymous mutations in D. pseudoobscura (see previous section), we find that λ₁ in Equation A2 is ∼0.960. From Equation A3, this means that the point estimates of α are slightly reduced below the values in Table 3; e.g., the estimate of 92% for the autosome in D. pseudoobscura from the LCBN method (assuming a gamma distribution) with an ancestral N_e of 1 million becomes 91%, and the corresponding estimate of 67% for the X chromosome becomes 66%. Any lower confidence interval that is <4% means that α is not significantly different from zero. Fortunately, the ostensibly significant estimates in Table 3 remain significant after this correction.

There is an additional problem with the EWK method; the model on which it is based assumes that all nonsynonymous mutations other than those that fall into the positively selected class are deleterious, so that all the mutations that get fixed by drift are deleterious. But in reality there is a two-way flux because of reverse mutations at nonsynonymous sites (Gillespie 1984); this is included in the LCBN method (Loewe et al. 2006). In general, the flux under the reversible mutation process will be larger than for the one-way mutation process, because of the additional contribution from slightly advantageous and neutral reverse mutations. An approximate method for correcting for the effect of ignoring the contribution of reverse mutations to estimates of α from the EWK method, together with the effect of selection on synonymous sites, is also described in the appendix (Equations A4–A7). With the autosomal data for D. pseudoobscura, this method gives a corrected point estimate of α of 0.87, with lower and upper 95% confidence bounds of 0.57 and 0.98. For the D. pseudoobscura X chromosome, the point estimate of α becomes 0.63, with lower and upper 95% confidence bounds of 0.34 and 0.92. The main effect of the correction is thus to reduce the values of the point estimates of α, but without greatly altering the conclusions.

Biases from gene selection:

One other potential difficulty with our results needs discussion. As mentioned in materials and methods, our genes were isolated using primers designed from coding sequences conserved between D. pseudoobscura and D. melanogaster, as done previously by Bartolomé and Charlesworth (2006) and Vicoso et al. (2008). This raises the question of whether our sequences might be biased in favor of genes with unusually high levels of selective constraint on their protein sequences. Our mean π_A-value of ∼0.6 × 10⁻⁴ is much smaller than the value for D. melanogaster of ∼2 × 10⁻³ (Shapiro et al. 2007), and the K_A/K_S values in Table 1 are ∼6%, somewhat lower than the value of ∼8% estimated for genes in high recombination regions in the melanogaster subgroup (Larracuente et al. 2008). Vicoso et al. (2008) found X-linked and autosomal mean K_A/K_S values of 14 and 8%, respectively, for divergence between D. pseudoobscura and D. affinis, despite using the same method as ours for most of their nonautosomal genes, other than not selecting coding sequences that were ∼1 kb long as we did; their X-linked value is highly significantly different from ours. However, the estimate of mean π_A for the D. miranda X-linked gene data set of Bachtrog (2008), which did not require conservation of primer sequences with D. melanogaster, is 4.4 × 10⁻⁴, close to our estimate of 3.4 × 10⁻⁴, with an identical value for the mean of π_S. Her mean K_A for D. miranda vs. D. pseudoobscura for these loci was 0.57%, and our X-linked loci yielded a value of 0.33%. In contrast, a comparison of 182 coding sequences from D. miranda BACs with the corresponding D. pseudoobscura sequences gave an overall K_A value of ∼0.8% (Marion De Procé et al. 2009).

This suggests that primer design criteria that select for long coding sequences that amplify in two or more species may generate polymorphism and divergence data sets that are biased in favor of more constrained sequences, consistent with the direction of differences between these three data sets. Purifying selection is more effective at reducing divergence than polymorphism, so that this will have more of an effect on divergence statistics than the polymorphism statistics. Until more extensive polymorphism data sets based on whole genome resequencing become available, we cannot easily quantify the extent of the bias in estimates of intensity of selection against amino acid mutations that is caused by this problem.

A partial solution to this is to take a subset of our genes with the highest K_A/K_S values, chosen such that its mean K_A/K_S is close to the typical mean value mentioned above. We found that choice of the subset of two-thirds of our genes gave reasonable mean K_A/K_S values, with values of 0.086 and 0.074 for X-linked and autosomal loci, respectively. Comparison of Tajima's D values for the subsets of genes with low and high mean K_A/K_S values (Table S1) suggests that this approach does indeed exclude the subset of genes that are under strongest selective constraints, since in all except one case these exhibit more negative Tajima's D values at both nonsynonymous and synonymous sites. For the LCBN method applied to the autosomal loci, most of the genes that were removed had also been removed because of anomalously low diversity values in D. pseudoobscura, so we did not analyze the modified data set by this method. Use of the simplified version of this method gave results that were very similar to those for the unselected data set, with only a small increase in the estimate of the proportion of amino acid mutations that are neutral, a small reduction in the estimate of N_es_h, and a negligible effect on the estimate of α (Table S2). For the EWK method, the main effect is to increase the estimate of the frequency of effectively neutral mutations (c_ne), giving point estimates and upper 95% confidence limits that are somewhat larger than those in Table 4; the largest effect is to increase the point estimate for D. pseudoobscura from 0.5 to 1.5% (Table S3). The estimates of α are not substantially affected, as is also the case for estimates from the Fay, Wyckoff, and Wu method (Table S4).

APPENDIX

Both the LCBN and EWK methods use the principle that the proportion of nonsynonymous fixed differences that have been fixed by positive selection (α) can be estimated by subtracting the proportion that have been fixed by genetic drift acting on weakly selected mutations from the observed value of K_A/K_S. The LCBN method assumes that nonsynonymous sites, other than those where positive selection is occurring, are subject to a flux of reversible mutations between the favored amino acid at each site and its deleterious alternatives. We write K_N for the rate of neutral substitutions, K_A for the total rate of nonsynonymous substitutions, and λ₀K_N for the rate of substitution of nonsynonymous mutations due to the flux of reversible mutations, where λ₀ represents the factor by which selection reduces the rate of substitution of these mutations relative to the neutral value and is computed as described by Loewe et al. (2006). The true value of α is then given by

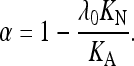(A1)

In the results described in the text, we equated K_N to K_S, the synonymous substitution rate. If there is weak selection acting on synonymous sites, then K_S is related to K_N by an expression of the form K_S = λ₁K_N, where λ₁ for an equilibrium population can be determined from the strength of selection on codon usage and the effective population size N_e (McVean and Charlesworth 1999). The value of α estimated from the data is thus

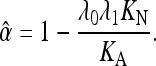(A2)

Substituting this into Equation A1, and rearranging, gives the corrected estimate of α as

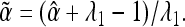(A3)

To apply this equation, it is necessary to have an estimate of λ₁. An approximate formula is given by

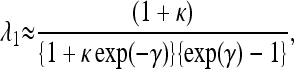(A4)

where γ is the product of 4N_e and the selection coefficient in favor of preferred codons, and κ is the mutational bias in favor of unpreferred codons, i.e., the ratio of mutation rates away from and to preferred codons.

This expression is obtained from Equation 6.11 of Charlesworth and Charlesworth (2010, p. 275), divided by the substitution rate for neutral mutations with the same mutational bias, 2uκ/(1 + κ), where u is the mutation rate from unpreferred to preferred codons. As discussed in the text, polymorphism data can be used to estimate γ and κ for synonymous sites and hence obtain an estimate of λ₁.

A further correction is needed for the EWK method, which assumes that amino acid mutations are always from favored to deleterious variants. In this case, for a given selection coefficient the predicted value of K_A/K_N is given by γ_A/{exp(γ_A) − 1}, where γ_A is the scaled selection coefficient against a deleterious amino acid mutation (Kimura 1983, p. 42). The net expected value of K_A/K_N, λ₂, is obtained by integrating this expression over the gamma distribution, using the values of a and b in Equation 2 that are estimated from the polymorphism data (Eyre-Walker and Keightley 2009). Thus, α is estimated as

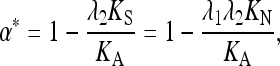(A5)

i.e., the value of λ₂ corresponding to the data is equivalent to .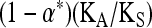

Given the estimated shape and location parameters of the gamma distribution that correspond to the estimate of λ₂, we can integrate a modification of Equation A4 for amino acid mutations subject to a flux between favored and deleterious states over the gamma distribution and obtain the corresponding estimate of the rate of substitution λ₃, which should more nearly represent the true situation. This can be done as follows.

As discussed by Loewe et al. (2006, p. 1082), a nonsynonymous site fixed for a favored amino acid mutation can mutate to up to three alternative nucleotides coding for a deleterious mutation. Any one of these can mutate to three alternatives, one of which corresponds to the favored amino acid, so that a reverse mutation to the favored state has a probability that is a fraction ζ of the mutation rate per nucleotide site, u. It has a probability (1 − ζ)u of mutating to another deleterious state, which we assume to be selectively equivalent to itself. 1/ζ is thus equivalent to the mutational bias parameter, κ, used above. In general, we expect ζ to take a value between 1 and 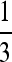, depending on the coding site in question and the extent of mutational biases (Loewe et al. 2006). This creates a dual process, in which a fraction (1 − ζ) of reverse mutations are neutral. If this is included in a forward and reverse model of substitutions between deleterious and favorable mutations, the equilibrium proportion of fixed sites that carry favored as opposed to deleterious variants, for a given scaled selection coefficient γ, is given approximately by the Li–Bulmer relation, x = ζ/{ζ + exp (−γ)} (Bulmer 1991). If the fixation probabilities for a given value of γ are Q₀ and Q₁ for deleterious and favorable nonsynonymous mutations, respectively, the net rate of substitution at sites with this selection coefficient relative to the neutral value is given by xQ₀ + (1 − x)ζQ₁ + (1 − ζ). Using the standard formulas for these fixation probabilities for semidominant mutations (Kimura 1962; Bulmer 1991), and integrating over the probability density of γ, φ(γ), whose parameters were estimated from the data, we obtain the following expression for the equilibrium substitution rate:

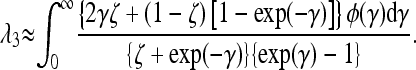(A6)

We can then obtain a corrected estimate of α, taking into account both selection on synonymous mutations and the flux of reversible amino acid mutations, as

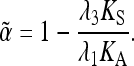(A7)

Low values of the shape parameter, a, of the gamma distribution imply a wide distribution of selection coefficients and a high rate of substitution of slightly deleterious mutations, giving low α*-values in Equation A5, while the reverse relations hold for high values of a. We can thus obtain an approximate joint confidence interval for a, α, and λ₂ by using the upper and lower 95% values of α* to determine the values of λ₂ corresponding to the lower and upper 95% values of a. The corresponding values of the mean of the gamma distribution are then used in Equation A6 to obtain the confidence intervals for λ₂ and hence for the corrected estimates of α (using Equation A7). Numerical investigations show that the results are not very sensitive to the value of ζ, with differences in at most the second significant number (data not shown); the values given in the text are for ζ = 0.5.