Fermi-surface collapse and dynamical scaling near a quantum-critical point

Abstract

Quantum criticality arises when a macroscopic phase of matter undergoes a continuous transformation at zero temperature. While the collective fluctuations at quantum-critical points are being increasingly recognized as playing an important role in a wide range of quantum materials, the nature of the underlying quantum-critical excitations remains poorly understood. Here we report in-depth measurements of the Hall effect in the heavy-fermion metal YbRh₂Si₂, a prototypical system for quantum criticality. We isolate a rapid crossover of the isothermal Hall coefficient clearly connected to the quantum-critical point from a smooth background contribution; the latter exists away from the quantum-critical point and is detectable through our studies only over a wide range of magnetic field. Importantly, the width of the critical crossover is proportional to temperature, which violates the predictions of conventional theory and is instead consistent with an energy over temperature, E/T, scaling of the quantum-critical single-electron fluctuation spectrum. Our results provide evidence that the quantum-dynamical scaling and a critical Kondo breakdown simultaneously operate in the same material. Correspondingly, we infer that macroscopic scale-invariant fluctuations emerge from the microscopic many-body excitations associated with a collapsing Fermi-surface. This insight is expected to be relevant to the unconventional finite-temperature behavior in a broad range of strongly correlated quantum systems.

Quantum criticality epitomizes the richness of quantum effects in macroscopic settings (1). The traditional description is based on the framework of Ginzburg and Landau (2), which focuses on the notion of an order parameter, a classical variable. The order parameter delineates the symmetry breaking of the macroscopic phases, while its fluctuations at ever-increasing length and time scales characterize the approach toward a second-order quantum phase transition. For metallic antiferromagnets, this theory appears in the form of a spin-density-wave quantum-critical point (QCP) (3, 4). Here, the macroscopic fluctuations of the order parameter are described by a Gaussian theory at the fixed point, with a vanishing effective coupling among the collective modes in the zero-temperature (T = 0), zero-energy (E = 0) and infinite-length limit. Consequently (5), the collective fluctuations will violate E/T scaling.

By contrast, an unconventional class of quantum criticality, emerging from studies in recent years (1), incorporates not only the slow fluctuations of the order parameter, but also some inherent quantum modes. For heavy-fermion metals, the additional quantum modes are associated with a critical breakdown of the Kondo screening effect and the concomitant single-electron Kondo resonance excitations (6–8). These additional critical modes can lead to a critical field theory that is interacting, instead of Gaussian, and the collective fluctuations will satisfy E/T scaling (9, 10). The critical Kondo effect itself is manifested in the nature of microscopic single-electron excitations, with the Fermi surface undergoing a severe reconstruction at the QCP.

To date, there has been no experiment to determine that the critical Kondo destruction is the underlying mechanism for the dynamical E/T scaling. In the heavy-fermion quantum-critical material CeCu_5.9Au_0.1, the magnetic dynamics have been shown to display such a scaling (9). In this material, however, the unconventional QCP appears only by tuning of chemical doping or pressure (11); consequently, it has so far not been possible to probe its Fermi surface and related single-electron properties with sufficient resolution. The heavy-fermion system YbRh₂Si₂ features an unconventional QCP that is accessible by the application of a relatively small magnetic field (12, 13), thereby allowing the study of magnetotransport across the QCP. Although indications of a rapid Fermi-surface change in YbRh₂Si₂ have appeared through the observation of a crossover in the Hall effect (14), no information has been extracted on the dynamical fluctuation spectra of either the magnetic or single-electron excitations. Moreover, the Hall crossover has alternatively been interpreted in terms of a background contribution in the nonmagnetic heavy-fermion phase through either minute valence variations (15) or Zeeman splitting of the bands (16, 17), leaving the nature of the quantum-critical single-electron excitations uncertain. In addition, the observation of sample dependences in the low-temperature Hall coefficient raises the important question of how these affect the Hall crossover (18, 19). To resolve these fundamental issues, we carry out comprehensive, in-depth Hall-effect measurements over a wide range of the control parameter, the magnetic field, down to very low temperatures. We establish a sample-dependent background component of the Hall crossover, which in turn allows us to isolate a critical component of the crossover with properties that are sample-independent. In addition, we identify a robustly linear-in-temperature width of the critical Hall crossover, which is compatible with a quantum-dynamical scaling of the critical single-electron excitations. Our findings lead to an unexpectedly direct linkage between the scale-invariant macroscopic fluctuations and the microscopic physics of a collapsing Fermi surface.

Results

We study the magnetotransport in tetragonal YbRh₂Si₂ using a crossed-field setup, in which two external magnetic fields are applied in perpendicular directions. This separation allows for a disentanglement between field tuning of ground states through B₂ and generation of Hall response through B₁: One field, B₁, along the magnetic hard c axis and perpendicular to the electrical current, is used to extract the initial slope of the Hall resistivity, ρ_H, i.e., the linear-response Hall coefficient, R_H (see SI Text I). The second field, B₂, applied within the magnetically easy ab plane and along the current direction, is used as the control parameter that tunes the system from an antiferromagnetic ground state at low fields across the QCP toward a high-field paramagnetic state. The adjacent phases on both sides of the QCP obey Fermi-liquid properties, like a quadratic temperature dependence of the resistivity (13). We consider two samples, which span the whole range of sample dependences in the Hall coefficient (see SI Text II).

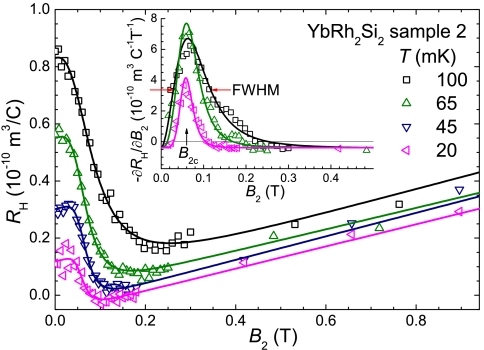
Fig. 1 shows the isothermal linear-response Hall coefficient of our highest-quality sample as a function of B₂. Two features are evident. First, for B₂ much larger than the quantum-critical field, B_2c, the Hall coefficient shows a sizable variation with the magnetic field; within the experimental error it is linear in B₂. This background feature is likely due to Zeeman splitting (17) because no indication for a valence change (15) has been observed. The identification of this background feature is possible only because we have measured in a substantially extended range of B₂ (see SI Text I). Second, there is a sharp crossover feature that rides on top of the background contribution. This sharp feature is located near B_2c and will henceforth be termed the critical Hall-crossover component.

Fig. 1.

Crossed-field Hall-effect results of YbRh₂Si₂. Selected isotherms of the initial-slope Hall coefficient R_H as a function of B₂ for sample 2 [which has the smallest residual resistivity (cf. SI Text II)]. The solid lines are best fits of the empirical crossover function given in Eq. 5 in Materials and Methods, extending up to 2 T. The anomalous contribution to the Hall effect can be neglected as explained in SI Text III. (Inset) Illustration of the decomposition of the crossover in R_H(B₂) into the critical and background components. Here, -∂R_H(B₂)/∂B₂ is plotted as a function of B₂ together with the derivatives of the fitted functions (solid lines). The background crossover term corresponds to the nonzero constant offset. The critical crossover term is represented by the sharp peak near B_2c (marked by vertical arrow), whose FWHM is defined as the crossover width (specified for one temperature by the red horizontal arrows). Standard errors of R_H are typically of the size of the symbols.

The inset of Fig. 1 further illustrates the systematic decomposition of the Hall crossover into the background and critical components. It plots -∂R_H/∂B₂ as a function of B₂. The background term appears as an underlying nonzero offset, whereas the critical term manifests itself as a sharp peak near B_2c. More quantitatively, Fig. 1 shows the separation of the two components using a fitting procedure specified in Materials and Methods.

The critical component is characterized by the difference between 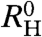, the Hall coefficient before the crossover, and 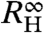, the Hall coefficient after the crossover. The temperature dependence of 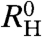and 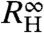in the low-T range for both samples is shown in Fig. 2A. The experimental finding of a pronounced quadratic temperature dependence of 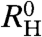below T_N allows a proper extrapolation to T → 0 yielding a finite difference between 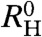and 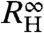persisting to zero temperature (see SI Text V). This difference is naturally associated with a change of the Fermi surface. 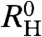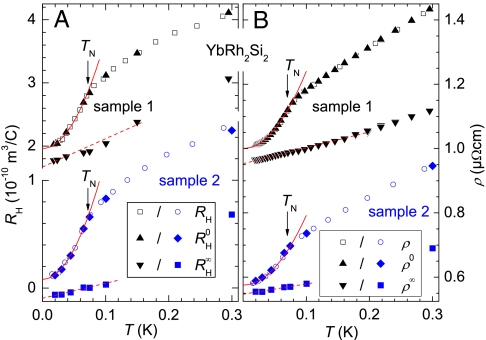The magnitudes of and 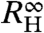, on the other hand, are different for the different samples rendering the sample dependences of the Hall coefficient a common property of the two phases at either side of the QCP. Recent ab initio calculations of the Hall coefficient in YbRh₂Si₂ suggest that these sample dependences are the effect of multiple Fermi-surface sheets. The “small” (4f-core) and “large” (4f-itinerant) Fermi surfaces at fields below and above B_2c in YbRh₂Si₂ are respectively dominated by two hole and one hole/one electron Fermi-surface sheets (19). Correspondingly, the step of R_H as B₂ increases through B_2c is expected to be negative, as is indeed seen here.

Fig. 2.

Limiting values of the Hall and magnetoresistivity crossover. (A) Fit parameters 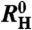and 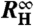of the crossover in R_H plotted for sample 1 and sample 2 as a function of temperature together with the measured initial-slope Hall coefficient R_H. The residual resistance ratios are 70 and 120 for sample 1 and sample 2, respectively. (B) Corresponding quantities ρ⁰ and ρ^∞ from the analogous analysis of the magnetoresistivity crossover (see SI Text IV). Solid lines correspond to fits of a quadratic temperature dependence below T_N (see SI Text V), as already observed previously for ρ(T) (13). Dashed lines are guides to the eye. Arrows indicate the Néel temperature. Standard deviations are smaller than the symbol size.

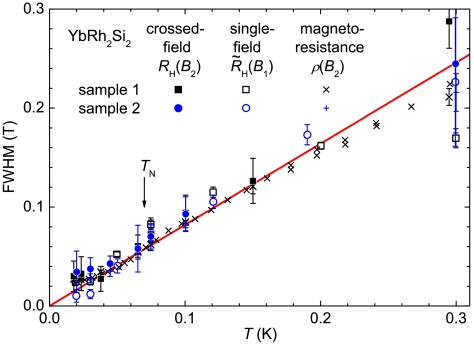
By contrast, the crossover position and the crossover width of the critical component show essentially no sample dependence within the experimental error. This is seen in Fig. 3, which plots the FWHM of ∂R_H/∂B₂ isotherms (Fig. 1 Inset), and in Fig. 4, which depicts the crossover field, B₀, extracted from the fits to R_H(B₂) for a range of low temperatures in the temperature-magnetic field phase diagram.

Fig. 3.

FWHM of the Hall crossover. The width was determined from the derivatives of the fits to R_H(B₂) in the crossed-field setup, to the simultaneously measured magnetoresistivity ρ(B₂), and to 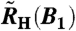of the single-field experiment, respectively. See Fig. 1 Inset for the definition of the FWHM. The values for 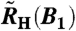were scaled by 1/11 = B_2c/B_1c (ref. 13) to account for the c axis vs. ab plane magnetic anisotropy of YbRh₂Si₂. The solid line represents a linear fit to all datasets with the magnetoresistivity data being well described up to 1 K; see SI Text IV. Within the experimental accuracy this fit intersects the ordinate at the origin. Where there is overlap, our magnetoresistivity results are in good agreement with the FWHM directly extracted from the derivative of ρ(B₂) presented in ref. 20. The crossed-field data obtained earlier in a very limited temperature range (14) are in good agreement with both our results and the linear fit. The different temperature dependence found earlier was dominated by the former single-field results differing from ours. This difference is likely a result of an improved orientation procedure that became possible only in a substantially improved setup (see SI Text I). Arrow indicates the Néel temperature. Error bars are standard deviations.

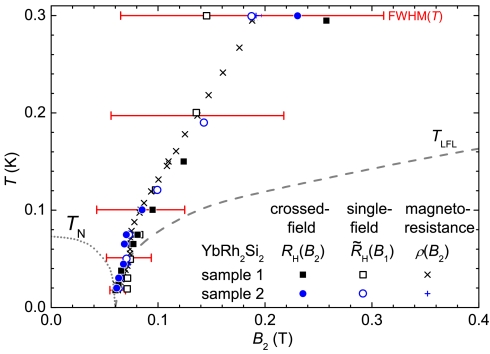
Fig. 4.

Position of the Hall crossover in the temperature-field phase diagram of YbRh₂Si₂. The crossover fields, B₀, are extracted from fits to R_H(B₂) of the crossed-field experiment, to 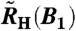of the single-field experiment, and to ρ(B₂) (cf. Materials and Methods). The values of the single-field Hall-effect experiment were scaled by 1/11 to account for the magnetic anisotropy of YbRh₂Si₂. The red horizontal bars reflect the FWHM at selected temperatures determined by the fit in Fig. 3, showing that the crossover fields of the various experiments and samples all lie within the range spanned by the FWHM. The dotted (dashed) line represents the boundary of the antiferromagnetic phase (Fermi-liquid regime) taken from ref. 13. Error bars are omitted in order to avoid confusion with the width of the crossover; with the exception of the data at 0.3 K and the single-field result of sample 2 at 0.19 K, the standard deviations are smaller than the symbol size.

To corroborate this fundamental finding, we have carried out two additional measurements. The standard single-field Hall-effect setup is used to monitor the differential Hall coefficient 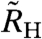as a function of the magnetic field B₁ applied along the crystallographic c axis (see SI Text I). In addition, the magnetoresistivity, ρ, is measured as a function of a single field, B₂, applied within the ab plane. Both ρ(B₂) and 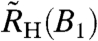can similarly be decomposed into background and critical terms (see SI Text IV), with the critical crossover terms occurring near the basal-plane critical field, B_2c, and near the c-axis critical field, B_1c, respectively; the ratio B_2c/B_1c will be used as the anisotropy ratio to convert the B₁ scale into an equivalent B₂. The zero-field and high-field values extracted from fits of the crossover function (Eq. 5) to magnetoresistivity (ρ⁰ and ρ^∞) and differential Hall coefficient ( 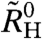and 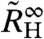) are presented in Fig. 2B and in SI Text V, respectively. Each quantity shows a similar sample dependence: As found for the crossed-field results, the differences ρ⁰ - ρ^∞ and 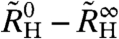remain finite in the zero-temperature limit even though the individual quantities differ for the different samples. The crossover positions extracted from all the properties are compiled in Fig. 4. They are largely compatible with each other, falling within a range spanned by the FWHM; they define a crossover energy scale (the T^⋆ line) (14, 20). Finally, the FWHM of the crossover in 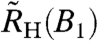and ρ(B₂) closely follow that of R_H(B₂) (see Fig. 3). We note that the onset of the quadratic form of 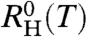at T_N (Fig. 2) is not accompanied by a similar signature in the FWHM at T_N (Fig. 3; see also SI Text IV). Therefore, the FWHM extrapolates to zero for T → 0 implying a jump of all three quantities (R_H(B₂), 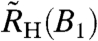and ρ(B₂)) at the QCP.

The sample independence of both the crossover position and the crossover FWHM strongly indicates that all the magnetotransport crossovers manifest the same underlying physics. Combined with the jump of the Hall coefficient and magnetoresistivity in the zero-temperature limit, they imply the interpretation in terms of a sharp Fermi-surface reconstruction at the magnetic QCP (14) over that based on the smooth physics of heavy quasiparticles (15, 17).

Having isolated the critical component of the Hall crossover from the background term, we are now in the position to discuss the detailed nature of the QCP. For this purpose, we have not only carried out crossed-field and single-field Hall and (single-field) magnetoresistivity measurements over an extended field range for each temperature, but have also done so for a large set of temperatures in the low-T range. These efforts allow us to reach the important conclusion that the crossover FWHM is proportional to temperature (Fig. 3).

The Fermi surface is a property of the single-electron excitation spectrum. In any Fermi liquid, it spans the momenta, k_F, at which the energy dependence of the single-electron Green’s function develops a pole at the Fermi energy. Hence, a reconstruction of the Fermi surface across the QCP implies that the single-electron Green’s function contains a singularity at the QCP. Indeed, the conduction-electron Green’s function of a Kondo lattice system can very generally be written as

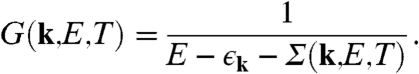[1]

In the absence of static Kondo screening, the self-energy Σ(k,E,T) is nonsingular. Correspondingly, the Fermi surface is smoothly connected to that of the conduction electrons alone; it is small (21). In the presence of static Kondo screening, Σ(k,E,T) develops a pole; for E and T small compared to the coherent Kondo scale, it takes the form

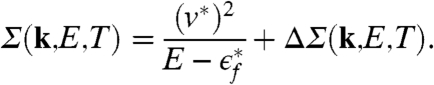[2]

Here v^∗ and 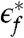specify the strength and energy of the Kondo resonance (22), and ΔΣ(k,E,T) is the nonsingular term of the self-energy. The existence of this pole in Σ(k,E,T) shifts the Fermi momenta from their positions on the small Fermi surface, k_F, to those on a large Fermi surface, 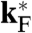. Approaching the point of critically destroyed Kondo effect, the quasiparticle weight vanishes (6, 7) in accordance with the divergence of the quasiparticle mass seen in specific heat and resistivity (13, 21). In particular, at the QCP, both the strength, v^∗, and the energy, 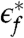, of the Kondo resonance (see Eq. 2) go to zero in the E → 0 and T → 0 limits. Moreover, the interacting nature of the fixed point implies an E/T scaling of the single-electron Green’s function: The reasoning is analogous to that for the dynamical spin susceptibility (6, 9), and the property can be illustrated by explicit calculations in simplified model settings for critical Kondo destruction (23). Similar forms of dynamical scaling of the single-electron spectra are likely a generic feature of other types of Kondo-destroying QCPs (7, 8, 24); they appear in related contexts as well (25–27). It is worth noting that the linear-in-temperature electrical resistivity cannot be used as evidence for E/T scaling of the single-electron excitations. Indeed, the temperature dependence of the electrical resistivity does not in general measure the temperature dependence of the single-electron relaxation rate and this is so even for spin-density-wave QCPs (28).

The scaling form for the single-electron Green’s function in the quantum-critical regime can be expressed as follows:

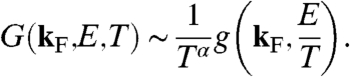[3]

The associated relaxation rate, defined in the quantum relaxational regime (E ≪ k_BT) according to

[4]

is linear in temperature: Γ(k_F,T) = cT, where c is a universal constant.

We can use these properties of the single-electron Green’s function to understand the crossover of the Hall coefficient. In the Fermi-liquid regimes on either side of the QCP, the Hall coefficient reflects the respective Fermi surface; it is, in particular, independent of the quasiparticle residue (29) (see SI Text VI). The distinct (large and small) Fermi surfaces in the two Fermi-liquid regimes yield different end values of the Hall coefficient. The central question is how the two Fermi surfaces are connected across the QCP. Because the single-electron Green’s function characterizes each of the two Fermi liquids, this is related to the critical relaxation rate, Γ(k_F,T), of the single-electron states. At zero temperature, Γ(k_F,T = 0) vanishes; the change from one Fermi surface to the other is sharp, occurring precisely at the QCP. The Hall coefficient must undergo a sharp jump in accordance with the experimental findings. At any nonzero temperature, a continuous crossover from one Fermi surface to the other is controlled by the single-electron relaxation rate Γ(k_F,T). Given the above-described behavior of the Hall coefficient in the adjacent Fermi-liquid regimes with well-defined but different Fermi surfaces, its crossover has to be related to the finite-temperature broadening of the critical single-electron states on the Fermi surface. Our observation of a linear-in-temperature width of the critical Hall crossover is therefore consistent with a linear-in-temperature relaxation rate. By contrast, our experimental finding is incompatible with the spin-density-wave picture of order parameter fluctuations and the concomitant Gaussian fixed point, which would be accompanied by a superlinear temperature dependence of the Hall-crossover width (see SI Text VI).

Discussion

The single-electron Green’s function serves as the proper means to specify whether a metal obeys the standard theory of solids—Landau’s Fermi-liquid theory. The fact that Eq. 2, with a nonzero v^∗, i.e., a large Fermi surface across the QCP, fails to describe our data is consistent with a breakup of the heavy-Fermi-liquid quasiparticles at the QCP. More generally Eq. 3, reminiscent of Green’s function of gapless interacting electrons in one dimension (30), invalidates any Fermi-liquid description. By using a single set of measurements on the same compound to probe both the collective fluctuations of the QCP and a critical destruction of the single-electron excitations, our work provides the most direct association between quantum criticality and non-Fermi-liquid behavior.

In summary, we have carried out in-depth magnetotransport measurements in a prototypical quantum-critical heavy-fermion metal, and we are able to distinguish a robust critical crossover from a sample-dependent background feature. By zooming into the vicinity of the QCP, we have shown that the width of the critical crossover is not only independent of sample quality but also proportional to temperature. This proportionality is consistent with the E/T form in the dynamical critical scaling. Coupled with the fact that the vanishing width in the zero-temperature limit implies a jump in the Fermi surface, our findings point to the microscopic many-body excitations of a collapsing Fermi surface as underlying the dynamical E/T scaling of the macroscopic critical fluctuations. Our results further establish the T^⋆ line as a means to probe the Kondo breakdown. This should hold even when the Kondo breakdown is separated from the paramagnetic-to-antiferromagnetic QCP (31). In addition, they might help to understand why the two coincide in stoichiometric YbRh₂Si₂ and its close vicinity. More generally, the linkage between microscopics and macroscopics is expected to be broadly relevant to the physics of strong correlations, considering that the finite-temperature properties are invariably abnormal in a wide array of quantum materials, and given that the Fermi surface and its evolution as a function of control parameters—e.g., from the underdoped high-temperature cuprate superconductors to the overdoped ones (32, 33)—are playing an increasingly central role in understanding these systems.

Materials and Methods

The Hall crossovers in both the crossed-field [R_H(B₂)] and single-field [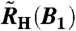] experiments (see SI Text I) were fitted with the empirical crossover function

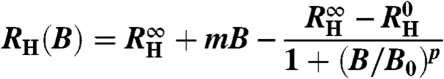[5]

that contains not only a critical component (14) but also a linear term mB to account for the background behavior. 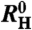and 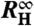are the zero-field and infinite-field values, respectively. The differential Hall coefficient and the magnetoresistivity curves were analyzed analogously leading to the corresponding parameters 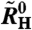, 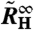and ρ⁰, ρ^∞, respectively. By fitting Eq. 5 to isotherms taken at different temperatures, the temperature dependences of the parameters were extracted. The FWHM was extracted from the derivative of the fitted function as illustrated in the inset of Fig. 1.