From cell death to embryo arrest: Mathematical models of human preimplantation embryo development

Abstract

Human preimplantation embryos exhibit high levels of apoptotic cells and high rates of developmental arrest during the first week in vitro. The relation between the two is unclear and difficult to determine by conventional experimental approaches, partly because of limited numbers of embryos. We apply a mixture of experiment and mathematical modeling to show that observed levels of cell death can be reconciled with the high levels of embryo arrest seen in the human only if the developmental competence of embryos is already established at the zygote stage, and environmental factors merely modulate this. This suggests that research on improving in vitro fertilization success rates should move from its current concentration on optimizing culture media to focus more on the generation of a healthy zygote and on understanding the mechanisms that cause chromosomal and other abnormalities during early cleavage stages.

Human preimplantation embryos produced in vitro are characterized by highly variable morphology and developmental potential. Only 25% of embryos that are transferred to patients 2 days after in vitro fertilization implant (1), resulting in low pregnancy rates (2). Approximately 75% of embryos exhibit varying degrees of cellular fragmentation and asymmetry (Fig. 1) (3). Finally, if embryos are cultured in vitro, ≈50% arrest during the first week (4). The reasons for this high rate of embryonic loss during early development are unclear but could include chromosomal abnormalities (5), suboptimal culture conditions (4, 6), or inadequate oocyte maturation (7).

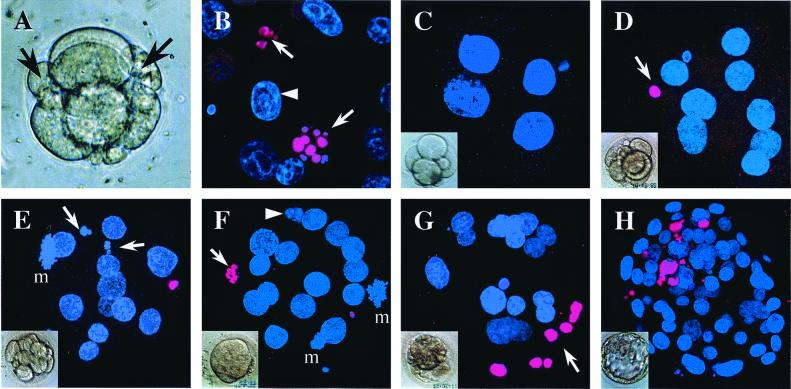
Figure 1.

Light and confocal micrographs showing cellular and nuclear morphology in human preimplantation embryos. Nuclei are labeled with 4′, 6-diamidino-2-phenylindole (blue). (A) Fragmenting day 2 human embryo, with fragments arrowed. (B) Nuclei from a day 6 blastocyst showing TUNEL-labeled (pink) fragmented nuclei () and healthy interphase nucleus (▸). (C) Day 2 4-cell embryo. (D) Day 4 8-cell embryo with TUNEL-labeled polar body (). (E) Day 4 embryo with 13 cells and 15 nuclei, including 2 fragmenting () and one in mitosis (m). Note TUNEL-labeled polar body. (F) Day 4 morula with 18 nuclei, including 2 in mitosis (m); 1 fragmented nucleus that is TUNEL-labeled () and 1 fragmented nucleus with no TUNEL labeling (▸). (G) Day 4 morula with 24 nuclei, including 7 condensed, TUNEL-labeled nuclei (). (H) Day 6 blastocyst with 87 nuclei, 12 of which are TUNEL-labeled and mostly localized to the region of the inner cell mass.

Both arrested and developing embryos contain varying proportions of cells with the classic features of apoptosis (3, 8–10), including cytoplasmic, nuclear, and DNA fragmentation (Fig. 1). Although the presence of similar cells in vivo in other species suggests a role for apoptosis in normal development (11), it has been proposed that apoptosis plays a significant role in embryonic arrest (9). However, the relationship between the rate of individual cell death and the level of whole embryo loss is very unclear and is complicated by the lack of information about crucial parameters such as the stage at which apoptosis begins, how long cells displaying features of apoptosis persist before clearance, and even the length of the cell cycle.

The Retrospective Data.

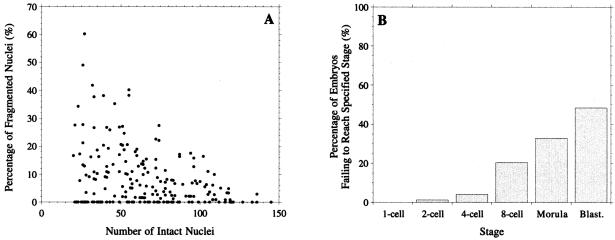
The study of apoptosis in human embryos is constrained by limited material. The starting point of our investigation was therefore a retrospective analysis of cell death and embryo arrest data accumulated over the last decade (shown in Fig. 2). This immediately raises two questions. First, are the levels of cell death seen in Fig. 2A sufficient to account for the levels of embryo loss in Fig. 2B or are additional mechanisms acting to arrest the whole embryo? Second, is the correlation suggested by the striking shape of the distribution in Fig. 2A a statistically significant one, so that embryos with more cells have lower rates of cell death?

Figure 2.

(A) Proportion of fragmented nuclei against number of intact nuclei for 203 day 6 blastocysts (10). Fragmenting and healthy nuclei were labeled with polynucleotide-specific fluorochromes and counted by using fluorescence microscopy (e.g., ref. 10). (B) Proportion of 994 embryos that have arrested by a given developmental stage. Accumulated retrospective control data from culture studies observing embryo development in vitro to day 6.

Both of these questions are difficult to answer directly, because the data in Fig. 2 are the end product of a number of generations during which individual cells can divide or die. The relationship between the rate of cell death for individual cells and the data in Fig. 2 is therefore complex, precluding the direct use of standard statistical tests. Instead, we construct a mathematical model of the cell division and cell death process that allows us to relate parameters such as individual cell death rates to global outcomes, such as the distribution of live and dead cell numbers or the arrest or survival of the whole embryo.

The Preliminary Model.

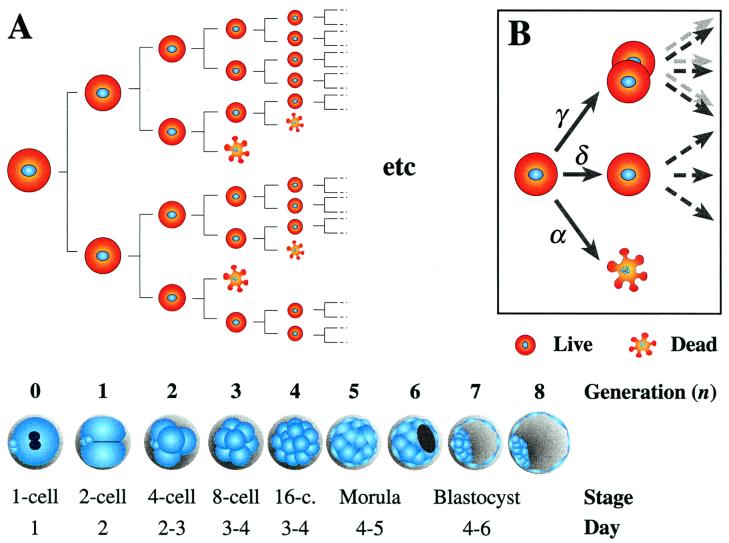
The most natural way to develop a model is in the form of a branching process. These have a well developed theory and are widely used to model a variety of biological growth phenomena [e.g., tissue proliferation or population growth; see for instance (12)]. The simplest model of this form for preimplantation embryo development is shown in Fig. 3A, where each cell either divides or dies during each generation. Each action occurs with a given probability, which may vary with time or with factors such as the number of cells in the embryo. It is assumed that this probability is the same for all cells in the same embryo, and that the choice of action for any given cell is independent of the choice for all other cells. These assumptions ignore the possibility of local communication between cells, and we hope to incorporate such effects in the future. To simplify matters further, our model evolves in discrete generations, i.e., we assume that cell cleavage is synchronous. Although there is a degree of asynchrony during cleavage even in mouse embryos (13), such an approximation sheds useful insight into the development of human embryos.

Figure 3.

(A; main figure) Schematic representation of branching process model of cell division and cell death in an embryo, and approximate correspondence between generations, developmental stages and chronological time, with day of oocyte retrieval being day 0. The equivalence between generations 0 to 4 and the 1- to 16- cell stages is straightforward, but that for subsequent generations is more imprecise. Confocal analysis of preimplantation human embryos indicates that compaction does not occur before the 16- to 32-cell stages (i.e., generations 4 and 5) (14). Newly expanded blastocysts of good morphology on day 5 were found to have, on average, 58 cells (8), which means that they were at about generation 6. Day 6 and 7 blastocysts had a mean of 84 and 126 cells, respectively. Thus we can assign generations 4 and 5 to the morula stage, and 6 to 8 to the blastocyst stage. To relate the model to the data in Fig. 2A, we make the simplest possible choice that each fragmented nucleus in Fig. 2A is equivalent to one cell dying during the last generation simulated by the model. This assumption was tested and found to be reasonable by extending the model to allow for different rates of dead cell clearance (see supplemental Appendix, www.pnas.org). (B Inset) Choice of actions and associated probabilities at each branch.

To specify the model mathematically, we have to decide what can occur at each branch and with what probability. We assume that in each generation a single cell can either die, with probability α; divide, with probability γ; or do neither, with probability δ (Fig. 3B). Note that we must have α + δ + γ = 1.

The behavior of the model depends on a number of parameters, including the probabilities α, δ, and γ, the starting stage at which cell death starts, and the number of subsequent generations that the embryo passes through. Different choices of these parameters will result in different final distributions of live and dead cell numbers. Thus, given a data set such as Fig. 2A, we can estimate these parameters by searching for values which give a final distribution that has the closest agreement with observed data. Some parameters will produce a distribution with a high likelihood of the model yielding the observed data, whereas others will have a much lower likelihood. Such a likelihood can be used as a measure of the fit of the model to the data; the higher the likelihood, the better the fit (e.g., ref. 14). Hence by maximizing the likelihood, we can derive quantities of biological interest (such as the cell death rate α or the stage at which cell death starts) from experimental observations (details are published in the Appendix, which is published as supplemental data on the PNAS web site, www.pnas.org).

Preliminary Model Results.

Values of α and γ maximizing the likelihood were found for models with cell death starting at the 1st, 2nd, 3rd, and 4th cleavage stages (n_s = 0, … , 3; Table 1) and ending at generation 8 to 10 inclusive (n_f = 8, … , 10; Table 1). The best fit was for cell death starting at the 4- to 8-cell transition (Fit I, Table 1). Having cell death start a generation earlier (Fit II) or the model finish a generation later (Fit III) gave plausible but much less likely fits (by a factor of at least 20). Fit IV was carried out to test the hypothesis that cell death starts at generation 0 (i.e., the 1-cell stage); it has a likelihood ratio of 4 × 10⁻¹⁷, and hence this hypothesis can be very confidently rejected. In every case, increasing the final generation n_f for a fixed value of starting stage n_s decreased the likelihood. The model thus suggests that the embryos in Fig. 2A have undergone on average eight cell divisions from the one-cell stage, consistent with the correspondence between generations and developmental stages presented in Fig. 3.

Table 1.

Different model fits

Fit	Generation		Death rate, α	Cell division, γ	Likelihood ratio
	Starting, ns	Final, nf
I	2	8	0.145	0.745	1 (Best Fit)
II	1	8	0.142	0.778	0.04
III	2	9	0.134	0.626	0.0485
IV	0	8	0.139	0.785	4 × 10−17
V	0	8	0.157	0.783	N/A

The starting generation n_sdetermines when cell death commences, with n_s = 0 corresponding to the one-cell zygote. Thus for instance n_s= 2 indicates that embryos divide without loss for two cleavage divisions to yield 4 cells before cell death is switched on. The final generation is denoted by n_f, which corresponds to the stage at which the data in Fig. 2A is observed. The model thus depicts a total of n_f − n_sgenerations. Because the data set contains embryos with more than 2⁷ = 128 cells, n_fmust be greater than 7. The parameters α and γ are respectively the probabilities of each cell dying or dividing in each generation (Fig. 3B). The last column gives the ratio of the likelihood of each fit to that of the best fit that has been found (Fit I) and thus provides a relative indication of the quality of each fit. The smaller the ratio, the less likely that the model gave rise to the data. Fit V corresponds to an extended data set, discussed below. Because this fit uses different data to that used in fits I–IV, it is meaningless to compute a likelihood ratio. 

The model thus makes a clear prediction that cell death does not start at the one-cell stage and most likely begins around the transition from the four- to eight-cell stage. This implies that cell death should first be seen experimentally in embryos at the eight-cell stage. We now go on to investigate this experimentally.

Experimental Verification.

Source of human embryos and embryo culture.

Patients underwent superovulation as described in ref. 1 by using recombinant follicle-stimulating hormone (Gonal F, Serono, Welwyn Garden City, UK). In vitro fertilization and embryo culture were carried out as described previously (1). After patients' informed consent, untransferred normally fertilized embryos were cultured for up to 4 days in Earle's Balanced Salt solution (GIBCO/BRL) containing 5.56 mM glucose and supplemented with 25 mM sodium bicarbonate (BDH), 0.47 mM pyruvic acid (Sigma), and 10% heat-inactivated maternal serum under a gas phase of 5% CO₂, in air. Only developing embryos of good morphology were included in the study. Arrested fragmented embryos were excluded. The work was approved by the research ethics committee of Imperial College School of Medicine, Hammersmith Hospital, and licensed by the United Kingdom Human Fertilisation and Embryology Authority.

Detection of apoptosis.

Morphological and biochemical features of apoptosis include fragmentation of both nuclei and DNA (ref. 15; Fig. 1B). Both of these features were examined in normally developing preimplantation human embryos at various developmental stages from the four-cell to the blastocyst (Fig. 1 C–H). Nuclear morphology was evaluated with 4′, 6-diamidino-2-phenylindole (DAPI) counterstaining, whereas in situ detection of fragmented DNA was performed by using TdT-mediated dUTP nick-end labeling (TUNEL) (16). Zona-free embryos were individually fixed (1 h) in 4% paraformaldehyde (Sigma), permeabilized (1 h) in 0.5% Triton-X-100 (Sigma), TUNEL labeled (1 h, 37°C, dark) in fluorescein-conjugated dUTP and TdT (Boehringer Mannheim), and mounted on a microscope slide in Vectashield containing 1.5 μg ml⁻¹ DAPI (Vector Laboratories). Embryos were thoroughly washed in PBS (GIBCO) supplemented with 3 mg ml⁻¹ polyvinylpyrrolidone (Sigma) between each treatment. The number of healthy nuclei and the proportion of nuclei showing DNA and/or nuclear fragmentation were assessed by using multichannel confocal microscopy.

Experimental Results.

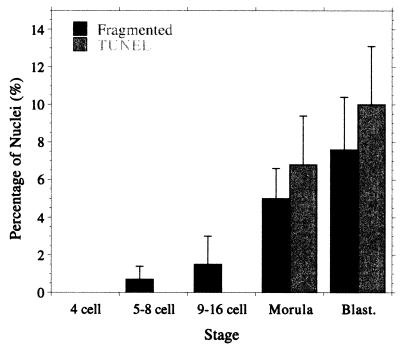
Sixty-six normally developing human preimplantation embryos were assessed for nuclear and DNA fragmentation (Fig. 1; see also Table 2, which is published as supplemental data in the PNAS web site). The majority of apoptotic nuclei were both fragmented and TUNEL labeled. TUNEL-labeled nuclei were not seen before compaction (Fig. 1 C–E and Table 2) but were observed at the morula (Fig. 1F) and blastocyst (Fig. 1H) stages. Fragmented nuclei were seen rarely before compaction and with increasing frequency at the morula and blastocyst stages (Fig. 1 F–H). The average percentage of nuclei showing features of apoptosis at each stage is summarized in Fig. 4.

Figure 4.

Cell death in normally developing embryos of good morphology: average percentage of nuclei in each embryo that is fragmented or TUNEL labeled; values are mean ± SEM.

These results unambiguously confirm our prediction that cell death does not occur in the early stages of embryo development. Thus fragmented nuclei are not seen until the eight-cell stage (exactly the prediction of our model) and TUNEL-labeled ones, not until the morula stage. In both cases, the levels increase at the blastocyst stage (Fig. 4). This variation in cell death rate with stage was not predicted by our model, but because the model a priori assumed that once cell death had started it occurred at a uniform rate, this is hardly surprising. Apart from this, the agreement with the model is remarkably good considering its highly simplistic nature.

Embryo Loss.

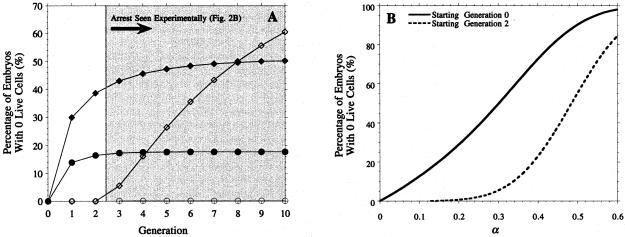
We next turned to whether the estimated levels of cell death could account for the embryo arrest rates presented in Fig. 2B. Although our model does not incorporate the notion of embryo arrest per se, it seems reasonable to assume that such embryos correspond to ones having no live cells, i.e., containing only fragmenting nuclei. The probability of having no live cells is straightforward to compute (see supplemental Appendix), and its dependence on α, n_s and n_f is illustrated in Fig. 5. Although our results above indicate that cell death is absent in early generations, we include some results for n_s = 0 in this figure, because they illustrate the significant role played by the timing of the start of cell death in determining the relationship between individual cell death and embryo loss.

Figure 5.

Embryo loss levels predicted by preliminary model. (A) Embryo loss rate at each generation for a choice of other parameters: ○ α = 0.145, n_s = 2 (Fit I, Table 1); ● α = 0.139, n_s = 0 (Fit IV, Table 1); .⋄ α = 0.485, n_s = 2; ♦ α = 0.3, n_s = 0. (B) Embryo loss rate at the 8th generation as a function of α, assuming cell death starts respectively at generation 0 and 2. In all cases, δ = 0.11, except for Fit IV, where δ = 0.076. The dependence of the embryo loss level on δ is much weaker than that on α or n_s and hence is not shown.

In Fig. 5A, we see the probability of embryo loss at each generation for a number of choices of α, δ, and n_s. For the best-fit parameters (Fit I, Table 1), the probability of the whole embryo dying is negligible (at most 0.15%). We can obtain much more significant levels of embryo loss if we assume that cell death starts from generation 0 (Fit IV, Table 1). This choice leads to an embryo loss rate of 18% by the 8th generation, still less than half the observed level (Fig. 2B). Fig. 5B shows the dependence of the embryo loss level at the eighth generation on the cell death rate α. It shows that to achieve the observed 50% embryo loss level, we require a cell death rate of approximately 30% if cell death starts at generation 0 (n_s = 0, α = 0.3) and 48.5% if it starts at the 2nd generation (n_s = 2, α = 0.485). The course of embryo loss for each of these values of α is also indicated in Fig. 5A. In the n_s = 0, α = 0.3 case, virtually all of the embryo loss occurs by the 2nd generation, i.e., by the 4-cell stage (and the same holds for the case of Fit IV discussed above). This is in contrast to our observed data (Fig. 2B), where significant embryo loss does not occur until the third generation, and there is a steady increase from that point on. This once again reinforces our prediction that cell death does not occur in the earliest stages. The time course for the n_s = 2, α = 0.485 case is much more realistic. However, it is difficult to accept a cell death rate of nearly 50% without strong supporting experimental evidence, and of course this rate is 3 times higher than that suggested by our best fit. Furthermore, the level of embryo loss continues to rise rapidly after the eighth generation, and in fact, with this choice of parameters, all embryos will eventually die in this model.

Fits I–IV in Table 1 were carried out using the data in Fig. 2A, which consists only of approximately the 50% of embryos that survive to the blastocyst stage. Fit V, Table 1, shows the effect of adding 203 “dead” embryos to the data in Fig. 2A. The embryo loss curve for this is very similar to that for fit II (data not shown) and hence still fails to account for the observed levels in Fig. 2B. Incorporating the dead embryos in the model fit thus leads to an inconsistent model. Together, these results indicate that an assumption of uniform cell death rate across all cells and all embryos cannot explain observed levels of embryo loss. This suggests that those embryos that fail to reach the blastocyst stage form a distinct subpopulation from those that develop normally.

Refined Models.

We therefore now refine our model to allow different embryos to have different underlying cell death rates by choosing the value of α at random for each embryo and then simulating its development by using that value as in the preliminary model. This modification can lead to quite a different relationship between cell death rate and embryos loss. Thus, for example, a population of embryos with a uniform intermediate death rate will exhibit almost no embryo arrest, whereas one with 50% of embryos having a low death rate and 50% a high rate will see almost 50% embryo arrest. To complete the description, we need to specify the probability distribution with respect to which α is chosen. The simplest possibility is to assume that α is selected from a finite number of possibilities α₁, … , α_m, with probabilities p₁, … , p_m respectively. Both α₁, … , α_m and p₁, … , p_m can be treated as parameters and estimated by using a maximum likelihood approach as before (subject to the constraint p₁ + … + p_m = 1).

Taking m = 3 gives three possible cell death rates α₁, α₂, and α₃, which we can interpret as low, intermediate, and high rates. The probabilities p₁, p₂, and p₃ then give the proportions of embryos exhibiting each of these rates. When fitted to the extended data set (consisting of the 203 points in Fig. 2A and an additional 203 dead embryos as in Fit V), assuming a starting generation n_s of 2 or later, this yielded values α₁ = 0.07, α₂ = 0.2, α₃ = 1.0 with probabilities p₁ = 0.25, p₂ = 0.27, and p₃ = 0.48 respectively. This suggests that approximately half the embryos have massive levels of cell death. Of the remainder, 25% have low levels (below 10%), and 25% have intermediate rates (in the region of 20%). From Fig. 5B, we see that even the intermediate cell death rate is insufficient to cause significant embryo loss, and hence all of the arresting embryos must belong to the α = 1.0 category. This result is consistent with the observation that approximately 50% of embryos fail to reach the blastocyst stage (Fig. 2B). Note that all those embryos with α = 1.0 will die as soon as cell death is switched on, and the model cannot determine when this occurs using only the data in Fig. 2A. We thus imagine that the embryos in this category die somewhere between the starting and final generations in a way that conforms to Fig. 2B. Increasing m above 3 (i.e., by using more categories) improved the fit but yielded no additional biological insight.

We have also extended the model in a different direction (see supplemental data) to test whether there is any dependence of the cell death rate on embryo cell number. We were able to detect a weak relationship but not one that was statistically significant. We are developing an explanation of the apparent contradiction of this result to the shape of Fig. 2A using our model and will present this in a subsequent paper.

Discussion

Time Course of Apoptosis.

By using a mixture of retrospective data, mathematical modeling, and experiment, we have shown that apoptosis does not occur during the early cleavage stages of human preimplantation development, and significant levels are not seen until the morula stage. This observation is consistent with previously reported results for other species, such as the mouse (11, 16), where cell death does not occur until the blastocyst stage. It has been proposed that unless cells receive signals from other cells or from survival factors, they die by apoptosis (17). However, cleavage-stage embryos are unique in that they are able to develop in the absence of serum or growth factors, and blastomeres can survive in isolation. Furthermore, embryos at these stages appear to have some resistance to chemical inducers of apoptosis such as staurosporine (18).

Early cleavage in the human is under maternal control (19, 20), using transcripts accumulated during oogenesis. This period, during which there is minimal embryonic arrest (Fig. 2B), coincides with limited cell–cell communication between undifferentiated cells (21), a large cytoplasmic to nuclear ratio, a predominance of undifferentiated mitochondria (22), and cell divisions that do not appear to be under the surveillance of cell cycle checkpoints (23). The onset of apoptosis coincides with compaction, an important developmental stage that immediately precedes the first differentiative event during embryogenesis: the formation of the blastocyst. Compaction is mediated by E-cadherin and accompanied by the development of gap junctions, desmosomes (21), and tight junctions. Recently, gap junctions have been shown to propagate apoptotic signals between cells (24). The appearance of apoptotic nuclei also closely follows activation of the embryonic genome. It remains to be seen whether it is this activation, the establishment of cell–cell communication, the ability to identify defective cells, or some other factor (such as the maturation of mitochondria, an important site for the regulation of apoptosis) that plays the most significant role in allowing apoptosis to occur.

Developmental Competence.

We have further examined the relationship between rates of cell death and levels of embryo arrest. We found that if all embryos are assumed to have the same underlying cell death rate, then it is difficult to reconcile observed levels of cell death (Fig. 4) with high rates of embryo loss seen in the human (Fig. 2B). This led us to refine the model to allow each embryo to be “programmed” at the one-cell stage with a different cell death rate, which is constant throughout its development. Fitting the refined model gave the estimate that 25% of embryos have low levels of cell death, 25% have intermediate levels, and 50% have very high levels. Almost all of the embryos in the latter group will arrest by the blastocyst stage. On the other hand, using the fact that cell death does not occur before generation two, we can deduce from Fig. 5B that levels of embryo loss in the first two categories are extremely small (less than 1%) under normal conditions.

However, the cell death rate (20%) in the intermediate group is such that increasing it, for instance because of adverse environmental conditions, can lead to a rapid increase in the level of embryo loss (Fig. 5B). We thus envisage that the 25% of embryos with low death rates will develop normally under most circumstances, those with intermediate rates will develop normally under favorable environmental circumstances but arrest under poor conditions, and the remaining 50% will always arrest. These predictions are consistent with experimental data observed in the literature. Reported rates of blastocyst formation in vitro vary considerably, ranging from 35% (i.e., 65% arrest rate) in a simple salt solution supplemented with BSA (25) to between 60 and 70% (i.e., 30–40% arrest rate) in more optimal media (25–28). Even when considering “ideal” conditions, either embryos in vivo (29) or embryos of only excellent morphology in vitro (3), there is still a significant incidence of embryonic arrest. This correlation between mathematical model and observed data strongly suggests that the factors predisposing an embryo to develop normally or arrest are largely determined at the one-cell stage. Environmental effects modulate these but only to a limited extent, so that there will always be a group of embryos that will arrest and a group that will survive even under significantly substandard conditions.

Causes and Timing of Arrest.

Assuming such a picture is correct and developmental potential is largely determined at or before the zygote stage, than likely causes of arrest include chromosomal abnormalities (5) and/or inadequate oocyte maturation (7). Most arrested embryos (70%) display gross chromosomal anomalies (5). The majority of these arise during oogenesis, at meiosis I (23, 30). It is thought that cell cycle checkpoint mechanisms are not operating at this stage (30), and it has been hypothesized that they may also not be functioning during early cleavage divisions (23) (as has been observed in Xenopus and Drosophila embryos). Lack of checkpoints would permit chromosomal abnormalities to survive until the eight-cell stage when arrest is first seen at significant levels (Fig. 2B). Additionally, this would allow chromosomal abnormalities to arise after fertilization, resulting in mosaic embryos, which have frequently been observed (5, 23). Such postzygotic chromosomal abnormalities could be the result of inadequate oocyte maturation with deficiencies in maternal transcript accumulation. Hence if the spindle or cytoskeleton is disorganized or deficient in the oocyte or early embryo, mitosis and cytokinesis could be impaired, giving rise to chromosomal abnormalities in some cells.

Conclusions

Currently it is thought that a major cause of embryonic arrest is suboptimal culture conditions, with considerable efforts being made to optimize culture media and improve blastocyst development. However, the combination of mathematical modeling with retrospective and prospective experimental observation suggests the embryo is already developmentally programmed at the one-cell stage. We suggest that it is now time to focus our attention on the generation of a healthy zygote, which will require an increased understanding of both male and female gametogenesis, in particular of the events during gamete maturation that lead to competence to undergo fertilization and successful healthy embryo development.

To our knowledge, this is the first time that the complex relationship between levels of cell death and survival of a small groups of cells has been elucidated. Such a relationship is difficult if not impossible to explore by using a purely experimental approach. We were able to overcome this difficulty by supplementing experiments with the development of increasingly sophisticated mathematical models. Similar ideas should be applicable to other problems involving the balance between apoptosis and proliferation, for instance in the early establishment of tumors.

Abbreviation

TUNEL

TdT-mediated dUTP nick-end labeling