Localization Microscopy Reveals Expression-Dependent Parameters of Chromatin Nanostructure

Abstract

A combined approach of 2D high-resolution localization light microscopy and statistical methods is presented to infer structural features and density fluctuations at the nuclear nanoscale. Hallmarks of nuclear nanostructure are found on the scale below 100 nm for both human fibroblast and HeLa cells. Mechanical measures were extracted as a quantitative tool from the histone density fluctuations inside the cell to obtain structural fluctuations on the scale of several micrometers. Results show that different mechanisms of expression of the same nuclear protein type lead to significantly different patterns on the nanoscale and to pronounced differences in the detected compressibility of chromatin. The observed fluctuations, including the experimental evidence for dynamic looping, are consistent with a recently proposed chromatin model.

Introduction

Chromatin nanostructure of eukaryotic cells has been hard to analyze by light optical techniques. Conventional light microscopy is limited physically to a resolution of ∼200 nm, the Abbe limit. Structures below this length scale cannot be resolved by these microscopes.

Chromatin structures above the level of single nucleosomes, however, are typically in the size range between 10 nm and some micrometers (1). The diameter of the presumed chromatin fiber between 10 nm and 45 nm renders it impossible to follow the path of the chromatin fiber by conventional light optical techniques. Thus, chromatin structure can only be inferred by using indirect approaches. Fluorescence in situ hybridization (FISH) has been applied to mark specific sites along the chromosome, measuring the physical distance between the FISH probes (2–5). Thus, a relationship between mean square displacement and genomic separation of two markers can be established. Large-scale organization on the level of the entire cell nucleus can be visualized by distributing FISH labels along the fiber (6) or by using fluorescent stains with a non-sequence-specific DNA binding affinity, such as 4′,6-diamidino-2-phenylindole (DAPI) (7). However, structural information from conventional confocal light microscopy is limited by ∼200 nm laterally and 600 nm axially. Confocal laser scanning fluorescence 4Pi microscopy, where laser light is focused from different sides, allowing for an axial resolution down to the 100-nm range (9), can be used to overcome these resolution limits (8).

The investigation of chromatin nanostructure, i.e., structures with dimensions <100 nm, still faces severe experimental problems. Electron microscopy (EM) has been applied to study both isolated chromatin segments in vitro and thin sections of chromatin in situ (10,11). Although actual optical resolution of nuclear structures in the 10-nm regime has been achieved using advanced EM methods (12), the general restrictions of EM that still remain make highly desirable the development of methods for light optical analyses of nuclear structure at an enhanced resolution beyond the Abbe limit.

In the last years, there have been advances in light optical techniques that have allowed for a resolution of single fluorescence-labeled molecules with localization accuracy ranging down to 20 nm (13–15). The basis of these techniques is the use of different spectral signatures of light from a pointlike source to localize positions of the fluorescent molecules, even if they are close together (<200 nm) (16). The first proof-of-principle experiments were done using spectral precision distance/spectral position determination microscopy (SPDM) (17,18). Since that time, an advanced method has been developed that uses reversibly bleached states of conventional fluorophores like green fluorescent protein (GFP) for localization microscopy (19). The stochastic recovery of fluorophores from the dark state yields to an optical isolation, which allows an accurate position determination far below the Abbe limit. Acquisition of a huge number of images over time results in a good reconstruction of the original distribution of fluorescent markers.

In this study, we present a method combining high-precision light microscopy with statistical methods to obtain information on structure on both the nanoscale and the scale of the nucleus by utilizing approaches from statistical physics. We apply this method to study the distribution of histone H2B inside the cell nucleus. We ask whether there is a recurrent chromatin nanostructure and whether this nanostructure shows differences depending on cell type. We investigate whether the observed nanostructure depends critically on the type of expression of the fluorescent dye. On a larger scale, the density fluctuations are investigated using the concept of compressibility analysis and compared to the predictions of polymer models.

Materials and Methods

Specimen preparation

VH7 diploid human fibroblast cells (kindly provided by Prof. Dr. Beauchamp from Deutsches Krebsforschungszentrum, Heidelberg, Germany) were cultivated in Dulbecco's modified Eagle medium supplemented with 10% FCS, 1% L-glutamine, and 1% penicillin/streptomycin in a standard CO₂ incubator. After the cells were seeded onto coverslips, they were allowed to attach and grow overnight. Using Organelle Lights (Invitrogen, Carlsbad, CA) according to the manufacturer's protocol, emGFP-conjugated histone proteins H2B were expressed. The cells were fixed with 4% formaldehyde in phosphate-buffered saline (PBS) and embedded with ProLong Gold antifade reagent (Invitrogen) 24 h after the transfection.

HeLa cells were cultivated in RPMI medium supplemented with 10% FCS, 1% L-glutamine, and 1% penicillin/streptomycin in a standard CO₂ incubator. HeLa cells of strain I were first seeded onto coverslips and allowed to attach and grow overnight. After using Organelle Lights (Invitrogen) according to the manufacturer's protocol, emGFP-conjugated histone proteins, H2B, were expressed. The cells were then fixed with 4% formaldehyde in PBS and embedded with ProLong Gold antifade reagent (Invitrogen) 20 h after transfection. HeLa cells of strain II (kindly provided by Dr. Tobias Knoch from University Rotterdam and Bioquant Center, University of Heidelberg, Heidelberg, Germany), which stably expressed histone H2B-GFP proteins, were seeded onto coverslips and allowed to attach and grow overnight. Afterward, the cells were fixed using 4% formaldehyde in PBS and embedded with ProLong Gold antifade reagent (Invitrogen).

SPDM setup

The microscopy was based on the principle of spectral precision distance/position determination microscopy (SPDM (17,20); for review, see Cremer et al. (21)). Here, a setup for SPDM with physically modifiable fluorophores (SPDM_PHYMOD) was used (22). Two-dimensional localization of single fluorescent molecules was achieved by stochastic switching. This method is based on a light-induced, reversibly bleached state of conventional fluorophores (23–25). By starting illumination of the sample with an excitation intensity in the range 10 to several hundred kW/cm², some molecules are bleached irreversibly ($M_{fl}\to M_{ibl}$), whereas others are transferred into a reversibly bleached state ($M_{fl}\to M_{rbl}$). The statistical recovery of fluorophores from this state ($M_{fl}\leftarrow M_{rbl}$) can be used for optical isolation of the single fluorescent molecules. For the experiments, only one laser source was needed at an excitation wavelength of λ = 488 nm (Ar488) (Lexel 95-4, Lexel Laser, Freemont, CA). It is used for fluorescence excitation, as well as for the reversible bleaching of fluorophores. After deflection at a mirror, the laser beam is expanded by a factor of 10 using a collimator built of two achromates with focal lengths of 10 mm and 100 mm (Linos Photonics, Göttingen, Germany). Then, an additional lens leads to a more focused spot in the object region so that one can achieve high laser intensity, which is necessary for the localization mode. Via a second mirror, a dichroic mirror (AHF Analysetechnik AG, Tübingen, Germany), and a lens, the beam is focused into the back focal plane of an oil immersion objective lens (100×, NA 1.4, Leica, Bensheim, Germany).

Image segmentation

The segmentation procedure aims at singling out all regions where the histone density was very low. To achieve this, we positioned a quadratic box of linear dimension b at each possible position (with a resolution of 30 nm) and determined the density ρ_b of points inside this box. If the density was below a certain percentage, p, of the maximum density, the region of the box is marked as outside of the analysis region. The box dimension was always set to b = 500 nm. The threshold percentage was set to p = 15% for the HeLa cells of strain I and p = 10% for those of strain II and the fibroblasts. These values were chosen by visual inspection to ensure that no region with little fluorophore content (low histone density) is used for analysis. By using a rather large box of dimension b we automatically excluded heterochromatin regions near the nuclear envelope (Fig. 1 D).

Figure 1.

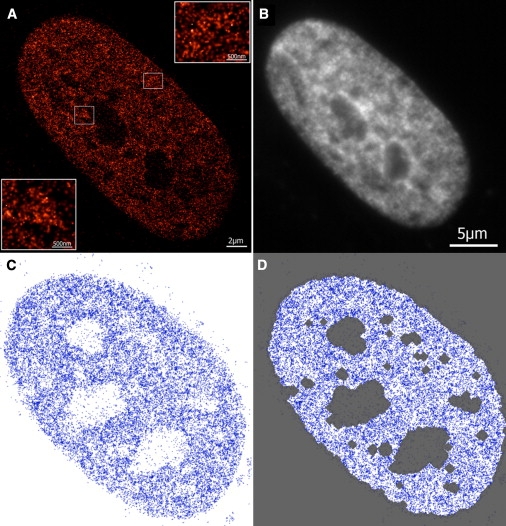
(A) Localization image of histones H2B in the nucleus of a human fibroblast cell labeled with emGFP. The localized fluorophores are blurred with a Gaussian corresponding to their individual localization accuracy. (Insets) Magnifications (4×) of the outlined areas. (B) A conventional wide-field image of the same nucleus as in A. The image was acquired in the conventional epifluorescence microscopy mode. (C) Localized histones of a different fibroblast cell after data processing. Each localized fluorophore is represented by a blue point. The average number of detected points is 124/μm². (D) Result of the segmentation procedure. Gray regions are not included in the data analysis. The image is segmented based on a density threshold procedure to exclude regions outside the nuclear membrane as well as chromatin-depleted regions inside the nucleus, e.g., nucleoli.

Molecular dynamics simulations of a Lennard-Jones fluid

Molecular dynamics simulations of a Lennard-Jones fluid (26) composed of N = 2048 particles and a density of ρ = 0.6σ⁻³ are performed in the NVT-ensemble using the software package Espresso (27). A time step of Δt = 0.005τ was chosen. The Langevin thermostat was initialized with a temperature parameter of T = 1ɛ and a friction of Γ = 0.5τ⁻¹, consistent with the values used in Limbach et al. (27).

Block density analysis

Statistical mechanics is a useful tool for the study of both structural and mechanical properties of a homogeneous system of particles (26). The localized fluorophores at positions r_i can be considered as particles in a volume, V, interacting via a certain potential, U({r_i}), which summarizes all interactions between fluorophores as well as interactions of fluorophores with other constituents of the cell in terms of an effective interaction. What does statistical mechanics tell us then about the system?

Consider now such a many-body system in a volume V. The volume can be subdivided into blocks, q_i, of linear dimension b. The densities inside these blocks yield a density distribution, P_b(ρ), which is still dependent on the block size. Indeed, if the particles were randomly distributed throughout the volume V, then P_b(ρ) should have a Gaussian form. From the block density distribution, P_b(ρ), the moments, 〈ρ_b〉, can be derived. In the case of a Gaussian distribution, the reduced fourth-order cumulant U_b,

$$U_b=1-\frac{{\mu }_4}{3{\mu }_2^2},$$ (1)

should exhibit a value of zero for a Gaussian distribution, i.e., for large b. Here, μ_k = $\langle {\left({\rho }_b-\langle {\rho }_b\rangle \right)}^k\rangle$ denote the centered kth moments.

In a typical fluid system, represented by a Lennard-Jones fluid, for example, the particles are not randomly distributed, but subjected to certain interactions. The typical length scale, ξ, of these interactions determines the scale, below which deviations from the expected Gaussian distribution should become visible. As soon as the block size, b, is larger than the correlation length, ξ, of the order parameters of the system but smaller than the total size of the system, V^1/3, all blocks represent one realization of the ensemble, resulting in a Gaussian distribution. Besides structural information, the density fluctuations contain information about mechanical properties of the system: The isothermal compressibility, κ_T, is related to the density fluctuations by (28)

$$b^2\left(\langle {\rho }_b^2\rangle -{\langle {\rho }_b\rangle }^2\right)={\langle {\rho }_b\rangle }^2{k}_{B}T{\kappa }_T^{\left(b\right)}\text{.}$$ (2)

The actual isothermal compressibility, κ_T, of the system is obtained by extrapolation to large block sizes. Thus, the block distribution is in a sense complementary to the radial distribution function, g(r). Although the latter gives information on the short scale, the compressibility is related to the system's large-scale behavior.

Dynamic loop model

Simulations were conducted using a lattice polymer model described in Bohn and Heermann (29). The lattice size chosen is L = 64, the density is ρ = 10% and the chain length is N = 256. The minimum distance two segments can approach is set to 30 nm, corresponding to a lattice unit of 45 nm in the bond fluctuation algorithm. A persistence length of l_p = 150 nm was used (3), requiring a bending potential U_θ = κ_θ(1 − cos θ) with κ_θ = 1.34 (see Materials and Methods in the Supporting Material). The localized histone distribution was simulated by distributing 5971 points randomly along the contour of the fiber, corresponding to a projected histone density of 150 points/μm².

Results

Data acquisition and image segmentation

To study the spatial distribution of histones and its dependence on cellular or expression parameters, we apply localization microscopy to two different cell types, human fibroblasts and HeLa cells. Two different HeLa strains were used (see Materials and Methods). The histones H2B of fibroblasts and HeLa strain I were labeled with emGFP by using Organelle Lights (Invitrogen) according to the manufacturers protocol. HeLa strain II is a stably transfected cell line expressing an H2B-GFP fusion protein. The measurements were made using an SPDM microscope setup for 2D localization of single fluorescent molecules (19,22,30). Using this microscopy setup, the lateral positions of single histone molecules were determined with localization accuracy in the range of a few tens of nanometers (Fig. 1 A).

After data acquisition and evaluation, the data are provided for each cell as a series of 2D coordinates (x ± Δx, y ± Δy), each point representing a localized fluorophore. An example of a cell after data processing is depicted in Fig. 1 C. To obtain information about structure, we applied a threshold-based density segmentation procedure that defines the region of pixels in which chromatin is found. The segmentation algorithm was parameterized such that regions outside the nuclear envelope, as well as regions within the nucleus that contained no or little chromatin (e.g., nucleoli) as defined by a low detected histone density, were excluded from the analysis (Materials and Methods). Fig. 1 D shows the nucleus depicted in Fig. 1 C with the segmentation results. To ensure that our results are not critically dependent on the segmentation procedure, we applied an independent segmentation approach based on Voronoi tessellation (31) (Section S1 of the Supporting Material).

In total, 74 cells were analyzed (28 fibroblasts, 37 strain I HeLas, and 9 strain II HeLas). The average labeling efficiency varied depending on cell type and strain, yielding average numbers of detected points/μm² of 124 (fibroblasts), 98 (HeLa strain I), and 206 (HeLa strain II). The local density distribution of detected histones is shown in Fig. 2 for a fibroblast cell.

Figure 2.

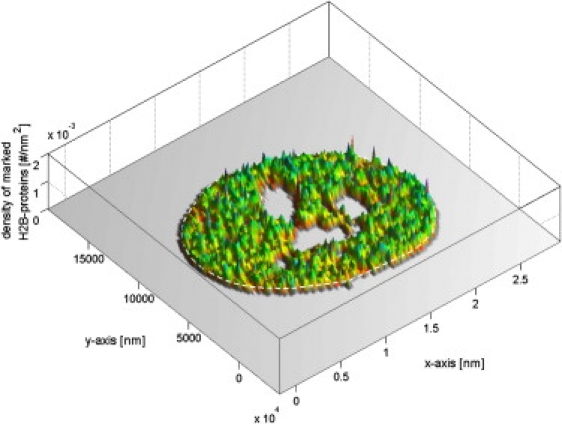
Local density distribution of localized histones after the segmentation procedure for a fibroblast cell. Strong fluctuations in the distribution are visible. Average number of histones is 124/μm².

Radial distribution function reveals structure on the nanoscale

How can we obtain information about chromatin structure at the nanoscale from localization microscopy data? Clearly, structure becomes visible by comparing it to a structureless, i.e., random, distribution of histones inside the cell nucleus. To examine nanostructure, we use the concept of the radial pair distribution function (RDF) g(r) from soft matter physics (26), where it is used to analyze structural properties of systems and transfer it to the context of analyzing cell contents. This RDF describes the variation of the surrounding matter's density as a function of distance. In fact, this RDF yields the factor by which the local histone density differs from a random distribution. The advantage of the RDF is that it can be easily calculated and is independent of localization density. Consider the illustration in Fig. 3 A. Here, a number of N = 20 particles (blue spheres) are distributed in the area of a circle of radius R = 4 around a histone sitting in the center of the coordinate system. The corresponding average density is ρ = N/V = 20/(πR²) ≈ 0.40. We now consider spherical shells of radial extension Δr = 1 and ask, what is the number of particles in these spherical shells (r, r + Δr)? The result is shown in Fig. 3 B (blue bars) together with the expected number of particles in case of a random distribution (gray bars). The RDF is now obtained by calculating the ratio between the actual particle number and the expected number for a random distribution. Thus, the RDF directly indicates deviations from a random distribution. The results are shown in Fig. 3 C. It is important to note that the first shell is depleted of particles, indicating a repulsive short-scale interaction between particles. The second shell is enriched in particles compared to a random distribution (gray line), indicating an attractive interaction at this distance.

Figure 3.

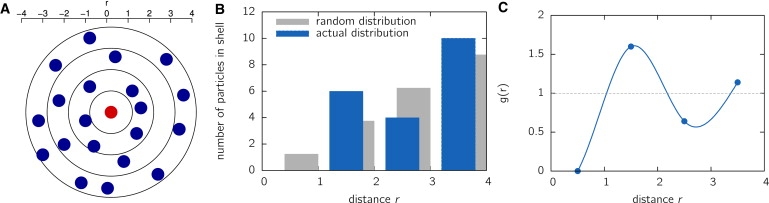
Illustration of the RDF. (A) A 2D system of N = 20 particles in a circle of radius R = 4. The particles arrange around the reference particle at the origin (red circle) in a certain manner. To determine the RDF, the circle is subdivided into spherical shells of thickness Δr = 1. (B) In the next step, the number of particles in each spherical shell is counted (blue bars). This is contrasted to the expected average number of particles if all 20 particles were randomly distributed inside the area (gray bars). (C) The RDF is now obtained by taking the ratio between actual density and average density. The model system shown here displays a particle depletion for short distances (r < 1), indicating a repulsive short-range potential.

Although it will become possible in the future to obtain 3D localization microscopy data, the available images from SPDM microscopy are 2D projections of 3D cells. Projections comprise ∼600 nm perpendicular to the focal plane, leading to a loss of structure information. We first studied a Lennard-Jones fluid as a model system to verify that projections do not conceal important structural information (Section 2 in the Supporting Material). It is clear that projections lead to a blurring of the maxima and minima in the RDF; however, they are still visible even for thick projection slices. To obtain a more quantitative comparison especially for polymer systems, we use simulations of linear chains (self-avoiding walks). The persistence length chosen is l_p = 150 nm, as has been used in other simulations of chromatin (32,33). Assuming such a homogeneous fiber, we have randomly distributed fluorophores along this fiber and performed a projection of a 600-nm slice. The results (Section 3 in the Supporting Material) clearly show that although structural features are blurred out by lowering the maxima, structure is still markedly visible. This finding indicates that although information gets lost by 2D images, the question of whether structure is present can still be answered.

To obtain the RDF for the microscopy data, an average over all localized histones has to be taken, each time determining the histone density in a certain shell (r, r + Δr) from this histone. It is important to note that we evaluate only the densities inside the region specified by our segmentation procedure, meaning that we do not take into account regions outside the cell nucleus or inside nucleoli and other chromatin-depleted regions. This masking procedure ensures that only rather homogeneous chromatin regions are sampled, excluding heterochromatic regions at the nuclear periphery.

The radial distribution function for the cell types studied is shown in Fig. 4 A. First, we observed for fibroblasts, as well as for both HeLa strains, significant differences from a random distribution of histones on a scale <100 nm, indicating the existence of distinct structures. Of more interest, the RDF shows pronounced differences for HeLa cells stably expressing histone H2B-GFP proteins (strain II) and emGFP-labeled cells (strain I). The emGFP-labeled fibroblasts showed the same structural features as strain I of HeLa. Thus, different mechanisms of expression of the same protein lead to a significantly different distribution of localized histones on the nanoscale. Error bars in Fig. 4 A represent the standard deviation in the ensemble of cells, showing that there is considerable structural variation from cell to cell.

Figure 4.

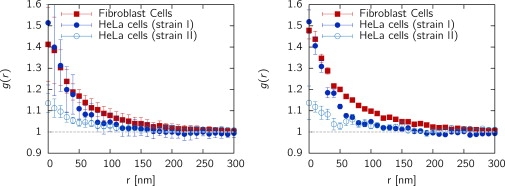
(left) Nanostructure of nuclear histone distribution observed by superresolution light microscopy (SPDM_PHYMOD). The projected RDF, g(r), reveals distinct differences from a random distribution (i.e., g(r) = 1), highlighting the existence of distinct structures on the scale below 100 nm. Results are shown for human fibroblasts and two HeLa strains prepared by different labeling methods. Error bars represent the cell-to-cell variation (standard deviation). Structural hallmarks are found for HeLa as well as fibroblasts independent of labeling methods, but quantitative differences exist. The gray horizontal line corresponds to the (normalized) average density, i.e., a random spatial distribution of histones. (right) For this panel, the average density of localized fluorophores has been adjusted to the minimal value found in the data by randomly removing points such that each cell has the same density. It is important to note that structures can be compared even with different localization efficiencies, as g(r) is a density-independent measure.

What is the effect of different densities of localized histones, as found for the different labeling methods used? To determine whether these have a significant impact on the observed structure of the RDF, we randomly removed detected histones from each cell such that the resulting labeling efficiency is equal in each cell for both fibroblasts and HeLa cells. The results are shown in Fig. 4 B. It is clear that the density does not affect the mean values; rather, the errors become large due to insufficient statistics. Note that the error bars shown in Fig. 4 B represent the standard errors of the cell-to-cell variation rather than the standard deviation. The independence of labeling efficiency is due to the RDF being defined so that it is independent of a particular particle density.

Density fluctuations on the large scale

How can we detect structural features of chromatin organization on a large scale? Again, we look for a measure that yields a constant value for a random histone distribution, i.e., the ideal gas system, such that deviations from a random distribution can be easily made visible.

Consider the case where the histones were randomly distributed throughout the cell. Imagine placing a box of linear size b inside the cell at some position, and count the number of histones, N_b, and the density, ρ_b = N_b/b², inside. Repeating this operation several times yields a density distribution, p(ρ_b), which is, according to the central limit theorem, a Gaussian. The so-called reduced fourth-order cumulant (28),

$$U_b=1-\frac{\langle {\left({\rho }_b-\langle {\rho }_b\rangle \right)}^4\rangle }{3{\langle {\left({\rho }_b-\langle {\rho }_b\rangle \right)}^2\rangle }^2},$$ (3)

is equal to zero for any Gaussian distribution. Thus, a first measure of having structure on the larger scale is given by the condition U_b ≠ 0.

Block density distribution reveals non-Gaussian distribution patterns

In Fig. 5, A and B, we have visualized the method of obtaining the density fluctuations for a fibroblast and a HeLa (strain I) cell, respectively. The cell is divided into blocks of size b = 500 nm and the density inside these blocks is indicated by the color of the blocks. From visual inspection, we found that nonrandom distribution patterns prevail in the cell over large length scales, e.g., the upper part of the fibroblast cell in Fig. 5 A seems to be depleted of fluorophores. This might be due to a heterochromatic region or to inaccessibility of the fluorophores to that region, in turn possibly related to chromatin density. Distinct connected regions with only a small density of localized points can be found throughout the cell spanning length scales of several micrometers. From the block densities, one obtains the density distribution function, P(ρ_b), which is displayed in Fig. 5 C for both fibroblast cells and HeLa cells (strain I) for block sizes of b = 200 nm, b = 500 nm, and b = 1000 nm. The distributions are scaled with the average density to obtain independence of labeling efficiency. As expected, clear deviations from a Gaussian shape are visible on the scale below 500 nm. For b = 1000 nm, deviations from a Gaussian cannot be distinguished by visual inspection; therefore, we apply the above measure, the reduced fourth-order cumulant, U_b (Eq. 3), which should become zero for a Gaussian distribution. It is interesting that the fourth-order cumulant does not vanish even for large block sizes up to b ≈ 1.5 μm (Fig. 5 D), indicating that histones are not randomly distributed throughout the nucleus even on the large scale.

Figure 5.

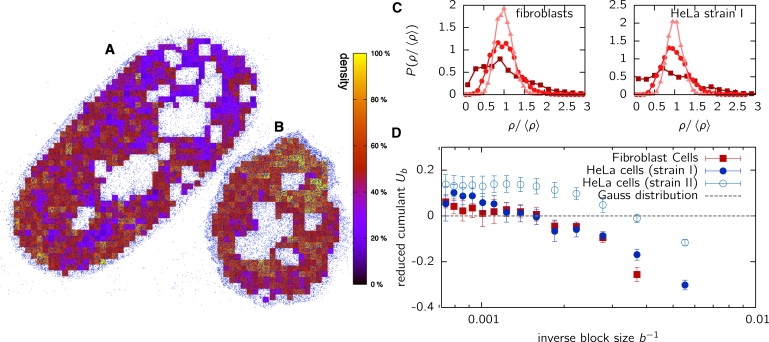
Visualized local densities for a fibroblast cell (A) and a HeLa cell of strain I (B). Shown are the densities of blocks of linear dimension b = 500 nm. They display strong deviation from a random distribution, indicating that structure in the histone distribution exists on that scale. (C) Block density distributions, P(ρ/ $\langle \rho \rangle$), for different values of block size b = 200 nm (squares), b = 500 nm (circles), and b = 1000 nm (triangles). Data are scaled with the average density, $\langle \rho \rangle$, to make the distribution independent of labeling efficiency. (D) The cumulants, U_b (Eq. 3), of the density distribution. For a thermodynamically equilibrated system, cumulants should display a value of zero (dashed line) above a block size b larger than the scale of density fluctuations.

Statistical methods reveal large-scale fluctuations

Statistical mechanics provides another useful measure to determine the scale ξ above which fluctuations in the system vanish. This measure is connected to the compressibility, κ, of a homogeneous equilibrium system and is given by

$${\kappa }_b/{\kappa }_0=b^2\left(\langle {\rho }_b^2\rangle -{\langle {\rho }_b\rangle }^2\right)/\langle {\rho }_b\rangle \text{.}$$ (4)

For an ideal gas, i.e., a random distribution of histones, we find κ_b/κ₀ = 1. Having short-range interactions in the system induces deviations from this value. To visualize this, we used simulations of the well-known Lennard-Jones fluid as a reference for comparison to the experimental histone distributions. Simulations were performed in three dimensions; for the analysis, however, the particle positions were projected on the xy plane. In Fig. 6 A, the block densities are visualized for a block size of b = σ (σ being the hard-sphere radius of the fluid particles), corresponding to the typical length scale ξ = σ of the system. The reduced fourth-order cumulant, U_b, asymptotically adopts the value 0 (Fig. 6 B), indicating a Gaussian shape of the distribution above the length scale ξ. As expected and in agreement with other studies (28), the isothermal compressibility converges to a constant value in the limit of $b\to \infty$ (Fig. 6 C). Strong deviations are visible on the scale below ξ = σ.

Figure 6.

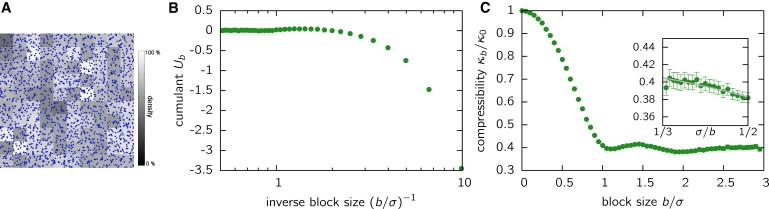
Block density analysis of a Lennard-Jones fluid. (A) Image of the local densities of a projected Lennard-Jones fluid with a block size b = σ. Each projected molecule is indicated by a point. Although σ is the hard-sphere radius of the particles, more than one particle can be found per block as we deal with projections. (B) The reduced fourth-order cumulant, U_b (Eq. 3), approaches the value zero for large b, indicating a Gaussian density distribution above the typical interaction length scale, ξ = σ, of the system. (C) The compressibility of the system. The inset shows that for length scales larger than σ, the block-size-dependent compressibility, κ_b, can be extrapolated to the limit $b\to \infty$, yielding the isothermal compressibility, κ_T/κ₀ = 0.45, of the system. Compressibilities are scaled with the isothermal compressibility of an ideal gas, κ₀, to obtain independence of the system average density.

In principle, the limit κ_b for large block sizes b corresponds to the mechanical compressibility of the system, whereas κ₀ is the compressibility of an ideal gas. Calculating the ratio κ_b/κ₀ renders the results density-independent and is therefore a good measure for investigating structural features of histone distributions independent of the underlying localization efficiency.

It is to be stressed that a direct relation to a real compressibility cannot be established without further assumptions, such as the homogeneity and equilibrium state of the system. We do not know to what extent equilibrium approaches are adequate for this polymer system. Although equilibrium polymer models have been applied successfully in the past to study the structural organization of chromatin (5,34–36), Rosa and Everaers suggested a nonequilibrium state of chromatin (32). Notwithstanding the question of whether chromatin is an equilibrium structure, the ratio in Eq. 4 can be applied to study whether fluorophores are randomly distributed throughout the cell or whether they are clustered. This clustering, which is probably dynamic as the formation of loops, leads to fluctuations in the density distribution, which can be detected using the method described. Fluctuations in the system thus show up in the higher-order moments 〈ρ_b^k〉 of the density distribution. Also, the typcial length scale, ξ, of these fluctuations can be determined: Above this scale, i.e., b > ξ, the resulting cumulant, U_b, becomes zero, whereas the compressibility ratio, κ_b/κ₀, should converge to a constant value here.

Fig. 7 shows the ratio κ_b/κ₀ for the three cell types studied. It is interesting that the data do not converge for stably transfected HeLas (strain II), indicating that fluctuations exist on a length scale far above 1 μm. Fibroblast cells display fewer fluctuations, resulting in a smaller κ_b/κ₀ ratio; however, pronounced differences are found for HeLa cells of strain I. The latter show a compressibility converging at ∼1 μm, indicating that typical chromatin fluctuations were in this size range. Thus, differences in the expression of the histone H2B protein lead to different structural patterns, not only on the short scale, as indicated by the RDF, g(r), but also on the scale of the nucleus. The compressibility strongly differs both for different cell types, suggesting that large-scale properties depend on the cell's differentiation state, and for different labeling methods. To exclude the possibility that insufficient statistics inside the cell is responsible for the observed behavior, we have simulated cells of the same shape and density using a random distribution of points. For all block sizes studied, the simulation shows no deviation from the expected value κ_b/κ₀ = 1, rendering statistics issues unlikely.

Figure 7.

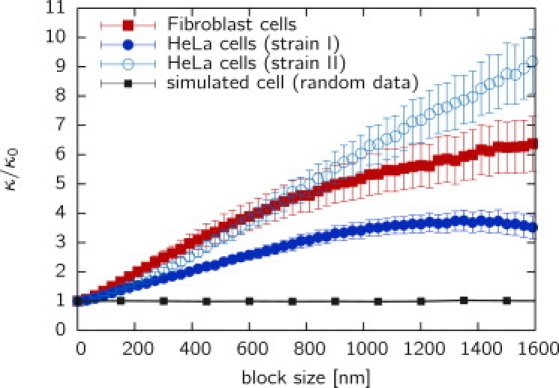
Compressibility ratio, κ_b/κ₀, versus block size, b. The compressibility, κ_b, is scaled with the compressibility of an ideal gas, κ₀ = (ρk_BT)⁻¹, to obtain density-independent values. Shown are the data for fibroblast cells and HeLa strains I and II. To eliminate the influence of finite-sized effects, cells of the same shape have been simulated with a random distribution of localized fluorophores, yielding the expected value of κ_b/κ₀ = 1. The nonconvergence of the compressibility indicates large-scale fluctuations of the histone distribution in the cell nucleus.

The observed fluctuations on the large scale might reflect regions with locally different chromatin density. Experimental studies indicate that gene-rich (ridges) as well as gene-poor (antiridges) regions spread over an average distance of up to 1–2 μm (5). This value corresponds to estimates of the average size of chromosome territories (37). Ridges and antiridges show pronounced differences in the compaction of chromatin, leading to histone density fluctuations.

It is interesting that the compressibility is markedly larger for all three cell types than for an ideal gas, i.e., a random distribution of points. This is somewhat unexpected, as interactions typically lower the strength of the fluctuations. The Lennard-Jones system, for example, shows a compressibility, κ_T, that is lower by a factor of ∼2 (Fig. 6 C) compared to the ideal gas system.

Loop formation induces observed fluctuations

Large-scale chromatin organization has been explained using polymer models with loops (5,34,35,38). Recently, dynamic loop formation was shown to act as a unified framework for chromatin folding (29), the results of this Dynamic Loop model being in agreement with a variety of experimental observations. This model correctly predicts, among other things, the folding of chromatin regions into a confined subspace of the nucleus and the formation of chromosome territories. Can such a polymer model explain observed density fluctuations on the large scale? To test such an assumption, we have simulated chromosomes with a persistence length of l_p = 150 nm (3) in a system of density ρ = 10%, close to the chromatin density inside the cell (39). Histones were then randomly distributed along the contour of the chromatin fiber with a density resembling the experimental density of localized histones. In the next step, the compressibility ratio was calculated from a 600-nm projection for different block sizes b. It is of interesting that the observed compressibilities, κ_b/κ₀, are much larger than the ideal gas value of unity (Fig. 8). Compared to the case of linear chains (self-avoiding walks), polymers with looping interactions display stronger fluctuations increasing with the looping probability, p. The block-size dependent compressibilities, κ_b, adopt a constant value in the limit of large b. Extrapolated compressibilities range from κ_b/κ₀ ≈ 2 (linear chains) up to κ_b/κ₀ ≈ 6.9 (0.56 loops/segment on average). It is interesting that dynamic loop formation induces strong fluctuations in the system similar to the experimental findings. Inhomogeneities can thus be interpreted as fluctuations due to dynamic looping without needing to refer to nonequilibrium polymer systems.

Figure 8.

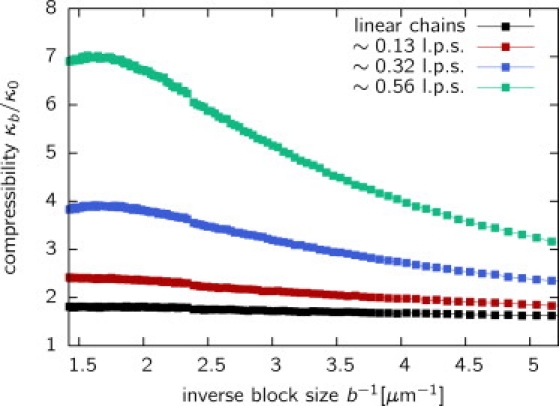
Block-size-dependent compressibility ratio, κ_b/κ₀, for the Dynamic Loop model (29). Shown are simulation results in a system at biological chromatin density, ρ = 10%, for various looping probabilities. The black line corresponds to the case of linear polymers (self-avoiding walks); other curves display looping polymers with various average numbers of loops per segment (l.p.s.). The compressibility is markedly larger than the ideal gas case, κ₀, for polymers with dynamic loops.

Conclusions

We have applied 2D localization light microscopy and statistical techniques to infer structural features and mechanical properties at the nuclear nanoscale. Superresolving localization microscopy allowed us to take a look at the chromatin nanostructure with a noninvasive method. Such light optical methods to resolve structures by optical isolation are well established and known to be able to resolve objects on the scale of single histones, allowing for the analysis of structures on the nanoscale.

To study the spatial distribution of histones and its dependency on cellular or expression parameters, we applied localization microscopy to two different cell types, human fibroblasts and HeLa cells. Two different HeLa strains were used. One HeLa strain is labeled with emGFP, the other strain is a stably transfected cell line expressing an H2B-GFP fusion protein.

Statistical analysis of the histone distribution revealed distinct differences from an average density distribution (Fig. 4). It could be shown that below the Abbe resolution limit of ∼200 nm, nucleosomal structures are existent in cell nuclei, a result which was shown to be robust with respect to cell type, strain, and labeling method. Our results furthermore indicate that different mechanisms of expression (plasmid, stable integration) of the same protein may lead to significantly different localization patterns on the nuclear nanoscale.

Structural and mechanical properties of the histone distribution were obtained by evaluating local density fluctuations inside the cell nucleus. We found that the histone distribution shows pronounced differences from an ideal gas or a simple fluid organization. Interestingly, density fluctuations exist on scales >1–2 μm, a result which is probably related to differences in large-scale chromatin compaction such as that found in ridges and antiridges. One mechanical measure directly derived from the histone distribution is the compressibility of chromatin (Fig. 7). Although only corresponding to a mechanical compressibility under the assumption of chromatin being in an equilibrium state, this measure obtains important information about fluctuations and can be used for comparison of different cell types. We found that the compressibility values deviate with respect to cell type and expression mechanism. A common feature of chromatin organization seems to be a higher compressibility compared to a fluid of equal density. This increase in compressibility, which is even larger than that found for the noninteracting ideal gas, is in agreement with the recently proposed Dynamic Loop model (29), suggesting that loop formation mediates the observed large fluctuations. It is important to note that our results show that cell-type-specific differences here might be related to different abundances of intrachromatin contacts. Thus, the compressibility ratio, κ_b/κ₀, offers a quantitative tool for distinguishing different cell types or expression mechanisms and allows for a comparison to polymer models of chromatin.

In this study, we found measures that show pronounced quantitative differences dependent on the expression mechanisms, whereas we could not find evidence of typical changes depending on specific cell type. It should be noted that the method at hand offers a tool that allows for a variety of applications, distinguishing between different cells or different states of cells. For example, the structure of chromosomes in both interphase and metaphase is still heavily under discussion. The method presented here can be used to perform a quantitative comparison between cells in interphase and metaphase, deriving structural differences both on the nanoscale and on the scale of the entire nucleus.

Recently, proof-of-principle experiments clearly showed that localization microscopy can be applied to two-color samples (30) as well as to FISH-labeled probes (40). These techniques offer completely new avenues for studying structural changes of chromosomes in cancer cells. It has been shown that certain chromosomes spread throughout the nucleus on tumorigenesis (41). The structure of such single cell types could be compared by combining FISH localization microscopy with our statistical tools. Similar expression-sensitive analysis methods could be used, for example, to study the nanostructure of gene-rich and highly transcribed regions in comparison to gene-poor regions with little transcriptional activity. These show different folding patterns on a scale of ∼0.5–2 μm (5,6), yet it is not clear whether differences exist on the nanoscale. Other interesting fields of analysis comprise organization of telomers and heterochromatin foci.

In general, the method might be useful to distinguish between cells in different states characterized by a variation in nanostructural chromatin organization. Thus, the combination of localization microscopy and statistical methods opens new possibilities for obtaining mechanistic insight into the nuclear structure and the fundamental processes of life.