Two-Dimensional Continuum Percolation Threshold for Diffusing Particles of Nonzero Radius

Abstract

Lateral diffusion in the plasma membrane is obstructed by proteins bound to the cytoskeleton. The most important parameter describing obstructed diffusion is the percolation threshold. The thresholds are well known for point tracers, but for tracers of nonzero radius, the threshold depends on the excluded area, not just the obstacle concentration. Here thresholds are obtained for circular obstacles on the continuum. Random obstacle configurations are generated by Brownian dynamics or Monte Carlo methods, the obstacles are immobilized, and the percolation threshold is obtained by solving a bond percolation problem on the Voronoi diagram of the obstacles. The percolation threshold is expressed as the diameter of the largest tracer that can cross a set of immobile obstacles at a prescribed number density. For random overlapping obstacles, the results agree with the known analytical solution quantitatively. When the obstacles are soft disks with a 1/r¹² repulsion, the percolating diameter is ∼20% lower than for overlapping obstacles. A percolation model predicts that the threshold is highly sensitive to the tracer radius. To our knowledge, such a strong dependence has so far not been reported for the plasma membrane, suggesting that percolation is not the factor controlling lateral diffusion. A definitive experiment is proposed.

Introduction

The size dependence of the diffusion coefficient of a species in the plasma membrane is of biophysical interest because the sizes of species in the membrane differ considerably: free fatty acids, cholesterol, phospholipids, proteins with single or multiple transmembrane helices, and protein complexes. A complication, of course, is that the dimension controlling obstruction for a particular pair of tracer and obstacle species may be the intracellular, transmembrane, or extracellular diameters.

The overall size dependence of the diffusion coefficient is affected by three factors.

First is the inherent size dependence in an unobstructed bilayer. The classical Saffman-Delbrück treatment indicates that this effect is small, with the diffusion coefficient approximately proportional to the logarithm of the particle radius (1). Later work suggests the effect may be larger (2).

Second is obstruction by the membrane skeleton. Diffusion across membrane skeleton barriers (3) may require fluctuations in the barrier, the membrane, or both that are large enough to allow the tracer to pass. This mechanism is likely to be highly sensitive to tracer size. Alternatively, diffusion may require dissociation of network segments from each other or the membrane. This mechanism would be less sensitive to tracer size. Analysis of either mechanism would require detailed modeling of the dynamics of the membrane skeleton and membrane (4).

Third, the factor considered here, is obstruction by immobile species in the membrane, such as proteins immobilized by attachment to the cytoskeleton.

The most important parameter describing diffusion in the presence of immobile obstacles is the percolation threshold, the obstacle concentration at which long-range conducting paths disappear and the long-range diffusion coefficient D goes to zero. To describe obstructed diffusion, it is more accurate to find the threshold directly than to extrapolate a low-density expansion in the obstacle concentration to find the concentration at which D = 0. Recent work by Novak et al. (5) showed that D in an obstructed system can be approximated well by a simple two-parameter equation in which the parameters are the percolation threshold and a scaling exponent.

Previous work (6) using a triangular lattice showed that the threshold is highly sensitive to the size of the diffusing particle, but the use of a lattice model gave low resolution. That work was restricted to point tracers and small hexagons. Here we extend the work to the continuum case, to eliminate the lattice approximation and to improve the resolution.

A further advantage is that the results are immediately in the appropriate form for comparison with experiment. The results of a lattice model are in abstract form; one can choose the lattice constant ℓ to be any length provided that the jump time τ is redefined according to

$$l^2=4D_0\tau ,$$

where D₀ is the diffusion coefficient in the unobstructed case. Here we use continuum Brownian dynamics, which has an inherent length scale, the characteristic length of the potential. The results are therefore in physical units, with obstacle concentrations given as a number density in particles/μm², and the percolation threshold given as the diameter in nanometers of the largest particle for which a percolating path exists.

Model

We consider two-dimensional diffusion of a tracer particle in the presence of a set of immobile obstacles. The goal is to find the largest tracer that can cross a given configuration of immobile obstacles. To generate the configuration, we place a prescribed number of mobile obstacles in a region of prescribed size and equilibrate them by either Brownian dynamics or Monte Carlo moves. Then we immobilize the equilibrated obstacles. (In the physics literature, this would be called a quenched-annealed system (7,8).) We find the diameter of the largest tracer that can cross that obstacle configuration by calculating a particular bond percolation threshold on a Voronoi diagram. Programming details are given in the Supporting Material. Preliminary results were presented earlier (9).

Earlier work

A similar approach was used long ago in the physics literature to study percolation in the void volume of spheres, the so-called Swiss cheese or void percolation model (10,11) and in the engineering literature for motion planning of robots among obstacles (12,13). Work was also done on the distinct but complementary problem of percolation of the obstacle phase (see for example (14)).

In the Swiss cheese model, the cheese phase is conducting and the holes are obstacles. The random widths of the necks—the narrow regions between obstacles—play a crucial role, different in two and three dimensions, as shown for electrical conductivity (analogous to diffusion), elasticity, and fluid permeability (15–17). Höfling and co-workers (18–20) examined this aspect of the problem by simulations and theory using the Lorentz model, in which a point particle moves by Newtonian mechanics among random immobile obstacles. These results are applicable to diffusion even though they are based on ballistic motion, because, first, the connectedness of the unobstructed region is the same for Newtonian and Brownian particles, and, second, the large number of collisions with the obstacles makes the large-scale motion diffusion-like.

An interesting series of articles by Sung and Yethiraj (21–23) used this Voronoi approach to examine diffusion in hard-sphere and hard-disk systems at nonzero tracer concentration. The emphasis was on evaluating diffusion coefficients and examining anomalous subdiffusion as well as finding percolation thresholds. They examined (22) the effect of different types of random arrangements of hard-sphere obstacles:

• 1.Random sequential insertion, stopping short of the parking limit;
• 2.An equilibrated hard-sphere fluid with random spheres removed; and
• 3.Equilibrated 16-bead chains of spheres.

The systems had different percolation thresholds and other properties, even though all the systems were hard spheres of the same diameter at the same number density, and differed only in their organization.

Voronoi methods were used recently to study percolation in filamentous networks (24). The approach used here and by Mickel et al. (24) is the same, but the articles are complementary. Mickel et al. examined three-dimensional obstruction by a collagen network characterized experimentally, and their article emphasized the morphological analysis techniques used to extract the network structure from images. We use standard computer models of two-dimensional fluids to examine obstruction by disks, and we emphasize the Voronoi analysis.

From the standpoint of the percolation literature, both this article and that of Mickel et al. (24) are somewhat nonstandard in that we express the percolation threshold in terms of the maximum diameter of a percolating particle, rather than an area fraction. This choice of variables is appropriate to the biological question. For completeness, we relate the percolation properties to the area fraction, and in the Supporting Material we present a scaling analysis in terms of the diameter.

Becker and Ziff (25) have recently published an extremely precise determination of the bond and site percolation thresholds for the Voronoi diagram and the Delaunay triangulation. The problem they treat, the standard bond percolation problem on Voronoi diagrams, is distinct from the problem treated here. In the standard problem, bonds are chosen to be nonconducting at random; here they are chosen based on the separation of the corresponding obstacle pair. The simulations of Sung and Yethiraj (21,23) directly showed that these problems are distinct; in two dimensions at the obstacle concentration chosen, the threshold based on separation was 0.526 but the threshold based on random assignment was 0.667.

A key principle underlying the entire argument is that the excluded area seen by tracers of a particular radius controls the percolation of those tracers. Obstruction of a tracer of radius R by point obstacles is equivalent to obstruction of a point tracer by obstacles of radius R (6,13,26).

The Voronoi diagram and bond percolation

The Voronoi diagram is a standard construction in computational geometry (27), with a wide variety of applications in fields ranging from physics to ecology. For a encyclopedic discussion see the book of Okabe et al. (28). Given a set of points in a plane, the Voronoi diagram divides the plane into, so to speak, “polygons of influence” for each point. Each polygon is that part of the plane closer to its central point than to any other points in the set. The Voronoi diagram decomposes the entire plane into distinct polygons in contact only at their edges or vertices, so it is said to be a tiling or tessellation.

The key property of the Voronoi diagram used here is that each edge of a Voronoi polygon is a line segment equidistant from a pair of obstacles, as shown in Fig. 1 a. We label each edge—or Voronoi bond—with the distance between the pair of obstacles defining the bond. This distance is the diameter of the largest tracer that can fit between these obstacles. The Delaunay triangulation is the dual of the Voronoi diagram (27,28), so we refer to the pair of obstacles defining a Voronoi bond as the dual pair of obstacles of that bond.

Figure 1.

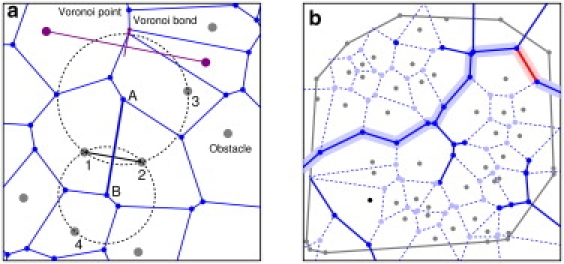
(a) A small part of a Voronoi diagram. (Gray) Obstacles. (Blue) Voronoi points and bonds. Bond AB is equidistant from obstacles 1 and 2, so the largest tracer that can move along bond AB is of diameter d₁₂. In terms of percolation, if d(tracer) < d₁₂, bond AB is conducting, and if d(tracer) > d₁₂, bond AB is nonconducting. Voronoi point A is equidistant from obstacles 1, 2, and 3. Voronoi point B is equidistant from obstacles 1, 2, and 4. A Voronoi bond and the line joining the dual pair of obstacles are perpendicular. The two lines often intersect inside the Voronoi bond but need not do so, as in the case (purple) of the short Voronoi bond, its extension, and the line joining the obstacles. (b) An example of the percolation threshold on a Voronoi diagram. (Gray circles) Obstacles. (Blue circles) Voronoi points (dark blue for connected points and light blue for unconnected). (Solid blue lines) Conducting bonds. (Dashed blue lines) Nonconducting bonds. (Highlighted line) Backbone. The tracer diameter is 0.1962, and this system percolates east-west but not north-south. (Red) Narrowest bond of the east-west backbone. When the tracer diameter is increased to 0.2011, this bond becomes nonconducting and the system no longer percolates in either direction. Also shown here are dangling ends, isolated clusters, and the convex hull of the obstacles (gray polygon).

In general, the bond percolation problem is this: In a system of conducting and nonconducting bonds, is there a continuous conducting path across the entire system in the limit of an infinite system? Here, more specifically, for a tracer of given diameter, is there a continuous conducting path across the entire system? Or to rephrase the question, for a given configuration of obstacles, what is the largest tracer for which there is a percolating path? There is a percolating path for any smaller tracer; there is no percolating path for any larger tracer.

Note that on a percolating path there are two types of bonds. Backbone bonds are actually part of the conducting path, whereas dangling bonds are dead ends that may simply trap the tracer temporarily. (Trapping by these dead ends is a major contributor to the anomalous subdiffusion of a tracer on the percolating cluster at the threshold, but the dead ends do not affect whether the cluster percolates.) There are also isolated clusters of bonds, that is, clusters of bonds not connected to the percolating cluster and too small to percolate themselves.

In principle, one can solve the problem as follows (Fig. 1). Label each bond with the distance d_ij between its dual pair of obstacles. Sort the list of bonds according to d_ij. In the sorted list, mark bonds as nonconducting, starting with the smallest d_ij and ending when the system no longer percolates. The values of d_ij just above and below the threshold give bounds on the percolation diameter d_c. In practice the threshold is found by bisection but the sorting method is a useful way to visualize the process and to verify that the program is working properly. In the tests for percolation, the north, south, east, and west edges of the system are defined by the quadrant in which the Voronoi bonds cross the convex hull of the obstacles. In the calculations, a set of 100–1000 obstacle configurations is generated and the thresholds (both north-south and east-west) are found. The distribution of thresholds is shown as the cumulative distribution function (CDF), and the percolation threshold is found by extrapolating the mean of the distribution of d_c to an infinite system.

Linearity in particle size

The basic procedure is to calculate the equilibrium configuration of obstacles of prescribed diameter, reduce them to immobile point obstacles, and find the percolation threshold for the point obstacles. Is this valid?

At the level of the individual Voronoi bond between an obstacle pair, the system is linear in the sense that obstruction is controlled entirely by the distance d between centers of the obstacle pair. The bond is conducting if, for example, the obstacle radius is 0 and the tracer radius is < d, or if the obstacle radii are d/3 and the tracer radius is < d/3. At the threshold, the single narrowest bond on the percolating path determines the threshold, and passage of this bond is determined by the sum of the tracer radius and the radii of the obstacles dual to that bond.

To verify the validity of this argument, a set of hard-disk obstacle configurations was generated by Monte Carlo methods, and the CDF was calculated for a range of tracer diameters. The resulting CDFs were identical, except that each was shifted by the corresponding tracer diameter. Of course, the excluded area for a tracer is not linear in the tracer radius on account of the overlap of excluded areas for neighboring obstacles, as will be examined later.

Results

We consider three model interactions in detail as a function of the number density of obstacles: random overlapping obstacles, for which exact theoretical results are available; soft disks with a power-law repulsion in equilibrium configurations from Brownian dynamics (29); and hard disks in equilibrium configurations from Metropolis Monte Carlo calculations (29). The potential used is

$$V\left(r\right)=V_0{\left(\sigma /r\right)}^n,$$ (1)

typically with V₀ = 1 kT and n = 12. Here σ = 4 nm is the disk diameter, k is the Boltzmann constant, and T is temperature. The choice of σ is somewhat arbitrary but it is the value used for mobile integral proteins in the work of Grasberger et al. (30) on crowding in membranes. As n increases, the potential steepens, and n → ∞ is the hard disk interaction. Later we examine the effect of changes in V₀ and n. In terms of number densities, the concentrations used are 4k, 8k, 16k, 24k, 32k, 40k, and 48k particles/μm² (1k = 1000). If area fractions are defined using a disk radius of σ/2, these number densities correspond to approximate area fractions of 0.05, 0.10, 0.20, 0.30, 0.40, 0.50, and 0.60 respectively. Fig. 2 shows the radial distribution functions g(r) for these concentrations. As the obstacle concentration increases, more structure is apparent, but the system is clearly fluid at all concentrations, as expected. The highest reduced density ρσ² = 0.7680 is well below the known values for transitions to a hexatic phase (1.000) or a solid phase (1.0198). (See Hurley and Harrowell (31) and references therein for molecular dynamics results for reduced densities between 0.91 and 0.98.)

Figure 2.

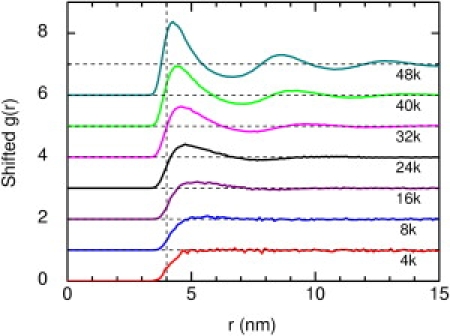
Radial distribution functions g(r) of obstacles for the indicated number densities (units: 1000 particles/μm²). For clarity, g(r) is offset vertically by one unit for each successive number density above 4k, and the limiting value g(r) = 1 is shown for each. The vertical line is σ = 4 nm.

CDF of percolation diameters

We find the percolation diameters for a prescribed number of independent obstacle configurations at a prescribed number density n of obstacles and system size L × L. The data is analyzed in terms of the CDF of the diameters.

As L increases, the fluctuations in the percolation diameter decrease and the CDF of the diameters steepens, as shown in Fig. 3. In the limit of an infinite system, the transition is infinitely sharp and occurs precisely at the percolation threshold. This sort of sharpening is a general feature of phase transitions in finite systems as they approach the thermodynamic limit.

Figure 3.

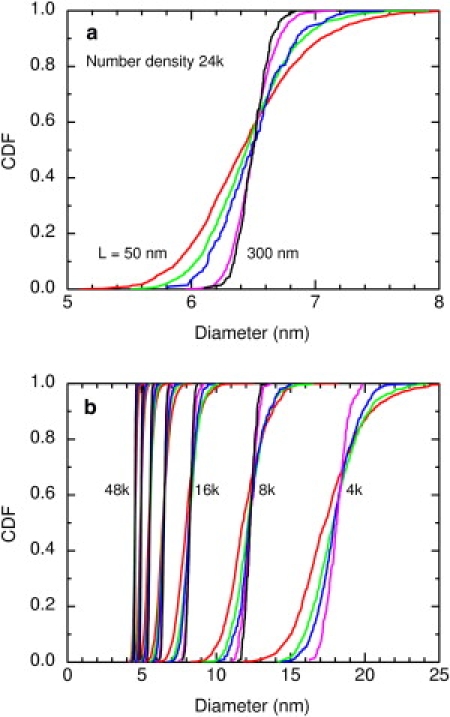
The cumulative distribution functions (CDFs) of the percolation diameters steepen as the system size increases and as the number density increases. (a) CDFs for a number density of 24k/μm². System sizes are L = 50, 76, 100, 200, and 300 nm, and the numbers of obstacles are 60, 139, 240, 960, and 2160. (b) CDFs for various system sizes for number densities of 4k, 8k, 16k, 24k, 32k, 40k, and 48k/μm². All results are for the standard soft repulsive potential.

Fig. 3 a shows the steepening of the CDF at a number density of 24k/μm². The transitions for the smallest system, L = 50 nm, is gradual, but the transition of the largest system, L = 300 nm, is much steeper. In a fluorescence photobleaching recovery experiment or a pulsed gradient spin echo experiment, the length scale is several micrometers so the percolation transition will be sharp, but a single-particle tracking experiment might see a more gradual transition. Fig. 3 b shows the steepening with system size over the entire range of number densities examined. The CDFs steepen as the system size increases at constant number density and as the number density increases at constant system size.

Percolation diameters

We evaluate the percolation diameters from the midpoints of the CDFs at a given number density for systems of various sizes L, as shown in Fig. 4 a for random overlapping disks and in Fig. 4 b for soft repulsive disks. In both cases, the percolation diameters are weakly dependent on system size. To obtain the final percolation diameters, we follow the standard procedure from the percolation literature and plot the percolation diameters versus 1/L^1/ν and extrapolate to infinite L. Here ν = 4/3 is a scaling exponent. Details are given in the Supporting Material.

Figure 4.

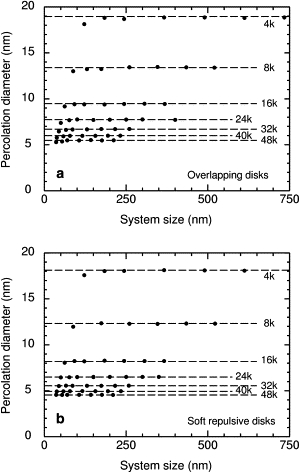
Percolation diameters d_c as a function of system size L for the indicated number densities, in units of 1000 obstacles/μm². (a) Thresholds for random overlapping disks rapidly approach their theoretical value as the system size is increased. (Points) Mean d_c from simulations. (Lines) Theoretical thresholds calculated from the known percolation threshold for overlapping disks on a continuum (Eq. 3). (b) Thresholds for 1/r¹² soft repulsive disks as a function of system size. (Points) Mean d_c from simulations. (Lines) Thresholds calculated for each number density by extrapolation to an infinite system.

Random overlapping disks are a useful test case because exact results are known. The percolation diameter d_c can be obtained trivially from the known percolation threshold for overlapping disks (32) ϕ_c = 0.6763475. Random overlapping disks are Poisson-distributed, so the area fraction at percolation is (33)

$${\varphi }_c=1-\exp \left(-{\eta }_c\right),$$ (2)

where η_c = ρπd_c²/4 is the reduced density at the percolation threshold and the number density ρ is the number of disk centers per unit area. So for a prescribed value of ρ, the percolation diameter is

$$d_c=\sqrt{\frac{4}{\pi \rho }\left[-\ln \left(1-{\varphi }_c\right)\right]}=\frac{1.1985}{\sqrt{\rho }},$$ (3)

which gives the calculated percolation diameters in Fig. 4 a. In the simplest possible estimate of d_c, if the obstacles are assumed to form a square lattice with lattice constant ℓ, the percolation threshold d_c(sq) is ℓ, the corresponding number density is ρ = 1/ℓ², and

$$d_c\left(sq\right)=1/\sqrt{\rho }\text{.}$$ (4)

That is, a back-of-the-envelope calculation is only off by 20%.

Earlier work (6) using the triangular lattice showed that the percolation threshold was strongly dependent on tracer radius. For random point obstacles, as the tracer size increased from points to hexagons of radius 1 to hexagons of radius 2, the threshold decreased from 0.4990 to 0.1156 to 0.04823. Here according to Eq. 3 if we prescribe d, the number density at percolation ρ_c ∝ 1/d², showing that in the continuum case the dependence on tracer size is also strong, though there does not appear to be a simple quantitative connection between the two problems.

Membrane proteins can be modeled more realistically as soft disks interacting by a power-law repulsive potential (Eq. 1). Random distributions of soft disks are generated by a Brownian dynamics calculation. After equilibration, the obstacle positions are fixed, and the percolation threshold is found as before.

As in the case of overlapping disks, the percolation diameters for the soft repulsive disks are only weakly dependent on system size (Fig. 4 b). Furthermore, the good agreement of theory and simulation for overlapping disks suggests that the system sizes for soft disks are large enough to give the limiting value of the threshold. The calculations for soft disks were done with the same system sizes and numbers of particles as those for overlapping disks. Only the interaction is changed, and it is short-ranged.

Fig. 5 shows the principal result of this work, the percolation diameter as a function of the number density of obstacles. The points are results for overlapping and soft disks. As expected, changing the obstacles from overlapping to soft reduces the size of the largest percolating tracer. That is, the overlapping obstacles obstruct less efficiently. The solid line is the theoretical curve (Eq. 3) for random overlapping disks. The calculated points agree well with the theoretical curve. Ratios of calculated to theoretical values range from 0.992 to 1.008, with a mean of 1.0007. Also shown are the results for hard disks. The dashed line is the curve for obstacles arranged in a square lattice. The results for soft disks are distinct from all of these curves, but the differences are relatively small. Given the uncertainties in the number density of immobile proteins in the plasma membrane, either Eq. 3 or Eq. 4 could be used as a first approximation.

Figure 5.

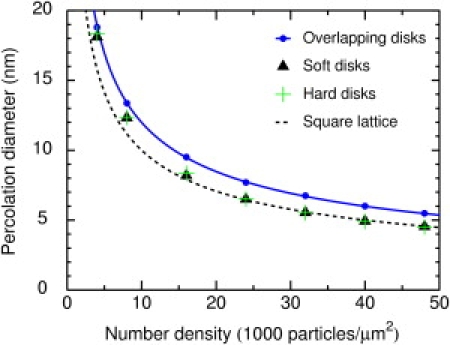
The percolation diameter as a function of number density for overlapping disks, 1/r¹² soft repulsive disks, and hard disks. (Upper curve) Theoretical curve (Eq. 3) for overlapping disks. (Upper circles) Data points for overlapping disks. (Triangles) Data points for soft disks. (Plus signs) Data points for hard disks. (Dashed line) Threshold for obstacles forming a square lattice.

Table 1 shows numerical values of the calculated percolation thresholds for various number densities of obstacles. The thresholds are given as diameters and area fractions. The area fractions are found as described later. The standard deviation for the percolation diameters is estimated to be 0.8% as discussed in the Supporting Material. For overlapping obstacles, the mean area fraction based on the Monte Carlo simulations is 0.6767 ± 0.0058, in good agreement with the literature value (32) for the percolation threshold of random overlapping disks, 0.6763475. This comparison is a useful check of the methods.

Table 1.

Percolation diameters d_c and area fractions

Number density	Overlapping obstacles		Soft obstacles
1/μm2	dc (nm)	Area fraction	dc (nm)	Area fraction
4,000	18.800	0.6663	17.952	0.6681
8,000	13.348	0.6715	12.342	0.6769
16,000	9.540	0.6790	8.176	0.6754
24,000	7.757	0.6774	6.490	0.6904
32,000	6.773	0.6831	5.550	0.7099
40,000	6.017	0.6796	4.931	0.7266
48,000	5.498	0.6801	4.541	0.7539

Disks with modified interactions

Modifying the interaction or boundary condition has little effect on the percolation diameters, as shown in Table 2. For the standard potential, V₀ = 1 kT and n = 12. The percolation diameter decreases as n increases at constant V₀ and as V₀ increases at constant n. The effects are small. The largest shift, for V₀ = 4, is only 1.5 times the estimated standard deviation but some shifts are real, as argued in the Supporting Material .

Table 2.

Effects of various parameters on d_c for number density 24k/μm²

	dc (nm)
Exponent
n = 6	6.556
n = 12	6.498
n = 18	6.460
Hard disk	6.512
Coefficient
V0 = 1	6.498
V0 = 2	6.454
V0 = 4	6.419
Boundary conditions
Periodic	6.520
Finite	6.498

If periodic boundary conditions are imposed in one direction and the threshold found in the other direction, the percolation diameter increases, as it must because the periodic boundary conditions allow conducting paths that would not otherwise exist. For all system sizes, d_c is consistently slightly greater for periodic boundary conditions, but the effect decreases as the system size increases. The effect did not disappear on extrapolation to zero, but the difference is well within the error bars of d_c.

As n increases, the disks become more strongly repulsive, overlap less, and become more effective obstacles, so the percolation diameter decreases. One might expect the trend to continue monotonically to the hard disk limit n → ∞, but it does not at this obstacle concentration. The trend can be understood in terms of the radial distribution functions in Fig. 6. The hard disks tend to clump together in contact, as shown by the peak of the hard-disk g(r), so the hard disks are less effective obstacles than those with finite n.

Figure 6.

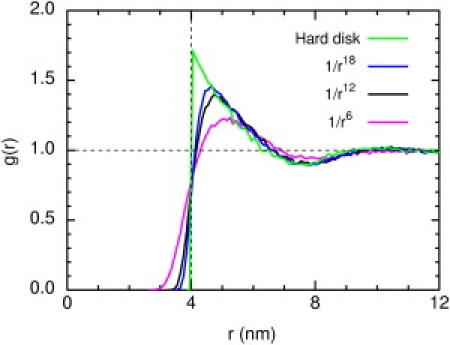
Radial distribution functions g(r) for power-law obstacles with exponents n = 6, 12, and 18, and hard disks of diameter σ, at a number density of 24k/μm².

Heyes and Brańka (34,35) have examined in great detail the behavior of three-dimensional power-law fluids, and found that a value of n ≥ 72 is required for a power-law fluid to approximate a hard-sphere fluid (35). Examining the approach to the hard-sphere limit is useful in studies of certain model colloids but is less important for applications to membrane proteins, so we do not pursue this question further.

Distributions of percolation diameters

The probability density functions of percolation diameters show the probability that a tracer smaller than d_c will by chance be blocked, or a larger tracer will by chance get through the obstacles, or a larger flexible tracer will squeeze through a gap. Fig. 3 showed the overall narrowing of the CDFs as the system size increases. But it is hard to visualize the distribution from the CDFs, so Fig. 7 shows the probability density functions of the percolation diameters for overlapping and soft repulsive disks. The distribution is considerably wider for overlapping disks (standard deviation 0.63) than for soft disks (standard deviation 0.28). The repulsive forces produce a more orderly structure with a narrower distribution of gaps through which a tracer can pass. The distributions are roughly Gaussian, but there is some asymmetry. The skewness and kurtosis are 0.31 and 3.24 for the overlapping case and 0.33 and 3.31 for the repulsive case, versus values of 0 and 3 for a Gaussian distribution.

Figure 7.

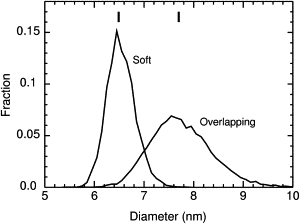
Probability distribution functions for percolation diameters for overlapping and 1/r¹² soft repulsive disks at a number density of 24k/μm². (Vertical bars) Means. To obtain better statistics, these simulations were done in small systems (L = 100 nm) with 5000 obstacle configurations.

Area fractions

So far the results have been presented in terms of the percolation diameter as a function of the number density of obstacles, so the results can be immediately tied to experiment. But for percolation theory and models of hindered diffusion, the usual variable is the excluded area fraction.

For random overlapping obstacles on the continuum, the excluded area fraction F is a simple function of the number density ρ and the tracer diameter r (33)

$$F\left(r\right)=1-\exp \left(-\rho \pi r^2\right)\text{.}$$ (5)

This is a CDF with corresponding probability density function

$$f\left(r\right)dr=\exp \left(-\rho \pi r^2\right)2\pi \rho rdr,$$ (6)

for which the mean is $1/2\sqrt{\rho }$ and the standard deviation is

$$\sqrt{1/\pi -1/4}/\sqrt{\rho }\approx 0.2614/\sqrt{\rho }\text{.}$$

In terms of the diameter, the 50% point of the area fraction CDF is

$$d_{0.50}=2\sqrt{-\left(\ln 0.5\right)/\pi }/\sqrt{\rho }\approx 0.9394/\sqrt{\rho },$$ (7)

close to the simple dimensional estimate of Eq. 4.

The excluded area fraction was calculated as a function of tracer diameter for the standard number densities of obstacles, as described in the Supporting Material. Fig. 8 a shows the results for random overlapping obstacles. On the scale of this plot, the calculated values agree well with Eq. 5. In a more stringent test in which the calculated results are transformed by plotting

$$-\ln \left[1-F\left(r\right)\right]/\pi \rho \text{versus}{\text{r}}^2,$$

some systematic error is evident at r > 10, presumably due to incomplete sampling of rare configurations with large gaps among obstacles. Fig. 8 b shows the corresponding plot for soft repulsive obstacles. The families of curves in the two panels are qualitatively very similar but the excluded area fraction increases more rapidly with tracer diameter for soft obstacles than for overlapping ones. That is, at the same number density of obstacles, soft disks are more effective obstacles than overlapping disks, as expected.

Figure 8.

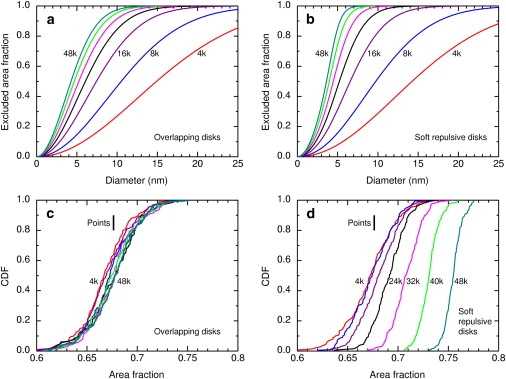
Excluded area analysis. (a and b) Excluded area fraction as a function of tracer diameter for the standard number densities 4k, 8k, 16k, 24k, 32k, 40k, and 48k/μm². Results are shown for the larger systems studied (see Supporting Material). (a) Overlapping disks. (b) Soft repulsive disks. (c and d) Distribution of percolation diameters as a function of the excluded area fraction for the same systems. (c) Overlapping disks. (d) Soft repulsive disks. (Vertical line) Literature value of the percolation threshold for a point tracer with random overlapping obstacles (32).

Finally, we combine numerically the CDF of percolation probability versus diameter (Fig. 3) with the CDF of the excluded area fraction versus diameter (Fig. 8, a and b) to obtain the CDF of percolation probability versus excluded area fraction (Fig. 8, c and d). (The method is described in the Supporting Material.) The thresholds for overlapping disks almost coincide for the full range of number densities, and are centered around the literature value of the percolation threshold. For soft repulsive disks, as the number density increases the thresholds move to higher area fraction and grow steeper.

Discussion

We have evaluated the percolation threshold in three systems of two-dimensional obstacles: random overlapping disks, soft repulsive disks, and hard disks. The threshold is obtained as the diameter of the largest tracer for which there is a percolating path. For random overlapping obstacles, the Monte Carlo results agree quantitatively with the theoretical expression. For soft obstacles or hard disks, the threshold is ≈80% or more of the value for overlapping obstacles. So as a first estimate one can use the formula for the overlapping case (Eq. 3), or the simplest approximation that the obstacles are arranged on a square lattice (Eq. 4).

The arrangement of immobile proteins in the plasma membrane is not likely to be random, but to reflect cytoskeletal structure. The repulsive fluid model presented here can be viewed as a first approximation to binding to a complex cytoskeletal network, or as a null hypothesis for a model involving detailed cytoskeletal structure.

The results are insensitive to changes in the softness of the repulsive potential, the magnitude of the potential, or the boundary conditions. The reason for this insensitivity is that the potentials are all purely repulsive, so the fluids have similar structure at a given number density and similar diameters. Using a screened Coulomb repulsion is unlikely to change the results much. But potentials such as the Lennard-Jones or an attractive lipid-mediated interaction may lead to formation of compact clusters, and therefore less efficient obstruction and higher threshold diameters. Formation of elongated clusters, such as membrane proteins bound to the cytoskeleton to form Kusumi-style picket fences (3), will lead to more effective obstruction and lower thresholds. These qualitative ideas were discussed earlier in terms of diffusion coefficients on lattices (36).

Hard versus soft systems

In the usual percolation problems in physics, the obstacles and tracers are rigid and the obstacles are immobile. The percolation thresholds are therefore absolute limits in the case of an infinite system. The only leeway is that, as a result of statistical fluctuations, the percolation transition is not infinitely sharp in a finite system.

But in a cell, both obstacles and tracers may be soft. The obstacles are anchored to the cytoskeleton, so the flexibility of the cytoskeleton and the anchoring groups leads to fluctuations in the positions of the obstacle anchorages. In addition, the obstacles may dissociate from the cytoskeleton. So the percolation threshold in the cell should not be taken as an absolute limit, but as the point at which the diffusion rate becomes dominated by the kinetics of dissociation and conformational fluctuation. Similar behavior is expected in other soft-matter systems.

Is percolation significant in the plasma membrane?

The plasma membrane contains species with a wide range of sizes. A percolation model predicts that diffusion depends strongly on the tracer diameter, with a steep cutoff for all species, but with allowance for squishiness and finite system size as already discussed.

No such cutoff has been reported, though small species tend to be mobile and large complexes tend to be immobile. It seems likely that if a sharp cutoff existed, it would have been observed by now, even though it would be obscured to some extent by the geometrical complexity and softness of the obstacles and tracers.

A rigorous experimental test would involve diffusion measurements in the same cell line for a variety of tracers differing in size. For the results to be cleanly interpretable, the tracers must be homologous, as in the pioneering work of Vaz and Criado (37) on monomers, dimers, and tetramers of the acetylcholine receptor, and in the highly precise and elegant work of the Petersen laboratory (Lee et al. (38) and Liu et al. (39)) where 1–6 fatty acids or transmembrane helixes were linked to macrocyclic polyamides.

This test can also be applied to anomalous subdiffusion. Recent work has begun to address the question of distinguishing the various mechanisms for anomalous subdiffusion (40–44). The definition of anomalous subdiffusion specifies only the second moment of the diffusion propagator, $\langle r^2\rangle \propto t^{\alpha },$ where 〈r²〉 is the mean-square displacement, t is time, and α < 1 is the anomalous diffusion exponent. The definition says nothing about higher moments. Several different mechanisms yield anomalous subdiffusion, most prominently the continuous-time random walk, fractional Brownian motion, and percolation (that is, a random walk on an infinite cluster of conducting sites at the percolation threshold). Anomalous subdiffusion has been reported for some species in the plasma membrane, cytoplasm, and nucleus. For a critical or maybe skeptical review, see Dix and Verkman (45). Identifying biological equivalents of the physicist's models of anomalous subdiffusion is of considerable interest, and the sensitivity of continuum percolation to tracer size may provide a highly specific experimental test.

Earlier work on random walks on a lattice (46) showed that when the obstacle concentration is below the percolation threshold, transient anomalous subdiffusion occurs, anomalous at short times and normal at long times. As the obstacle concentration increases toward the percolation threshold, diffusion becomes more anomalous for longer times. At the threshold, diffusion is purely anomalous at all times, as is well known. Similar behavior is expected here as the tracer diameter approaches the percolation threshold diameter. As a result, obstruction can account for anomalous subdiffusion for only a limited range of tracer sizes.