Estimating Disease Prevalence Using Relatives of Case and Control Probands

Summary

We introduce a method of estimating disease prevalence from case-control family study data. Case-control family studies are performed to investigate the familial aggregation of disease; families are sampled via either a case or a control proband, and the resulting data contain information on disease status and covariates for the probands and their relatives. Here, we introduce estimators for overall prevalence and for covariate-stratum-specific (e.g., sex-specific) prevalence. These estimators combine the proportion of affected relatives of control probands with the proportion of affected relatives of case probands and are designed to yield approximately unbiased estimates of their population counterparts under certain commonly-made assumptions. We also introduce corresponding confidence intervals designed to have good coverage properties even for small prevalences. Next, we describe simulation experiments where our estimators and intervals were applied to case-control family data sampled from fictional populations with various levels of familial aggregation. At all aggregation levels, the resulting estimates varied closely and symmetrically around their population counterparts, and the resulting intervals had good coverage properties, even for small sample sizes. Finally, we discuss the assumptions required for our estimators to be approximately unbiased, highlighting situations where an alternative estimator based only on relatives of control probands may perform better.

1. Introduction

The gold standard approach to estimating prevalence involves first obtaining a cross-sectional (or prevalence) sample from the population of interest, then assessing whether the disease is present in the sampled individuals, and finally calculating the proportion of sampled individuals with the disease, often with individuals weighted to reflect the probability that they were sampled and responded. Frequently, though, researchers do not have access to an existing cross-sectional sample that is relevant to both the population and the disease of interest, and the cost of collecting one would be prohibitive. However, if researchers do have access to a case-control family sample that was originally collected to investigate familial aggregation of the disease in the population of interest, we show here that it can be used to obtain valid estimates of prevalence.

Case-control family studies are conducted to investigate the extent to which a disease aggregates (with itself) within families, or co-aggregates with other diseases within families (Hudson, Laird, and Betensky, 2001). In these studies, researchers select case probands who are affected by the disease and control probands who are not, and then select relatives from among the case and control probands’ family members (e.g., first-degree relatives). The resulting data consist of information on disease status and covariates for the case and control probands and their relatives. (When the data are used to investigate familial aggregation, the most basic analysis entails comparing the proportion of affected relatives for case probands to the proportion of affected relatives for control probands.) Here, we refer to an example that is a case-control family study of major depressive disorder (MDD) conducted at Innsbruck University Clinics in Innsbruck, Austria (Hudson et al., 2003). In the study, 64 adults with MDD (case probands) were selected from the psychiatric unit, and 58 adults without MDD (control probands) were selected from the surgical and ophthalmology units. Three hundred and thirty of the probands’ adult first-degree relatives (parents, siblings, children) consented to participate in the study. Table 1 presents the numbers of relatives with and without MDD, by proband disease status and sex of the relative.

Table 1.

Number of relatives with (without) major depressive disorder^*

Proband disease status	Sex of relatives
	Male	Female
Case	8 (65)	25 (80)
Control	4 (69)	8 (71)

^*MDD was diagnosed by interviewing probands and their relatives using the German translation (Wittchen et al., 1996) of the Structured Clinical Interview for DSM-IV (First et al., 1994).

The probands provide no information on prevalence because the proportion of affected (or case) probands is fixed by design. The relatives, on the other hand, do provide information on prevalence, but the simple proportion of affected relatives is a biased estimate of prevalence if the disease aggregates in families because, in that case, the relatives’ probability of selection depends on their disease status, albeit indirectly (through the probands’ disease statuses). However, by using only the relatives and conditioning on the disease status of the probands through which the relatives were selected, we can obtain valid estimates and confidence intervals for overall and stratum-specific (e.g., sex-specific) prevalence, provided that certain commonly-made assumptions about sampling and the population structure hold. Under these assumptions, our method yields estimates that are only slightly biased (typically, downwards) for their population counterparts. Further, when these assumptions hold and familial aggregation is non-negligible, our method, which combines the proportion of affected relatives of control probands with the proportion of affected relatives of case probands, yields estimates that are less downwardly biased than a preexisting method, known as the proband or propositus method (Kendler and Eaton, 1988; Strömgren, 1948), that uses just the proportion of affected relatives of control probands as an estimate of prevalence. (Note that the “proband method” as described here refers to a method of prevalence estimation, not to the same-named method used in segregation analysis to estimate segregation ratios—both methods make use of relatives of probands, but use them to estimate different quantities.) Our method performs very well when applied to case-control family study data sampled from fictional populations with various degrees of familial aggregation: the resulting estimates vary closely and symmetrically around their population counterparts, with only a very small downwards bias, and the resulting intervals have good coverage properties, even for small sample sizes.

The paper is organized as follows. Section 2 introduces our estimators for overall prevalence and stratum-specific prevalence, as well as the assumptions on which they rely. In Section 3, we apply our estimators (and corresponding confidence intervals) to the data from the Austrian case-control family study of MDD. Section 4 presents the results of simulation experiments, and Section 5 is a discussion of the advantages and limitations of the method that highlights situations where the proband/propositus method may perform better. Web Appendices A and B contain proofs that the overall and stratum-specific estimators, respectively, are approximately unbiased for their population counterparts. Finally, Web Appendix C introduces standard errors and confidence intervals for overall and stratum-specific prevalence.

2. Estimation

Before presenting estimators for overall and stratum-specific prevalence, it is necessary to introduce some notation, as well as several assumptions. These assumptions are commonly, if implicitly, made when analyzing data from case-control family studies; here, they are used to guarantee that the proposed estimators will be approximately unbiased. The assumptions describe a simplified model for the underlying population and for the ascertainment of case-control families from it. Although not a perfect representation of reality, this simplified model is an adequate approximation to reality when the size of the population is sufficiently large (relative to the sizes of the families that comprise the population and relative to the number of probands ascertained in the study). Further, the results of the simulation experiments in Section 4 suggest that our method is robust to violations of some of the assumptions underlying the simplified model.

We will assume that the population of interest is finite (but very large) and that it can be partitioned into F mutually exclusive and exhaustive families. These families are indexed by i. Family i has N_i members, who are indexed by ij, where j = 1, …, N_i. For individual ij, we use Y_ij to denote disease status, with 1 corresponding to presence of the disease and 0 corresponding to absence of the disease. The population prevalence, π, is defined as f(Y_ij = 1), where individual ij is randomly selected from the population. Similarly, the stratum-specific prevalence, π^x, is defined as f(Y_ij = 1|X_ij = x), where X_ij is a categorical variable whose levels define covariate strata of interest (e.g., males and females); x is a particular value of X_ij (e.g., the female stratum); and individual ij is randomly selected from the population in stratum x. Note that X_ij may result from coarsening the values of a continuous variable (e.g., age) or from crossing the levels of multiple categorical variables (e.g., sex and race).

Families are ascertained for the case-control family study via F_A unrelated probands with the disease and F_U unrelated probands without the disease. Once families have been ascertained, they are renumbered, as are their members. The re-numbered families are now indexed by i^*, where, for the sake of convenience, the values i^* = 1, …, F_A refer to families ascertained via case probands, the values i^* =F_A + 1, …, F_A +F_U refer to families ascertained via control probands, and the values i^* = F_A + F_U + 1, …, F refer to unascertained families. For ascertained family i^*, disease status and covariate information is obtained for only n_i* −1 of the N_i* − 1 remaining (i.e., non-proband) family members. The re-numbered members of ascertained family i^* are now indexed by i^*j^*, where j^* = 1 refers to the proband, j^* = 2, …, n_i* refer to the sampled relatives, and j^* = n_i* + 1, …, n_i* + N_i* refer to the unsampled relatives. The original index j, which refers to an individual as a member of a family in the population, has a 1:1 mapping to the index j^*, which refers to the individual as a member of his or her family once it has been ascertained. We use r_i(j) to refer to the renumbered index for the j^th member of the i^th family in the population once his or her family has been ascertained.

Below, we show how data from a case-control family study can be used to obtain estimates of overall prevalence and stratum-specific prevalence. Several more assumptions must hold for the proposed estimators to yield approximately unbiased estimates:

1. Availability of Relatives: Each member of the population of interest has at least one living relative.

2. Family Size and Disease Status are Uncorrelated: $\text{Cor}(N_i,N_i^A/N_i)=0$, where $N_i^A={\sum }_{j=1}^{N_i}\text{I}(Y_{ij}=1)$, the number of affected members in family i.

3. Sampling of Probands: The case probands are randomly sampled from the affected members of the population, and the control probands are randomly sampled from the unaffected members of the population.

4. Single Ascertainment: The number of case (control) probands is sufficiently small relative to the number of affected (unaffected) members of the population to guarantee that no family will be selected via more than one proband.

5. Sampling of Relatives: Given that family i has been ascertained, the probability that individual i^*j^* (j^* ≠ 1) is included in the study is a constant (referred to as s) and, thus, does not depend on Y_i*j* (his or her disease status), X_i*j* (his or her covariates), Y_i*(−j*) (the disease statuses for the other members of the family), X_i*(−j*) (the covariates for the other members of the family), or on N_i* (the family’s size).

6. Disease Status is Independent of Other Family Members’ Covariates: For individual ij, Y_ij (his or her disease status) is independent of X_i(−j) (the covariates for the other members of the family), conditional on X_ij (the individual’s covariate)

We can use Assumption (i) about the availability of relatives to expand the definition of prevalence as follows

$$\pi \equiv f(Y_{ij}=1)=f(Y_{ij}=1\mid Y_{{ij}^{\prime }}=1)f(Y_{{ij}^{\prime }}=1)+f(Y_{ij}=1\mid Y_{{ij}^{\prime }}=0)f(Y_{{ij}^{\prime }}=0),$$ (1)

where j′ ≠ j and where individual ij′ is randomly selected from among Y_ij’s relatives with disease status Y_ij′. We can rewrite Equation (1) as

$$\pi =f(Y_{ij}=1\mid Y_{{ij}^{\prime }}=1)\pi +f(Y_{ij}=1\mid Y_{{ij}^{\prime }}=0)(1-\pi ),$$ (2)

which can then be rearranged to give

$$\pi =\frac{{\pi }_U}{1-{\pi }_A+{\pi }_U},$$ (3)

where π_U ≡ f(Y_ij = 1|Y_ij′ = 0) and π_A ≡ f(Y_ij = 1|Y_ij′ = 1). Replacing the parameters on the right-hand side of Equation (3) with estimators yields the following estimator for overall prevalence:

$$\widehat{\pi }=\frac{p_U}{1-p_A+p_U},$$ (4)

where p_A is the proportion of case probands’ relatives who are affected,

$$p_A=\frac{{\displaystyle \sum _{i^{\ast }=1}^{F_A}}{\displaystyle \sum _{j^{\ast }=2}^{n_{i^{\ast }}}}\text{I}(Y_{i^{\ast }{j}^{\ast }}=1)}{{\displaystyle \sum _{i^{\ast }=1}^{F_A}}{\displaystyle \sum _{j^{\ast }=2}^{n_{i^{\ast }}}}1};$$ (5)

and p_U is the proportion of control probands’ relatives who are affected,

$$p_U=\frac{{\displaystyle \sum _{i^{\ast }=F_A+1}^{F_A+F_U}}{\displaystyle \sum _{j^{\ast }=2}^{n_{i^{\ast }}}}\text{I}(Y_{i^{\ast }{j}^{\ast }}=1)}{{\displaystyle \sum _{i^{\ast }=F_A+1}^{F_A+F_U}}{\displaystyle \sum _{i^{\ast }=2}^{n_{i^{\ast }}}}1}.$$ (6)

If Assumptions (i)–(v) hold, then the estimator in Equation (4) is approximately unbiased at the first-order for the overall prevalence of disease in the population (see Web Appendix A for a proof). Further, we can show that the slight bias introduced by the second-order terms is downward when F_A ≈ F_U (the number of case probands is approximately equal to the number of control probands) and when E(1 − p_U) > E(p_A) (the expected proportion of control probands’ relatives who are unaffected is greater than the expected proportion of case probands’ relatives who are affected).

Note that the estimator in (4) adjusts p_U, an estimate of prevalence based on relatives of control probands only, by the factor 1/(1 − p_A + p_U). Since E(p_A) > E(p_U) for diseases that aggregate in families, this adjustment will usually have the effect of moving the prevalence estimate upwards from p_U. As a result, if the disease aggregates in families and the above assumptions hold, using p_U alone as an estimate of overall prevalence—an approach that, as noted above, is referred to as the proband or propositus method and that has been widely used in genetic-epidemiologic studies of psychiatric disorders (Kendler and Eaton, 1988; Strömgren, 1948)—will result in greater downward bias than using the estimator in (4). Thus, the proband/propositus method, unlike our method, requires the additional assumption that the disease of interest does not aggregate in families in order for the estimator to be approximately unbiased. However, the proband/propositus method, unlike our method, does not use case probands and thus does not require that the case probands be representative of affected members of the population (the first part of Assumption (iii)). Therefore, in situations where familial aggregation is small and where the first part of Assumption (iii) appears to be violated, the bias of the proband/propositus method may be smaller than the bias of (4), a point that we discuss further in Section 5. As for using p_A alone as an estimate of overall prevalence, similar arguments reveal that doing so overestimates prevalence when the above assumptions hold and disease aggregates in families.

Next, if Assumptions (i)–(vi) hold, then the following estimator is biased only slightly at the first-order for the prevalence of disease in stratum x (see Web Appendix B for a proof):

$${\widehat{\pi }}^x=p_A^x\widehat{\pi }+p_U^x(1-\widehat{\pi }),$$ (7)

where $p_A^x$ is the proportion of case probands’ relatives who have covariate value x and are affected

$$p_A^x=\frac{{\displaystyle \sum _{i^{\ast }=1}^{F_A}}{\displaystyle \sum _{j^{\ast }=2}^{n_{i^{\ast }}}}\text{I}(X_{i^{\ast }{j}^{\ast }}=x)\text{I}(Y_{i^{\ast }{j}^{\ast }}=1)}{{\displaystyle \sum _{i^{\ast }=1}^{F_A}}{\displaystyle \sum _{j^{\ast }=2}^{n_{i^{\ast }}}}\text{I}(X_{i^{\ast }{j}^{\ast }}=x)};$$ (8)

and $p_U^x$ is the proportion of control probands’ relatives who have covariate value x and are affected

$$p_U^x=\frac{{\displaystyle \sum _{i^{\ast }=F_A+1}^{F_A+F_U}}{\displaystyle \sum _{j^{\ast }=2}^{n_{i^{\ast }}}}\text{I}(X_{i^{\ast }{j}^{\ast }}=x)\text{I}(Y_{i^{\ast }{j}^{\ast }}=1)}{{\displaystyle \sum _{i^{\ast }=F_A+1}^{F_A+F_U}}{\displaystyle \sum _{j^{\ast }=2}^{n_{i^{\ast }}}}\text{I}(X_{i^{\ast }{j}^{\ast }}=x)}.$$ (9)

Further, we can show that the slight first-order bias is downwards when, again, F_A ≈ F_U and E(1 − p_U) > E(p_A). Note that, as above, an examination of Equation (7) reveals that using only the relatives of control probands to estimate stratum-specific prevalence results in more serious underestimation than using the estimator in (7) when the above assumptions hold and disease aggregates in families.

In Web Appendix C, we provide approximate standard errors and confidence intervals for π̂ and π̂^x. The standard errors and confidence intervals are appropriate for dependent observations since disease status will be positively correlated within families when the disease aggregates in families. The confidence intervals are based on the same concept as the Agresti-Coull (1998) interval, which modifies the standard Wald interval for binomial proportions so that it will attain actual coverage levels near the nominal coverage level even for small proportions. The modification, which has strong roots in the work of Wilson (1927), involves replacing the maximum likelihood estimate of the proportion used to calculate the center and standard error of the Wald interval with an estimate that is smoothed towards the uniform probability distribution by adding a small number (e.g., two) of successes and the same number of failures to the observed data. Because the Agresti-Coull interval appears to perform well for small independent samples (Agresti and Coull, 1998) and, more relevantly for our data, medium-sized dependent samples (Miao and Gastwirth, 2004), we use a similar approach to form confidence intervals: the intervals’ center and spread are calculated using p̃_A, p̃_U, ${\stackrel{\sim }{p}}_A^x$, and ${\stackrel{\sim }{p}}_U^x$, which smooth p_A, p_U, $p_A^x$, and $p_U^x$, respectively, towards the uniform distribution by adding two failures and two successes for every 100 observations.

3. Austrian Case-Control Family Study Example

To illustrate the use of our method, we apply it to the data from the Austrian case-control family study.

We begin by addressing whether the six assumptions enumerated in Section 2 are valid for our example. Regarding Assumption (i), the proportion of individuals in the Tyrol (the region including Innsbruck) who are without any first-degree relatives is unknown, but expected to be small. Further, violations of this assumption are not problematic unless Assumption (ii) is also violated. To examine Assumption (ii), we compare the sizes of the families identified through case probands versus control probands. Control families are slightly larger, but only by 0.5 relatives on average, a non-significant difference. Regarding Assumption (iii), we utilize additional data on whether individuals also have a comorbid anxiety disorder to examine whether case probands represent particularly severe cases of MDD, a potential concern because the case probands were sampled from a psychiatric clinic rather than from the community. Approximately 41% of case probands have comorbid anxiety disorders, compared with 52% of affected (with MDD) relatives of case probands and 25% of affected (with MDD) relatives of control probands; the first proportion does not differ significantly from the second or third. This suggests that case probands are not significantly more severe, at least with respect to anxiety comorbidity. Regarding Assumption (iv), no families were multiply ascertained in the Austrian study. As for Assumption (v), its validity is difficult to assess without follow-up data on non-interviewed relatives. Finally, regarding Assumption (vi), in a logistic regression using the data, the disease status of relatives is not associated with (odds ratio = 1.0) the sex of their other family members, conditional on the sex of the relatives themselves.

When we apply our method to the data, Equations (4) and (C.3) yield an estimate of 8.8% and a 95% confidence interval of [5.9%, 15%], respectively, for the overall lifetime prevalence of MDD in the Tyrol region. Equations (7) and (C.4) yield an estimate of 6.0% and a 95% confidence interval of [2.3%, 13%] for male lifetime prevalence, and 11.3% and [6.4%, 20.0%] for female lifetime prevalence. Note that our overall, male, and female prevalence estimates are slightly larger than the proportions of all control relatives, male control relatives, and female control relatives who are affected (7.9%, 5.5%, and 10.1%, respectively), which are the estimates produced by the proband/propositus method. In contrast, our overall, male, and female prevalence estimates are considerably smaller than the proportions of all case relatives, male case relatives, and female case relatives who are affected (18.5%, 11.0%, and 23.8%, respectively). It is difficult to validate the estimates produced using our method because no comparable estimates of the lifetime prevalence of DSM-IV MDD in the Tyrol Region of Austria could be located in the English or German literature. However, our estimate of 8.8% is approximately half the National Comorbidity Survey Replication (Kessler et al., 2005) estimate (= 16.6%) for the lifetime prevalence of MDD in the United States, a fact that is noteworthy in light of the findings of an earlier study that the prevalence of MDD in the Upper Bavarian Region of Germany was approximately half the comparable rate in the United States (Fichter et al., 1996).

4. Simulation Results

We conducted simulation experiments in order to investigate how well the estimators from Section 2 and the confidence intervals from Web Appendix C perform in practice. The experiments were designed to mimic the Austrian case-control family study of MDD, which is at the very small end of case-control family studies.

We created four fictional populations, each with a different level of disease aggregation within families. The populations contained approximately 500, 000 individuals each, a number that corresponds to the number of people between 18 and 70 years old reported to be living in the Tyrol region of Austria in 2003, the catchment area for the Austrian study (Statistik Austria, 2003). To create populations of this size, we generated data for approximately 125, 000 families, which involved three steps: (a) generating family sizes (from 2 to 9 members) based roughly on the distribution of family sizes in the Austrian data; (b) generating the sexes of and relationships between (e.g., siblings, parents, etc.) family members based on the percentage of females between 18 and 70 years in the Tyrolean population in 2003 (=50.5%) and the distribution of family relationships and sex in the Austrian data, and; (c) generating lifetime disease statuses for the family members conditional on their sexes and relationships, based on parameter estimates from the Austrian data.

To generate the disease statuses in step (c), we used the ACE (A = additive genetic effects, C = common or shared family environment, and E = unique environment) model for case-control family data (Javaras, Hudson, and Laird, 2009). In this model, a subject is affected if his or her ‘liability to the disease’ exceeds a threshold that corresponds to disease prevalence for the relevant covariate stratum. The liabilities for subjects from family i are modeled by an N_i-variate normal distribution with mean vector set to zero and correlations that are a function of a² (the percentage of variation in liability due to A) and c² (the percentage of variation in liability due to C). In our experiments, we set a² and c² to different values for each of the four populations: for the ‘No Aggregation’ population, we set a² to 0.0 and c² to 0.0; for the ‘Low Aggregation’ population, we set a² to 0.10 and c² to 0.10; for the ‘Medium Aggregation’ population, we set a² to 0.40 and c² to 0.10; and for the ‘High Aggregation’ population, we set a² to 0.70 and c² to 0.10. Note that the Medium Aggregation population most closely resembles the level of familial aggregation (â² = 0.44 and ĉ² = 0.07) found when the ACE model was fitted to the actual MDD data (Javaras, Hudson, and Laird, 2009, Section 6). In all four populations, we set lifetime disease prevalence among males to 5.9%, and lifetime disease prevalence among females to 11.5%. Note that the male and female prevalences, along with the proportion of females, determine the overall lifetime prevalence of disease (= 8.7%) for the fictional populations.

Next, we sampled 1, 000 small case-control family datasets from each of the fictional populations. Each dataset was formed by selecting F_A = 64 case probands and F_U = 58 control probands, and then including all of the probands’ family members (s = 1). (F_A, F_U, and s were set equal to their values in the Austrian study.) For each sampled dataset, Equation (4) was used to estimate overall prevalence, and Equation (7) was used to estimate the male and female prevalences. In addition, we used Equation (C.3) to form 95% confidence intervals for the overall prevalence, and we used Equation (C.4) to form 95% confidence intervals for the male and female prevalences.

In the 4, 000 case-control family datasets sampled, the number of included individuals (relatives plus probands) ranged between approximately 450 and 550. Even for this relatively small study size, the population was not sufficiently large to ensure that Assumption (iv) about single ascertainment held. (In contrast, all other assumptions listed in Section 2 held in the simulation experiments.) Assumption (iv) was only violated to an extremely small extent, however: of the almost 500, 000 families sampled, only approximately 0.05% were multiply ascertained. In multiply-ascertained families, the first family member selected as a proband was retained as the sole proband for his or her family, and all other family members were treated as relatives. This simple approach is, in general, not an appropriate one for handling multiple ascertainment. However, due to the extremely small extent of multiple ascertainment in the simulation experiments, the reported results from this simple approach were identical to those from a more complicated approach (results not reported), where, in multiply-ascertained families, all family members selected as probands were retained as probands, and the remaining family members were treated as relatives and counted multiple times (once for each proband) in the relevant numerators and denominators of p_A, p_U, $p_A^x$, and $p_U^x$, as is done in the proband method for estimating the segregation ratio (see Sham, 1998).

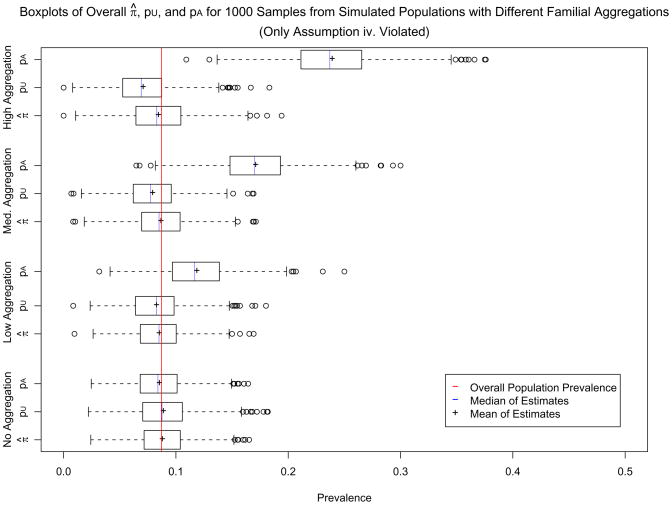
For each of the four populations, Figure 5 presents boxplots of the 1, 000 values of π̂, as well as boxplots of the 1, 000 values of p_U and p_A that went into estimating π̂. Similarly, for each of the four populations, Web Figures 1 and 2 present boxplots of the 1, 000 values of the male and female π̂^xs, respectively, as well as boxplots of the 1, 000 values of $p_U^x$ and $p_A^x$ that went into estimating the male and female π̂^xs. The plots reveal that, for all four populations, π̂ and π̂^x vary symmetrically and closely around the corresponding population prevalences, which are indicated by vertical red lines. Their estimated downward bias (presented in Table 2) is extremely small, especially relative to the length of the confidence intervals. Although π̂ and π̂^x do become slightly more downwardly biased when the disease aggregates in families, the downward bias is very small even for the High Aggregation population. In contrast, p_U and $p_U^x$ become considerably more downwardly biased as familial aggregation increases; for medium and high levels of familial aggregation, they are considerably more downwardly biased than π̂ and π̂^x, respectively.

Table 2.

Simulation experiment results for π̂ and π̂^x

	Mean of π̂ or π̂x	Bias of π̂ or π̂x (%)	2-sided CI coverage (%)	2-sided CI length
Overall
No aggregation	0.088	1.4	93.1	0.093
Low aggregation	0.085	−2.4	94.7	0.097
Medium aggregation	0.087	−0.7	94.8	0.104
High aggregation	0.084	−3.5	94.5	0.112
Female
No aggregation	0.115	1.1	95.4	0.150
Low aggregation	0.113	−1.7	95.4	0.152
Medium aggregation	0.113	−2.1	95.5	0.158
High aggregation	0.110	−4.1	94.9	0.167
Male
No aggregation	0.060	1.6	95.3	0.125
Low aggregation	0.057	−3.7	96.9	0.125
Medium aggregation	0.060	2.1	95.0	0.130
High aggregation	0.058	−3.0	96.3	0.135

Table 2 also presents lengths and coverage probabilities for the 95% confidence intervals for overall, male, and female prevalences in all four populations. Although the confidence intervals are fairly wide, especially for such small estimates, this is to be expected due to the positive correlation of MDD status within families and the small number of case and control probands used in the simulation experiments. Note that the confidence intervals attain actual coverage levels very close to the nominal level of 95%.

The simulation experiments suggest that the prevalence estimators in (4) and (7) are approximately unbiased and reasonably efficient, even when the population size is relatively small and the assumption of single ascertainment does not hold. As would be expected, the prevalence estimators are even more efficient in additional simulation experiments (not described here) that are identical to those described above except for being based on a larger number of case and control probands (150 of each) and a larger fictional population (over 2 million individuals).

5. Discussion

We have introduced a method of forming estimates and confidence intervals for overall and stratum-specific prevalence based on case-control family data.

It is clear from the simulation experiments (Section 4) and proofs (Web Appendices A and B) that the proposed estimators and intervals yield valid information about the prevalence of disease. The ability to glean valid information about disease prevalence from case-control family data is useful to medical investigators when no population-based data (from a cross-sectional sample) are available for the population of interest. Knowledge of prevalence augments epidemiological understanding of the disease and also informs resource allocation. In addition, knowledge of prevalence makes it possible to estimate other parameters of epidemiological interest. For instance, data from a case-control sample can be weighted to create data representative of the population by using weights equal to the inverse sampling probabilities for the cases and controls, the calculation of which requires knowledge of prevalence. The weighted data that result can be used to obtain approximately unbiased estimates of population parameters, such as the exposure-disease risk difference and the exposure-disease risk ratio, that cannot be obtained from case-control studies unless the sampling fractions of cases and controls is known. (In contrast, the exposure-disease odds ratio can, of course, be obtained from case-control data without weighting them.)

Several limitations should be noted. For one, when the disease of interest aggregates in families, disease status will be positively correlated for individuals within the same family, which will have the effect of inflating the errors and intervals for π̂ and π̂^x. Thus, in this case, the prevalence estimators in Equations (4) and (7) will be less precise than corresponding estimators based on the same number of unrelated individuals from a cross-sectional sample. Further, the estimators and intervals would probably not perform well in very small samples (or even in larger samples if the true prevalence were very small), but these caveats would also apply to estimators and intervals calculated from cross-sectional samples.

Second, the prevalence estimators may no longer be approximately unbiased if one or more of the assumptions enumerated in Section 2 are violated. Beginning with Assumption (ii), one example of a violation is when smaller families have a greater proportion of affected individuals, a scenario that would result in prevalence being underestimated (Kendler and Eaton, 1988). (In situations where smaller families have lower proportions of affected individuals, one would expect the opposite: overestimation of prevalence.) The former scenario is plausible for early-onset diseases that impair individuals’ ability to have children or for diseases that result in early death. To investigate the impact of this violation on our estimators, we performed a second set of simulation experiments identical to the first set described in Section 4 except that families with three or fewer members had larger proportions of affected members than families with four or more members. When smaller families had twice the proportion of affected individuals as larger families, a very extreme scenario, our method yielded estimates that were downwardly biased by approximately −25%. (Web Appendix A contains a more detailed description of these experiments, but full results are not presented for the sake of brevity.) Although Assumption (ii) pertains to the underlying population, the case-control family data can be used to get a sense of whether the assumption is violated, for example by comparing the distribution of family sizes for case probands to the distribution of family sizes for control probands. If it is suspected that the assumption is violated, one option is to use a multiple-outputation-based (Follman et al., 2003) variant of our method since multiple outputation derives from a within-cluster resampling method (Hoffman et al., 2001) developed for situations where cluster size is non-ignorable, as is the case when Assumption (ii) is violated. In the multiple-outputation-based variant of our method, the estimator in (4) or (7) is repeatedly applied to each of a large number of reduced samples that consist of only one randomly-selected relative per proband; the resulting estimates are then averaged. When this variant of our method (with 1000 resamples) was applied in the very extreme scenario described above, the resulting estimates were downwardly biased by only small amounts similar to those seen when Assumption (ii) holds (see Table 2), albeit at the expense of greater variance.

Turning to Assumption (iii), one example of a violation is when probands are selected based not only on disease status but also on measured covariates such as sex or age. However, in this scenario, valid estimates of stratum-specific prevalence can still be obtained by applying Equation (7) only to the relatives of those probands who belong to the stratum of interest. Further, in some instances, the resulting stratum-specific prevalence estimates can be combined with external data on the stratum frequencies in the population of interest to obtain estimates of overall prevalence. A more concerning example of a violation of Assumption (iii) is when case probands are selected based not only on their disease status but also on disease severity, a scenario in which p_A, and thus π̂, would be upwardly biased (Begg, 2002). To investigate the impact of this type of violation on our estimators, we performed a third set of simulation experiments similar to the first set described in Section 4 except that only affected population members with very high underlying liabilities were chosen as case probands. When only affected population members with liabilities greater than 0.5 were selected as case probands, an extreme scenario, our method yielded estimates that were upwardly biased by approximately 50% for a population with medium familial aggregation. (Further details and results of these experiments are not presented here for the sake of brevity.) Thus, in scenarios where case probands are thought to be unrepresentative of affected population members with respect to disease severity, using the proband/propositus estimator (p_U) may be preferable because it will have only slight downwards bias if the disease does not aggregate highly in families. Of course, if control probands are also unrepresentative of controls with respect to underlying disease liability, then p_U, too, may be biased. One way to check whether case probands are representative of cases is to compare the case probands to the affected relatives in terms of disease severity, risk factors for the disease, and other relevant variables that are measured. A similar approach can be used for control probands by comparing them to unaffected relatives.

As for violations of Assumption (iv), the simulation experiments in Section 4 suggests that our method is robust to at least small departures from single ascertainment. Next, if the affected relatives of the probands are less likely to participate in the study, a violation of Assumption (v), then prevalence will be underestimated. Finally, if the disease of interest is extremely common or if it is somewhat common and aggregates extensively in families, then it may not be true that E(1 − p_U) > E(p_A). It is easy to see why this inequality will not hold if the disease in question is extremely common (prevalence over 50%), since in that case E(p_A) will be large and E(1 − p_U) will be small even if the disease does not aggregate in families. Another case where the inequality will not hold is when the disease aggregates in families to such an extent that E(p_A) is large and when the disease is common enough so that E(1 − p_U) is not large. However, for most diseases (including MDD), the inequality will hold. Further, since the assumption that E(1 − p_U) > E(p_A) is required only to ensure that the bias in π̂ is downwards, our method will still be approximately unbiased even when this assumption is violated.

In general, though, our method appears to be reasonably robust to at least some of the assumptions. The most crucial assumption is likely to be the one about relative sampling, which assumes that individuals with the disease are no more or less likely to be included in the sample than individuals without the disease. This assumption would apply equally to cross-sectional samples. The next-most crucial assumption is likely to be the assumption that case (control) probands are sampled randomly from cases (controls), followed by the assumption that family size and disease status are uncorrelated in the population of interest. If these crucial assumptions hold, as they should in a well-executed case-control family study, then our method of estimating disease prevalence from case-control family data is a useful tool, especially for diseases and populations where no cross-sectional samples are available.

Figure 1.

Boxplots of overall π̂, p_U, and p_A values calculated for 1000 samples drawn from four different populations with varying degrees of disease familiality.