Decoding the Large-Scale Structure of Brain Function by Classifying Mental States Across Individuals

Abstract

Brain-imaging research has largely focused on localizing patterns of activity related to specific mental processes, but recent work has shown that mental states can be identified from neuroimaging data using statistical classifiers. We investigated whether this approach could be extended to predict the mental state of an individual using a statistical classifier trained on other individuals, and whether the information gained in doing so could provide new insights into how mental processes are organized in the brain. Using a variety of classifier techniques, we achieved cross-validated classification accuracy of 80% across individuals (chance = 13%). Using a neural network classifier, we recovered a low-dimensional representation common to all the cognitive-perceptual tasks in our data set, and we used an ontology of cognitive processes to determine the cognitive concepts most related to each dimension. These results revealed a small organized set of large-scale networks that map cognitive processes across a highly diverse set of mental tasks, suggesting a novel way to characterize the neural basis of cognition.

Neuroimaging has long been used to test specific hypotheses about brain-behavior relationships. However, it is increasingly being used to infer the engagement of specific mental processes. This is often done informally, by noting that previous studies have found an area to be engaged for a particular mental process and inferring that this process must be engaged whenever that region is found to be active. Such reverse inference has been shown to be problematic, particularly when regions are unselectively active in response to many different cognitive manipulations (Poldrack, 2006). However, recent developments in the application of statistical classifiers to neuroimaging data provide the means to directly test how accurately mental processes can be classified (e.g., Hanson & Halchenko, 2008; Haynes & Rees, 2006; O’Toole et al., 2007).

In this study, we first examined how well classifiers can predict which of a set of eight cognitive tasks a person is engaged in, on the basis of patterns of activation from other individuals, and we found that such predications can be highly accurate. We next examined the dimensional representation of brain activity underlying this classification accuracy and found that the differences among these tasks can be described in terms of a small set of underlying dimensions. Finally, we examined how these distributed neural dimensions map onto the component cognitive processes that are engaged by the same eight diverse tasks, by mapping each task onto an ontology of mental processes. The results demonstrate how neuroimaging can in principle be used to map brain activity onto cognitive processes, rather than onto tasks.

There is increasing interest in using the tools of machine learning to identify signals that can allow brain-reading, or prediction of mental states or behavior directly from neuroimaging data (O’Toole et al., 2007). These tools, known as classifiers, are first trained on functional magnetic resonance imaging (fMRI) data from one subset of the participant’s data (in-sample data) and then used to make predictions about patterns in a different subset of the same person’s data set (out-of-sample data). Such methods typically show perfect classification on the in-sample training data, and classification ranges between 70 to 90% correct for out-of-sample data, which is quite exceptional given the noisiness of the fMRI signal. For example, it is now well established that fMRI data from the ventral temporal cortex provide sufficient information to accurately predict what class of object (e.g., faces, houses) a person is viewing (Hanson & Halchenko, 2008; Hanson, Matsuka, & Haxby, 2004; Haxby et al., 2001). In other kinds of tasks, one can tell whether the subject is conscious of visual information (Haynes & Rees, 2005), or can even “read out” the intention of the subject prior to his or her behavioral response (Haynes et al., 2007). Thus, it is possible to reliably identify mental states for a given individual who is engaged in a specific task, using training data from the same individual. There have also been some demonstrations of accurate prediction to new individuals (Mourao-Miranda, Bokde, Born, Hampel, & Stetter, 2005; Shinkareva et al., 2008) when a relatively limited set of stimulus classes has been used.

CLASSIFYING TASKS ACROSS INDIVIDUALS

To investigate classification of tasks across individuals, we combined data from eight fMRI studies (performed in the first author’s laboratory) that included a total of 130 participants performing a wide range of mental tasks (see Table 1). The data were all collected on the same 3-T MRI scanner with consistent acquisition parameters, and were analyzed using the same data-analysis procedures (described in the Supporting Information available on-line—see p. XXX). This large-scale and methodologically consistent data set allowed us to investigate whether it is possible to tell which mental task a person is engaged in solely on the basis of fMRI data.

Table 1.

Tasks in the Data Set

Task name	Number of subjects	Design type
Risk taking (balloon-analogue risk task)	16	Event-related
Classification (probabilistic classification, no feedback)	20	Event-related
Rhyme judgments (pseudowords)	13	Blocked
Working memory (tone counting)	17	Blocked
Gambling decisions (50/50 gain/loss gambles)	16	Event-related
Semantic judgments (living/nonliving decision on mirror-reversed words)	14	Event-related
Reading aloud (pseudowords)	19	Event-related
Response inhibition (stop-signal task)	15	Event-related

Note. Only one scanning run was available for the rhyme-judgments and working memory tasks.

For each subject, a single statistical parametric (z) map was obtained for a contrast comparing the task condition with a baseline condition. These z-statistic data were submitted to classification using a multiclass linear support vector machine (SVM; Boser, Guyon, & Vapnik, 1992; Hsu & Lin, 2002; Schölkopf & Smola, 2002). SVM analysis provides a computationally tractable means to classify extremely high-dimensional data (in this case, the data included more than 200,000 features). Accuracy at predicting which task a subject was performing was computed using leave-one-out cross-validation: The classifier was trained on all subjects except for one and then tested on that out-of-sample individual, and this method was repeated for each individual (Supplementary Fig. 1 in the Supporting Information available on-line provides an overview of the analysis).

Using data from the intersection set of in-mask voxels (which included 214,000 voxels across the entire brain), we achieved 80% classification accuracy for subjects in the out-of-sample generalization set. Similar levels of accuracy were obtained using neural network classifiers (for an exhaustive list of classifier results with this data set, see Supplementary Table 1 in the Supporting Information available on-line). Table 2 presents the confusion matrix for this analysis, which shows that all tasks were classified with relatively high accuracy, though there was some variability across tasks. Statistical significance of the classification accuracy achieved (vs. accuracy levels expected by chance) was assessed using a randomization approach to obtain an empirical null distribution. Mean chance accuracy was 13.3%, and according to this analysis, accuracy greater than 18.5% is significantly greater than chance at p < .05.

Table 2.

Confusion Matrix for the Support Vector Machine Analyses

Predicted task
True task	Risk taking	Classification	Rhyme judgments	Working memory	Gambling decisions	Semantic judgments	Reading aloud	Response inhibition	Accuracy
Risk taking	14	0	0	0	1	0	1	0	87.50%
Classification	0	18	0	0	0	0	1	1	90.00%
Rhyme judgments	1	2	8	0	1	1	0	0	61.54%
Working memory	0	0	0	14	0	0	0	3	82.35%
Gambling decisions	0	3	0	0	11	2	0	0	68.75%
Semantic judgments	0	2	0	0	1	11	0	0	78.57%
Reading aloud	0	1	0	0	0	0	17	1	89.47%
Response inhibition	0	0	0	1	0	0	3	11	73.33%

Note. The table presents results obtained using leave-one-out cross-validation. The numbers in each row indicate how many subjects were classified as performing each task when they were actually performing the task indicated by the row label.

When the classifier was trained on one run and then generalized to a second run for the same individuals (for the six tasks that had multiple runs), 90% classification accuracy was achieved for the second run (for the confusion matrix for this analysis, see Supplementary Table 2a in the Supporting Information available on-line). Thus, the accuracy of task classification across individuals was nearly as high as the accuracy of the generalization across runs within individuals. It is difficult to compare these accuracy levels with those obtained in previous studies of within-subjects classification, because those studies have often used much smaller image sets or single images to perform classification, whereas we used summary statistical images in the present analysis.

If this classification ability relies on general cognitive features of the tasks, then it should be possible to classify individuals performing different versions of the same tasks on which the classifier was trained. We examined this possibility with data from two additional studies, which used slightly different versions of two of the tasks on which the classifier was trained (probabilistic classification and response inhibition). These data sets were collected from subjects who were included in the original training set, but for different tasks (working memory and reading aloud, respectively). When the classifier was trained excluding the data from these subjects from the original set, accurate classification (84%) was obtained for the new data sets (see Supplementary Table 2b in the Supporting Information available on-line). Thus, the classifier trained on the original data was able to accurately generalize to different studies using different versions of the same mental tasks. When the data sets from those same subjects (performing different tasks) were included in the training set, accuracy was reduced but still high (66%; see Supplementary Table 2c in the Supporting Information). This decrease in accuracy reflects the fact that the classifier was somewhat sensitive to individual characteristics of the training examples; in particular, subjects who performed the response-inhibition task in the test data but the reading-aloud task in the training data were often (7 out of 20 subjects) misclassified as performing reading aloud in the test. No such misclassification occurred for the probabilistic classification task. These results demonstrate that the classifier was more sensitive to task-relevant information than to idiosyncratic activation patterns of individual subjects, but did retain some sensitivity to task-independent patterns within individuals.

LOCALIZING THE SOURCES OF CLASSIFICATION ACCURACY

To determine the anatomical sources of the information that drove classification accuracy, we used two independent sensitivity methods to identify anatomical areas that were potentially diagnostic for correct classification by the SVM classifier. First, we looked at the predictive power of activation within each of a set of independent anatomical regions of interest (ROIs) using an SVM classifier within each ROI. Second, for every voxel we applied a localized SVM that was centered at that voxel and had a fixed radius of 4 mm (Hanson & Gluck, 1990; Kriegeskorte, Goebel, & Bandettini, 2006; Poggio & Girosi, 1990). Results of these analyses tended to be consistent and indicated that many regions throughout the cortex provided information that allowed some degree of accurate prediction (30–50%) of cognitive states (Fig. 1; see Supplementary Table 3 in the Supporting Information available on-line).

Fig. 1.

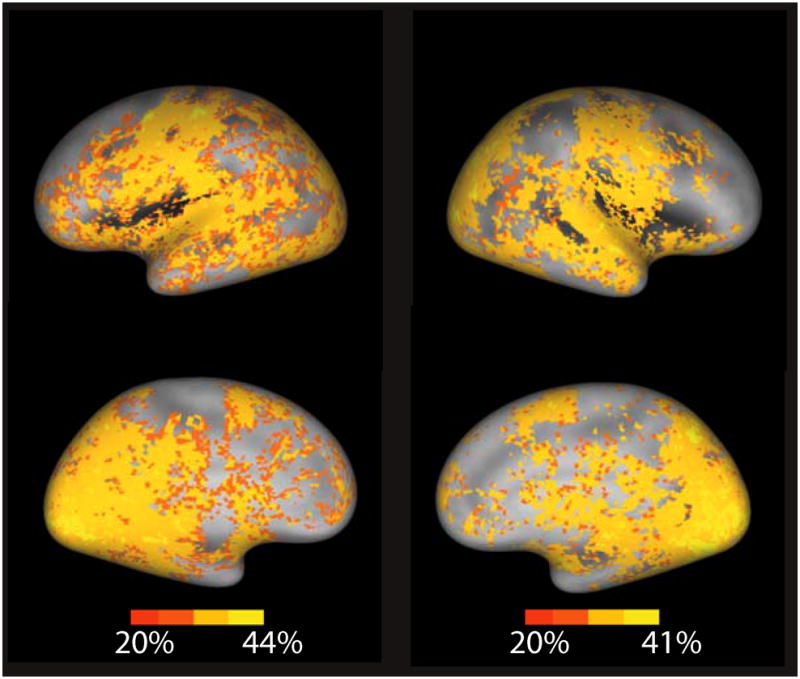
Localized accuracy of reverse inference from brain activity to task engagement across the eight cognitive tasks. Accuracy for each voxel was determined using a searchlight technique (localized support vector machine applied within a region of interest centered at that voxel and having a 4-mm radius). Results were overlaid on a population-average surface using CARET software (Van Essen, 2005). The left panel presents lateral (top) and medial (bottom) views of the left hemisphere, and the right panel presents corresponding views of the right hemisphere.

Sensory cortices provided substantial predictability. Given the fact that the different studies varied substantially in characteristics of the visual stimuli and also varied in whether auditory stimuli were present, this was not surprising. These results suggested that the classification did not necessarily reflect the higher-order cognitive aspects of the tasks. However, a number of regions in the prefrontal cortex, including the premotor and anterior cingulate cortices, also showed substantial ability to predict tasks. Strikingly, when the local kernel extent in the localized SVM analysis was expanded to 8 mm, one of the only regions not providing substantial classification accuracy was in the bilateral dorsolateral prefrontal cortex (see Supplementary Fig. 2 in the Supporting Information available on-line). This could reflect the fact that this region is equally engaged across mental tasks (Duncan & Owen, 2000), that substantial individual variability renders it nonpredictive across subjects, or that the radial ROIs were too small for the classifier to detect relevant interregional interactions.

These sensitivity analyses demonstrated which regions provide information that might be useful for task classification, but did not tell us which regions are diagnostic for particular tasks. In order to determine this, we performed an analysis that measured the diagnosticity of each voxel—that is, the degree to which activity in each voxel was predictive of a specific task. We determined which voxels from the whole-brain data set had the greatest effect on the classifier’s error, which is equivalent to determining the effect of removing voxels individually to see which ones have the greatest effect on the classification (for details, see Supplementary Methods in the Supporting Information available on-line). The results of this analysis (see Supplementary Fig. 3 in the Supporting Information) showed that the set of voxels identified as diagnostic for each task heavily overlapped with, but was much smaller than, the set of voxels that were identified as active in a standard general linear model (GLM) analysis. These analyses had different goals: For the GLM, the goal was detection of active voxels, whereas for the classifier analysis, the goal was identification of voxels that are diagnostic for tasks; the latter kind of analysis is more stringent, but has the potential for higher specificity (Hanson & Halchenko, 2008).

RELATING NEURAL AND PSYCHOLOGICAL SIMILARITY SPACES

The ability to accurately classify mental tasks using brain-imaging data requires that brain patterns from the same task are more similar to each other in the high-dimensional voxel space than they are to patterns from different tasks. Therefore, we next set out to examine how this neural similarity space is related to the psychological similarity space of the specific tasks used in the data set. We accomplished this by visualizing the location of each subject’s brain data in a brain activation space with greatly reduced dimensionality.

The SVM analysis provided strong evidence for a valid classification function based on whole-brain data (200,000 features). Although the identified support vectors were diagnostic of the boundaries of the decision surface, by design they could not at the same time provide probabilistic information about the underlying feature space or the class-conditional probability distributions. However, given the impressive performance of the SVM classifier, it was likely that a conservatively chosen feature-selection/-extraction approach could be used to approximate the classification function identified and at the same time (unlike the classifier) allow visualization of the feature space and provide information on the class-conditional probability distribution.

One candidate for this classification approximation was a related learning method: neural networks, which are additive sigmoidal kernel function approximators. Neural networks have the ability to both select exemplar patterns (as SVMs do) and find prototypes based on “interesting” projections in the feature space. Unsupervised dimensionality-reduction methods, such as principal- or independent-components analysis, can also identify lower-dimension projections of fMRI data, but are not constrained at the same time by the particular classification problem, as is a neural network. However, one limitation of neural networks is that, depending on the complexity of the decision surface, they are limited to processing about 10,000 features because of memory and computational constraints. Thus, the present data set required feature selection in order for us to apply a neural network analysis.

We performed feature selection by computing the relative entropy in each voxel over all brains and tasks; compared with feature selection using variance within features, this approach provided a more sensitive measure of voxel sensitivity to brain and task variation. At a threshold of p < .01, this measure of relative entropy identified 2,173 voxels; the selected voxels were sparsely distributed throughout the brain (see Supplementary Fig. 4 in the Supporting Information available on-line). These voxels were used to train a sigmoidal neural network (with a varied number of hidden units), which was able to produce classification accuracy similar to that obtained with the SVM analyses using whole-brain data (accuracy was 71% when the model included six hidden units, and including more hidden units resulted in little improvement; see Supplementary Table 1 in the Supporting Information). To further confirm the validity of entropy-based feature selection, we used these voxels with an SVM classifier, which achieved accuracy (72%) that was slightly reduced from that obtained in the original analysis using more than 200,000 voxels. Thus, feature selection produced a compression factor of 100 to 1.

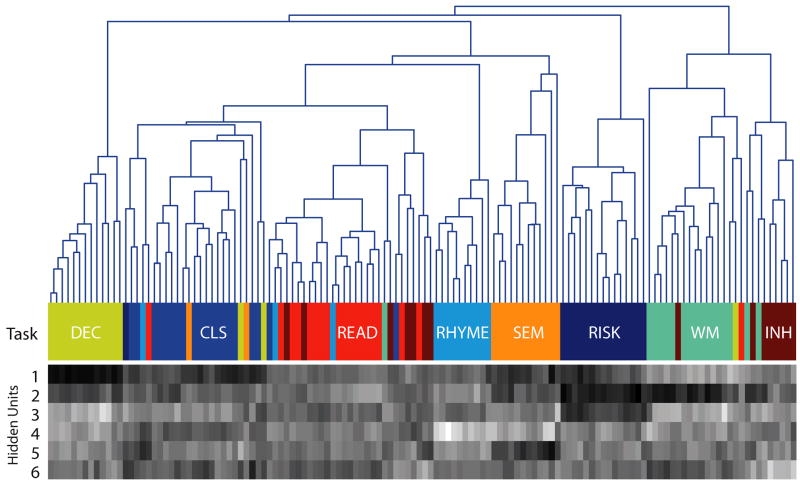
The neural network classifier was trained on all exemplars and was able to achieve high classification accuracy and simultaneously project (by extraction of new features) the data into a lower-dimensional subspace (six hidden units). To further characterize this space, we first performed an agglomerative hierarchical cluster analysis (for details, see Supplementary Methods in the Supporting Information available on-line) in the six-dimensional space derived from the hidden units of the network. Figure 2 illustrates the results. It was clear from this cluster space that the neural activity patterns not only preserved task differences, but also reflected the similarity structure of the mental tasks. For example, the three tasks that required linguistic processing (reading aloud, rhyme judgments, and semantic judgments) were adjacent, as were the two tasks that required attention to auditory stimuli (working memory and response inhibition).

Fig. 2.

Visualization of the reduced-dimension data set. The cluster tree is based on a hierarchical clustering solution using the six-dimension data obtained from the hidden-unit activity in a neural network presented with each individual’s data. The data for each component for each subject are presented in gray-scale form in the lower panel; brighter shadings represent higher values on each component. Each final branch in the tree and each column in the gray-scale component map represents a single individual. The color bar between the tree and the component map represents the task that each subject actually performed in the data set. (For additional information about the tasks, see Table 1.)

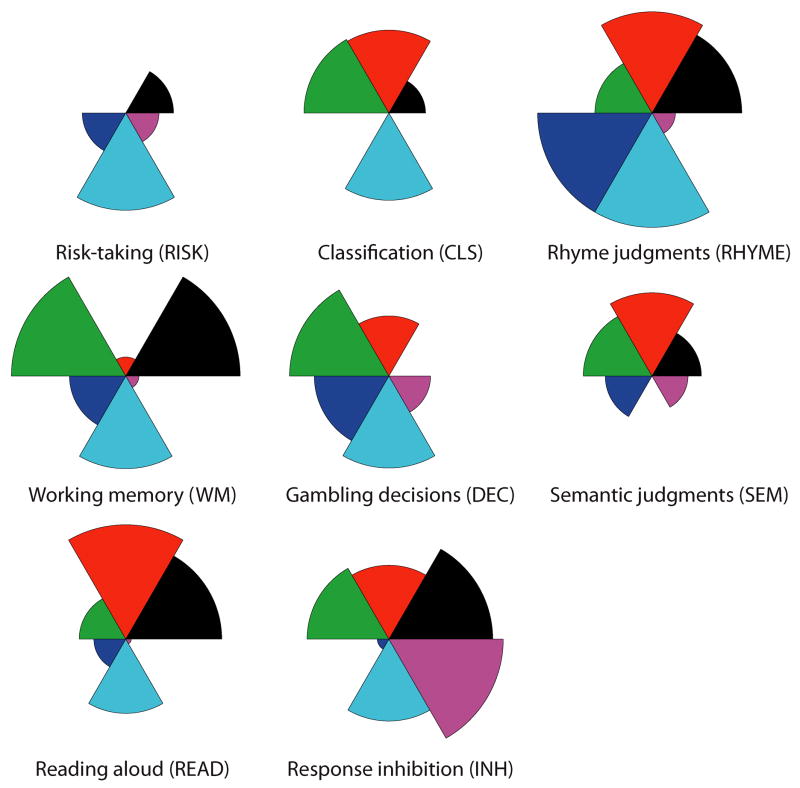
In order to characterize the derived dimensionality of the task space, we constructed a visualization of the dimensions for each task using star plots, which coded the contribution of each dimension to each task. These plots (Fig. 3) revealed that brain functions across these diverse tasks were organized on a small set (three to six) of unknown functional features, which suggests that all the tasks recruited similar brain networks, to different degrees.

Fig. 3.

Dimensional loadings for each task. The six dimensions were extracted from the neural network trained on the reduced feature set. The coefficient loading for each dimension in each task is coded by the relative size of that dimension’s wedge in the plot.

MAPPING NEURAL AND MENTAL SPACES USING ONTOLOGIES

To characterize the neural dimensions obtained from the neural network analysis in terms of basic mental processes, we coded each task according to the presence or absence of a number of such processes (as depicted in Supplementary Fig. 5 in the Supporting Information available online). These processes were then projected onto all six functional dimensions in order to characterize which cognitive processes were most strongly related to each neural processing dimension (Fig. 4).

Fig. 4.

Visualization of the loading of mental concepts onto brain systems. The slice images show regions that exhibited positive (red or yellow) loading on each of the six dimensions identified in the neural network analysis; the original voxel loading maps were smoothed in order to create these images. The tag clouds above the images represent the strength of association between a set of cognitive concepts and these dimensions; larger words (darker shades) were more strongly associated with the indicated dimension.

Dimension 1 loaded most heavily on the cognitive concept “audition,” and the neural pattern associated with this dimension was primarily centered on the superior temporal gyrus (i.e., auditory cortex) and precentral gyrus. Dimension 2 was associated with language processes, and engaged a bilateral network including Broca’s and Wernicke’s areas and their right-hemisphere homologues, as well as parahippocampal gyrus, medial parietal, and medial prefrontal regions. Dimensions 3 and 4 were associated with learning and memory and decision-making processes, and engaged highly overlapping sets of neural structures, including the thalamus, striatum, amygdala, medial prefrontal cortex, and parietal cortex. Dimension 5 was mostly strongly associated with memory and vision, and was tightly focused on the dorsomedial thalamus and dorsal striatum. Finally, Dimension 6 showed a pattern of loading that was very similar to activation observed in studies of response inhibition (right inferior frontal gyrus, basal ganglia, and medial prefrontal cortex; e.g., Aron & Poldrack, 2006), and the mental concept most associated with this pattern was indeed “response inhibition.” In each case, the pattern was not restricted to the concepts just indicated; Figure 4 shows that other concepts had strong loadings on these dimensions as well. These data suggest that the functions of these networks are only partially captured by the specific terms we have used; however, the relatively small number of tasks included in the analysis certainly biased the particular associations that were observed.

DISCUSSION

The results presented here show that fMRI data contain sufficient information to accurately determine an individual’s mental state (as imposed by a mental task) by using classifiers trained on data from other individuals. This finding generalizes previous results, which have demonstrated accurate classification within individuals (Hanson et al., 2004; Haxby et al., 2001; Haynes & Rees, 2005) and between individuals (Mourao-Miranda et al., 2005; Shinkareva et al., 2008), and provides a proof of concept that fMRI can be used to detect a broad range of cognitive states in previously untested individuals. The results also demonstrate how large-scale neuroimaging data sets can be used to test theories about the organization of cognition. Whereas previous imaging studies have nearly always focused on determining the neural basis of a particular cognitive process using specific task comparisons to isolate that process, the approach outlined here shows how data from multiple tasks can be used to examine the neural basis of cognitive processes that span across tasks. To the degree that cognitive theories make predictions regarding the similarity structure of different tasks, these theories could be tested using neuroimaging data.

Relation to Standard Neuroimaging Analyses

The standard mass-univariate approach to fMRI analysis is aimed at answering the following question: What regions are significantly active when a specific mental process is manipulated? Examination of the statistical maps associated with each of the eight tasks in the present study revealed substantial overlap between different sets of tasks, as well as some distinctive features. Our classifier analysis answered a very different question: What task is the subject most likely engaged in, given the observed pattern of brain activity? In the neuroimaging literature, it is common for researchers to use univariate maps to infer the engagement of specific mental processes from univariate analyses (i.e., reverse inference), but without using a classification technique, it is impossible to determine the accuracy of such inferences. More directly, our diagnosticity analysis shows that the set of voxels that are activated by a task is much larger than the set of voxels whose activity is diagnostic for engagement in a particular task. This suggests that informal reverse inference is almost certain to be highly inaccurate in task domains like those we examined and that approaches like the one used here are necessary in order to make strong inferences about cognitive processes from neuroimaging data.

Ontologies for Cognitive Neuroscience

The use of formal ontologies (Bard & Rhee, 2004), such as the Gene Ontology (Ashburner et al., 2000), has become prevalent in many areas of bioscience as a means to formalize the relation between structure and function. The results of our analysis, in which a simple ontology of mental processes was mapped onto dimensions of neural activity, provide a proof of concept for the utility of cognitive ontologies as a means to better understand how mental processes map to neural processes (cf. Bilder et al., 2009; Price & Friston, 2005). Currently, it is not possible to determine how well the methods we used could scale to a larger analysis using a complete ontology of mental states. Such analyses would require large databases of statistical results from individual subjects, which are not currently available. The present results suggest that such databases could be of significant utility to the cognitive-neuroscience community. In addition, it is likely that differences in acquisition parameters will have significant effects on the ability to classify and cluster neuroimaging data across studies. The development of neuroimaging consortia that use standardized data-acquisition parameters could help reduce this problem.