Abstract
The time it takes an enzyme to complete its reaction is a stochastic quantity governed by thermal fluctuations. With the advent of high-resolution methods of single-molecule manipulation and detection, it is now possible to observe directly this natural variation in the enzymatic cycle completion time and extract kinetic information from the statistics of its fluctuations. To this end, the inverse of the squared coefficient of variation, which we term nmin, is a useful measure of fluctuations because it places a strict lower limit on the number of kinetic states in the enzymatic mechanism. Here we show that there is a single general expression for the substrate dependence of nmin for a wide range of kinetic models. This expression is governed by three kinetic parameters, which we term NL, NS, and α. These parameters have simple geometric interpretations and provide clear constraints on possible kinetic mechanisms. As a demonstration of this analysis, we fit the fluctuations in the dwell times of the packaging motor of the bacteriophage φ29, revealing additional features of the nucleotide loading process in this motor. Because a diverse set of kinetic models display the same substrate dependence for their fluctuations, the expression for this general dependence may prove of use in the characterization and study of the dynamics of a wide range of enzymes.
Keywords: statistical kinetics, enzyme dynamics, single molecule, molecular motors
An enzymatic reaction can be seen as a sequence of distinct kinetic states separated by energy barriers. The energy needed to cross these barriers is provided by spontaneous thermal fluctuations and, as a result, the time to complete an enzymatic cycle is stochastic: two identical enzymes executing the same kinetic mechanism will complete their cycles in different times. Nonetheless, these fluctuations are not useless noise. The enzymatic mechanism determines how thermal fluctuations are transformed into variation in the cycle completion time. Thus, statistical measures of these fluctuations promise to provide new insight into enzyme dynamics (1–3).
Experimental advances in the methods of single-molecule manipulation and detection as well as synchronized ensemble methods have made the measurement of these fluctuations increasingly routine (4–7). However, observation of these fluctuations alone is not enough to create new insights into the enzymatic mechanism. Fluctuations must be quantified and classified, and statistical measures must be related to constraints on possible mechanisms. For measurements of the mean cycle completion time as a function of substrate concentration such classification is typically provided by the well-studied Michaelis-Menten expression and its parameters, kcat and KM (8, 9) or the more general Hill expression (8, 10). With these expressions and their parameters, the behavior of different enzymes can be succinctly reported and compared, and basic limits can be placed on the enzymatic mechanism (8). Unfortunately, no analogous expressions exist for enzymatic fluctuations.
Before fluctuations can be characterized and classified, they must be quantified. One particularly simple and useful statistical measure is the squared coefficient of variation—the variance in the cycle completion times normalized by the mean squared time. This measure is used in the study of a wide variety of random systems, ranging from telecommunications (11) to gene expression (12). In single-molecule enzymology, the squared coefficient of variation has been related to the randomness parameter (1, 13, 14), the mechanicity (15), and the zero frequency component of a Fourier analysis of fluctuations (16, 17). In some cases (18, 19), this value can be estimated even when the individual enzymatic cycles are obscured by experimental noise (1, 13, 14, 16, 17).
Here we consider the inverse of the squared coefficient of variation,
 |
[1] |
where 〈τ〉 is the mean time to complete the enzymatic cycle and 〈τ2〉-〈τ〉2 is the variance in this time. We adopt the term nmin for this ratio because, remarkably, it provides a strict lower limit on the number of kinetic states that must compose the enzymatic mechanism. Explicitly, if a given kinetic model has N kinetic states, the measured value of nmin must obey
| [2] |
This inequality applies for any stochastic process composed of distinct Markov states with exponentially distributed lifetimes (20)—reasonable assumptions that are common in kinetic modeling (3). Because [2] is based on general assumptions, the measured value of nmin can be used to eliminate candidate kinetic models with very little a priori knowledge of the kinetic mechanism. Simply put, any model with fewer kinetic states than the measured value of nmin need not be considered. This model independence is a feature not shared by most methods of fluctuation analysis where it is typically required that a specific kinetic model or family of models must first be assumed before fluctuations can be analyzed.
The inequality in [2] can yield more than a single constraint on potential mechanisms. As external parameters such as substrate concentration or force are varied, kinetic rates will change, and different sets of kinetic states will become rate-limiting (8, 21). Thus, nmin, as an estimate of the number of “effective” rate-limiting states, will vary with substrate concentration. Such substrate dependence has been calculated for a variety of specific kinetic models (1, 13, 15, 19, 22–27), and these expressions have been fit to experimental measurements (when available) (13, 15, 28). However, by assuming a specific kinetic model, the expressions derived previously are only applicable to the assumed models, and, thus, do not exploit the model independence of [2]. What is needed is a general expression for the substrate dependence of nmin applicable for a large family of kinetic models—an expression analogous to the Michaelis-Menten equation.
Here we consider the substrate concentration dependence of nmin for an important family of kinetic models and show that there is a single, compact expression that contains, as a subset, all previous equations (1, 13, 15, 19, 22–27). We discuss the kinetic parameters introduced by this expression and derive the mechanistic constraints they provide. Finally, we conclude by applying our expression to fluctuation data collected for the packaging motor of the bacteriophage φ29 (29).
Results
Assumptions and Schematic Proof.
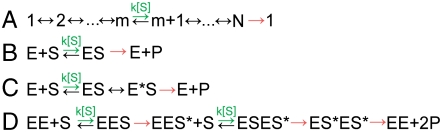
We model enzymatic dynamics as a first passage process through a series of discrete kinetic states, each of which has an exponentially distributed lifetime and transition rates that depend only on the current kinetic state (3). We further restrict our analysis to an important class of kinetic models: the nearest neighbor models as depicted in Fig. 1A. This class of models contains all kinetic mechanisms in which every state is on-pathway, i.e., there are no off-pathway branches and no parallel catalytic pathways, and includes the text-book Michaelis-Menten mechanism (Fig. 1B), mechanisms with multiple intermediate states (Fig. 1C), and even systems that involve the binding of multiple substrate molecules (Fig. 1D).
Fig. 1.
Kinetic Models. (A) A schematic diagram of the nearest neighbor kinetic models considered here. Each kinetic state, i, can transition to either the state before it, i - 1, or the state after it, i + 1. One or more of these transitions (green) corresponds to the binding of a substrate molecule and occurs with a rate constant proportional to the substrate concentration, ki[S]. The transition from the final state in the cycle, state N, is assumed to be irreversible (red) and to produce a detectable signal that marks the end of one cycle and the beginning of the next. This family of kinetic models includes (B) the common Michaelis-Menten mechanism as well as generalizations of this mechanism with (C) intermediate states (E*S) and (D) additional substrate binding events.
In addition, we consider only models that display a Michaelis-Menten-like substrate dependence for the mean cycle completion time:
 |
[3] |
where [S] is the substrate concentration (8, 9). kcat, the “effective” catalysis rate, determines the maximum rate of the reaction while KM, the “Michaelis” constant, determines the substrate concentration at which the reaction proceeds at half the maximal speed. This substrate dependence can also be exhibited by mechanisms that require the binding of multiple substrate molecules as long as these binding events are separated by irreversible transitions (29) (Fig. 1D; SI Text).
Finally, we require that the enzymatic reaction concludes with an irreversible transition that produces a measurable signal. For the case of a molecular motor, this transition might correspond to a physical movement such as a discrete step or rotation (3, 8), but, more generally, this transition could be an internal conformational change or the formation of the enzymatic product, revealed, perhaps, by a change in fluorescence (5, 6). The final irreversible transition is not needed if reverse reactions can be identified and analyzed separately (19) though it simplifies our analysis here.
Given these assumptions, our proof of the general form for the substrate dependence of nmin proceeds as follows: we start with the closed-form, analytic solutions for the mean cycle completion time and the variance in these times as a function of the individual rate constants for all nearest neighbor kinetic models (19, 30). We then derive the necessary and sufficient restrictions required to produce a Michaelis-Menten substrate dependence for the mean dwell time and apply these restrictions to the expression for the variance in the cycle times. With the substrate dependence of the mean and the variance, we derive the general substrate dependence of nmin via the definition in [1]. The full proof is provided in the SI Text.
The General Substrate Dependence of nmin.
Under the above assumptions, we find that the general substrate dependence of nmin is described by
 |
[4] |
Eq. 4 defines a family of curves governed by the same KM that appears in Eq. 3 and three dimensionless parameters, NL, NS, and α. In general, these parameters are complicated functions of both the number of kinetic states and their interconversion rates (SI Text: Equations S22–S25). However, for all of the models considered here, the individual kinetic rates combine in such a way that they can be captured with just these parameters, hiding the individual complexity of different models.
Geometric Interperation of the nmin Parameters.
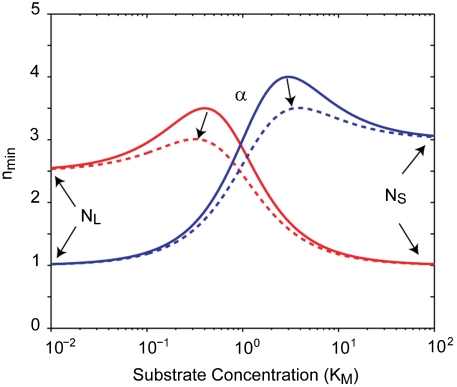
The nmin parameters have simple geometric interpretations (see Fig. 2). NL is the value at asymptotically low or Limiting substrate concentrations,
 |
[5] |
while NS is the value at asymptotically high or Saturating substrate concentrations,
 |
[6] |
Between these two asympotic values, nmin can peak to a value greater than either of the two limits. α controls the properties of this peak. When α < min(NL, NS), there is a peak in nmin while there is no peak when α is between NS and NL. If α is larger than both NS and NL, nmin does not peak, but rather drops to a local minimum. Such a situation seems unphysical since at this point both increasing and decreasing substrate concentration would produce more rate-limiting events; thus, we propose that α ≤ max(NL, NS).
Fig. 2.
General Substrate Dependence of nmin. nmin vs. substrate concentration, measured in units of KM. NL determines the asymptotic limit at low substrate concentrations while NS determines the asymptotic limit at saturating substrate concentrations. The parameter α determines the height of the peak between these two asymptotic limits. The solid red curve corresponds to NL = 2.5, NS = 1, and α = 0. The solid blue curve corresponds to NL = 1, NS = 3, and α = 0. The dashed lines correspond to the same values as the solid curves but with α = 0.3.
If there is a peak in nmin, the value at this peak is
 |
[7] |
and it occurs at a substrate concentration of
 |
[8] |
For small α, max(nmin) ∼ NL + NS - 2α. Thus, α is roughly half the difference between the peak value and the sum of the two asymptotic limits. If α = 0, then the maximum of nmin is NL + NS and it occurs at [S]max = KMNS/NL. The substrate concentration at which this maximum occurs can be either below or above the KM depending on the larger of NL and NS.
Physical Interpretation of the nmin Parameters.
As we show in the SI Text, the three nmin parameters place clear limits on possible kinetic mechanisms. First, if the underlying kinetic model has N = NB + Nother kinetic states, where NB is the number of substrate binding states and Nother is the number of other states, then the value of NS provides a strict lower limit on the actual number of non-substrate-binding kinetic states in the cycle:
| [9] |
Moreover, NS = Nother if and only if the system visits each kinetic state once and only once and the lifetimes of each kinetic state are equal, i.e., all transitions are irreversible with the same transition rate. Any difference in the transition rates or reversibility in the cycle will result in a value of NS < Nother.
The value of nmin at asymptotically low substrate concentration, NL, has a similar interpretation. If the enzyme only binds one substrate molecule, i.e., NB = 1, then NL = 1. However, if the enzyme binds multiple substrate molecules, NL provides a strict lower limit on the number of molecules that bind each cycle:
| [10] |
In general, NL is a complicated function of the individual kinetic rates that are involved in the binding and commitment of each substrate molecule (SI Text: Eqs. S7, S23). The average rate at which this process occurs, the catalytic efficiency of binding (8), is βi = kcat,i/KM,i where kcat,i and KM,i are the Michaelis-Menten parameters for the binding of each substrate molecule. Despite its complex dependence on individual rate constants, NL has as a simple dependence on the catalytic efficiencies:
 |
[11] |
This relationship should allow catalytic efficiencies to be inferred or constrained from the measured value of NL with no a priori knowledge of the specific mechanism by which substrate is bound and committed to the cycle.
Eq. 11 implies that NL = NB if and only if the catalytic efficiencies for binding each of the substrate molecules are identical. In contrast to NS, this equality need not imply that the binding of substrate molecules is irreversible or even that each binding process involve exactly the same kinetic states with the same rates. Rather, multiple substrate molecules may be bound via very different mechanisms, yet if the catalytic efficiencies of these processes are the same, NL will be equal to the number of substrate molecules that bind.
For the nearest neighbor models considered here, we find that NL, NS≥1. Thus, an observed value of NL, NS < 1 necessarily implies that the enzymatic mechanism must have features not treated here, e.g., parallel catalytic pathways or off-pathway pause states. This conclusion is supported by theoretical studies on enzymatic systems that display dynamic disorder—i.e., a large or infinite set of parallel catalytic pathways—in which it is shown that nmin < 1 (23, 31). Similarly, it is possible to measure a value of nmin < 1 when a population of enzymes display heterogenous dynamics, i.e., static disorder.
Finally, the value of the parameter α places some physical restrictions on the enzymatic mechanism. Under the assumption that the underlying kinetic mechanism contains no off-pathway branches or parallel pathways (Fig. 1A), α = 0 if and only if i) the binding of substrate molecules is strictly irreversible and ii) the binding state is not in equilibrium with the previous kinetic state. In other words, a measured value of α = 0 indicates that the binding of substrate must obey:
| [12] |
where E′ is the kinetic state that proceeds the binding state, E is the binding competent state, ES is the substrate docked state, and the arrows represent irreversible transitions. If the enzyme binds multiple substrate molecules, then these conditions must hold for each binding transition.
Application to the Packaging Motor of the Bacteriophage φ29.
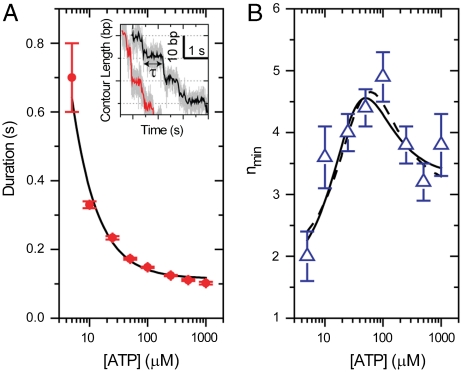
As an illustration of the use of Eq. 4 and its parameters, we have applied this analysis to recent data collected on the packaging motor of the bacteriophage φ29. This bacteriophage utilizes a pentameric ring (32) of identical ATPase subunits to drive the compaction of its dsDNA genome into a proteinacous precursor capsid during viral self-assembly (33). Recent high-resolution optical trapping measurements (29) have revealed the discrete, 10 base pair, increments of DNA packaged each cycle of the motor. The observation of the discrete steps of this motor makes it possible to compile the exact time between steps—the dwell times of the enzyme. Both the average dwell time and the variance in these times as a function of [ATP] were determined, as was nmin for all [ATP] under conditions of low opposing load (see Fig. 3). Additional measurements at high opposing loads revealed that after the dwell, the DNA was packaged not in a single step, but in a burst of four 2.5-bp steps. The observation of four steps per cycle strongly suggests that the motor loads four ATPs to four different subunits during the observed dwells (29).
Fig. 3.
Statistical Properties of the Dwell Times for the Packaging Motor of the Bacteriophage φ29. (A) Mean dwell time for the packaging motor of the Bacteriophage φ29 as a function of [ATP] with a Michaelis-Menten fit (solid black). Inset: Example packaging traces for 5 and 10 μM [ATP] (black and red, respectively). Light gray corresponds to 1.25 kHz data averaged to 100 Hz in color. (B) nmin vs. [ATP] with fits to Eq. 4 with either KM floating (dashed) or fixed (solid). Fit values are listed in Table 1. Data are reproduced with permission from Ref. (29), Macmillan publishers Ltd: Nature © 2009.
Previous work (29, 34) has shown that the mean dwell time is well described by a Michaelis-Menten [ATP] dependence; thus, we expect that the substrate dependence of nmin is fit by Eq. 4. To test this hypothesis, we first fit the nmin data with Eq. 4, allowing all four parameters to vary. Fig. 3B shows that the resulting fit describes well the substrate dependence of the data (solid black line), producing a KM = 36 ± 18 μM consistent with the value measured directly from the mean dwell time, KM = 23 ± 7 μM. The agreement between the KM measured from 〈τ〉 and from nmin lends support to both the data and the theoretical treatment considered above. We then refit the nmin values using the KM measured from the mean dwell time, which is better constrained than the value measured from a fit to nmin directly. Again, Fig. 3B shows that the data are well fit by Eq. 4 (dashed black line). Table 1 lists the values of NL, NS, α, and their uncertainties for these fits.
Table 1.
Fit Parameters for Fig. 3
| Parameter | Michaelis-Menten | nmin Floating KM | nmin Fixed KM |
| kcat | 8.7 ± 0.2 s-1 | N/A | N/A |
| KM | 23 ± 7 μM | 36 ± 18 μM | 23 μM |
| NL | N/A | 1.9 ± 0.4 | 1.6 ± 0.3 |
| NS | N/A | 3.1 ± 0.3 | 3.3 ± 0.2 |
| α | N/A | 0.2 ± 0.3 | 0.2 ± 0.3 |
The specific fit values of the nmin parameters have several implications for the kinetic mechanism of the packaging motor. In particular, the values of NL and NS indicate that each cycle must contain no less than two ATP binding states and no less than four additional, non-ATP-binding states. Previously, similar conclusions were drawn from the measured value of nmin at the highest and lowest concentrations of ATP (5 μM and 1,000 μM ATP), under the assumption that these conditions were sufficiently limiting or saturating for ATP (29). However, limiting or saturating concentrations of [ATP] for the mean dwell time need not be limiting or saturating for nmin, and, thus, it was not necessarily obvious that the values of nmin measured at the lowest and highest [ATP] were accurate estimates of the asymptotic values of this parameter. The fit to Eq. 4 confirms the previous interpretations while eliminating the need to argue that a specific [ATP] is sufficiently “saturating” or “limiting.” Moreover, the fit to Eq. 4 provides estimates of the asymptotic values of nmin that are better constrained and less biased by single measurements. For example, at saturating [ATP] the uncertainty in the asymptotic value drops from ± 0.5 (the single measurement at 1,000 μM) to ± 0.2 (Table 1). Furthermore, Fig. S1 shows that removing each of the measured values of nmin at different [ATP] does not significantly change the values of the fit parameters, indicating that the asymptotic values are determined from all measurements not just those at the lowest and highest [ATP].
Finally, the measured value of α is consistent with a small, perhaps zero, value for this parameter. From previous work, it has been established that the binding of ATP likely involves an initial, reversible docking process followed by a tight binding transition, which is irreversible and commits the nucleotide to the hydrolysis cycle (29, 34). A measured value of α consistent with zero suggests that this initial docking process is not highly reversible. However, the large uncertainty on this parameter prohibits more detailed claims on the degree to which ATP binding is irreversible.
Specific Restrictions on Catalytic Efficiencies.
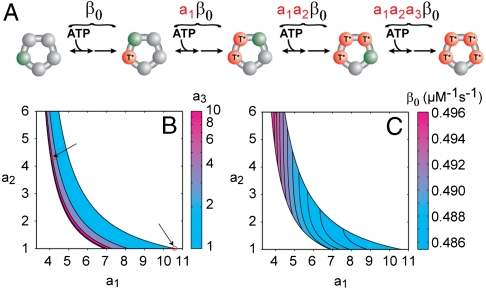
In addition to formalizing previous interpretations, the specific values of the nmin parameters allow us to extract additional information from fluctuations. In particular, under the assumption that four ATPs load each cycle (29), we can restrict the relative catalytic efficiency of binding ATP to each subunit from the measured value of NL by using Eq. 11. We first adopt a convenient parameterization: the subunits are ordered from smallest catalytic efficiency to largest, and the catalytic efficiency of each subunit is described as function of the previous subunit (see Fig. 4A). By requiring that a1, a2, and a3≥1 , we consider each combination of catalytic efficiencies only once. The numbering of the individual subunits should not be confused with the physical ordering of the subunits within the motor ring. Eq. 11 treats all subunits identically, so rearranging the order of the subunits would not change the measured value of NL.
Fig. 4.
Relationship between the catalytic efficiencies of the different subunits. (A) The ATP loading cycle of the pentameric packaging motor of φ29. The catalytic efficiency for each subunit increases, βi, by the geometric factors a1, a2, and a3. Green corresponds to subunits competent to bind ATP while red (T*) corresponds to subunits loaded with ATP. (B) Contour plot of the permitted values of a1, a2, and a3. Arrows highlight specific combinations of a1, a2, and a3 mentioned in the text. (C) Contour plot of the smallest catalytic efficiency in the ring for permitted values of a1 and a2.
Under this parameterization, Eq. 11 becomes
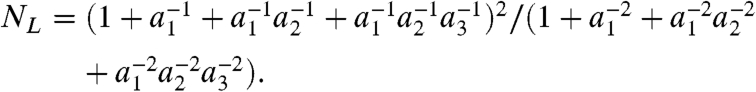 |
[13] |
Combined with the measured value of NL = 1.6, this expression defines a unique three-dimensional surface that constrains the possible catalytic efficiencies in the ring, shown in Fig. 4B. This surface reveals that not all combinations of a1 and a2 are permissible rather a1 and a2 must be within a narrow set of values to produce the measured NL. Remarkably, a1 = a2 = a3 = 1 is not a solution; thus, despite the fact that the individual ATPase subunits in the packaging motor are chemically identical, they cannot have identical catalytic efficiencies. This observation implies that the conformation of a given subunit must be a function of the catalytic state of the surrounding subunits. While no high-resolution structure exists for the packaging motor, the structural asymmetries needed to produce this kinetic asymmetry has been observed for related ring ATPases (35).
There are two combinations of catalytic efficiencies that are of particular interest. First, if one and only one subunit is distinct from the others, i.e., a2 = a3 = 1, then this “special” subunit must have a catalytic efficiency 10.7 ± 5.2 times smaller than the other three (the uncertainty is due to the uncertainty in NL). In such a model, one might imagine that the first or last subunit would sense the asymmetry in the ring and as a result bind and commit ATP to the hydrolysis cycle more slowly than the other three. Alternatively, each subunit might know its exact position in the ring, first, second, etc., and each position might correspond to a different catalytic efficiency for binding. In this case, it is useful to consider a model in which the catalytic efficiency of each subunit increases with respect to the previous subunit by the same geometric amount, i.e., a1 = a2 = a3. To produce the measured value of NL, this geometric factor must be 4.3 ± 1.7. Thus, on average, the catalytic efficiencies between the different subunits in the packaging motor must increase (or decrease) by a factor of ∼4 as each subunit loads ATP.
The absolute values of the catalytic efficiencies can also be constrained. The inverse of the total catalytic efficiency at which ATP is loaded to the ring is simply the sum of the inverse of the efficiencies of the individual subunits (SI Text: Eq. S15); thus, each set of a1, a2, and a3 in Fig. 4B corresponds to a specific set of catalytic efficiencies. Fig. 4C shows that β0, the smallest catalytic efficiency, varies remarkably little, < 5%, across the permissible range of a1, a2, and a3. It is interesting to note that had we simply assumed that the four catalytic efficiencies were equal we would have estimated a value three times larger, ∼1.5 μM-1 s-1.
Discussion
Enzymatic dynamics are dominated by fluctuations, and techniques for quantifying these fluctuations directly are becoming increasingly routine (1–7). In this article, we extend fluctuation analysis by proving that for a wide range of kinetic models the substrate dependence of a useful measure of fluctuations, nmin, is governed by a single, general expression. Moreover, we show that this expression is parameterized by just three kinetic parameters: NL which sets the value of nmin at asymptotically limiting substrate concentrations, NS which sets the value of nmin at asymptotically saturating substrate concentrations, and α which parameterizes the difference between the maximum value of nmin and the sum of the two asymptotic limits. These parameters provide powerful constraints on the underlying kinetic mechanism of the enzyme. In particular, NL and NS place strict lower bounds on the number of substrate-binding events and non-substrate-binding events, respectively, while the specific value of α provides information on the degree to which the binding of substrate is reversible. Finally, we illustrate the power of this analysis by using it to capture the substrate dependence of the fluctuations observed for the packaging motor of the bacteriophage φ29. The values we derive from fits to previous data not only rigorously confirm previous conclusions by providing the true asymptotic values of nmin at low and high substrate concentration, they also allow us to greatly restrict the possible values of the catalytic efficiencies for the different subunits.
In contrast to the expressions currently in use (1, 13, 15, 19, 22–27), Eq. 4 makes very limited assumptions about the underlying kinetic model. More importantly, one of the assumptions that it does make—that the mean dwell time has a substrate dependence described by the Michaelis-Menten expression—can be easily verified experimentally. While our proof of Eq. 4 assumes a specific family of kinetic models, a cursory analysis of specific kinetic models with off-pathway states or parallel catalytic pathways suggests that Eq. 4 is not restricted to the linear, unbranched kinetic models we consider here (36). Rather, we conjecture that the specific substrate dependence for nmin corresponds to any kinetic model in which the mean dwell time has a Michaelis-Menten substrate dependence and that the mechanistic constraints implied by its parameters also hold for more general kinetic schemes.
The general expression for the substrate dependence of nmin derived here provides several practical and theoretical benefits. First, extensive theoretical studies of the mean enzymatic behavior as a function of different experimental conditions have revealed that there are only a small number of basic substrate dependencies for the mean velocity: the Michaelis-Menten expression and the more general Hill expression (8). Knowning these general forms allows experimentalists to classify the behavior of their enzyme and to extract the relevant kinetic parameters, such as kcat and KM. In this sense, the general substrate dependence for nmin should allow enzymes to be classified based on the measured values of NL, NS, and α in addition to the values of kcat and KM.
Second, a general substrate dependence provides experimentalists with a way to quantitatively determine if truly saturating or limiting conditions have been probed. Given that much of the informative power of nmin comes from its values at asymptotically low and high substrate concentrations, an understanding of what signifies a saturating or limiting concentration of substrate is crucial to extracting information from fluctuations. Of course, truly saturating or limiting substrate concentrations can never be probed, but by specifying the dependence of nmin on different substrate concentrations, Eq. 4 allows the asymptotic limits of nmin to be inferred from measurements over a finite range of substrate concentrations.
Finally, and more fundamentally, a general substrate dependence for nmin provides a clear indication of the information content of such measurements. The mean dwell time or nmin can be measured at many different substrate concentrations, yet these measurements are not independent of one another. For example, a mean dwell time that is described by the Michaelis-Menten expression is completely determined by just two independent parameters, kcat and KM. After two different substrate concentrations have been probed, additional measurements only serve to better constrain these two parameters. Because a general kinetic model may have many more than two independent kinetic rates, measurements of the mean dwell time as a function of substrate concentration cannot uniquely constrain typical models.
In this light, the results we provide here reveal the information content of the variance in the cycle completion time. Specifically, if the nmin of a given system has a substrate dependence described by Eq. 4, then these measurements will provide only three additional constraints on the underlying kinetic mechanism. Once these parameters are specified, additional measurements at new substrate concentrations will only better constrain these parameters, not yield new constraints on the system. Since there is a large degree of degenerecy in the types of kinetic models that produce a given substrate dependence for both the mean dwell time and nmin, care should be taken before touting the validity of specific kinetic models on the basis of their fit to the experimental data. Rather, experimental data should be used to dictate features of the kinetic scheme
The mechanistic constraints provided by the measurements of substrate dependence of enzymatic flucuations are fundamentally different than those provided by measurements of the mean. In practice, the specific values of kcat or KM say little about the individual kinetic rates or binding affinities of the underlying kinetic model. In contrast, the parameters of nmin provide fundamental limits on the enzymatic mechanism, placing firm constraints on the number of kinetic states that a candidate model must contain. The ability to place restrictions on candidate models from statistical measures of fluctuations is a reflection of the fact that there are fundamental differences between the stochastic dynamics of enzymes that are goverened by different kinetic models—properties which are now amenable to direct measurement.
Supplementary Material
Acknowledgments.
We thank A. Kaplan and A. R. Subramaniam for a critical reading of the manuscript. J.R.M. was supported by the National Science Foundation’s Graduate Research Fellowship. Y.R.C. was supported by the Burroughs Welcome Fund’s Career Awards at the Scientific Interface. This work was supported by National Institutes of Health (NIH) Grants GM-071552, DE-003606, and GM-059604 awarded to C.B.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1006997107/-/DCSupplemental.
References
- 1.Schnitzer MJ, Block SM. Statistical kinetics of processive enzymes. Cold Spring Harbor Symposia on Quantitative Biology. 1995;60:793–802. doi: 10.1101/sqb.1995.060.01.085. [DOI] [PubMed] [Google Scholar]
- 2.Xie SN. Single-molecule approach to enzymology. Single Mol. 2001;2:229–236. [Google Scholar]
- 3.Kolomeisky AB, Fisher ME. Molecular motors: a theorist’s perspective. Annu Rev Phys Chem. 2007;58:675–695. doi: 10.1146/annurev.physchem.58.032806.104532. [DOI] [PubMed] [Google Scholar]
- 4.Sakmann B, Neher E. Patch clamp techniques for studying ionic channels in excitable membranes. Annu Rev Physiol. 1984;46:455–472. doi: 10.1146/annurev.ph.46.030184.002323. [DOI] [PubMed] [Google Scholar]
- 5.Cornish PV, Ha T. A survey of single-molecule techniques in chemical biology. ACS Chem Biol. 2007;2:53–61. doi: 10.1021/cb600342a. [DOI] [PubMed] [Google Scholar]
- 6.Greenleaf WJ, Woodside MT, Block SM. High-resolution, single-molecule measurements of biomolecular motion. Annu Rev Biophys Biomol Struct. 2007;36:171–190. doi: 10.1146/annurev.biophys.36.101106.101451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Moffitt JR, Chemla YR, Smith SB, Bustamante C. Recent advances in optical tweezers. Annu Rev Biochem. 2008;77:205–228. doi: 10.1146/annurev.biochem.77.043007.090225. [DOI] [PubMed] [Google Scholar]
- 8.Segel IH. Enzyme kinetics. New York: John Wiley & Sons, Inc; 1975. pp. 346–462. [Google Scholar]
- 9.Michaelis L, Menten ML. The kenetics of the inversion effect. (Translated from German) Biochem Z. 1913;49:333–369. [Google Scholar]
- 10.Hill AV. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J Physiol. 1910;40:iv–vii. [Google Scholar]
- 11.Breuer L, Baum D. An introduction to queueing theory and matrix-analytic methods. Dordrecht, Netherlands: Kluwer Academic Publishers; 2005. pp. 169–178. [Google Scholar]
- 12.Paulsson J. Models of stochastic gene expression. Phys Life Rev. 2005;2:157–175. [Google Scholar]
- 13.Schnitzer MJ, Block SM. Kinesin hydrolyses one ATP per 8-nm step. Nature. 1997;388:386–390. doi: 10.1038/41111. [DOI] [PubMed] [Google Scholar]
- 14.Svoboda K, Mitra PP, Block SM. Fluctuation analysis of motor protein movement and single enzyme kinetics. Proc Natl Acad Sci USA. 1994;91:11782–11786. doi: 10.1073/pnas.91.25.11782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fisher ME, Kolomeisky AB. Simple mechanochemistry describes the dynamics of kinesin molecules. Proc Natl Acad Sci USA. 2001;98:7748–7753. doi: 10.1073/pnas.141080498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Charvin G, Bensimon D, Croquette V. On the relation between noise spectra and the distribution of time between steps for single molecular motors. Single Mol. 2002;3:43–48. [Google Scholar]
- 17.Neuman KC, et al. Statistical determination of the step size of molecular motors. Journal of Physics: Condensed Matter. 2005;17:S3811–S3820. doi: 10.1088/0953-8984/17/47/012. [DOI] [PubMed] [Google Scholar]
- 18.Shaevitz JW, Block SM, Schnitzer MJ. Statistical kinetics of macromolecular dynamics. Biophys J. 2005;89:2277–2285. doi: 10.1529/biophysj.105.064295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chemla YR, Moffitt JR, Bustamante C. Exact solutions for kinetic models of macromolecular dynamics. J Phys Chem B. 2008;112:6025–6044. doi: 10.1021/jp076153r. [DOI] [PubMed] [Google Scholar]
- 20.Aldous D, Shepp L. The least variable phase type distribution is erlang. Stoch Models. 1987;3:467–473. [Google Scholar]
- 21.Bustamante C, Chemla YR, Forde NR, Izhaky D. Mechanical processes in biochemistry. Annu Rev Biochem. 2004;73:705–748. doi: 10.1146/annurev.biochem.72.121801.161542. [DOI] [PubMed] [Google Scholar]
- 22.Kolomeisky AB, Fisher ME. A simple kinetic model describes the processivity of Myosin-V. Biophys J. 2003;84:1642–1650. doi: 10.1016/S0006-3495(03)74973-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kou SC, Cherayil BJ, Min W, English BP, Xie XS. Single-molecule Michaelis-Menten equations. J Phys Chem B. 2005;109:19068–19081. doi: 10.1021/jp051490q. [DOI] [PubMed] [Google Scholar]
- 24.Goedecke DM, Elston TC. A model for the oscillatory motion of single dynein molecules. J Theor Biol. 2005;232:27–39. doi: 10.1016/j.jtbi.2004.07.017. [DOI] [PubMed] [Google Scholar]
- 25.Xu W, Kong JS, Chen P. Single-molecule kinetic theory of heterogeneous and enzyme catalysis. J Phys Chem C. 2009;113:2393–2404. [Google Scholar]
- 26.Tinoco I, Wen JD. Simulation and analysis of single-ribosome translation. Phys Biol. 2009;6:025006. doi: 10.1088/1478-3975/6/2/025006. [DOI] [PubMed] [Google Scholar]
- 27.Garai A, Chowdhury D, Chowdhury D, Ramakrishnan TV. Stochastic kinetics of ribosomes: Single motor properties and collective behavior. Phys Rev E. 2009;80:011908–011915. doi: 10.1103/PhysRevE.80.011908. [DOI] [PubMed] [Google Scholar]
- 28.Visscher K, Schnitzer MJ, Block SM. Single kinesin molecules studied with a molecular force clamp. Nature. 1999;400:184–189. doi: 10.1038/22146. [DOI] [PubMed] [Google Scholar]
- 29.Moffitt JR, et al. Intersubunit coordination in a homomeric ring ATPase. Nature. 2009;457:446–450. doi: 10.1038/nature07637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Derrida B. Velocity and diffusion constant of a periodic one-dimensional hopping model. J Stat Phys. 1983;31:433–450. [Google Scholar]
- 31.English BP, et al. Ever-fluctuating single enzyme molecules: Michaelis-Menten equation revisited. Nat Chem Biol. 2006;2:87–94. doi: 10.1038/nchembio759. [DOI] [PubMed] [Google Scholar]
- 32.Morais MC, et al. Defining molecular and domain boundaries in the Bacteriophage φ29 DNA packaging motor. Structure. 2008;16:1267–1274. doi: 10.1016/j.str.2008.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Grimes S, Jardine PJ, Anderson D. Bacteriophage φ29 DNA packaging. Adv Virus Res. 2002;58:255–294. doi: 10.1016/s0065-3527(02)58007-6. [DOI] [PubMed] [Google Scholar]
- 34.Chemla YR, et al. Mechanism of force generation of a viral DNA packaging motor. Cell. 2005;122:683–692. doi: 10.1016/j.cell.2005.06.024. [DOI] [PubMed] [Google Scholar]
- 35.Enemark EJ, Joshua-Tor L. On helicases and other motor proteins. Curr Opin Struc Biol. 2008;18:243–257. doi: 10.1016/j.sbi.2008.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Moffitt JR, Chemla YR, Bustamante C. Methods in statistical kinetics. Methods in Enzymology. 2010;475:221–257. doi: 10.1016/S0076-6879(10)75010-2. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.