All joint moments significantly contribute to trunk angular acceleration

Abstract

Computationally advanced biomechanical analyses of gait demonstrate the often counter intuitive roles of joint moments on various aspects of gait such as propulsion, swing initiation, and balance. Each joint moment can produce linear and angular acceleration of all body segments (including those on which the moment does not directly act) due to the dynamic coupling inherent in the interconnected musculoskeletal system. This study presents the quantitative relationships between individual joint moments and trunk control with respect to balance during gait to show that the ankle, knee, and hip joint moments all affect the angular acceleration of the trunk. We show that trunk angular acceleration is affected by all the joints in the leg with varying degrees of dependence during the gait cycle. Furthermore, it is shown that inter-planar coupling exists and a two dimensional analysis of trunk balance neglects important out-of-plane joint moments that affect trunk angular acceleration.

Introduction

Dynamic balance during walking consists in large part of stabilization of the trunk. Trunk angular sway has been indicated as a reliable measure of balance stability (Allum et al., 2001; Adkin et al., 2005; Allum et al., 2005); however, there are inconsistencies in the literature as to how each of the lower extremity joint moments affect trunk angular acceleration.

Previous studies have argued that because the inertia of the trunk about the ankle joint is nearly eight times the inertia of the trunk about the hip joint, the ankle muscles would need nearly eight times the moment-of-force relative to provide the same angular acceleration of the head, arms, and trunk segment as the hip muscles (Winter, 1990; Winter et al., 1990; Winter, 1995). They concluded that the central nervous system (CNS) may recognize this and utilize the hip muscles as the primary actuator for trunk angular control with little involvement of the ankle muscles during gait (Winter et al., 1990). Alternatively, EMG studies have concluded that the role of distal musculature is as important as proximal hip musculature in maintaining balance using a movable platform to allow for perturbations (Tang et al., 1998). Similar observations, using joint power and muscle EMG patterns, show that reactive balance control is more likely a synchronized effort of the lower extremity joint moments to prevent collapse during perturbations (Ferber et al., 2002).

Although the contribution of each muscle (or joint moment) has been explored with regards to trunk propulsion and support and segmental power flow (e.g., Neptune et al., 2001; Kepple et al., 1996; Zajac et al., 2002; Zajac et al., 2003), similar relationships to trunk angular acceleration have been relatively unexplored. In the present study, we use a three dimensional model and the resulting forward dynamic equations of motion to identify the relative contribution of each joint moment to the trunk angular acceleration and assess whether one joint more strongly accelerates the trunk than the others. We also analyze the contribution of sagittal plane moments on frontal plane trunk accelerations that are made possible through dynamic coupling (Zajac and Gordon, 1989), along with the contribution of frontal plane moments on sagittal plane accelerations, to assess whether caution is necessary when interpreting trunk angular acceleration with only sagittal plane analysis (McKinnon and Winter, 1993).

Methods

Subject

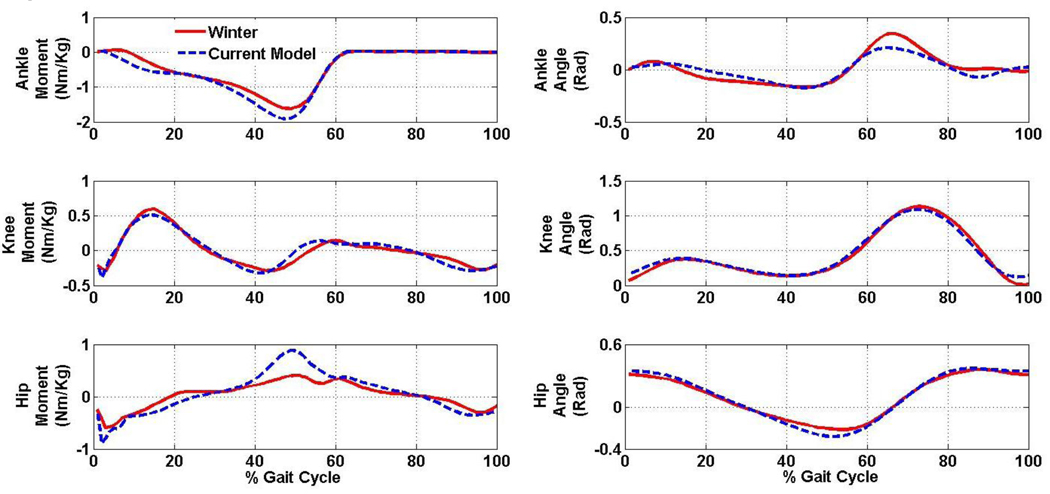
A single subject whose joint moments and joint angular velocities are consistent with published data used in similar trunk control research (e.g., Winter, 1991) (Fig. 1) was used for demonstration purposes. The subject walked at self-selected speed on an instrumented treadmill (Techmachine, Andrezieux Boutheon, France) for three trials of thirty seconds each.

Figure 1.

Comparison of the current model (blue) to data from previously published work (red) (Winter 1991).

Data collection

Kinematic data were collected using a 12 camera VICON system and sampled at 100Hz to capture spatial positions of markers placed on the subject in a modified Helen Hayes configuration. Rigid clusters of markers were placed on the feet, left and right shanks, left and right thighs, pelvis, trunk, head, and upper and lower arms to allow for six degree of freedom orientation measurement of each segment. Hip joint centers were determined using the CODA algorithm (Bell et al., 1989; Bell et al., 1990). In this work we have assumed that treadmill and overground gait are similar enough to make this study relevant to overground walking. We believe this is justified because each muscle will still accelerate all segments in exactly the same way in each mode of walking.

Model

A 12 segment rigid body model consisted of two feet, shanks, thighs, forearms, and upper arms, a head, and a combined pelvis and trunk segment. Each segment’s inertial characteristics were defined using Visual 3D (C-motion, Germantown, Maryland). The equations of motion were derived using a standard d’Alembert approach and a sensitivity matrix relating the joint moments to trunk accelerations was derived (see Appendix A). The joint constraints are defined by equation 4 in Appendix A. This equation assumes a ball and socket joint for all joints. The laboratory axes have the x-axis directed to the subject’s right, the y-axis directed forward, and the z-axis directed vertically. Note, to express the three-dimensional vectors in a sense that is most comparable with previously performed two-dimensional analysis, moments are expressed with reference to axes that remain parallel with the laboratory axes but with an origin at the proximal end of the corresponding segment (c.f., anatomically defined axes).

Results and Discussion

Trunk angular acceleration sensitivity

Sagittal plane

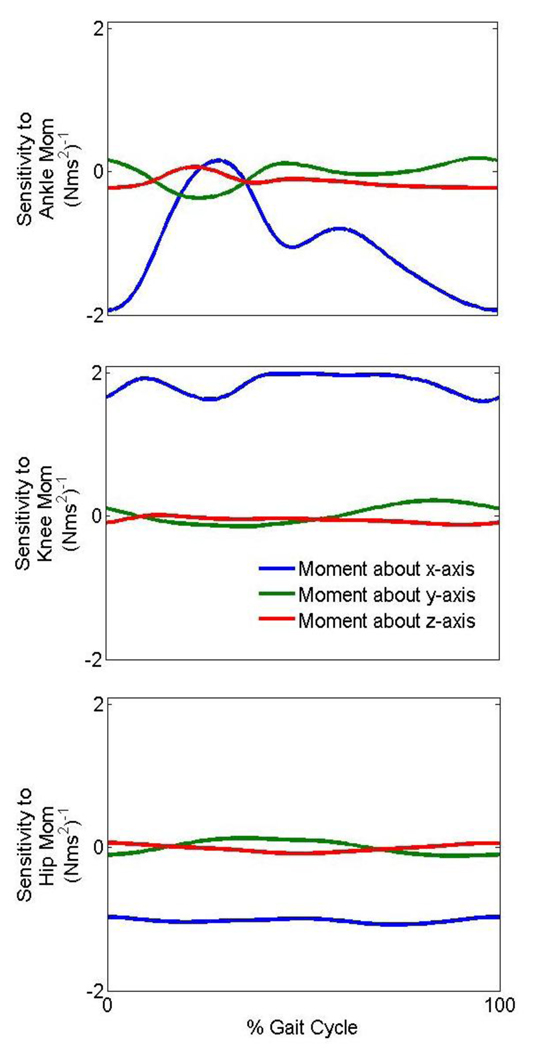
The elements of the sensitivity matrix (angular acceleration per N-m of moment produced) which affect the sagittal plane trunk angular acceleration are shown in Figure 2. The sagittal plane trunk angular acceleration depends little on non-sagittal plane moments.

Figure 2.

The sensitivity of the trunk angular acceleration about the x-axis to the joint moments during gait. A negative sensitivity implies that a positive moment about an axis causes a negative acceleration about the same axis and vice versa.

The sagittal plane trunk angular acceleration has a negative sensitivity to the moment generated at the ankle for most of the gait cycle (Fig. 2). Thus, an increase in plantar flexion moment (a more negative ankle moment about the x-axis) can cause the trunk to have an angular acceleration that leans the trunk posteriorly (shoulders back relative to hips, which is a positive angular acceleration about the x-axis). Similarly, an increase in a knee extension moment has the potential to cause an angular acceleration that leans the trunk posteriorly while an increase in hip flexion moment causes an angular acceleration that leans the trunk anteriorly. It should be noted that when the trunk angular acceleration is sensitive to a moment, it does not imply that the moment is influencing the trunk angular acceleration. If the moment is low, and the sensitivity is high, the joint may not influence the trunk angular acceleration. Thus, the sensitivity to a joint moment must always be considered in conjunction with the joint moment to assess the actual influence on the trunk angular acceleration.

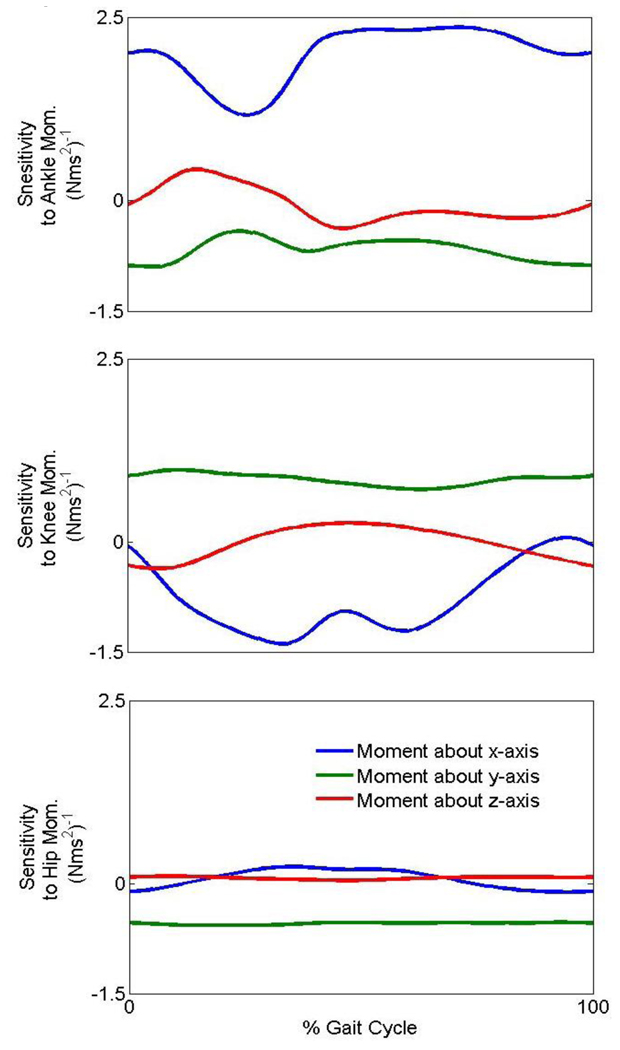
Frontal plane

The frontal plane trunk angular acceleration is similarly dependent on moments at all joints (Fig. 3). In addition to the importance of the moment at the hip, an increase in left ankle plantar flexion moment or left knee extension moment each could possibly cause a trunk angular acceleration to the right (Fig. 4).

Figure 3.

The sensitivity of the trunk angular acceleration about the y-axis to the joint moments of the leg during gait. A negative sensitivity implies that a positive moment about an axis causes a negative acceleration about the same axis and vice versa.

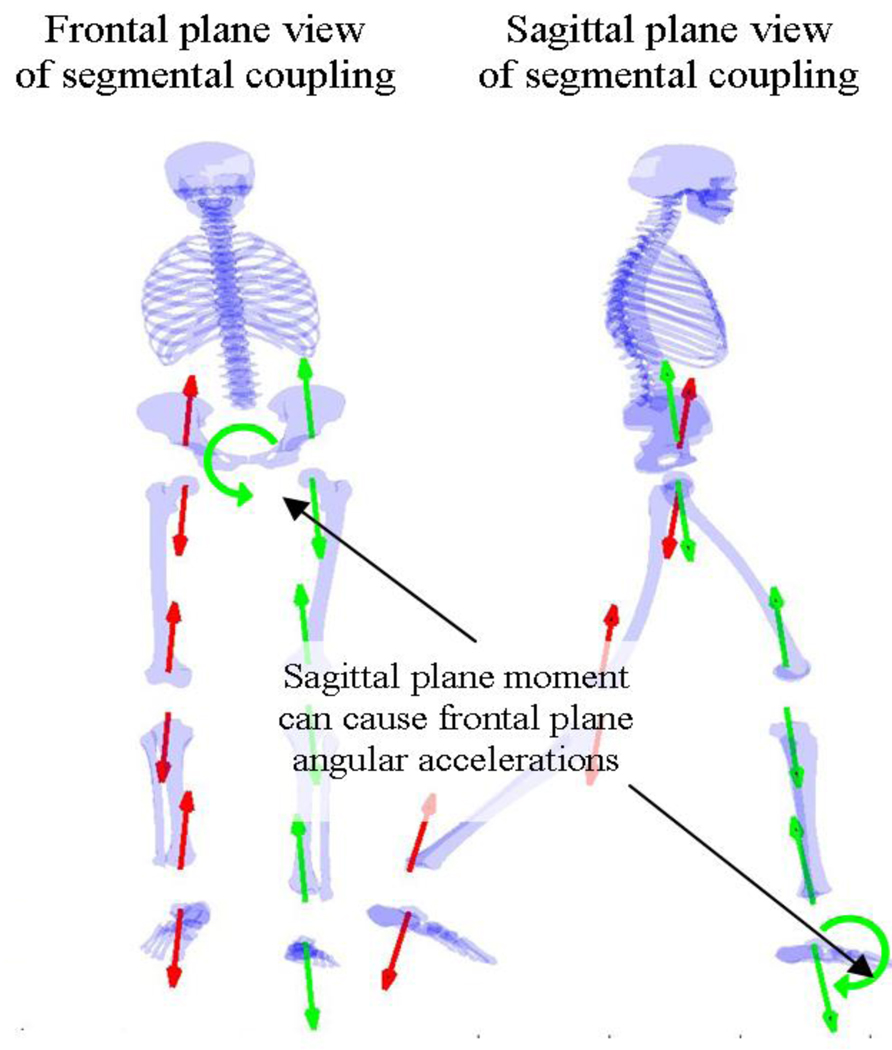
Figure 4.

Frontal and sagittal plane views illustrate how a sagittal moment can cause frontal plane accelerations by means of reaction forces along the kinematic chain.

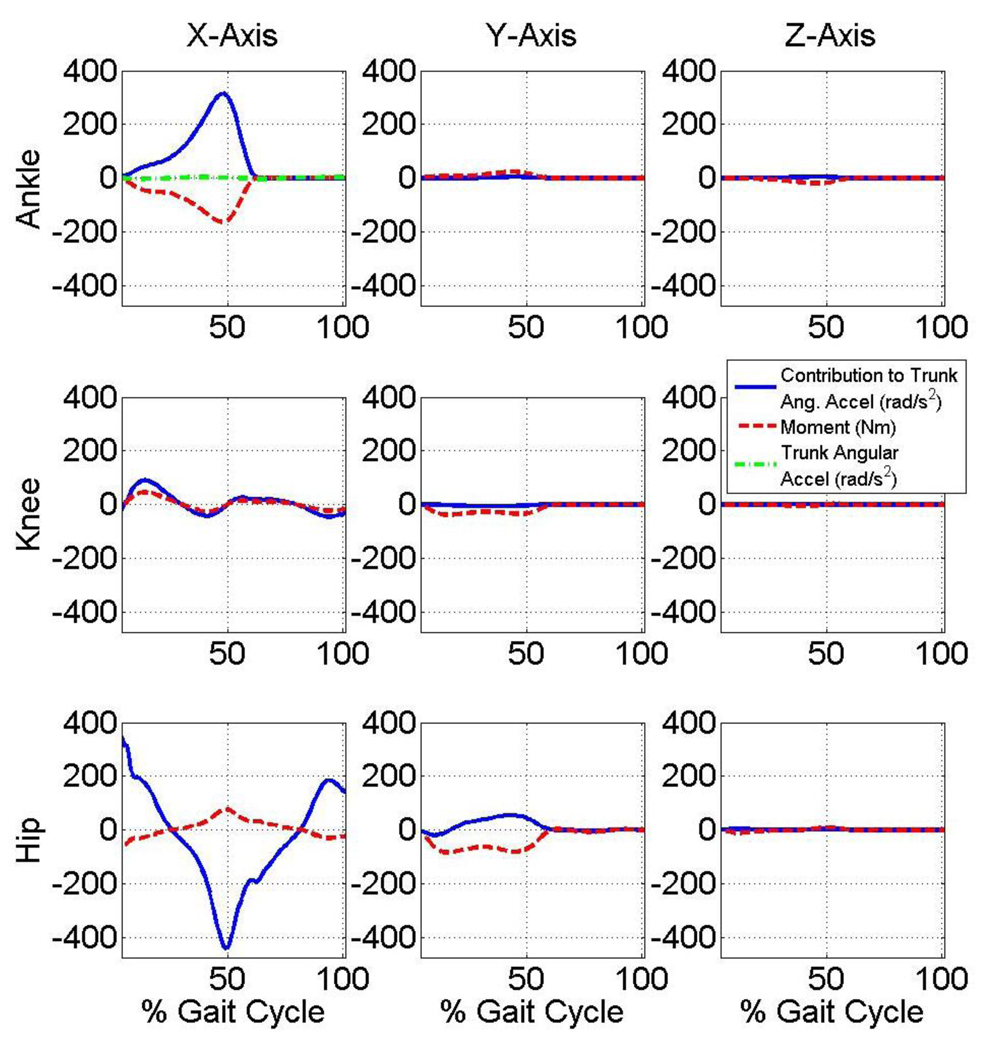
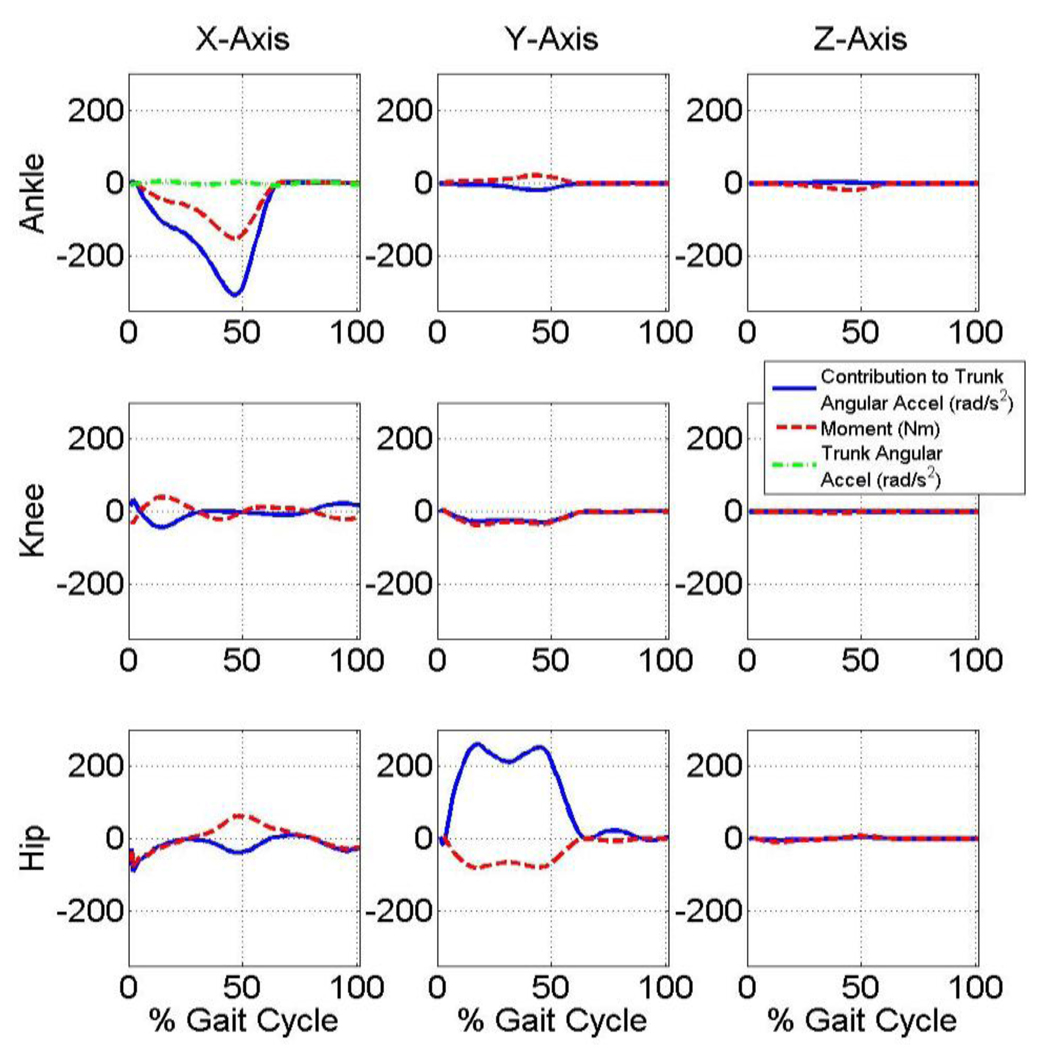
Joint moment contributions to trunk angular accelerations

Joint moments multiplied by their sensitivity yields results in units of acceleration with the result from each moment being superimposed to yield the total trunk angular acceleration. Note that each joint moment’s contribution to the trunk angular acceleration in the sagittal and frontal planes are thus quantified and the extent and the magnitude of each moment’s contribution varies throughout the gait cycle (Fig. 5 and Fig. 6, respectively). Note that at approximately 50% gait cycle: 1) sagittal plane plantarflexion and hip flexion moments approximately counteract one another with respect to their effect on trunk sagittal plane angular acceleration; and 2) sagittal plane plantarflexion moment approximately counteracts frontal plane hip moment with respect to their effect on trunk frontal plane angular acceleration.

Figure 5.

Contribution of each joint moment to trunk angular acceleration in the sagittal plane. The summation of the contributions is equal to the total trunk angular acceleration in the sagittal plane.

Figure 6.

Contribution of each joint moment to trunk angular acceleration in the frontal plane. The summation of the contributions is equal to the total trunk angular acceleration in the frontal plane.

Control of trunk angular acceleration by the CNS

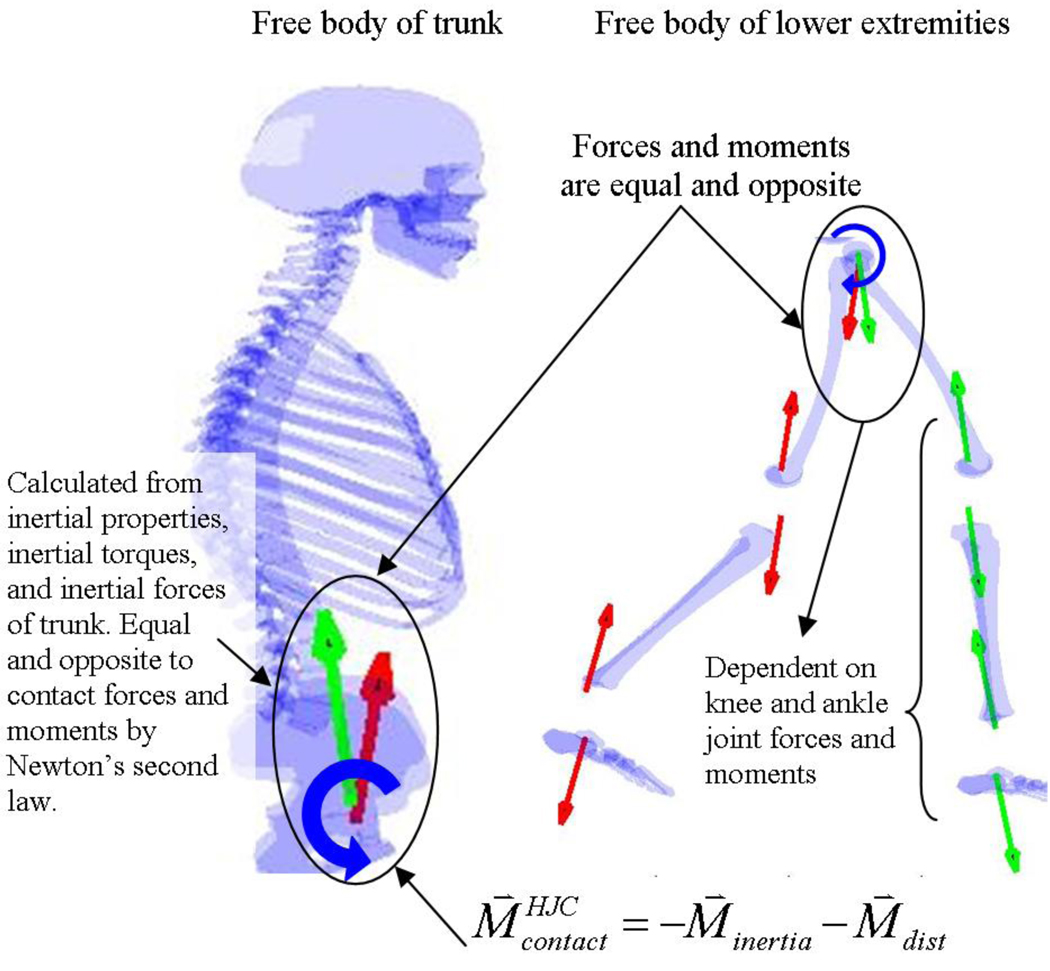
The contact moments acting on the trunk will almost be equal and opposite to the inertial torques since the gravitational torque is minimal due to the upright trunk causing the gravity vector to pass close to the center-of-mass (Fig. 7). Thus, the inertial torque is almost equal and opposite to the contact torques on the trunk as a result of the fundamental laws of mechanics (see Equation 1 in Appendix A). Furthermore, since distal joint moments can generate linear forces at the base of the trunk (Fig 4, Fig 7), it is possible that the CNS utilizes these forces to alter the angular acceleration of the trunk. An example of such a control system is the inverted-pendulum-cart problem in which linear forces at the base of the inverted pendulum can control pendulum balance (rotation) yet still progress the pendulum horizontally. If the trunk is modeled as an inverted pendulum with its base at the hip joint center, then the linear reaction forces (which are a function of distal joint moments) at the base of the trunk are an effective means to control balance of the trunk and maintain forward progression. Since both the forces and moments at the base of the human trunk can be used to control its angular acceleration, it is possible that the CNS uses both to control trunk balance.

Figure 7.

Two methods of calculating the contact moments are illustrated by taking free bodies of the trunk and lower extremity. These methods illustrate why the contact moments on the trunk are mathematically equal and opposite to the inertial forces and moments acting on the trunk.

Conclusion

The importance of a three dimensional analysis should be considered when investigating trunk angular acceleration (Fig. 4). Although frontal plane moments do not have significant contributions to trunk angular accelerations in the sagittal plane, the sagittal plane moments, especially the ankle moment, have large contributions to trunk angular accelerations in the frontal plane.

All the moments are simultaneously controlled to result in a very stable angular acceleration at the trunk (Fig. 6 and Fig. 7). A synergistic effort from all the lower extremity joints to influence trunk angular acceleration is likely, as previous EMG and perturbation studies suggest (Tang et al., 1998; Ferber et al., 2002).