Skip to main content
NCBI home page
Bioinformatics logoLink to Bioinformatics
. 2009 May 5;25(13):1662–1668. doi: 10.1093/bioinformatics/btp295

Evaluating reproducibility of differential expression discoveries in microarray studies by considering correlated molecular changes

Min Zhang 1,†,✉, Lin Zhang 2,†,✉, Jinfeng Zou 1, Chen Yao 2, Hui Xiao 1, Qing Liu 1, Jing Wang 1, Dong Wang 1, Chenguang Wang 1, Zheng Guo 1,2,*
PMCID: PMC2940240  PMID: 19417058

Abstract

Motivation: According to current consistency metrics such as percentage of overlapping genes (POG), lists of differentially expressed genes (DEGs) detected from different microarray studies for a complex disease are often highly inconsistent. This irreproducibility problem also exists in other high-throughput post-genomic areas such as proteomics and metabolism. A complex disease is often characterized with many coordinated molecular changes, which should be considered when evaluating the reproducibility of discovery lists from different studies.

Results: We proposed metrics percentage of overlapping genes-related (POGR) and normalized POGR (nPOGR) to evaluate the consistency between two DEG lists for a complex disease, considering correlated molecular changes rather than only counting gene overlaps between the lists. Based on microarray datasets of three diseases, we showed that though the POG scores for DEG lists from different studies for each disease are extremely low, the POGR and nPOGR scores can be rather high, suggesting that the apparently inconsistent DEG lists may be highly reproducible in the sense that they are actually significantly correlated. Observing different discovery results for a disease by the POGR and nPOGR scores will obviously reduce the uncertainty of the microarray studies. The proposed metrics could also be applicable in many other high-throughput post-genomic areas.

Contact: guoz@ems.hrbmu.edu.cn

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The reproducibility problem is one of the fundamental issues in validation of high-throughput biological discoveries (Marshall, 2004; Ransohoff, 2004; Ransohoff, 2005) because it is often considered that ‘a study that cannot be reliably reproduced has little value’ (Klebanov et al., 2007). However, lists of differentially expressed genes (DEGs) detected from different microarray studies for a disease are often highly inconsistent (Ein-Dor et al., 2005; Michiels et al., 2005; Tan et al., 2003), which frequently raises doubts about the reliability of microarrys (Ein-Dor et al., 2005; Frantz, 2005; Miklos and Maleszka, 2004). It has been suggested that many factors such as large biological variations, small sample sizes (Ein-Dor et al., 2005; Ein-Dor et al., 2006; Zhang et al., 2008) and improper statistical methods (Klebanov et al., 2007; Shi et al., 2006; Tong et al., 2006) may produce inconsistent DEG lists for a disease. Recently, we demonstrated that in the presence of small technical noise and wide differential expressions in a cancer, it is still highly likely that the observed percentage of overlapping genes (POG) of DEG lists from two studies is low, although each DEG list may comprise mostly true DEGs (Zhang et al., 2008).

Up to now, the concept of reproducibility of DEG lists for a disease is often intuitively defined, using terms such as concordance (Shi et al., 2006), agreement (Shi et al., 2006), stability (Ein-Dor et al., 2006; Qiu et al., 2006) or rediscovery rate (Xu and Li, 2003). Most metrics for evaluating the consistency between two gene lists, including the frequently used POG (Ein-Dor et al., 2006; Irizarry et al., 2005; Shi et al., 2006), rely on counting gene overlaps and treat genes as if they would be completely independent with each other. However, a complex disease is often characterized with many coordinated molecular changes (Klebanov et al., 2006; Qiu et al., 2005), which should be taken into account when evaluating whether different studies have actually detected the same or similar results for a disease.

In this article, considering the correlated molecular changes in a complex disease, we propose a novel metric termed percentage of overlapping genes-related (POGR) and its normalized formation nPOGR for evaluating consistency between two DEG lists for the disease. Obviously, to be utilized as a disease marker, a DEG should have a steady expression pattern in the disease. Thus, we also consider genes' upregulated or downregulated status when evaluating their reproducibility. Based on microarray datasets for three diseases, we show that though there are few genes shared between the DEG lists from different studies for a disease, most of the POGR and nPOGR scores are rather high, suggesting high reproducibility of the DEG lists in the sense that the apparently inconsistent DEG lists are significantly correlated. After normalizing the effects of list lengths and random data correlations in datasets, the nPOGR metric may be more appropriate for comparing the consistency levels of DEG lists with different lengths and from different studies.

2 METHODS

2.1 Datasets

For prostate cancer, the cDNA microarray data consist of 62 tumors and 41 normal prostate samples (Lapointe et al., 2004), while the oligo microarray (Affymetrix U95Av2) data contain 52 tumor and 50 non-tumor samples (Singh et al., 2002). A total of 6797 genes were measured by both platforms. For lung cancer, the cDNA microarray data consist of 13 squamous cell lung cancer and five normal lung specimens (Garber et al., 2001), while the data by Affymetrix human U95A oligonucleotide arrays consist of 21 squamous cell lung carcinomas and 17 normal lung specimens (Bhattacharjee et al., 2001). A total of 5530 genes were measured by both platforms. The two datasets for Duchenne muscular dystrophy (DMD) are based on Affymetrix (Santa Clara, CA) HG-U95Av2 and HG-U133A GeneChip, respectively. One dataset contains 24 samples from 12 DMD patients and 12 unaffected controls (Haslett et al., 2002) and the other consists of 36 samples from 22 DMD patients and 14 controls (Pescatori et al., 2007). A total of 8572 genes were measured by both platforms. For each disease, we only analyze the genes that are present on both platforms.

The cDNA data is log2 transformed and then normalized as median 0 and standard deviation 1 per array, as adopted in Oncomine database (Rhodes et al., 2007). The CloneIDs with missing rates above 20% are deleted, and the other missing values are replaced by using the kNN imputation algorithm (k = 15) (Troyanskaya et al., 2001). The Affymetrix GeneChip data are preprocessed by RMA (Robust Multi-array Analysis). The most recent (July, 2008) SOURCE database (Diehn et al., 2003) is used for annotating CloneIDs to GeneIDs.

2.2 DEGs and co-expression gene pairs

DEGs are most commonly defined as genes with non-zero expression difference between two groups. Usually, each gene is tested against the null hypothesis of equal means of expression levels across groups, while the multiple tests are controlled by false discovery rate (FDR) (Benjamini and Hochberg, 1995) loosely defined as the expected percentage of false positives among the claimed DEGs. When using the conventional t-test to select DEGs, small per-gene variances could make genes with small fold-changes statistically significant. To deal with this problem, Tusher et al. (2001) proposed the significance analysis of microarrays (SAM) method to select DEGs by adding a small ‘fudge factor’ to the denominator of the t-test statistic as follows:

graphic file with name btp295m1.jpg (1)
graphic file with name btp295m2.jpg (2)

where x1(i) and x2(i) are the expression vectors of gene i in n1 disease samples and n2 control samples, respectively. The ‘fudge factor’ s0 is chosen to minimize the coefficient of variance of d(i).

Because the FDR estimation procedure of SAM might be overly conservative (Xie et al., 2005; Zhang, 2007), we apply the FDR estimation method suggested by (Zhang, 2007) to the SAM program (samr_1.25 R package).

Similarly as Carter et al. (2005) did, in each dataset, we estimate the random correlation distribution by independently permuting the sample labels of each gene and then compute the Pearson correlation coefficients for all the gene pairs. For an observed correlation r between two genes in the original data, the P-value is calculated as the percentage of the permutated correlations exceeding r. The FDR control procedure proposed by (Benjamini and Hochberg, 1995) is used to select gene pairs with significantly positive correlation.

2.3 POG and POGR scores

The POG metric is usually used to measure the consistency of gene lists by simply counting overlapped genes between the lists without considering the regulation directions of genes (Chen et al., 2007; Shi et al., 2005). We can evaluate reproducibility of DEG lists in such a broad sense by just counting the overlapped and related genes, as briefly shown in ‘Results’ section (Section 3.3). However, a DEG for a disease should be regulated in the same direction (up-regulated or down-regulated) in different datasets. Thus, strictly, we define a gene is shared by two gene lists only if it is both overlapped and regulated in the same direction in both datasets. In the following text, we mainly analyze the reproducibility of gene lists with such a strict definition.

Suppose k genes are shared between list 1 with length l1 and list 2 with length l2, then the POG score from list 1 to list 2 is POG12 = k/l1, and the score from list 2 to list 1 is POG21 = k/l2.

Then, considering the correlated molecular changes in a disease, we define the POGR metric to evaluate the consistence between two DEG lists. Let Or12 (or Or21) represent the number of genes in list 1 (or list 2) which are not shared but significantly positively correlated with at least one gene in list 2 (or list 1), then the POGR scores are calculated as:

graphic file with name btp295m3.jpg (3)

Both the POG and POGR scores take values ranging from 0 to 1. Usually, a high POG or POGR score is desired for two discovery lists for a disease. However, both metrics are dependent on the list lengths (see ‘Results’ section) and thus lack statistical significance. Also, when expressions of genes are widely correlated in a disease, the POGR score between two gene lists randomly extracted from the original datasets may be high. To partially solve this problem, for an obtained POGR score, we can estimate the probability (P-value) of observing the score in the original datasets by random chance. The null hypothesis is that the POGR score of two DEG lists (with lengths l1 and l2) is the same as the expected score for pairs of gene lists (with lengths l1 and l2) randomly extracted from the original datasets. Here, the P-value is calculated as, among the scores of the 10 000 random pairs of gene lists, the proportion of the scores exceeding the observed one. Similarly to the basic idea of gene set enrichment analysis (GSEA) (Klebanov et al., 2007; Subramanian et al., 2005), which tests whether the members of a gene set are randomly distributed throughout all ranked genes according to correlations of their expressions with the sample labels, we test whether the expression correlations are randomly distributed throughout all genes or primarily among DEGs.

Here, two genes are defined as a correlated pair if and only if they are significantly positively correlated in both datasets. We note that other choices exist. For example, for a DEG list reported in a previous study, it is reasonable to evaluate its reproducibility in a new study by only requiring significant correlation in the new dataset, especially when the original data of the previous study are unavailable. The negatively correlated gene pairs are excluded because we specifically require that the related genes should be regulated in the same direction. However, negatively correlated genes may be also biologically meaningful, which warrants further investigation.

2.4 Normalization of the POG and POGR scores

Because the POG and POGR scores depend on list length, both metrics cannot be applied to compare the consistence levels of pairs of gene lists with different lengths. Thus, we propose an approach to normalize the effect of list lengths on POG and POGR scores. Additionally, we also normalize the POGR scores to reduce the effects of general data correlations in datasets.

For two lists (with lengths l1 and l2) randomly extracted from two datasets, suppose E(k) is the expected number of their shared genes, then the POG expectation is E(POG12) = E(k)/l1 or E(POG21)= E(k)/l2. Similarly to the kappa metric (Fleiss, 1971), we normalize the POG score between two DEG lists (with lengths l1 and l2) as the proportion of the observed scores beyond chance to the corresponding maximum potential scores beyond chance as follows:

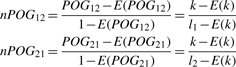graphic file with name btp295m4.jpg (4)

where k is the observed number of the shared genes between the two DEG lists. The E(POG12) [or E(POG21)] can be estimated by the average of the scores for10 000 pairs of random lists (with lengths l1 and l2).

We normalize the POGR in a similar way. For two lists (with lengths l1 and l2) randomly extracted from two datasets, suppose E(Or12) [or E(Or21)] is the expected number of genes in list 1 (or list 2), which are not shared but significantly correlated with at least one gene in list 2 (or list 1), then the POGR score expected by random chance is E(POGR12)= [E(k)+E(Or12)]/l1 [or E(POGR21)= [E(k)+E(Or21)]/l2]. The POGR score can be normalized as:

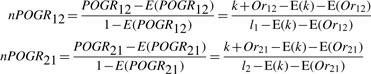graphic file with name btp295m5.jpg (5)

where E(Or12) [or E(Or21)] can be estimated as the average number of genes in list 1 (or list 2). which are not shared but significantly positively correlated with genes in list 2 (or list 1) in 10 000 pairs of gene lists (with lengths l1 and l2) randomly extracted from two datasets.

When the POGR score of two DEG lists (with lengths l1 and l2) is less than the expected score for pairs of gene lists (with lengths l1 and l2) randomly extracted from the original datasets, the nPOGR score will be negative. In this situation, we set the score as 0. Thus, the nPOGR score achieves 0 if and only if POGR ≤ E(POGR) < 1. It achieves 1 if and only if POGR = 1 and E(POGR) < 1. Note that the score is invalid when E(POGR) = 1, such as in the extreme situation that all genes are significantly correlated in both datasets for a disease. However, this does not appear in the datasets for the three diseases under this study and would rarely appear in other real applications. Because an nPOGR score is a ratio, it is better to interpret the score together with the maximum potential agreement beyond chance [1 – E(POGR)] it can achieve for pairs of lists with the same lengths from the original datasets.

We can estimate the significance level (P-value) for an observed nPOGR score of two DEG lists (with lengths l1 and l2) to test the null hypothesis that this score is the same as the expected score for pairs of gene lists (with lengths l1 and l2) randomly extracted from the original datasets. This P-value can be calculated from the same set of 10 000 pairs of random gene lists for calculating the P-value of the corresponding POGR score. According to formula (5), for a pair of gene lists randomly extracted from the original datasets, its nPOGR score will be larger than the observed nPOGR score if and only if its POGR score is larger than the observed POGR score, since the E(POGR) is a constant estimated from the 10 000 random gene list pairs. Thus, estimated as the proportion of the random nPOGR scores exceeding the observed nPOGR score, the P-value of the observed nPOGR score is the same as the P-value of the corresponding POGR score.

After excluding the effects of list lengths and general data correlations on chance agreement, the nPOGR score may be more appropriate for comparing the consistency levels of DEG lists with different lengths and from different studies. On the other hand, because the nPOGR score measures the relative agreement beyond chance, it should be necessary to use the POGR scores to reflect the apparent agreement of DEG lists based on the original data correlation.

3 RESULTS

3.1 Reproducibility of studies for three diseases

For prostate cancer, by SAM with 1% FDR control, we detect 1054 and 1343 DEGs in the datasets of oligo and cDNA microarrays, respectively. The reproducibility of the two studies is measured in two directions. In one direction, for the list of DEGs detected in the oligo microarray data, we measure its reproducibility in the cDNA microarray data as the percentage of these DEGs, which also appear in the cDNA result. The POG12 score is as low as 38% and the nPOG12 score is only 30%, intuitively suggesting that most of the results from the oligo microarray data are irreproducible in the cDNA microarray result. Then, considering significantly co-expressed gene pairs with 0.1% FDR control, the POGR12 score achieves 90%, intuitively suggesting that the DEG list from the oligo microarray data may be highly reproducible in the cDNA microarray data when considering correlated molecular changes. The corresponding nPOGR is 74%, indicating that after subtracting the POGR score by random chance, the observed score achieves a high proportion of the maximum potential agreement beyond chance (0.38). In another direction, for the DEG list detected in the cDNA data, we measure its reproducibility in the oligo microarray data as the percentage of the detected DEGs, which also appear in the oligo microarray result. For the full DEG lists, although the POG21 score is only 30% and the nPOG21 is as low as 23%, the POGR21 score reaches 90% and the nPOGR is as high as 76%, with the maximum potential agreement value as 0.40.

Similar results can be observed for the lists of the top-ranked DEGs from the two studies. For example, although the two lists of the top-10 DEGs from the two datasets share only three genes, the POGR12 score is as high as 90%. The corresponding nPOGR12 is 89%, reaching a high proportion of the maximum potential value of 0.94. In another direction, both the POGR21 and nPOGR21 scores are 100%, indicating that the list of the top 10 DEGs from the oligo microarray data is fully reproducible in the cDNA microarray data when considering correlated molecular changes.

Then, we study the reproducibility of two relatively small-scaled experiments for lung cancer. By SAM with 1% FDR control, we detect 2157 DEGs in the oligo microarray data with 38 samples and only 336 DEGs in the cDNA microarray data with 18 samples. Finding significant correlations with 0.1% FDR control, most of the POGR and nPOGR scores are low and only slightly higher than the corresponding POG and nPOG scores (Table 1). Loosening the FDR level to 5% for significant correlations, the DEG lists from the cDNA microarray data are highly reproducible in the larger oligo microarray data, with all the POGR scores and most of the corresponding nPOGR scores reaching above 90% (all with P < 2 × 10−3) (see Supplementary Table S1). In another direction, all the POGR and nPOGR scores for the lists of the top-ranked 10, 50 and 100 DEGs increase to above 70%. However, for the list of all the 2157 DEGs from the larger oligo microarray data, the POGR12 and nPOGR12 scores measuring its reproducibility in the smaller cDNA microarray data are only 40% and 34%, respectively. This could be explained by the fact that the smaller samples of the cDNA microarray data may have insufficient statistical power in identifying enough DEGs to characterize the disease.

Table 1.

Consistence scores between DEG lists for the same disease when using 0.1% FDR control for significant correlations

Datasets DEGs POG nPOG POGR nPOGR Maxa DEGs POG nPOG POGR nPOGR Maxa
From 102 samples to 103 samplesb
 From 103 samples to 102 samplesb
Top 10 0.30 0.30 0.90 0.89 0.94 Top 10 0.30 0.30 1.00 1.00 0.94
Prostate cancer Top 50 0.14 0.14 0.78 0.69 0.70 Top 50 0.14 0.14 0.92 0.89 0.73
Top100 0.15 0.14 0.80 0.66 0.60 Top100 0.15 0.14 0.94 0.90 0.63
1054 vs. 1343 0.38 0.30 0.90 0.74 0.38 1343 vs. 1054 0.30 0.23 0.90 0.76 0.40
From 38 samples to 18 samplesb
 From 18 samples to 38 samplesb
Top 10 0.00 0.00 0.00 0.00 1.00 Top 10 0.00 0.00 0.00 0.00 1.00
Lung cancer Top 50 0.20 0.19 0.20 0.19 0.99 Top 50 0.20 0.19 0.20 0.19 0.99
Top100 0.31 0.30 0.32 0.31 0.99 Top100 0.31 0.30 0.31 0.30 0.99
2157 vs. 336 0.13 0.09 0.13 0.09 0.96 336 vs. 2157 0.82 0.75 0.82 0.75 0.72
From 24 samples to 36 samplesb
 From 36 samples to 24 samplesb
Top 10 0.20 0.20 0.70 0.70 1.00 Top 10 0.20 0.20 0.80 0.80 1.00
DMD Top 50 0.42 0.42 0.92 0.92 0.99 Top 50 0.42 0.42 0.80 0.80 0.99
Top100 0.54 0.54 0.94 0.94 0.98 Top100 0.54 0.54 0.85 0.85 0.98
805 vs. 800 0.53 0.50 0.72 0.68 0.89 800 vs. 805 0.53 0.49 0.65 0.61 0.89
Open in a new tab

aMax means the maximum potential agreement beyond chance (see ‘Methods’ section).

bTwo datasets for each disease are marked by their sample sizes. ‘From dataset1 to dataset2’ means that the reproducibility of a DEG list detected in dataset1 is evaluated in dataset2.

Finally, for a non-cancer disease (DMD), by SAM with 1% FDR control, we detect 805 and 800 DEGs in two datasets, respectively. For the full lists, the POG and nPOG scores are at a rather high level around 50%. Considering significant correlations with 0.1% FDR control level, the POGR and nPOGR scores in both directions increase to above 60%. Notably, for the top-ranked DEG lists, most POGR and nPOGR scores are above 80%, much higher than the corresponding POG and nPOG scores (Table 1). For example, for the list of the top 10 DEGs from the dataset with 24 samples, the POG and nPOG scores for evaluating its reproducibility in the dataset with 36 samples are both 20%, while the corresponding POGR and nPOGR scores are both 70%. In another direction, the corresponding POGR and nPOGR scores are both 80%. Thus, the DEG lists from one of the two studies are highly reproducible in another from the view of correlated molecular changes.

Here, all the POG and POGR scores in Table 1 are significantly higher than the average POG and POGR scores of the random list pairs extracted from the corresponding original datasets (P < 1 × 10−4).

3.2 Factors affecting the scores

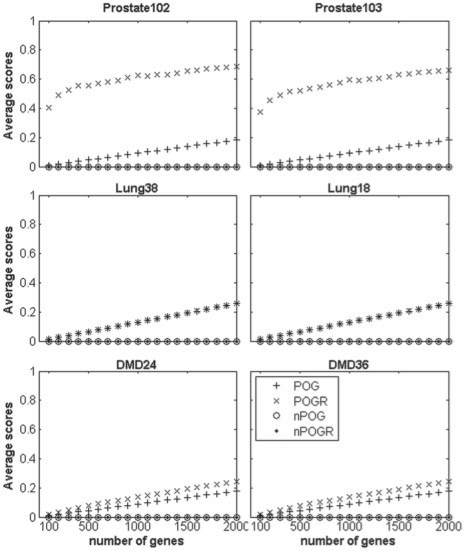
As shown in Figure 1, for 10 000 pairs of lists with the same length randomly selected from each dataset, both of the average POG and POGR scores increase as the list length increases.

Fig. 1.

Fig. 1.

Open in a new tab

The effect of list lengths on POG, nPOG, POGR and nPOGR. The x-axis represents list lengths ranging from 100 to 2000, and the y-axis represents the average scores of 10 000 pairs of gene lists randomly selected from the original datasets. Here, 0.1% FDR level is used for detecting significant correlations. The legend for all the six subgraphs is the same as shown within the last one.

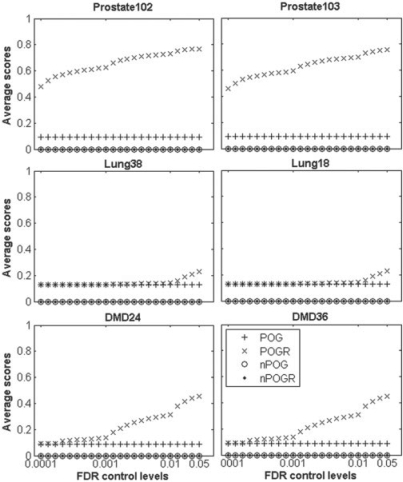
On the other hand, both the corresponding nPOG and nPOGR scores fluctuate around zero as the list length increases (Fig. 1). Thus, compared with their non-normalized counterparts, the normalized metrics nPOG and nPOGR are more stable and independent of the list lengths and general data correlations in the datasets. For randomly extracted lists, when using less stringent FDR control levels for selecting significant correlations, the nPOGR scores are still around zero though the POGR scores may increase (Fig. 2).

Fig. 2.

Fig. 2.

Open in a new tab

The effect of FDR control levels on POG, nPOG, POGR and nPOGR. The x-axis represents FDR cotnrol levels ranging from 0.01% to 5%. The y-axis represents the average scores of 10 000 pairs of gene lists with a given length (1000) randomly selected from the original datasets. The legend for all the six subgraphs is the same as shown within the last one.

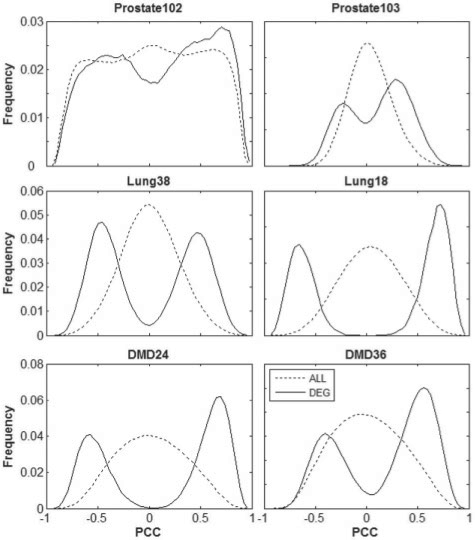
As shown in Figure 3, in each of the datasets for prostate cancer, the correlation distribution for all gene pairs is similar to the correlation distribution for DEG pairs selected by SAM with 1% FDR control, indicating that the expressions of genes in the prostate cancer data tend to be widely correlated. In such a situation, the nPOGR scores decrease obviously from the POGR scores (Table 1). In the two datasets for lung cancer, the distributions of the correlations of DEG pairs are distinct from the distributions of all gene pairs, indicating that the expression correlations in these datasets are largely limited to DEGs. Similar results are observed in the two datasets for DMD. In this situation that most non-DEGs are not significantly correlated, the nPOGR scores decrease slightly from the POGR scores (Table 1).

Fig. 3.

Fig. 3.

Open in a new tab

The distributions of the PCC of expressions of gene pairs in three pairs of datasets. The legend for all the six subgraphs is the same as shown within the last one.

3.3 Comparison between DEG lists from different diseases

Finally, we analyze the consistence of DEG lists from datasets for different diseases, using the larger dataset for each disease. The DMD dataset shares a total of 9200 and 8495 genes with the prostate and lung cancer datasets, respectively, and the two cancer datasets have 6797 genes in common. Similarly to the above analysis, DEGs are selected by SAM with 1% FDR control and the correlated gene pairs are determined with 0.1% FDR control.

As shown in Table 2, the POGR and nPOGR scores of DEG list pairs from different diseases are obviously much smaller than the scores from the same disease. For example, the nPOGR score is 0 for the full DEG lists from prostate and DMD, while the nPOGR score is 74% for the full DEG lists from two prostate cancer datasets and 68% for the full DEG lists from two DMD datasets. For DEG lists from a cancer dataset and a DMD dataset, most of the POG and POGR scores are not much different from the scores for gene lists randomly selected from the original datasets (P > 1%). When using looser FDR control levels for selecting correlated genes, the nPOGR scores of DEG lists from DMD and cancer still fluctuate around zero (Supplementary Table S2).

Table 2.

Consistence scores between DEG lists for different diseases when using 0.1% FDR control for significant correlations

Datasets DEGs POG nPOG POGR nPOGR Maxa DEGs POG nPOG POGR nPOGR Maxa
From Prostate to DMDb
 From DMD to Prostateb
Top 10 0.00 0.00 0.00 0.00 0.98 Top 10 0.00 0.00 0.00 0.00 0.98
Prostate vs. DMD Top 50 0.02 0.02 0.04 0.00 0.93 Top 50 0.02 0.02 0.04 0.00 0.93
Top100 0.01 0.00 0.05 0.00 0.89 Top100 0.01 0.00 0.06 0.00 0.89
1842 vs. 801 0.05 0.00 0.16 0.00 0.68 801 vs. 1842 0.11 0.01 0.37 0.00 0.52
From Lung to DMDb
 From DMD to Lungb
Top 10 0.00 0.00 0.00 0.00 1.00 Top 10 0.00 0.00 0.00 0.00 1.00
Lung vs. DMD Top 50 0.00 0.00 0.00 0.00 1.00 Top 50 0.00 0.00 0.00 0.00 1.00
Top100 0.00 0.00 0.00 0.00 0.99 Top100 0.00 0.00 0.00 0.00 0.99
3303 vs. 797 0.05 0.00 0.05 0.00 0.95 797 vs. 3303 0.21 0.02 0.21 0.02 0.81
From Prostate to Lungb From Lung to Prostateb
Top 10 0.00 0.00 0.00 0.00 1.00 Top 10 0.00 0.00 0.00 0.00 1.00
Prostate vs. lung Top 50 0.02 0.02 0.02 0.02 1.00 Top 50 0.02 0.02 0.02 0.02 1.00
Top100 0.04 0.03 0.04 0.03 0.99 Top100 0.04 0.03 0.04 0.03 0.99
1353 vs. 2763 0.35 0.15 0.35 0.15 0.77 2763 vs. 1353 0.17 0.06 0.17 0.07 0.89
Open in a new tab

Indicated as in Table 1.

Notably, the nPOGR scores between the DEG lists from the two cancers are higher than the scores between DMD and cancer (Table 2 and Supplementary Table S2), suggesting that the expression patterns of the altered genes in different cancers may be more consistent. For example, between the full DEG lists from prostate and lung cancer, the nPOGR12 score is 15% and the corresponding POGR12 score is 35%, which is significantly higher than the average score of randomly selected lists.

As mentioned in ‘Methods’ section (Section 2.3), we can also evaluate the reproducibility of DEG lists in a broad sense by just counting the overlapped and correlated genes, without regulation direction requirement. Calculated similarly as the approaches described in ‘Methods’ section, for DEG lists selected from the datasets for the same disease, all the scores are almost unchanged (Supplementary Table S3 and Table S4), reflecting that DEGs from the same disease are regulated in a similar way. However, interestingly, for DEG lists from the cancer and DMD datasets, some scores are unexpectedly high (Supplementary Table S5 and Table S6), especially when using less stringent FDR control levels for selecting correlated gene pairs. To understand these surprising results, we find that the full DEG list from DMD are non-randomly overlapped with the full DEG list from the prostate cancer data (POG = 30%, P < 1 ×10−4) as well as the full DEG list from the lung cancer data (POG = 53%, P < 1 ×10−4), indicating that many genes (DEGs) disturbed in DMD are also differentially expressed in cancer. Without the requirement for regulation direction, the overlapped DEGs between DMD and cancer tend to be correlated with other DEGs in each disease and thus will introduce higher POGR as well as nPOGR scores. However, when considering regulation directions of genes, all the scores become rather low, suggesting that the genes differentially expressed in different diseases may be regulated in different ways. Thus, it is important to consider the regulation directions of DEGs when evaluating their reproducibility.

4 DISCUSSION

Intuitively, a high POG score is expected for two studies for a disease. Similarly, a high POGR score suggests apparently high reproducibility of DEG lists in the sense that different studies have actually detected similar results for a disease. Because both POG and POGR scores are dependent on list lengths, they cannot be simply used to compare the reproducibility of gene lists with different lengths. Statistically, for each obtained POG or POGR score, we can calculate the P-value of observing the score in random lists from the original data, which may help interpret the intuitive score.

However, even a small P-value for a POG or POGR score cannot guarantee a high percentage of shared genes between two lists. By normalizing the effects of list length and correlation distribution in datasets, the proposed nPOGR metric suggests a more appropriate way for comparing the reproducibility of gene lists with different lengths and from different studies.

As previously demonstrated by us (Zhang et al., 2008), though DEG lists from current small-scaled microarray studies may only capture a small fraction of DEGs in a disease and thus show low POG scores, each separately determined list may comprise mostly true DEGs. Usually, the global expression changes of genes in a disease may introduce great uncertainty to the findings at the individual genes level. Under such a situation, even if there are many ‘true’ DEGs in a disease, we may be only interested in analyzing the most significant ones. The proposed POGR metric is especially helpful for evaluating such short lists of interesting genes. It should be noted that distinct methods for selecting DEGs, such as SAM (Tusher et al., 2001), analysis of variance (ANOVA) (Hardeo and Mohammed, 2000) and empirical Bayes with t-statistic (Efron et al., 2001; Oshlack et al., 2007), may capture different statistical aspects of expression changes and contribute to the observed inconsistency between the derived DEGs (Jeffery et al., 2006; Qiu et al., 2006). Thus, it warrants further investigation to study the reproducibility of DEG lists found by different DEG selection approaches.

At the functional module level, the strikingly inconsistent gene lists generated in different experiments for a disease could be rather functionally consistent (Guo et al., 2006; Hosack et al., 2003; Zhu et al., 2007). Specifically, we have demonstrated functional modules related to a disease could be captured by only a small fraction of DEGs in the disease (Yang et al., 2008). Therefore, similarly to POGR metric, a metric considering gene overlaps from the view of functional similarity will probably provide another way for evaluating the reproducibility of the apparently inconsistent discoveries in microarray studies, which deserves our future work. Other metrics or views could be considered for observing different discovery results for a disease. Notably, Mao et al (2009) showed that the discriminating genes identified in a study may preserve their disease discriminating ability in another study though these genes might not be selected independently in the later dataset because they might not be the optimum ones in both studies. Their result implies high concordance of DNA microarrays by the signals and classifier transferability of the discriminating genes, rather than simply relying on counting gene overlaps. This concept is somewhat similar to ours. However, our proposed metrics should be more statistically interpretable and applicable in classical studies on evaluating differential gene expressions in diseases.

Finally, we note that the irreproducibility problem of finding disease markers also exists in other post-genomic areas such as proteomics (Ransohoff, 2005), metabolismics (David I. and Douglas B., 2006) and large-scale screens for cancer mutations (Chen et al., 2007; Frantz, 2005). The apparently inconsistent discoveries generated in these post-genomic areas could also be evaluated by considering correlated disease markers. Because this problem is of fundamental importance in the field of systems biology, it deserves our future researches.

Supplementary Material

[Supplementary Data]
btp295_index.html (786B, html)

ACKNOWLEDGEMENTS

National Natural Science Foundation of China (Grant Nos. 30170515, 30370388, 30571034).

Conflict of Interest: none declared.

REFERENCES

  1. Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Series B (Methodol.) 1995;57:289–300. [Google Scholar]
  2. Bhattacharjee A, et al. Classification of human lung carcinomas by mRNA expression profiling reveals distinct adenocarcinoma subclasses. Proc. Natl Acad. Sci. USA. 2001;98:13790–13795. doi: 10.1073/pnas.191502998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Carter SL, et al. Redefinition of Affymetrix probe sets by sequence overlap with cDNA microarray probes reduces cross-platform inconsistencies in cancer-associated gene expression measurements. BMC Bioinformatics. 2005;6:107. doi: 10.1186/1471-2105-6-107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chen J, et al. Reproducibility of microarray data: a further analysis of microarray quality control (MAQC) data. BMC Bioinformatics. 2007;8:412. doi: 10.1186/1471-2105-8-412. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. David IB, Douglas BK. Statistical strategies for avoiding false discoveries in metabolomics and related experiments. Metabolomics. 2006;2:s11306–11006- 10037. [Google Scholar]
  6. Diehn M, et al. SOURCE: a unified genomic resource of functional annotations, ontologies, and gene expression data. Nucleic Acids Res. 2003;31:219–223. doi: 10.1093/nar/gkg014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Efron B, et al. Empirical Bayes analysis of a microarray experiment. J. Am. Stat. Assoc. 2001;96:1151–1160. [Google Scholar]
  8. Ein-Dor L, et al. Outcome signature genes in breast cancer: is there a unique set? Bioinformatics. 2005;21:171–178. doi: 10.1093/bioinformatics/bth469. [DOI] [PubMed] [Google Scholar]
  9. Ein-Dor L, et al. Thousands of samples are needed to generate a robust gene list for predicting outcome in cancer. Pro.c Natl Acad. Sci. USA. 2006;103:5923–5928. doi: 10.1073/pnas.0601231103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Fleiss JL. Measuring nominal scale agreement among many raters. Psychol. Bull. 1971;76:378–382. [Google Scholar]
  11. Frantz S. An array of problems. Nat. Rev. Drug Discov. 2005;4:362–363. doi: 10.1038/nrd1746. [DOI] [PubMed] [Google Scholar]
  12. Garber ME, et al. Diversity of gene expression in adenocarcinoma of the lung. Proc. Natl Acad. Sci. USA. 2001;98:13784–13789. doi: 10.1073/pnas.241500798. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Guo L, et al. Rat toxicogenomic study reveals analytical consistency across microarray platforms. Nat. Biotechnol. 2006;24:1162–1169. doi: 10.1038/nbt1238. [DOI] [PubMed] [Google Scholar]
  14. Hardeo S, Mohammed A. Analysis of Variance: Fixed, Random and Mixed Models. Boston: Birkhauser; 2000. [Google Scholar]
  15. Haslett JN, et al. Gene expression comparison of biopsies from Duchenne muscular dystrophy (DMD) and normal skeletal muscle. Proc. Natl Acad. Sci. USA. 2002;99:15000–15005. doi: 10.1073/pnas.192571199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hosack DA, et al. Identifying biological themes within lists of genes with EASE. Genome Biol. 2003;4:R70. doi: 10.1186/gb-2003-4-10-r70. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Irizarry RA, et al. Multiple-laboratory comparison of microarray platforms. Nat. Methods. 2005;2:345–350. doi: 10.1038/nmeth756. [DOI] [PubMed] [Google Scholar]
  18. Jeffery IB, et al. Comparison and evaluation of methods for generating differentially expressed gene lists from microarray data. BMC Bioinformatics. 2006;7:359. doi: 10.1186/1471-2105-7-359. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Klebanov L, et al. A multivariate extension of the gene set enrichment analysis. J Bioinform Comput Biol. 2007;5:1139–1153. doi: 10.1142/s0219720007003041. [DOI] [PubMed] [Google Scholar]
  20. Klebanov L, et al. A new type of stochastic dependence revealed in gene expression data. Stat. Appl. Genet. Mol. Biol. 2006;5 doi: 10.2202/1544-6115.1189. Article7. [DOI] [PubMed] [Google Scholar]
  21. Klebanov L, et al. Statistical methods and microarray data. Nat. Biotechnol. 2007;25:25–26. doi: 10.1038/nbt0107-25. author reply 26–27. [DOI] [PubMed] [Google Scholar]
  22. Lapointe J, et al. Gene expression profiling identifies clinically relevant subtypes of prostate cancer. Proc. Natl Acad. Sci. USA. 2004;101:811–816. doi: 10.1073/pnas.0304146101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Mao S, et al. Evaluation of inter-laboratory and cross-platform concordance of DNA microarrays through discriminating genes and classifier transferability. J. Bioinform. Comput. Biol. 2009;7:157–173. doi: 10.1142/s0219720009004011. [DOI] [PubMed] [Google Scholar]
  24. Marshall E. Getting the noise out of gene arrays. Science. 2004;306:630–631. doi: 10.1126/science.306.5696.630. [DOI] [PubMed] [Google Scholar]
  25. Michiels S, et al. Prediction of cancer outcome with microarrays: a multiple random validation strategy. Lancet. 2005;365:488–492. doi: 10.1016/S0140-6736(05)17866-0. [DOI] [PubMed] [Google Scholar]
  26. Miklos GL, Maleszka R. Microarray reality checks in the context of a complex disease. Nat. Biotechnol. 2004;22:615–621. doi: 10.1038/nbt965. [DOI] [PubMed] [Google Scholar]
  27. Oshlack A, et al. Normalization of boutique two-color microarrays with a high proportion of differentially expressed probes. Genome Biol. 2007;8:R2. doi: 10.1186/gb-2007-8-1-r2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Pescatori M, et al. Gene expression profiling in the early phases of DMD: a constant molecular signature characterizes DMD muscle from early postnatal life throughout disease progression. FASEB J. 2007;21:1210–1226. doi: 10.1096/fj.06-7285com. [DOI] [PubMed] [Google Scholar]
  29. Qiu X, et al. The effects of normalization on the correlation structure of microarray data. BMC Bioinformatics. 2005;6:120. doi: 10.1186/1471-2105-6-120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Qiu X, et al. Assessing stability of gene selection in microarray data analysis. BMC Bioinformatics. 2006;7:50. doi: 10.1186/1471-2105-7-50. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Ransohoff DF. Rules of evidence for cancer molecular-marker discovery and validation. Nat. Rev. Cancer. 2004;4:309–314. doi: 10.1038/nrc1322. [DOI] [PubMed] [Google Scholar]
  32. Ransohoff DF. Lessons from controversy: ovarian cancer screening and serum proteomics. J. Natl Cancer Inst. 2005;97:315–319. doi: 10.1093/jnci/dji054. [DOI] [PubMed] [Google Scholar]
  33. Rhodes DR, et al. Oncomine 3.0: genes, pathways, and networks in a collection of 18,000 cancer gene expression profiles. Neoplasia. 2007;9:166–180. doi: 10.1593/neo.07112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Shi L, et al. The microarray quality control (MAQC) project shows inter- and intraplatform reproducibility of gene expression measurements. Nat. Biotechnol. 2006;24:1151–1161. doi: 10.1038/nbt1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Shi L, et al. Cross-platform comparability of microarray technology: intra-platform consistency and appropriate data analysis procedures are essential. BMC Bioinformatics. 2005;6(Suppl 2):S12. doi: 10.1186/1471-2105-6-S2-S12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Singh D, et al. Gene expression correlates of clinical prostate cancer behavior. Cancer Cell. 2002;1:203–209. doi: 10.1016/s1535-6108(02)00030-2. [DOI] [PubMed] [Google Scholar]
  37. Subramanian A, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl Acad. Sci. USA. 2005;102:15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Tan PK, et al. Evaluation of gene expression measurements from commercial microarray platforms. Nucleic Acids Res. 2003;31:5676–5684. doi: 10.1093/nar/gkg763. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Tong W, et al. Evaluation of external RNA controls for the assessment of microarray performance. Nat. Biotechnol. 2006;24:1132–1139. doi: 10.1038/nbt1237. [DOI] [PubMed] [Google Scholar]
  40. Troyanskaya O, et al. Missing value estimation methods for DNA microarrays. Bioinformatics. 2001;17:520–525. doi: 10.1093/bioinformatics/17.6.520. [DOI] [PubMed] [Google Scholar]
  41. Tusher VG, et al. Significance analysis of microarrays applied to the ionizing radiation response. Proc. Natl Acad. Sci. USA. 2001;98:5116–5121. doi: 10.1073/pnas.091062498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Xie Y, et al. A note on using permutation-based false discovery rate estimates to compare different analysis methods for microarray data. Bioinformatics. 2005;21:4280–4288. doi: 10.1093/bioinformatics/bti685. [DOI] [PubMed] [Google Scholar]
  43. Xu R, Li X. A comparison of parametric versus permutation methods with applications to general and temporal microarray gene expression data. Bioinformatics. 2003;19:1284–1289. doi: 10.1093/bioinformatics/btg155. [DOI] [PubMed] [Google Scholar]
  44. Yang D, et al. Gaining confidence in biological interpretation of the microarray data: the functional consistence of the significant GO categories. Bioinformatics. 2008;24:265–271. doi: 10.1093/bioinformatics/btm558. [DOI] [PubMed] [Google Scholar]
  45. Zhang M, et al. Apparently low reproducibility of true differential expression discoveries in microarray studies. Bioinformatics. 2008;24:2057–2063. doi: 10.1093/bioinformatics/btn365. [DOI] [PubMed] [Google Scholar]
  46. Zhang S. A comprehensive evaluation of SAM, the SAM R-package and a simple modification to improve its performance. BMC Bioinformatics. 2007;8:230. doi: 10.1186/1471-2105-8-230. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Zhu J, et al. GO-2D: identifying 2-dimensional cellular-localized functional modules in gene ontology. BMC Genomics. 2007;8:30. doi: 10.1186/1471-2164-8-30. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
btp295_index.html (786B, html)
btp295_bioinf-2008-1636-File001.doc (165KB, doc)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES