Patterns and Processes of Genome-Wide Divergence Between North American and African Drosophila melanogaster

Abstract

Genomic tools and analyses are now being widely used to understand genome-wide patterns and processes associated with speciation and adaptation. In this article, we apply a genomics approach to the model organism Drosophila melanogaster. This species originated in Africa and subsequently spread and adapted to temperate environments of Eurasia and the New World, leading some populations to evolve reproductive isolation, especially between cosmopolitan and Zimbabwean populations. We used tiling arrays to identify highly differentiated regions within and between North America (the United States and Caribbean) and Africa (Cameroon and Zimbabwe) across 63% of the D. melanogaster genome and then sequenced representative fragments to study their genetic divergence. Consistent with previous findings, our results showed that most differentiation was between populations living in Africa vs. outside of Africa (i.e., “out-of-Africa” divergence), with all other geographic differences being less substantial (e.g., between cosmopolitan and Zimbabwean races). The X chromosome was much more strongly differentiated than the autosomes between North American and African populations (i.e., greater X divergence). Overall differentiation was positively associated with recombination rates across chromosomes, with a sharp reduction in regions near centromeres. Fragments surrounding these high F_ST sites showed reduced haplotype diversity and increased frequency of rare and derived alleles in North American populations compared to African populations. Nevertheless, despite sharp deviation from neutrality in North American strains, a small set of bottleneck/expansion demographic models was consistent with patterns of variation at the majority of our high F_ST fragments. Although North American populations were more genetically variable compared to Europe, our simulation results were generally consistent with those previously based on European samples. These findings support the hypothesis that most differentiation between North America and Africa was likely driven by the sorting of African standing genetic variation into the New World via Europe. Finally, a few exceptional loci were identified, highlighting the need to use an appropriate demographic null model to identify possible cases of selective sweeps in species with complex demographic histories.

THE study of genetic differentiation between populations and species has recently been empowered by the use of genomic techniques and analysis (e.g., Noor and Feder 2006; Stinchcombe and Hoekstra 2008). In the past decade, genetic studies of adaptation and speciation have taken advantage of emerging molecular techniques to scan the genomes of diverging populations for highly differentiated genetic regions (e.g., Wilding et al. 2001; Emelianov et al. 2003; Beaumont and Balding 2004; Campbell and Bernatchez 2004; Scotti-Saintagne et al. 2004; Achere et al. 2005; Turner et al. 2005; Vasemagi et al. 2005; Bonin et al. 2006, 2007; Murray and Hare 2006; Savolainen et al. 2006; Yatabe et al. 2007; Nosil et al. 2008, 2009; Turner et al. 2008a,b; Kulathinal et al. 2009). As a result, genome scans can identify candidate regions that may be associated with adaptive evolution between diverging populations and, more broadly, are able to describe genome-wide patterns and processes of population differentiation (Begun et al. 2007; Stinchcombe and Hoekstra 2008).

Genome scans in well-studied genetic model species such as Drosophila melanogaster gain particular power because differentiated loci are mapped to a well-annotated genome. Moreover, the evolutionary history of D. melanogaster is rich with adaptive and demographic events with many parallels to human evolution. Most notable is the historical out-of-Africa migration and subsequent adaptation to temperate ecological environments of Europe, Asia, North America, and Australia. This has resulted in widespread genetic and phenotypic divergence between African and non-African populations (e.g., David and Capy 1988; Begun and Aquadro 1993; Capy et al. 1994; Colegrave et al. 2000; Rouault et al. 2001; Takahashi et al. 2001; Caracristi and Schlötterer 2003; Baudry et al. 2004; Pool and Aquadro 2006; Schmidt et al. 2008; Yukilevich and True 2008a,b). Further, certain populations in Africa and in the Caribbean vary in their degree of reproductive isolation from populations in more temperate regions (Wu et al. 1995; Hollocher et al. 1997; Yukilevich and True 2008a,b). In particular, the Zimbabwe and nearby populations of southern Africa are strongly sexually isolated from all other populations, designating them as a distinct behavioral race (Wu et al. 1995).

D. melanogaster has received a great deal of attention from the population geneticists in studying patterns of sequence variation across African and non-African populations. Many snapshots have been taken of random microsatellite and SNP variants spread across X and autosomes, and these have generated several important conclusions. Polymorphism patterns in European populations are characterized by reduced levels of nucleotide and haplotype diversity, an excess of high frequency-derived polymorphisms, and elevated levels of linkage disequilibrium relative to African populations (e.g., Begun and Aquadro 1993; Andolfatto 2001; Glinka et al. 2003; Haddrill et al. 2005; Ometto et al. 2005; Thornton and Andolfatto 2006; Hutter et al. 2007; Singh et al. 2007). These results have been generally interpreted as compatible with population size reduction/bottlenecks followed by recent population expansions. On the other hand, African populations are generally assumed either to have been relatively constant in size over time or to have experienced population size expansions. They generally show higher levels of nucleotide and haplotype diversity, an excess of rare variants, and a deficit of high frequency-derived alleles (Glinka et al. 2003; Ometto et al. 2005; Pool and Aquadro 2006; Hutter et al. 2007; but see Haddrill et al. 2005 for evidence of bottlenecks in Africa).

Previous work also shows that the ratio of X-linked to autosomal polymorphism deviates from neutral expectations in opposite directions in African and European populations with more variation on the X than expected in Africa and less variation on the X than expected in Europe (Andolfatto 2001; Kauer et al. 2002; Hutter et al. 2007; Singh et al. 2007). The deviation from neutrality in the ratio of X-autosome polymorphism may be explained by positive selection being more prevalent on the X in Europe and/or by a combination of bottlenecks and male-biased sex ratios in Europe and female-biased sex ratios in Africa (Charlesworth 2001; Hutter et al. 2007; Singh et al. 2007). The selective explanation stems from the argument that, under the hitchhiking selection model, X-linked loci are likely to be more affected by selective sweeps than autosomal loci (Maynard Smith and Haigh 1974; Charlesworth et al. 1987; Vicoso and Charlesworth 2006, 2009).

The relative contribution of selective and demographic processes in shaping patterns of genomic variation and differentiation is highly debated (Wall et al. 2002; Glinka et al. 2003; Haddrill et al. 2005; Ometto et al. 2005; Schöfl and Schlötterer 2004; Thornton and Andolfatto 2006; Hutter et al. 2007; Singh et al. 2007; Shapiro et al. 2007; Stephan and Li 2007; Hahn 2008; Macpherson et al. 2008; Noor and Bennett 2009; Sella et al. 2009). This is especially the case in D. melanogaster because derived non-African populations have likely experienced a complex set of demographic events during their migration out of Africa (e.g., Thornton and Andolfatto 2006; Singh et al. 2007; Stephan and Li 2007), making population genetics signatures of demography and selection difficult to tease apart (e.g., Macpherson et al. 2008). Thus it is still unclear what role selection has played in shaping overall patterns of genomic variation and differentiation relative to demographic processes in this species.

While there is a long tradition in studying arbitrarily or opportunistically chosen sequences in D. melanogaster, genomic scans that focus particularly on highly differentiated sites across the genome have received much less attention. Such sites are arguably the best candidates to resolve the debate on which processes have shaped genomic differentiation within species (e.g., Przeworski 2002). Recently, a genome-wide scan of cosmopolitan populations in the United States and in Australia was performed to investigate clinal genomic differentiation on the two continents (Turner et al. 2008a). Many single feature polymorphisms differentiating Northern and Southern Hemisphere populations were identified. Among the most differentiated loci in common between continents, 80% were differentiated in the same orientation relative to the Equator, implicating selection as the likely explanation (Turner et al. 2008a). Larger regions of genomic differentiation within and between African and non-African populations have also been discovered, some of them possibly being driven by divergent selection (e.g., Dopman and Hartl 2007; Emerson et al. 2008; Turner et al. 2008a, Aguade 2009). Despite this recent progress, we still know relatively little about large-scale patterns of genomic differentiation in this species, especially between African and non-African populations, and whether most of this differentiation is consistent with demographic processes alone or if it requires selective explanations.

In this work, we explicitly focus on identifying differentiated sites across the genome between U.S., Caribbean, West African, and Zimbabwean populations. This allows us to address several fundamental questions related to genomic evolution in D. melanogaster, such as the following: (1) Do genome-wide patterns of differentiation reflect patterns of reproductive isolation? (2) Is genomic differentiation random across and within chromosomes or are some regions overrepresented? (3) What are the population genetics properties of differentiated sites and their surrounding sequences? (4) Can demographic historical processes alone explain most of the observed differentiation on a genome-wide level or is it necessary to involve selection in their explanation?

In general, our findings revealed that most genomic differentiation within D. melanogaster shows an out-of-Africa genetic signature. These results are inconsistent with the notion that most genomic differentiation occurs between cosmopolitan and Zimbabwean reproductively isolated races. Further, we found that the X is more differentiated between North American and African populations and more strongly deviates from pure neutrality in North American populations relative to autosomes. Nevertheless, our article shows that much of this deviation from neutrality is broadly consistent with several demographic null models, with a few notable exceptions. Athough this does not exclude selection as a possible alternative mechanism for the observed patterns, it supports the idea that most differentiation in D. melanogaster was likely driven by the sorting of African standing genetic variation into the New World.

MATERIALS AND METHODS

Isofemale lines:

In the summer of 2004, R. Yukilevich collected and established isofemale lines from the southeastern United States (Tuscaloosa, AL: 18 lines; Columbus, MI: 15 lines) and the Caribbean (High Rock, South Andros Island: 20 lines; Port Nelson, Rum Cay: 22 lines; Spring Point, Acklins Island: 16 lines). For further details about the U.S. and Caribbean populations, see Yukilevich and True (2008a,b). African isofemale lines were acquired from J. Pool and C. Aquadro in 2005 and consisted of a population from West Africa (Mbalang-Djalingo, West Cameroon: 31 lines collected by J. Pool in 2004) and a population from southeast Africa (Sengwa, Zimbabwe: 13 lines collected in 1990 and described by Begun and Aquadro 1993).

DNA extraction and purification:

DNA was extracted from pooled individuals of multiple isofemale lines for each of the seven locations described above. First, we collected an equal number of males and females from each isofemale line of a given location and froze the flies at −80°. We then created three replicates, each containing 100 pooled individuals, per location. In total, this yielded 21 samples (3 replicates from 7 locations). For each 100-fly pooled sample, we used a phenol:chloroform extraction to isolate the initial DNA extract. We then performed ethanol precipitation and resuspended the DNA in 38 μl of H₂O. To eliminate RNA, we added 1 μl of RNAse. To check the concentration of DNA, we ran λDNA (350 ng/μl) in parallel with all 21 diluted samples on 1% agarose gels. Before DNA fragmentation, the amount of DNA for each of the 21 samples was standardized to ∼7.8 μg/100-fly sample.

DNA fragmentation and labeling:

DNA samples of volume 39 μl were fragmented with a mix of 4 μl of 10× One-Phor-All buffer (Amersham Biosciences), 0.14 μl of acetylated BSA (Invitrogen), and 0.64 μl of DNase1 (Promega) (total mix = 4.78 μl) per sample. Fragmentation of all 21 samples was done simultaneously in a PCR thermocycler at 37° for 16 min, 99° for 15 min, and 12° for 15 min, and then the DNA was stored at −20°. Fragmentation of DNA was assessed by running 3 μl of DNA fragment on 2% agarose gels. Mean fragment sizes of all samples were ∼35 bp, with similar intensity and variance when separated in a 1% agarose gel. Labeling was done with 2 μl of Biotin-N6-ddATP (Enzo) and 3 μl of RTdT enzyme (Promega) mix added to each sample. RTdT was first diluted from 30 to 15 units/μl enzyme by mixing a ratio of 5:1:4 of RTdT enzyme, RTdT 5× buffer, and H₂O. PCR conditions for labeling were 37° for 90 min, 99° for 15 min, and 12° for 5 min, and then the DNA was stored at −20°. Labeling was done simultaneously on all 21 samples using the same master mix.

Affymetrix tiling array hybridization and data extraction:

Each of the 21 samples was hybridized to a single Affymetrix tiling array. Hybridization was done at the University of California Davis Genome Center (Affymetrix facility) following standard protocols for this array. All hybridization data, including raw CEL files and normalized files (see below), have been deposited with the EMBL-European Bioinformatics Insitute (EBI)/MassArray library (accession no. E-MEXP-2667). It has been established that hybridization intensity of DNA to a microarray depends on sequence similarity (Winzeler et al. 1998; Borevitz et al. 2003; Gresham et al. 2006). Differentiated sites in the genome can therefore be identified when different DNA samples hybridize to an array with different affinities (Borevitz et al. 2003; Turner et al. 2008a; see below). Limitations of this technique may include variable sensitivity of hybridization intensity across the genome and a possible nonlinear relationship between DNA sequence divergence and hybridization intensity (Zhang et al. 2003). Several approaches were used to minimize these effects (see below).

National Center for Biotechnology Information megablast was used to identify array probes with a single perfect match to version 5.3 of the D. melanogaster reference genome. We retained 3,015,075 probes throughout the genome, including 2,950,143 probes on the major chromosomal arms, 24,726 probes on the “dot” fourth chromosome, and 32,256 probes in heterochromatic regions of chromosomes X, 2, and 3. This corresponds to ∼63% of the D. melanogaster genome.

Data normalization:

We normalized the data to partially control for heterogeneous and spatially nonrandom patterns of signal intensities on chips (Borevitz et al. 2003). Briefly, we divided each array into 1600 subarrays of 64 × 64 probes and log-transformed raw intensity values. We then divided the intensity of each oligo by the median intensity of unique probes on each local 64 × 64 probe subarray (following Turner et al. 2008a). We normalized the data further by using quantile normalization (Gautier et al. 2004).

Nested ANOVA:

A nested ANOVA analysis was performed on all 3,015,075 normalized mean hybridization intensities of U.S., Caribbean, West African, and Zimbabwean locations using the following model design: Y = geographical region + population (geographical region) + replicate [population (geographical region)]. The ANOVA results have been deposited along with the above hybridization data with the EMBL-EBI. We divided our populations into four geographical regions: the United States, the Caribbean, West Africa, and Zimbabwe because these four regions have been previously shown to have phenotypic and behavioral differences (Wu et al. 1995; Hollocher et al. 1997; Yukilevich and True 2008a,b). U.S. and Caribbean regions contained several local populations, while West Africa and Zimbabwe each had a single population. Every local population had three replicates. Since our focus was to describe genomic differentiation between the United States, Caribbean, West Africa, and Zimbabwe, the nested ANOVA allowed us to generate a list of probes that were significantly differentiated only between these geographical regions (i.e., were significantly homogeneous within the United States and within the Caribbean).

Upon generating a list of probes with their associated P-values, we used a Bonferroni correction for multiple testing (P-value × 3,015,075 probes) and then calculated the false discovery rate (FDR) of each probe P-value. FDRs were estimated as the expected/observed number of probes below a given P-value, where the expected number is the P-value × the number of tests [which assumes a uniform distribution of P-values from 0 to >1 as the null (Benjamini and Hochberg 1995; Storey and Tibshirani 2003)].

Phylogenetic patterns of population differentiation:

To assess which geographical regions were differentiated within a given significant probe, we estimated the phylogenetic relationship of local populations among our most differentiated probes. First, we generated a genetic distance matrix for each probe based on the absolute hybridization signal intensity difference between a pair of populations. A neighbor-joining algorithm (Felsenstein 2004) was used to group populations within each probe on the basis of their genetic distance matrix. We then employed a hierarchical gene-clustering algorithm (average linkage clustering) to cluster genes into larger groups on the basis of their phylogenetic relationships with the software Gene Cluster 3.0 (de Hoon et al. 2004). Using the companion software Tree View (version 1.1.3), we identified distinct clusters of phylogenetic relationships among localities and determined their relative frequencies among our differentiated probes.

We also generated an overall phylogenetic tree based on all of our differentiated probes by using the average Euclidean distance between localities with the software PASSAGE (Rosenberg 2004). The overall clustering was performed with NEIGHBOR and DRAWTREE programs of software PHYLIP 3.6 (Felsenstein 2004). Bootstrap values were also determined on the basis of 1000 bootstrap replicates using the CONSENSE program of the software PHYLIP 3.6 (Felsenstein 2004).

Sanger DNA sequencing of differentiated probes:

We sequenced 41 probes to validate the tiling array results, to determine sequence differentiation within the probes, and to characterize molecular divergence of our differentiated sites. All forward and reverse primers were ∼150 bp from the center of the probe, with a mean fragment size of 142 bp (SD ±42.8). We chose relatively small fragments because linkage disequilibrium is substantially weakened at >200 bp from the target site in D. melanogaster (Haddrill et al. 2005; Ometto et al. 2005). We genotyped single individuals from 20 isofemale lines from the United States, from 30 lines from the Caribbean, from 10 lines from West Africa (Cameroon), and from 10 lines from Zimbabwe (Sengwa). PCR products were checked on 1% agarose gels. Then PCR products were purified using either Qiagen Qiaquick PCR purification kits or exonuclease I-shrimp alkaline phosphatase to remove residual primers and unincorporated nucleotides. Amplicons were then sequenced using ABI BigDye terminator version 3.1. Sequencing reactions were then purified using Sephadex G-50 columns, and sequence data were collected on an ABI 3100 genetic analyzer. Sequence data have been deposited with the EMBL/GenBank data libraries under accession nos. FR657549–FR660150.

Population genetics statistics and F_ST values:

We identified polymorphisms in U.S., Caribbean, West African, and Zimbabwean populations within each sequenced fragment using Sequencher 4.8 software (Gene Codes, Ann Arbor, MI). We then extracted aligned sequences into DnaSP5 software (Rozas et al. 2003) to determine population genetics statistics. This included the polarity of allelic ancestry within the probe, designated as the sequence that is present in one or both of the closely related species D. simulans and D. sechellia, and the allelic frequency within the probe. We also determined population genetics statistics on the basis of the whole fragment: haplotype (gene) diversity, H_d, (Nei 1987), nucleotide diversity per site, π (Nei 1987), θ per site assuming Watterson's estimate, θ_W (Nei 1987), Tajima's D statistic (Tajima 1989), and Fay and Wu's H (Fay and Wu 2000; Zeng et al. 2006) to test the hypothesis of selective neutrality of the probe. The significance of Tajima's D (D) and Fay and Wu's H (FWH) was determined by comparing each statistic against the distribution generated by 10,000 coalescent simulations under the standard neutral model (SNM) with constant population size, with and without recombination, panmixis, and an infinite-sites model, using DnaSP5 software (Rozas et al. 2003). See below for significance based on a specialized demographic coalescent model.

To determine the level of genetic differentiation between populations on the basis of our sequenced probes, we calculated the F_ST values, assuming the Weir and Cockerham (1984) calculations, using the DnaSP5 software (Rozas et al. 2003). The F_ST value is a measure of between-population variability relative to within-population variability and may therefore be affected by the level of the latter (Charlesworth 1998). Thus, we also calculated the absolute nucleotide divergence statistic D_xy, defined as the average number of nucleotide substitutions per site between populations (Nei 1987, equation 10.20), and the relative divergence statistic D_net (also known as D_a), defined as the number of net nucleotide substitutions per site between populations within each fragment (Nei 1987, equation 10.21).

Demographic coalescent null models:

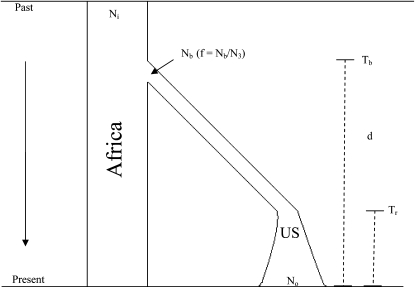
We further tested whether alternative demographic null models could explain our observed average values of Tajima's D and Fay and Wu's H among the X-linked and autosomal fragments surrounding our high F_ST probes. We used a general two-population bottleneck/population expansion model (described in Figure 1; Hudson 2002). In this model, the initial ancestral effective population size (N_i) is assumed to be constant over time. At T_b generations ago, a derived bottleneck population is established at an effective size of N_b. At T_r generations ago, the bottlenecked population experiences a recovery with an exponential growth to the present population size of N_o. The difference in time between T_b and T_r is the duration of the bottleneck (d). All times in the simulation are measured in units of 4N_o generations. Thus, the severity of the bottleneck (f) is here defined in terms of N_b/N_o. We assumed only between-fragment recombination. We assumed N_{i_X} = 2.5 million for X chromosome and N_{i_auto} = 3,417,722 for autosomes to preserve the observed 3/4 ratio of the ancestral effective population size (see below). The X-chromosome estimate is based on Haddrill et al. (2005) and Thornton and Andolfatto (2006). The parameters, T_b, T_r, and f reflected the difference in the effective population sizes of the X chromosome and autosomes. We assumed that the number of generations per year is 10.

Figure 1.—

An illustration of the general bottleneck/expansion demographic model used to test various population genetics statistics of high-F_ST fragments (see Table 5 for specific parameters and results). Initial effective population size in Africa (N_i) is assumed to be constant over time (see Haddrill et al. 2005; Thornton and Andolfatto 2006). N_b is the effective population size of the bottlenecked population derived from Africa T_b generations ago. At T_r, the derived U.S. population is assumed to experience a recovery with an exponential growth to the present effective population size, N_o. The duration time from T_b to T_r is referred to as d. Migration rate between Africa and the United States is assumed to be effectively zero after T_b to the present (see text).

Input and simulated parameters:

For each demographic scenario, we specified the number of chromosomes to be sampled and four input parameters of the model, T_b, T_r, f, and the average θ (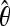) among simulated fragments. The 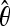is an estimate of the population parameter 4N_eu, where N_e is the effective population size and u is the neutral mutation rate. Because the true θ is uncertain under complex demographic history, we explored a range of 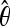values under different demographic scenarios (Haddrill et al. 2005; D. Hudson, personal communication; see Table S4). In each case, the four simulation input parameters were scaled to match the observed data among our fragments in terms of (1) the average value of k [referred to as “pi” in Hudson's (2002) ms document], which equals the average number of pairwise differences between haplotypes within a population, and (2) the average number of segregating sites, ss, within a population. Particular attention was also given to matching the variance of k and ss between simulated and observed fragment data (see similar treatment in Glinka et al. 2003; Haddrill et al. 2005; Thornton and Andolfatto 2006). Because our fragments are nonrandom across the genome and are strongly biased toward high F_ST values (highly differentiated sites in the genome), we sampled fragments without replacement that best matched the F_ST distribution among our observed data. Thus our simulations also matched the F_ST distribution of our observed fragments.

Output statistics to test demographic model scenarios:

To test whether a given demographic model scenario is consistent with the observed data, we focused on two summary statistics, Tajima's D and Fay and Wu's H (see above for description). For each simulation replicate, we calculated the average D and FWH values among our simulated fragments. Thus, for each demographic scenario, we analyzed four types of fragment sets, 19 X-linked random fragments, 19 X-linked biased in F_ST fragments, 20 autosomal random fragments, and 20 autosomal biased in F_ST fragments (see Table 5 for details). To determine significance for random sets, we sampled 19 X-linked or 20 autosomal fragment sets 5000 times and determined the conditional probability (P-value) of observing more negative means of both D and FWH statistics among simulated sets than among the observed sets. To determine significance for biased F_ST sets, we sampled 19 X-linked or 20 autosomal fragment sets, which matched the F_ST mean and variance of the observed data, 100 times. We then determined the conditional probability (P-value) of observing more negative means of both D and FWH statistics among the biased F_ST simulated sets than among the observed data. All simulations were run with Hudson's ms program and auxiliary custom R scripts that analyzed F_ST values between ancestral and derived populations (Hudson 2002). Command lines of the ms program are provided in Table S4.

TABLE 5.

Average nucleotide diversity estimates for X-linked and autosomal loci

Location	θW (X)	θW (auto)	θW (X/A)	π(X)	π(auto)	π(X/A)
The Netherlandsa	0.0033	0.0068	0.49	0.0043	0.0063	0.68
U.S. Northeast (Maine)b	0.011	0.0115	0.96	0.008	0.011	0.73
U.S. Southeast (Mississippi, Alabama)	0.01	0.0159	0.63	0.0068	0.013	0.52
U.S. Southeast (Florida)b	0.008	0.0119	0.67	0.01	0.012	0.83
U.S. (California, North Carolina)c	0.0082	0.0094	0.87	—	—	—
Caribbean (Bahamas)	0.0065	0.0124	0.52	0.005	0.013	0.38
West Africa (Cameroon)	0.0083	0.0116	0.72	0.008	0.012	0.67
South Africa (Malawi)c	0.0173	0.01779	0.97	—	—	—
Zimbabwe (Sengwa)	0.0075	0.01	0.75	0.008	0.011	0.73
Zimbabwe (Lake Kariba,Victoria Falls)a	0.0096	0.011	0.87	0.011	—	—

Data are based on 22 X-linked loci and 23 autosomal loci (see text). θ_W is the Watterson's diversity estimate, and π is the average pairwise divergence (Tajima 1989). Diversity estimates are per site.

^aData from Glinka et al. (2003) and Haddrill et al. (2005) based on 115 X-linked loci and from Hutter et al. (2007) based on 377 autosomal loci.

^bData from Turner et al. (2008a) based on 7 X-linked loci and 25 autosomal loci.

^cData from Singh et al. (2007) based on 8 X-linked loci and 8 autosomal loci.

Single-fragment analysis:

In addition to determining whether a given demographic model can explain the average population statistics, we also asked whether any of our sequenced fragments deviate significantly from various demographic models. First, we determined the P-value for having a lower Tajima's D and FWH statistics in the U. S. population compared to SNM expectations. This was determined using DnaSP5 software based on 100,000 coalescent simulations (Rozas et al. 2003). In addition, we determined the probability (P-value) of having a lower D and FWH statistics in the U.S. population than expected, given the most acceptable demographic null model from our simulations (see below for details). To replicate our sampling of the most differentiated probes, our significance was based on running 1,000,000 coalescent simulations of this particular model and then considering only the top 1% most differentiated fragments (highest F_ST fragments). We then corrected for multiple testing by using the FDR adjustment based on the Benjamini and Yekutieli (2001) FDR method.

RESULTS

Nested ANOVA and overall geographical differentiation across the genome:

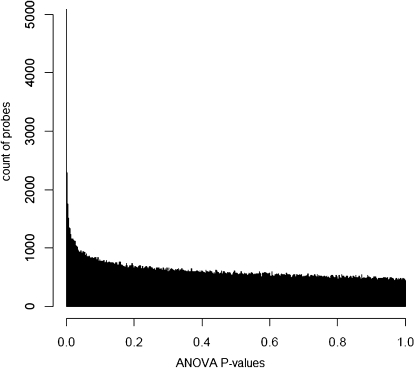
Our analysis generated a distribution of individual probe P-values, with the characteristic exponential curve, indicating an excess of low P-values (Figure 2). Under the model of no differentiation, a uniform distribution from 0 to 1 is expected (Storey and Tibshirani 2003). We identified the top 681 probes as the largest set expected to contain less than 1 false discovery (FDR = 0.00147% with the least significant P-value = 3.31 × 10⁻⁷; Table S1), which is a highly conservative estimate. For comparison, an FDR of 1% contains 2773 probes with 28 expected false discoveries, and an FDR of 5% contains 9826 probes with 491 expected false discoveries. These probes were significantly homogeneous within U.S. and within Caribbean regions.

Figure 2.—

Histogram of 3,015,075 probe P-values from nested ANOVA analysis based on mean probe hybridization signal intensities of four geographical locations: the United States, Caribbean, Cameroon (West Africa), and Zimbabwe (see materials and methods for location information). P-values reflect the significance associated with differentiation only between geographical regions (i.e., the geographical region effect in the nested ANOVA design; see text for details).

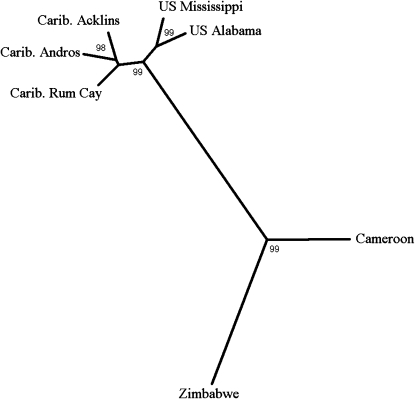
To determine the overall pattern of geographical differentiation between localities, we grouped populations using an unrooted neighbor-joining (NJ) algorithm based on pairwise Euclidean distances of the 681 most significant hybridization signal intensities (Figure 3). This revealed that the strongest differentiation in most probes is between North American and African populations. We also found that the two U.S. populations and the three Caribbean populations grouped according to geographical region and with each other, indicating similar hybridization signal intensities within these regions. Zimbabwean and West African populations are themselves differentiated, but to a lesser degree than Africa and North America are differentiated. Finally, North America is more differentiated from Zimbabwe than from West Africa (Figure 3).

Figure 3.—

Unrooted neighbor-joining tree based on pairwise Euclidean distances of the 681 most differentiated probe hybridization signal intensities from the nested ANOVA analysis (see text). Euclidean distances were generated using PASSAGE software (Rosenberg 2004). Qualitatively similar results are obtained when analyzing exclusively X-linked or autosomal differentiated probes (data not shown). Clustering was performed using NEIGHBOR and DRAWTREE programs. Bootstrap values are shown as percentages based on 1000 bootstrap replicates using CONSENSE program. All programs were run with PHYLIP 3.6 (Felsenstein 2004).

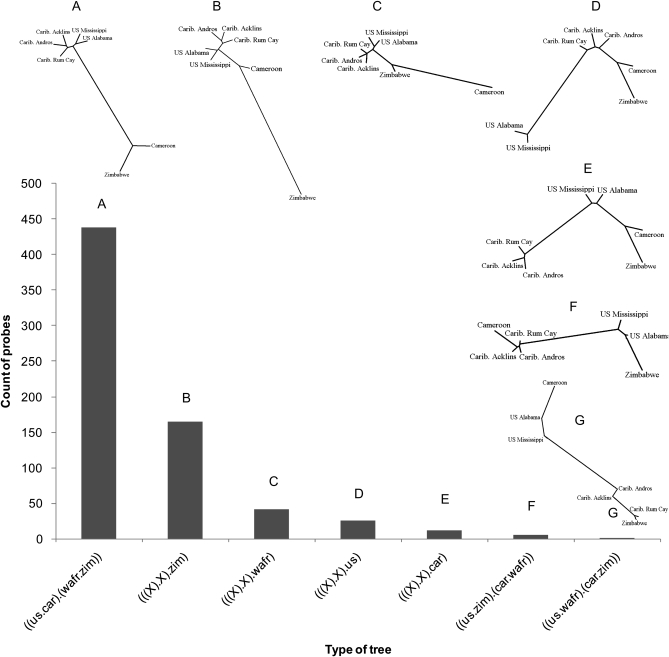
We then studied the distribution of phylogenetic relationships among the 681 most significant probes by first constructing the NJ tree for each probe and then by identifying seven distinct phylogenetic clusters among probes (see materials and methods; Figure 4). We found that 437 probes (64%) are characterized by the North America–Africa differentiation (from here on referred to as “out-of-Africa” divergence). The next most common cluster of differentiation occurs for 163 probes (24%) where Zimbabwe is a strong geographical outlier (from here on referred to as “cosmopolitan–Zimbabwe” divergence). West Africa is an outlier for 39 probes (6%), while the United States and the Caribbean are outliers for 24 and 12 probes, respectively (Figure 4). This analysis allowed us to rank the various patterns of genomic differentiation among our populations as follows: out-of-Africa divergence ≫ cosmopolitan–Zimbabwe divergence ≫ West African divergence > U.S. divergence.

Figure 4.—

Distribution of different clusters of neighbor-joining (NJ) trees among the 681 most differentiated probes from the nested ANOVA analysis. The NJ tree for each probe was based on the absolute difference in the mean hybridization signal intensity between populations. The tree shown for each cluster is based on Euclidean distances of mean hybridization values of probes using PASSAGE software (Rosenberg 2004). NJ trees were generated using NEIGHBOR and DRAWTREE programs of PHYLIP 3.6 (Felsenstein 2004).

Patterns of differentiation within the genome:

We then tested whether the most differentiated probes are randomly distributed among and within chromosomes. First, to test whether differentiation is randomly distributed among chromosomes, we determined the expected frequency of differentiated probes among all chromosomes, which is based on the total number of probes situated on each chromosome (Table 1). On the basis of these random expectations, we found that probes showing divergence between North American and African populations are strongly overrepresented on the X chromosome relative to autosomes (Table 1; χ² test, P < 0.00001). Compared to the expected 18%, between 49% and 71% of differentiated probes were situated on the X, with out-of-Africa probes having the most extreme bias (Table 1). In contrast, probes where the United States was a major outlier (i.e., where Caribbean lines are genetically closer to Africa), did not deviate from random expectation across chromosomes (Table 1; χ² test, P = 0.57; also see Turner et al. 2008a for similar results between eastern U.S. populations). The above results indicate that the X chromosome has experienced a much greater level of nucleotide differentiation compared to autosomes particularly between North American and African populations.

TABLE 1.

Chromosomal distribution of the most differentiated probes among the most common phylogenetic clusters in Figure 4

Chromosome	Expected frequency	Out-of-Africa	Zimbabwean outlier	West African outlier	U.S. outlier
X	0.18%	0.71%	0.49%	0.64%	0.21%
3R	0.25%	0.07%	0.13%	0.08%	0.33%
3L	0.20%	0.08%	0.18%	0.18%	0.25%
2R	0.18%	0.07%	0.10%	0.10%	0.13%
2L	0.19%	0.07%	0.10%	0.03%	0.08%
No. of probes:		437	163	39	24
χ2 test (P-values)		<0.0001	<0.0001	<0.0001	0.57

Expected percentage is based on total number of probes per chromosomal arm.

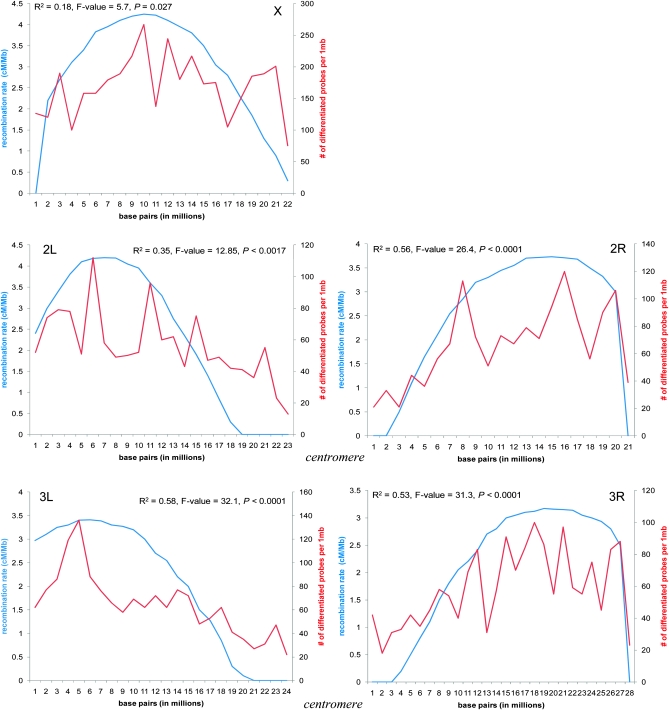
We next turn to subchromosomal patterns of differentiation. We mapped both the recombination rate and the number of differentiated probes from the ANOVA analysis along 1-million-bp windows across each chromosomal arm (see Figure 5). To avoid many chromosomal regions with zero differentiated probes, we used a less stringent 5% FDR cutoff level (9286 total probes; see above). Our results showed that there was a positive and highly significant association between recombination rate and the level of differentiation along all chromosomes, especially within autosomes. This result was driven by reduced differentiation at telomeres and especially at centromeres (Figure 5). A weaker, but still significant, relationship on the X chromosome occurred because the X showed a heightened level of differentiation across nearly the whole chromosome. In total, it is clear that genomic differentiation peaks in the middle of each chromosome or arm and falls off toward its ends. Similar reduction in divergence near centromeres was recently observed between the species pair D. pseudoobscura and D. persimilis (Kulathinal et al. 2008). A more general relationship between divergence rates and nucleotide polymorphism also has been seen in the D. melanogaster species group (Begun et al. 2007).

Figure 5.—

Relationship between recombination rate (blue) and the number of differentiated probes (red) from the nested ANOVA for each 1-million-bp window along the chromosome arm. Recombination rate data were acquired from http://petrov.stanford.edu/cgi-bin/recombination-rates_updateR5.pl. and were estimated by plotting Marey maps of the genetic positions of molecular markers (in centimorgans, cM) against their physical position (in megabase pairs, Mb). For this analysis, we used 9286 probes identified at the 5% FDR level from the nested ANOVA. Adjusted regression coefficients and their significance are shown.

Sanger sequencing of candidate probes:

To validate the above results, we sequenced 41 candidate probes across U.S., Caribbean, Cameroon, and Zimbabwean lines (see materials and methods). In addition to sampling from 681 most differentiated probes with less than one expected false discovery, we sampled probes of less stringent criteria with more than one expected false discovery (Table 2). Probes were equally represented across X and autosomes and between coding and noncoding sites (including introns and intergenic regions) from the top 80,000 probes with the lowest ANOVA P-values.

TABLE 2.

Basic features of the 41 sequenced probes chosen from the nested ANOVA and of six random probes

Gene name	Rank	FDR	No. of FDs	Fragment (bp)	Recombination Rate (cM/Mb)	Chromosome	Probe location	Site type	Synonymous/nonsynonymous	Ancestral allele	Derived allele
period	2	0.0000016	<1	222	1.84	X	2,579,880–2,579,904	5′ UTR	—	SNP: A	T(ref.); Indel: (15bp. insertion in N.A.)
235.468	4	0.0000124	<1	194	3.46	X	15,156,739–15,156,763	Intergenic	—	A….GG	A…..GC > G……TC(ref.)
5097.1107	20	0.0000222	<1	107	2.82	X	7,322,927–7,322,951	Intergenic	—	A.G	A.A(ref. N.A.) or T.G(Africa)
fred	74	0.0000744	<1	51	2.76	2L	3,921,381–3,921,405	Intron	—	C…G(ref.)	A…G > A….T
Cyp6a22	75	0.0000756	<1	158	1.46	2R	10,760,407–10,760,431	Intron	—	TA..T	AC..T(ref. N.A.) or TA..Cor AA..C(Africa)
1857.837	107	0.0001210	<1	153	3.17	X	20,876,262–20,876,286	Intergenic	—	T	C(ref.)
FucT6	108	0.0001345	<1	158	3.32	X	11,602,351–11,602,375	CDS	Syn	G…G	A…C(ref.)
CG2694	224	0.0003093	<1	100	1.85	X	2,608,335–2,608,359	CDS	Syn	T(ref.)	C
couch potato	245	0.0003394	<1	183	0.88	3R	13,790,151–13,790,175	Intron	—	T(ref.)	A
Atapalpha	246	0.0003387	<1	69	1.25	3R	16,781,505–16,781,529	Intron	—	G	T(ref.)
CG15293	257	0.0003581	<1	174	3.52	2L	14,108,392–14,108,416	CDS	NonS	GAGGG..GGG	TGAAC..GAA(ref.)
E2f	442	0.0008782	<1	103	1.32	3R	17,461,287–17,461,311	Intron	—	C(ref.)	T
2555.2470	574	0.0011381	<1	159	3.36	X	18,578,377–18,578,401	Intergenic	—	T	C(ref.)
CG14998	672	0.0014177	<1	142	3.03	3L	4,126,308–4,126,332	CDS	NonS	G	A(ref.)
Tak1	699	0.0014919	1	122	3.22	X	20,388,005–20,388,029	CDS	NonS	GCC	CTT(ref.)
2375.2501	908	0.0022309	2	183	0	X	1,229,872–1,229,896	Intergenic	—	C…G	A…G or C…T > G…T(ref.)
Nmdar2	919	0.0022462	2	167	0	X	1,394,893–1,394,917	Intron	—	Indel: CAT^GG	CAT..[114 bp deletion]..GG(ref.)
Btk29A	1,201	0.0030002	4	152	3.44	2L	8,271,429–8,271,453	Intron	—	C….C	T…C(ref.) or C…A
75.618	1,263	0.0031734	4	195	3.45	X	14,440,737–14,440,761	Intergenic	—	G	A(ref.)
Eip75B	1,890	0.0056572	11	137	2.73	3L	17,985,031–17,985,055	Intron	—	T(ref.)	G
CG32635	2,105	0.0066248	14	152	3.42	X	13,389,886–13,389,910	CDS	NonS	T	A(ref.)
CG7728	2,119	0.0067023	14	109	2.83	3L	17,011,993–17,012,017	CDS	Syn	G(ref.)	A
CG11106	2,250	0.0073320	16	88	3.28	X	11,096,487–11,096,511	CDS	NonS	T	G(ref.)
CG2898	2,546	0.0087331	22	159	3.2	X	10,269,933–10,269,957	CDS	NonS	G….G	C…G > C…A(ref.)
sphinx1	2,649	0.0093497	25	147	3.19	3L	7,431,854–7,431,876	CDS	Syn	G…T(ref.)	A…G
feo	2,830	0.0103741	29	183	3.24	X	10,747,118–10,747,142	CDS	Syn	C	T(ref.)
Cad96Cb	3,971	0.0165277	66	93	1.64	3R	21,051,158–21,051,182	CDS	Syn	G	A(ref.)
Shaker	6,638	0.0319373	212	200	3.4	X	17,847,304–17,847,328	CDS	—	—	—
Spn	6,876	0.0335110	230	88	2.91	3L	2,540,498–2,540,522	Intron	—	C…G(ref.)	A…G or C…C
ligand	8,725	0.0438968	383	170	0	2R	3,959,855–3,959,879	CDS	—	—	—
Gr28b	8,761	0.0441712	387	108	3.36	2L	7,456,562–7,456,586	Intron	—	A…C	G…T(ref.)
Pxd	9,154	0.0463209	424	97	0.75	3R	12,847,742–12,847,766	Intron	—	T	C(ref.)
CG12115	10,331	0.0523437	541	132	3.06	X	9,083,537–9,083,561	CDS	Syn	G….G	A…Gor G….T(ref.) > A….T
CG11261	11,819	0.0604584	715	145	3.13	3L	13,003,921–13,003,945	CDS	NonS	T	C(ref.)
CG15764	17,016	0.0873993	1487	117	2.55	X	5,763,338–5,763,362	CDS	—	TorC	T(ref.)orC
CG15894	19,306	0.0974121	1881	260	2.63	X	6,214,894–6,214,918	CDS	NonS	GG	CA(ref.)
Ob50b	24,055	0.1181299	2842	99	1.38	2R	10,259,477–10,259,501	CDS	NonS	T..A..G..G	G..T..C..A(ref.)
pathetic	32,325	0.1499259	4846	111	3.21	3L	9,488,908–9,488,932	CDS	Syn	G..A	A..G(ref.)
ham	50,670	0.2063295	10455	134	0	2L	18,765,080–18,765,104	CDS	NonS	A(ref.)	T
CG33213	>57,763	>0.224	>12944	174	1.81	3R	23,744,914–23,744,938	CDS	Syn	G	A(ref.)
CG1745	>57,763	>0.224	>12944	132	3.3	X	11,350,112–11,350,136	CDS	Syn	A…Cor G…G	A….Cor G…G(ref.)
Flo-2	Random	NA	NA	190	3.46	X	14,802,654–14,802,844	Intron	—	A	T(ref.)
sgg	Random	NA	NA	245	1.84	X	2,542,804–2,543,048	Intron	—	AA(ref.)	CC
CG3655	Random	NA	NA	311	0	X	1,018,839–1,019,436	Intron	—	G..A..G	A..G..T(ref.)
chb	Random	NA	NA	260	0	3L	21,170,325–21,170,584	Intron	—	T	G(ref.)
intergene	Random	NA	NA	190	2.1	2L	1,302,500–1,302,648	Intergenic	—	G(ref.)	A
Trp1	Random	NA	NA	149	0.38	2R	5,647,602–5,647,724	Intron	—	A	G(ref.)

CDS, (protein) coding site: the change is synonymous (Syn) or nonsynonymous (NonS). The polarity of the single feature polymorphism is determined on the basis of the sequence of D. simulans/D. sechelia (presumed ancestral state). The D. melanogaster reference sequence (ref.) is shown. Two sequenced probes (in Shaker and ligand loci) were false discoveries (see above). Probe within the locus CG15764 was polymorphic, but with very low F_ST values (see Table S2 for details).

Table 2 shows the rank, FDR, and the number of expected false discoveries (FDs) of each sequenced probe. Because our focus of interest is on the sites immediately adjacent to each probe, where linkage disequilibrium is highest (e.g., Haddrill et al. 2005; Ometto et al. 2005), we chose to study relatively small fragment sizes. Thus the average length of our sequenced fragments was 142 bp for a total 5827 bp. We determined that 2 of the 41 sequenced probes were false discoveries, defined as having no sequence variation within these fragments and an F_ST of zero. Thus, our overall sequence FDR was 4.9%. The two probes were ranked 6638th (P-value: 7 × 10⁻⁵) and 8725th (P-value: 0.000127), well beyond the 681 most significant probes considered in the analyses above. These false discoveries are expected since, if all probes with P-values <0.000127 are considered together, we would expect an FDR of 4.4%. Among 39 true discoveries, two probes correspond to indel mutations (15 and 114 bp). From the remaining 37 probes, 17 probes contain more than one high-F_ST SNP (46%).

Patterns of F_ST values across the genome:

First, we determined the relationship between probe differentiation based on tiling array data and differentiation based on actual sequence divergence. To test this relationship, we correlated the mean hybridization signal intensity difference and the F_ST value based on allelic frequency differences at each probe. We tested the above relationship among 39 probes for each pairwise independent geographical comparison (e.g., the United States vs. the Caribbean). We observed highly significant positive correlations across all six pairwise geographical comparisons (n = 39 for each comparison: R²_US-Carib. = 0.41, P < 0.0001, R²_US-W.Afr. = 0.35, P < 0.0001, R²_US-Zimb. = 0.33, P < 0.0001, R²_{Carib.-W.Afr.} = 0.35, P < 0.0001, R²_Carib.-Zimb. = 0.28, P = 0.0004, R²_W.Afr.-Zimb. = 0.30, P = 0.0002). When hybridization intensity within a probe differed by ≥0.2 between a pair of populations, F_ST values were always positive (data not shown). In total, our results indicate that the tiling array hybridization data are powerful in assessing F_ST values based on an allelic frequency difference of sequences.

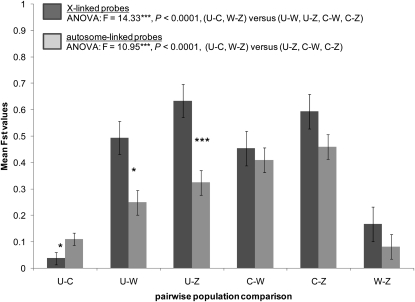
Further, we found that the mean F_ST values were much higher in North American–African comparisons relative to U. S.–Caribbean or to Cameroon–Zimbabwe comparisons, and this holds for both X-linked and autosomal probes (Figure 6; ANOVA: F-values 14.33 and 10.95, respectively; P < 0.0001). These results complement our earlier finding that, among the highly divergent probes, most differentiation occurs between North America and Africa (e.g., see Figure 4). We also found that, for U. S.–African comparisons, F_ST values on the X were significantly higher than on the autosomes (Figure 6). Caribbean–African comparisons show a similar, but not significant, trend. Thus for North American–African comparisons, in addition to having more differentiated probes on the X relative to autosomes (see above), the probes that are differentiated also have relatively higher F_ST values on the X. Interestingly, we observed the opposite pattern for the U. S.–Caribbean comparison with significantly higher mean F_ST values on the autosomes compared to the X (Figure 6). In general, these results are consistent with greater differentiation on the X between North American and African populations, but not within North America (see Table 1).

Figure 6.—

Mean F_ST values (Weir and Cockerham's) among 19 X-linked (solid bars) and 20 autosomal (shaded bars) sequenced probes between six pairwise geographical comparisons: United States–Caribbean (U-C), United States–West Africa Cameroon (U-W), United States–Zimbabwe (U-Z), Caribbean–West Africa Cameroon (C-W), Caribbean–Zimbabwe (C-Z), and West Africa Cameroon–Zimbabwe (W-Z). ANOVAs describe significant differentiation between geographical comparisons for both X and autosomal probes. Asterisks designate significant differentiation (t-test) between X and autosomal probes for each geographical comparison (*P < 0.05, ***P < 0.0001).

Given that F_ST may be influenced by within-population diversity (Charlesworth 1998; Haddrill et al. 2005), we tested the above patterns of genomic differentiation using other measures of sequence divergence, D_xy and D_net, with D_xy being the absolute measure (see materials and methods). Both of these measures once again revealed much greater divergence among North American–African comparisons relative to within each continent (see Table 3 and Table 4). However, we failed to find significantly greater differentiation on the X relative to autosomes for U. S.–African comparisons, but interestingly, did find it for Caribbean–African comparisons (Table 3 and Table 4). These results provide a mixed picture of the role of within-population diversity in contributing to the greater X divergence pattern between North America and Africa.

TABLE 3.

Patterns of the D_xy statistic as an uncorrected measure of absolute sequence divergence between populations

Pairwise comparisons	X-linked	SE	Autosomal	SE	F-value	P-value
United States–Caribbean	0.43	0.06	0.7	0.06	8.86	0.005
United States–West Africa	0.82	0.03	0.87	0.04	0.94	0.33
United States–Zimbabwe	0.93	0.02	0.94	0.02	0.12	0.74
Caribbean–West Africa	0.79	0.05	0.65	0.04	4.47	0.04
Caribbean–Zimbabwe	0.92	0.03	0.71	0.04	13.6	0.0007
West Africa–Zimbabwe	0.46	0.07	0.42	0.07	0.18	0.67

The sample size per location is 21 X-linked loci and 23 autosomal loci. ANOVA: X-linked pairwise—F-value = 14.15, P < 0.0001; autosomal pairwise—F-value = 18.87, P < 0.0001; Measures of D_xy are scaled within each fragment by the maximum pairwise value to compare D_xy at the same scale across fragments.

TABLE 4.

Patterns of the Dnet statistic as a corrected (relative) measure of sequence divergence between populations

Pairwise comparisons	X-linked	SE	Autosomal	SE	χ2	P-value
United States–Caribbean	0.03	0.04	0.07	0.02	4.63	0.03
United States–West Africa	0.18	0.04	0.16	0.02	0.02	0.88
United States–Zimbabwe	0.21	0.04	0.17	0.02	0.1	0.75
Caribbean–West Africa	0.19	0.04	0.11	0.02	4.05	0.044
Caribbean–Zimbabwe	0.22	0.04	0.12	0.02	4.16	0.041
West Africa–Zimbabwe	0.07	0.04	0.05	0.02	0.35	0.55

The D_net values were square rooted for better fit to normal distribution. The sample size per location is 21 X-linked loci and 23 autosomal loci. Kruskal–Wallis test: X-linked—χ² value = 36.6, P < 0.0001; autosomal—χ² value = 30.2, P < 0.0001.

We also tested if there was relationship between F_ST and the local recombination rate of the fragment. However, unlike the positive relationship between recombination rate and number of differentiated probes on the chromosome (see above), the relationship between recombination rate and F_ST values was not significant (see Table S3). Finally, we also found that NJ trees based on hybridization signal intensity differences and based on F_ST values agreed well with each other (see Figure S1; χ² test: P = 0.158). Both distributions showed the majority of probes to have an out-of-Africa phylogenetic signature followed by probes with a cosmopolitan–Zimbabwean signature. These results provide strong support for our observed overall patterns of differentiation (see Figures 3 and 4).

Population-specific statistics of sequenced probes:

We further analyzed the population genetics statistics among our sequenced high-F_ST probes and their surrounding regions. Thus, for each of the 39 sequenced fragments, we estimated the direction and frequency of derived alleles, various measures of genetic and nucleotide diversity (see below), and the sign and value of Tajima's D and Fay and Wu's H statistics (see materials and methods for raw data; Table S2). The Tajima's D and Fay and Wu's H statistics measure a skew in allelic distribution from selective neutrality within a population, with Tajima's D indicating a skew in the frequency of rare alleles and Fay and Wu's H indicating a skew in the frequency of derived alleles (Fay and Wu 2000; Przeworski 2002; Haddrill et al. 2005; Zeng et al. 2006).

We asked if North America and Africa significantly differ on average with respect to the above genetic parameters of high-F_ST fragments. In following previous studies of random sequenced fragments, we analyzed X and autosomal loci separately (Andolfatto 2001; Kauer et al. 2002; Hutter et al. 2007; Singh et al. 2007). In effect, we extended previous X-autosome comparisons to high-F_ST sites and their immediately neighboring regions. For comparison, we also sequenced six random fragments of similar average base-pair length (224 bp) on both X and autosomes for a total of 1345 bp. However, these fragments also showed at least one high-F_ST SNP (see Table S2).

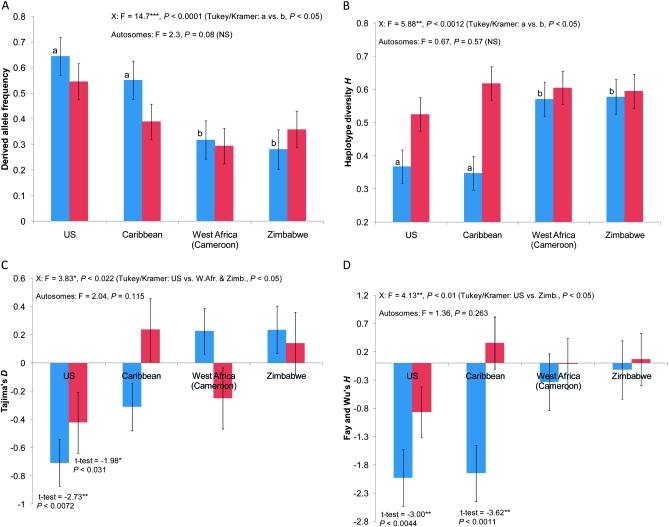
First, we found that the mean frequency of derived alleles within high-F_ST probes is much higher in North America relative to Africa on the X (55–65% vs. 28–30%, respectively; blue bars in Figure 7A). Even though a similar pattern exists on the autosomes, it is not statistically significant (red bars in Figure A). In general, we found only 7 of the total 39 probes with derived alleles having high frequencies in Africa and low frequencies in North America, with all other probes showing the opposite pattern (see Table S2; sign test, two-tailed, P < 0.0001). This result is in agreement with previous findings between European and African populations (Glinka et al. 2003; Sezgin et al. 2004; Haddrill et al. 2005; Hutter et al. 2007) and our random sequenced fragments (see Table S2). This supports the general phenomenon that non-African populations are more derived across the entire genome.

Figure 7.—

Population genetics statistics across U.S., Caribbean, West African (Cameroon), and Zimbabwean localities among 19 X-linked probes (blue bars), and 20 autosomal probes (red bars). (A) Frequency of derived allele within probes (relative to D. simulans/D. sechelia). (B) H (haplotype diversity). (C) Tajima's D and (D) Fay and Wu's H based on sequence of the whole fragment.

Second, the mean haplotype diversity, H_d, of sequenced fragments surrounding our high-F_ST probes is sharply reduced in North America relative to Africa on the X, but not on the autosomes (compare X and autosome bars in Figure 7B). Similar reduction in H_d was found in European populations relative to African populations on the X (Glinka et al. 2003), but was apparently not analyzed among autosomes (Hutter et al. 2007). The reduction in H_d is also found among our random sequenced fragments (see Table S2).

Third, we estimated the nucleotide diversity per site (both θ_W and π) among our fragments. We did not find any significant difference in θ_W and π estimates between high-F_ST fragments vs. random fragments (data not shown). Thus, all comparisons of these estimates between localities are based on pooled fragment data. Our results indicated that the X/autosome ratios of average θ_W and π are lower in North America than in Africa (see Table 5). Thus, the θ_W on the X is significantly lower than on the autosomes only in North America (θ_{US_X} = 0.01; θ_{US_auto} = 0.0159; F-value = 4.06; P-value = 0.05; θ_{Carib._X} = 0.0065; θ_{Carib._auto} = 0.0124; F-value = 10.01; P-value = 0.003). These results are consistent with previous estimates of X/A ratios in non-African vs. African populations (Singh et al. 2007). It is also apparent that all North American samples show higher X/A ratios relative to The Netherlands (see Table 5).

Perhaps most surprisingly, we found that nucleotide diversity in North America is not significantly reduced relative to Africa (see means in data columns 1–2 and 4–5 of Table 5; for X-linked loci comparison, F-value = 1.19; P-value = 0.32; for autosomal loci comparison F-value = 1.96; P-value = 0.13). This seems to be a rather general phenomenon that is not limited to our particular data set. In Table 5, we show that other recent North American surveys of Maine, California, North Carolina, and Florida have discovered similarly high diversity values (Singh et al. 2007; Turner et al. 2008a). It is also apparent that all of these North American diversity estimates are substantially higher on the X and autosomes compared to previous observations in The Netherlands (Table 5).

Consistent with these findings, we also observed that the number of segregating sites per fragment in North America and Africa is not significantly different on either the X or autosomes (for X-linked means: United States: 6.4; Caribbean: 4.4; West Africa: 4.0; Zimbabwe: 3.6; Wilcoxon/Kruskal–Wallis test, P-value = 0.24; for autosomal means: United States, 8.0; Caribbean: 6.26; West Africa: 4.7; Zimbabwe: 4.1; Wilcoxon/Kruskal–Wallis test: P-value = 0.16). Both data sets suggest that North American populations are likely to be less bottlenecked than European populations. These results are consistent with previous findings between the United States and Europe based on microsatellites (Caracristi and Schlötterer 2003).

Fourth, we analyzed Tajima's D and Fay and Wu's H statistics of our high-F_ST fragments. We found that, on average, both D and FWH values were significantly different between U.S. and African populations on the X (Figure 7, C and D). In particular, we found that D and FWH values in the United States were sharply negative. Autosomes exhibited a weaker pattern with only D estimates in the United States being significantly different from zero (see Table S2 for raw data). Similarly, the Caribbean populations also showed negative D and FWH averages among these fragments, but only the FWH mean is significantly different from zero (Figures 7, C and D). Even though our sample size for random fragments is small, it also showed negative values of D and FWH on the X chromosome in both the U. S. and the Caribbean samples (see Table S2).

The combination of strongly negative Tajima's D and Fay and Wu's H among our high-F_ST fragments indicates that there is a significant excess of rare alleles and high frequency-derived alleles in North America, especially in the United States. We performed explicit demographic coalescent simulations to infer the nature of these patterns.

Testing population genetics statistics of high-F_ST fragments in the United States against demographic null models:

Past demographic events may leave a diagnostic signature of deviation from neutrality revealed through Tajima's D and Fay and Wu's H statistics (Fay and Wu 2000; Przeworski 2002; Haddrill et al. 2005; Thornton and Andolfatto 2006; Zeng et al. 2006). Here we determine whether the sharply negative mean D and FWH statistics among our nonrandom set of fragments (high-F_ST probes) in North America can be explained by demographic models. We focus on the U.S. population since it shows the most extreme deviation from zero in D and FWH statistics. African population statistics did not deviate from the SNM (data not shown).

Our model assumed two populations. The ancestral population is assumed to be of constant size. The derived population diverges from its ancestor by a colonization/bottleneck event and then experiences a subsequent population expansion (see Figure 1). The relative effective population sizes of X and autosomes are based on the observed ratios of X to autosome polymorphism among our sequences (see materials and methods). We do not consider simple bottleneck or population expansion models because these generate extremely different combinations of D and FWH statistics from those observed (data not shown). We also do not consider selection in these analyses because our aim is to determine if demography can be rejected as a possible explanation.

In addition to generating the outputs of θ_π, the number of segregating sites, and D and FWH statistics of simulated fragments, our simulations also generated the F_ST statistic of each fragment as a result of divergence between ancestral and derived populations (see materials and methods). Thus our analysis simulated (1) random fragments that best matched the genetic variance statistics of our observed data, k and ss, and (2) sampling nonrandom fragments with high-F_ST values that mimicked the observed F_ST distribution of our sequenced fragments.

Population analysis:

Table 6 shows the general results of our simulations. We explored a range of bottleneck/expansion scenarios, ranging from weak to strong bottlenecks (N_b: 500,000 to 20,000, respectively) and from old to relatively recent bottlenecks (T_b: 16,000 to 8500 years ago, respectively). We also explored short to long durations of bottlenecks (500 to 8500 years, respectively). First, our results clearly indicated that a combination of bottleneck and subsequent population expansion is sufficient in producing nucleotide sequence differentiation (positive F_ST values) across the whole genome (Table 6). However, it was also apparent that weak bottlenecks were unable to generate substantial genome-wide differentiation (i.e., nearly zero average F_ST for the Bot/Exp1 scenario among random fragments). By introducing subsequent gene flow between ancestral and derived populations, not surprisingly, we observed significantly lower F_ST values across the genome (data not shown). Migration was not considered any further.

TABLE 6.

Results of testing D and FWH statistics of U.S. population against a bottleneck/expansion coalescent demographic null model

	X-linked						Autosome-linked
	k	ss	FSTa	D	FWH		k	ss	FSTa	D	FWH
Observed values:	1.66	6.37	0.57	−0.71	−2.03	P-valueb	2.11	8.45	0.29	−0.42	−0.87	P-valueb
Standard neutral	1.40	6.73	NA	−0.06	0.00	<0.0001	1.79	8.63	NA	−0.06	0.00	0.001
Bot/Exp1_weak_and_old bot (random)	1.54	6.64	0.03	0.20	−0.02	<0.0001	1.98	8.73	0.03	0.16	−0.06	0.001
Bot/Exp1_weak_and_old bot (bias in FST)	1.56	6.75	0.23	0.23	0.00	0.02	2.02	8.91	0.15	0.18	−0.13	0.05
Bot/Exp2_weak_and_old bot (random)	1.69	6.24	0.16	0.36	−0.15	<0.0001	2.10	8.70	0.03	0.34	−0.14	<0.0001
Bot/Exp2_weak_and_old bot (bias in FST)	1.83	6.43	0.29	0.20	−0.28	<0.0001	2.14	8.66	0.18	0.40	−0.17	0.02
Bot/Exp3_medium_and_old bot (random)	1.69	6.24	0.16	0.42	−1.00	<0.0001	2.23	8.26	0.17	0.64	−1.06	0.0004
Bot/Exp3_medium_and_old bot (bias in FST)	1.83	6.43	0.52	0.51	−0.87	<0.0001	2.20	8.16	0.29	0.60	−1.10	0.001
Bot/Exp4_medium_and_old_to_recent_bot (random)	1.53	6.40	0.24	−0.23	−1.13	0.01	2.15	8.30	0.20	0.22	−1.59	0.02
Bot/Exp4_medium_and_old_to_recent_bot (bias in FST)	1.59	6.60	0.54	−0.21	−1.05	0.02	2.02	8.84	0.29	0.25	−1.65	0.03
Bot/Exp5_medium_and_old_to_more_recent_bot (random)	1.55	6.86	0.27	−0.53	−1.17	0.051NS	2.20	8.07	0.23	0.07	−1.73	0.076NS
Bot/Exp5_medium_and_old_to_more_recent_bot (bias in FST)	1.82	7.44	0.54	−0.47	−1.13	0.09NS	2.21	8.06	0.29	0.03	−1.74	0.13NS
Bot/Exp6_stronger_and_old_to_more_recent_bot (random)	1.25	6.18	0.28	−0.77	−0.89	0.06NS	2.08	8.11	0.25	−0.25	−1.66	0.24NS
Bot/Exp6_stronger_and_old_to_more_recent_bot (bias in FST)	1.41	6.48	0.54	−0.71	−0.94	0.05NS	2.12	8.09	0.29	−0.20	−1.59	0.23NS
Bot/Exp7_medium_and_recent_bot (random)	1.77	6.08	0.18	0.78	−0.78	<0.0001	2.48	8.29	0.08	1.00	−0.82	<0.0001
Bot/Exp7_medium_and_recent_bot (bias in FST)	1.90	6.50	0.53	0.65	−0.82	<0.0001	2.42	8.16	0.26	0.98	−0.76	<0.0001

“k” is the average number of pairwise differences between haplotypes [labeled “pi” in Hudson's (2002) ms code document]. The ss is the average number of segregating sites.

All simulations sampled 136 total chromosomes, with 67 chromosomes from the ancestral population and 69 from the derived population. Specific parameters of the models are the following: SNM_X—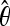 = 1.4; SNM_A— 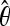= 1.8. For X-linked loci: N_{e Africa} = 2,500,000; N_{e US} = 3,164,557; For autosomal loci: N_{e Africa} = 3,417,722; N_{e US} = 5,031,646. The 2.5 million value is based on previous estimates for African X-linked loci (Thornton and Andolfatto 2006), while all other estimates of effective population size are based on the observed relative θ_W values in Table 5. All simulations assumed that N_bottleneck retains the ancestral Africa X/A ratio of 0.731. This assumes that the ancestral X/A ratio was conserved until a population expansion in United States. Bot/Exp1: T_b = 16,000, T_r = 15,000, N_{b_X} = 500,000, N_{b_A} = 683,544; Bot/Exp2: T_b = 16,000, T_r = 15,000, N_{b_X} = 250,000, N_{b_A} = 341,772; Bot/Exp3: T_b = 16,000, T_r = 15,000, N_{b_X} = 25,000, N_{b_A} = 34,177; Bot/Exp4: T_b = 16,000, T_r = 10,000, N_{b_X} = 25,000, N_{b_A} = 34,177; Bot/Exp5: T_b = 15,000, T_r = 6,500, N_{b_X} = 24,000, N_{b_A} = 32,810; Bot/Exp6: T_b = 15,000, T_r = 6,500, N_{b_X} = 20,000, N_{b_A} = 27,342; Bot/Exp7: T_b = 7500, T_r = 6500, N_{b_X} = 24,000, N_{b_A} = 32,810. Note that T_b and T_r are presented as generations and are not shown with respect to N_o (see Table S4 for exact command lines).

^aObserved F_ST is based on the average F_ST in U. S.–West Africa and U. S.–Zimbabwe comparisons among fragments.

^bP-value is based on the probability of having both D and FWH statistics less than the observed within the same sample. Number of replicates in simulations: for random fragment analysis, we simulated 5000 sets of fragments and determined their means; for biased fragments in high F_ST, we simulated 100 sets of fragments and determined their means. “NS” indicates that the observed combination of D and FWH statistics among our fragments is not significantly different from the simulated data.

In general, the results showed that weak bottlenecks (N_b: 500,000) alone were inconsistent with our observed data because they generated near zero or even positive values of D and FWH statistics. It is also clear that a given historical scenario either is unable to explain both X- and autosomal-linked data or is able to explain both simultaneously (Table 6). Further, simulated fragments biased in F_ST did not differ in their statistics from genome-wide simulated fragments (Table 6). Therefore, the above statistics are relatively insensitive to local differentiation values.

We found that only two similar demographic scenarios, Bot/Exp5 and Bot/Exp6, were broadly consistent with our observed negative values of D and FWH statistics and produced a comparable level of F_ST differentiation. In these models, the bottleneck was of roughly medium strength (∼20,000–24,000 N_e), started relatively long ago (16,000 years ago), and had a long duration with a recovery starting relatively recently (6500 years ago). Much stronger bottlenecks (<15,000 N_e) were unable to match the observed θ_π and number of segregating sites in our data set and were thus not considered any further. Very recent bottleneck/expansion scenarios (<6500 years ago) produced positive D and negative FWH values, akin to a simple bottleneck scenario (data not shown). Although the true demographic history of U.S. populations is no doubt more complex than is modeled here and may likely involve selection (e.g., Turner et al. 2008a) and some migration, these results demonstrate that a fairly simple demographic model is able to explain the gross features of our observed data.

Single-fragment analysis:

In addition to testing average patterns of deviations from selective neutrality among our fragments, we also asked whether there are any X-linked or autosomal fragments that individually deviated from various demographic models. Table S2 shows that many fragments on both the X and the autosomes had significant D and FWH statistics against the SNM. However, given that the SNM is clearly violated genome-wide in our U. S. population, it is not appropriate to use this model as the null (e.g., Thornton and Andolfatto 2006). Thus, we asked whether any of the sequenced fragments significantly deviated in their D and FWH statistics from the most acceptable demographic null model (Bot/Exp6). After correcting for multiple testing using the Benjamini and Yekutieli (2001) FDR method, we found four fragments with significant D and FWH deviations and one more fragment with a suggestive deviation from Bot/Exp6 expectations (see boldface and underlined P-values in Table S2).

These fragments included a coding region of the gene CG7728 on 3L, giving rise to a synonymous substitution and four X-linked fragments, an intergenic region (2305.468, ranked the fourth most differentiated probe in our genomic survey), and three coding regions of the genes CG2898, CG32635, and Tak1, all giving rise to nonsynonymous amino acid substitutions (see Table S2). With the exception of a fragment at CG7728, all other fragments had the derived allele being nearly fixed in North America and the ancestral allele nearly fixed in Africa. Note that many of the same fragments also showed similarly negative D and FWH values in the Caribbean, providing further support for the biological reality of our observed deviations (Table S2). These results indicate that a few exceptional fragments likely exist in our data set even when P-values are based on the most acceptable bottleneck-expansion demographic model. These fragments are excellent candidates for further selective sweep analyses, which are beyond the scope of the present study.

DISCUSSION

In this study, we used DNA tiling arrays to identify highly differentiated sites (probes) between North American (United States and Caribbean) and African (Cameroon and Zimbabwe) populations across 63% of the D. melanogaster genome. While previous studies detailed population genetics patterns of arbitrarily chosen sequenced fragments (e.g., Andolfatto 2001; Glinka et al. 2003; Haddrill et al. 2005; Ometto et al. 2005; Hutter et al. 2007; Singh et al. 2007), very little was known about overall patterns of differentiation between African and non-African genomes or about the statistical properties of highly differentiated sites and the processes that have shaped this differentiation. Below we discuss how our data help clarify our understanding of the evolution of X-linked and autosomal differentiation in D. melanogaster.

General patterns of genomic differentiation:

First, using tiling array probes, we found that most differentiation in D. melanogaster at the whole-genome level is associated with divergence between populations living in Africa vs. outside of Africa, with all other geographic differences being less important. This is reflected in both the relative number of highly differentiated sites in the genome and the relatively high F_ST values in each of the differentiated probes. In general, these findings are inconsistent with the notion that most genomic differentiation is between cosmopolitan and Zimbabwean behavioral races (e.g., Wu et al. 1995; Hollocher et al. 1997). Our results suggest that factors associated with reproductive isolation between cosmopolitan and Zimbabwean populations do not follow overall patterns of genomic differentiation in this species. Haddrill et al. (2005) obtained similar results on the basis of 10 loci on the X chromosome, supporting our whole-genome observations. This adds to the growing list of studies revealing that the evolution of reproductive isolation is often disassociated from general patterns of genomic differentiation among incipient species or races (e.g., Ford and Aquadro 1996).

We also found that as much as 71% of all differentiated probes between African and North American populations were situated on the X chromosome, which is highly overrepresented relative to random expectations of 18%. In addition to more probes being differentiated between North America and Africa on the X, sequencing revealed that these probes also have on average higher F_ST values compared to probes on the autosomes. Although many studies have found lower nucleotide diversity among various sequences on the X relative to autosomes in non-African populations (e.g., Andolfatto 2001; Kauer et al. 2002, 2003; Hutter et al. 2007; Singh et al. 2007), greater differentiation on the X compared to autosomes is primarily documented from microsatellite data in D. melanogaster (Kauer et al. 2003; also see Ford and Aquadro 1996 for similar results in D. athabasca).

F_ST values may be a by-product of how F_ST is calculated when populations differ in their relative genetic diversity rather than due to absolute sequence divergence (e.g., Charlesworth 1998; Haddrill et al. 2005; Schofl et al. 2005). This seems to be the case for microsatellite data. The greater F_ST values of microsatellites on the X relative to autosomes are accompanied by substantially reduced variance on the X in Europe compared to Africa (e.g., Kauer et al. 2002, 2003). Our sequence results provide a mixed picture with respect to this question.

On the one hand, absolute measures of divergence such as D_xy, as well as the relative measure D_net, are not significantly greater on the X relative to autosomes in U.S.–African comparisons. Thus, at least for the United States, the reduced haplotype diversity on the X does play a major role in increasing F_ST values that is not reflected in absolute nucleotide divergence. In retrospect, this may not be too surprising. Any process that drives derived sequences to high frequency will necessarily reduce the ancestral haplotype diversity and lead to high-F_ST values.

On the other hand, D_xy and D_net values are significantly greater on the X relative to autosomes in Caribbean–African comparisons. Therefore, there does seem to be evidence for greater X divergence in some North American–African comparisons beyond the difference in relative genetic diversity. We also find that this greater X divergence is a particularly out-of-Africa phenomenon because the very opposite pattern (i.e., divergence greater on autosomes) is observed in the U. S.–Caribbean comparison. Greater X divergence is also not observed among eastern U.S. populations (see Turner et al. 2008a). Below we discuss what processes may have led to these genomic patterns of differentiation between North American and African populations.

Patterns of sequence variation of highly differentiated regions:

To gain insight into the population genetics properties of our highly differentiated probes, we sequenced candidate probes and their surrounding regions and random fragments of similar length. By analyzing X and autosomal fragments separately, we found that only X-linked probes exhibited significant differences in various population genetics statistics between North America and Africa. These included significantly higher frequencies of derived alleles, lower haplotype diversity, and lower negative Tajima's D and Fay and Wu's H statistics in North America compared to Africa. The high frequency of derived alleles and the reduced haplotype diversity is consistent with previous analyses of X-linked fragments in a Netherlands sample and with our random fragments, implying that these patterns are a general feature of non-African populations (Glinka et al. 2003).

However, nucleotide diversity in North America is consistently greater than in Europe and may even be comparable to African estimates. Even though this seems rather surprising in light of analyses based on European samples, we have shown that our estimates are consistent with other recent surveys of North American populations among both random and highly differentiated loci (Singh et al. 2007; Turner et al. 2008a). This interesting finding implies that U.S. populations maybe less bottlenecked than European populations. The elevated nucleotide diversity in North America relative to Europe may also be due to the possible secondary infusion of African alleles, perhaps as a result of the trans-Atlantic slave trade, into the Caribbean (David and Capy 1988; Caracristi and Schlötterer 2003; Yukilevich and True 2008b). In this context, it is interesting that Caribbean populations tend to exhibit the most reduction in nucleotide diversity in North America, approaching values seen in Europe. However, this may be due to secondary bottlenecks in the Caribbean. Such a scenario is consistent with anecdotal evidence based on field collections, suggesting very low population densities in these Caribbean islands (R. Yukilevich, unpublished data). This hypothesis requires further investigation.

In addition, Singh et al. (2007) have shown that the large difference in the ratio of X to autosome nucleotide diversity that was observed between European and African populations (e.g., Hutter et al. 2007) does not necessarily hold in North America. Our data also show that the X/A ratio in nucleotide diversity is substantially higher in North America relative to Europe. Taken together, these results clearly indicate that North American and European populations contain real biological differences in several important genetic statistics. Therefore, they should be studied independently in subsequent analyses.

Coalescent simulation models of highly differentiated fragments:

The strongly negative values of Tajima's D and Fay and Wu's H statistics among our differentiated regions indicated that the sequences surrounding high-F_ST probes have an excess of rare alleles and an excess of high frequency-derived alleles, respectively. This is especially the case in U.S. populations, but is also seen in the Caribbean. We have also shown that these statistics are significantly more negative among X-linked loci than among autosomal loci. It has been argued that the combination of strongly negative values of Tajima's D and Fay and Wu's H is indicative of selective sweeps (Fay and Wu 2000; Zeng et al. 2006). Such a result would be consistent with theoretical arguments that selection of beneficial alleles should be more efficient on the X relative to autosomes (i.e., “faster-X evolution”; see review by Vicoso and Charlesworth 2006). Indeed, African populations often exhibit an elevated X/A ratio of polymorphism, which has been recently shown to favor selection on the X under a wide range of mutational dominances (Vicoso and Charlesworth 2009). However, these patterns may also result from purely demographic processes because a bottleneck may initially lead to the loss of rare alleles and to an excess of high frequency-derived alleles while a subsequent expansion may replenish rare alleles (e.g., Haddrill et al. 2005).

Our simulation results have shown that the observed patterns of high-F_ST fragments are largely compatible with a demographic process in which a derived population splits off from its ancestor and experiences a bottleneck and a subsequent population expansion. Such a scenario can generate a similar level of F_ST values as well as strongly negative Tajima's D and Fay and Wu's H statistics within a derived population. Similarly, the greater deviation from selective neutrality on the X relative to autosomes is consistent with the greater reduction in effective population size of the X in North America. Since females carry two-thirds of the X chromosomes in a population, but only one-half of the autosomes, a relative reduction in the female population size during or after the bottleneck could have been responsible for the shift in the observed X/A relative diversity and differentiation patterns (e.g., Charlesworth 2001; Wall et al. 2002; Hutter et al. 2007).

The above results imply that genome-wide differentiation between North America and Africa may have been primarily driven by the sorting of African genetic variation into North America during its colonization (see also Orr and Betancourt 2001; Schofl and Schlotterer 2004). This can also explain why we observed recombination rate to be significantly associated with divergence across all chromosomes. In African D. melanogaster, regions of high recombination maintain greater sequence variation compared to regions of low recombination (e.g., Aguade et al. 1989; Begun and Aquadro 1993, 1995; Langley et al. 1993). Thus, those regions of greater ancestral genetic variation would have been able to diverge more easily due to bottlenecks and expansions in derived populations (also see Kulathinal et al. 2008). This process alone can generate the observed relationship between recombination rate and divergence without selection. While we accept a demographic explanation for our observed data, we emphasize that, because we did not simulate models based on selection alone or based on demography plus selection, alternative scenarios involving selection cannot be completely ruled out. Nevertheless, it is clear that our observed deviations from selective neutrality are not striking enough to claim that selection has been largely responsible for genome-wide high-F_ST sites.

Our analysis has also shown that not all bottleneck/expansion scenarios are compatible with our observed data. Only a few demographic scenarios were largely consistent with both X-linked and autosomal data in U.S. populations. These scenarios required a medium-strength bottleneck (∼20,000–23,000 N_e) that started ∼16,000 years ago and continued to ∼6500 years ago at which point the population experienced an expansion. Interestingly, anecdotal historical evidence suggests that North American D. melanogaster were colonized from Europe and subsequently rapidly expanded only ∼130 years ago (Keller 2007). However, because such a scenario produces a deficit in rare alleles, akin to a standard bottleneck model, simulations clearly rejected this as a viable possibility (data not shown). It is also peculiar that our simulations are largely consistent with demographic results of European populations in terms of the strength of the bottleneck and the general timing of population expansion (Baudry et al. 2004; Thornton and Andolfatto 2006). Both pieces of evidence suggest that these features of U.S. population genetics statistics likely stem from its ancestral European demographic history. However, as already discussed above, other statistical differences exist between U.S. and European populations.

In addition to testing broad genomic patterns, we also tested each fragment against the SNM as well as against the most acceptable demographic null model. While many individual fragments significantly deviated from SNM, only four loci showed significant deviations from the acceptable demographic model and one had a suggestive deviation after correcting for multiple testing. We suggest that these fragments are excellent candidates for further selective sweep analyses. Our study highlights the need to use appropriate demographic null models to identify candidate loci for possible selective sweeps since the SNM is strongly rejected in this case (also see Thornton and Andolfatto 2006).

Our overall findings are broadly consistent with the view that signatures of selection within the genome may be difficult to identify when a species has undergone recent bottlenecks and population expansions (e.g., Hamblin et al. 2006; Thornton and Andolfatto 2006; Macpherson et al. 2008). We emphasize that the major reason for this is because most of the genome-wide differentiation appears to have been driven by demographic processes between such populations as North American and African D. melanogaster. The flip side of this argument, however, is that we may be able to identify selection more readily between other more appropriate populations that share a similar demographic history (e.g., Turner et al. 2008a). In D. melanogaster, an excellent case may be between U.S. and Caribbean populations since these resemble the cosmopolitan–African phenotypic and behavioral differentiation, but share an out-of-Africa demographic history (Yukilevich and True 2008a,b). If the Caribbean populations are truly of more recent African ancestry, then the admixture between U.S. and Caribbean flies should have shuffled the genome except for loci experiencing divergent selection (i.e., “a genomic island” view of divergence). This intriguing possibility requires further testing.

In conclusion, this study contributes to the recent growing use of modern genomic tools to understand the broad patterns of genomic differentiation between diverging taxa.