Inferring Bacterial Genome Flux While Considering Truncated Genes

Abstract

Bacterial gene content variation during the course of evolution has been widely acknowledged and its pattern has been actively modeled in recent years. Gene truncation or gene pseudogenization also plays an important role in shaping bacterial genome content. Truncated genes could also arise from small-scale lateral gene transfer events. Unfortunately, the information of truncated genes has not been considered in any existing mathematical models on gene content variation. In this study, we developed a model to incorporate truncated genes. Maximum-likelihood estimates (MLEs) of the new model reveal fast rates of gene insertions/deletions on recent branches, suggesting a fast turnover of many recently transferred genes. The estimates also suggest that many truncated genes are in the process of being eliminated from the genome. Furthermore, we demonstrate that the ignorance of truncated genes in the estimation does not lead to a systematic bias but rather has a more complicated effect. Analysis using the new model not only provides more accurate estimates on gene gains/losses (or insertions/deletions), but also reduces any concern of a systematic bias from applying simplified models to bacterial genome evolution. Although not a primary purpose, the model incorporating truncated genes could be potentially used for phylogeny reconstruction using gene family content.

GENE content variation as a key feature of bacterial genome evolution has been well recognized (Garcia-Vallvé et al. 2000; Ochman and Jones 2000; Snel et al. 2002; Welch et al. 2002; Kunin and Ouzounis 2003; Fraser-Liggett 2005; Tettelin et al. 2005) and gained increasing attention in recent years. Various methods have been employed to study the variation of gene content in the form of gene insertions/deletions (or gene gains/losses); there are studies of population dynamics (Nielsen and Townsend 2004), birth-and-death evolutionary models (Berg and Kurland 2002; Novozhilov et al. 2005), phylogeny-dependent studies including parsimony methods (Mirkin et al. 2003; Daubin et al. 2003a,b; Hao and Golding 2004), and maximum-likelihood methods (Hao and Golding 2006, 2008b; Cohen et al. 2008; Cohen and Pupko 2010; Spencer and Sangaralingam 2009). The pattern of gene presence/absence also contains phylogenetic signals (Fitz-Gibbon and House 1999; Snel et al. 1999; Tekaia et al. 1999) and has been used for phylogenetic reconstruction (Dutilh et al. 2004; Gu and Zhang 2004; Huson and Steel 2004; Zhang and Gu 2004; Spencer et al. 2007a,b). All these studies make use of the binary information of gene presence or absence and neglect the existence of gene segments or truncated genes.

Bacterial genomes are known to harbor pseudogenes. An intracellular species Mycobacterium leprae is an extreme case for both the proportion and the number of pseudogenes: estimated as 40% of the 3.2-Mb genome and 1116 genes (Cole et al. 2001). In free-living bacteria, pseudogenes can make up to 8% of the annotated genes in the genome (Lerat and Ochman 2004). Many pseudogenes result from the degradation of native functional genes (Cole et al. 2001; Mira et al. 2001). Pseudogenes could also result from the degradation of transferred genes and might even be acquired directly via lateral gene transfer. For instance, in plant mitochondrial genomes, which have an α-proteobacterial ancestry, most, if not all, of the laterally transferred genes are pseudogenes (Richardson and Palmer 2007). Furthermore, evidence has been documented that gene transfer could take place at the subgenic level in a wide range of organisms, e.g., among bacteria (Miller et al. 2005; Choi and Kim 2007; Chan et al. 2009), between ancient duplicates in archaea (Archibald and Roger 2002), between different organelles (Hao and Palmer 2009; Hao 2010), and between eukaryotes (Keeling and Palmer 2001). A large fraction of pseudogenes have been shown to arise from failed lateral transfer events (Liu et al. 2004) and most of them are transient in bacterial genomes (Lerat and Ochman 2005). Zhaxybayeva et al. (2007) reported that genomes with truncated homologs might erroneously lead to false inferences of “gene gain” rather than multiple instances of “gene loss.” This raises the question of how a false diagnosis of gene absence affects the estimation of insertion/deletion rates. Recently, we showed that the effect of a false diagnosis of gene absence on estimation of insertion/deletion rates is not systematic, but rather more complicated (Hao and Golding 2008a). To further address the problem, a study incorporating the information of truncated genes is highly desirable. This will not only yield more accurate estimates of the rates of gene insertions/deletions, but also provide a quantitative view of the effect of truncated genes on rate estimation, which has been understudied in bacterial genome evolution.

In this study, we developed a model that considers the information of truncated genes and makes use of a parameter-rich time-reversible rate matrix. Rate variation among genes is allowed in the model by incorporating a discrete Γ-distribution. We also allow rates to vary on different parts of the phylogeny (external branches vs. internal branches). Consistent with previous studies, the rates of gene insertions/deletions are comparable to or larger than the rates of nucleotide substitution and the rates of gene insertions/deletions are further inflated in closely related groups and on external branches, suggesting high rates of gene turnover of recently transferred genes. The results from the new model also suggest that many recently truncated genes are in the process of being rapidly deleted from the genome. Some other interesting estimates in the model are also presented and discussed. One implication of the study, though not primary, is that the state of truncated genes could serve as an additional phylogenetic character for phylogenetic reconstruction using gene family content.

METHODS

Phylogenetic analysis and genome comparison:

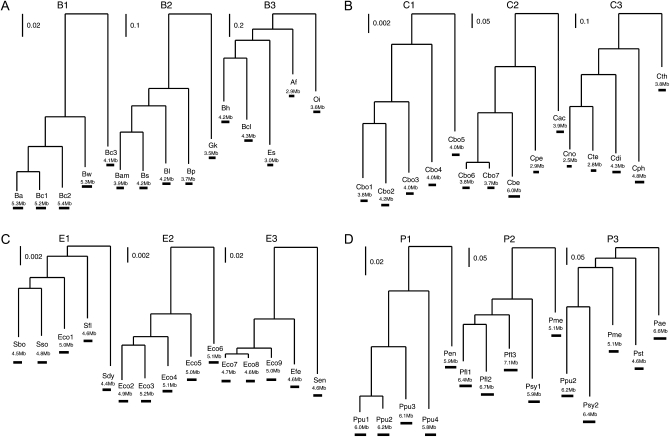
Four bacterial groups with an abundance of completely sequenced congeneric species/strains and relatively large genome sizes were selected (listed in Table 1 with outgroup information shown in supporting information, Table S1). The four groups are Bacillaceae, Clostridium, Escherichia/Shigella (Escherichia, for simplicity), and Pseudomonas. Within each group, analyses were conducted separately in three clades with different levels of divergence (Figure 1). A large number of universally present nonduplicated genes from each clade were extracted and examined to obtain a robust phylogenetic tree. The numbers of concatenated genes (and characters) are 325 genes (335,380 characters) for clades B1 and B2; 329 genes (362,583 characters) for clade B3; 108 genes (130,531 characters) for clades C1, C2, and C3; 755 genes (809,248 characters) for clades E1, E2, and E3; and 434 genes (516,571 characters) for clades P1, P2, and P3. Alignment of each gene was generated individually using MUSCLE (Edgar 2004) followed by a concatenation of individual alignments into a single giant alignment for each clade. A maximum-likelihood tree was generated for each clade on the concatenated sequences using the PHYLIP package (Felsenstein 1989) version 3.67 and the rate variation parameter α in a Γ-distribution was estimated using the PUZZLE program (Strimmer and von Haeseler 1996). The sum of branch lengths for each tree was used as an indicator for the divergence of the clade.

TABLE 1.

Strain information from a variety of phylogenetic groups

Clade	Tree length	Species/strain name	Abbreviation	Accession
B1	0.366	Bacillus anthracis str. Ames	Ba	NC_003997
		B. cereus ATCC 10987	Bc1	NC_003909
		B. cereus ATCC 14579	Bc2	NC_004722
		B. weihenstephanensis	Bw	NC_010184
		B. cereus subsp. cytotoxis	Bc3	NC_009674
B2	1.981	B. amyloliquefaciens	Bam	NC_009725
		B. subtilis	Bs	NC_000964
		B. licheniformis ATCC 14580	Bl	NC_006322
		B. pumilus	Bp	NC_009848
		Geobacillus kaustophilus	Gk	NC_006510
B3	3.274	B. halodurans	Bh	NC_002570
		B. clausii	Bcl	NC_006582
		Oceanobacillus iheyensis	Oi	NC_004193
		Exiguobacterium sibiricum	Es	NC_010556
		Anoxybacillus flavithermus	Af	NC_011567
C1	0.055	Clostridium botulinum A str. Hall	Cbo1	NC_009698
		C. botulinum A2 str. Kyoto	Cbo2	NC_012563
		C. botulinum B1 str. Okra	Cbo3	NC_010516
		C. botulinum Ba4 str. 657	Cbo4	NC_012658
		C. botulinum A3 str. Loch Maree	Cbo5	NC_010520
C2	1.415	C. botulinum B str. Eklund 17B	Cbo6	NC_010674
		C. botulinum E3 str. Alaska E43	Cbo7	NC_010723
		C. beijerinckii NCIMB 8052	Cbe	NC_009617
		C. perfringens SM101	Cpe	NC_008262
		C. acetobutylicum ATCC 824	Cac	NC_003030
C3	2.958	C. novyi NT	Cno	NC_008593
		C. tetani E88	Cte	NC_004557
		C. difficile 630	Cdi	NC_009089
		C. phytofermentans ISDg	Cph	NC_010001
		C. thermocellum ATCC 27405	Cth	NC_009012
E1	0.039	Shigella boydii Sb227	Sbo	NC_007613
		S. sonnei Ss046	Sso	NC_007384
		Escherichia coli E24377A	Eco1	NC_009801
		S. flexneri 5 str. 8401	Sfl	NC_008258
		S. dysenteriae Sd197	Sdy	NC_007606
E2	0.044	E. coli 536	Eco2	NC_008253
		E. coli ED1a	Eco3	NC_011745
		E. coli APEC 01	Eco4	NC_008563
		E. coli O127:H6 str. E2348/69	Eco5	NC_011601
		E. coli IAI39	Eco6	NC_011750
E3	0.387	E. coli IAI1	Eco7	NC_011741
		E. coli HS	Eco8	NC_009800
		E. coli S88	Eco9	NC_011742
		E. fergusonii ATCC 35469	Efe	NC_011740
		Salmonella enterica subsp. arizonae serovar 62:z4,z23	Sen	NC_010067
P1	0.312	Pseudomonas putida F1	Ppu1	NC_009512
		P. putida KT2440	Ppu2	NC_002947
		P. putida GB-1	Ppu3	NC_010322
		P. putida W619	Ppu4	NC_010501
		P. entomophila L48	Pen	NC_008027
P2	0.885	P. fluorescens Pf0-1	Pfl1	NC_007492
		P. fluorescens SBW25	Pfl2	NC_012660
		P. fluorescens Pf-5	Pfl3	NC_004129
		P. syringae pv. phaseolicola 1448A	Psy1	NC_005773
		P. mendocina ymp	Pme	NC_009439
P3	1.118	P. putida KT2440	Ppu2	NC_002947
		P. syringae pv. tomato str. DC3000	Psy2	NC_004578
		P. mendocina ymp	Pme	NC_009439
		P. stutzeri A1501	Pst	NC_009434
		P. aeruginosa PA7	Pae	NC_009656

Figure 1.—

(A–D) Phylogenies with varied levels of divergence. Clade names and strain abbreviations are as in Table 1. Horizontal scale bar indicates genome size.

In addition to the two states, “p” for gene presence and “a” for gene absence, a new state “f” for fragment (truncated genes) was introduced. The method to identify members of a gene family was modified from Hao and Golding (2004), and all paralogs in each genome were clustered as a single gene family and only one member was retained for further analysis. First, annotated protein sequences were clustered into gene families following a criterion of E-value ≤10⁻²⁰ and match length ≥85% in a BLASTP search (Altschul et al. 1997). Gene families retained for further analysis were required to have >100 amino acids in at least one gene member, since similarity searches using BLAST have low power to detect homologs in short sequences (Altschul et al. 1997). Genes clustered in gene families were considered as gene presence or p. Second, we further analyzed the genomes that do not have annotated protein sequences for each gene family by conducting a TBLASTN search (Altschul et al. 1997) using an annotated protein sequence as the query sequence. When a gene family has more than one annotated member, the protein sequence with the median length (the shorter of the two median genes in the case of an even number of genes) of the family was chosen as the query sequence. When no annotated protein sequence for a gene family was found in a genome, there are three possible conditions of the gene: the gene could be present (but not annotated), truncated (short in length), or genuinely absent: (1) gene presence (p) was inferred, if the BLAST hit has an E-value ≤10⁻²⁰ and match length ≥85%; (2) gene truncation (f) was inferred, if the BLAST hit has an E-value ≤10⁻²⁰ but match length <85%; and (3) hits that have an E-value >10⁻²⁰ were considered as gene absence (a). The observed patterns of gene presence/absence/truncation are shown in Table S2, Table S3, Table S4, and Table S5. To access the robustness of the analysis, a different criterion of E-value ≤10⁻¹⁰ and match length ≥70% in both BLASTP and TBLASTN searches was used in gene family identification (Table S6, Table S7, Table S8, and Table S9 and Figure 2).

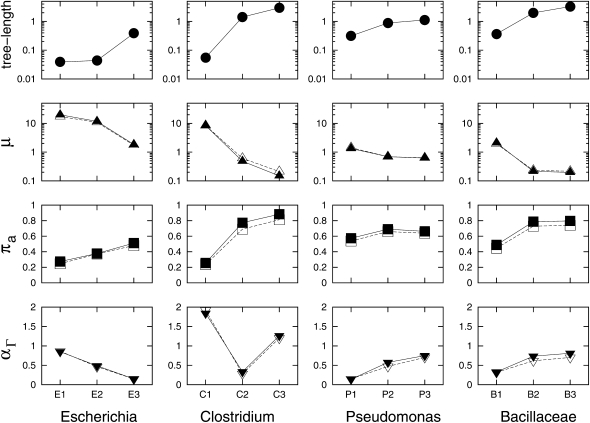
Figure 2.—

Association between estimated parameters and phylogenetic divergence in each group. Three maximum-likelihood estimates (MLEs), μ, π_a, and α_Γ, are estimated under the M₀ + π model using different cutoff thresholds in BLASTP/TBLASTN searches. Solid symbols represent MLEs using a criterion of E-value ≤10⁻²⁰ and match length ≥85%, while open symbols represent MLEs using a criterion of E-value ≤10⁻¹⁰ and match length ≥70%. The four groups are sorted from the least diverse group (Escherichia) on the left to the most diverse group (Bacillaceae) on the right. Although shown along with three estimates, tree length is not an estimate from the gene insertion/deletion model. Indeed, it is the sum of branch lengths based on nucleotide substitution and used as an indicator for the degree of divergence in the clade.

As in Hao and Golding (2004), the “single link” method (Friedman and Hughes 2003) was employed to define gene families (e.g., if A and B are in a family and B and C are in a family, then A, B, and C are in a family). By doing this, there is an increased risk of a truncated gene being mistakenly identified as “present” (Hao and Golding 2008a). The risk would become higher, when more genomes are compared. To avoid such a problem as much as possible, we limit the number of taxa in each clade to five, which also makes the computation less demanding.

The mathematical model:

The transitions among p's, f's, and a's are defined by a 3 × 3 instantaneous rate matrix Q with stationary probabilities (π_a, π_f, π_p). Here π_a + π_f + π_p = 1, and the matrix Q is reversible,

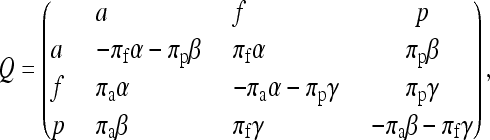(1)

where α, β, and γ are the rate ratios between the state pairs af, ap, and fp, respectively. They are also known as the exchangeability terms. For instance, ∀x, y ∈ {a, f, p}, x ≠ y, Q(x, y) is the rate at which state x changes to state y, and all entries satisfy π_xQ(x, y) = π_yQ(y, x). When gene truncation is not considered, there is no f state and the matrix would be reduced to

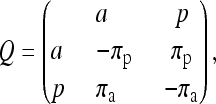(2)

which has been used in previous studies (Cohen et al. 2008; Spencer and Sangaralingam 2009; Cohen and Pupko 2010). When π_a = π_p = 0.5, the matrix entries Q(a, p) and Q(p, a) = 1 (see Equation 3 below for detail), or

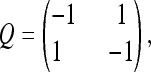and the model is equivalent to that used in Hao and Golding (2006, 2008b) and Cohen et al. (2008). This model is labeled M₀₀ in Table 3. To reduce the number of parameters to be optimized, the α-parameter in the Q_3×3 matrix was fixed to be 1. It is a standard practice to allow only calibrated rate matrices; i.e., Q satisfies

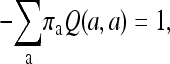(3)

so that a rate parameter (shown as μ below) is the average number of transition events per gene family per evolutionary time. The transition probability matrix is

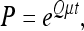(4)

where t is the branch length based on nucleotide sequences, and μ is a rate parameter.

TABLE 3.

Maximum log-likelihood comparison of different evolutionary models considering only gene presence/absence (p/a)

			Bacillaceae			Clostridium			Escherichia			Pseudomonas
Scenario	Model	Parameter	B1	B2	B3	C1	C2	C3	E1	E2	E3	P1	P2	P3
f → a	M00a	μ	1.886	0.463	0.388	5.459	1.061	0.441	12.125	8.250	1.723	1.450	1.038	0.870
		ln L	−13,682	−15,268	−21,207	−6,491	−19,623	−23,554	−10,428	−10,080	−12,546	−14,607	−24,708	−26,670
	M0a	μ	2.474	0.483	0.381	7.611	1.041	0.444	17.150	11.306	2.495	1.736	1.084	0.884
		ln L	−13,970	−15,487	−20,743	−6,444	−19,359	−22,168	−10,457	−10,195	−12,766	−14,961	−25,029	−26,803
	M0 + π	μ	1.842	0.185	0.173	7.514	0.440	0.093	16.075	9.785	1.570	1.138	0.577	0.542
		πa	0.510	0.816	0.831	0.286	0.807	0.933	0.345	0.407	0.534	0.616	0.745	0.725
		ln L	−13,681	−14,866	−20,017	−6,404	−18,705	−21,012	−10,362	−10,062	−12,543	−14,572	−24,253	−26,154
		Δ ln Lb	289	621	726	40	654	1156	95	133	223	389	776	649
f → p	M00	μ	1.490	0.393	0.356	4.593	0.912	0.416	8.072	6.969	1.405	1.289	0.894	0.741
		ln L	−12,470	−14,472	−20,761	−5,902	−19,171	−23,250	−8,578	−9,293	−11,857	−13,785	−23,565	−25,408
	M0	μ	2.045	0.419	0.337	6.747	0.873	0.377	12.813	10.198	2.116	1.605	0.956	0.762
		ln Lb	−12,579	−14,613	−20,443	−5,794	−18,990	−22,318	−8,425	−9,296	−11,944	−13,989	−23,749	−25,478
	M0 + π	μ	1.681	0.209	0.191	6.686	0.471	0.156	12.765	9.263	1.555	1.207	0.639	0.567
		πa	0.442	0.745	0.774	0.242	0.753	0.857	0.238	0.341	0.460	0.534	0.657	0.639
		ln L	−12,460	−14,274	−20,070	−5,784	−18,635	−21,804	−8,425	−9,249	−11,853	−13,782	−23,402	−25,243
		Δ ln Lb	119	339	373	10	355	514	0	47	91	207	347	235

In the two extreme scenarios, all truncated genes were entirely classified as absent (f → a) or present (f → p).

^aAs described in methods, model M₀₀ is the special case of M₀ + π when π_a = π_p = 0.5, while M₀ is the special case of M₀ + π when π_a and π_p are the frequencies of each character in the data.

^bΔ ln L's are shown as (M₀ + π) vs. M₀. Since 2Δ ln L ≈ χ², Δ ln L's > 1.97 (d.f. = 1) are considered significant.

Since some patterns are not observable, we calculate the likelihood conditional on a pattern being observable, 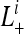as suggested in Felsenstein (1992),

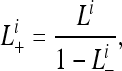(5)

where Lⁱ_– is the likelihood of unobservable patterns for gene family i. For cases where a number of patterns are unobservable, each such pattern is a disjoint event, and summation is taken over all unobservable patterns to get Lⁱ_–,

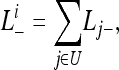(6)

where U is the set of unobservable patterns (Table S10), and L_j− is the likelihood of the jth unobservable pattern. Here Lⁱ₋ has the same value for all i.

Rate variation was also considered in a similar manner to nucleotide rate heterogeneity in phylogeny reconstruction (Yang 1994; Felsenstein 2001). A discrete Γ-model with eight rate categories (M = 8 categories) was implemented in the maximum-likelihood estimation. The likelihood on gene family i is the sum of likelihoods for each rate category ν for that gene family weighted by the category probabilities p_ν,

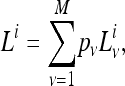(7)

where 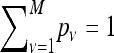. After incorporating a discrete Γ-model as done in Spencer and Sangaralingam (2009), the likelihood of observing the pattern of gene family i will be

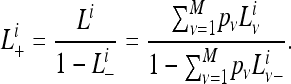(8)

First, parameters were estimated by assuming π_a, π_f, and π_p to be the frequencies of each character state in the data. This is called model M₀. In the case of only two characters (a, p), model M₀ is when π_a and π_p are the frequencies of each character state in the data, and another model, in which π_a and π_p = 0.5, was introduced (called model M₀₀) since it has been used in previous studies (Hao and Golding 2006, 2008b; Cohen et al. 2008). Then π_a, π_f, and π_p were treated as parameters to be optimized and hence called model M₀ + π. Finally, a discrete Γ-distribution was incorporated (model M₀ + Γ + π). All free parameters were estimated such that they maximize the likelihood of the data. This was achieved using the Nelder–Mead simplex method (Nelder and Mead 1965), which is slower than some gradient-based methods and the EM method but less likely to be misled to local maxima (Yap and Speed 2005; R Development Core Team 2008). To further reduce the chance of being trapped in local maxima, different initial values were used, and the final estimates with the highest likelihood were picked.

RESULTS

In this study, information on truncated genes was incorporated into the maximum-likelihood model. Analyses were conducted in four bacterial groups, and each group contains three clades with different levels of divergence (Table 1 and Figure 1). The results reveal that closely related clades have higher rates of gene insertions/deletions (μ) than distantly related clades (Figure 2 and Table 2). This trend holds throughout all four groups, and the use of different cutoff thresholds on identifying gene families yields remarkably similar results (Figure 2 and Table S11). This is consistent with previous findings that recently acquired genes have high rates of gene turnover (Daubin and Ochman 2004; Hao and Golding 2004, 2006). Under the M₀ + π model (Figure 2), the stationary probability π_a is positively associated with the tree length of each clade. It is important to clarify that the tree length is not an estimate from the gene insertion/deletion model. Indeed, it is the sum of branch lengths based on nucleotide substitution and it was used as an indicator for the degree of divergence in the clade.

TABLE 2.

Maximum log-likelihood comparison of different evolutionary models

		Bacillaceae			Clostridium			Escherichia			Pseudomonas
		B1	B2	B3	C1	C2	C3	E1	E2	E3	P1	P2	P3
Model	Parameter	(5,453)c	(5,614)	(6,813)	(3,546)	(6,526)	(7,645)	(4,681)	(5,063)	(5,307)	(6,505)	(8,761)	(9,140)
M0	μ	2.705	0.515	0.404	8.315	1.041	0.478	20.143	12.774	2.683	1.847	1.162	0.947
	β	0.577	1.281	1.700	0.326	2.430	1.851	0.372	0.285	0.439	0.587	1.117	1.466
	γ	1.311	2.096	2.725	0.590	3.498	3.050	0.686	0.495	0.817	0.831	1.703	2.209
	ln L	−16,551	−18,432	−24,799	−7,424	−22,783	−27,618	−13,019	−12,016	−15,071	−17,175	−29,926	−32,327
M0 + π	μ	2.102	0.214	0.197	8.385	0.482	0.149	19.805	11.699	1.837	1.332	0.695	0.619
	β	0.440	0.845	1.314	0.315	1.578	1.191	0.335	0.259	0.353	0.535	0.892	1.364
	γ	1.900	3.862	4.489	0.728	4.397	4.742	0.860	0.704	1.109	1.210	2.638	3.254
	πa	0.487	0.788	0.797	0.255	0.774	0.883	0.274	0.377	0.511	0.574	0.691	0.662
	πf	0.041	0.036	0.035	0.029	0.036	0.037	0.074	0.040	0.044	0.041	0.047	0.055
	ln L	−16,243	−17,799	−24,069	−7,385	−22,112	−26,491	−12,924	−11,876	−14,822	−16,787	−29,169	−31,715
	Δ AICa	−612	−1,262	−1,456	−74	−1,338	−2,250	−186	−276	−494	−772	−1,510	−1,220
M0 + Γ + π	μ	3.811	0.264	0.285	8.446	1.623	0.193	22.112	14.150	8.257	4.123	0.948	0.809
	αΓb	0.330	0.736	0.811	1.839	0.334	1.263	0.850	0.487	0.150	0.139	0.575	0.751
	ln L	−15,861	−17,553	−23,738	−7,370	−21,312	−26,253	−12,830	−11,728	−13,951	−16,334	−28,674	−31,325
	Δ AICa	−762	−490	−660	−28	−1598	−474	−190	−294	−1740	−904	−988	−778

^aAkaike's information criteria (Δ AICs) are shown as (M₀ + π) vs. M₀ and (M₀ + Γ + π) vs. (M₀ + π). By definition, AIC = 2(−ln L + K), where K is the number of parameters that are estimated from the data; thereafter, Δ AIC = 2(−Δ ln L + ΔK). The model that best approximates the data is the one with smallest AIC.

^bThis is the shape parameter in a Γ-distribution, which is traditionally described as α. The use of α_Γ is to distinguish it from the symbol α used in the instantaneous rate matrix.

^cThe number of gene families for each clade is shown in parentheses underneath the clade name.

To further access the robustness of using two different cutoff thresholds, we plotted the distribution of length variation in reciprocal best BLASTP hits from 24 selected genome pairs (see Figure S1 for details). Genome pairs Cph–Cth in C3 and Sfl–Sdy in E1 show the highest level of length variation (Figure S1). Then we plotted the DNA distance and K_a/K_s ratio of these homologs (Figure S2). All examined genome pairs have a median DNA distance <1.0 and a median K_s/K_s ratio <0.2 (Figure S2). Among the examined genome pairs, Cph–Cth is the most diverse, while Sfl–Sdy and Eco5–Eco6 are the least diverse. After that, we simulated the expected distribution of match length at given sequence divergence and functional constraints with no indels allowed. It is shown that the number of imperfect matches increases when the homologous pairs are more diverse (Figure S3) and the query sequences are shorter (Figure S4). Compared with the simulated data, reciprocal best BLASTP hits show a significantly higher level of length variation than expected. The most extreme case is the Sfl–Sdy pair, which has a remarkably low level of sequence divergence (Figure S2) but a significantly high level of length variation (Figure S1). The K_s/K_s ratios in the Sfl–Sdy pair are significantly higher than those in either Eco5–Eco6 or Efe–Sen (each with P < 0.0001 in a Wilcoxon rank test), suggesting that many genes are under relaxed functional constraints in at least one of the two genomes in Sfl–Sdy. In fact, the Shigella flexneri genome (Sfl) has been documented to undergo genome reduction and gene pseudogenization (Wei et al. 2003; Lerat and Ochman 2004; Dagan et al. 2006). The high level of length variation in the Cph–Cth pair can be explained in part by the high degree of sequence divergence. Importantly, the observed level of length variation in all genome pairs is always higher than that of the simulated data at a similar level of sequence divergence. Some of the inflated length variation could have been introduced by problematic annotations. However, during the annotation process closely related genomes are routinely used as references for gene identification and the annotations are frequently updated. It is reasonable to believe that some of the annotated genes might indeed have been affected by gene truncation. Finally we plotted the observed distribution of match length of the TBLASTN hits in the examined genomes (Figure S5). It is shown that the imperfect TBLASTN hits are not uniformly distributed; instead, the number of imperfect TBLASTN hits increases as match length increases. Possible explanations would be that (1) truncated genes are selectively disadvantageous and shorter gene lengths would likely result in a greater disadvantage, and (2) some truncated genes failed to be detected and more such failures occur when longer stretches of gene sequences are missing. During the TBLASTN search, we used the longest, median, and shortest sequences from each gene family as query sequences (see Figure S5 for details). Furthermore, a smaller word size (−W 2) in the TBLASTN search was used in addition to the default word size (−W 3). It shows that using the longest, median, or shortest sequences as query sequences and using a smaller word size in the search led to remarkably similar results in our examined genomes (Figure S5).

When the clade is more diverse, more gene families that were once present in the ancestral genome are lost from some descendants. Figure S6 illustrates a decreasing trend of the number of commonly present gene families (with the exception of a slight increase from E1 to E2) and an increasing trend of the number of strain-specific gene families when clades become more diverse. The most parsimonious explanation for the decrease of commonly present gene families in more diverse clades is the loss of ancient gene families during evolution. The increase of strain-specific gene families also supports the loss of some ancient genes. If genome size stays relatively constant over time, the increase of recently acquired genes should be a reflection of the decrease of ancient genes. Furthermore, the stationary probability π_a appears to be greater than the observed frequency of a in each clade (Figure S7). This is expected since the genes that were once present but have been deleted from all the descendants are unobservable in the current data (Table S10), but have been taken into account in the maximum-likelihood estimation (Equation 5). The rate variation parameter α (shown as α_Γ in Table 2) has a positive association with tree length in the Pseudomonas and Bacillaceae groups (Figure 2). These data are in agreement with Hao and Golding (2008b) that closely related groups tend to have high degrees of rate variation for gene insertions/deletions among genes, while distantly related groups tend to have low degrees of rate variation for gene insertions/deletions. However, such a positive association was not found in the Escherichia and Clostridium groups. We suspect that the low divergence in the E1, E2, and C1 clades and the relatively low absolute numbers of gene insertions/deletions do not provide enough statistical power for the estimation of the rate variation parameter despite the high estimated rates. A lack of statistical power was previously documented in some phylogenetic groups with small genome sizes and/or closely related species (Hao and Golding 2008b). Indeed, the removal of the E1, E2, and C1 clades yields a strong positive association (with P-value = 0.0054) between tree length and α_Γ in the remaining nine clades (Figure S8).

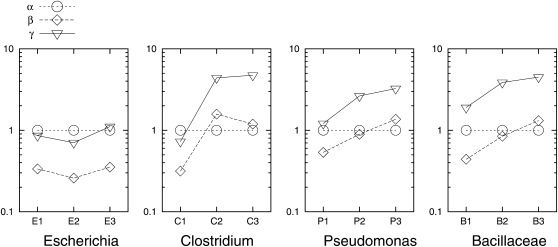
In the instantaneous rate matrix, α, β, and γ are the rate ratios between the state pairs af, ap, and fp, respectively, and are also known as the exchangeability terms. They are plotted for each clade in Figure 3. Here, α was fixed to be 1, and β and γ were estimated under the M₀ + π model. The trend seems to be that the β- and γ-values increase as the clades become more diverse. There are two exceptions (in two clades, E1 and C3) to this trend:

1. The β- and γ-values in the E1 clade are larger than those in the E2 clade. This could possibly be due to the low number of commonly present gene families in E1 (Figure S6), which is very likely associated with the process of genome reduction and gene pseudogenization in the S. flexneri (Sfl) genome (Wei et al. 2003; Lerat and Ochman 2004; Dagan et al. 2006). By contrast, the number of commonly present gene families generally decreases as the clade divergence increases. Furthermore, the similar level of divergence between E1 and E2 could potentially lead to the lack of statistical power to estimate parameters in very closely related clades as suggested in Hao and Golding (2008b).

2. The β-value in the C3 clade is smaller than the β-value in the C2 clade. Genome size was found to vary greatly in both clades, e.g., from 2.9 to 6.0 Mb in the C2 clade and from 2.5 to 4.8 Mb in the C3 clade. In the C2 clade, Cbe is significantly larger than the remaining four genomes, while in the C3 clade, Cno and Cte are significantly smaller than the remaining three genomes. We sought to address whether the unexpected pattern of the β-parameter in the instantaneous rate matrix could be explained by the highly variable genome sizes. A separate instantaneous rate matrix was assumed on the branches associated with the strain(s) with substantially different genome sizes (Cbe in C2, Cno and Cte in C3). The parameters β and γ are higher on the branch leading to the large genome (Cbe) and lower on the branches associated with the two small genomes (Cno and Cte), compared with on the rest of the phylogeny (Figure S9). The β-values on the rest of the phylogeny are 1.224 for C2 and 1.486 for C3, and they yield an increasing trend from C1 (β = 0.315 in C1) to C2 and to C3. Such a trend has been observed in Pseudomonas and Bacillaceae (Figure 3).

Figure 3.—

Estimated parameters of the instantaneous rate matrix in each clade. As described in methods, α was fixed to be 1, and β and γ were estimated under the M₀ + π model.

Furthermore, we computed the product of the scaled instantaneous rate matrix Q and the rate parameter μ (Table S12), which presents the instantaneous rates for all possible transitions. There is a clear trend that the instantaneous rates for all parameters increase as the clade becomes more closely related. As a part of the picture, the increased rates associated with character f in more closely related clades suggest that many truncated genes are in the process of being rapidly deleted from the genome.

We then sought to address the question whether a false diagnosis of gene absence systematically overestimates the rates of gene insertion/deletion. First, we conducted an analysis as in Hao and Golding (2006), in which the truncated genes were classified as absent (f → a), in a false diagnosis of gene absence in Zhaxybayeva et al. (2007). To make a comparison, we conducted another set of analyses by forcing all truncated genes to be classified entirely as present (f → p). Maximum-likelihood estimation was then conducted for both scenarios and the MLEs are shown in Table 3. When all truncated genes were classified as present (f → p), rather than absent (f → a), all 12 clades showed a lower μ under the M₀ model. Under the M₀ + π model, 5 clades (B1, C1, E1, E2, and E3) showed a lower μ, while the remaining 7 clades showed a higher μ. This is consistent with Hao and Golding (2008a) that the effect of false diagnosis of gene absence does not lead to a systematic bias but rather has a more complicated effect. As expected from the change of the frequency of state a, the stationary probability π_a became smaller in every clade after all truncated genes were classified as present, compared with when truncated genes were classified as absent.

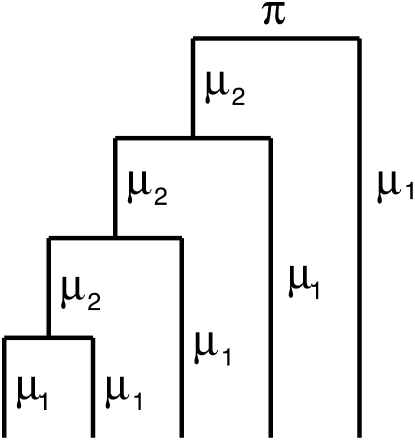
Finally, gene insertion/deletion rates were distinguished on different parts of the phylogeny, namely between external branches and internal branches (as shown in Figure 4). Table 4 shows that nine clades have significant improvement when rates on external branches and internal branches were distinguished. All nine clades show higher rates of gene insertions/deletions on external branches than on internal branches. Similar results were observed previously in Bacillaceae strains, Streptococcus strains, and Corynebacterium strains (Hao and Golding 2006; Marri et al. 2006, 2007). The three clades that do not show significant improvement are B2, B3, and C3 (Table 4), and they are the three most diverse clades in the study (Table 1 and Figure 2). Since most of the dynamics of gene insertions/deletions occur at the tip of the phylogeny (Hao and Golding 2006, 2008b), it is perhaps not surprising that little or no difference in the rates of gene insertions/deletions was found between external branches and internal branches in such diverse clades. In fact, substantially different results were observed on gene gains/losses by applying similar parsimony methods on distantly related species (Mirkin et al. 2003) vs. on closely related species (Hao and Golding 2004).

Figure 4.—

Rate parameters estimated on a five-taxon phylogeny. Rates on external branches are μ₁, and rates on internal branches are μ₂.

TABLE 4.

Rate comparison on different branches under the M0 + π model

	Bacillaceae			Clostridium			Escherichia			Pseudomonas
Model	B1	B2	B3	C1	C2	C3	E1	E2	E3	P1	P2	P3
μ1 = μ2	2.102	0.214	0.197	8.385	0.482	0.149	19.805	11.699	1.837	1.332	0.695	0.619
ln L	−16,243.9	−17,799.0	−24,069.1	−7,384.6	−22,112.1	−26,490.9	−12,924.1	−11,875.9	−14,822.4	−16,787.4	−29,169.0	−31,715.2
μ1	3.169	0.215	0.200	10.949	0.661	0.146	22.154	15.765	2.533	1.750	0.764	0.644
μ2	0.180	0.210	0.180	0.000058	0.199	0.158	5.797	2.161	0.737	0.556	0.454	0.558
ln L	−15,879.1	−17,798.9	−24,067.8	−7,233.0	−21,879.1	−26,489.6	−12,888.7	−11,722.1	−14,722.1	−16,608.3	−29,128.4	−31,710.8
Δ ln La	364.8	0.1	1.3	151.6	233.0	1.43	35.4	153.8	100.3	79.1	40.6	4.4

^aΔ ln L's > 1.94 (d.f. = 1) are considered significant. As a result, B2, B3, and C3 are not significant.

DISCUSSION

Here, we are primarily interested in modeling gene insertions/deletions with consideration for truncated genes. We have not attempted to infer the functionality of any truncated genes. First, there has never been a standard criterion in the literature for pseudogene identification (Chain et al. 2004; Lerat and Ochman 2004). Second, detection of pseudogenes requires extensive knowledge of each gene's transcription and its protein's function but this is beyond the scope of this study. Finally, the boundary between gene and pseudogene might rather be ambiguous (Zheng and Gerstein 2007). Presence of an annotated gene within a genome does not necessarily suggest its functionality, but ironically, some shortened homologs might still carry out some function (Ogata et al. 2001).

Our current study classifies genes into three categories (presence/absence/fragment) and makes no attempt to examine any sequence divergence at the gene or subgenic levels. If a whole gene or a fraction of it was replaced via a lateral transfer with a similar gene, the methods employed here would fail to detect these transfers. In other words, homologous recombination (HR) would not directly contribute to any rate changes under our current model. However, if HR has occurred in the genes we used for phylogeny reconstruction, it might affect the maximum-likelihood estimates (MLEs) since our estimation was based on the gene phylogeny (e.g., t in Equation 4 is branch length). The effect of such HRs on the MLEs is likely complex. If HR has occurred between two examined genomes in a clade and the observed sequence diversity is likely to have been diminished, the branch lengths on the gene phylogeny would have been underestimated and the estimated rates of gene insertions/deletions might have been overestimated. If HR has occurred between one examined genome and any unsampled distantly related genome, the recombined branch length would have been overestimated and, as a result, the estimated rates of gene insertions/deletions might have been underestimated. If HR has occurred and even altered the branching order(s), the estimated rates of gene insertions/deletions would likely have been overestimated, since one generally expects to infer more evolutionary events on a less parsimonious tree. If HR has occurred in the combination of two scenarios or more, the effect on the MLEs could be even more complex. In our study, the phylogeny of each clade was constructed using concatenated sequences of a large number of single-copy genes. Although not completely immune to lateral transfer (Yap et al. 1999; Brochier et al. 2000), commonly present single-copy genes have been shown to exhibit mostly vertical descent (Hooper and Berg 2003; Wellner et al. 2007). We therefore believe that the effect of any potential HRs in the genes used for phylogeny reconstruction should be small.

As in previous studies (Hao and Golding 2006, 2008b; Cohen et al. 2008), we initially assumed a constant rate of gene insertions/deletions on each phylogeny. This simplifying assumption is not realistic. Since the number of gene insertions/deletions is proportional to μt, here t is the branch length; when the rate of gene insertions/deletions μ is constant, the number of gene insertions/deletions would be proportional to the corresponding branch length. The assumption of a constant rate μ would result in a bias that high numbers of gene insertions/deletions are inferred on the fast-evolving branches. This bias exists as long as the members of a clade do not evolve at the exact same rate. Clearly, the members in each studied clade do not all evolve at the exact same rate since none of the studied clades support a strict molecular clock tree (Figure 1). Furthermore, previous studies have shown that the inferred rates of gene insertions/deletions are not constant, and instead, recent branches tend to have higher numbers of gene insertions/deletions (Hao and Golding 2006). Given the use of a simplifying model in the study, it is essential to address the robustness of the results upon such an assumption. Our findings reveal that there is a strong negative association between the rate parameter μ and the degree of divergence in the clade (Figure 2). The same trend was found in a previous study on groups with different sets of genomes (Hao and Golding 2008b). Both studies showed that closely related clades tend to have high rates of gene insertions/deletions, suggesting many recently transferred genes are to be rapidly deleted from the genome. Importantly, the same conclusion can be drawn by comparing the rates of gene insertions/deletions between recent branches and ancient branches in the same phylogeny. Table 4 shows that the rates of gene insertions/deletions on external branches, when significant, are always higher than those on internal branches. This pattern has also been found in Hao and Golding (2006) and Marri et al. (2006). Furthermore, branch lengths, when estimated from the sequence data, have often been systematically overestimated on recent branches (Ho et al. 2005). In our study, we observed high rates of gene insertions/deletions on recent branches. One can easily imagine that the high rates of gene insertions/deletions on recent branches will be further inflated after correcting for the overestimation of the recent branch lengths.

Currently our method assumes reversibility in the transition processes among genes present (p), fragment (f), and absent (a). This is not likely realistic. For instance, the transition from p to f could easily be explained by gene truncation, while the reverse is not so clear. In our data, the state changes from f to p could result from homologous recombination or acquisition of a new full-length homolog. First, homologous recombination has been widely reported in bacterial genomes, especially between closely related strains (Guttman and Dykhuizen 1994; Gogarten et al. 2002; Fraser et al. 2007; Lefebure and Stanhope 2007), and recombination could involve long stretches of sequences (Didelot et al. 2007; Sheppard et al. 2008). When the recombinant sequences are long, truncated genes embedded in the recombinant region could potentially be converted to full-length genes. Second, the three different states are for gene families rather than for individual genes, and full-length genes with “truncated” paralogs are always classified as p. As a consequence, acquisition of full-length homolog(s) will result in the change of gene state from f to p. Since the rates of gene insertions are high (Hao and Golding 2006) and genes with high duplicability are more prone to gene transfer (Wellner et al. 2007), it should be appropriate to consider the transition from f to p. Although the transitions and their reverse forms are all possible, there is no good reason to believe that the actual transitions are mathematically reversible. Our current model assumes reversibility and assigns a single instantaneous rate parameter to both directions of each transition. For instance, the instantaneous rate parameter for the state pair fp is γ (Equation 1). Further improvement can be made in future studies by distinguishing the two directions of each transition and ultimately introducing an irreversible rate matrix. Future studies by incorporating an irreversible rate matrix would be able to further improve the MLEs and address how asymmetric each transition is in the instantaneous rate matrix. In the data f's are very much outnumbered by a's and p's (Table S2, Table S3, Table S4, Table S5, Table S6, Table S7, Table S8, and Table S9). We suspect that the asymmetry between f and p and between f and a might not result in dramatic changes of MLEs when genome size remains roughly constant. On the flip side, when genome size varies significantly among taxa, models incorporating an irreversible rate matrix would be highly desirable. Furthermore, our current study assumes one instantaneous rate matrix on the entire phylogeny. This is also not likely realistic, especially when genome size varies among genomes (as shown in Figure S9). A more thorough study on genome size variation is in progress and will be reported later. Future studies by incorporating an irreversible rate matrix would shed new light on understanding the dynamics of genome size during bacterial genome evolution.

This study models insertions/deletions (or gains/losses) of gene families and requires the identification of the full-length gene in at least one genome in each examined clade. Recently Didelot et al. (2009) presented a method to reconstruct genomic flux on the basis of raw genomic sequences without relying on gene identification. In their study, each sequence rather than each gene was treated as a unit and sequence gains/losses were modeled on the basis of the presence or the absence of each sequence unit. One advantage of their method is its ability to model genomic flux beyond the gene boundary, since gene transfer could occur both at subgenic levels (Riley and Labedan 1997; Miller et al. 2005; Chan et al. 2009) and in large gene clusters (Lawrence 1999). However, their model, as with previous models that consider a gene family as a unit, does not allow any intermediate states other than sequence presence or absence. In contrast, our study identifies truncated genes by comparing the full-length gene in a closely related species and should yield more accurate estimates of gene insertion/deletion events. Adding an intermediate state and considering insertions/deletions in the unit of genes, our method has a potential to model gene decay, which could be frequent and rapid in some genomes (Cole et al. 2001; Dagan et al. 2006).

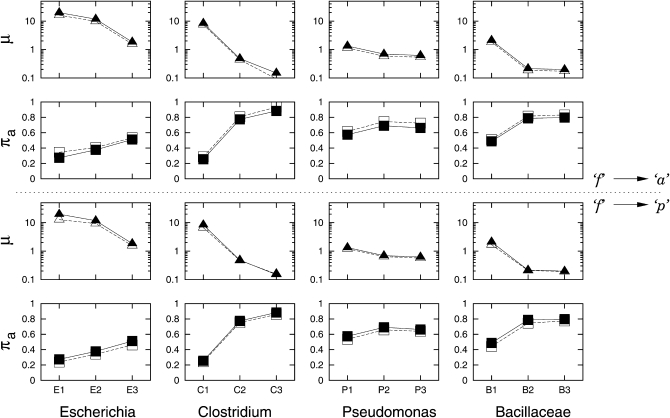
It is noteworthy that the rates of gene insertion/deletion were estimated from the data of currently present gene families. If gene deletion largely takes place in recently transferred genes, the number of anciently transferred genes will decrease during the course of evolution and will be reflected by a small number of gene gains or a slow rate of gene gains/losses in estimations (for a detailed illustration, see Hao and Golding 2010). This study reveals that closely related clades have high rates of gene insertions/deletions, while distantly related clades have low rates of gene insertions/deletions (Figure 2). This suggests that the fate of many recently transferred genes is to be deleted from the genome. When rates were distinguished between external branches and internal branches, the rate on external branches is, when significant, always higher than the one on internal branches (Table 4). These data are consistent with our previous observations (Hao and Golding 2004, 2006) that many of the recently transferred genes have a fast turnover. Several lines of evidence have previously documented that truncated genes are involved in the fast turnover of laterally transferred genes. An early study has shown that truncated genes arose from failed lateral gene transfer events (Liu et al. 2004). We reported that many of the truncated genes are recently acquired into the host genome (Hao and Golding 2008a) and are associated with gene translocation and gene deletion (Hao and Golding 2009). To address whether a false diagnosis of gene absence leads to systematic overestimation of any estimates, the maximum-likelihood estimates considering truncated genes were compared with the estimates after forcing truncated genes to be classified as either absent or present (Figure 5). Classifying truncated genes as absent does not always yield smaller rates (μ) than classifying truncated genes as present. As suggested in Hao and Golding (2008a), the effect of false diagnoses is not systematically biased, but rather complex. A more thorough understanding of the effect of false diagnoses requires further studies. Under the M₀ + π model in the study, the rate parameter μ with truncated genes is almost always (with one exception in C3) slightly higher than the rate when classifying truncated genes as either absent or present (Figure 4). We believe that the higher rates observed when considering truncated genes are likely due to the richness of parameters. An analogous situation is often seen in observing greater nucleotide substitution distances when the substitution model is more parameter rich [e.g., from JC (Jukes and Cantor 1969) to K2P (Kimura 1980) and then to HKY (Hasegawa et al. 1985)].

Figure 5.—

Comparison of MLEs with (solid symbols) or without (open symbols) considering truncated genes in the model. MLEs were estimated under the M₀ + π model. When not considering truncated genes, truncated genes were entirely classified as absent (top half) or present (bottom half).

The expected equilibrium frequencies of the three character states (π_a, π_f, π_p) were also assumed to be the frequencies at the ancestral node. Although the stationary probabilities are associated with the empirical frequencies of the character states in the data, they may deviate from the empirical frequencies since the stationary probabilities have taken into account the gene families that were once present in the ancestral genome but are no longer observable in the current data. One should expect a higher frequency of a in the stationary probability than in the empirical data. In fact, the stationary probability π_a is always higher than the observed frequency of a (Figure S7). One should not misinterpret it as any systematic bias that might favor more gene losses. In the results, the stationary probability π_a is positively associated with the tree length of each clade (Figure 2). These data suggest that a large number of ancient gene families have been lost in highly diverse clades, while only a small number of ancient gene families have been lost in low diversity clades. However, the large value of π_a in a more diverse clade might not necessarily suggest a smaller ancestral genome size of the clade, since an accurate estimation of ancestral genome size relies on the total number of gene families including the absolute number of unobservable patterns. When truncated genes were forced to be classified as present, the estimate of π_a became smaller in every clade compared to when truncated genes were considered. While if truncated genes were forced to be classified as absent, the estimate of π_a became larger in every clade compared to when truncated genes were considered (Figure 2). These estimates might be a reflection of the change of frequency of state a among clades.

It is widely acknowledged that gene family data contain phylogenetic signals (Fitz-Gibbon and House 1999; Snel et al. 1999; Tekaia et al. 1999) and many studies have used such data for the reconstruction of phylogenetic trees (Dutilh et al. 2004; Gu and Zhang 2004; Huson and Steel 2004; Zhang and Gu 2004; Spencer et al. 2007a,b) and phylogenetic topologies in more complex forms (Rivera and Lake 2004; Lake 2008). Even though the primary purpose of our study is to infer the dynamics of gene content during bacterial genome evolution, the model incorporating truncated genes could be potentially applied for phylogeny reconstruction using gene family data. We note that using three characters (p, f, a), compared with using only two characters (p, a) increased the –ln L values (Tables 2 and 3). In Figure S10, we plotted the –ln L values of using two gene characters against the ln L differences after adding the third gene character f. It is clear that there is a significantly positive association between the –ln L values and the ln L differences. This suggests a significant improvement in the probability of observing the data given three rather than two characters.

Given the nature of high rates of gene insertions/deletions in closely related species and low rates of gene insertions/deletions in distantly related species, the model presented in this study is expected to be useful among closely related taxa but less so for deep phylogeny questions.

The results from the improved model reveal fast rates of gene insertions/deletions/truncations on recent branches. This holds true when comparing different rates both between internal branches and external branches and among clades with different levels of divergence. The estimates of the rate ratio parameters suggest that many recently truncated genes are in the process of being rapidly deleted from the genome. We also demonstrated that using simplifying models, in which truncated genes are classified as absent, does not result in a systematic bias, but has a complex effect on rate estimates. Furthermore, the improved model is sensitive to the variation of genome size, and it opens the door to more thorough and comprehensive studies on the variation and dynamics of genome size during bacterial genome evolution.