Abstract
Microsatellites are abundant in eukaryotic genomes and have high rates of strand slippage-induced repeat number alterations. They are popular genetic markers, and their mutations are associated with numerous neurological diseases. However, the minimal number of repeats required to constitute a microsatellite has been debated, and a definition of a microsatellite that considers its mutational behavior has been lacking. To define a microsatellite, we investigated slippage dynamics for a range of repeat sizes, utilizing two approaches. Computationally, we assessed length polymorphism at repeat loci in ten ENCODE regions resequenced in four human populations, assuming that the occurrence of polymorphism reflects strand slippage rates. Experimentally, we determined the in vitro DNA polymerase-mediated strand slippage error rates as a function of repeat number. In both approaches, we compared strand slippage rates at tandem repeats with the background slippage rates. We observed two distinct modes of mutational behavior. At small repeat numbers, slippage rates were low and indistinguishable from background measurements. A marked transition in mutability was observed as the repeat array lengthened, such that slippage rates at large repeat numbers were significantly higher than the background rates. For both mononucleotide and dinucleotide microsatellites studied, the transition length corresponded to a similar number of nucleotides (approximately 10). Thus, microsatellite threshold is determined not by the presence/absence of strand slippage at repeats but by an abrupt alteration in slippage rates relative to background. These findings have implications for understanding microsatellite mutagenesis, standardization of genome-wide microsatellite analyses, and predicting polymorphism levels of individual microsatellite loci.
Keywords: microsatellites, polymorphism, indel mutations, threshold, strand slippage, DNA polymerase fidelity
Introduction
Microsatellites are tandem repeats of short (1–6 bp) DNA motifs and are ubiquitous in eukaryotic genomes. Germline microsatellite mutation rates are high in humans, leading to ample polymorphisms within populations (Ellegren 2000). Due to their abundance and high polymorphism levels, microsatellites have become popular markers in association studies, population genetics, and forensics. Most microsatellites are thought to evolve neutrally; however, some of them affect gene expression, splicing, or protein sequence (Meloni et al. 1998; Li et al. 2002, 2004; Rockman and Wray 2002; Ruggiero et al. 2003; Iglesias et al. 2004; Hammock and Young 2005; Martin et al. 2005; Zhang et al. 2006), and thus are subject to selection. Over 40 functionally relevant microsatellites are implicated in, or are risk factors for, human diseases (Pearson et al. 2005). Allele length polymorphisms in not only trinucleotide but also highly abundant [A/T]n and [GT/CA]n microsatellites are genetic risk factors in several human diseases. A well-described example of this is the [GT]n and [T]n allele length changes that affect CFTR gene expression via altered splicing efficiency, which consequently affects cystic fibrosis disease status (Chu et al. 1993; Cuppens et al. 1998). Similarly, the length of a polymorphic, intronic [CA]n allele is inversely correlated with transcription of the EGFR gene, and interethnic differences in [CA]n allele lengths are associated with varying EGFR levels in breast cancer patients (Gebhardt et al. 1999; Buerger et al. 2004). Finally, the length of a pure, exonic [A/T]n allele within the APC gene affects the onset of familial adenomatous polyposis cancer (Laken et al. 1997).
The most commonly proposed model for microsatellite mutation is strand slippage during DNA synthesis (Levinson and Gutman 1987). According to this model, a nascent DNA strand transiently dissociates from a template strand, and, due to the complementarity within a microsatellite sequence, strand misalignment upon reassociation occurs with an increased probability. This DNA strand misalignment usually results in addition or deletion of repeat units. The characteristics of microsatellite mutations observed in vitro by numerous DNA polymerases (see references below) and in genome analyses (Ellegren 2004; Webster and Hagberg 2007; Brandstrom and Ellegren 2008; Kelkar et al. 2008) support the strand slippage model. Additionally, we and others have recently shown that a large proportion of mutation rate variation at microsatellites can be explained by sequence features intrinsic to a microsatellite locus itself—repeat number, motif size, and sequence (Kelkar et al. 2008). These results are concordant with several experimental investigations (reviewed in Eckert and Hile 2009) as well as pedigree and polymorphism studies (Wierdl et al. 1997; Brinkmann et al. 1998; Huang et al. 2002). However, most of these investigations have focused on microsatellites with sizeable repeat numbers, leaving sequences with small repeat numbers largely unexplored (Zhu et al. 2000; Noor et al. 2001; Dieringer and Schlötterer 2003; Ellegren 2004).
One of the most contentious issues in microsatellite studies relates to the very definition of a microsatellite. Indeed, when does a sequence consisting of short tandem repeats qualify as a microsatellite? According to the threshold hypothesis, a repeat sequence is required to exceed a certain critical size (a threshold) in order to become a hotspot for strand slippage and thus to constitute a microsatellite. Depending on the data and approach used, different studies have reached varying conclusions about the exact value of the threshold. Messier et al. (1996) observed that once a tandem repeat expands above a threshold size (4–5 repeats for di- and 2 for tetranucleotide microsatellites, respectively), it exhibits a high degree of variation in repeat numbers among primate species. Many other studies have defined the threshold as a tandem repeat number above which the repetitive loci are overrepresented in a genome as compared with random nucleotide co-occurrence because such overrepresentation is likely a result of strand slippage (de Wachter 1981; Tautz et al. 1986; Cox and Mirkin 1997; Dechering et al. 1998; Rose and Falush 1998; Pupko and Graur 1999; Zhu et al. 2000). Within this view, a universal threshold of 8–10 bp was proposed for yeast microsatellites (Rose and Falush 1998), and a threshold of 7–10 bp (depending on species) was suggested for mononucleotide microsatellites in eukaryotes (Dechering et al. 1998). The threshold for human microsatellites was found to depend on their motif size (9 repeats for mononucleotide and 4 repeats for di-, tri-, and tetranucleotide microsatellites [Lai and Sun 2003]), whereas another study found that the threshold length depended on motif identity (3 and 9 bps for [A/T]n and [C/G]n, respectively; [Dieringer and Schlötterer 2003]). Implicit in most of the above work is the definition of the threshold as the smallest tandem repeat number at which strand slippage occurs. However, several studies provided evidence of slippage-related insertions and deletions even at repeat numbers that were much lower than the proposed threshold values (Zhu et al. 2000; Noor et al. 2001; Dieringer and Schlötterer 2003). Consequently, the very existence of a microsatellite threshold and its usefulness in defining microsatellites has been doubted (Pupko and Graur 1999; Zhu et al. 2000; Noor et al. 2001; Dieringer and Schlötterer 2003).
Experimental models of DNA polymerase fidelity, which use vector constructs to assess repeats occurring in protein-coding regions, have clearly demonstrated that strand slippage (frameshift) errors occur at a low but detectable frequency within very short mononucleotide sequences (e.g., [G]2, [C]3 or [T]4) during DNA synthesis (Kunkel 1990; Garcia-Diaz and Kunkel 2006). Such frameshifts are greatly biased toward one base deletion events (Kunkel and Alexander 1986). Frameshifts produced by purified DNA polymerases arise in a manner that is consistent with the strand slippage model. For example, a positive correlation was observed between the length of a [T]n repeated sequence (n = 3–8 bases) and the polymerase error frequency (Kroutil et al. 1996). In contrast, polymerase frameshift errors within nonrepetitive sequences are initiated primarily by base mispairing rather than by strand misalignment (Bebenek and Kunkel 1990). Previously, we have demonstrated that mammalian DNA polymerases α and β produce errors within [GT/CA]10, [TC/AG]11, and [TTCC/AAGG]9 microsatellites at rates that are 10- to 100-fold higher than the rate of errors produced at short repeated mononucleotide sequences of 2–4 bases within a protein-coding sequence (Eckert et al. 2002; Hile and Eckert 2004; Eckert and Hile 2009). Such results allow us to experimentally define microsatellite-specific errors as those that occur at a rate higher than other strand slippage-mediated errors within coding sequences.
Here, to resolve the controversy surrounding the definition of microsatellites, we investigated the dynamic nature of mutations within short tandem repeats as a function of repeat number. In the “computational analysis,” we assessed repeat polymorphism occurrence at ten ENCODE regions resequenced in 48 humans (International HapMap Consortium 2005; Legendre et al. 2007). Our premise was that the presence of polymorphism at repeats with a certain number of units reflects their increased slippage rates. In the “experimental analysis,” we modified our published HSV-tk in vitro mutagenesis system (Eckert et al. 2002) to directly quantify DNA polymerase error frequencies within tandem repeats differing by one-unit increments. In both approaches, we considered microsatellites to be tandem repeat loci with slippage rates significantly exceeding background slippage rates in the genome. With results combining computational and experimental evidence, we aim to set a standard for what loci should be called microsatellites in future studies. This is critical for the development of polymorphic markers, for commencing inquiries into microsatellite life cycle (Buschiazzo and Gemmell 2006), and for meaningful comparisons among microsatellite studies.
Materials and Methods
Computational Analysis
Public Data Utilized
We used human resequencing data generated by the HapMap-ENCODE resequencing and genotyping project (International HapMap Consortium 2003). As part of this project, 500 kb from each of the ten ENCODE regions—ENr112, ENr131, ENr113, ENm010, ENm010, ENm013, ENm014, ENr321, ENr232, ENr123, and ENr213 (supplementary table S1, Supplementary Material online)—were amplified in fragments and sequenced using the Sanger method in 48 unrelated individuals belonging to four human populations (16 Yoruban Africans, 16 Europeans, 8 Han Chinese, and 8 Japanese). We obtained the corresponding single-pass DNA sequencing reads from the NCBI Trace Archive. For each of the ten ENCODE regions, reads were mapped to the reference human genome (hg18) using the Consed and Cross_match programs (Gordon et al. 1998) with default parameters.
Identification of Repeats
The microsatellite search methods can dramatically influence results (Merkel and Gemmell 2008), therefore we provide all parameters used in the present study below, to insure reproducibility. Using Sputnik (Abajian, unpublished data) with default parameters, an initial scan of microsatellites within the reference human genome sequence of the ten ENCODE regions was conducted. As very low numbers of tri- and tetranucleotide microsatellites with repeat number greater than four were found (data not shown), the following procedure was restricted to mono- and dinucleotide microsatellites. An in-house pipeline consisting of custom Perl scripts with few parameters was created to extract positions and sequences of uninterrupted and interrupted mono- and dinucleotide repeats within the human reference genome and also within each ENCODE resequencing read, using a microsatellite search algorithm similar to the one introduced by Mudunuri and Nagarajaram (2007). In this pipeline, initially, all “seeds” of mononucleotide and dinucleotide repeats, that is, uninterrupted [A/T]n, [G/C]n, [GT/CA]n, [AG/TC]n, [CG/GC]n, and [TA/AT]n repeats, n ≥ 1, are extracted from each sequence read. The seeds undergo the elongation process, wherein they are progressively extended into flanking bases by incorporating interruptions, if present. In this elongation process, the immediate neighborhood of each seed is examined for the presence of seeds with the same motif that are separated by one nonrepeat nucleotide in case of mononucleotide repeats or by at most two nonrepeat nucleotides in case of dinucleotide repeats. If neighboring seeds are discovered, then the initial seed is extended to include them, with the separating interruptions. The search for neighboring seeds is continued iteratively beyond the extended boundaries of the seed, until no such neighboring seed is identified. Seeds that are not extended and those that are extended are classified as uninterrupted and interrupted repeats, respectively. Only the repeats that were at least 10 bp away from nearest identified repeats were used for further analysis. Thus, adjacent repeats that constituted compound microsatellites were discarded. The interrupted repeats identified above were later discarded (below), and the mutational dynamics of only uninterrupted repeats were analyzed.
Detection of Indels at Repeat Loci
Because the reads were generated by Sanger sequencing of polymerase chain reaction products derived from diploid samples, PolyScan (Chen et al. 2007) was used with default settings to delineate the two allele states at heterozygous repeat loci. Positions of inferred indels at long repeats (repeat number n > 4) were validated by manual inspection. Repeat loci having reads with low sequence quality (PHRED scores of less than 20) at any nucleotide within a repeat in any individual were usually removed. We retained the repeat loci when, at a repeat sequence having only terminal nucleotides with low sequence quality, two conditions were satisfied: 1) PolyScan inferred heterozygous indels and 2) the sequence quality deterioration within a repeat locus was in the direction of the sequencing reaction (following the repeat). At each repeat locus, allele states in terms of repeat numbers were determined for each individual, after confirming that the inferred insertions and deletions were made up of multiples of the repeated motif. Repeats mapping to the same position of the reference sequence were grouped among different individuals to collect population-wide repeat-number polymorphism at that locus (we pooled data from the four human populations for this analysis).
Filtering of Repeat Loci
Four filtering steps were implemented to ensure correct inference of polymorphism levels at repeat loci. First, loci with interruptions were excluded if the allele frequency of interrupted alleles among humans was greater than 10%. If an interrupted allele had low frequency (<10% of the individuals considered), then only this allele (and not the whole locus) having interruptions within repeat loci was filtered out. Second, to exclude loci with possible incorrect local sequence alignment, the similarity of sequences flanking a repeat locus was examined among all individuals. For each individual represented at a locus, 10 bps of flanking sequence were extracted upstream and downstream of the locus and concatenated into a single 20-bp flanking sequence. We discarded loci at which the most common concatenated flanking sequence, and flanking sequences more than 90% identical to it, were present in less than 90% of individuals analyzed. For the remaining loci, individuals with rare flanking sequences were omitted from further analysis of the locus. Third, we excluded loci overlapping with [C/G]n mononucleotide microsatellites, non-[GT/AC]n dinucleotide microsatellites, tri- or tetranucleotide microsatellites, as identified by Sputnik (Abajian, unpublished data). This ensures that slippage mutations at repeats of interest are independent of those at such microsatellites (loci overlapping with penta- and hexanucleotide microsatellites were retained as Sputnik identified very few of such loci in the reference sequence of the ten resequenced ENCODE regions). Fourth and finally, to exclude loci that overlapped the untranslated regions and coding regions of genes, human annotations of known genes were used as available at the UCSC Genome Browser (Rhead et al. 2010). Thus, only the insertion and deletion dynamics of uninterrupted, intergenic, and intronic [A/T]n and [GT/CA]n repeats was examined.
Computing the Proportion of Polymorphic Loci
At Repeat Loci
Repeat loci were divided into bins, based on the modal allele at a locus. For each of these bins, the proportion of polymorphic repeat loci (PPRL), considering only polymorphisms in terms of differences in repeat number, was calculated. Subsequently, within each bin, we resampled loci with replacement, thus creating 1,000 bootstrap samples for each bin. The PPRL was calculated for each bootstrap sample, and the 2.5th and 97.5th percentiles of the resulting PPRL values were used to create the 95% bootstrap bands in figures 1 and 2.
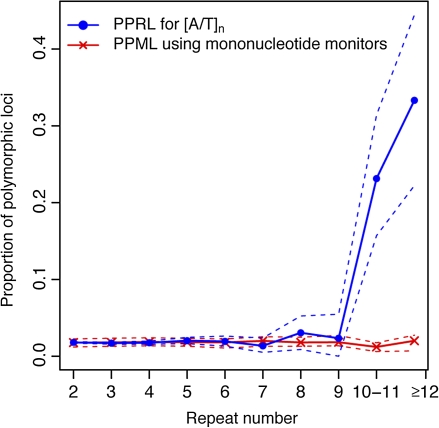
FIG. 1.—
Dependence of polymorphism prevalence at [A/T]n repeats (PPRL) on repeat number in relation to mononucleotide monitors (PPML) sampled from their immediate neighborhoods. PPRL is denoted by circles, with dashed blue lines denoting the 95% CIs. PPML is denoted by ‘x’s, with the 95% CIs denoted by dashed red lines.
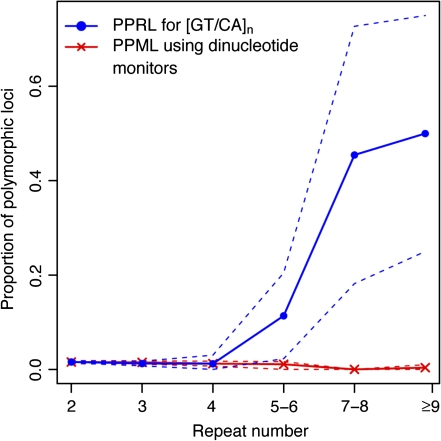
FIG. 2.—
Dependence of polymorphism prevalence at [GT/CA]n repeats (PPRL) on repeat number in relation to dinucleotide monitors (PPML) sampled from their immediate neighborhoods. PPRL is denoted by circles, with dashed blue lines denoting the 95% CIs. PPML is denoted by ‘x’s, with the 95% CIs denoted by dashed red lines.
At Monitors
In order to contrast slippage rates at repeat loci versus background slippage rates, while also taking potential regional variation in slippage rates into account, we examined polymorphism levels at “monitor loci” selected in the neighborhood of each repeat locus. We defined monitors as a subset of the repeat loci; namely, uninterrupted repeat loci having at least one allele with two repeats (the minimal number required for slippage to occur) and no alleles with greater than three repeats. Thus, we considered the two simplest slippage scenarios: [X]2->[X]1 and [X]2->[X]3 (where X denoted a repeating motif, and the subscript denotes the repeat number). For each repeat locus, we collected 20 adjacent monitor loci—10 upstream and 10 downstream, positioned at the most 5,000 bp from the repeat (monitors located within 10 bp of the repeat were excluded to ensure that slippage events at repeat loci and monitors were independent of each other). Twenty mononucleotide monitors were collected for each mononucleotide repeat, whereas for each dinucleotide repeat, we collected 20 dinucleotide and 20 mononucleotide monitors. Next, for each repeat locus, we calculated the proportion of polymorphic monitor loci (PPML) among its closest 20 monitors (this was done separately for mononucleotide and dinucleotide monitors of each dinucleotide repeat). The mean PPML of repeats from each bin was plotted in figures 1 and 2. Initially, polymorphism occurrence for different monitor motifs with the same size (either mono- or dinucleotide) was measured separately. However, as their PPMLs were very similar (data not shown), in our final procedure for each repeat, we selected monitors regardless of their motif sequence. Therefore, [A/T]2 and [C/G]2 were considered jointly as mononucleotide monitors, and [GT/CA]2, [AG/CT]2, and [AT/TA]2 were considered jointly as dinucleotide monitors. [CG/GC]2 loci were not used as monitors, due to their high susceptibility to point mutations (Bulmer 1986; Britten et al. 1988).
Subsequently, within each bin, we resampled monitor loci with replacement, thus creating 1,000 bootstrap samples for each bin. The PPML was calculated for each bootstrap sample, and the 2.5th and 97.5th percentiles of the resulting PPML values were used to create the 95% PPML bootstrap bands in figures 1 and 2. This was done separately for mono- and dinucleotide monitors of dinucleotide repeats.
Population-Specific Threshold Values
To investigate the effect of population history on the determination of threshold size, PPRL (for repeats) and PPML (for monitors) as well as the associated 95% bootstrap confidence bands for mononucleotide repeats were determined individually for each of the studied populations—African (YRI), European (CEU), and combined Eastern Asian (CHB + JPT; CHB and JPT were pooled in a single Eastern Asian population due to their recent split). We did not determine population-specific thresholds for [GT/CA]n because, in addition to the small number of loci at longer repeats (for instance, only seven loci in repeat range of n = 8–9), the reduction in the number of individuals per locus to less than three (due to quality filtering) in some instances rendered the threshold computation unreliable. In contrast, at least three individuals per locus were always available for our original analysis, where we did not separate the data into populations.
Using Orthologous Chimpanzee Sequences as Ancestral States
For each locus of interest, orthologous chimpanzee alleles were obtained from the hg18-panTro2 pair-wise alignments using Galaxy (http://g2.bx.psu.edu). Loci at which the orthologous chimpanzee sequence possessed different motif were discarded. PPRL (for repeats) and PPML (for monitors) as well as the associated 95% bootstrap confidence bands for [A/T]n and [GT/AC]n repeats were determined by binning the human repeat loci depending on the repeat numbers of the orthologous chimpanzee repeat loci.
Experimental Analysis
Reagents
Oligonucleotides used to construct the tandem repeat sequences were synthesized by Integrated DNA Technologies. Restriction endonucleases were supplied by Roche or New England Biolabs and were used according to manufacturer's instructions. 5-Fluoro-2'-deoxyuridine (FUdR) and all antibiotics were purchased from Sigma Chemical Co. Recombinant DNA pol β was purified as described previously (Opresko et al. 2000).
Construction of Vectors
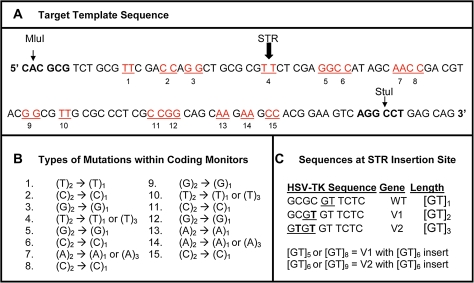
The HSV-tk-containing vector pSStu1 is a derivative of pGem3Zf(-) phagemid and has been previously described in Hile and Eckert (2008). Dinucleotide vectors containing the [GT/CA]4,7,10 series were constructed as described in Eckert and Yan (2000), by inserting 3, 6, or 9 tandem repeats in-frame between bases 111 and 112 of the target HSV-tk gene, in the sequence context GT^TCTC. To create the in-frame [GT/CA]5, [GT/CA]6, [GT/CA]8, and [GT/CA]9 motifs, sequences immediately flanking the insertion site were mutated to extend the repeated sequence (fig. 3). The [GT]5 and [GT]8 motifs contain a C→T substitution at position 109 along with an in-frame insertion of 3 or 6 units, respectively. The [GT]6 and [GT]9 motifs contain two C→T substitutions at positions 109 and 107 along with in-frame motif insertions. To ensure that the base substitutions introduced to create the [GT/CA] series did not disrupt HSV-tk protein function and subsequent selection, the HSV-tk phenotype was confirmed by selective plating in the presence 2 μg/ml trimethoprim, an antibiotic that selects for bacteria carrying a wild-type, plasmid-encoded HSV-tk gene.
FIG. 3.—
Design of the HSV-tk experimental assay. (A) Sequence of the MluI to StuI mutational target (sense strand). The arrow indicates the point of in-frame insertion of tandem repeats of varying length. Sequences and location of the 15 dinucleotide monitors are indicated. (B) Examples of experimentally observed mutations at monitor loci. (C) Base substitution changes immediately flanking the short tandem repeat (STR) insertion site that were used to generate variant HSV-tk sequences and create a series of tandem repeat lengths that are in-frame and vary by one unit increments.
In Vitro HSV-tk Mutagenesis Assay
Linear DNA fragments and ssDNA were prepared and used to construct gapped duplex (GD) molecules for each construct, as described (Eckert et al. 2002; Hile and Eckert 2008). The in vitro reactions contained 1 pmol of template DNA at 40 nM concentration. Two independent polymerase reactions were performed for each [GT] and [CA] tandem repeat-containing template. Reaction conditions for pol β were as described (Eckert et al. 2002), except that 10 pmol of enzyme were used. To sample reaction products for mutations, small fragments were prepared by Mlu I and Stu I restriction digestion and hybridized to the corresponding GD as described (Eckert et al. 2002; Hile and Eckert 2008). Successful hybridization to GD was achieved for all reactions, as determined by gel electrophoresis. An aliquot of DNA from the final hybridization was used to transform Escherichia coli strain FT334 by electroporation, and selection for mutants was performed (Eckert et al. 1997). Briefly, to select for HSV-tk mutant plasmids, bacteria were plated in the presence of 40 mM FUdR and 50 mg/ml chloramphenicol. The HSV-tk mutant frequency is defined as the number of FUdR-resistant + CmR colonies divided by the total number CmR colonies. To control for preexisting mutations present within the DNA synthesis template, we determined the HSV-tk mutation frequency for each ssDNA by electroporation of FT334, followed by selective plating on media containing 250 μg/ml carbenicillin in place of chloramphenicol, with or without FUdR. For each template, the polymerase error frequency was calculated by subtracting the ssDNA background mutation frequencies from the observed pol β HSV-tk mutation frequencies. To determine the polymerase error frequency within each target region, a mutational spectrum was generated for pol β using each template. For each spectrum, independent mutants were isolated from at least two independent polymerase reactions per template. The DNA sequence changes within the Mlu I-Stu I region were determined by dideoxy sequencing analyses. The polymerase error frequency of a specific type of error (e.g., indel within the repeat or indel at a monitor locus) was calculated from the proportion of the specific mutants (among the total sequenced) multiplied by polymerase error frequency for each template. Because the [GT/CA] motif is one target site, whereas the monitor frequency is the summation of errors occurring over 15 sites, we normalized the monitor error frequency by dividing it by the number of detectable sites.
Computing Confidence Intervals
Only a small portion of the DNA polymerase synthesis reaction products is analyzed for mutations. Therefore, we computed confidence intervals (CIs) to estimate the error associated with sampling, for each [GT/CA] template. The fraction of mutants having indels at the short tandem repeat and/or monitor loci is known for a finite number (64–109) of FUdR− + Cm-resistant colonies, as determined by selective plating and direct sequencing (supplementary table S3, Supplementary Material online). To calculate the 95% CIs for the estimates of tandem repeat and monitor indel frequencies, we carried out a bootstrap procedure. For each template, we resampled the sequenced mutants with replacement, thus creating 1,000 bootstrap samples. For each such bootstrap sample, the indel frequency at the [GT/CA] motif was calculated, and the 2.5th and 97.5th percentiles of the resulting frequencies were used to create 95% bootstrap CIs for [GT/CA] indel frequency (supplementary table S3, Supplementary Material online). Similarly, for each bootstrap sample, indel frequency at monitor loci was calculated, and the 2.5th and 97.5th percentiles of the frequencies were used to create 95% bootstrap CIs for monitor indel frequency (fig. 4).
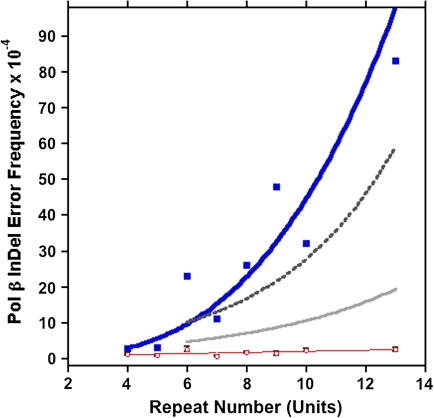
FIG. 4.—
The dependence of pol β indel error frequency at [GT/CA]n repeats and at two-unit mononucleotide monitors on repeat number. Blue symbols: summed indel error rate at GT and CA repeats (overall pol β error frequencies, CIs, and numbers of mutants observed within each motif and on each strand are given in supplementary table S3 and fig. S4, Supplementary Material online). Blue line, best curve fit of the data to the equation, y = 0.042756 × x3.0138; R = 0.94062. Red symbols: summed monitor indel error rate per site. Red line, best fit of the data to the equation, y = 0.29756 + 0.1658x; R = 0.62378. Black bars: 95% bootstrap-based confidence bands around the red symbols (in some cases, the bar is so narrow as to be indistinguishable from the data point). Dark gray dashed line: pol β error rate on the CA strand, best fit of the data to the exponential equation y = 2.2228 × e0.25245x; R = 0.98989. Light gray line, pol β error rate on the GT strand, best fit of data to the exponential equation y = 1.4048 × e0.20202x; R = 0.57692 (for a more detailed presentation of the data, see supplementary fig. S4, Supplementary Material online).
Results
To determine what constitutes a microsatellite, we employed two different approaches—computational and experimental. Both approaches are based on the same working definition of microsatellites, that is, tandem repeats having a minimal number of units that is required for the production of unit-based indel mutations at a frequency greater than the average frequency of indel mutations within the genome overall.
Computational Definition of Microsatellites
Computationally, we used an assumption that, as a reflection of dynamic mutational activity, microsatellites are expected to exhibit significantly higher prevalence of intraspecific polymorphism than nonmicrosatellite repeat loci in the genome. We utilized human population resequencing data and contrasted the PPRL with various repeat numbers to that at two-unit repeat “monitor” sites of potential indel errors.
Identification of Repeat Loci
Mono- through tetranucleotide repeat loci (with at least n = 2 repeats) were identified in ten 0.5-Mb ENCODE regions that were resequenced in 48 humans (supplementary table S1, Supplementary Material online) as part of the HapMap-ENCODE project (International HapMap Consortium 2003; International HapMap Consortium 2005). We restricted our analysis to simple (i.e., containing a single motif) uninterrupted repeats. Different repeated motifs were analyzed separately because mutational properties of repeats are, in part, determined by motif identity (Hile et al. 2000; Kelkar et al. 2008; Eckert and Hile 2009).
We focused our analysis on [A/T]n and [GT/CA]n repeats, as, after rigorous filtering, these were the only motifs for which we obtained substantial numbers of loci over a wide range of repeat lengths (we required at least seven loci per repeat number bin to obtain a reliable polymorphism occurrence estimate, see below) in the ENCODE resequencing data set (supplementary table S2, Supplementary Material online; data not shown). Specifically, we discarded loci that 1) contained reads with low sequence quality, 2) exhibited elevated sequence diversity in their flanking sequences, or 3) overlapped with or were immediately adjacent to either other repeat loci or coding regions of genes (supplementary table S2, Supplementary Material online). After this filtering, our final data set consisted of 201,102 and 25,052 [A/T]n and [GT/CA]n repeat loci, respectively.
Polymorphism at Repeat Loci
Repeats ([A/T]n and separately [GT/CA]n) were binned according to the repeat number of the modal (most frequent and hence likely ancestral) allele at each locus. Next, the PPRL, that is, the proportion of loci with at least two alleles differing in repeat number, was calculated for each bin. Slippage mutations at a neutrally evolving repeat locus lead to differences in repeat number, that is, polymorphism, among its alleles. Therefore, the differences in polymorphism prevalence among bins can be attributed to distinct slippage-induced mutation rates at loci depending on repeat number, with the PPRL statistic functioning as a proxy for slippage rates. As most polymorphic loci had only two alleles, polymorphism prevalence (a binary metric—either presence or absence of polymorphism) and not polymorphism level was estimated for each bin.
We observed that indeed polymorphism prevalence grows with repeat number (figs. 1 and 2)—however, it does so with qualitatively different regimes, suggestive of two distinct modes of mutational behavior. More specifically, polymorphism prevalence was low and almost constant at small repeat numbers (relatively low mutability) but grew markedly at large repeat numbers (hypermutability). For [A/T] repeats, less than 3% of loci with nine or less repeats were polymorphic; in contrast, >20% and >30% of loci with n = 10–11 and n ≥ 12 repeats were polymorphic, respectively (fig. 1). Polymorphism occurrence for [GT/CA] repeats exhibited a comparable pattern; it increased with repeat number above 4, with a pronounced rise at n = 5–6 repeats and particularly at n = 7–8 repeats, where ∼50% of loci were polymorphic (fig. 2).
Comparing Slippage Rates at Repeats with Background Slippage Rates
A statistically significant departure of slippage rates at loci with a certain repeat number from background slippage rates is expected to indicate the onset of the dynamic mutational activity that is characteristic of microsatellites, and thus to provide an effective definition for the latter. The background rate of strand slippage was assessed computationally by measuring polymorphism occurrence at two-unit repeats that served as monitors. Here, monitors of background slippage were defined as nonmicrosatellite loci that nonetheless experience polymerase slippage; however, being smaller than microsatellites, they are not hotspots for slippage. Two-unit tandem repeats were employed as monitors of background slippage rate because they are the smallest repeats at which slippage can occur; however, due to their abundance, such loci can be used to measure the background slippage rates within the genome. Indels at nonrepetitive sequences are initiated almost exclusively by base mispairing (Bebenek and Kunkel 1990; Kunkel 1990); they exhibit extremely low slippage rates (Field and Wills 1998; Zhu et al. 2000; Eckert et al. 2002; Nishizawa M and Nishizawa K 2002; Brandstrom and Ellegren 2008), and thus cannot be called microsatellites.
The [A/T]n slippage rates were contrasted with the background slippage rates measured at monitor [A/T]2 and [C/G]2 loci (we pooled these because polymorphism occurrence was similar at monitors with different motifs). Similarly, the [GT/CA]n slippage rates were contrasted with the background rates measured at monitor two-unit dinucleotide motifs (again, dinucleotide monitors with different motifs were considered jointly). In all cases, slippage rates were approximated by polymorphism occurrence, with only unit-based indel mutations allowed among alleles. To control for possible regional variation (Hardison et al. 2003), the background slippage rate at monitors in the neighborhood of each tandem repeat was measured as the PPML among the 20 closest to the repeat (10 most adjacent upstream and downstream), and the average PPML was computed for each repeat number bin.
Interestingly, the observed two-regime mutational behavior of repeat loci (figs. 1 and 2) corresponds to two distinct relationships with the background slippage rates. The [A/T]n polymorphism prevalence below 10 repeats is not significantly different from that of monitor loci—as evident from the consistent overlap of the bootstrap bands of mean PPML and PPRL (the bootstrap bands for PPRL become wider as repeat number grows, due to a paucity of available loci). This implies that loci with repeat numbers below 10 have slippage rates indistinguishable from background slippage rates (low or background mutability). In stark contrast, polymorphism prevalence at [A/T]n loci with 10 repeats or more is significantly higher than those for monitor loci—as evident from the nonoverlapping bootstrap bands of mean PPRL and PPML. This suggests that loci above nine repeats exhibit the dynamic mutational behavior characteristic of microsatellites (hyper- or microsatellite mutability). Accordingly, we define a repeat number around 10 to be the minimal size for [A/T]n microsatellites, that is, the size at which slippage rates at [A/T]n loci significantly exceed the background slippage rates.
A similar biphasic behavior relative to the background slippage rates was observed for [GT/CA]n loci. Below 5–6 repeats, polymorphism occurrence and thus slippage rates at [GT/CA]n are statistically indistinguishable from those at monitor loci mutating at background slippage rates (fig. 2). At ≥5–6 repeats, [GT/CA]n loci exhibit a statistically significant increase in polymorphism occurrence over those at monitors (even though the separation of the PPRL and PPML bootstrap bands is not large). Therefore, the high incidence of polymorphism and thus the hypermutable behavior of [GT/CA]≥5–6 loci become evident, with inferred slippage rates significantly above the background slippage rates, and such loci can be considered microsatellites. We also measured the PPML at [GT/CA]n loci using mononucleotide monitors in their neighborhoods. The polymorphism levels for mono- and dinucleotide monitors were very similar (supplementary fig. S1, Supplementary Material online). Therefore, the background slippage rates can be effectively measured with the use of either mono- or dinucleotide monitors.
Population Differences
Populations with different histories may harbor different levels of polymorphism and this might affect estimation of the transition length required for a locus to become a microsatellite. To investigate whether the transition in mutability is population specific, we focused on mononucleotide repeats. These were abundant (>50 of loci for each bin), allowing for statistically reliable estimates of polymorphism for each population (we lacked data to perform a similar population-specific analysis for dinucleotide repeats). The [A/T]n repeat was investigated separately in the three populations—Africans, represented by Yoruba people in Ibadan, Nigeria (YRI), Northern, and Western Europeans, represented by individuals from Utah (CEU), and Eastern Asians, represented by individuals from Beijing, China, and Tokyo, Japan (CHB + JPT). Our results (supplementary fig. S2, Supplementary Material online) indicate that the [A/T]n transition value for all populations is identical to the one determined by combining these populations together (fig. 1). Also, the statistical power in identifying the transition value remains high within populations (nonoverlapping bootstrap bands above n = 9 in all panels of supplementary fig. S2, Supplementary Material online). This suggests that the biphasic relationship of PPML to repeat number is not population specific but rather species wide. In agreement with previous studies (International HapMap Consortium 2005), Africans exhibited higher polymorphism levels above 9 units, as compared with Europeans and East Asians whose populations went through recent population bottlenecks (Watkins et al. 2001).
Using Chimpanzee Sequence to Infer the Ancestral state of Human Alleles
As an alternative way to infer the ancestral state at each locus, instead of using the modal human repeat number, we utilized the repeat number of an orthologous chimpanzee microsatellite. We selected only those loci (95% of the total) for which the chimpanzee allele was present in at least one individual resequenced in human populations. In spite of the smaller number of loci investigated, our results (supplementary fig. S3, Supplementary Material online) indicate that the [A/T]n as well as [AC/GT]n transition values identified using this approach are identical to those obtained above.
Experimental Definition of Microsatellites
The intriguing biphasic dependence of polymorphism prevalence on repeat number and its relationship with polymorphism occurrence at monitor loci prompted us to test the very assumption of the computational definition of microsatellites; namely, that polymorphism incidence indeed reflects slippage-induced mutational dynamics. If this assumption is correct, then we expect to observe a similar biphasic relationship between DNA polymerase slippage rates and repeat number. Alternatively, the rise in polymorphism incidence with increasing repeat number could result from loss of effective DNA mismatch repair correction of strand slippage errors (Harfe and Jinks-Robertson 2000; Gragg et al. 2002). We used our previously published HSV-tk experimental system to investigate the mutational dynamics of one of the two repeated motifs investigated computationally, [GT/CA]n. Sequence-specific transcriptional frameshifting within poly [A/T] tracts by E. coli RNA polymerase (Wagner et al. 1990) precludes our ability to use the HSV-tk system to measure mutations within [A/T]n tandem repeats longer than 9 units (Hile and Eckert 2008).
Design of the DNA Polymerase Assay
We carried out an in vitro mutation assay for [GT/CA]n repeats, using two-unit repeat loci from their flanking sequences as monitors of background slippage. In our published experimental system (Eckert et al. 2002; Hile and Eckert 2008), polymerase errors are analyzed using DNA vectors that encode an HSV-tk gene containing an artificial, in-frame, short tandem repeat. Forward mutations that inactivate the HSV-tk protein are scored after transfection of E. coli and selective plating. Polymerase errors that add or delete any number of bases within the tandem repeat that are not a multiple of three will result in a frameshift mutation and inactivate the HSV-tk protein. Base substitutions, frameshifts, and large deletions are also detectable within the surrounding HSV-tk coding sequence. Therefore, mutations occurring in either the tandem repeat or the HSV-tk coding sequence motif produce an inactive thymidine kinase protein that is detectable by the same selection scheme. Importantly, our HSV-tk target sequence (Hile and Eckert 2008) is very sensitive for the detection of slippage-mediated DNA polymerase errors at short repeats and contains 15 two-unit mononucleotide monitor sequences (AA, TT, GG, and CC; fig. 3). (This target sequence contains only four, two-unit dinucleotide motifs, which is too few to use as monitor loci; we also showed above that either mono- or dinucleotide monitors can effectively assess background slippage rates—supplementary fig. S1, Supplementary Material online.) We measured polymerase frameshift errors at the monitors to evaluate the background polymerase strand slippage error frequency within a representative coding sequence, analogous to the background slippage rates measured using repeat size polymorphism for monitors in the computational analysis above. To determine the mutational behavior of repeats of various sizes, we further engineered the HSV-tk gene to contain a series of tandem [GT/CA] motifs that differ in increments of one unit, from 4 through 13 units (fig. 3). Importantly, all alleles encode a wild-type HSV-tk gene, so that both insertion and deletion polymerase errors within the short tandem repeat as well as errors within the HSV-tk coding sequence monitors can be scored using the forward mutation assay.
All DNA polymerases studied in vitro to date, including the E. coli Klenow fragment polymerase and bacteriophage T4 and T7 DNA polymerases, display strand slippage when utilizing templates containing long microsatellites (Schlötterer and Tautz 1992; Kroutil et al. 1996; da Silva and Reha-Krantz 2000). In this study, we used mammalian DNA polymerase β (pol β) as a model to test the relationship between tandem repeat allele length and slippage-induced mutational dynamics, for several reasons. First, pol β contains no associated 3'→5' proofreading exonuclease activity, which affects the frequency of both frameshift and microsatellite mutations (Kroutil et al. 1996; Eckert and Hile 2009). Second, we have shown previously that pol β produces a significant number of slippage-mediated errors within the HSV-tk coding sequence and that pol β errors within 2-unit mononucleotide sequences occur at a low but detectable frequency (Eckert et al. 2002). Third, we have demonstrated that pol β creates both unit-based indel errors and interruptions within the [GT/CA]10 microsatellite (Eckert et al. 2002). Thus, using pol β allows us to examine mechanisms of the microsatellite mutation process in a manner that will not be biased by the inherent error specificity of the polymerase.
Experimental Observation of Polymerase Errors within [GT/CA]n Motifs
We measured the pol β error frequency on each complementary DNA strand, as the number of [GT] or [CA] units increased from 4 to 13 (supplementary table S3, Supplementary Material online). After DNA sequence analyses of ∼60–100 independent mutants for each template, polymerase errors were classified as arising within the tandem repeat sequence (unit-based indels or interruptions) or within the HSV-tk sequence monitors (supplementary table S3, Supplementary Material online). The [CA]4 and [CA]5 tandem repeats exhibited a very low frequency of indel errors (∼10−4). However, a significant increase in indel error frequency was observed for the [CA]6 template (10−3; supplementary fig. S4A, Supplementary Material online), and we observed a strictly exponential relationship between the pol β error frequency and [CA] length, as the number of repeats increased further, from 6 to 13 units (fig. 4; supplementary fig. S4A, Supplementary Material online). A similar relationship between indel error rate and repeat number was observed for the [GT] strand, although the pol β error rate was more variable than observed for the [CA] strand (supplementary fig. S4A, Supplementary Material online). We attribute this variability to a difference in the 5′ sequence context of the V2 HSV-tk allele, which was the parent sequence for the [GT]6 and [GT]9 motifs, relative to the wild-type and V1 HSV-tk sequences (see fig. 3C). Nevertheless, a greater than linear relationship between the pol β indel error rate and repeat number was observed for [GT] motifs of 6–13 units in length (supplementary fig. S4A, Supplementary Material online).
In order to compare these experimental results with the computational analyses, we summed the observed average pol β indel error rates for the [CA] and [GT] strands and determined the average indel error rate at the 15 monitor sites observed for all 16 templates (supplementary table S3, Supplementary Material online). Pol β errors were randomly distributed among the 15 monitor sites on both strands, with the characteristic appearance of mutational hotspots and coldspots, depending on the sequence context (supplementary fig. S5, Supplementary Material online). The average frequency of pol β HSV-tk indel errors per monitor site was 1.6 ± 1.7 × 10−4 (95% CI 0.42–3.9 × 10−4) (fig. 4). This indel error rate at two-unit mononucleotide monitors thus serves as the background error frequency against which we can directly compare polymerase errors generated within [GT/CA]n motifs of varying length, in a manner similar to the computational analyses presented above.
As shown in figure 4, we observe an increasing indel error rate as the tandem repeat number increases, with a marked transition above an array of five units. The indel error frequency within [GT/CA]4 (2.6 × 10−4; CI, 0.61–4.9 × 10−4) is not greater than the average error frequency at monitors. Similarly, the pol β indel error frequency within [GT/CA]5 is 3.1 × 10−4 (CI, 1.2–6.4 × 10−4), within the monitor frequency CI. In contrast, the indel frequency for [GT/CA]6 is 14-fold greater and that for [GT/CA]7 is 7-fold greater than the average monitor frequency. The indel frequency continued to be greater than the monitor frequency and markedly increased as the number of tandem GT/CA units increased through 13 units. We also observed differences in the types of pol β indel errors (insertions vs. deletions) produced within the [GT/CA]n motifs of varying lengths. Interestingly, we observe a statistically significant linear trend of an increasing proportion of expansion errors with length, for motifs ≥7 units (P = 0.0009, χ2 test). Motifs of 10 units or more represent robust, mature microsatellites that display the attribute of dynamic mutation equally in both directions (supplementary fig. S4B, Supplementary Material online).
Definition of a Microsatellite Based upon Mutational Behavior
Our in vitro mutagenesis (experimental) and population genomic (computational) analyses of alterations in the mutational behavior of [GT/CA]n repeats with increasing length are in remarkable agreement. At small repeat numbers (n ≤ 4 units), both polymerase error frequencies and the prevalence of polymorphism in human populations are low, very similar to the corresponding measurements at two-unit monitor loci. A marked transition in mutability is observed as the tandem repeat array lengthens, such that at large repeat numbers (at ≥5–6 units), polymerase error frequencies and the prevalence of polymorphism are significantly higher than those at monitor loci. These results validate the use of polymorphism incidence as a proxy for slippage rates. Thus, we can define microsatellites based on the dynamics of strand slippage, their major mutational mechanism.
Discussion
In an attempt to define a microsatellite DNA sequence, we investigated the mutational dynamics of two microsatellite motifs with variable repeat numbers, employing population genomic and in vitro mutagenesis approaches. Importantly, our results uncovered a conspicuous, biphasic mutational behavior of repetitive loci that depends on repeat number. Below a transitional repeat number (10 repeats for [A/T]n and 5–6 repeats for [GT/CA]n), the rate of slippage is low and indistinguishable from the background slippage rate; thus, the repeats cannot be considered microsatellites. Above these repeat numbers, the rate of slippage becomes significantly higher than the background slippage rate; therefore, the repeats can be identified as microsatellites. In the case of [GT/CA]n, consistent transitional values were obtained with the use of both computational (fig. 2) and experimental (fig. 4) approaches.
Our analysis suggests that, to become a sustainable microsatellite, a short tandem repeat needs to meet a minimal size requirement that allows it to acquire slippage rates higher than the overall genome slippage error rate and, according to our experimental results, to overcome the directionality bias that favors deletion errors. From this turning point onward, the strand slippage rates escalate in a manner that is characteristic of microsatellites. We emphasize that strand slippage errors occur at both microsatellites and shorter repeats; however, the dynamic mutational behavior is acquired only as the tandem repeat array lengthens. Therefore, our results argue for the existence of a microsatellite threshold that is determined not simply by the presence/absence of strand slippage at repeats (Dechering et al. 1998; Rose and Falush 1998; Lai and Sun 2003) but by an abrupt alteration in slippage rates and directionality relative to background slippage rates.
Although a transition in slippage rates occurring at a certain repeat number has been previously noted, this is the first study that effectively identifies this transition in relation to background slippage rate. Thus, this transition corresponds not to the onset of slippage but to the size at which a repeat can be usefully distinguished from its genomic background.
A Comparison of Threshold Values among Studies
The transition values obtained here are comparable with threshold values obtained in several investigations; for instance, our 10-repeat threshold for the mononucleotide [A/T]n is consistent with the ones identified by Lai and Sun (2003) (9 repeats) and by Dechering et al. (1998) (≥10 repeats). However, it is substantially higher than the value obtained by Dieringer and Schlötterer (2003) (3 repeats), who proposed the threshold as a boundary between length-independent and length-dependent slippage at low and high repeat numbers, respectively. Although our results agree with this observation qualitatively, quantitatively we identify a different turning point between these two behaviors for [A/T]n. For the dinucleotide [GT/CA]n, our 5–6 threshold is somewhat higher than the one identified for humans by Lai and Sun (2003) (4 repeats) and than the transition between low and high polymorphism levels for chicken dinucleotide repeats (4–5 repeats [Brandstrom and Ellegren 2008]). Our results clearly demonstrate that the onset of hypermutability for dinucleotide repeats occurs above 4 units, which is higher than 2 repeats suggested by Dieringer and Schlötterer (2003).
Mechanistic Basis for the Alteration in Repeat Mutational Behavior
The mutational behavior transition points we observed for mono- and dinucleotide repeats correspond to a similar total array length (10–12 nucleotides). This length also corresponds to a transition in mutational behavior of intronic and exonic trinucleotide repeats, as noted by Molla et al. (2009). This suggests that the change in mutational behavior depends on the total length of the repetitive array, corroborating some previous studies (Rose and Falush 1998; Dieringer and Schlötterer 2003). This observation may seem counterintuitive at first because strand slippage mutations lead to unit-based alterations in length, and thus the probability of slippage is expected to be influenced by repeat unit number. However, we emphasize that the relationship between microsatellite mutability and repeat length is more complex than simply the influence of repeat number on the probability of strand slippage (Eckert et al. 2002; Kelkar et al. 2008; Eckert and Hile 2009).
Our computational approach reflects the summation of mutational forces within a cell that contribute to microsatellite sequence variation, including errors created by several cellular polymerases during DNA synthesis (Sweasy et al. 2006) as well as repair processes (e.g., mismatch repair) (Harfe and Jinks-Robertson 2000; Eckert and Hile 2009). Additionally, repeat mutations are investigated in their native genomic environment and for multiple genomic loci (eventually genome wide) simultaneously. Therefore, the study of a single DNA polymerase cannot be used to directly describe microsatellite mutagenesis in human cells. Intriguingly, however, we observed a striking similarity in the transition lengths obtained for the [GT/CA] motif computationally and experimentally, using a model eukaryotic DNA polymerase. Such a concordance may imply that the transition length observed in the genome studies is driven primarily by the effects of repeat number on DNA strand slippage rates during DNA synthesis. We will test the extent to which such agreement between experimental and computational approaches can be generalized in future studies using the complementary HSV-tk shuttle vector microsatellite mutagenesis assay and repair-proficient human cells (Eckert et al. 2002; Shah and Eckert 2009).
What might account for the observed length-dependent alteration in tandem repeat mutational dynamics? Assuming that strand slippage during DNA synthesis is a driving force, we propose three mechanistic models, which are not mutually exclusive. First, the length-dependent transition may reflect a change in the thermodynamic properties of the bulged (misaligned) DNA premutational intermediates resulting from strand slippage. Examinations of DNA bulges in solution have shown that translocation of the bulge into several positions within a repeated sequence is less thermally destabilizing, relative to nonbulged DNA (Woodson and Crothers 1987; Rosen et al. 1992). In this scenario, the low mutability of small tandem repeats may reflect the fact that the bulged DNA intermediates are relatively unstable; increasing the allele length above the threshold results in stabilization of the bulged intermediates by allowing the bulge to be present at multiple positions throughout the tandem array. However, this model does not readily explain why the transition point for mono- and dinucleotide alleles corresponded to a similar total length (in nucleotides) rather than a similar number of units because the bulged bases within tandem repeats are expected to be the respective units (A/T or GT/CA).
A second explanation for the length-dependent change in mutational behavior is that alternative, non-B-form DNA structures are stabilized within the repetitive array after the transition length has been reached. DNA polymerase discrimination against errors during DNA synthesis depends on direct minor groove interactions of the protein with the DNA primer template, and disruptions in N3 purine and O2-pyrimidine atom positioning decreases polymerase fidelity (reviewed in Kunkel and Bebenek 2000). In physical structures, (CA)2 tracts exhibit shifted base pairing, in which bases are not paired with their Watson–Crick complements but with their direct 5′ neighbors on the opposite strand (Timsit et al. 1991). Such an unusual structure has been described as a preslipped DNA form that may account for the high mutability of [GT/CA]n repeats (Timsit 1999). Sequences as short as 8 bps of alternating purine–pyrimidine nucleotides may form Z-DNA structures (Rich et al. 1984; Kim et al. 1996), and poly(A/T) sequences longer than 7 bp create uniformly bent DNA structures (Nadeau and Crothers 1989; Crothers et al. 1990). Both of these alternative DNA structures display changes in helical parameters that will alter the positioning of minor groove functional groups (Sinden 1994). Furthermore, repeated sequences assume non-B DNA conformations with motif-specific thermodynamic properties (Baldi and Baisnee 2000). This structure-based model predicts that the transition length for mutability of a tandem repeat will depend on the repeated motif sequence.
Third, the length-dependent transition from low to high mutability may represent loss of the stabilizing influence of the DNA polymerase protein bound to the DNA. The footprint length of bound DNA differs among DNA polymerases but generally includes several nucleotides downstream (duplex DNA primer stem) and upstream (ssDNA template) of the nascent base pair (Kunkel and Bebenek 2000), such that at least 9–11 nucleotides are occluded by the enzyme (Rajendran et al. 1998; Swan et al. 2009). Therefore, short repeat arrays will be completely bound by the polymerase during DNA synthesis, whereas longer arrays will have the potential for the formation of bulges away from the site of DNA synthesis. A recent study has suggested that the structure of an unpaired (looped) base at the primer-template junction is distinctly different from the structure of a bulge in duplex DNA and is less thermally stable (Baase et al. 2009). Also, the structure of DNA within polymerase active sites is more characteristic of A-form than B-form DNA, a fact that has been proposed to negatively affect the formation of preslipped DNA within (CA)n tracts (Timsit 1999). Finally, it has been suggested that increasing the distance between bulged nucleotides and the polymerase active site elevates the probability of efficient DNA polymerase extension of misaligned DNA substrates, thus increasing the likelihood of successful slippage-related indel errors (Garcia-Diaz and Kunkel 2006). Because the number of nucleotides bound and the structure of DNA within the active site vary among DNA polymerases, this model predicts that the identity of the DNA polymerase will influence the observed transition length for mutability. In conclusion, we emphasize that none of the above models are mutually exclusive and that several mechanisms may cooperatively contribute to the dramatic change in mutational behavior that is observed upon increasing the length of a tandemly repeated sequence.
Applications
We have presented a novel, combined computational and experimental approach to define a microsatellite. Semantics aside, our study has several important applications. First and significantly, we provide a means of determining which repeats are expected to be polymorphic in a genome (those with a number of repeats above the transition from low to high mutability), and, if situated in functionally important regions, they should be investigated in future association studies. Indeed, length polymorphisms within the two motifs examined in our study are well known modifiers of gene expression and human disease risk (Chu et al. 1993; Cuppens et al. 1998; Gebhardt et al. 1999; Buerger et al. 2004; Hui et al. 2005). Thus, the transition values obtained here for human [A/T]n and [GT/CA]n repeats can be utilized directly for the purpose of developing markers for future association studies. Transition values for other repeated motifs in the human genome can be obtained computationally (once more abundant polymorphism data for a larger number of loci become available, e.g., from the 1,000 Genomes Project; www.1000genomes.org) and confirmed experimentally in future studies.
Second, our approach, once its application to the majority of microsatellite motifs becomes possible (see above), should set a standard for more direct comparisons among microsatellite studies. Various microsatellite search algorithms implement different cut-off values in terms of either repeat or nucleotide numbers (Leclercq et al. 2007), which are taken from previous determinations of threshold values or chosen to reduce program running time. Apart from this, large-scale genomic microsatellite surveys have used different cut-off values to extract microsatellite sequences (Denver et al. 2004; Prasad et al. 2005; Brandstrom and Ellegren 2008; Kelkar et al. 2008). This has prevented broad comparisons of microsatellite mutation dynamics across different studies, and the approach presented here is expected to alleviate this limitation.
Third, the model of microsatellite mutational behavior put forth here can be readily applied to the definition of microsatellite births. According to the microsatellite life cycle hypothesis (Amos 1999; Buschiazzo and Gemmell 2006), crossing the transition length propels a repeat locus toward high mutation rates, which are the defining feature of the “adulthood” stage. Our characterization of the microsatellite threshold based on mutation dynamics of repeats reflects this fundamental property of microsatellite birth in the life cycle.
Limitations
Our computational approach depends on determining the intraspecific polymorphism prevalence, which might be influenced by population parameters. As indicated by our results, polymorphism occurrence at loci with various repeat numbers is representative of the actual strand slippage rates, which are expected to be similar for all populations belonging to a species and does not depend on human populations analyzed in the present study. However, more dramatic population history effects in other species (e.g., a bottleneck) may reduce variation at repeats of all sizes, including the two-unit monitors and, thus, might reduce the statistical power of detecting differences in slippage rates as inferred from polymorphism prevalence at repeat loci. Although we expect such situations to be rare, it is still critical to sample a large number of individuals per locus (at least 30) or a large number of loci per individual in such populations.
As we pooled all loci from the ten resequenced ENCODE regions, we were limited in investigating the possibility of regional genomic features—for instance, proximity to recombination hotspots, regional nucleotide composition, and substitution rates—in influencing regional mutational dynamics at repeat loci (Brandstrom et al. 2008).
The ENCODE-HapMap resequencing data set used in the computational component of our analysis is limiting in the number of motifs that could be studied. As we calculated polymorphism prevalence for bins that have at least seven loci, we could not extend this analysis to motifs other than [A/T]n and [GT/AC]n, as, after filtering, other motifs had at most three loci at bin sizes above 4 repeats. Other resequencing data sets accessible at the time of writing do not offer the key advantage of the ENCODE-HapMap data set, namely, the availability of a significant number of intronic and intergenic loci sequenced in a large group of individuals from which polymorphism presence/absence can be rigorously investigated.
Lack of sufficient number of [GT/AC]n in the resequencing data set restricted our population-specific determination of threshold values to [A/T]n alone. Although the similarity of population-specific threshold values for [A/T]n is assumed to extend to other motifs and motif sizes, further investigations (e.g., using the data of the 1,000 Genomes Project) will be required to test this hypothesis.
Summary
We have used two mechanistic approaches to examine the very property that characterizes microsatellites—the dynamic behavior of slippage-related mutations. The computational approach utilized here, assessing size polymorphism at repeat loci, presents an instantaneous computational view of strand slippage acting in the genome because the presence of indel polymorphisms reflects few, relatively recent mutational events. This approach differs from previous studies, which primarily analyzed the genome-wide repeat size distributions, whose relationship with actual slippage rates is still debated. The experimental approach directly quantifies DNA polymerase strand slippage indel rates at repeats with varying numbers. Our combined study demonstrates that the mutational behavior of repeat loci changes from low mutability at small repeat numbers, similar to overall genome background slippage rates, to hypermutability at large repeat numbers, characteristic of microsatellites. The striking agreement of the dynamic repeat mutational behavior of [GT/CA]n as inferred by two very different approaches—population genomic and in vitro mutagenesis—lends credence to our proposal that the microsatellite threshold is not a magic integer number of repeat units but corresponds to real differences in slippage-induced mutational dynamics between the DNA and the polymerase during genome replication.
Supplementary Material
Supplementary figures S1–S5 and tables S1–S3 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).
Acknowledgments
We are thankful to the members of Eckert's and Makova's laboratories for helpful discussions. Funding for this project was provided by the National Institutes of Health (R01GM087472 to K.D.M., K.A.E., and F.C.; R01CA100060 to K.A.E.), by the PA Department of Health (SAP#4100047645 to K.A.E.), and by the Huck Institute of Life Sciences (Penn State University).
References
- Amos W. A comparative approach to study the evolution of microsatellites. In: Goldstein DB, Schlötterer C, editors. Microsatellites: evolution and applications. Oxford: Oxford University Press; 1999. p. xv. p. 352. [Google Scholar]
- Amos W, Sawcer SJ, Feakes RW, Rubinsztein DC. Microsatellites show mutational bias and heterozygote instability. Nat Genet. 1996;13:390–391. doi: 10.1038/ng0896-390. [DOI] [PubMed] [Google Scholar]
- Baase WA, Jose D, Ponedel BC, von Hippel PH, Johnson NP. DNA models of trinucleotide frameshift deletions: the formation of loops and bulges at the primer-template junction. Nucleic Acids Res. 2009;37:1682–1689. doi: 10.1093/nar/gkn1042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldi P, Baisnee PF. Sequence analysis by additive scales: DNA structure for sequences and repeats of all lengths. Bioinformatics. 2000;16:865–889. doi: 10.1093/bioinformatics/16.10.865. [DOI] [PubMed] [Google Scholar]
- Bebenek K, Kunkel TA. Frameshift errors initiated by nucleotide misincorporation. Proc Natl Acad Sci U S A. 1990;87:4946–4950. doi: 10.1073/pnas.87.13.4946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandstrom M, Bagshaw AT, Gemmell NJ, Ellegren H. The relationship between microsatellite polymorphism and recombination hot spots in the human genome. Mol Biol Evol. 2008;25:2579–2587. doi: 10.1093/molbev/msn201. [DOI] [PubMed] [Google Scholar]
- Brandstrom M, Ellegren H. Genome-wide analysis of microsatellite polymorphism in chicken circumventing the ascertainment bias. Genome Res. 2008;18:881–887. doi: 10.1101/gr.075242.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brinkmann B, Klintschar M, Neuhuber F, Huhne J, Rolf B. Mutation rate in human microsatellites: influence of the structure and length of the tandem repeat. Am J Hum Genet. 1998;62:1408–1415. doi: 10.1086/301869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Britten RJ, Baron WF, Stout DB, Davidson EH. Sources and evolution of human Alu repeated sequences. Proc Natl Acad Sci U S A. 1988;85:4770–4774. doi: 10.1073/pnas.85.13.4770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buerger H, et al. Allelic length of a CA dinucleotide repeat in the egfr gene correlates with the frequency of amplifications of this sequence—first results of an inter-ethnic breast cancer study. J Pathol. 2004;203:545–550. doi: 10.1002/path.1542. [DOI] [PubMed] [Google Scholar]
- Bulmer M. Neighboring base effects on substitution rates in pseudogenes. Mol Biol Evol. 1986;3:322–329. doi: 10.1093/oxfordjournals.molbev.a040401. [DOI] [PubMed] [Google Scholar]
- Buschiazzo E, Gemmell NJ. The rise, fall and renaissance of microsatellites in eukaryotic genomes. Bioessays. 2006;28:1040–1050. doi: 10.1002/bies.20470. [DOI] [PubMed] [Google Scholar]
- Chen K, et al. PolyScan: an automatic indel and SNP detection approach to the analysis of human resequencing data. Genome Res. 2007;17:659–666. doi: 10.1101/gr.6151507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu CS, Trapnell BC, Curristin S, Cutting GR, Crystal RG. Genetic basis of variable exon 9 skipping in cystic fibrosis transmembrane conductance regulator mRNA. Nat Genet. 1993;3:151–156. doi: 10.1038/ng0293-151. [DOI] [PubMed] [Google Scholar]
- Cox R, Mirkin SM. Characteristic enrichment of DNA repeats in different genomes. Proc Natl Acad Sci U S A. 1997;94:5237–5242. doi: 10.1073/pnas.94.10.5237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crothers DM, Haran TE, Nadeau JG. Intrinsically bent DNA. J Biol Chem. 1990;265:7093–7096. [PubMed] [Google Scholar]
- Cuppens H, et al. Polyvariant mutant cystic fibrosis transmembrane conductance regulator genes. The polymorphic (Tg)m locus explains the partial penetrance of the T5 polymorphism as a disease mutation. J Clin Invest. 1998;101:487–496. doi: 10.1172/JCI639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- da Silva EF, Reha-Krantz LJ. Dinucleotide repeat expansion catalyzed by bacteriophage T4 DNA polymerase in vitro. J Biol Chem. 2000;275:31528–31535. doi: 10.1074/jbc.M004594200. [DOI] [PubMed] [Google Scholar]
- Dechering KJ, Cuelenaere K, Konings RN, Leunissen JA. Distinct frequency-distributions of homopolymeric DNA tracts in different genomes. Nucleic Acids Res. 1998;26:4056–4062. doi: 10.1093/nar/26.17.4056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denver DR, Morris K, Kewalramani A, Harris KE, Chow A, Estes S, Lynch M, Thomas WK. Abundance, distribution, and mutation rates of homopolymeric nucleotide runs in the genome of Caenorhabditis elegans. J Mol Evol. 2004;58:584–595. doi: 10.1007/s00239-004-2580-4. [DOI] [PubMed] [Google Scholar]
- de Wachter R. The number of repeats expected in random nucleic acid sequences and found in genes. J Theor Biol. 1981;91:71–98. doi: 10.1016/0022-5193(81)90375-1. [DOI] [PubMed] [Google Scholar]
- Dieringer D, Schlötterer C. Two distinct modes of microsatellite mutation processes: evidence from the complete genomic sequences of nine species. Genome Res. 2003;13:2242–2251. doi: 10.1101/gr.1416703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckert KA, Hile SE. Every microsatellite is different: intrinsic DNA features dictate mutagenesis of common microsatellites present in the human genome. Mol Carcinog. 2009;48:379–388. doi: 10.1002/mc.20499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckert KA, Hile SE, Vargo PL. Development and use of an in vitro HSV-tk forward mutation assay to study eukaryotic DNA polymerase processing of DNA alkyl lesions. Nucleic Acids Res. 1997;25:1450–1457. doi: 10.1093/nar/25.7.1450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckert KA, Mowery A, Hile SE. Misalignment-mediated DNA polymerase beta mutations: comparison of microsatellite and frame-shift error rates using a forward mutation assay. Biochemistry. 2002;41:10490–10498. doi: 10.1021/bi025918c. [DOI] [PubMed] [Google Scholar]
- Eckert KA, Yan G. Mutational analyses of dinucleotide and tetranucleotide microsatellites in Escherichia coli: influence of sequence on expansion mutagenesis. Nucleic Acids Res. 2000;28:2831–2838. doi: 10.1093/nar/28.14.2831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckert KA, Yan G, Hile SE. Mutation rate and specificity analysis of tetranucleotide microsatellite DNA alleles in somatic human cells. Mol Carcinog. 2002;34:140–150. doi: 10.1002/mc.10058. [DOI] [PubMed] [Google Scholar]
- Ellegren H. Microsatellite mutations in the germline: implications for evolutionary inference. Trends Genet. 2000;16:551–558. doi: 10.1016/s0168-9525(00)02139-9. [DOI] [PubMed] [Google Scholar]
- Ellegren H. Microsatellites: simple sequences with complex evolution. Nat Rev Genet. 2004;5:435–445. doi: 10.1038/nrg1348. [DOI] [PubMed] [Google Scholar]
- Field D, Wills C. Abundant microsatellite polymorphism in Saccharomyces cerevisiae, and the different distributions of microsatellites in eight prokaryotes and S. cerevisiae, result from strong mutation pressures and a variety of selective forces. Proc Natl Acad Sci U S A. 1998;95:1647–1652. doi: 10.1073/pnas.95.4.1647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia-Diaz M, Kunkel TA. Mechanism of a genetic glissando: structural biology of indel mutations. Trends Biochem Sci. 2006;31:206–214. doi: 10.1016/j.tibs.2006.02.004. [DOI] [PubMed] [Google Scholar]
- Gebhardt F, Zanker KS, Brandt B. Modulation of epidermal growth factor receptor gene transcription by a polymorphic dinucleotide repeat in intron 1. J Biol Chem. 1999;274:13176–13180. doi: 10.1074/jbc.274.19.13176. [DOI] [PubMed] [Google Scholar]
- Gordon D, Abajian C, Green P. Consed: a graphical tool for sequence finishing. Genome Res. 1998;8:195–202. doi: 10.1101/gr.8.3.195. [DOI] [PubMed] [Google Scholar]
- Gragg H, Harfe BD, Jinks-Robertson S. Base composition of mononucleotide runs affects DNA polymerase slippage and removal of frameshift intermediates by mismatch repair in Saccharomyces cerevisiae. Mol Cell Biol. 2002;22:8756–8762. doi: 10.1128/MCB.22.24.8756-8762.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammock EA, Young LJ. Microsatellite instability generates diversity in brain and sociobehavioral traits. Science. 2005;308:1630–1634. doi: 10.1126/science.1111427. [DOI] [PubMed] [Google Scholar]
- Hardison RC, et al. Covariation in frequencies of substitution, deletion, transposition, and recombination during eutherian evolution. Genome Res. 2003;13:13–26. doi: 10.1101/gr.844103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harfe BD, Jinks-Robertson S. DNA mismatch repair and genetic instability. Annu Rev Genet. 2000;34:359–399. doi: 10.1146/annurev.genet.34.1.359. [DOI] [PubMed] [Google Scholar]
- Hile SE, Eckert KA. Positive correlation between DNA polymerase alpha-primase pausing and mutagenesis within polypyrimidine/polypurine microsatellite sequences. J Mol Biol. 2004;335:745–759. doi: 10.1016/j.jmb.2003.10.075. [DOI] [PubMed] [Google Scholar]
- Hile SE, Eckert KA. DNA polymerase kappa produces interrupted mutations and displays polar pausing within mononucleotide microsatellite sequences. Nucleic Acids Res. 2008;36:688–696. doi: 10.1093/nar/gkm1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hile SE, Yan G, Eckert KA. Somatic mutation rates and specificities at TC/AG and GT/CA microsatellite sequences in nontumorigenic human lymphoblastoid cells. Cancer Res. 2000;60:1698–1703. [PubMed] [Google Scholar]
- Huang QY, et al. Mutation patterns at dinucleotide microsatellite loci in humans. Am J Hum Genet. 2002;70:625–634. doi: 10.1086/338997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hui J, et al. Intronic CA-repeat and CA-rich elements: a new class of regulators of mammalian alternative splicing. EMBO J. 2005;24:1988–1998. doi: 10.1038/sj.emboj.7600677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iglesias AR, Kindlund E, Tammi M, Wadelius C. Some microsatellites may act as novel polymorphic cis-regulatory elements through transcription factor binding. Gene. 2004;341:149–165. doi: 10.1016/j.gene.2004.06.035. [DOI] [PubMed] [Google Scholar]
- International HapMap Consortium. The International HapMap Project. Nature. 2003;426:789–796. doi: 10.1038/nature02168. [DOI] [PubMed] [Google Scholar]
- International HapMap Consortium. A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelkar YD, Tyekucheva S, Chiaromonte F, Makova KD. The genome-wide determinants of human and chimpanzee microsatellite evolution. Genome Res. 2008;18:30–38. doi: 10.1101/gr.7113408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Yang C, DasSarma S. Analysis of left-handed Z-DNA formation in short d(CG)n sequences in Escherichia coli and Halobacterium halobium plasmids. Stabilization by increasing repeat length and DNA supercoiling but not salinity. J Biol Chem. 1996;271:9340–9346. doi: 10.1074/jbc.271.16.9340. [DOI] [PubMed] [Google Scholar]
- Kroutil LC, Register K, Bebenek K, Kunkel TA. Exonucleolytic proofreading during replication of repetitive DNA. Biochemistry. 1996;35:1046–1053. doi: 10.1021/bi952178h. [DOI] [PubMed] [Google Scholar]
- Kunkel TA. Misalignment-mediated DNA synthesis errors. Biochemistry. 1990;29:8003–8011. doi: 10.1021/bi00487a001. [DOI] [PubMed] [Google Scholar]
- Kunkel TA, Alexander PS. The base substitution fidelity of eucaryotic DNA polymerases. Mispairing frequencies, site preferences, insertion preferences, and base substitution by dislocation. J Biol Chem. 1986;261:160–166. [PubMed] [Google Scholar]
- Kunkel TA, Bebenek K. DNA replication fidelity. Annu Rev Biochem. 2000;69:497–529. doi: 10.1146/annurev.biochem.69.1.497. [DOI] [PubMed] [Google Scholar]
- Lai Y, Sun F. The relationship between microsatellite slippage mutation rate and the number of repeat units. Mol Biol Evol. 2003;20:2123–2131. doi: 10.1093/molbev/msg228. [DOI] [PubMed] [Google Scholar]
- Laken SJ, et al. Familial colorectal cancer in Ashkenazim due to a hypermutable tract in APC. Nat Genet. 1997;17:79–83. doi: 10.1038/ng0997-79. [DOI] [PubMed] [Google Scholar]
- Leclercq S, Rivals E, Jarne P. Detecting microsatellites within genomes: significant variation among algorithms. BMC Bioinformatics. 2007;8:125. doi: 10.1186/1471-2105-8-125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legendre M, Pochet N, Pak T, Verstrepen KJ. Sequence-based estimation of minisatellite and microsatellite repeat variability. Genome Res. 2007;17:1787–1796. doi: 10.1101/gr.6554007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levinson G, Gutman GA. Slipped-strand mispairing: a major mechanism for DNA sequence evolution. Mol Biol Evol. 1987;4:203–221. doi: 10.1093/oxfordjournals.molbev.a040442. [DOI] [PubMed] [Google Scholar]
- Li YC, Korol AB, Fahima T, Beiles A, Nevo E. Microsatellites: genomic distribution, putative functions and mutational mechanisms: a review. Mol Ecol. 2002;11:2453–2465. doi: 10.1046/j.1365-294x.2002.01643.x. [DOI] [PubMed] [Google Scholar]
- Li YC, Korol AB, Fahima T, Nevo E. Microsatellites within genes: structure, function, and evolution. Mol Biol Evol. 2004;21:991–1007. doi: 10.1093/molbev/msh073. [DOI] [PubMed] [Google Scholar]
- Martin P, Makepeace K, Hill SA, Hood DW, Moxon ER. Microsatellite instability regulates transcription factor binding and gene expression. Proc Natl Acad Sci U S A. 2005;102:3800–3804. doi: 10.1073/pnas.0406805102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meloni R, Albanese V, Ravassard P, Treilhou F, Mallet J. A tetranucleotide polymorphic microsatellite, located in the first intron of the tyrosine hydroxylase gene, acts as a transcription regulatory element in vitro. Hum Mol Genet. 1998;7:423–428. doi: 10.1093/hmg/7.3.423. [DOI] [PubMed] [Google Scholar]
- Merkel A, Gemmell NJ. Detecting microsatellites in genome data: variance in definitions and bioinformatic approaches causes systematic bias. Evol Bioinform Online. 2008;4:1–6. doi: 10.4137/ebo.s420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messier W, Li SH, Stewart CB. The birth of microsatellites. Nature. 1996;381:483. doi: 10.1038/381483a0. [DOI] [PubMed] [Google Scholar]
- Molla M, Delcher A, Sunyaev S, Cantor C, Kasif S. Triplet repeat length bias and variation in the human transcriptome. Proc Natl Acad Sci U S A. 2009;106:17095–17100. doi: 10.1073/pnas.0907112106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mudunuri SB, Nagarajaram HA. IMEx: Imperfect Microsatellite Extractor. Bioinformatics. 2007;23:1181–1187. doi: 10.1093/bioinformatics/btm097. [DOI] [PubMed] [Google Scholar]
- Nadeau JG, Crothers DM. Structural basis for DNA bending. Proc Natl Acad Sci U S A. 1989;86:2622–2626. doi: 10.1073/pnas.86.8.2622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishizawa M, Nishizawa K. A DNA sequence evolution analysis generalized by simulation and the Markov chain Monte Carlo method implicates strand slippage in a majority of insertions and deletions. J Mol Evol. 2002;55:706–717. doi: 10.1007/s00239-002-2366-5. [DOI] [PubMed] [Google Scholar]
- Noor MA, Kliman RM, Machado CA. Evolutionary history of microsatellites in the obscura group of Drosophila. Mol Biol Evol. 2001;18:551–556. doi: 10.1093/oxfordjournals.molbev.a003834. [DOI] [PubMed] [Google Scholar]
- Opresko PL, Shiman R, Eckert KA. Hydrophobic interactions in the hinge domain of DNA polymerase beta are important but not sufficient for maintaining fidelity of DNA synthesis. Biochemistry. 2000;39:11399–11407. doi: 10.1021/bi000698t. [DOI] [PubMed] [Google Scholar]
- Pearson CE, Nichol Edamura K, Cleary JD. Repeat instability: mechanisms of dynamic mutations. Nat Rev Genet. 2005;6:729–742. doi: 10.1038/nrg1689. [DOI] [PubMed] [Google Scholar]
- Prasad MD, et al. Survey and analysis of microsatellites in the silkworm, Bombyx mori: frequency, distribution, mutations, marker potential and their conservation in heterologous species. Genetics. 2005;169:197–214. doi: 10.1534/genetics.104.031005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pupko T, Graur D. Evolution of microsatellites in the yeast Saccharomyces cerevisiae: role of length and number of repeated units. J Mol Evol. 1999;48:313–316. doi: 10.1007/pl00006474. [DOI] [PubMed] [Google Scholar]
- Rajendran S, Jezewska MJ, Bujalowski W. Human DNA polymerase beta recognizes single-stranded DNA using two different binding modes. J Biol Chem. 1998;273:31021–31031. doi: 10.1074/jbc.273.47.31021. [DOI] [PubMed] [Google Scholar]
- Rhead B, et al. The UCSC Genome Browser database: update 2010. Nucleic Acids Res. 2010;38:D613–D619. doi: 10.1093/nar/gkp939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rich A, Nordheim A, Wang AH. The chemistry and biology of left-handed Z-DNA. Annu Rev Biochem. 1984;53:791–846. doi: 10.1146/annurev.bi.53.070184.004043. [DOI] [PubMed] [Google Scholar]
- Rockman MV, Wray GA. Abundant raw material for cis-regulatory evolution in humans. Mol Biol Evol. 2002;19:1991–2004. doi: 10.1093/oxfordjournals.molbev.a004023. [DOI] [PubMed] [Google Scholar]
- Rose O, Falush D. A threshold size for microsatellite expansion. Mol Biol Evol. 1998;15:613–615. doi: 10.1093/oxfordjournals.molbev.a025964. [DOI] [PubMed] [Google Scholar]
- Rosen MA, Live D, Patel DJ. Compartive NMR study of An-bulge loops in DNA duplexes: intrahelical stacking of A, A-A, and A-A-A bulge loops. Biochemistry. 1992;31:4004–4014. doi: 10.1021/bi00131a016. [DOI] [PubMed] [Google Scholar]
- Ruggiero T, et al. Deletion in a (T)8 microsatellite abrogates expression regulation by 3'-UTR. Nucleic Acids Res. 2003;31:6561–6569. doi: 10.1093/nar/gkg858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlötterer C, Tautz D. Slippage synthesis of simple sequence DNA. Nucleic Acids Res. 1992;20:211–215. doi: 10.1093/nar/20.2.211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah SN, Eckert KA. Human postmeiotic segregation 2 exhibits biased repair at tetranucleotide microsatellite sequences. Cancer Res. 2009;69:1143–1149. doi: 10.1158/0008-5472.CAN-08-3499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinden RR. DNA structure and function. San Diego (CA): Academic Press; 1994. [Google Scholar]
- Swan MK, Johnson RE, Prakash L, Prakash S, Aggarwal AK. Structural basis of high-fidelity DNA synthesis by yeast DNA polymerase delta. Nat Struct Mol Biol. 2009;16:979–986. doi: 10.1038/nsmb.1663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sweasy JB, Lauper JM, Eckert KA. DNA polymerases and human diseases. Radiat Res. 2006;166:693–714. doi: 10.1667/RR0706.1. [DOI] [PubMed] [Google Scholar]
- Tautz D, Trick M, Dover GA. Cryptic simplicity in DNA is a major source of genetic variation. Nature. 1986;322:652–656. doi: 10.1038/322652a0. [DOI] [PubMed] [Google Scholar]
- Timsit Y. DNA structure and DNA polymerase fidelity. J Mol Biol. 1999;293:835–853. doi: 10.1006/jmbi.1999.3199. [DOI] [PubMed] [Google Scholar]
- Timsit Y, Vilbois E, Moras D. Base-pairing shift in the major groove of (CA)n tracts by B-DNA crystal structures. Nature. 1991;354:167–170. doi: 10.1038/354167a0. [DOI] [PubMed] [Google Scholar]
- Wagner LA, Weiss RB, Driscoll R, Dunn DS, Gesteland RF. Transcriptional slippage occurs during elongation at runs of adenine or thymine in Escherichia coli. Nucleic Acids Res. 1990;18:3529–3535. doi: 10.1093/nar/18.12.3529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watkins WS, et al. Patterns of ancestral human diversity: an analysis of Alu-insertion and restriction-site polymorphisms. Am J Hum Genet. 2001;68:738–752. doi: 10.1086/318793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webster MT, Hagberg J. Is there evidence for convergent evolution around human microsatellites? Mol Biol Evol. 2007;24:1097–1100. doi: 10.1093/molbev/msm051. [DOI] [PubMed] [Google Scholar]
- Wierdl M, Dominska M, Petes TD. Microsatellite instability in yeast: dependence on the length of the microsatellite. Genetics. 1997;146:769–779. doi: 10.1093/genetics/146.3.769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodson SA, Crothers DM. Proton nuclear magnetic resonance studies on bulge-containing DNA oligonucleotides from a mutational hot-spot sequence. Biochemistry. 1987;26:904–912. doi: 10.1021/bi00377a035. [DOI] [PubMed] [Google Scholar]
- Zhang L, et al. Conservation of noncoding microsatellites in plants: implication for gene regulation. BMC Genomics. 2006;7:323. doi: 10.1186/1471-2164-7-323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Y, Strassmann JE, Queller DC. Insertions, substitutions, and the origin of microsatellites. Genet Res. 2000;76:227–236. doi: 10.1017/s001667230000478x. [DOI] [PubMed] [Google Scholar]