Lipid Bilayer Domain Fluctuations as a Probe of Membrane Viscosity

Abstract

We argue that membrane viscosity, η_m, plays a prominent role in the thermal fluctuation dynamics of micron-scale lipid domains. A theoretical expression is presented for the timescales of domain shape relaxation, which reduces to the well-known η_m = 0 result of Stone and McConnell in the limit of large domain sizes. Experimental measurements of domain dynamics on the surface of ternary phospholipid and cholesterol vesicles confirm the theoretical results and suggest domain flicker spectroscopy as a convenient means to simultaneously measure both the line tension, σ, and the membrane viscosity, η_m, governing the behavior of individual lipid domains.

As a first step to understanding the biophysics of plasma membranes (1), model membrane systems have been developed to mimic aspects of biomembranes under controlled, simplified laboratory conditions (2). Much work has focused on vesicles composed of ternary phospholipid/cholesterol mixtures, where physical properties of lipid domains can be characterized by fluorescence microscopy (3–6).

Among the most biologically important physical properties of inhomogeneous membrane systems are the line tension between coexisting phases σ and the membrane viscosity η_m. Line tensions influence the distribution of domain sizes (7), and viscosities set diffusion coefficients for lipid domains (8) and membrane proteins (9). Measurements of line tension via microscopy are well known, particularly for lipid monolayers (10–12); recent “domain flicker spectroscopy” (6) experiments were developed to measure the line tension on the surface of ternary vesicles. The membrane viscosity is not as simple to measure, though it may be estimated by fitting diffusion coefficients to the Saffman-Delbrück (SD) form (8,13) or by microrheology (14).

In this letter, we show that flicker spectroscopy may be used to measure not only σ, but also η_m. Our theoretical work exploits hydrodynamic analysis introduced by Stone and McConnell (SM) (15), but extends their results to a physical regime where membrane viscosity is relevant. Our experiments show that domain relaxation times do deviate from the η_m = 0 SM predictions. By combining theory with experiment, it becomes possible to directly measure η_m.

Our analysis of domain fluctuations assumes an isolated domain of constant area within a large flat membrane (Fig. 1). We assume that the boundary energy is given by E = σL, with σ the line tension and L the domain perimeter. It is convenient, theoretically (15) and experimentally (6,11), to express the domain shape in Fourier modes, $r\left(\theta ,t\right)=R\left(1+\frac{1}{2}{\sum }_{n\ne 0}{u}_n\left(t\right)e^{in\theta }\right),$ with n from –N/2 to N/2. To second order in u_n(t), the energy cost of deviations from the minimum energy circle with radius R is (6)

$$\Delta E=\frac{\sigma \pi R}{2}\sum _{n=2}^{N/2}\left(n^2-1\right){\left|u_n\right|}^2\text{.}$$ (1)

The equipartition theorem (as applied to the Fourier components of a real-valued physical quantity (16)) immediately leads to the spectrum of equilibrium shape fluctuations (11),

$$\langle {\left|u_n\right|}^2\rangle =\frac{2k_{\text{B}}T}{\sigma \pi R\left(n^2-1\right)},$$ (2)

and a direct experimental route to the determination of σ via measurement of 〈|u_n|²〉 (6).

Figure 1.

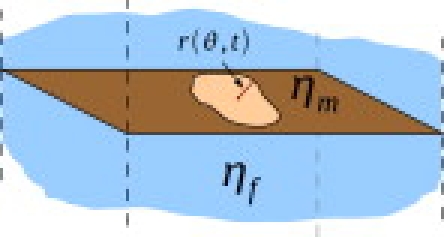
The shape of a quasicircular lipid domain within a thin, flat membrane is specified by the distance from the domain center of mass to the boundary as a function of the polar angle θ. Both lipid phases are assumed to share the surface viscosity η_m (17). The membrane is surrounded by a bulk fluid of viscosity η_f.

The time-dependence associated with fluctuations in u_n(t) may be calculated within the hydrodynamic model introduced by Saffman and Delbrück (9), namely a single, thin, flat fluid sheet with surface viscosity η_m surrounded by a bulk fluid of viscosity η_f treated within the creeping-flow approximation (Fig. 1). (17). This picture neglects the dual leaflet structure of the bilayer and applies only to symmetric bilayers with domains that are in registry across both leaflets. The available experimental (19), theoretical (20), and simulation (21) evidence suggests that domain registry is nearly perfect in ternary model membrane systems, with interleaflet domain mismatch confined to areas of tens of lipids for an entire domain (20,21). The picture from Saffman and Delbrück (9) is expected to be completely adequate to describe domain dynamics over the optical length-scales observed experimentally.

Relaxation of a general domain shape is driven by the line tension σ, with the radially directed force per unit length at the domain boundary given by the functional derivative f_r(θ, t) = –R⁻¹δ(ΔE(t))/δr(θ, t) (22), which is, to linear order in u_n(t),

$$f_r\left(\theta ,t\right)=-\frac{\sigma }{2R}\sum _{n=-N/2}^{N/2}\left(n^2-1\right)u_n\left(t\right)e^{in\theta }\equiv \frac{1}{2}\sum f_n\left(t\right)e^{in\theta }\text{.}$$ (3)

This force drives flow within the bilayer and in the bulk fluid. In particular, the radial velocity at the domain boundary $v_r\left(\theta ,t\right)=\frac{d}{dt}r\left(\theta ,t\right)=\frac{R}{2}\sum {\stackrel{.}{u}}_n\left(t\right)e^{in\theta }$ may be obtained through application of the techniques of SM (15), or by use of the more general formalism developed by Lubensky and Goldstein (22). The result is conveniently cast in terms of the Fourier modes (see the Supporting Material for further details)

$$v_n\left(t\right)=R{\stackrel{.}{u}}_n\left(t\right)=\frac{n^{2}R}{{\eta }_m}{I}_n(\Lambda )f_n\left(t\right),$$ (4)

where the integral $I_n(\Lambda )={\int }_0^{\mathrm{\infty }}dx{J}_n^2\left(x\right)/\left[x^2\left(x+\Lambda \right)\right],J_n\left(x\right),$ is a Bessel function of the first kind and $\Lambda =2R{\eta }_f/{\eta }_m\text{.}$ Combining Eqs. 3 and 4 leads to ${\stackrel{.}{u}}_n\left(t\right)=-u_n\left(t\right)/{\tau }_n$, with the solution $u_n\left(t\right)=u_n\left(0\right)e^{-t/{\tau }_n}$, where

$${\tau }_n=\frac{{\eta }_{m}R}{\sigma }\frac{1}{n^2\left(n^2-1\right)}{\left[\underset{0}{\overset{\mathrm{\infty }}{\int }}dx\frac{J_n^2\left(x\right)}{x^2\left(x+\Lambda \right)}\right]}^{-1}\text{.}$$ (5)

The fluctuation-dissipation theorem (23) provides the connection between the relaxation of u_n(t) and the equilibrium correlation functions measured in flicker spectroscopy,

$$\langle u_n\left(t\right)u_{-n}\left(0\right)\rangle =\langle |u_n{|}^2\rangle e^{-t/{\tau }_n}\text{.}$$ (6)

Equation 5 is the primary theoretical result of this letter; the expression is evaluated for a few representative parameters in Fig. 2. Though there is no general closed-form solution for the integral in Eq. 5, it reduces to two simple results in appropriate limits. For large domains and sufficiently small n (Λ ≫ n), dissipation in the bulk fluid dominates the dynamics, η_m may be neglected, and Eq. 5 approaches a result generally attributed to SM (15,24),

$${\tau }_n^{\text{fluid}}=\frac{2\pi R^2{\eta }_f}{\sigma }\frac{n^2-1/4}{n^2\left(n^2-1\right)}\text{.}$$ (7)

In the opposite limit (Λ ≪ n), the membrane viscosity dominates and η_f may be neglected, recovering the result of Mann et al. (24)

$${\tau }_n^{\text{membrane}}=\frac{4{\eta }_{m}R}{n\sigma }\text{.}$$ (8)

Because both Eq. 7 and Eq. 8 neglect a source of dissipation, τ_n ≥ ${\tau }_n^{\text{membrane}}$, ${\tau }_n^{\text{fluid}}$. The crossover between regimes occurs where the wavelength of the fluctuations (∼R/n) becomes comparable to the SD length scale L_sd = η_m/2η_f. Membrane viscosities generally fall within (0.1–10) × 10⁻⁶ surface poise (poise-cm, or grams/s) (8,13,25), leading to SD lengths L_sd ∼0.1–10 μm. Recent experimental measurements (6) on domains with radii of a few microns, unlike the much larger domains originally studied by SM and co-worker (10,15), are thus expected to deviate from the SM result (see Fig. 2).

Figure 2.

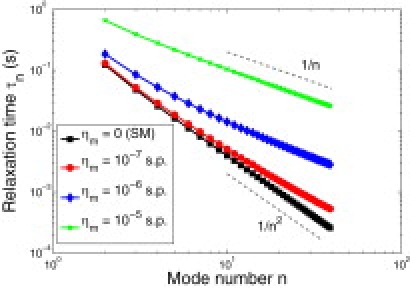
Relaxation times (Eq. 5) as a function of mode number for several membrane viscosities assuming a domain with R = 2.5μm, σ = 0.1 pN, and η_f = 0.01 Poise (water). As membrane viscosity is increased, the relaxation times increase, and the scaling with n changes from τ_n ∼ n⁻² for R/n ≫ L_sd (Eq. 7) to τ_n ∼ n⁻¹ for R/n ≪ L_sd (Eq. 8).

To test the above analysis, giant unilamellar vesicles of a ternary mixture of phospholipids, namely, dipalmitoylphosphatidylcholine (DPPC) and diphytanoylphosphatidylcholine (DiPhyPC) and cholesterol, were studied experimentally using the flicker spectroscopy technique (see (6) for details). Twenty-eight r(θ, t) traces from individual domains were analyzed, each from a vesicle with 25:55:20 molar ratios of DiPhyPC/Chol/DPPC at 20 ± 1°C (see the Supporting Material). Note that DiPhyPC was chosen over dioleoylphosphatidylcholine (DOPC) used in Esposito et al. (6) for its greater photostability (26). Domain images were thresholded to find r(θ, t), which was Fourier-transformed to yield u_n(t). Line tensions (σ) were extracted from the variance in Fourier modes u_n via Eq. 2 (with mean σ = 0.23 pN over all 28 traces) and relaxation times (τ_n) were determined by fitting 〈u_n(t)u_–n(0)〉 to single exponential decay. With σ, R, and η_f known, Eq. 5 has a single unknown parameter: η_m. The relaxation times over all measured n values were simultaneously fit to our general result (Eq. 5) using η_m as the fit parameter. A typical fit is shown in Fig. 3. Applying this procedure to all traces determined the mean membrane surface viscosity η_m = (4 ± 1) × 10⁻⁶ s.p., consistent with the low-temperature values observed from fitting diffusion constants. For comparison, Petrov and Schwille (13) use the data of Cicuta et al. (8) and find viscosities of ≈2 × 10⁻⁶ s.p. at a similar temperature, though for different lipids. A similar analysis based on the SM expression for the τ_n (Eq. 7) was also attempted (see the Supporting Material for further details). Because SM neglects η_m, there are no free parameters in ${\tau }_n^{\text{fluid}}$ and relaxation times are predicted immediately from σ. The SM theory predicts relaxation times in clear disagreement with the measurements (Fig. 3); additional dissipation from the bilayer itself must be considered to explain the data. We note that prior successful fits of the SM theory to experimental results using DOPC/Cholesterol/DPPC lipid mixtures (6) were only apparent. Equation 2 of this work corrects Eq. 3 of Esposito et al. (6). Also, the extraction of τ_n from correlations in u_n(t) (via Eq. 6) corrects the procedure of Esposito et al. (6), which was based upon correlations in |u_n(t)|². Experimental relaxation times that appeared consistent with SM in Esposito et al. (6) are actually four-times longer than SM predictions when the analysis is carried out properly. This level of disagreement between SM and experiment is similar to results summarized in Fig. 3.

Figure 3.

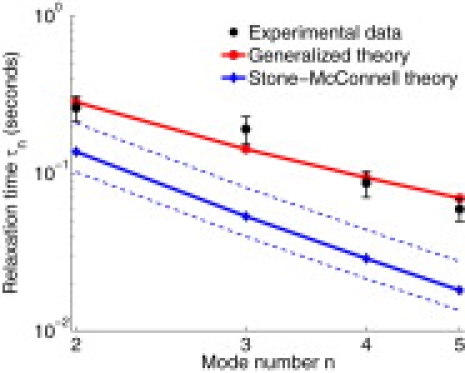
DiPhyPC/Cholesterol/DPPC relaxation times for a single domain trace with R = 3.8 μm. (Error bars) 95% confidence intervals for the fit to Eq. 6. The fit membrane surface viscosity η_m is 3.25 × 10⁻⁶ s.p. Also plotted is the SM theory for the relaxation times (Eq. 7). The theoretical results assume σ = 0.19 pN, as extracted from the variance in u_n (Eq. 2). (Dotted lines) Uncertainty in the SM predictions from adjusting σ by one standard deviation. Uncertainty in σ cannot account for the deviation between SM and experiment.

We have proposed a simple extension to the usual SM theory for relaxation times of domain fluctuations (Eq. 5) and have verified it against experimental data. The experimental results suggest that membrane viscosity significantly affects these relaxation times for the smallest wavelength modes observable by microscopy. By combining equilibrium measurements of line tension (via Eq. 2) with the measurement of dynamic relaxation, the viscosity of a lipid bilayer may be determined.